Some algorithms to correct a geometry in order to create a finite element mesh

SOME ALGORITHMS TO CORRECT A GEOMETRY IN ORDER TO CREATE A FINITE ELEMENT MESH

R. Ribó, G. Bugeda, and E. Oñate

International Center for Numerical Methods in Engineering (CIMNE)

Universidad Politécnica de Cataluña; Campus Norte UPC; 08034 Barcelona; Spain

web page: http://cimne.upc.es/

fax.: +34 93 4016517, e-mail: bugeda@cimne.upc.es

Abstract

keywords Mesh generation, geometry correction, NURBS.

1 INTRODUCTION

Mesh generation using structured and unstructured grids is still

nowadays one of the bottlenecks in the practical application of the

finite element method (FEM). See [1] and [2].

Geometrical models created for finite element mesh generation purposes

are typically created by the mesh generation software or imported from

an external CAD system. In both cases, the geometrical model must

satisfy a series of quality constraints.

Normally, geometrical models are constructed as a set of NURBS lines

and trimmed surfaces. These entities can be mathematically correct and

suitable for other uses like visualization or CAM but, in many cases,

they are not good enough for meshing operations. In these cases, it

is necessary to adapt/repair the geometrical entities by changing

their mathematical description while maintaining the same geometrical

shape. The final entities should be better suited for the mesh

generation operations. See [3] and [4].

The algorithms proposed in this paper are considered as a set of

filters that will be applied to a geometry definition just after being

imported or created. The algorithms are:

• collapse of entities

• correction of the list of knots

• reparametrization

• conversion to similar cubic entity

• union of curves

• reorientation of the boundary of the surfaces

• collapse of small angles

With the help of these algorithms, it is possible to automate the

process of importing geometry from CAD and mesh on it while maintaining an

acceptable level of quality criteria. This process should be performed

without the need of manual intervention.

To understand better what follows, a short description of the NURBS lines

and surfaces entities is given. A deeper description can be found in []

farin-cadg and [5].

1.1 NURBS lines

A NURBS line is a geometrical entity, described as a parametric line in the

3D space, that is defined with a set of knots, a set of control points, and a set of weights if it is rational.

Figure 1: Example of a quadratic NURBS line with 4 control points evaluated for a given value of $u$.

The knots are a list of non-decreasing numbers ${\textstyle u_{0},\dots ,u_{L+n}}$

that begin in the lower range of the parameter space (usually 0.0) and

finish in the high range of it (usually 1.0). A knot has

multiplicity ${\textstyle r}$ if its value is repeated ${\textstyle r}$ times inside the list of knots. The initial and the end knots must have multiplicity ${\textstyle r=n+1}$, where ${\textstyle n}$ is the degree of the curve.

The control points ${\textstyle {\vec {P}}_{1},\dots ,{\vec {P}}_{L}}$ are a list of points

in the 3D space that are part of the NURBS definition. The line will

interpolate the first and the last point and will smoothly approximate the

other points.

The weights ${\textstyle \omega _{1},\dots ,\omega _{L}}$ are a set of non-negative real

numbers, one for every control point. They allow the shape of the

curve to change and also to have an exact representation of conic curves like circles

or ellipses.

The number of knots, ${\textstyle N_{k}}$ must be equal to ${\textstyle N_{k}=N_{p}+n+1}$, where ${\textstyle N_{p}}$ is the number of control points.

The evaluation of a NURBS curve for a given value of the parameter ${\textstyle u}$ can be

done in a recursive manner. First, it is necessary to identify the interval ${\textstyle [u_{I},u_{I+1}]}$ in the list of knots that contains the value of ${\textstyle u}$ (${\textstyle u\in [u_{I},u_{I+1}]}$). Next, the following recursive expression can be applied:

${\vec {P}}_{i}^{k}(u)={\frac {(1-\alpha _{i}^{k})\omega _{i-1}^{k-1}{\vec {P}}_{i-1}^{k-1}(u)+\alpha _{i}^{k}\omega _{i}^{k-1}{\vec {P}}_{i}^{k-1}(u)}{\omega _{i}^{k}}}\quad {\hbox{with: }}\left|{\begin{array}{l}k=1,\dots ,n-r\\i=I-n+k+1,\dots ,I+1\\{\vec {P}}_{i}^{0}(u)={\vec {P}}_{i}\\\omega _{i}^{0}=\omega _{i}\end{array}}\right.$ (4) $\alpha _{i}^{k}={\frac {u-u_{i-1}}{u_{i+n-k}-u_{i-1}}}$ $\omega _{i}^{k}=(1-\alpha _{i}^{k})\omega _{i-1}^{k-1}+\alpha _{i}^{k}\omega _{i}^{k-1}$ then: ${\vec {s}}(u)={\vec {P}}_{I+1}^{n-r}(u)$

1.2 NURBS surfaces

A NURBS surface is the extension of the NURBS line to one additional

dimension in the parametric space. Most of the properties of the NURBS

curves applies here. There is a list of knots for every parametric

direction ${\textstyle u}$ and ${\textstyle v}$. The control points are a set of ${\textstyle P_{ij}}$

points with ${\textstyle i\in \lbrack 1,\dots ,L_{u}]}$ and ${\textstyle j\in \lbrack 1,\dots ,L_{v}]}$

.

Figure 2: NURBS surface with the corresponding control polygon.

The evaluation of the surface can be made in different ways:

• To evaluate first the NURBS curve corresponding to one of the

parametric directions ${\textstyle u}$ (maintaining ${\textstyle v}$ constant) and obtain a NURBS

line. Then, to evaluate the resulting NURBS curve in the second direction ${\textstyle v}$

.

• Recursive evaluation. Similar to the expression (1) given for the

NURBS curve.

• Evaluation by means of the b-spline base. This technique is

also usable for curves.

The evaluation with the b-spline base is done by defining a base of

b-splines, ${\textstyle N_{i}}$, as a recursive function in the following recursive

way:

$N_{i}^{0}(u)=\left\{{\begin{array}{l}1\qquad {\hbox{if }}u_{i-1}\leq u<u_{i}\\0\qquad {\hbox{if not.}}\end{array}}\right.$ $N_{i}^{n}(u)={\frac {u-u_{i-1}}{u_{i-n-1}-u_{i-1}}}N_{i}^{n-1}(u)+{\frac {u_{i+n}-u}{u_{i+n}-u_{i}}}N_{i+1}^{n-1}(u)$ Then, the following expression is applied: ${\vec {s}}(u,v)={\frac {\sum _{i}\sum _{j}\omega _{ij}{\vec {P}}_{ij}N_{i}^{m}(u)N_{j}^{n}(v)}{\sum _{i}\sum _{j}\omega _{ij}N_{i}^{m}(u)N_{j}^{n}(v)}}$

(6)

2 COLLAPSE OF ENTITIES

The standard CAD exchange formats (IGES, VDA,...) do not contain the

topological connection between the different surface patches defining a

closed geometry. These files just contain the mathematical description of

the patches. Nevertheless, in order to proceed with a correct mesh

generation it is necessary to check the correctness of the 3D geometry by

ensuring, for example, that it is defined by a completely closed surface. In addition,

many mesh generation algorithms need to know the neighboring relation between patches

in order to advance in their work. For this reason, it is necessary to obtain the topological connection

between the different surface patches.

An important additional difficulty is that, very often, the boundary curves

defining neighboring patches are very similar, but not identical. Normally,

the corresponding pairs of curves are close enough for the different

visualization or CAM operations, but not for the necessary operations for

the analysis. This makes the task of identifying neighbor

patches very difficult.

In order to solve this difficulty it is necessary to define a geometrical

tolerance. When two different geometrical entities are separated by a

distance smaller than the prescribed tolerance they are considered to be

identical and they are collapsed. This tolerance can be specified by the

user or can be obtained in an automatic way as a certain percentage of the

total size of the geometrical model.

The collapse procedure reduces the initial four curves to only three.

Figure 3: The collapse procedure reduces the initial four curves to only three.

Given a geometrical tolerance ${\textstyle \epsilon }$, the collapse criteria for the

different geometrical entities are the following:

• Two points are collapsed into a single one if:

$\Vert {\vec {P}}_{1}-{\vec {P}}_{2}\Vert <\epsilon$

where ${\textstyle {\vec {P}}_{i}}$ is the vector of coordinates of point ${\textstyle i}$.

• Two curves are collapsed if they share their end points and the

maximum distance between them is smaller than ${\textstyle \epsilon }$. In addition, they

are also collapsed if a curve belongs to the interior of another

one. This last property means that, in addition to the first criterion, its

end points ${\textstyle {\vec {P}}_{i}}$ accomplish

$\mathrm {dist} ({\vec {P}}_{i},L)<\epsilon$

where ${\textstyle {\vec {L}}(t)}$ is the second curve. In the latter case, the final result

of the collapse operation is not a single curve but a group of curves

as shown in Figure 3.

• Two patch surfaces are collapsed if they share their boundary curves

and a similar maximum distance criterion is accomplished.

• Two volumes are considered as equivalent if they share their

boundary surfaces.

The computation of the maximum distance between different curves or

surfaces is made in an approximated way as follows: a fixed number of

points ${\textstyle {\vec {P}}_{i}}$ are chosen in the interior of the curve or surface

depending on their geometrical characteristics. The distance

point-curve or point-surface ${\textstyle d_{i}}$ is computed for each of the

selected points. Then, ${\textstyle d_{max}}$ is approximated as

${\textstyle d_{max}=max(d_{i})}$.

In general, a big number of control points and a high degree of the line or surface

formulations will imply a bigger geometrical complexity. For this reason,

the number of selected points will be related to the two mentioned values.

In the computation of the ${\textstyle d_{i}}$ values the ${\textstyle {\vec {P}}_{i}^{\prime }}$ point

is obtained as the mapping of the original point over the

geometrical entity and ${\textstyle d_{i}=\|{\vec {P}}_{i}-{\vec {P}}_{i}^{\prime }\|}$. The

mapping operation is the transformation of an original point to

the closest point contained into a geometrical entity like a curve or

surface. This procedure is described in [5].

Saving of elements when unnecessary details are eliminated.

Figure 4: Saving of elements when unnecessary details are eliminated.

The collapse operation is also useful to eliminate small details of the

geometry that can be of no relevance for the analysis. If some lines or surface

patches are smaller than the tolerance, they can disappear and their

neighbor entities are reconnected. This operation is normally called feature reduction. From the practical point of view, many details that are

crucial for the design task, can be totally irrelevant for the analysis.

This operation can save a lot of elements and degrees of freedom in the

final finite element mesh. In Figure 4 a graphical

example of this possibility is shown.

3 CORRECTION OF THE LIST OF KNOTS

The list of knots is a set of non decreasing real values that

belong to the parametric space and are used for the definition of a

NURBS. A more detailed definition of knot can be obtained

in [6].

In the formulation of a NURBS curve or surface the list of knots

cannot contain any knot with a multiplicity higher than the degree of

the mathematical entity. Nevertheless, in many cases the standard exchange

files contain this type of error. In these cases, it is necessary to correct

the list of knots by eliminating the overdefined knot and the

associated weights and points. In this way, if we have a ${\textstyle n}$ degree NURBS

curve defined by ${\textstyle L}$ points with the following list of knots:

$k_{0},\dots ,k_{i},k_{i+1},\dots ,k_{i+n+p},\dots ,k_{L+n}\qquad {\hbox{with:}}\quad k_{i}=k_{i+1}=\dots =k_{i+n+p}$ (7) ${\vec {P}}_{1},\dots ,{\vec {P}}_{L}$ (8) $\omega _{1},\dots ,\omega _{L}$ (9)

the list (7) will be reduced to:

$k_{0},\dots ,k_{i},k_{i+1},\dots ,k_{i+n},k_{i+n+p+1},\dots ,k_{L+n}$

and the list of control points (8) and weights (9) to:

${\vec {P}}_{1},\dots ,{\vec {P}}_{i+1},{\vec {P}}_{i+p+2},\dots ,{\vec {P}}_{L}$ (10) $\omega _{1},\dots ,\omega _{i+1},\omega _{i+p+2},\dots ,\omega _{L}$ (11)

Note that the new list will have ${\textstyle L-p}$ control points and that the

resulting curve will be an approximation to the original one, being

the original one a mathematically incorrect representation of a curve.

4 REPARAMETRIZATION

A very desiderable property for the mesh generation algorithm is

to use the arc length as the defining parameter over the curve or surface. This

property is not normally available in the NURBS curves or surfaces.

This can be partially corrected by using a constant distance between

each pair of consecutive control points. Nevertheless, in order to

obtain the best possible quality during the mesh generation process it

is convenient to improve the parametrization from the very beginning.

The corresponding changes that are produced in the curves or surfaces

during the improvement of their parametric definition are named

reparametrization.

Comparison between the derivatives of the curve before and after the reparametrization.

Figure 5: Comparison between the derivatives of the curve before and after the reparametrization.

A major problem arises when there are big discrepancies between the

spacing of distances between the control points and the spacing between the orresponding

associated points of the curves or surfaces. This problem can be detected by

a comparison between the modulus of the derivatives in the following way:

${\frac {1}{F}}<{\frac {\left\|\left.{\frac {d{\vec {L}}}{dt}}\right|_{t=k_{i-}}\right\|}{\left\|\left.{\frac {d{\vec {L}}}{dt}}\right|_{t=k_{i+}}\right\|}}<F$

(12)

where the ${\textstyle k_{i}}$ in (12) represents an interior knot

and ${\textstyle F}$ is a maximum acceptable parameter that,

for acceptable parametrizations, can have values between 4 and 5. In

this formula, ${\textstyle {\vec {L}}(t)}$ represent the curve.

The first step of the correcting process consists of decomposing the

curve into the addition of the set of the equivalent Bézier curves.

This can be done by inserting multiple knots until a

multiplicity equal to the order of the mathematical entityi is reached. The process of

inserting knots is described in [6].

From the geometrical and the parametrization points of view, the defined curve is completely equivalent to the original one.

If we have a ${\textstyle n}$ degree curve and ${\textstyle L}$ defining points with the following values:

$k_{0},\dots ,k_{i},\dots ,k_{L+n}$ (13) ${\vec {P}}_{1},\dots ,{\vec {P}}_{L}$ new knots are inserted with the same value of the already existing knots into (13) until they all have a multiplicity of the same order as the curve $\underbrace {k_{0},\dots ,k_{0}} _{n+1},\dots ,\underbrace {k_{i},\dots ,k_{i}} _{n+1},\dots ,\underbrace {k_{L+n},\dots ,k_{L+n}} _{n+1}$ (14)

After inserting these knots, the number of control points of the curve

will increase. The new number of points will Bézier equal to the sum

of the difference between the original multiplicities and

the order of each of the original knots.

Taking the list of points and grouping them in sets of ${\textstyle n+1}$ points,

it is possible to buid successive Bézier curves with the same degree

than the original curve and the same continuity between successive

Bézier curves. These new curves will not depend on the list of

knots and, therefore, their shape will not change if any of the

knots is moved. Consequently, the increments between each

groups of knots can be recomputed in order to obtain a better

parametrization. A possible modification based in the chord length parametrization consists in creating the following new list:

$k_{0},\dots ,k_{n},\dots ,k_{i},\dots ,k_{i+n},\dots ,k_{L^{\prime }},\dots ,k_{L^{\prime }+n}$ (15) $k_{0}=\dots =k_{n}\qquad k_{i}=\dots =k_{i+n}\qquad k_{L^{\prime }}=\dots =k_{L^{\prime }+n}$ (16) $k_{i+n+1}-k_{i+n}={\frac {l_{c}}{l_{tot}}}$ (17)

where ${\textstyle l_{c}}$ in (17) is the length of the corresponding Bezier

curve and ${\textstyle l_{tot}}$ is the total length.

The new curve parametrized in this way will have the same geometrical shape

than the original one but with a different parametric definition. Figure 

fig:conv-to-bezier shows the typical improvement than can be obtained with

the described algorithm.

5 CONVERSION TO SIMILAR CUBIC ENTITY

In some cases, the correction described in the last section is not

enough for ensuring a good parametrization. Typically, these cases

arise when one or more control points are repeated, or else when the

orders of magnitude of the distances between points have big

discrepancies between them.

File:Draft Ribó 247186029-picture-b42e7c.png	Conversion of a NURBS to an approximated interpolant cubic NURBS.
Figure 6: Conversion of a NURBS to an approximated interpolant cubic NURBS.

In these cases it is acceptable to use a new curve or surface not

identical to the original one but with a good enough approximation. We

should keep in mind that the exchange of CAD files is always carried

out with different geometrical tolerances. Hence, it seem logical to

allow geometrical changes below the limits of this

tolerance.

The process consists of computing a set of points ${\textstyle {\vec {P}}_{i}}$

belonging to the interior of the curve. These points will be the base

of an interpolation algorithm that will be used for the definition of

the new curve with the required approximation to the original one. The

criteria for the selection of the number of points ${\textstyle L_{I}}$ is obtained

by correlating the number of control points ${\textstyle L}$ with the accepted

tolerance. A new cubic curve can be interpolated from the new set of

points using different procedures like the one described in

[6]. Figure 6 shows an example of

this type of conversion. In this case, the discrepancy between both

curves is high due to a point with ${\textstyle C^{0}}$ continuity.

6 UNION OF CURVES

It is possible to convert a set of connected NURBS curves into a single

curve. Normally, it is advantageous to keep the number of curves as

small as possible because it can make the mesh generation task easier.

Typically, the presence of extremely small segment lines can increase

the complexity of the mesh generation.

Different criteria for accepting (or not) the union of curves.

Figure 7: Different criteria for accepting (or not) the union of curves.

The criteria for joining different curves are the following:

1. Enough degree of continuity between the different segments must

exist. Typically, a ${\textstyle C^{1}}$ continuity is considered as enough.

2. None of the segments can support any individual surface patch. The

set of segments to be joined must belong to the boundaries of the same

surface patches.

Figure 7 shows different examples of these situations.

Before the union can proceed, the different curves must have the

same degree. Hence, the degree of all the segments will be increased

until they reach the maximum value ${\textstyle n}$. Next, the different control

points will be joined and a new list of knots will be computed

starting from the original ones in the following way:

$k_{A,0},\dots ,k_{A,L_{A}+n}\qquad {\hbox{curve A}}$ (18) $k_{B,0},\dots ,k_{B,L_{B}+n}\qquad {\hbox{curve B}}$ (19) The new list will be: $\alpha k_{A,0},\dots ,\alpha k_{A,L_{A}+n},\alpha k_{A,L_{A}+n}+\beta k_{B,0},\dots ,\alpha k_{A,L_{A}+n}+\beta k_{B,L_{B}+n}$ (20) $\alpha ={\frac {l_{A}}{l_{A}+l_{B}}}\qquad \beta ={\frac {l_{B}}{l_{A}+l_{B}}}$ (21)

where ${\textstyle l_{A}}$ and ${\textstyle l_{B}}$ in (21) are the respective lengths of the

curves.

7 SUBDIVISION OF CURVES

Some of the algorithms related with the mesh generation task solve

small non linear systems of equations that involve the derivatives of

the analytical expression defining the curves. The presence of

strong changes of these derivatives inside the curve can produce

convergence difficulties in the solution of the mentioned systems. Due

to this reason, it is very convenient to maintain a ${\textstyle C^{1}}$ continuity

over the whole curve (In practice, small angle discontinuities can

also be allowed). Hence, it is convenient to subdivide (cut) the

original curves at points not satisfying the required

continuity.

This subdivision is made through the insertion of additional knots at

the required cutting points until a multiplicity equal to the order

of the curve is reached. The new curves will be:

$k_{0},\dots ,\underbrace {k_{i},\dots ,k_{i}} _{n+1},\dots ,k_{L+n}$ ${\frac {k_{0}}{k_{i}}},\dots ,{\frac {k_{i}}{k_{i}}}\qquad {\hbox{ curve A}}$ ${\frac {k_{i+n+1}-k_{i+n+1}}{k_{L+n}-k_{i}}},\dots ,{\frac {k_{L+n}-k_{i+n+1}}{k_{L+n}-k_{i}}}\qquad {\hbox{ curve B}}$

The control points will be simply spread depending on the number of knots corresponding to each curve.

8 REORIENTATION OF THE BOUNDARY OF THE SURFACES

Some of the mesh generation algorithms require a proper orientation of all

the boundary curves. A curve ${\textstyle {\vec {L}}(t)}$ that belongs to the boundary of a

surface with a normal vector ${\textstyle {\vec {N}}}$ is considered as well oriented if the

vector ${\textstyle {\vec {V}}}$ defined by

${\vec {V}}={\vec {N}}\times {\frac {d{\vec {L}}}{dt}}$

always points towards the interior of the surface.

Criterion of signs and orientations of the trimming lines of a trimmed surface.

Figure 8: Criterion of signs and orientations of the trimming lines of a trimmed surface.

In some cases, the information imported from a CAD system does not

satisfy the mentioned criterion. It is then convenient to check this

possibility and to change the corresponding orientation when necessary.

Nevertheless, some times it is not easy to identify the interior of

a surface. In this work, we use the fact that for non trimmed surfaces the

curves must belong to the boundary of a NURBS surface. For

trimmed surfaces, it is necessary to look for any of the trimming curves

placed on the surface.

A boundary line of a NURBS surface patch is well oriented if:

${\frac {d{\vec {L}}(t)}{dt}}\cdot {\frac {\delta {\vec {S}}(u,v)}{\delta u}}>0\qquad {\vec {L}}\in v=0$ (22) ${\frac {d{\vec {L}}(t)}{dt}}\cdot {\frac {\delta {\vec {S}}(u,v)}{\delta u}}<0\qquad {\vec {L}}\in v=1$ (23)

where ${\textstyle {\vec {S}}(u,v)}$ is the parametric surface. If the curve lays on

${\textstyle u=0}$ or ${\textstyle u=1}$ the corresponding similar expressions will be used.

An additional convenient check consists of computing the normal

vector to the surface in its center and to compute the approximated

normal vector to the boundary curves. The approximate normal vector

can be computed as:

${\vec {N}}_{L}=\sum _{i}{\vec {L}}(t_{i})-{\vec {C}}\times {\vec {L}}(t_{i}+\Delta t_{i})-{\vec {C}}$

(24)

where ${\textstyle {\vec {C}}}$ is the center of the surface. The boundary curves will be

well oriented if:

${\vec {N}}\cdot {\vec {N}}_{L}>0$

9 COLLAPSE OF SMALL ANGLES

A very common problem in files imported from CAD systems is that some

of the surfaces contain almost null angles that make impossible the

generation of a proper mesh. In those cases, it is convenient to

collapse part of the lines that define these angles until converting

the angles into bigger ones allowing to place acceptable mesh elements.

Collapse of a too small angle. The collapse will be accepted if L is bigger than a minimum value.

Figure 9: Collapse of a too small angle. The collapse will be accepted if $L$ is bigger than a minimum value.

The collapsing angle will be computed depending on the given tolerance ${\textstyle \epsilon }$. In general, the resulting criterion should guarantee that

the size of the resulting curve is in agreement with the rest of the

contiguous curves (see Figure 9).

10 EXAMPLES

The algorithms presented in previous sections have been implemented

into the GiD pre/postprocessing system[7] developed at

CIMNE. The following examples are a set of representative applications

of these algorithms for the preparation of different geometries in

order to be meshed. Typically, the geometry has been defined using a

CAD system and the corresponding information has been introducind into

GiD using standard CAD files (IGES, VDA, ...). In all cases, the use

of the presented algorithms has carried out the

improvements/reparations needed to allow meshing of the geometry

without the necessity of any additional operation.

10.1 Geometry of a set of casting teeth

This example (see Figures 10 and 11),

corresponds with the generation of a finite element mesh over the solid

model of a casting set of teeth. The number of surface patches used for the geometry

definition is around 400. In this particular case, before the mesh generation it has been necessary

to correc the geometry in order to create a closed volume (without gaps). The final obtained mesh has

around 40,000 elements.

10.2 Tarazona cathedral

Figures 12 and 13 represent a structural analysis model

with a non-linear damage material model of the Tarazona cathedral.

In this case, it has been necessary to correct many of the surfaces used

to describe the fine details of the shape in some parts of the

geometry. The final mesh has around 40,000 elements.

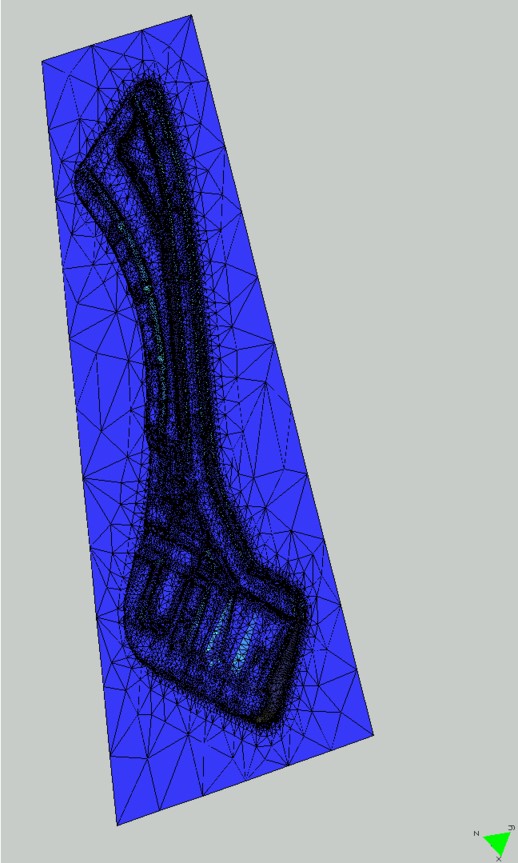
10.3 Sheet stamping processes

This is a typical case corresponding with a sheet stamping analysis (see Figure 14). The

geometry has been modeled using traditional

CAD systems and before proceeding to the classical mesh generation operations

it has been necessary to use all the

correction algorithms presented in these pages. Some of the problems

that usually appear in this type of geometries are:

• Some surfaces are too small and must disappear.

• Other surfaces have a bad mathematical description.

• Some of them are correctly defined but with some properties that

are not suitable for meshing on them.

• Some of the geometrical details are very small and produce extremely complex geometries.

Figure 14 shows a typical mesh for this type of cases with around 400,000 finite elements.

10.4 Aluminium casting

These type of geometrical models have the same problems as the previous one.

However, they are more complicated to improve due to the

inherent complexity of their surface patches. See

Figures 15 and 16.

Figure 10: Geometry of a set of casting teeth for construction machines. This set is the one used in the casting process.

Figure 11: Fotorrealistic render of the previous geometry.

Figure 12: Geometry of the Tarazona cathedral (Spain).

Figure 13: Mesh of the cathedral.

Figure 14: Analysis of sheet stamping processes.

Figure 15: Mesh of an aluminium casting model.

Figure 16: Detail of the previous mesh.

11 CONCLUSIONS

CAD models are not always best suited as starting points for mesh generation.

CAD models and the corresponding exchange files are more

suited for design and CAM operations than for the analysis task. For this

reason, it is normally necessary to repair the CAD models in order to make

them suitable for mesh generation.

The proposed algorithms have shown to be efficient in dealing with three

different problems:

• The elimination of some small features that are necessary for the

design but are not important for the numerical analysis.

• The correction of some mistakes and accuracies that are found in many

geometrical interchange files.

• The change in the mathematical definition of some entities in order

to make them better suited for mesh generation.

All these algorithms can be executed automatically as a filter to the

imported or created geometry reducing the human interaction to a minimum and

facilitating a lot the mesh generation task.

An academic version of the GiD pre/postprocessing system, where the

algorithms presented in this paper have been implemented, can be

freely downloaded at

http://gid.cimne.upc.es

curve-surface-fitting

BIBLIOGRAPHY

[1] R. Löhner and P. Parikh. (1988) "Generation of three-dimensional unstructured grids bythe advancing front method". Int. j. numer. methods fluids. 8

[2] P. L. George. (1991) "Automatic Mesh Generation. Application to Finite Element Methods". Wiley

[3] J M Le Gouez and M A Boheas and C J Miles. (1995) "Data requirements for analysis modelling". NAFEMS

[4] NAFEMS. (1996) "Integrate CAD and Analysis"

[5] Ramon Ribó. (2000) "Development of an integrated system for the geometry dealing, mesh generationand data for the finite element analysis"

[6] Gerald Farin. (1973c1993) "Curves and surfaces for CADG". ACADEMIC PRESS, INC., Third Edition

[7] Ramon Ribó and others. (1998) "GiD reference manual". CIMNE

[8] D.N.Knuth. (1973) "The art of computer programming, Vol. 3". Addison-Wesley

[9] Hoschek, Josef and Dieter Lasser. (1993) "Fundamentals of computer aided geometric design". Addison-Wesley

[10] Foley and van Dam and Feiner and Hughes. (1993) "Computer Graphics. Principles and practice". Addison-Wesley, second Edition

[11] O. C. Zienkiewicz and R. Taylor. (2000) "The Finite Element Method", Volume I. John Wiley and Sons, 5 Edition

[12] Adi Levin. (1999) "Interpolating nets of curves by smooth subdivision surfaces". Computer Graphics Proceedings (SIGGRAPH)

[13] Eugenio Oñate. (1995) "Cálculo de estructuras por el método de los elementos finitos". CIMNE