Magnetic properties and applications of glass-coated ferromagnetic microwires

1 Introduction

Magnetically soft wires can present magnetic properties suitable for industrial applications such as the giant magnetoimpedance (GMI) effect or magnetic bistability related to the large and single Barkhausen jump [1-9].

Although these versatile properties can be observed either in crystalline or in amorphous magnetic wires, amorphous magnetic wires present several advantages, such as superior mechanical properties, the absence of the microstructure defects (grain boundaries, crystalline texture, dislocations, point defects,…) [3,10]. and therefore long and precise post-processing is not required. For these reason, amorphous wires have attracted considerable attention since the 70-s [1-10].

Amorphous materials can be prepared using rapid quenching from the melt [1, 11,12]. There are several families of amorphous wires those can be prepared using rapid melt quenching methods [1, 3,11-14]

One of the trends of modern applications is related to use of materials with reduced dimensionality [3]. Reduced dimensionality allows critical materials saving and provides new functionalities [3, 14]. The finest amorphous magnetic wires- glass-coated microwires can be prepared using so-called Taylor-Ulitovsky technique [3,10,14]. Typically glass-coated magnetic microwires consist of metallic nucleus with diameters from 0.5 to 50 μm covered by flexible, insulating and biocompatible glass with thickness from 0.5 up to 30 μm [15,16]. It is worth mentioning that the Taylor-Ulitovsky method for glass-coated microwires preparation is known since the 60-s [17,18]. However, this technique become commonly used for magnetic microwires preparation starting from 90-s [1-4].

The presence of non-magnetic glass coating considerably affects magnetic properties of glass-coated microwires [1-4]. This influence is related to the magnetoelastic anisotropy. Indeed, in amorphous materials the magnetocrystalline anisotropy is absent. Therefore, the magnetoelastic anisotropy becomes one of the most important parameters affecting the magnetic properties of amorphous magnetic materials [3,4,18-21].

The magnetoelastic anisotropy, K_me,is given as [3,4]:

${\textstyle {K}_{me}=3/2{\lambda }_{S}{\sigma }_{i}}$

(1)

where λ_S is the magnetostriction coefficient and σ_i is the internal stresses value.

In the case of glass-coated microwires the magnetoelastic anisotropy contribution is even more relevant than in other families of amorphous wires since the Taylor-Ulitovsky preparation process involves simultaneous solidification of the metallic nucleus surrounded by the glass-coating with rather different thermal expansion coefficients [3,4,19-21]. The strength of internal stresses, σ_i, is basically affected by the three main factors: i) quenching stresses associated to the melt quenching of the metallic alloy; ii) stresses related to the different thermal expansion coefficients of metallic ingot and glass simultaneously solidifying and iii) stresses associated to the drawing of solidifying wire [19-21].

On the other hand The magnetostriction coefficient, λ_s, value in amorphous alloys can be tailored by the chemical composition [22,23]. Generally Fe-rich compositions present positive λ_s -values (typically λ_s ≈ 20 - 40 x 10⁻⁶), while for the Co-rich alloys, λs –values are negative, typically λ_s ≈ -5 to - 3 x 10⁻⁶. Consequently nearly-zero λ_s –values can be achieved in the Co_xFe_1-x (0≤x ≤1) or Co_xMn_1-x (0≤x ≤1) systems at x about 0,03-0,08 [22,23 ].

Consequently, as regarding magnetic properties the as-prepared microwires are usually classified into three main groups:

• Fe-based microwires with positive (λ_s≈ 10^-5) λ_s -values presenting spontaneous magnetic bistability (rectangular hysteresis loop);

• Co-based wires with negative (λ_s≈ - 10^-6) λ_s -values exhibiting almost non-hysteretic linear magnetization curves with rather high magnetic anisotropy field;

• Co-based wires with vanishing λ_s –values (λ_s≈ - 10^-7) presenting best magnetic softness [22,23].

Aforementioned excellent magnetic properties of glass-coated microwires are suitable for prospective applications in magnetic sensors [24-28]

Fe-rich glass-coated microwires usually present the magnetic bistability effect and hence fast magnetization switching by rapid domain wall (DW) propagation [7]. However, as-prepared Fe-based microwires do not present high GMI effect. On the other hand Fe-rich glass-coated microwires are less-expensive and present a number of advantages, i.e. higher saturation magnetization [3,4,7].

Accordingly, Fe-based microwires are preferable for large scale applications.

Therefore, certain efforts have been paid to optimization of the magnetic softness and GMI effect in Fe-rich microwires [29-31]

One of the routes for GMI effect improvement of Fe-rich microwires consists of devitrification of amorphous precursor allowing drastic decreasing of the magnetostriction coefficient [28]. But the disadvantage of nanocrystalline materials is poorer mechanical properties limiting possible applications.

The alternative route is the development of the induced transverse magnetic anisotropy by specially designed annealing allowing keeping the amorphous structure and hence maintaining superior mechanical properties. Recently, we demonstrated that the magnetic anisotropy induced by stress-annealing with transverse easy magnetization direction is beneficial for improvement of magnetic softness and GMI ratio [3,29,31].

It is worth mentioning that the main technological interest in soft magnetic wires is related to the GMI effect for which high circumferential magnetic permeability observed in properly processed magnetic wires is essentially important. The GMI effect provides excellent opportunity for design of magnetic sensors and magnetometers owing to extremely high magnetic field sensitivity (few hundred percent change of impedance under low external magnetic field reported for amorphous wires) [1-8].

The GMI effect is usually characterized by the GMI ratio, ΔZ/Z, defined as:

${\textstyle \Delta Z/Z=\left[Z\left(H\right)-Z\left({H}_{max}\right)\right]/Z\left({H}_{max}\right)}$

(2)

where H_max is the maximum applied DC magnetic field.

The origin of the GMI is commonly attributed
to the classical skin effect of magnetic conductor [1-8].

Up to now the highest GMI ratio is reported for Co-rich glass-coated microwires with nearly-zero magnetostriction coefficient [4, 32-34]. However in most of cases special post processing for GMI effect improvement is needed [32,34]

Consequently, in this paper we present our recent experimental results on post- processing of magnetic microwires with aim to achieve better magnetic softness and GMI effect.

2 Experimental method and techniques

2.1 Materials

We selected typical Fe-rich (Fe₇₅B₉Si₁₂C₄) and Co-rich (Co_69.2Fe_4.1B_11.8Si_13.8C_1.1) alloys in which the phase diagram presents deep eutectic. Such chemical compositions were used previously for preparation of amorphous Fe-rich and Co-rich microwires [3,4]. Glass-coated Fe₇₅B₉Si₁₂C₄ (metallic nucleus diameter, d=15.2 μm, total diameter, D=17.2 μm) and Co_69.2Fe_4.1B_11.8Si_13.8C_1.1 (d=25.6 μm, D=30.2 μm) microwires with positive and low negative magnetostriction coefficients, λ_s, respectively have been prepared by Taylor-Ulitovsky technique described elsewhere [3,4].

Samples annealing has been performed in a conventional furnace. The tensile stress has been applied during the annealing as well as during the sample cooling with the furnace. The mechanical load has been attached to the microwire during the annealing and slow cooling with the furnace. The stress value applied during the annealing and measurements within the metallic nucleus and glass shell has been evaluated as described earlier [31]:

${\textstyle {\sigma }_{m}={\frac {K.P}{\,K\,\,{S}_{m}{+S}_{gl}}}{\sigma }_{gl}={\frac {P}{\,K\,\,{S}_{m}{+S}_{gl}}}}$,

(3)

where K =E₂/E₁, E_i are the Young’s moduli of the metal (E₂) and the glass (E₁) at room temperature, P is the applied mechanical load, and S_m and S_gl respectively are the cross sections of the metallic nucleus and glass coating.

The stress has been applied during the annealing as well as during the sample cooling with the furnace.

2.2 Experimental methods

Hysteresis loops have been measured using fluxmetric method previously described elsewhere [3,7,9]. We represent the normalized magnetization, M/M₀ versus magnetic field, H, where M is the magnetic moment at given magnetic field and M₀ is the magnetic moment of the sample at the maximum magnetic field amplitude, H_m.

For GMI characterization we used GMI ratio, ΔZ/Z, defined by eq. (2).

As previously described [35], we used micro-strip sample holder placed inside a sufficiently long solenoid that creates a homogeneous magnetic field, H. The sample impedance, Z, was measured using vector network analyzer from the reflection coefficient S₁₁ using expression [35]:

${\textstyle Z={Z}_{0}\left(1+{S}_{11}\right)/\left(1-{S}_{11}\right)}$

(4)

where Z₀=50 Ohm is the characteristic impedance of the coaxial line. Employed GMI measurements method allows evaluation of the GMI effect in extended frequency, f, range up to GHz frequencies.

The DW velocity, v, was evaluated using modified Sixtus-Tonks-like setup described elsewhere [7,9]. In this setup 3 pick-up coils are mounted along the microwire placed inside the long solenoid allowing measurement of the DW velocity at different external magnetic field [7,8].

The propagating DW induces electromotive force (emf) in the coils which are picked up by the digital oscilloscope. Then, the DW velocity is estimated as:

${\textstyle \nu ={\frac {l}{\Delta t}}}$

(5)

where l is the distance between a pair of pick-up coils and Δt is the time difference between the maximum in the induced emf.

The DSC measurements were performed using DSC 204 F1 Netzsch calorimeter in Ar atmosphere at a heating rate of 10 K/min up to temperature, T, of 900 ^oC.

3 Experimental results and discussion

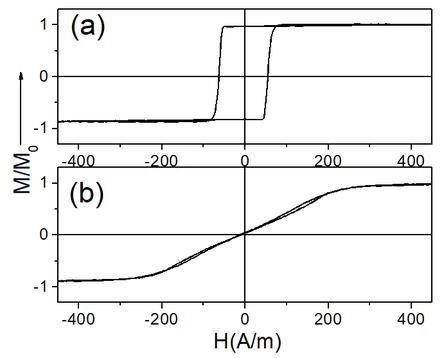
Studied Co-rich and Fe-rich as-prepared microwires present rather different magnetic properties and hence GMI effect: Fe₇₅B₉Si₁₂C₄ microwires present perfectly rectangular hysteresis loops typical for Fe-rich microwires with high and positive magnetostriction coefficient, λ_s, (λ_s ≈35x10^-6) exhibiting magnetic bistability. In contrast Co_69.2Fe_4.1B_11.8Si_13.8C_1.1 microwires present linear hysteresis loops previously reported for Co-based glass-coated microwires with low and negative λ_s (λs ≈ -10^-7) [3,4] (see Fig. 1a and
Fig. 1b). Coercivity, H_c, of Fe₇₅B₉Si₁₂C₄ microwires (about 55 A/m) is about an order of magnitude higher that of Co_69.2Fe_4.1B_11.8Si_13.8C_1.1 microwires.

Figure 1. Hysteresis loops of as-prepared Fe₇₅B₉Si₁₂C₄ (a) and (b) Co_69.2Fe_4.1B_11.8Si_13.8C_1.1 microwires.

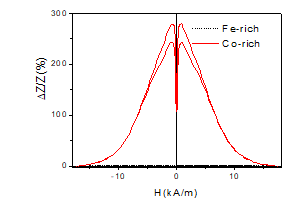
Accordingly, magnetically softer Co_69.2Fe_4.1B_11.8Si_13.8C_1.1 microwires exhibit an order of magnitude higher GMI ratio than Fe₇₅B₉Si₁₂C₄ microwires (see Fig. 2).

Figure 2. ΔZ/Z(H) dependences of as-prepared Co_69.2Fe_4.1B_11.8Si_13.8C_1.1and Fe₇₅B₉Si₁₂C₄ measured at 100 MHz.

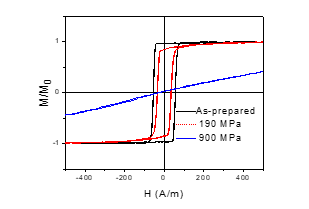
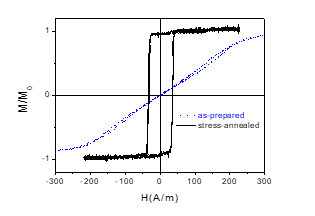
Stress annealing of Fe based microwires allows considerable magnetic softening (H_c decrease) and inducing of transverse magnetic anisotropy as can be observed from hysteresis loops measured in stress-annealed Fe₇₅B₉Si₁₂C₄ microwires (Fig. 3). Magnetic properties are considerably affected by the stress, σ_m, applied during the stress annealing: induced transverse magnetic anisotropy becomes more noticeable with increasing of σ_m -values.

Figure 3 Hysteresis loops of as-prepared and stress-annealed at T_ann=300^o C (upon ${\textstyle {\sigma }_{m}=}$190 and 900 MPa) Fe₇₅B₉Si₁₂C₄ microwires.

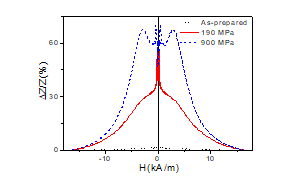
Accordingly, remarkable improvement of GMI ratio is observed in stress-annealed Fe₇₅B₉Si₁₂C₄ microwires: improvement of ΔZ/Z –values by an order of magnitude is achieved (Fig. 4).

Observed ΔZ/Z(H) dependencies present irregular shape that can be interpreted as the superposition of double-peak ΔZ/Z(H) dependence (more appreciable for the sample stress-annealed under σ_m = 900 MPa) and decay of ΔZ/Z with magnetic field, H.

Observed effect of frequency on ΔZ/Z(H) dependence can be explained considering frequency dependence of the skin penetration depth, δ, as well as magnetic anisotropy distribution within the metallic nucleus.

It is well established [3-6], that the penetration skin depth decreases with the frequency increasing.

Figure 4. ΔZ/Z(H) dependencies of as-prepared and stress-annealed at T_ann=350^o C (upon ${\textstyle {\sigma }_{m}=}$190 and 900 MPa) Fe₇₅B₉Si₁₂C₄ microwires measured at 100 MHz.

The penetration depth of the AC current, δ, is given by [3-6]:

${\textstyle \delta ={\left(\pi \sigma \cdot {\mu }_{\phi }\cdot f\right)}^{-1/2}}$

(6)

where σ is the electrical conductivity and μ_ϕ - the circumferential magnetic permeability.

At relatively low frequency of 10 MHz, the skin depth is comparable and even higher than the microwire radius and the current is flowing through the whole ferromagnetic nucleus.

On the other hand, experimentally confirmed [9,36] that the magnetic domain structure of magnetic wires consists of outer domain shell with circular magnetization orientation and inner axially magnetized core.

Observed influence of stress-annealing on hysteresis loop of Fe₇₅B₉Si₁₂C₄ microwires can be associated with changes of domain structure after stress-annealing.

The inner axially magnetized core radius, R_c, that can be estimated from squireness ratio, M_r/M_s as [3,37]:

${\textstyle {R}_{c}=R{\left({M}_{r}/{M}_{S}\right)}^{1/2}}$

(7)

being R- microwire radius.

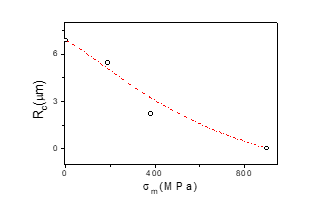
Consequently, from M_r/M_s values we evaluated the dependence of the radius of inner axially magnetized core, R_c, on σ_m. As can be observed from Fig. 5, R_c -values progressively decrease with increasing of σ_m -values.

Figure 5. Dependence of radius of inner axially magnetized core, R_c, on stress applied during the annealing in Fe₇₅B₉Si₁₂C₄ microwire.

Considering results presented in Fig. 5 we can explain the observed influence of stress-annealing on ΔZ/Z(H) dependencies as following:

For low σ_m -values the volume of the outer domain shell is small (at σ_m =190 MPa R_c is only slightly lower than R). Consequently, stress annealed Fe₇₅B₉Si₁₂C₄ (190 MPa) microwire presents predominantly axial anisotropy (as confirmed by Fig. 4). Increasing the σ_m -values the volume of the outer domain shell grows. Therefore, double-peak ΔZ/Z(H) dependence becomes more evident (as also confirmed by Fig. 4).

As recently reported elsewhere [38,39] upon annealing the hysteresis loop of Co-rich microwires becomes rectangular presenting considerable magnetic hardening.

Stress-annealed Co_69.2Fe_4.1B_11.8Si_13.8C_1.1 microwires also present rectangular hysteresis loop and remarkable magnetic hardening (see Fig. 6). However stress-annealed Co_69.2Fe_4.1B_11.8Si_13.8C_1.1 microwires present lower coercivity as compared to annealed without stress microwires.

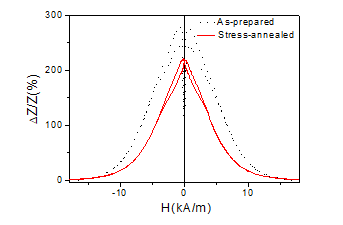
In spite of magnetic hardening and rectangular hysteresis loop stress-annealed Co_69.2Fe_4.1B_11.8Si_13.8C_1.1 microwires still present high GMI effect of the order of 200% (at 100 MHz, see Fig. 7).

Figure 6. Hysteresis loops of as-prepared and
stress-annealed (σ_m≈ 80 MPa) at 300 ^ºC for 60 min
Co_69.2Fe_4.1B_11.8Si_13.8C_1.1 microwires.

Figure 7. Comparison of ΔZ/Z (H) dependencies of as-prepared and stress-annealed Co_69.2Fe_4.1B_11.8Si_13.8C_1.1 microwire (T_ann = 300 ⁰C, t_ann = 5 min, σ_m= 80 MPa).

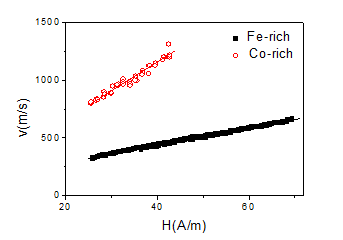
Hysteresis loops of Co-rich microwires observed after stress-annealing present features similar to that of Fe-rich microwires and annealed Co-rich microwires, i.e. rectangular shape that must be related to presence of single and large Barkhausen jump and induced magnetic bistability. Therefore, similarly to annealed without stress Co-rich microwires [39] stress-annealed Co_69.2Fe_4.1B_11.8Si_13.8C_1.1 microwires present single domain wall (DW) propagation. From Fig. 8 we can observe that similarly to Fe₇₅B₉Si₁₂C₄ microwire stress-annealed Co_69.2Fe_4.1B_11.8Si_13.8C_1.1 microwires present linear dependence of DW velocity, v, on magnetic field, H (see Fig. 8). However, v-values observed in stress-annealed Co_69.2Fe_4.1B_11.8Si_13.8C_1.1 microwires at the same H-values are almost twice superior to those of Fe₇₅B₉Si₁₂C₄ microwire (Fig. 8).

Figure 8. v(H) dependencies of as-prepared Fe₇₅B₉Si₁₂C₄ and stress-annealed (T_ann = 300 ⁰C, t_ann = 60 min, σ_m= 80 MPa) Co_69.2Fe_4.1B_11.8Si_13.8C_1.1microwires.

Consequently, stress annealing of ferromagnetic microwires allows achievement of interesting combination of magnetic properties. In the Fe-rich microwires stress-annealing allows remarkable improvement of magnetic softness and GMI effect. Stress-annealed Co-rich microwires can simultaneously present single and fast domain wall (DW) propagation and high GMI effect.

The origin of stress-induced anisotropy in amorphous materials is previously discussed in terms of either “back stresses” or directional pair ordering [40-42].

Generally, pair ordering mechanism is assumed for amorphous alloys with two or more magnetic elements. Since one of studied microwire (Fe₇₅B₉Si₁₂C₄) contains only one transition metal we consider that the back stresses mechanism of stress-induced anisotropy is more probable.

4 Conclusions

We observed that the stress-annealing allows remarkable improvement of GMI effect in Fe-rich microwires and observation of unique combination of magnetic properties in Co-rich microwires: simultaneous observation of single domain wall propagation and still high GMI effect in Co-rich microwires. An order of magnitude GMI ratio and magnetic softness improvement in Fe-rich microwires is demonstrated.

Unusual ΔZ/Z(H) dependence in stress-annealed Fe-rich microwires has been explained considering frequency dependence of the skin penetration depth, δ, as well as magnetic anisotropy distribution within the metallic nucleus.

For interpretation of observed effect of stress annealing we considered internal stresses relaxation after annealing and interplay of compressive “back-stresses” arising after stress annealing and axial internal stresses and change of the spatial distribution of the magnetic anisotropy and hence the domain structure inside the microwire and near the surface.

Acknowledgements

This work was supported by Spanish MCIU under PGC2018-099530-B-C31 (MCIU/AEI/FEDER, UE), by the Basque Country Government under the Elkartek (RTM 4.0) project and by the University of Basque Country under scheme of “Ayuda a Grupos Consolidados” (Ref.: IT954- 16). The authors thank for technical and human support provided by SGIker of UPV/EHU (Medidas Magneticas Gipuzkoa) and European funding (ERDF and ESF).

References

[1] D. C. Jiles, Recent advances and future directions in magnetic materials, Acta Mater., 51 (2003) pp. 5907-5939.

[2] M.H. Phan, H.X. Peng, Giant magnetoimpedance materials: Fundamentals and applications, Progr. Mater. Sci. 53 (2) (2008) 323-420.

[3] A. Zhukov, M. Ipatov, M. Churyukanova, A. Talaat, J. M. Blanco and V. Zhukova, Trends in optimization of giant magnetoimpedance effect in amorphous and nanocrystalline materials, J. Alloys Compd., 727 (2017) pp. 887-901.

[4] A. Zhukov, M. Ipatov and V. Zhukova, Advances in Giant Magnetoimpedance of Materials, Handbook of Magnetic Materials, ed. K.H.J. Buschow, Vol. 24, 2015, pp. 139-236 (chapter 2).

[5] L.V. Panina and K. Mohri, Magneto-impedance effect in amorphous wires, Appl Phys Lett. 65 (1994) 1189-1191.

[6] M. Knobel, M. Vazquez, L. Kraus, Giant magnetoimpedance, Handbook of magnetic materials ed. E. Bruck 15 (2003) pp.497-563.

[7] V. Zhukova, J. M. Blanco, V. Rodionova, M. Ipatov and A. Zhukov, Domain wall propagation in micrometric wires: Limits of single domain wall regime, J. Appl. Phys. 111 (2012) 07E311.

[8] R. Beach and A. Berkowitz, Giant magnetic field dependent impedance of amorphous FeCoSiB wire, Appl. Phys. Lett. 64 (1994) 3652-3654.

[9] V. Zhukova, J. M. Blanco, M. Ipatov and A. Zhukov, Effect of transverse magnetic field on domain wall propagation in magnetically bistable glass-coated amorphous microwires, J. Appl. Phys. 106 (2009) 113914.

[10] A. Zhukov, M. Ipatov, A. Talaat, J. M. Blanco,B. Hernando, L. Gonzalez-Legarreta, J. J. Suñol and V Zhukova, “Correlation of Crystalline Structure with Magnetic and Transport Properties of Glass-Coated Microwires”, Crystals Vol. 7, p. 41, 2017, doi:10.3390/cryst7020041

[11] G .Herzer, Amorphous and nanocrystalline soft magnets, in Proceedings of the NATO Advanced Study Insititute on Magnetic Hysteresis in Novel Materials, Mykonos, Greece, 1-12 July 1996 ed. George C. Hadjipanayis, NATO ASI Series (Series E:Applied Sciences) Vol. 338, pp.711-730. Kluwer Academic Publishers (Dordrecht/Boston/London) 1997.

[12] I. Ogasawara and S. Ueno. Preparation and properties of amorphous wires, IEEE Trans. Magn. 31 (2) (1995) 1219-1223.

[13] P. Rudkowski, G. Rudkowska, J.O. Strom-Olsen, The fabrication of fine metallic fibers by continuous melt extraction and their magnetic and mechanical properties, Mater. Sci. Eng. A 133 (1991) 158-161.

[14] H. Chiriac, S. Corodeanu, M. Lostun, G. Ababei, and T.-A. Óvári, Rapidly solidified amorphous nanowires, J. Appl. Phys., vol. 107, (2010) 09A301.

[15] D. Kozejova, L. Fecova, P. Klein, R. Sabol, R. Hudak, I. Sulla, D. Mudronova, J. Galik, R. Varga, “Biomedical applications of glass-coated microwires”, J. Magn. Magn. Mater., 470, (2019) pp. 2-5.

[16] A. Talaat, J. Alonso, V. Zhukova, E. Garaio, J. A. García, H. Srikanth, M. H. Phan and A. Zhukov, Ferromagnetic glass-coated microwires with good heating properties for magnetic hyperthermia, Sci. Reports, 6 (2016) 39300

[17] A.V. Ulitovsky, I.M. Maianski, A.I. Avramenco, Method of continuous casting of glass coated microwire, Patent No128427 (USSR), 15.05.60, Bulletin, No10, p.14.

[18] R. Gemperle, L. Kraus and J. Schneider, Magnetization reversal in amorphous (Fe1−xNix)80P10B10 microwires, Czezh. J. Phys. B 28 (1978) 1138-1145.

[19] A. Zhukov, J. Gonzalez, A. Torcunov, E. Pina, M.J. Prieto, A.F. Cobeño, J.M. Blanco, V. Larin and S. Baranov, Ferromagnetic resonance and Structure of Fe-based Glass-coated Microwires, J. Magn. Magn. Mater. 203 (1999) 238-240.

[20] H. Chiriac, T.A. Ovari and Gh. Pop, Internal stress distribution in glass-covered amorphous magnetic wires, Phys Rev B 42 (1995) 10105.

[21] S. A. Baranov, V. S. Larin and A. V. Torcunov, “Technology, Preparation and Properties of the Cast Glass-Coated Magnetic Microwires”, Crystals, 7 (2017) 136

[22] A. Zhukov, M. Churyukanova, S. Kaloshkin, V. Sudarchikova, S. Gudoshnikov,M. Ipatov, A. Talaat, J.M. Blanco and V. Zhukova, “ Magnetostriction of Co-Fe-based amorphous soft magnetic microwires”, J. Electr. Mater. (2016), 45(1), pp 226-234

[23] Y. Konno, K. Mohri, Magnetostriction measurements for amorphous wires, IEEE Trans Magn. 25 (1989) 3623-3625.

[24] A. F. Cobeño, A. Zhukov, J. M. Blanco, V. Larin and J. Gonzalez, Magnetoelastic sensor based on GMI of amorphous microwire, Sens. Actuators A, 91, (2001) pp. 95-98.

[25] A. Zhukov, A.F. Cobeño, J. Gonzalez, J.M. Blanco, P. Aragoneses and L. Dominguez, Magnetoelastic sensor of level of the liquid based on magnetoelastic properties of Co-rich microwires, Sens. Actuators A, 81/1-3, (2000) pp. 129-133.

[26] D. Makhnovskiy, N. Fry, A. Zhukov, On different tag reader architectures for bistable microwires, Sens. Actuators A-Phys., 166, (2011) pp. 133-140.

[27] D. Praslička, J. Blažek, M. Šmelko, J.Hudák, A. Čverha, I. Mikita, R.Varga and A. Zhukov, Possibilities of Measuring Stress and Health Monitoring in Materials Using Contact-Less Sensor Based on Magnetic Microwires, IEEE Trans. Magn., 49(1) (2013) pp. 128-131.

[28] F.X. Qin, H.X. Peng, M.H. Phan, L.V. Panina, M. Ipatov, A. Zhukov, Effects of wire properties on the field-tunable behaviour of continuous-microwire composites, Sens. Actuators A, 178 (2012) pp. 118– 125.

[29] V. Zhukova, J. M. Blanco, M. Ipatov, M. Churyukanova, S. Taskaev and A. Zhukov, Tailoring of magnetoimpedance effect and magnetic softness of Fe-rich glass-coated microwires by stress- annealing, Sci. Reports, 8 (2018) 3202

[30] A. P. Zhukov, A. Talaat, M. Ipatov, J. M. Blanco, L. Gonzalez-Legarreta, B. Hernando, and V. Zhukova, Effect of Nanocrystallization on Magnetic Properties and GMI Effect of Microwires, IEEE Trans. Magn. 50 (6) ( 2014) 2501905.

[31] V. Zhukova, J.M. Blanco, M. Ipatov, J. Gonzalez, M. Churyukanova A., Zhukov, “Engineering of magnetic softness and giant magnetoimpedance effect in Fe-rich microwires by stress-annealing”, Scripta Materialia Vol. 142, 1 January 2018, 10–14, doi: 10.1016/j.scriptamat.2017.08.014

[32] K.R. Pirota, L. Kraus, H. Chiriac, M. Knobel, Magnetic properties and GMI in a CoFeSiB glass-covered microwire, J.Magn. Magn. Mater. 21 (2000) L243-L247.

[33] A. Zhukov, V. Zhukova, J.M. Blanco and J. Gonzalez, Recent research on magnetic properties of glass-coated microwires, J. Magn. Magn. Mater. 294 (2005) 182-192.

[34] P. Corte-León , V. Zhukova, M. Ipatov, J.M. Blanco, J. Gonzalez, A. Zhukov, “Engineering of magnetic properties of Co-rich microwires by joule heating”, Intermetallics 105 (2019) 92-98, DOI: https://doi.org/10.1016/j.intermet.2018.11.013

[35] A.Zhukov, A. Talaat, M. Ipatov, and V. Zhukova, “Tailoring the high-frequency giant magnetoimpedance effect of amorphous Co-rich microwires,” IEEE Magn. Lett., vol. 6, 2015, Art. ID 2500104, 10.1109/LMAG.2015.2397877

[36] Yu. Kabanov, A. Zhukov, V. Zhukova and J. Gonzalez, Magnetic domain structure of microwires studied by using the magneto-optical indicator film method, Appl. Phys. Lett. 87 (2005) 142507.

[37] M.Vázquez and D.-X.Chen, The magnetization reversal process in amorphous wires, IEEE Trans. Magn. 31 (2) (1995)1229-1239.

[38] A.Zhukov, K.Chichay, A.Talaat, V.Rodionova, J.M.Blanco, M.Ipatov, V. Zhukova, “Manipulation of magnetic properties of glass-coated microwires by annealing”, J. Magn. Magn. Mater. 383 (2015) 232–236.

[39] A. Zhukov, A. Talaat, M. Ipatov, J.M. Blanco, V. Zhukova, “Tailoring of magnetic properties and GMI effect of Co-rich amorphous microwires by heat treatment”, J. Alloys Compounds 615 (2014) 610–615.

[40] F. E. Luborsky and J. L. Walter, Magnetic Anneal Anisotropy in Amorphous Alloys, IEEE Trans.Magn. Mag-13, No2 (1977) 953-956.

[41] J. Haimovich, T. Jagielinski, and T. Egami, Magnetic and structural effects of anelastic deformation of an amorphous alloy, J. Appl. Phys. 57 , 3581 (1985); doi: 10.1063/1.335013

[42] A. Zhukov, V. Zhukova, V. Larin , J.M. Blanco and J. Gonzalez, ”Tailoring of magnetic anisotropy of Fe-rich microwires by stress induced anisotropy”, Physica B 384 (2006) 1-4.