Combination of 3D solid finite elements with rotation-free beam elements for non-linear analysis of fiber reinforced polymer rebars

Abstract

We present a combination of three dimensional (3D) solid elements and rotation-free beam elements for non-linear analysis of fiber-reinforced polymer (FRP) of rebars. The matrix material is modelled by 3D solid elements while the fibers are modelled with rotation-free beam elements. The absence of rotation variables in the beam elements allows the straightforward coupling of 3D solid and beam elements using a formulation with displacement nodal degrees of freedom only. Both solid and beam elements are formulated in an updated Lagrangian description. The behavior of the matrix and the fiber material are modelled with an elastic-damage model. The efficiency and accuracy of the combined 3D-beam element formulation are verified in examples of application to the analysis of FRP rebars up to fracture in axial, bending and shear tests for which experimental results are available.

Keywords: 3D solid finite elements, rotation-free beam elements, polymer fiber rebars

1. Introduction

There is an increasing interest in the use of non-metallic materials, such as polymers, in the building and construction (B&C) sector as an alternative to standard materials, such as steel and cement [1,2]. These new materials have many advantages, compared to traditional ones, in terms of strength-weight and stiffness-weigh ratios, corrosion resistance to chemical agents, and fatigue performance, to name a few. All these advantages can extend the life-frame of structures and minimize the maintenance required, thus contributing to improve the sustainability of the sector. Current research efforts aim to develop resistant, sustainable and cost-effective materials incorporating polymers for a number of applications in building and construction.

Polymers and composite materials can be used in B&C in many forms: as external reinforcements of concrete beams and slabs [3,4], as short fibers embedded in concrete [5], or as pultruded elements which can be used as rebars for concrete reinforcement [6] or as beams elements to construct different structures such as bridges [7], or lighthouses [8] (Figures 1a and 1b), to name some examples.

(a) (b)

Figure 1. Applications of pultruded beams in construction [7,8]

The use of pultruded FRP as reinforcement in concrete has several advantages compared to steel reinforcement such as corrosion resistance, high longitudinal (unidirectional) strength (2 or 3 times higher than steel for equivalent bar diameter), high fatigue endurance (which depends on the type of reinforcing fiber and bar), magnetic transparency, lightweight (25% of steel weight) and low thermal and electric conductivity (for glass and aramid fibers) [9]. Glass fibers are the common choice due to their good performance and reduced cost, compared to other synthetic fibers that have improved properties but are more expensive, such as carbon. Research efforts are currently carried out for developing new families of rebars with synthetic fibers, as reinforcement for concrete structures [10,11]. This type of synthetic fiber rebars could be an alternative to current FRP rebars using glass fibers, and even to steel rebars for specific applications.

Pultrusion beams are obtained by pulling the reinforcement fibers, which have previously impregnated with a matrix resin, through a heated die where the composite is cured [12]. The shape of the die defines the shape of the final beam produced. Due to the fabrication process, the final composite contains mainly fibers aligned with the beam axis, and the efficiency of the method allows having fiber participations that can reach 80% of the total composite weight content [13].

This paper presents a new computational approach for assessing the non-linear behavior of pultruded composites beams using a combination of 3D solid finite elements with rotation-free beam elements. These last ones are included in the model to characterize the longitudinal performance of the composite.

The formulation presented is of special interest for pultruded beams, as in these elements fibers are mainly oriented in the longitudinal direction, which simplifies the distribution of the rotation-free beams in the numerical model. As it will be shown, the adaptability of the beam elements in the model geometry allows characterizing complex failure mechanisms such as shear failure, which depends highly on the tensile forces taken by the fibers once the matrix has failed. To do so, the geometrical non-linear effects in the solid and beam elements are taken into account by using an updated Lagrangian description, allowing for large displacements effects that can occur in specific loading cases, such as in shear tests and in post-failure situations. The fact that both the 3D solid elements and the rotation-free beam element are formulated in terms of displacement degrees of freedom (DOFs) only facilitates the integration of both types of elements in a unified formulation. An elastic-damage model is used for characterizing the behavior of both the matrix and the fibers.

The content of the paper is as follows. In the next section we present the overall finite element approach for non-linear analysis of FRP rebars combining solid elements and rotation-free beam elements. Then we describe the 3D solid finite element formulation for modelling the behavior of the matrix material. This is followed by the finite element formulation for the fibers using rotation-free beam elements based on a cell-vertex approach. The coupling of 3D-solid elements and rotation-free beam elements is detailed. The finite element formulation is validated in the non-linear analysis up to failure of FRP bar specimens formed by an epoxy matrix and carbon fibers tested under axial, bending and shear loads. Numerical results are compared with experimental results for the same tests. Excellent agreement is obtained in the comparison.

2. Combination of 3D solid elements and rotation-free elements for analysis of polymer fiber rebars

Figure 2 depicts the modelling strategy for analysis of FRP rebars with the FEM [14,15]. The procedure proposed dissociates the longitudinal contribution of fibers to the composite strength and stiffness, from their contribution in the transversal and shear directions. This is done by modeling a transverse reinforced resin, that accounts for the resin and the transverse and shear performance of the fibers, with standard 3D solid elements; and by modeling the longitudinal contribution of fibers to the composite with a collection of beams embedded in the 3D solid model.

Figure 2. Finite element modelling of FRP rebar

Both the 3D solid elements and the beam elements are formulated using an updated Lagrangian description in order to account for geometrically non-linear effects in the deformation of the FRP bars. Following standard finite element procedures, the discretized equilibrium equation for the bar structure, expressed in the current configuration at time ${\textstyle t}$, can be written in the following quasi-static form [15]

${}^{t}{\boldsymbol {r}}({}^{t}{\boldsymbol {a}}):={}^{t}{\boldsymbol {p}}({}^{t}{\boldsymbol {a}})-{}^{t}{\boldsymbol {f}}=0$

(1)

with

${}^{t}{\boldsymbol {p}}({}^{t}{\boldsymbol {a}})=\int _{{}^{t}V}{}^{t}{\boldsymbol {B}}{}^{t}{\boldsymbol {\sigma }}dV$

(2)

In Eqs.(1) and (2), ${\textstyle {\boldsymbol {r}}}$ is the vector of residual forces, ${\textstyle {\boldsymbol {a}}}$ is the vector of nodal displacement, ${\textstyle {\boldsymbol {p}}}$ is the vector of internal nodal forces, ${\textstyle {\boldsymbol {B}}}$ is the strain matrix relating the strains with the nodal displacements, ${\textstyle {\boldsymbol {\sigma }}}$ is the Cauchy stress vector, ${\textstyle {\boldsymbol {f}}}$ is the vector of equivalent nodal forces, ${\textstyle V}$ is the volume of the FRP bar and the upper left index ${\textstyle t}$ denotes the time ${\textstyle t}$.

The vector of internal forces ${\textstyle {}^{t}{\boldsymbol {p}}}$ is computed by sum of the contributions from the solid elements and the beam elements, i.e.

${}^{t}{\boldsymbol {p}}({}^{t}{\boldsymbol {a}})={}^{t}{\boldsymbol {p}}_{s}({}^{t}{\boldsymbol {a}})+{}^{t}{\boldsymbol {p}}_{b}({}^{t}{\boldsymbol {a}})$

(3)

where indices ${\textstyle s}$ and ${\textstyle b}$ denote the contribution of the 3D solid elements and the beam elements to vector ${\textstyle {}^{t}{\boldsymbol {p}}}$, respectively.

The equilibrium solution at time ${\textstyle t+\Delta t}$ is found by solving Eq.(1) using a standard Newton-Raphson procedure briefly outlined below.

For each iteration of the Newton-Raphson scheme [15] we perform the following computations:

Computation of displacement increments

${}^{t}{\boldsymbol {K}}_{T}\Delta {\boldsymbol {a}}^{i}=-{}^{t}{\boldsymbol {r}}^{i}$

(4)

with

${}^{t}{\boldsymbol {r}}^{i}={}^{t}{\boldsymbol {p}}({}^{t+\Delta t}{\boldsymbol {a}}^{i})-{}^{t+\Delta t}{\boldsymbol {f}}$

(5)

Displacement update

${}^{t+\Delta t}{\boldsymbol {a}}^{i+1}={}^{t+\Delta t}{\boldsymbol {a}}^{i}+\Delta {\boldsymbol {a}}^{i}$

(6)

Stress update

$\Delta {\boldsymbol {\varepsilon }}^{i}={}^{t}{\boldsymbol {B}}\Delta {\boldsymbol {a}}^{i}$

(7)

$\Delta {\boldsymbol {\sigma }}^{i}={\boldsymbol {D}}_{T}\Delta {\boldsymbol {\varepsilon }}^{i}$

(8)

${}^{t+\Delta t}{\boldsymbol {\sigma }}^{i+1}={}^{t+\Delta t}{\boldsymbol {\sigma }}^{i}+\Delta {\boldsymbol {\sigma }}^{i}$

(9)

Residual force vector computation

${}^{t+\Delta t}{\boldsymbol {r}}^{i+1}=\int _{{}^{t+\Delta t}V}{}^{t+\Delta t}{\boldsymbol {B}}{}^{t+\Delta t}{\boldsymbol {\sigma }}^{i+1}dV-{}^{t+\Delta t}{\boldsymbol {f}}$

(10)

Convergence check

The iteration stop when

$\Vert {}^{t+\Delta t}r^{i+1}\Vert <{\boldsymbol {\varepsilon }}$

(11)

where ${\textstyle {\boldsymbol {\varepsilon }}}$ is a prescribed error value. In our computations we have taken ${\textstyle \varepsilon =10^{-3}}$.

In Eq.(4) ${\textstyle {}^{t}{\boldsymbol {K}}_{T}}$ is the tangent stiffness matrix. We have computed this matrix as

${}^{t}{\boldsymbol {K}}_{T}={}^{t}{\boldsymbol {K}}_{T_{s}}+{}^{t}{\boldsymbol {K}}_{T_{b}}$

(12)

where indices ${\textstyle s}$ and ${\textstyle b}$ denote the contribution of the solid elements and the beam elements to the tangent stiffness matrix, respectively. These contributions are computed as

${}^{t}{\boldsymbol {K}}_{T_{r}}=\int _{V_{r}}{}^{t}{\boldsymbol {B}}_{r}^{T}{}^{t}{\boldsymbol {D}}_{T_{r}}{}^{t}{\boldsymbol {B}}_{r}dV\,,\qquad {\mbox{with }}\,\,\,r=s,b$

(13)

where ${\textstyle {}^{t}{\boldsymbol {B}}_{r}}$ and ${\textstyle {}^{t}{\boldsymbol {D}}_{T_{r}}}$ with ${\textstyle r=s,b}$ denote the deformation matrix and the tangent constitutive matrix for the solid elements and the beam elements, respectively at time ${\textstyle t}$.

The computation of these matrices is detailed in the next sections.

3. Formulation of 3D solid elements for the transverse reinforced resin material

3.1 Definition of displacements, strains and stresses

Let us consider a FRP rebar discretized using 3D-solid elements of ${\textstyle n}$ nodes. The displacement field within the element can be expressed in terms of the nodal displacements in the standard finite element form as [14,15]

${\boldsymbol {u}}=[u,v,w]^{T}={\boldsymbol {N}}^{e}{\boldsymbol {a}}^{e}$

(14)

where ${\textstyle {\boldsymbol {u}}}$ is the displacement vector, ${\textstyle u,v}$ and ${\textstyle w}$ are the displacements along the cartesian axes ${\textstyle x,y,z}$, respectively, ${\textstyle {\boldsymbol {N}}^{e}}$ and ${\textstyle {\boldsymbol {a}}^{e}}$ are the shape functions matrix and the nodal displacement vector for the element ${\textstyle e}$ given by

${\boldsymbol {N}}^{e}=[{\boldsymbol {N}}_{1}^{e},{\boldsymbol {N}}_{2}^{e},\cdots ,{\boldsymbol {N}}_{n}^{e}]\quad ,\quad {\boldsymbol {a}}^{e}=\left\{{\begin{matrix}{\boldsymbol {a}}_{1}^{e}\\{\boldsymbol {a}}_{2}^{e}\\\vdots \\{\boldsymbol {a}}_{n}^{e}\end{matrix}}\right\}$

(15)

where

${\boldsymbol {N}}_{i}^{e}=N_{i}^{e}\left[{\begin{matrix}1&0&0\\0&1&0\\0&0&1\end{matrix}}\right]\quad ,\quad {\boldsymbol {a}}^{e}=\left\{{\begin{matrix}u_{i}\\v_{i}\\w_{i}\end{matrix}}\right\}$

(16)

are the nodal components of matrix ${\textstyle {\boldsymbol {N}}^{e}}$ and vector ${\textstyle {\boldsymbol {a}}^{e}}$, and ${\textstyle N_{i}^{e}}$ is the shape function matrix of node ${\textstyle i}$.

The strains within the element can be readily expressed in terms of the nodal displacements as

${\boldsymbol {\varepsilon }}={\boldsymbol {B}}^{e}{\boldsymbol {a}}^{e}$

(17)

where

${\boldsymbol {\varepsilon }}=\left\{{\begin{matrix}\varepsilon _{x}\\\varepsilon _{y}\\\varepsilon _{z}\\\gamma _{xy}\\\gamma _{xz}\\\gamma _{yz}\end{matrix}}\right\}=\left\{{\begin{matrix}\displaystyle {\frac {\partial u}{\partial x}}\\\displaystyle {\frac {\partial v}{\partial y}}\\[.3cm]\displaystyle {\frac {\partial w}{\partial z}}\\[.3cm]\displaystyle {\frac {\partial u}{\partial y}}+\displaystyle {\frac {\partial v}{\partial x}}\\[.3cm]\displaystyle {\frac {\partial u}{\partial z}}+\displaystyle {\frac {\partial w}{\partial x}}\\[.3cm]\displaystyle {\frac {\partial v}{\partial z}}+\displaystyle {\frac {\partial w}{\partial y}}\end{matrix}}\right\}\quad ,\quad {\boldsymbol {B}}^{e}=[{\boldsymbol {B}}_{1}^{e},{\boldsymbol {B}}_{2}^{e},\cdots ,{\boldsymbol {B}}_{n}^{e}]\quad ,\quad {\boldsymbol {B}}_{i}=\left[{\begin{matrix}\displaystyle {{\partial N_{i}} \over {\partial x}}&0&0\\[.3cm]0&\displaystyle {{\partial N_{i}} \over {\partial y}}&0\\[.3cm]0&0&\displaystyle {{\partial N_{i}} \over {\partial z}}\\[.3cm]\displaystyle {{\partial N_{i}} \over {\partial y}}&\displaystyle {{\partial N_{i}} \over {\partial x}}&0\\[.4cm]\displaystyle {{\partial N_{i}} \over {\partial z}}&0&\displaystyle {{\partial N_{i}} \over {\partial x}}\\[.4cm]0&\displaystyle {{\partial N_{i}} \over {\partial z}}&\displaystyle {{\partial N_{i}} \over {\partial y}}\\\end{matrix}}\right]$

(18)

where ${\textstyle {\boldsymbol {B}}^{e}}$ and ${\textstyle {\boldsymbol {B}}_{i}^{e}}$ are the strain matrices for the element and the ${\textstyle i}$th node, respectively.

The stress-strain relationship is written in incremental form (neglecting initial strains and initial stressed) as

$d{\boldsymbol {\sigma }}={\boldsymbol {D}}_{T}d{\boldsymbol {\varepsilon }}$

(19)

where

${\boldsymbol {\sigma }}=[\sigma _{x},\sigma _{y},\sigma _{z},\tau _{xy},\tau _{xz},\tau _{yz}]^{T}$

(20)

is the Cauchy stress vector and ${\textstyle {\boldsymbol {D}}_{T}}$ is the tangent constitutive matrix. In our computations we have modelled the matrix material with an elastoplastic model based on a Drucker-Prager yield functions and an elastic-plastic-damage model. The damage model is described in the next section.

The expressions of the strain matrix and the Cauchy stress vector are used for computing the nodal forces (Eq.(2)) and the tangent constitutive matrix.

The validation examples presented in the paper have been solved using three-linear 8-noded hexahedral elements [14].

3.2 Material model for solid elements

The material model defined for the solid elements has to reproduce the performance of what has been called transverse reinforced resin. This is, a resin with improved properties in its transversal and shear directions, due to the presence of fibers. The transversal directions are defined as those directions perpendicular to the fiber longitudinal orientation.

As stated by Rastellini et al. when defining the serial parallel mixing theory [17] and used by Martinez et al. in the simplified model presented in [16], the contribution of the fibers to the composite in the transversal and shear directions can be captured by applying the inverse mixing theory. This states that the constitutive matrix of the composite (${\textstyle {\hat {\boldsymbol {D}}}}$) can be obtained by the inverse combination of the stiffness matrix of its constituents (${\textstyle {\boldsymbol {D}}_{m}}$ and ${\textstyle {\boldsymbol {D}}_{f}}$), proportionally to their volumetric participation (${\textstyle V_{m}}$ and ${\textstyle V_{f}}$), being ${\textstyle m}$ and ${\textstyle f}$ matrix and fiber, respectively. This is

${\hat {\boldsymbol {D}}}^{-1}=V_{m}{\boldsymbol {D}}_{m}^{-1}+V_{f}{\boldsymbol {D}}_{f}^{-1}$

(21)

The constitutive matrices ${\textstyle {\boldsymbol {D}}_{m}}$ and ${\textstyle {\boldsymbol {D}}_{f}}$ are shown in Eq.(22)

${\boldsymbol {D}}_{i}=\left[{\begin{matrix}H_{i}&F_{i}&F_{i}&0&0&0\\&H_{i}&F_{i}&0&0&0\\&&H_{i}&0&0&0\\&&&G_{i}&0&0\\&&&&G_{i}&0\\Sym.&&&&&G_{i}\end{matrix}}\right]\,,\quad i=m,f$

(22)

with

$H_{i}=\displaystyle {\frac {E_{i}(1-\nu _{i})}{(1+\nu _{i})(1-2\nu _{i})}}\,,\quad F_{i}=\displaystyle {\frac {E_{i}\nu _{i}}{(1+\nu _{i})(1-2\nu _{i})}}\,,\quad G_{i}=\displaystyle {\frac {(1-2\nu _{i})}{2(1-\nu _{i})}}$

(23)

We note that the constitutive matrix ${\textstyle {\hat {\boldsymbol {D}}}}$ accounts for the effect of the fiber matrix ${\textstyle {\boldsymbol {D}}_{f}}$ where ${\textstyle H_{f}}$ has a null value in the fiber direction (in practice a small value is chosen to avoid numeric instability). The stiffness in the fiber direction is provided by the RFB elements.

The distinct form of matrices ${\textstyle {\boldsymbol {D}}_{f}}$ and ${\textstyle {\boldsymbol {D}}_{m}}$ is needed in order to accurately reproduce the shear stiffness in the resulting matrix ${\textstyle {\hat {\boldsymbol {D}}}}$. In this manner, the combination of solid elements and RFB elements can reproduce a parallel mixed material behavior along the longitudinal direction of the RFB elements (deformations in the fiber direction are compatible between all materials) and a serial mixed material behavior in the orthogonal direction to the fibers (stresses in the normal fiber direction are compatible between all materials), according to the inverse mixing theory [17]. An advantage of this approach versus the standard serial-parallel material mixing model is the compatibility between the stresses in the concrete and the fibers in the orthogonal direction to the fibers, which facilitates the convergence of the nonlinear iterative process.

Non-linear effects in the response of the material are modelled by a simple isotropic damage model [18,19]. According to this, Eq.(21) is modified as

${\hat {\boldsymbol {D}}}^{-1}=V_{m}\left[{\boldsymbol {D}}_{m}(1-d_{m})\right]^{-1}+V_{f}\left[{\boldsymbol {D}}_{f}(1-d_{f})\right]^{-1}$

(24)

where ${\textstyle {\hat {\boldsymbol {D}}}}$ is the damaged constitutive matrix for the solid element and the damage parameters ${\textstyle d_{i}(i=m,f)}$ are an scalar numbers between 0 and 1 defined as

$d_{i}={\frac {2\left({\sigma }_{0_{i}}-{\sigma }_{I}\right)\left(E_{i}G_{i}-h{\sigma }_{0_{i}}\right)}{(2E_{i}G_{i}-h{\sigma }_{0_{i}}){\sigma }_{I}}}\quad \quad i=m,f$

(25)

In Eq.(25) ${\textstyle \sigma _{0_{i}}}$ is the elastic limit, ${\textstyle \sigma _{I}}$ is the maximum principal stress, ${\textstyle G_{i}}$ is the fracture energy, ${\textstyle E_{i}}$ is the Young's modulus and index ${\textstyle i}$ (${\textstyle i=m,f}$) refers to the matrix or fiber material, respectively. In addition, ${\textstyle h}$ is the characteristic length of the element.

The above constitutive model can accurately reproduce axial and pure bending stress states in which the RFB elements are mainly subjected to tensile forces. The model has proved to work well in shear-dominated regions in which two different stress situations appear in the shear zone and in the region where the loads are applied. In the shear zone the matrix material is soon fully damaged (i.e. ${\textstyle {\hat {\boldsymbol {D}}}\to 0}$) and the stiffness is mainly contributed by the fibers as they rotate and change their orientation. In zones where the loads are applied in a direction orthogonal to the fibers, the fibers are agglomerated in packages that allow the transmission of compression stresses to the resin material, inducing damage. The contribution of matrix ${\textstyle {\hat {\boldsymbol {D}}}}$ is important in these zones. This distinct phenomenon has been modelled by limiting the maximum value of the damage parameters in Eq.(25) in these regions as

$0\leq d_{i}\leq 0.5\quad \quad i=m,f$

(26)

4. Formulation of rotation-free beam elements for the fibers

The elimination of the rotations as nodal degrees of freedom in bending-type elements (such as beams, plates and shells) leads to the so-called rotation-free elements [20,21,22]. Rotations can be simply eliminated by expressing the curvature field in a node, or a point within an element, in terms of the displacements of nodes contained in an appropriate patch of elements surrounding the node or the point. This procedure emanates from the efforts of finite difference practitioners for analysis of thin plates based on Kirchhoff plate theory using displacement variables only [20]. The idea evolved in the last decades of the 20th century and lead to the formulation of different families of rotation-free elements for analysis of plates and shells. Oñate and Zárate [20] developed a unified formulation for this type of rotation-free plate and shell elements combining ideas from the finite volume method with the FEM. Some of the rotation-free shell elements have enjoyed much popularity for non-linear analysis of shells structures under dynamic and impact loads and sheet stamping processes using explicit and implicit dynamic formulations [23].

The use of rotation-free beam elements has been less popular in practice. The derivation of this type of elements based on Euler-Bernoulli beam theory can be found in [14,22,24]. Extensions of these elements to account for shear deformation effect was reported by Zarate and Oñate [21].

A distinct feature of all rotation-free elements is that the discretized equilibrium equations can be expressed in terms of displacement degrees of freedom only. This makes these elements advantageous for their coupling with solid elements, that are also formulated in terms of nodal displacement DOFs, in a straightforward manner. In this work we will model the mechanical behavior of the fibers with rotation-free Euler-Bernoulli beam elements formulated using an updated Lagrangian description and a cell-vertex approach [14,20]. We present below details of the element formulation.

4.1 Straight cell-vertex rotation-free beam elements

A particular class of rotation-free beam element can be derived by computing the curvature at each node using a finite difference scheme. The resulting element is termed CVB (for Cell-Vertex Beam element) [14,20].

For the sake of simplicity we will show the derivation of the stiffness equation of a rotation-free straight beam element that bends in the ${\textstyle x-z}$ plane (Figure 3). A similar process can be followed for deriving the stiffness equations for bending in the ${\textstyle x-y}$ plane. Due to the particular one-dimensional (1D) features of the rebars considered in this work, we will neglect torsional effects in the fibers.

Figure 3. Modelling strategy for analysis of FRP with the FEM

Let us formulate the deformation of a straight beam element for a current configuration at time ${\textstyle t}$. The bending behavior of the beam is modelled by considering the control domain formed by half of the lengths of the elements adjacent to a node. The curvature at node ${\textstyle i}$ is computed as

$\kappa _{i}={1 \over l_{i}}\left[\left({\partial w \over \partial x}\right)_{\!\scriptscriptstyle R_{i}}-\left({\partial w \over \partial x}\right)_{\!\scriptscriptstyle L_{i}}\right]$

(27)

where ${\textstyle l_{i}={1 \over 2}(l^{e}+l^{e-1})}$ and subscripts ${\textstyle R_{i}}$ and ${\textstyle L_{i}}$ denote the midpoints of the elements located at the right and left of node ${\textstyle i}$ (Fig. 4). The curvature ${\textstyle \kappa _{i}}$ is assumed to be constant in the control domain ${\textstyle l_{i}}$ assigned to node ${\textstyle i}$ (Figure 4).

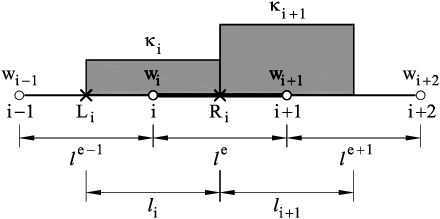
Figure 4. CVB element. Control domains around two nodes $i$ and $i+1$

The rotations ${\textstyle \left(\displaystyle {\partial w \over \partial x}\right)_{\!\scriptscriptstyle R_{i}}}$ and ${\textstyle \left(\displaystyle {\partial w \over \partial x}\right)_{\!\scriptscriptstyle L_{i}}}$ are expressed in terms of the nodal deflections as

$\left({\partial w \over \partial x}\right)_{\scriptscriptstyle R}={w_{\scriptscriptstyle i+1}-w_{\scriptscriptstyle i} \over l^{e}}\quad ,\quad \left({\partial w \over \partial x}\right)_{\scriptscriptstyle L}={w_{\scriptscriptstyle i}-w_{\scriptscriptstyle i-1} \over l^{e-1}}$

(28)

Substituting Eqs.(28) into (27) gives

$\kappa _{i}={2 \over l^{e}l^{e-1}(l^{e}+l^{e-1})}[l^{e},-(l^{e}+l^{e-1}),l^{e-1},0]\left\{{\begin{matrix}w_{\scriptscriptstyle i-1}\\w_{\scriptscriptstyle i}\\w_{\scriptscriptstyle i+1}\\w_{\scriptscriptstyle i+2}\end{matrix}}\right\}={\boldsymbol {B}}_{i}{\bar {\boldsymbol {w}}}^{(e)}$

(29)

where

${\boldsymbol {B}}_{i}={2 \over l^{e}l^{e-1}(l^{e}+l^{e-1})}[l^{e},-(l^{e}+l^{e-1}),l^{e-1},0]~~,~~{\bar {\boldsymbol {w}}}^{(e)}=\left\{{\begin{matrix}w_{\scriptscriptstyle i-1}\\w_{\scriptscriptstyle i}\\w_{\scriptscriptstyle i+1}\\w_{\scriptscriptstyle i+2}\end{matrix}}\right\}$

(30)

Similarly, the curvature at node ${\textstyle i+1}$ is found as

$\kappa _{\scriptscriptstyle i+1}={2 \over (l^{e}+l^{e+1})}\left[{w_{\scriptscriptstyle i+2}-w_{\scriptscriptstyle i+1} \over l^{e+1}}-{w_{\scriptscriptstyle i+1}-w_{\scriptscriptstyle i} \over l^{e}}\right]={\boldsymbol {B}}_{\scriptscriptstyle i+1}{\bar {\boldsymbol {w}}}^{(e)}$

(31)

with

${\boldsymbol {B}}_{i+1}={1 \over l^{e}l^{e+1}(l^{e}+l^{e+1})}[0,l^{e+1},-(l^{e}+l^{e+1}),l^{e}]$

(32)

The internal virtual work over the element ${\textstyle e}$ is obtained by adding up the contributions from the two control domains ${\textstyle l_{i}}$ and ${\textstyle l_{i+1}}$ as

$\delta U^{(e)}=\int _{l_{i} \over 2}\delta \kappa _{i}(E_{f}I)\kappa _{i}dx+\int _{l_{i+1} \over 2}\delta \kappa _{\scriptscriptstyle i+1}(E_{f}I)\kappa _{\scriptscriptstyle i+1}dx$

(33)

Substituting Eqs.(27) and (31) into (33) and following the standard assembly process of the FEM yields the element stiffness matrix as

${\boldsymbol {K}}^{(e)}={\boldsymbol {K}}_{i}^{(e)}+{\boldsymbol {K}}_{\scriptscriptstyle i+1}^{(e)}$

(34.a)

where

${\begin{array}{l}\displaystyle {\boldsymbol {K}}_{i}^{e}=\int _{l_{i} \over 2}{\boldsymbol {B}}_{i}^{T}(E_{f}I){\boldsymbol {B}}_{i}dx={l_{i} \over 2}{\boldsymbol {B}}_{i}^{T}(E_{f}I)^{(e)}{\boldsymbol {B}}_{i}\\[.5cm]\displaystyle {\boldsymbol {K}}_{\scriptscriptstyle i+1}^{e}=\int _{l_{i+1} \over 2}{\boldsymbol {B}}_{i+1}^{T}(E_{f}I){\boldsymbol {B}}_{i+1}dx={l_{\scriptscriptstyle i+1} \over 2}{\boldsymbol {B}}_{i+1}^{T}(E_{f}I)^{(e)}{\boldsymbol {B}}_{\scriptscriptstyle {i+1}}\end{array}}$

(34.b)

In Eqs.(33) and (34) ${\textstyle E_{f}}$ and ${\textstyle I}$ are the Young modulus of the fiber material and the moment of inertia of the fiber section with respect the bending axis, respectively. In the computation of the above integrals, we have assumed that ${\textstyle E_{f}}$ and ${\textstyle I}$ are constant over the control domains.

Note that, as it is usual in rotation-free beam, plate and shell elements, the stiffness matrix of an element involves the nodal deflections of the adjacent elements.

The global equivalent nodal force ${\textstyle {f}_{i}}$ is computed

${f}_{i}={P}_{z_{i}}+{f}_{z_{i}}{(l^{e}+l^{e+1}) \over 2}$

(35.a)

with

${f}_{z_{i}}={1 \over 2}\left[f_{z}^{(e)}+{f}_{z}^{(e+1)}\right]$

(35.b)

where ${\textstyle {P}_{z_{i}}}$ is the external nodal force acting at node ${\textstyle i}$ and and ${\textstyle {f}_{z}^{(e)}}$ and ${\textstyle {f}_{z}^{(e+1)}}$ are uniformly distributed loads acting in the vertical direction over elements ${\textstyle e}$ and ${\textstyle e+1}$, respectively.

4.2 Boundary conditions

The prescribed values for the deflection are imposed when solving the global system of equations, as usual. We briefly explain next how to compute the curvature at a free end and at simply supported and clamped nodes. For details see [14].

The curvature at a free end node and at a simply supported node is zero. This condition is implemented by neglecting the contribution of the boundary node to the element stiffness matrix. For a boundary element with a free or simply supported node the stiffness matrix is (Figure 5a)

${\boldsymbol {K}}^{(e)}={\boldsymbol {K}}_{\scriptscriptstyle i+1}^{(e)}\quad {\hbox{if }}\quad \kappa _{i}=0$

(36.a)

${\boldsymbol {K}}^{(e)}={\boldsymbol {K}}_{\scriptscriptstyle i}^{(e)}\quad {\hbox{if }}\quad \kappa _{i+1}=0$

(36.b)

Figure 5. CVB element. (a) Boundary condition of zero curvature at a free or simply supported node $B$. (b) Control domain for a clamped or symmetry node

The curvature at a clamped or symmetry left-end node ${\textstyle i}$ is computed as (Figure 5b)

$\kappa _{i}={2 \over l^{e}}{(w_{\scriptscriptstyle i+1}-w_{\scriptscriptstyle i}) \over l^{e}}={2 \over (l^{e})^{2}}[1,-1,1,0]\left\{{\begin{matrix}w_{\scriptscriptstyle i-1}\\w_{\scriptscriptstyle i}\\w_{\scriptscriptstyle i+1}\\w_{\scriptscriptstyle i+2}\end{matrix}}\right\}={\boldsymbol {B}}_{i}{\bar {\boldsymbol {w}}}^{(e)}$

(37)

where ${\textstyle w_{\scriptscriptstyle i-1}}$ is an auxiliary fictitious deflection.

Similarly, for a right-end clamped or symmetry node (Figure 5b)

$\kappa _{\scriptscriptstyle i+1}={2 \over l^{e}}{(w_{\scriptscriptstyle i+1}-w_{\scriptscriptstyle i}) \over l^{e}}={2 \over (l^{e})^{2}}[0,-1,1,1]\left\{{\begin{matrix}w_{\scriptscriptstyle i-1}\\w_{\scriptscriptstyle i}\\w_{\scriptscriptstyle i+1}\\w_{\scriptscriptstyle i+2}\end{matrix}}\right\}={\boldsymbol {B}}_{\scriptscriptstyle i+1}{\bar {\boldsymbol {w}}}_{i}$

(38)

where ${\textstyle w_{\scriptscriptstyle i+2}}$ is an auxiliary fictitious deflection.

The element stiffness matrix is computed in both cases by Eq.(36) with ${\textstyle {\boldsymbol {B}}_{i}}$ or ${\textstyle {\boldsymbol {B}}_{\scriptscriptstyle i+1}}$ equal to zero, as appropriate. The fictitious nodal deflections ${\textstyle w_{i-1}}$ or ${\textstyle w_{i+2}}$ (and indeed ${\textstyle w_{i}}$) are prescribed to a zero value when solving the global system of equations.

The above rotation-free formulation can be extended to account for the bending behavior of the beam in the ${\textstyle y-z}$ plane in a straightforward manner. The nodal degrees of freedom are the vertical displacement along the ${\textstyle y}$ and ${\textstyle z}$ axes [14].

The extension of the bending formulation of rotation-free beam element to account for transverse shear deformation effect is possible. The details can be found in [21].

4.3 Material model for the rotation-free beam element

The material behavior of the rotation-free CVB element is simply characterized by the Young modulus. Accounting for non-linear effects in the fiber material under axial stresses has been modelled with a standard one-dimensional elastic-damage constitutive law, i.e.

${\hat {E}}_{f}=E_{f}(1-d_{f}^{b})$

where ${\textstyle {\hat {E}}_{f}}$ and ${\textstyle E_{f}}$ are the Young modulus of the fiber in the undamaged and damaged states, respectively.

The evolution of the damage parameter ${\textstyle d_{f}^{b}}$ for the beam element is governed the maximum deformation of the fiber at failure, i.e.

$d_{f}^{b}=1+{\frac {\sigma _{0_{f}}(\varepsilon -2\varepsilon _{0_{f}}+\varepsilon _{u_{f}})}{\varepsilon E_{f}(\varepsilon _{0_{f}}+\varepsilon _{u_{f}})}}$

where ${\textstyle \varepsilon }$ is the axial deformation of the fiber, ${\textstyle \varepsilon _{0_{f}}}$ is the deformation at the elastic limit, ${\textstyle \sigma _{0_{f}}}$, and ${\textstyle \varepsilon _{u_{f}}}$ is the deformation at the ultimate (fracture) strength value.

4.4 Extension to curved rotation-free CVB elements

A curved rebar will be modelled by a collection of straight rotation-free CVB elements. Figure 6 shows a curved rebars under bending loads in a plane ${\textstyle x-z}$, discretized with three CVB elements.

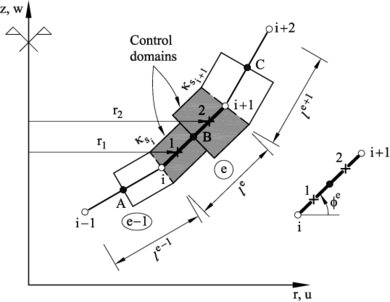
Figure 6. Cell-vertex rotation-free beam element. Control domains for computing the average curvature. A, B and C are element mid-points

The stiffness matrix is obtained as the sum of the axial stiffness matrix (${\textstyle {\boldsymbol {K}}_{A}}$) and the bending stiffness matrix (${\textstyle {\boldsymbol {K}}_{B}}$).

4.4.1 Axial stiffness matrix

The axial strain matrix ${\textstyle {\boldsymbol {B}}_{a}}$ is obtained as

$\varepsilon _{a}={\frac {\partial u'}{\partial x'}}=\lambda _{s}={\partial u' \over \partial x'}={\frac {1}{l^{e}}}[-1,1]\left\{{\begin{matrix}{u'}_{i}^{e}\\{u'}_{i+1}^{e}\end{matrix}}\right\}=\underbrace {{\frac {1}{l^{e}}}[{\boldsymbol {0}},-{\boldsymbol {t}}^{e},{\boldsymbol {t}}^{e},{\boldsymbol {0}}]} _{{\boldsymbol {B}}_{a}}{\boldsymbol {a}}^{e}={\boldsymbol {B}}_{a}{\boldsymbol {a}}^{e}$

(39)

with ${\textstyle {\boldsymbol {t}}^{e}=[\cos \phi ^{e},\sin \phi ^{e}]}$ and ${\textstyle ()'}$ denotes variables in the local coordinates system.

The axial stiffness matrix is computed as

${\boldsymbol {K}}_{A}^{e}=(E_{f}I)^{(e)}{\boldsymbol {B}}_{a}^{T}{\boldsymbol {B}}_{a}l^{e}$

(40)

4.4.2 Bending stiffness matrix

The procedure for computing the bending stiffness matrix is an extension of that followed for straight CVB elements in Section 4.2.

The curvature at node ${\textstyle i}$ is computed in terms of the gradients of the normal deflection at points ${\textstyle A}$ and ${\textstyle B}$ (Figure 6)

$\kappa _{i}={\frac {2}{l^{e}+l^{e-1}}}\left[\left({\partial w' \over \partial x'}\right)_{B}-\left({\partial w' \over \partial x'}\right)_{A}\right]={\frac {2}{l^{e}+l^{e-1}}}\left[{\frac {{w'}_{i+1}^{e}{-w_{i}'}^{e}}{l^{e}}}-{\frac {{w'}_{i}^{e-1}-w_{i-1'}^{e-1}}{l^{e-1}}}\right]=$ $=\underbrace {{\frac {1}{l^{e}l^{e-1}(l^{e}+l^{e-1})}}[l^{e},-l^{e},-l^{e-1},l^{e-1}]} _{{{\bar {\boldsymbol {B}}}'}_{b_{i}}}\left\{{\begin{matrix}{w'}_{i-1}^{e-1}\\{w'}_{i}^{e-1}\\{w'}_{i+1}^{e}\\{w'}_{i+1}^{e}\end{matrix}}\right\}={{\boldsymbol {B}}'}_{b_{i}}\mathbf {w} ^{'}={\boldsymbol {B}}_{b_{i}}{\boldsymbol {a}}^{e}$

(41.a)

In Eqs.(41.a) ${\textstyle {w'}_{j}}$ are the nodal deflections in the local axes of the element defined in Figure 7 and

${\boldsymbol {B}}_{b_{i}}={{\boldsymbol {B}}'}_{b_{i}}{\boldsymbol {T}}\quad {\hbox{with }}~{\boldsymbol {T}}=\left[{\begin{matrix}{\boldsymbol {n}}^{e-1}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}\\{\boldsymbol {0}}&{\boldsymbol {n}}^{e-1}&{\boldsymbol {0}}&{\boldsymbol {0}}\\{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {n}}^{e}&{\boldsymbol {0}}\\{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {n}}^{e}\end{matrix}}\right]$

(41.b)

and

${\boldsymbol {a}}^{e}=\left\{{\begin{matrix}{\boldsymbol {a}}_{i-1}\\{\boldsymbol {a}}_{i}\\{\boldsymbol {a}}_{i+1}\\{\boldsymbol {a}}_{i+2}\end{matrix}}\right\}\quad {\hbox{with}}\quad {\boldsymbol {a}}_{i}=\left\{{\begin{matrix}u_{i}\\w_{i}\end{matrix}}\right\}$

(41.c)

Figure 7. Local coordinate system of curved rotation-free CVB element bending in the $xz$ plane

Similarly, for node ${\textstyle i+1}$

$\kappa _{i+1}={\frac {2}{l^{e}+l^{e+1}}}\left[\left({\partial w' \over \partial x'}\right)_{C}-\left({\partial w' \over \partial x'}\right)_{B}\right]={\frac {2}{l^{e}+l^{e+1}}}\left[{\frac {{w'}_{i+2}^{e+1}{-w'}_{i+1}^{e}}{l^{e+1}}}-{\frac {{w'}_{i+1}^{e}-w_{i'}^{e}}{l^{e}}}\right]=$ $=\underbrace {{\frac {2}{l^{e}l^{e+1}(l^{e}+l^{e+1})}}[l^{e+1},-l^{e+1},-l^{e},l^{e}]} _{{\bar {\boldsymbol {B}}}_{b_{i+1}}}\left\{{\begin{matrix}{w'}_{i}^{e}\\{w'}_{i+1}^{e}\\{w'}_{i+1}^{e+1}\\{w'}_{i+2}^{e+1}\end{matrix}}\right\}={{\boldsymbol {B}}'}_{b_{i+1}}\mathbf {w} ^{'}={\boldsymbol {B}}_{b_{i+1}}{\boldsymbol {a}}^{e}$

(42.a)

with

${\boldsymbol {B}}_{b_{i+1}}={{\boldsymbol {B}}'}_{b_{i+1}}{\boldsymbol {T}}$

(42.b)

and

${\boldsymbol {T}}=\left[{\begin{matrix}{\boldsymbol {n}}^{e-1}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}\\{\boldsymbol {0}}&{\boldsymbol {n}}^{e-1}&{\boldsymbol {0}}&{\boldsymbol {0}}\\{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {n}}^{e+1}&{\boldsymbol {0}}\\{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {n}}^{e+1}\end{matrix}}\right]\quad ,\quad {\boldsymbol {n}}^{e}=[-\sin \phi ^{e},\cos \phi ^{e}]\quad ,\quad {\boldsymbol {0}}=[0,0]$

(42.c)

The bending stiffness matrix for the CVB element is expressed as the sum of the stiffness contributions from the two control subdomains 1 and 2 that form the element (Figure 6), i.e.

${\boldsymbol {K}}_{B}^{e}=l^{e}{\Bigl [}{\boldsymbol {B}}_{i}^{T}(E_{f}I){\boldsymbol {B}}_{i}+{\boldsymbol {B}}_{i+1}^{T}(E_{f}I){\boldsymbol {B}}_{i+1}{\Bigr ]}$

(43)

The total stiffness matrix for the element is finally obtained by

${\boldsymbol {K}}^{e}={\boldsymbol {K}}_{A}^{e}+{\boldsymbol {K}}_{B}^{e}$

(44)

where ${\textstyle {\boldsymbol {K}}_{A}}$ is given by Eq.(40).

We note that the size of ${\textstyle {\boldsymbol {K}}^{(e)}}$ for the CVB element bending in the ${\textstyle x-z}$ plane is ${\textstyle 8\times 8}$, as it involves the two DOFs of nodes ${\textstyle i-1,i,i+1}$ and ${\textstyle i+2}$. A similar procedure will be followed for the case of bending in the plane ${\textstyle y-z}$ [14].

The assembly process follows the general rule of the FEM [14].

5. Coupling of 3D solid elements and rotation-free beam elements

Figure 8 shows a conceptual representation of a FRP bar of rectangular section containing of a number of fibers embedded in the (bulk) matrix material. The bar geometry is discretized into 3D solid elements (8-noded hexahedral are shown). The fibers contained within each solid element are assumed to be concentrated in one-dimensional (1D) packs of fibers distributed within the 3D solid elements. Figure 8 shows the concentration of fibers in four 1D packs placed at the ${\textstyle 2\times 2}$ Gauss points locations in each cross section [14]. Each fiber pack is modelled as a rotation-free beam element with a cross-section area equivalent to the amount of fibers considered in the pack.

The displacements of the rotation-free beam element nodes are related to the nodal displacement of the 3D solid element by a simple interpolation.

Figure 8. Patch of 3D solid and rotation-free beam elements

The discretized equilibrium equations for the coupled solid-beam system can be written as explained in Section 2. The numerical response of the FRP bars for different incremental load up to failure is computed using the standard Newton-Raphson iterative procedure described in Eqs.(4)-(13).

6. Examples of application

6.1 Composite material properties

The three examples shown hereafter demonstrate the good behavior of the formulation described for analysis of FRP rebars. The examples include the analysis of a FRP rebar in three standard laboratory tests: an axial test, a three-point bending test and a shear test. The numerical results are compared with results from laboratory tests carried out at the experimental lab for structural materials of the Centro de Investigación en Materiales Estructurales (CIME) of the Technical University of Madrid (UPM), using rebars made of ECR-Glass and a matrix of DERAKANE${\textstyle \_}$8084${\textstyle \_}$Epoxy${\textstyle \_}$Vinyl${\textstyle \_}$ester.

The rebar nominal diameter is 10mm, including helicoidal ribs. As these ribs are manufactured by machining the originally pultruded rebars, the effective diameter of the bars is reduced to 9.58 mm, on average. This diameter is the one adopted for creating the model of the bar geometries.

The mechanical parameters of the fibers are: Young modulus: 74.61 GPa, Poisson ratio: 0.22, Elastic limit (tension): 1,653 MPa, Elastic limit (compression): 1,322 MPa, Fracture energy: 126,778 J/m2, Deformation at failure: 0.0277, Volume fraction: 70%

The mechanical parameters of the matrix material are: Young modulus: 3.17 GPa, Poisson coefficient: 0.38, Elastic limit: 72 MPa, Fracture energy: 45,657 J/m2, Deformation at failure: 0.11, Volume fraction 30%

6.2 Axial tension test

Figure 9 shows the bar modelled with 960 8-noded hexahedral elements and 1197 nodes. The fibers have been modelled using 1140 RFB elements. The length of the sample is 100 mm long with 9.58 mm diameter. Symmetry conditions have been considered by prescribing a zero axial displacement in the normal direction to the surface at a bar end, while the other end has a prescribed axial displacement condition to induce tensile stresses in the bar. The bar axis has the displacements in the normal plane yz constrained to zero.

Figure 9. Tensile test geometry: 3D solid and RFB elements mesh

Figure 10 shows a typical bar tested at UPM after failure.

Figure 10. Tensile test of the PFR performed at UPM

The numerical results obtained are shown in Figures 11 and 12. The displacement field obtained presents a linear distribution, until the rebar reaches brittle failure.

Figure 11. Displacement field [m] in deformed geometry

Figure 12. Axial tension tests stress-strain curves. Numerical and experimental values

The numerical load-displacement curve obtained is converted into a stress-strain curve to be compared with the experimental results. A good correlation can be seen between the numerical and experimental values (Figure 12).

Table 1 shows the good correlation between the numerical and experimental stiffness and strength magnitudes.

Table 1. Tensile test. Comparison of numerical and experimental results

Property	Lab tests	Numerical
Tensile strength (MPa)	1150 ${\boldsymbol {\pm }}$ 34 (MPa)	1173.33 (MPa)
Strain to max strength	2.3 $\pm$ 0.1 (%)	2.22 (%)
Young Modulus (GPa)	55 $\pm$ 4 (GPa)	53.03 (GPa)

6.3 Bending test

The experiment performed for measuring the bending properties, corresponds to the standard three-point bending test showed in Figure 14. The tests were carried out on bars of full circular section, instead of using cut specimens as indicated in the ASTMD-4476 norm. Figure 13 shows the bar modelled with 5400 8-noded hexahedral elements (6327 nodes) and 6156 rotation-free beam elements. The length of the bar sample is 100 mm long with 9.58 mm diameter. Symmetry and boundary conditions have been considered, as shown in Figure 13. To avoid problems with the stress concentration at the loading points, a small part of the beam (the blue zone in Figure 13) has been defined with an unbreakable material. The elastic properties of this material are the same as for the rest of the bar.

Figure 13. Three point bending test for PFR rebar. Dimensions, FEM mesh and boundary conditions

Figure 14 shows a snapshot of the laboratory test for the FRP rebar in a three-point bending configuration. Note the rollers used as a pin-supports of the beam.

Figure 14. Three-point bending test of FRP rebars performed at UPM

Figure 15 shows the strain distribution over the deformed bar (Figure 15a) and the mesh of hexahedra (Figure 15b) in a load state close to the onset of damage. The damage distribution for each element is displayed in Figure 16.

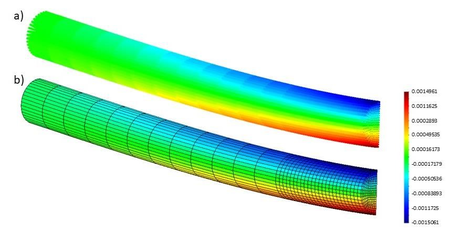
Figure 15. Three-point bending tests. Numerical results. Deformed bar. (a) Strain distribution for RFB elements. (b) Strain distribution in 3D solid elements

Figure 16. Contour field of damage variable in longitudinal and transverse sections on the deformed geometry (1x)

In Figure 17, the numerical load-deflection curve is shown together with that obtained in the laboratory for comparison purposes. The maximum loading force and the flexural stiffness captured by the numerical simulation are in good agreement with the experimental results.

Figure 17. Three-point bending tests. Force-deflection curves for shearing testing. Numerical results compared with laboratory tests

At the laboratory, samples of 240mm of total length were cut for the 10mm diameter full cylinder tests. The span of the tests was set to 200mm. Tests were carried out under displacements control, with a crosshead displacement velocity of 3mm/min. Figure 18 shows the test set-up and one specimen after failure.

Figure 18. Three-point bending tests. Failed specimen of PFR rebar

6.4 Shear test

The experiment carried out for evaluating the shear properties, corresponds to the ASTM-7617 standard test showed in Figure 19 [25]. For the numerical analysis, the symmetry of the geometry and the imposed displacement have been taken into account as shown in Figure 20a in order to speed up the calculations. Figure 20b displays the bar modelled with 5225 8-noded hexahedral elements (4608 nodes) and 5016 rotation-free beam elements. The length of the sample is 100 mm long with 9.58 mm diameter.

Figure 19. Shear test. Double shear fixture according to ASTM D-7617 standard [25]

(a) (b)

Figure 20. Shear test geometry. (a) Boundary conditions. (b) Mesh and dimensions

In Figure 20 a gap of 0.001 m can be observed between the loaded and supported zones of the specimen. This zone is necessary to capture accurately the shear forces and to avoid stress concentration in the numerical model.

Figure 21 shows a representative configuration of the numerical results. Figure 21a displays the deformed bar and the localized damage in the resin material at the shear zone. Figure 21b is a close-up of the shear zone were the RFB are presented. The curvature of these elements due to the shear deformation is depicted.

Figure 22 shows the numerical load-deflection curve superimposed to a set of curves obtained in the laboratory tests for comparison purposes. In the curves the non-linear load phenomena of the fiber reorientation can be clearly observed. For an applied load slightly larger than 5kN there is an initial plateau in the experimental tests, also reproduced by the numerical model, that corresponds to the cracking of the matrix. At this point there is a fiber reorientation that provides the stiffness increase and the final composite failure, due to fiber failure, for a load close to 35kN. The good agreement obtained between the numerical and the experimental results, especially in this case, highly non-linear, proves the validity of the proposed procedure to simulate pultruded fiber reinforced polymer rebars.

Figure 21. Shear test. Contour field of damage variable in the matrix. Deformed geometry (1x)

Figure 22. Shear test. Force-deflection curves. Numerical results compared with laboratory tests

7. Concluding remarks

The combination of 3D solid finite elements with rotation-free beam elements has shown to be adequate for modelling axial, bending and shear deformation states in fiber reinforced polymer rebars. The fact that both types of elements are formulated in terms of displacement DOFs only simplifies the combination of the best features of both elements for modelling the 3D behavior of the matrix material and the 1D behavior of the fibers, as well as the coupling interactions during complex deformation modes.

The good agreement of the numerical results for several benchmark laboratory tests with experimental data for the same tests have, validated the accuracy of the combined 3D-1D model presented. The combined model can be therefore be used confidently in practical applications of the fiber polymer rebars as reinforcement of concrete structures.

The approach presented in this work for combining 3D solid elements with rotation-free beam elements can be implemented in more sophisticated formulations for modelling fiber reinforced materials, such as that proposed in [26].

Data Availability Statement

Some or all data, models, or code that support the findings of this study are available from the corresponding author upon reasonable request.

Acknowledgements

This research was carried out as a part of the project “Development of polymer fiber reinforced rebars” funded by Saudi Aramco. The authors also acknowledge the financial support from the Spanish Ministry of Economy and Competitiveness, through the “Severo Ochoa Programme for Centres of Excellence in R&D” (CEX2018-000797-S).

References

[1] Pacheco-Torgal F., Jalali S., Labrincha J., John V.M. Eco-efficient concrete. Woodhead Publishing Series in Civil and Structural Engineering, pp. 624, 2013.

[2] Bank L.C. Composites for construction: Structural design with FRP materials. John Wiley & Sons, Inc., pp. 560, 2006.

[3] Marí A.R., Oller E., Bairán J.M. Predicting the response of FRP-strengthened reinforced-concrete flexural members with nonlinear evolutive analysis models. J. Compos. Constr., 15(5):799–809, 2011.

[4] Martínez X., Oller S., Rastellini F., Barbat A.H. A numerical procedure for simulating RC structures reinforced with FRP using the serial/parallel mixing theory. Computers & Structures, 86(15-16):1604-1618, 2008. doi:10.1016/j.compstruc.2008.01.007

[5] Nogales A., Tosić N., de la Fuente A. Rotation and moment redistribution capacity of fiber-reinforced concrete beams: Parametric analysis and code compliance. Struct. Concr., 23(1):220-239, 2021.

[6] Pultron Composites [Online]. Available: https://www.pultron.com/products/features/. [Accessed: 17-Apr-2020].

[7] Lleida GFRP Pedestrian Bridge [Online]. Available: http://www.pedelta.com/lleida-gfrp-pedestrian-bridge-p-52-en. [Accessed: 17-Apr-2020].

[8] Hernández S., et al. Design and development of an innovative structural system based on composites applied on the constrction of maritme lighthouses with lower maintenance requeriments (FAROCOMP). Mater. Compuestos, 3(2):54–58, 2019.

[9] GangaRao H.V.S., Taly N., Vijay P.V. Reinforced concrete design with FRP composites. 1st Edition, CRC Press, pp. 400, 2019.

[10] Sharifianjazi F., Zeydi P., Bazli M., Esmaeilkhanian A., Rahmani R., Bazli L., Khaksar S. Fibre-reinforced polymer reinforced concrete members under elevated temperatures: A review on structural performance. Polymers, 14(3):472, 2022. 10.3390/polym14030472

[11] Sagar B., Sivakumar M.V.N. Performance evaluation of basalt fibre-reinforced polymer rebars in structural concrete members–a review. Innovative Infrastructure Solutions, 6(2):1-18, 2021. 10.1007/s41062-020-00452-2

[12] Strau S., Senz A., Ellinger J. Comparison of the processing of epoxy resins in pultrusion with open bath impregnation and closed-injection pultrusion. J. Compos. Sci., 3(3):87, 2019.

[13] Starr T.F. Pultrusion for engineers. Woodhead Publishing Series in Composites Science and Engineering, pp. 336, 2000.

[14] Oñate E. Structural analysis with the finite element method. Linear statics. Vol 1: Basis and solids, 2009. Vol. 2: Beams, plates and shells, 2013, Springer-CIMNE.

[15] Zienkiewicz O.C., Taylor R.L. The finite element method for solids and structural mechanics. 6th edition, Elsevier, 2005.

[16] Martínez X., Rastellini F., Oller S., Flores F., Oñate E. Computationally optimized formulation for the simulation of composite materials and delamination failures. Composites Part B: Engineering, 42(2):134-144, 2011. 10.1016/j.compositesb.2010.09.013

[17] Rastellini F., Oller O., Salomón O., Oñate E. Composite materials non-linear modelling for long fibre-reinforced laminates: Continuum basis, computational aspects and validations. Computers & Structures, 86(9):879-896, 2008. 10.1016/j.compstruc.2007.04.009

[18] Oller S., Oñate E., Oliver J., Lubliner J. Finite element non-linear analysis of concrete structures using a plastic-damage model. Int. Journal of Engineering Fracture Mechanics, 35(1/2/3):219-231, 1990. 10.1016/0013-7944(90)90200-Z

[19] Lubliner J., Oller S., Oliver J., Oñate E. A plastic damage model for concrete. Int. Journal of Solids and Structures, 25(3):299-326, 1989. 10.1016/0020-7683(89)90050-4

[20] Oñate E., Zárate F. Rotation-free triangular plate and shell elements. Int. J. Numer. Meth. Engng., 47(1-3):557-603, 2000. <557::AID-NME784>3.0.CO;2-9 10.1002/(SICI)1097-0207(20000110/30)47:1/3<557::AID-NME784>3.0.CO;2-9

[21] Oñate E., Zárate F. Extended rotation-free plate and beam elements with shear deformation effects. Int. J. Numer. Meth. Engng., 83(2):196-227, 2010. 10.1002/nme.2836

[22] Jovicevic J., Oñate E. Analysis of beams and shells using a rotation - free finite element - finite volume formulation. Monograph M43, CIMNE, ISBN: 84-89925-36-4, Barcelona, 1999.

[23] Oñate E., Flores F.G. Advances in the formulation of the rotation-free basic shell triangle. Computer Methods in Applied Mechanics and Engineering, 194(21-24):2406-2443, 2005. 10.1016/j.cma.2004.07.039

[24] Flores F., Oñate E. Rotation-free finite element for the non-linear analysis of beams and axisymmetric shells. Computer Methods in Applied Mechanics and Engineering, 195(41-43):5297-5315, 2006. 10.1016/j.cma.2005.08.021

[25] ASTM-International, ASTM D7617/D7617M - 11(2017) Standard Test Method for Transverse Shear Strength of Fiber-reinforced Polymer Matrix Composite Bars, West Conshohocken, PA, 2017.

[26] Khristenko U., Schuß S., Krüger M., Schmidt F., Wohlmuth B., Hesch C. Multidimensional coupling: A variationally consistent approach to fiber-reinforced materials. Computer Methods in Applied Mechanics and Engineering, 382:113869, 2021. 10.1016/j.cma.2021.113869