Structural analysis of a railway bridge using the FEM-DEM technique

Resumen

Los objetivos del presente trabajo se enfocan en dar una respuesta a los problemas presentados en la operación de un puente ferroviario, haciendo uso de la técnica numérica FEM-DEM considerando cargas estáticas y dinámicas. La finalidad es averiguar los mecanismos de rotura existentes en el puente.

Desde un aspecto social, existe la preocupación por el posible colapso del puente, con la correspondiente pérdida económica y, eventualmente, pérdidas humanas. Por ello, el interés e implicación social del estudio repercute no solo en los mecanismos de reparación que se puedan adoptar, sino también en la posible revisión de los aspectos de cálculo y diseño en este tipo de obras.

La técnica FEM-DEM desarrollada por Zárate et al. [1,2] ha sido validada en diversos ensayos de laboratorio [3-5]. Debido a las características del problema esta técnica es la herramienta idónea para estudiar el comportamiento estructural del puente desde un punto de vista estático y dinámico. La consideración del acero de refuerzo en el puente es fundamental para realizar el análisis estructural, por lo que se describe la implementación de este tipo de refuerzo en la formulación FEM-DEM.

Palabras clave: Técnica FEM-DEM, aplicaciones de ingeniería computacional, puente ferroviario, dinámica ferroviaria

Abstract

The objectives of this work are focused on giving an answer to the problems presented in the operation of a railway bridge, using the FEM-DEM numerical technique considering static and dynamic loads. The purpose is to find out the existing breakage mechanisms in the bridge.

From a social aspect, there is concern about the possible collapse of the bridge, with the corresponding economic loss and eventually human losses; therefore, the interest and social involvement of the study has repercussions not only on the repair mechanisms that can be adopted but also on the possible revision of the calculation and design aspects in this type of works.

The FEM-DEM technique developed by Zárate et al. [1,2] has been validated in various laboratory tests [3-5]. Due to the characteristics of the problem, the technique used is an ideal tool to study the structural behaviour of the bridge from a static and dynamic point of view. Considering the reinforcing steel in the bridge is fundamental to carry out the structural analysis, which is why the implementation of this type of reinforcement in the FEM-DEM formulation is described.

Keywords: FEM-DEM technique, computer science applications, railway bridge, railway dynamics

1. Introducción

La estructura denominada Paso Inferior de Ferrocarril (PIF) se localiza en las intersecciones de la Avenida Insurgentes y Ferrocarril Central, en el Barrio de San Antonio, Celaya, Gto. México, como se puede observar en la Figura 1.

Figura 1. Ubicación del PIF. (a) Vista cenital. (b) Vista en perspectiva

Con referencia a la normativa mexicana N-PRY-CAR-6-01-001/01 [6], la estructura se clasifica como un Paso Inferior de Ferrocarril. La superestructura está compuesta por dos puentes paralelos a base de trabes de hormigón reforzado y losa del mismo material. La subestructura se compone con coronas de concreto reforzado y estribos a base de muros de mampostería. En base a una revisión in situ, no se aprecian dispositivos de apoyo. La cimentación no se ha podido verificar debido a que no es un elemento visible. El gálibo vertical promedio es de 4.20 metros y el gálibo horizontal medio de 11.75 metros.

La obra data de finales de la década de los años 1950 [7] y no se tiene conocimiento de información referente a la memoria de cálculo, planos de diseño o planos “as built”.

La estructura presenta daños bastante evidentes después de más de 60 años de servicio, y corre el riesgo de colapsar. En un análisis in situ [7] se han detectado problemas en la operación tales como:

• Deflexiones apreciables en la superestructura del PIF.

• Vibraciones importantes en la superestructura con el paso de los ferrocarriles.

• Drenes obstruidos que inducen filtraciones y humedades excesivas en la estructura.

• El tablero de ambos puentes presenta agrietamientos en el centro del claro, con patrones típicos asociados a esfuerzos de flexión, con filtraciones de humedad.

• El tablero del puente norte presenta además un descascarillado a una tercera parte de la luz, con exposición de varillas de refuerzo, mismas que se encuentran en un estado de deterioro grave con corrosión, exfoliación y laminación (pérdida de sección efectiva), así mismo probables efectos de carbonatación en el concreto.

• Se aprecian filtraciones de arcillas en las grietas con restos de resina epoxi, probablemente producto de reparaciones superficiales deficientes sin la preparación adecuada a los materiales, realizados con anterioridad en la estructura.

• En la parte superior del tablero, se aprecian una serie de grietas longitudinales localizadas en el centro y que recorren todo el desarrollo del puente.

En la Figura 2 se muestran las grietas en la parte inferior del tablero, mientras que en la Figura 3 (a) se muestran las grietas en el centro del tablero y el descascarillado con exposición del acero de refuerzo en la Figura 3 (b). La Figura 4 muestra el sellado de las grietas en la cara superior del tablero, encontradas después de retirar el balasto y las traviesas.

Figura 2. Ubicación de las grietas en la cara inferior del tablero del puente norte

Figura 3. Detalle de las grietas localizadas en el puente norte. a) Grieta al centro de la luz. b) descascarillado, con exposición de varillas de refuerzo

Figura 4. Detalle del sellado de las grietas localizadas en la cara superior del tablero del puente norte

El artículo se organiza de la siguiente manera. Primeramente, se describe la problemática encontrada en la obra civil bajo estudio. Posteriormente, se realiza un pequeño esbozo de la técnica FEM-DEM y se formula la inclusión del acero de refuerzo. Tras ello, se presentan los distintos resultados de los estudios estáticos y dinámicos efectuados.

2. La metodología FEM-DEM

Existen diferentes enfoques de acoplamiento entre el método de los elementos discretos (DEM, por sus siglas en ingles) y el método de los elementos finitos (FEM, por sus siglas en inglés) en la literatura, aprovechando las ventajas de ambos métodos numéricos. En Oñate y Rojeck [22,23] y Monteiro y Lemos [24], se utiliza el DEM para caracterizar las fracturas, mientras que el FEM discretiza el resto del dominio, existiendo un solapamiento de ambos con el fin de compatibilizar fuerzas y desplazamientos entre ellos, utilizando partículas circulares para el análisis 2D y esféricas para el 3D. En Katagiri y Takada [25], Moharnmadi et al. [26], Munjiza y Owen [27], Munjiza [28], Han et al. [29] y Han et al. [30] se presenta un método combinado de elementos finitos-discretos basado en elementos discretos en forma de bloque los cuales cubren todo el dominio e interactúan entre ellos a través de fuerzas de cohesión y contacto. Cada bloque se encuentra discretizado por elementos finitos a fin de proporcionar las propiedades elásticas correspondientes al material simulado.

Para estos estudios se ha utilizado el método FEM-DEM, implementado en el código implícito FEM2DEM desarrollado en CIMNE [1,2]. El método FEM-DEM ha sido propuesto por Zárate et al. [1,2], el cual discretiza el continuo usando triángulos lineales de 3 nodos (en 2D) y tetraedros de 4 nodos (en 3D) cuyos nodos definen la posición de un elemento discreto (virtual). Estos elementos discretos se introducen en el proceso de simulación cuando aparecen grietas. Las fuerzas normales de contacto entre elementos discretos se calculan integrando la matriz de rigidez del triángulo lineal a lo largo de sus lados que conectan las partículas discretas. El problema mecánico en la región libre de grietas se resuelve usando el FEM estándar y un modelo de daño apropiado. En los ejemplos que se muestran en este capítulo, el inicio y la evolución del daño se rigen por un criterio de falla de Mohr-Coulomb.

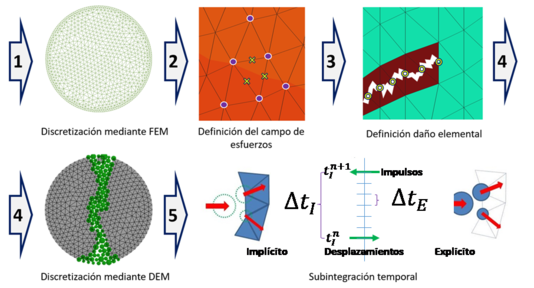
Esta formulación se puede simplificar en cinco etapas que se describen en [5] y que se resumen a continuación, haciendo uso de la gráfica en la Figura 5:

1. El dominio a analizar es inicialmente discretizado por una malla de elementos finitos (triángulos de 3 nodos en 2D y tetraedros de 4 nodos en 3D) [14].
2. Sobre la estructura se aplican las cargas a las que se encuentra sometida. Estas cargas se van incrementado por un coeficiente temporal que empieza en 0 hasta llegar al valor unitario si se trata de un análisis cuasi-estático, o bien, en un análisis dinámico se aplican siguiendo una variación temporal predefinida. En cada paso de tiempo (o pseudotiempo) se evalúa la respuesta estructural mediante el FEM. En el caso de un análisis dinámico la respuesta estructural se calcula con un esquema de integración en el tiempo implícito. Para cada nivel de carga se evalúan las tensiones en el punto medio de las aristas de cada elemento, utilizando una parcela súper-convergente [8]. Con dichas tensiones se evalúa el daño en el centro de cada arista de cada elemento, utilizando un sencillo modelo de daño isótropo [9,10].
3. El daño en cada uno de los elementos bidimensionales (2D) de la malla se evalúa como el promedio de los dos mayores valores del daño calculado sobre las aristas del elemento. En el caso 3D el daño elemental en cada elemento tetraédrico será el mayor obtenido como el promedio del daño sobre las aristas que intersectan cualquiera de los posibles planos de corte sobre el tetraedro.
4. Cuando el daño elemental alcanza un valor cercano a la unidad, el correspondiente elemento se elimina y en sus vértices se generan elementos discretos (discos circulares en 2D y esferas en 3D). A partir de ese momento el dominio de estudio contiene elementos finitos y elementos discretos.
5. El incremento de tiempo sobre los elementos discretos es función de los contactos entre ellos y los elementos finitos. Como es usual en el DEM, la integración temporal del movimiento de los elementos discretos se realiza mediante un esquema de integración explicito, por otra parte, para calcular el movimiento de los elementos finitos se utiliza un esquema implícito. Es obvio que el incremento de tiempo entre ambos esquemas es muy diferente, por lo que al inicio del tiempo ${\textstyle {t}_{I}^{n}}$ se resuelve el movimiento de los elementos discretos con incrementos de tiempo ${\textstyle \Delta {t}_{E}}$ hasta el tiempo ${\textstyle {t}_{I}^{n+1};}$ acumulando a lo largo del proceso el impulso debido a todos los contactos ocurridos. El contacto friccional entre los elementos discretos y los lados (en 2D) o las caras y las aristas (en 3D) de los elementos se trata con técnicas usuales del método de elementos discretos [7,8].

Figura 5. Descripción esquemática de la técnica FEM DEM

Al llegar al tiempo ${\textstyle {t}_{I}^{n+1}}$, los impulsos son transformados a fuerzas en dicho tiempo para así resolver el esquema implícito con el incremento ${\textstyle \Delta {t}_{I}}$ para encontrar los nuevos desplazamientos de la malla FEM en ${\textstyle {t}_{I}^{n+1}}$.

De esta forma, los desplazamientos del DEM se encuentran definidos por la solución del esquema implícito y los desplazamientos del FEM por el esquema explícito. Una consideración importante es que el paso de tiempo explicito no puede ser muy grande pues puede provocar inconsistencias entre los desplazamientos de los elementos discretos respecto a los elementos finitos.

La formulación FEM-DEM utilizada en este trabajo ha sido ampliamente verificada en diversas aplicaciones del estudio de la rotura de estructuras de hormigón y mampostería [1–5,19-21], así como en problemas de interacción fluido-estructura [20,21], demostrando en todos los casos su robustez, versatilidad y exactitud.

3. Modelización del acero de refuerzo

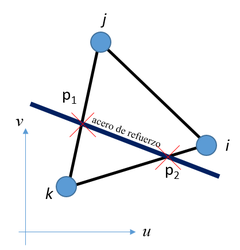
Con la finalidad de poder incluir la rigidez aportada por la armadura de acero en la formulación utilizada, se evalúa la intersección de las varillas de acero sobre los elementos asumiendo una adherencia perfecta entre ambos materiales, tal como se muestra en la Figura 6. De esta forma es posible conocer la rigidez aportada por los elementos de acero en función de los desplazamientos de los nodos del elemento de acuerdo con la ecuación (1)

${\textstyle {\boldsymbol {K}}_{}^{({e}_{1\rightarrow 2})}={\boldsymbol {N}}_{\left({p}_{1x}\,,{p}_{1y}\right)}^{T}\left({\frac {EA}{{l}_{1\rightarrow 2}}}\right)\left[{\begin{matrix}1&-1\\1&1\end{matrix}}\right]{\boldsymbol {N}}_{\left({p}_{1x}\,,{p}_{1y}\right)}}$

(1)

donde ${\textstyle E}$ es el módulo de elasticidad del acero de refuerzo, ${\textstyle A}$ el área de la sección transversal y ${\textstyle {l}_{1\rightarrow 2}}$ la distancia entre el punto ${\textstyle {p}_{1}\,}$ y ${\textstyle {p}_{2}.\,}$ En dicha ecuación es posible modelar una adherencia no perfecta del acero minorando el módulo de elasticidad en función de los esfuerzos en el refuerzo; sin embargo, en este estudio se considera la adherencia perfecta dado que aparentemente no ocurre deslizamiento del acero en el caso de estudio.

Figura 6. Descripción esquemática de la técnica FEM DEM

Los desplazamientos ${\textstyle {\left(u,v\right)p}_{1}}$ y ${\textstyle {\left(u,v\right)}_{p2}}$ se obtienen en función de los desplazamientos de los vértices del elemento evaluando las correspondientes funciones de forma en los puntos de intersección ${\textstyle \,{p}_{1}\,}$ y ${\textstyle \,{p}_{2}}$:

${\textstyle {\boldsymbol {u}}_{{p}_{1},{p}_{2}\,}={{\boldsymbol {\,N}}\left({p}_{1x}\,,{p}_{1y}\right)}_{\,}{\boldsymbol {u}}^{(e)}}$

(2)

donde:

${\textstyle {\boldsymbol {u}}_{{p}_{1},{p}_{2}}^{\,}=\,{\left[{\begin{matrix}{\begin{matrix}{u}_{1}&{v}_{1}\end{matrix}}&{\begin{matrix}{u}_{2}&{v}_{2}\end{matrix}}\end{matrix}}\right]}^{T}}$

(3)

${\textstyle \,{\boldsymbol {N}}_{\left({p}_{1x}\,,{p}_{1y}\right)}=}$$\left[{\begin{matrix}{\begin{matrix}{N}_{i}\left({p}_{1x}\,,{p}_{1y}\right)\\0\\{N}_{i}\left({p}_{2x}\,,{p}_{2y}\right)\\0\end{matrix}}&{\begin{matrix}0\\{N}_{i}\left({p}_{1x}\,,{p}_{1y}\right)\\0\\{N}_{i}\left({p}_{2x}\,,{p}_{2y}\right)\end{matrix}}&{\begin{matrix}{N}_{j}\left({p}_{1x}\,,{p}_{1y}\right)\\0\\{N}_{j}\left({p}_{2x}\,,{p}_{2y}\right)\\0\end{matrix}}\end{matrix}}\,\,{\begin{matrix}{\begin{matrix}0\\{N}_{j}\left({p}_{1x}\,,{p}_{1y}\right)\\0\\{N}_{j}\left({p}_{2x}\,,{p}_{2y}\right)\end{matrix}}&{\begin{matrix}{N}_{k}\left({p}_{1x}\,,{p}_{1y}\right)\\0\\{N}_{k}\left({p}_{2x}\,,{p}_{2y}\right)\\0\end{matrix}}&{\begin{matrix}0\\{N}_{k}\left({p}_{1x}\,,{p}_{1y}\right)\\0\\{N}_{k}\left({p}_{2x}\,,{p}_{2y}\right)\end{matrix}}\end{matrix}}\right]$

(4)

${\textstyle {\boldsymbol {u}}^{(e)}=\,{\left[{\begin{matrix}{\begin{matrix}{u}_{i}&{v}_{i}\end{matrix}}&{\begin{matrix}{u}_{j}&{v}_{j}\end{matrix}}&{\begin{matrix}{u}_{k}&{v}_{k}\end{matrix}}\end{matrix}}\right]}^{T}}$

(5)

Finalmente, la rigidez del elemento se evalúa como la suma de ambas rigideces:

${\textstyle {\tilde {\boldsymbol {K}}}_{\,}^{(e)}={\boldsymbol {K}}_{\,}^{(e)}+}$${\boldsymbol {K}}_{\,}^{({e}_{1\rightarrow 2})}$

(6)

La extensión de esta formulación al caso tridimensional resulta trivial. La sencillez y el buen comportamiento de este modelo de hormigón armado queda patente en [4,5].

4. Estrategia de análisis del puente

El estudio se divide en dos partes: un primer análisis pseudo-estático con las cargas de diseño actuales y seguidamente un análisis dinámico considerando el paso de un boge sobre el puente a distintas velocidades. Dado que la estructura se encuentra formada por dos puentes similares, solo se analiza uno de ellos.

El análisis pseudo-estático se realiza considerando la simetría longitudinal del puente, tomando en cuenta las cargas muertas debidas a la estructura, el balasto, las traviesas y las vías. Las cargas vivas corresponden al tren de cargas Cooper E80 [11]. Dicho tren de cargas es aplicado de forma gradual en el tiempo observando la respuesta en desplazamiento del centro del vano, hasta llegar al equilibrio.

Con la finalidad de conocer la posición más desfavorable del tren de cargas, se considera un pequeño modelo de viga simplemente apoyada mediante elementos finitos de Euler-Bernoulli por donde se hace avanzar el tren de cargas y en cada paso se determina el momento máximo en la viga, el cual no necesariamente se encuentra a la mitad del vano, debido a que la distribución del tren de cargas no suele ser simétrico respecto al punto medio de la luz de la viga. Una vez definida la posición más desfavorable del tren de cargas, se realiza un análisis estático con un modelo 3D, considerando el refuerzo de acero, para así determinar la capacidad resistente de la estructura. Adicionalmente, se evalúan las frecuencias fundamentales del puente mediante el uso de la transformada de Fourier, aplicada al desplazamiento del centro del vano, ante este tipo de carga.

El segundo análisis corresponde a la respuesta dinámica del puente frente al paso de un boge de dos ejes característico del tipo de vagón empleado sobre el puente, el cual se hace circular a distintas velocidades, en el modelo 3D. El objetivo es conocer las frecuencias del puente en cada caso y determinar el daño estructural.

En todos los casos, se utilizó la misma discretización de elementos finitos, de manera que la aproximación de la malla no sea fuente de errores al comparar los resultados.

5. Geometría y materiales

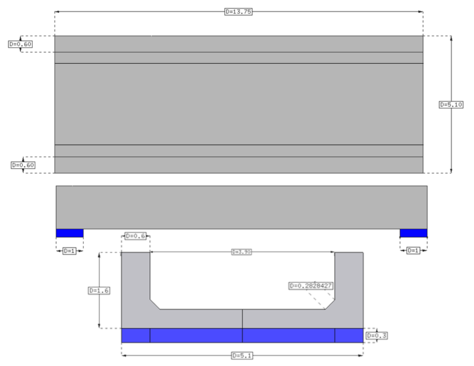
La definición geométrica de la estructura proviene de un levantamiento realizado in situ, debido a la inexistencia de planos constructivos. La Figura 7 muestra las dimensiones en metros, del puente, así como los apoyos de neopreno (azul).

Figura 7. Definición geométrica de la estructura (en metros)

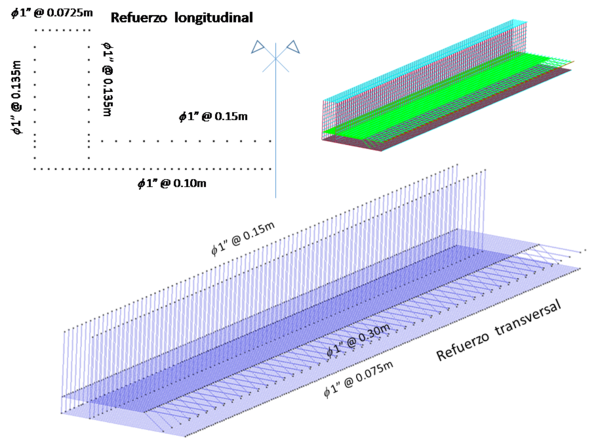
Para definir el armado de la estructura se han considerado las observaciones hechas en la zona del descascarillado, así como algunas pequeñas catas y pruebas de reconocimiento magnético para determinar el espaciamiento y tipo de refuerzo. Sin embargo, el armado presenta una gran incertidumbre, por lo que se ha considerado lo que sería lo más cercano al tipo de obra y características constructivas de la época. Los planos de armado se muestran en la Figura 8.

Figura 8. Planos de armado del acero de refuerzo. Diámetros en pulgadas

En cuanto a los materiales utilizados, el hormigón ha sido caracterizado mediante un análisis por esclerómetro, de acuerdo a la Norma Oficial Mexicana NMX-C 192- ONNCCE-2018 [12], para conocer la resistencia a compresión máxima. La resistencia media ha sido de 470 Kg/cm$^{2}$. Cabe añadir que el muestreo se ha realizado en zonas donde el hormigón no presenta daño o agrietamiento. Sin embargo, pruebas de compresión realizadas sobre corazones de hormigón extraídas reportan una resistencia a compresión de 350 Kg/cm$^{2}$ [13], de manera que se supondrá para este estudio el valor de 350 Kg/cm$^{2}$.

Respecto al acero y el neopreno utilizado, se consideran las propiedades estándares de estos materiales. En la Tabla 1 se resumen las propiedades mecánicas de los materiales del puente.

Tabla 1. Propiedades mecánicas de los materiales utilizados

		Hormigón F’c 350	Neopreno	Acero de refuerzo
Módulo de Elasticidad	N/m2	31.971e09	7.00e06	210.00e09
Coeficiente de Poisson		0.20	0.20	0.20
Peso específico	N/m3	25 000.00	9 200.00	25 120.00
Límite elástico a tracción	N/m2	3.43e6	900.00e9	411.00e06
Limite elástico a compresión	N/m2	34.32e6	900.00e9	411.00e06
Energía de fractura a tracción	J/m2	100.00	75 000.00	300.00
Energía de fractura a compresión	J/m2	10 000.00	75 000.00	300.00

5.1 Análisis estático

Como se ha comentado, en primer lugar, se realizó un análisis estático lineal del puente con las consideraciones de los materiales que lo conforman. Para ello se ha considerado el uso del tren de cargas Cooper E80 [11], recomendado por las especificaciones técnicas para la construcción y ampliación de vías particulares del manual de mantenimiento y recursos operativos de FERROMEX y amplificado por un coeficiente de impacto [17].

Cabe hacer notar que este tren de cargas se considera relativamente reciente, ya que ha sido recomendado a partir de mediados de los años 1990 [18], debido al incremento del peso y capacidad de los trenes modernos, por lo que es muy probable que el puente haya sido diseñado considerando el tren de cargas Cooper E60 propuesto en 1914 [18]. Esto sugiere que actualmente el puente haya sobrepasado su capacidad resistente, como lo demuestran los daños apreciados y estudios similares [16].

5.1.1 Cargas estáticas (CE)

Las cargas estáticas son el peso propio y las cargas repartidas sobre el tablero del puente y se resumen en las Tablas 2 y 3.

Tabla 2. Cargas de peso propio (N/m$^{3}$)

Cargas volumétricas	Observaciones	Carga por unidad de volumen (N/m$^{3}$)
Hormigón armado		25 000.00

Tabla 3. Cargas estáticas sobre el tablero (N/m$^{2}$)

Cargas sobre el tablero	Observaciones	Carga por unidad de área (N/m2)
Balasto	El peso específico del balasto se considera de 2 700 Kg/m$^{3}$ Se considera una cama de 0.4 m	1 080.00
Railes	El peso por rail considerado es de 490 N/m	251.00
Traviesas	El peso por traviesa se considera de 300 Kg Con una distancia entre traviesas de 0.60 m	1 260.00

5.1.2 Cargas dinámicas (CD)

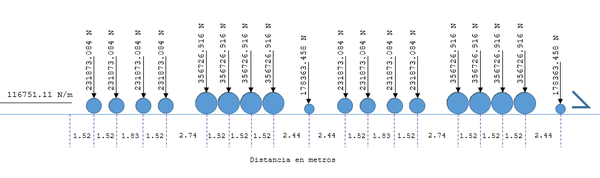
El tren de cargas Cooper E80 [11,17] considerado se muestra en sistema internacional en la Figura 9. Dicho tren se amplifica por un factor de impacto [17] de acuerdo con la siguiente expresión:

${\textstyle \Phi =1+{\frac {\,CD}{CE+CD}}<1.60}$

(7)

Donde ${\textstyle L}$ es la longitud del puente, CE la carga estática, CD la carga dinámica y ${\textstyle \Phi \,}$ el factor de impacto que en este caso es de 1.40

Figura 9. Tren de carga Cooper E 80. Unidades en metros y Newtons

Con objeto de evitar errores en la consideración simultanea de las envolventes de cargas asociadas al tren de cargas descrito, se ha realizado un análisis elástico lineal mediante elementos finitos, utilizando elementos de viga de Euler-Bernoulli mediante el código MAT-FEM [14,15]. El análisis toma en cuenta las cargas estáticas y el tren de carga (aumentado por el coeficiente de impacto) avanzando sobre el puente en intervalos de 0.001 m. El puente se ha discretizado en 1375 elementos de 0.01 m de longitud, considerando una luz de 13.75 m una sección transversal de 2.87 m$^{2}$ y una inercia de 0.742876 m$^{4}$. El material se caracteriza con un módulo de elasticidad de 30.68E9 Pa, y un peso específico equivalente a las cargas de peso propio y cargas sobre el tablero de 3169.5 N/m$^{3}$.

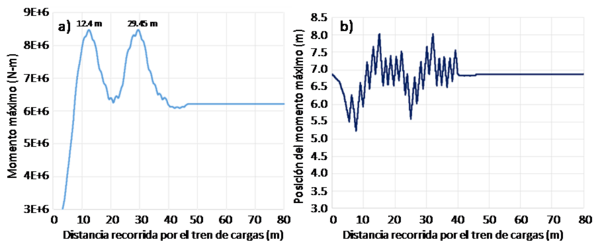
La Figura 10 (a) muestra el valor del momento máximo generado sobre la viga en función del avance del tren de cargas, mientras que la Figura 10 (b) corresponde a la posición del momento máximo sobre el puente. En la Figura 10 (a) se puede observar que existen dos posiciones del tren de carga en donde el momento es máximo. El primero corresponde a un avance del tren de 12.4 m y el segundo a un avance de 29.45 m. El momento generado en ambos casos es idéntico e igual a 7 729 355.20 Nm. Esto es debido a la periodicidad del tren de carga. En ambas figuras se puede observar como la carga uniformeme repartida asociada al tren de cargas se mantiene constante sobre el puente después de que el tren de cargas avance 46.93 m.

Figura 10. Variación del momento máximo (a) y su posición en la viga (b) conforme el tren de cargas avanza sobre el puente

5.1.3 Análisis en 3D mediante la técnica FEM-DEM

Conocida la posición más desfavorable del tren de cargas sobre el puente, se realiza un análisis en 3D mediante el código FEM-DEM [13,14]. La Figura 11 muestra la posición más desfavorable del tren de cargas y su valor. Se ha considerado que las cargas puntuales del tren se distribuyen de forma homogénea sobre el área de acción de las traviesas y de estas al tablero del puente. A efectos de reducir el tiempo de cálculo se ha analizado la mitad del puente aprovechando su simetría longitudinal. La malla utilizada tiene 316758 nodos, 110853 elementos lineales que conforman el armado y 498628 tetraedros con un tamaño medio de 0.08 m de arista. El puente se encuentra asentado sobre dos elementos de neopreno, como se muestra en la Figura 7.

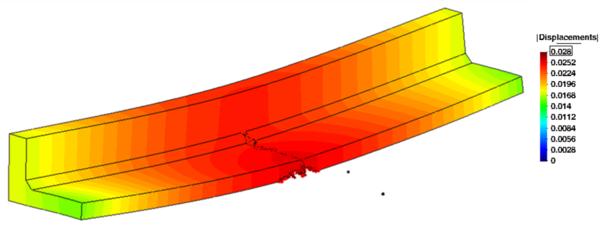
Los resultados obtenidos se muestran en las Figuras 12, 13 y 14. La Figura 12 muestra las iso-áreas de desplazamiento en donde el desplazamiento máximo se localiza al centro del vano con un valor de 2.8 mm.

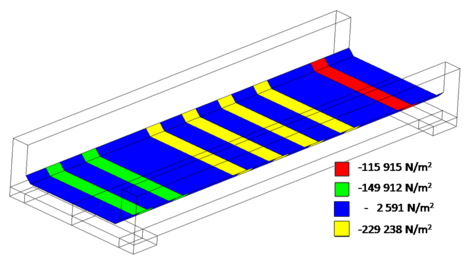
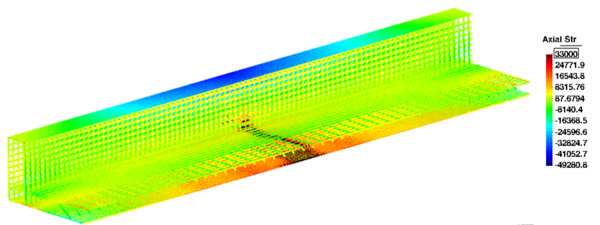
La Figura 13 muestra los esfuerzos axiles en el emparrillado de acero. Se puede observar que en ningún caso se alcanza el limite elástico del acero por lo que se considera en este sentido que el acero no expuesto se encuentra en buen estado. Se observa que los esfuerzos se encuentran por debajo de los 170 MPa, de manera que no existe riesgo de fatiga.

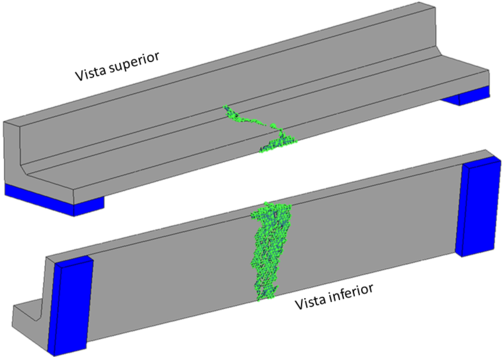
La Figura 14 muestra una fractura en la mitad longitudinal del tablero, tanto en su parte superior como inferior y en donde los elementos dañados son reemplazados por elementos discretos. Es interesante observar que este resultado coincide con lo observado in situ, como se muestra en las Figuras 2 y 3 (a). Sin embargo, no se generan el resto de grietas observadas. Por lo que su origen debe ser de carácter dinámico.

Finalmente, con la finalidad de confirmar el tipo de material y la distribución del acero, se ha realizado el mismo análisis considerando un tren de cargas Cooper E60, el cual es 0.75 veces el tren de cargas E80, verificando que no existe daño en la estructura, por tanto, se puede afirmar que la estructura fue diseñada, en su momento, de manera correcta.

Figura 11. Distribución más desfavorable del tren de cargas sobre el tablero del puente

Figura 12. Deformada (x50) y distribución de las iso-áreas de desplazamiento (m)

Figura 13. Distribución de los esfuerzos axiles (Pa) en el refuerzo de acero

Figura 14. Agrietamiento en el tablero

5.1.4 Análisis de frecuencias

Con la finalidad de conocer la frecuencia de vibración libre de la estructura, se ha realizado un análisis dinámico, considerando solo el peso propio de la estructura como única excitación dinámica. En la Figura 15 (a) se muestra el registro del desplazamiento vertical del punto central del tablero del puente durante los primeros 6 segundos, en los cuales se observa la oscilación alrededor del desplazamiento de dicho punto en equilibrio.

Para conocer la frecuencia de oscilación se ha llevado a cabo un análisis de frecuencias mediante la transformada de Fourier discreta. Los resultados se muestran en la Figura 15 (b) en donde claramente se observa que la frecuencia de vibración es muy cercana a los 2.14 Hz.

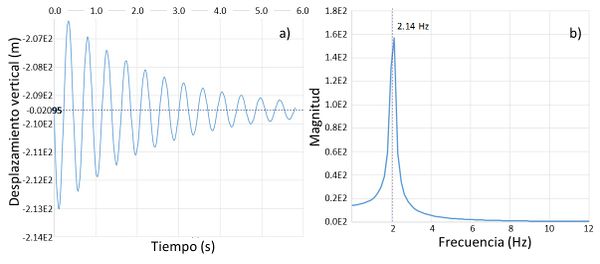
Figura 15. (a) Registro del desplazamiento vertical del punto central del tablero bajo excitación dinámica. (b) Análisis de las frecuencias de vibración

5.2 Análisis dinámico

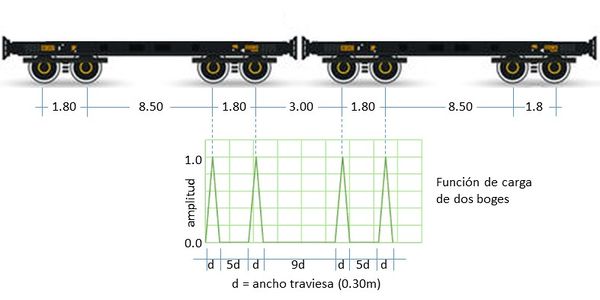
Debido al anacronismo de las cargas definidas por el estándar E80, y con el objeto de conocer mejor el comportamiento dinámico del PIF, se simula el paso de un convoy de vagones a distintas velocidades. La Figura 16 muestra dos vagones de carga y la separación de los ejes de rodamiento entre ellos. A efectos del análisis se consideran dos boges consecutivos, en los cuales el peso de cada eje se reparte de forma homogénea sobre el área de influencia de cada traviesa, de acuerdo con la función de carga representada en la misma figura.

Figura 16. Función de carga de dos boges consecutivos

De acuerdo con el tipo de vagón mayormente utilizado en la región, se considera una carga máxima de cada vagón corresponde a 1272191.38 N que incluye tanto el peso de vagón como su capacidad máxima. Dicha carga se considera soportada por cuatro ejes y es aumentada por un coeficiente dinámico de 1.40 a fin de considerar el movimiento de la carga sobre los amortiguadores de cada boge, obteniendo una presión de 190000 N/m$^{2}$. Esta presión es multiplicada por la amplitud de la función de carga a fin de determinar en cada instante de tiempo la presión ejercida en el tablero.

La velocidad de paso del conjunto de boges que se analiza es de 15, 20, 30 y 40 k/m. Se muestrea el desplazamiento vertical en intervalos de 0.002 segundos con la finalidad de conocer las vibraciones del punto en el centro del claro.

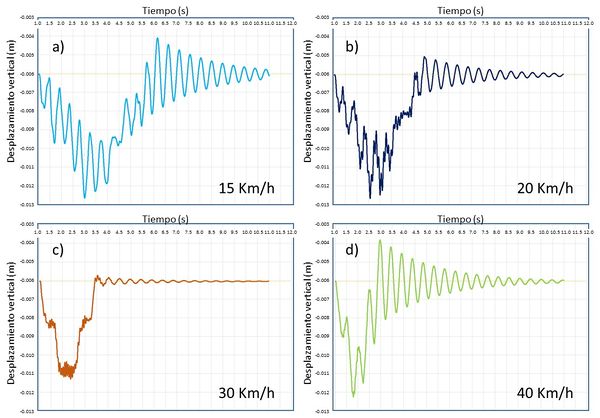
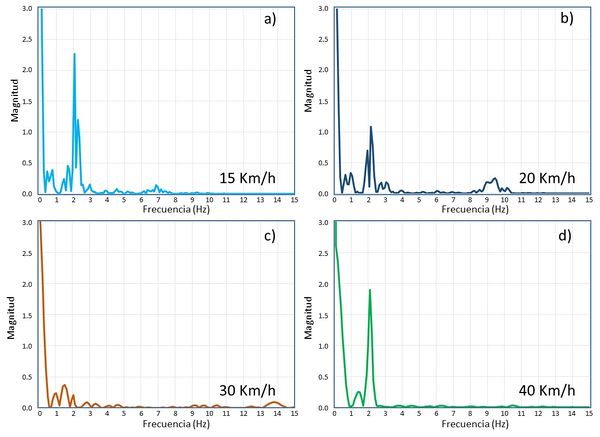
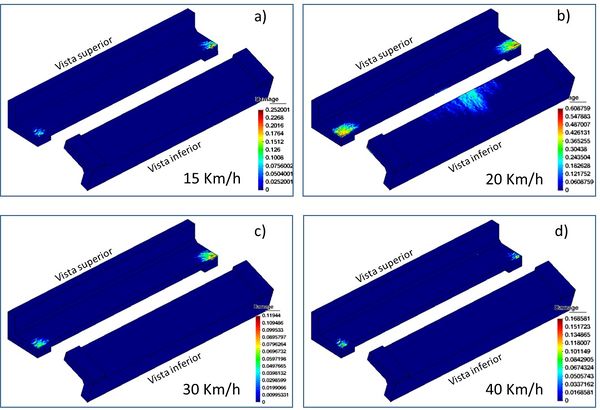
El cálculo parte del equilibrio del puente mediante un análisis cuasiestático realizado durante el primer segundo y, a partir de aquí, se estudia la vibración durante 10 segundos. La Figura 17 muestra el desplazamiento vertical del punto central del puente durante y después del paso del convoy. La Figura 18 muestra el análisis en frecuencias de dicha vibración, obtenida mediante la transformada discreta de Fourier y la Figura 19 representa el daño en la estructura.

Es interesante observar que a una velocidad de crucero de 15 Km/h la frecuencia a la que el puente vibra (2 Hz) es prácticamente la frecuencia de vibración libre de la estructura (2.14 Hz), por lo que este movimiento puede ser percibido in situ. Adicionalmente, se excitan frecuencias entre 0 y 1 Hz y entre 6 y 8 Hz pero con una energía muy inferior a la observada a 2 Hz.

A una velocidad de 20 Km/h se observa que las frecuencias excitadas están en 2Hz y en un rango de 0 a 1 Hz y de 8 y 10 Hz. Todas ellas con una energía comparable. Es interesante observar que el desplazamiento máximo encontrado es el máximo de todas las velocidades analizadas.

A 30 Km/h la excitación se concentra en frecuencias relativamente muy altas entre 9 y 14 Hz, disminuyendo considerablemente la energía en la frecuencia de 2 Hz.

Figura 17. Desplazamiento vertical del punto central del puente con distintas velocidades de circulación del convoy. (a) 15 Km/h. (b) 20 Km/h. (c) 30 Km/h. (d) 40 Km/h

Figura 18. Frecuencias de vibración del puente con distintas velocidades de circulación del convoy. (a) 15 Km/h. (b) 20 Km/h. (c) 30 Km/h. (d) 40 Km/h

Figura 19. Daño obtenido en el PIF al final del análisis numérico con distintas velocidades de circulación del convoy. (a) 15 Km/h. (b) 20 Km/h. (c) 30 Km/h. (d) 40 Km/h

Finalmente, a 40 Km/h la frecuencia excitada es cercana a la frecuencia de vibración libre del PIF, pero debido a los efectos inerciales la amplitud de vibración es más pequeña que a 15 Km/h. También se observa que la energía usada en la frecuencia de 2 Hz es inferior al caso de 15 Km/h y no presenta vibraciones importantes por arriba de dicha frecuencia.

La Figura 19 muestra el daño en el PIF al finalizar el análisis. Como se puede observar, los resultados son muy dispares. En la Figura 19 (d), con una velocidad del convoy de 40 Km/h, se observa un daño prácticamente nulo en la estructura el cual es entendible al efecto inercial de una carga aplicada rápidamente, ya que no permite que se genere una vibración importante en la estructura como se observa en la Figura 18 (d). Igualmente, las aceleraciones inducidas en el PIF permiten resistir la carga aplicada.

La Figura 19 (c) muestra un daño pequeño en las cabeceras de la plataforma del PIF. Este daño se ha apreciado in situ y obviamente no es atribuible a un efecto estático, ni mucho menos capturable con un análisis de las mismas características. El paso del convoy a 30 Km/h muestra excitaciones de frecuencias altas tal como se ha comentado. De hecho, en la figura 18 c) se observa que la energía disipada se distribuye en una amplia serie de frecuencias por lo que el daño en la estructura es relativamente pequeño.

El daño observado a 15 y 20 Km/h sugiere una correlación entre el daño y la energía de las frecuencias entre 6 y 11 Hz observadas en las Figuras 19 (a) y (b). En el primer caso (15 Km/h) se aprecia un daño pequeño en las cabeceras de la plataforma, al tiempo que las frecuencias entre 6 y 8 Hz presentan una energía baja. Más interesante es el caso de 20 Km/h que muestra un daño similar al apreciado in situ, y que, de acuerdo con la Figura 19 (b), muestra una alta excitación de las frecuencias comprendidas entre 8 y 11 Hz. En este caso, el daño en las cabeceras de la plataforma es superior al 60% lo que indica la presencia de microgrietas que permiten la filtración de agua y la oxidación del acero de refuerzo. Además, en este caso, existe también daño en la cara inferior de la plataforma de PIF, que se corresponde con las grietas encontradas en el puente.

6. Conclusiones

Es interesante remarcar que el tren de cargas Cooper fue propuesto inicialmente en 1894 [18], basado en el tipo de trenes existentes en la época y muy diferentes en configuración y peso de los actuales, por lo que no representa de forma adecuada las cargas que actualmente actúan sobre el puente, siendo exclusivamente una referencia de solicitación para diseño. Es por esto que el daño encontrado en el análisis estático no corresponde totalmente a las patologías mostradas. Por otra parte, el análisis dinámico resalta la importancia de la velocidad de circulación de un convoy. Las velocidades cercanas a los 20 Km/h han mostrado ser las más perjudiciales y el estudio sugiere que el comportamiento estructural del PIF es mejor a velocidades superiores, siendo la de 30 Km/h la que menos vibraciones y daño induce.

Actualmente el puente se encuentra en proceso de reparación mediante el uso de fibras de carbono adheridas a la parte inferior del tablero.

Agradecimientos

Los autores agradecen la colaboración desinteresada del Colegio de Ingenieros Civiles de Celaya, A.C., así como de la empresa FERROMEX (Grupo México Transportes GMxT), por sus observaciones y comentarios sobre este estudio. Igualmente, agradecen al Prof. Eugenio Oñate su apoyo y valiosas observaciones.

Referencias

[1] Zárate F., Oñate E. A simple FEM-DEM technique for fracture prediction in materials and structures. Computational Particle Mechanics, 2(3):301–314, 2015.

[2] Zárate F., Cornejo A., Oñate E. A three-dimensional FEM-DEM technique for predicting the evolution of fracture in geomaterials and concrete. Computational Particle Mechanics, 5:411–420, 2018.

DOI 10.1007/s40571-017-0178-z

[3] Zárate F., Gomez A., Oñate E. Ensayos experimentales y numéricos de rotura en piezas de hormigón. Hacia el Laboratorio Virtual. Rev. int. métodos numér. cálc. diseño ing., 35(1):1-14, 2019. URL https://www.scipedia.com/public/Zarate_et_al_2018d

[4] Zárate F., Cuellar J., Regalado A. La simplificación en ingeniería, ventajas e inconvenientes. Revista Mexicana de Métodos Numéricos, 2, 1, 2018. URL https://www.scipedia.com/public/Zarate_et_al_2018a

[5] Zárate F., Oñate E. Fractures prediction in concrete structures combining the finite and discrete element methods. Hormigón y Acero, 69(1):53-69, 2018. URL https://www.scipedia.com/public/Onate_Zarate_2019a

[6] Norma N-PRY-CAR-6-01-001/01. Instituto Mexicano del Trasporte y La Secretaría de Comunicaciones y Transportes, México 2001. URL https://normas.imt.mx/normativa/N-PRY-CAR-6-01-001-01.pdf

[7] Dictamen preliminar de verificación estructural mediante inspección visual. Informe Interno del Colegio de Ingenieros Civiles de Celaya, A.C. Celaya, Gto. México, 2021.

[8] Zienkiewicz O.C., Zhu J.Z. The superconvergent patch recovery (spr) and adaptive finite element refinement. Comput. Methods App. Mech. Engng., 101:207-224. 1992.

[9] Lopez J., Oller S., Oñate E., Lubliner J. A homogeneous constitutive model for masonry. Int. J. Numer. Meth. Engng., 46:1651-1671. 1999.

[10] E. Oñate. Desarrollos y aplicaciones de modelos de fractura en la Escuela de Ingenieros de Caminos de Barcelona. Centro Internacional de Métodos Numéricos en Ingeniería (CIMNE), PI201, 2000.

[11] Manual for Railway Engineering. American Railroad Engineering and Maintenance-of-Way Association (AREMA), USA, 2002.

[12] Industria de la Construcción - Concreto-Determinación del Número de Rebote Utilizando el Dispositivo Conocido como Esclerómetro - Método de Ensayo. Diario Oficial de la Federación, México, 2019.

[13] Examen preliminar de verificación estructural mediante inspección visual. Consultora Mexicana de Ingeniería S.A. de C.V. México, 2021.

[14] Oñate E. Structural analysis with the finite element method. Linear statics: Vol. 1: Basis and solids. Springer, Barcelona, 2009.

[15] Oñate E. Structural analysis with the finite element method. Linear statics: Vol. 2: Beams, plates and shells. Springer, Barcelona, 2013.

[16] Tobias D.H., Foutch D.A., Choros J. Loading spectra for railway bridges under current operating conditions. Journal of Bridge Engineering, 1(4):127-134, 1996.

[17] Manual for Railway Engineering. Chapter 15, AREMA, Washington D.C., 2018.

[18] Coopers Loading System, [http:// http://]en.wikipedia.org, https://en.wikipedia.org/wiki/Theodore_Cooper, 2021.

[19] Cornejo A., Mataix V., Zárate F., Oñate E. Combination of an adaptive remeshing technique with a coupled FEM–DEM approach for analysis of crack propagation problems. Computational Particle Mechanics, 7:735-752, 2020.

[20] Cornejo A., Franci A., Zárate F., Oñate E. A fully Lagrangian formulation for fluid-structure interaction problems with free-surface flows and fracturing solids. Computers & Structures, 250:106532, 2021.

[21] Oñate E., Cornejo A., Zárate F., Kashiyama K., Franci A. Combination of the finite element method and particle-based methods for predicting the failure of reinforced concrete structures under extreme waterforces. Engineering Structures, 251:113510, 2021.

[22] Oñate E., Rojek J. Combination of discrete element and finite element methods for dynamic analysis of geomechanics problems. Comput. Meth. Appl. Mech. Engrg., 193:3087–3128, 2004.

[23] Rojek J., Oñate E. Multiscale analysis using a coupled discrete/finite element method. Interaction and Multiscale Mechanics: An International Journal (IMMIJ), 1:1–31, 2007.

[24] Monteiro N., Lemos J.V. Hybrid discrete element/finite element method for fracture analysis. Computer Methods in Applied Mechanics and Engineering, 195, 4579-4593, 2006.

[25] Katagiri S., Takada S. Development of FEM-DEM combined method for fracture analysis of a continuos media. Memoirs of the Graduate School of Science and Technology, Kobe University Japan, 20A:65–79, 2003.

[26] Moharnmadi S., Owen D.R.J., Peric D. A combined finite/discrete element algorithm for delamination analysis of composites. Finite Elements in Analysis and Design, 28:321–336, 1998.

[27] Munjiza A., Owen D.R.J., Bicanic N. A combined finite-discrete element method in transient dynamics of fracturing solids. Engineering Computations, 12:145–174, 1995.

[28] Munjiza A. The combined finite-discrete element method. Wiley, 2004.

[29] Han K., Peric D., Owen D.R.J., Yu J. A combined finite/discrete element simulation of shot peening processes–Part II: 3D interaction laws. Engineering Computations, 17:680–702, 2000.

[30] Han K., Owen D.R.J., Peric D. Combined finite/discrete element and explicit/implicit simulations of peen forming process. Engineering Computations, 19:92–118, 2002.