Triangular element for two-dimensional elasticity with z stress and z strain constant and different from zero.

Elemento triangular para elasticidad bidimensional con σz y εz constantes y diferentes de cero.

Francisco Zárate ^a,b , Núria Zárate ^c

^aCentre Internacional de Mètodes Numèrics en Enginyeria (CIMNE) www.cimne.com

^bUniversitat Politècnica de Catalunya (UPC),

Gran Capitan s/n, Campus Nord, 08034 Barcelona, España.
^cUniversitat de Barcelona (UB)
Gran Via de les Corts Catalanes, 585, 08007 Barcelona, España.

zarate@cimne.upc.edu

Resumen

Este trabajo describe como obtener un elemento bidimensional de tres nodos a partir de un elemento sólido prismático de seis nodos, suponiendo que la tensión normal a las caras triangulares es constante y diferente de cero.

Se presenta también un ejemplo numérico en donde se comparan los resultados obtenidos con el elemento desarrollado y con elementos tridimensionales, poniendo de manifiesto el buen comportamiento del elemento desarrollado.

Palabras clave. Método de elementos finitos, Tensión y deformación plana, Mecánica de sólidos.

1.- Introducción

La gran utilidad de las simplificaciones de la elasticidad tridimensional en problemas de dos dimensiones queda fuera de toda duda pues la reducción en el número de variables permite resolver este tipo de problemas en un tiempo más que razonable, en comparación con el mismo problema resuelto mediante la teoría tridimensional.

Es la elasticidad plana quien estudia la solución particular del problema elástico general en el conjunto de aplicaciones técnicas donde el estado de tensión-deformación es reducible a problemas planos o bidimensionales partiendo de que el dominio de estudio sea un cuerpo prismático. Concretamente se definen dos estados de elasticidad bidimensional: Tensión plana y Deformación plana [1].

Un sólido prismático con una de sus dimensiones mayor que la otras dos es susceptible de ser simplificado en un estado de deformación plana. Para ello se descompone en rebanadas idénticas y se estudia sobre una de estas rebanadas la distribución de deformaciones como un problema bidimensional usando únicamente dos coordenadas ${\textstyle \left(x,y\right)}$ para definir la posición de cada punto sobre la rebanada. Una condición esencial es que todas las cargas aplicadas estén contenidas en el plano de cada rebanada, y dichas cargas sean las mismas para todas las rebanadas del sólido. De esta manera se genera la hipótesis que define nula la deformación normal a cada una de las rebanadas ${\textstyle \left({\epsilon }_{z}=\right.}$$\left.0\right)$ .

Por otra parte, el estado de Tensión plana se puede aplicar a un sólido prismático en el cual una de sus dimensiones es menor que las otras dos, y las cargas aplicadas se encuentran contenidas en la sección media cuya normal es paralela al lado más corto. En este caso, la tensión en dirección a dicha normal se considera nula ${\textstyle \left({\sigma }_{z}=\right.}$$\left.0\right)$ .

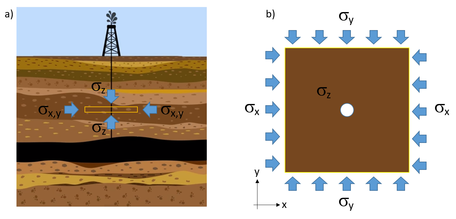
Sin embargo, estas dos hipótesis no llegan a cubrir la totalidad de los problemas que se pueden simplificar a dos dimensiones. Por ejemplo, el estudio del estado tensional del terreno de un pozo vertical a cierta profundidad como se muestra en la Figura 1, en la cual tanto la deformación como la tensión en dirección vertical son constantes pero diferentes de cero. En este caso es posible definir una rebanada normal a la dirección de perforación del pozo, pero debido a la existencia de una presión normal en la dirección de la rebanada elegida, no es posible aplicar las hipótesis de tensión plana, ni las de deformación plana.

Figura 1. Aplicación bidimensional donde ${\textstyle {\sigma }_{z}\not =0}$

En el ejemplo mostrado en la Figura 1 se puede considerar que la tensión normal es diferente de cero, pero constante en todo el dominio bidimensional.

Para poder reducir este problema a un estado bidimensional se parte de un elemento finito prismático asociado a un estado de elasticidad tridimensional en donde se aplican las hipótesis de tensión y deformación normal constantes y diferentes de cero.

2.- Formulación del elemento prismático.

2.1- Hipótesis iniciales

Como se ha comentado, la formulación del elemento parte del estado tensional tridimensional, en donde se consideran las siguientes hipótesis:

1. El dominio de análisis corresponde a una laja del dominio de espesor h.

2. La deformación ${\textstyle {\epsilon }_{z}\,}$ es constante en cualquier punto y diferente de cero.

3. La tensión ${\textstyle {\sigma }_{z}\,}$ es constante en cualquier punto y diferente de cero.

Como corolario de estas hipótesis se sigue que:

4. Los movimientos en el plano xy son constantes a lo largo de la posición z.

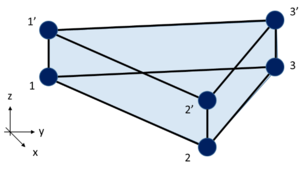
Estas hipótesis se aplican sobre un elemento prismático tridimensional de seis nodos como el mostrado en la Figura 2.

Figura 2. Elemento prismático base.

De manera que siguiendo las hipótesis 2 y 3 se puede definir el estado tensional y de deformaciones en el sólido considerado:

	${\sigma }_{x}\not =0\,;\,{\sigma }_{y}\not =0\,;\,{\sigma }_{z}=cte\,;\,{\tau }_{xy}\not =0\,\,;$
	$\,\,{\tau }_{xz}=0\,;\,{\tau }_{yz}=0\,\,$	(1)

	${\epsilon }_{x}\not =0\,;\,{\epsilon }_{y}\not =0\,;\,{\epsilon }_{z}=$$cte\,;\,{\gamma }_{xy}\not =0\,\,;$
	$\,\,{\gamma }_{xz}=0\,;\,{\gamma }_{yz}=0\,\,$	(2)

por lo que describiendo las ecuaciones (1) y (2) en forma vectorial se obtienen las ecuaciones (3) y (4) respectivamente.

$\,\,{\boldsymbol {\sigma }}^{T}=\left[{\begin{matrix}{\sigma }_{x}&{\sigma }_{y}&{\sigma }_{z}&{\tau }_{xy}\end{matrix}}\right]$

(3)

$\,{\epsilon }^{T}=\left[{\begin{matrix}{\epsilon }_{x}&{\epsilon }_{y}&{\epsilon }_{z}&{\gamma }_{xy}\end{matrix}}\right]$

(4)

Y de acuerdo con la teoría de la elasticidad tridimensional, la relación tensión deformación entre (3) y (4) se expresa por:

$\left[{\begin{matrix}{\begin{matrix}{\sigma }_{x}\\{\sigma }_{y}\\{\sigma }_{z}\end{matrix}}\\{\begin{matrix}{\tau }_{xy}\end{matrix}}\end{matrix}}\right]=$$\left[{\begin{matrix}{d}_{11}&{d}_{12}&{d}_{12}&0\\{d}_{12}&{d}_{11}&{d}_{12}&0\\{d}_{12}&{d}_{12}&{d}_{11}&0\\0&0&0&{d}_{44}\end{matrix}}\right]\left[{\begin{matrix}{\begin{matrix}{\epsilon }_{x}\\{\epsilon }_{y}\\{\epsilon }_{z}\end{matrix}}\\{\begin{matrix}{\gamma }_{xy}\end{matrix}}\end{matrix}}\right]$

(5)

siendo

${d}_{11}={\frac {E\left(1-\upsilon \right)}{\left(1+\upsilon \right)\left(1-2\upsilon \right)}}\,;\,\,{d}_{12}=$${\frac {E\upsilon }{\left(1+\upsilon \right)\left(1-2\upsilon \right)}}\quad ;\,{d}_{44}=$${\frac {E}{2\left(1+\upsilon \right)}}\,\,$

(6)

2.2- Discretización

De la hipótesis 4 es posible establecer las siguientes relaciones entre los desplazamientos nodales del elemento:

	${u}_{1}={u}_{{1}^{'}}\,;\,{v}_{1}={v}_{{1}^{'}}\,\,;$
	${u}_{2}={u}_{{2}^{'}}\,;\,{v}_{2}={v}_{{2}^{'}}\,;$
	${\textstyle {u}_{3}={u}_{{3}^{'}}\,;\,{v}_{3}={v}_{{3}^{'}}}$ ;	(7)
	${\textstyle {w}_{1}={w}_{2}={w}_{3}}$ ;
	${w}_{{1}^{'}}={w}_{{2}^{'}}={w}_{{3}^{'}}\,$

Ahora bien, se propone usar un campo bilineal ( ${\textstyle \varnothing =}$$a+bx+cy$) en el plano ${\textstyle x,\,y\,}$ para definir el movimiento de los puntos en dicho plano y, como se ha mencionado, dicho plano es constante a lo largo del eje ${\textstyle \,z}$; por lo que a largo de dicho eje se define un campo lineal e independiente del anterior ( ${\textstyle \varnothing =}$$d+ez$). Siendo las funciones de forma que describen el campo bilineal las mostradas en las ecuaciones (8) y las descritas para el eje z las presentadas en las ecuaciones (9).

	${N}_{1}={\frac {1}{2A}}\left({a}_{1}+{b}_{1}x+{c}_{1}y\right)$
	${N}_{2}={\frac {1}{2A}}\left({a}_{2}+{b}_{2}x+{c}_{2}y\right)$	(8)
	${N}_{3}={\frac {1}{2A}}\left({a}_{3}+{b}_{3}x+{c}_{3}y\right)$
	${\textstyle {N}_{A}={\frac {1}{h}}\left(h-z\right)}$  ; ${\textstyle {N}_{B}=}$${\frac {1}{h}}\left(z\right)$	(9)

Donde ${\textstyle A}$ es el área de la base del elemento prismático de la Figura 2 y ${\textstyle h\,}$ su altura. Las variables ${\textstyle {a}_{i},\,{b}_{i}}$ y ${\textstyle {c}_{i\,}}$vienen dadas por las expresiones siguientes, donde los índices ${\textstyle i,\,j,\,k}$ son cíclicos.

	${a}_{i}={x}_{j}{y}_{k}-{x}_{k}{y}_{j}\,$
	${b}_{i}={y}_{j}-{y}_{k}$	(10)
	${c}_{i}={x}_{k}-{x}_{j}\,\,;\,\,i,j,k=1,2,3$

Si bien, podría bastar un campo constante a lo largo del eje z en lugar de uno lineal como se propone, se ha optado por utilizar un campo lineal a fin de mantener lo más homogénea la descripción de las variables nodales.

Las deformaciones definidas en la ecuación (4) quedarán definidas como:

	${\epsilon }_{x}=\,{\frac {\partial {N}_{1}}{\partial x}}{u}_{1}+{\frac {\partial {N}_{2}}{\partial x}}{u}_{2}+$${\frac {\partial {N}_{3}}{\partial x}}{u}_{3}\,\,;\,{\epsilon }_{y}=\,{\frac {\partial {N}_{1}}{\partial y}}{v}_{1}+$${\frac {\partial {N}_{2}}{\partial y}}{v}_{2}+{\frac {\partial {N}_{3}}{\partial y}}{v}_{3}$
	${\epsilon }_{z}=\,{\frac {\partial {N}_{A}}{\partial z}}{w}_{1}+{\frac {\partial {N}_{B}}{\partial z}}{w}_{{1}^{'}}$	(11)
	${\gamma }_{xy}=\,{\frac {\partial {N}_{1}}{\partial x}}{v}_{1}+{\frac {\partial {N}_{2}}{\partial x}}{v}_{2}+$${\frac {\partial {N}_{3}}{\partial x}}{v}_{3}+{\frac {\partial {N}_{1}}{\partial y}}{u}_{1}+$${\frac {\partial {N}_{2}}{\partial y}}{u}_{2}+{\frac {\partial {N}_{3}}{\partial y}}{u}_{3}$

Y la descripción del vector de desplazamientos viene dada por:

${\boldsymbol {a}}^{T}=\left[{\begin{matrix}{u}_{1}&{v}_{1}&{u}_{2}&{v}_{2}&{u}_{3}&{v}_{3}&{w}_{1}&{w}_{{1}^{'}}\end{matrix}}\right]$

(12)

Por lo que, haciendo uso de las funciones de forma descritas, la matriz B de deformaciones queda definida como:

${\boldsymbol {B}}=\left[{\begin{matrix}{\frac {{b}_{1}}{2A}}&0&{\frac {{b}_{2}}{2A}}&0&{\frac {{b}_{3}}{2A}}&0&0&0\\0&{\frac {{c}_{1}}{2A}}&0&{\frac {{c}_{2}}{2A}}&0&{\frac {{c}_{3}}{2A}}&0&0\\0&0&0&0&0&0&-{\frac {1}{h}}&{\frac {1}{h}}\\{\frac {{c}_{1}}{2A}}&{\frac {{b}_{1}}{2A}}&{\frac {{c}_{2}}{2A}}&{\frac {{b}_{2}}{2A}}&{\frac {{c}_{3}}{2A}}&{\frac {{b}_{3}}{2A}}&0&0\end{matrix}}\right]$

(13)

De aquí es muy sencillo obtener la matriz de rigidez del elemento aplicando el principio de los trabajos virtuales:

${\boldsymbol {K}}^{(e)}=\int _{{A}^{(e)}}^{}{\boldsymbol {B}}^{T}{\boldsymbol {DB}}hd{A}^{(e)}$

(14)

2.3- Simplificación de variables

La matriz de rigidez mostrada en la ecuación (14) es de ${\textstyle 8\times 8}$ y responde a las variables nodales definidas en la ecuación (12) por lo que es necesario eliminar las variables ${\textstyle {w}_{1}}$ y ${\textstyle {w}_{{1}^{'}}.}$

De la relación tensión deformación para la elasticidad 3D, mostrada en la ecuación (5) y dado que se considera que ${\textstyle {\sigma }_{z}=}$$cte$ en todo el dominio, se puede escribir:

${\sigma }_{z}=\,{d}_{12}\,{\epsilon }_{x}+\,{d}_{12}\,{\epsilon }_{y}+\,{d}_{11}\,{\epsilon }_{z}$

(15)

de donde se desprende que:

${\epsilon }_{z}=\,{\frac {1}{{d}_{11}}}\left({{\sigma }_{z}-d}_{12}\,{\epsilon }_{x}-\right.$$\left.\,{d}_{12}\,{\epsilon }_{y}\,\right)$

(16)

y por lo tanto, la elongación del segmento ${\textstyle {\overline {{\,w}_{1}\,{w}_{{1}^{'}}}}{=d}_{z}}$que se define como

${d}_{z}=h{\epsilon }_{z}=\,{\frac {h}{{d}_{11}}}\left({{\sigma }_{z}-d}_{12}\,{\epsilon }_{x}-\right.$$\left.\,{d}_{12}\,{\epsilon }_{y}\,\right)$

(17)

Por lo que si el desplazamiento ${\textstyle {w}_{1}=0}$ entonces

${w}_{{1}^{'}}={\frac {h}{{d}_{11}}}\left({{\sigma }_{z}-d}_{12}\,{\epsilon }_{x}-\right.$$\left.\,{d}_{12}\,{\epsilon }_{y}\,\right)$

(18)

Obsérvese ahora que las dos variables asociadas al espesor del elemento han sido eliminadas pues ${\textstyle {w}_{1}=}$$0$ y ${\textstyle {w}_{{1}^{'}}}$ es ahora función de ${\textstyle {\epsilon }_{x},\,{\epsilon }_{y}\,}$ y ${\textstyle {\sigma }_{z}}$ por lo que se define un nuevo vector de variables nodales ${\textstyle {\boldsymbol {a}}_{1}}$ como:

${\boldsymbol {a}}_{1}^{T}=\left[{\begin{matrix}{u}_{1}&{v}_{1}&{u}_{2}&{v}_{2}&{u}_{3}&{v}_{3}&{\sigma }_{z}\end{matrix}}\right]$

(19)

De manera que la relación entre ${\textstyle {\boldsymbol {a}}_{1}}$ y ${\textstyle {\boldsymbol {a}}}$ queda definida por:

${\boldsymbol {a}}={\boldsymbol {V}}{\boldsymbol {a}}_{\mathit {\boldsymbol {1}}}$

(20)

en donde

${\boldsymbol {V}}=\left[{\begin{matrix}1&0&0&0&0&0&0\\0&1&0&0&0&0&0\\0&0&1&0&0&0&0\\0&0&0&1&0&0&0\\0&0&0&0&1&0&0\\0&0&0&0&0&1&0\\0&0&0&0&0&0&0\\{\frac {-{d}_{12}{b}_{1}h}{{2Ad}_{11}}}&{\frac {-{d}_{12}{c}_{1}h}{2A{d}_{11}}}&{\frac {-{d}_{12}{b}_{2}h}{2A{d}_{11}}}&{\frac {-{d}_{12}{c}_{2}h}{{2Ad}_{11}}}&{\frac {-{d}_{12}{b}_{3}h}{2A{d}_{11}}}&{\frac {-{d}_{12}{c}_{2}h}{2A{d}_{11}}}&{\frac {h}{{d}_{11}}}\end{matrix}}\right]$

(21)

Al utilizar la definición de ${\textstyle {\boldsymbol {a}}_{1}}$como variables nodales elementales en la ecuación de equilibrio se tiene:

${\boldsymbol {K}}_{\mathit {\boldsymbol {v}}}^{\mathit {\boldsymbol {(e)}}}{\boldsymbol {a}}_{\mathit {\boldsymbol {1}}}^{\mathit {\boldsymbol {(e)}}}=$${\boldsymbol {f}}^{\mathit {\boldsymbol {(e)}}}$

(22)

en donde

${\boldsymbol {K}}_{\mathit {\boldsymbol {v}}}^{\mathit {\boldsymbol {(e)}}}={\boldsymbol {K}}_{}^{\mathit {\boldsymbol {(e)}}}{\boldsymbol {V}}^{\mathit {\boldsymbol {(e)}}}$

(23)

La matriz de rigidez ${\textstyle {\boldsymbol {K}}_{\mathit {\boldsymbol {v}}}^{({\mathit {\boldsymbol {e}}})}}$ que se obtiene es de ${\textstyle 8\times 7}$. Sin embargo, la séptima ecuación del sistema mostrado en (22) puede ser eliminar directamente ya que resulta ser una ecuación linealmente dependiente de las demás y está asociada al desplazamiento ${\textstyle {w}_{1}\,}$ cuyo valor es conocido e igual a 0, quedando un sistema de ${\textstyle 7\times 7}$.

Finalmente, dado que ${\textstyle \,{\sigma }_{z}}$ no es una incógnita sino un valor conocido y constante en todo el domino, es posible eliminar la ecuación asociada, actualizando el vector ${\textstyle {\boldsymbol {f}}^{({\mathit {\boldsymbol {e}}})}}$ con el producto de ${\textstyle {\,K}_{i,7\,}\ast \,{\sigma }_{z}}$ obteniendo una matriz de 6 x 6 dependiente exclusivamente de los desplazamientos en el plano ${\textstyle x,\,y\,\,}$ del dominio por analizar.

El ensamblaje y solución del problema se sigue de la manera estándar a cualquier problema bidimensional, como se muestra en el siguiente apartado.

Esta formulación se ha implementado en el código FEM2DEM desarrollado en CIMNE y siguiendo la formulación propuesta en [2-4].

3.- Ejemplos.

En este apartado se muestran dos ejemplos, el primero corresponde a la verificación de los desplazamientos en un dominio rectangular debido a la existencia de un esfuerzo ${\textstyle {\sigma }_{z}}$. Los resultados se comparan con los obtenidos mediante un programa de solidos tridimensionales a fin de verificar que los resultados obtenidos sean iguales.

El segundo ejemplo corresponde a una sección de un pozo de perforación en donde además de considerar la profundidad se evalúa el efecto de la presión interna del ducto de perforación.

3.1- Ejemplo de validación.

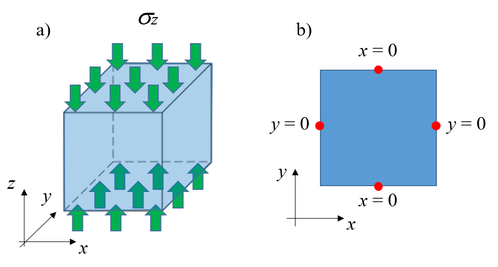
Este ejemplo corresponde a un cubo de dimensiones ${\textstyle 1.2\times 1.2\times 1.2\,m.}$ el cual está sujeto a una presión axial de ${\textstyle 1\times {10}^{7\,}\,N/{m}^{2}}$ en compresión y donde las propiedades del material son: ${\textstyle E=}$$2.1\times {10}^{11}\,N/{m}^{2}$, ${\textstyle \nu =0.20\,}$ . En la Figura 3 se muestran las condiciones de carga (Fig. 3 a) y de apoyo (Fig. 3 b) el cual restringe, sobre ambas superficies de carga, el movimiento del punto medio de las aristas en dirección normal. Por otra parte, no es necesario restringir el desplazamiento vertical dado que las cargas de compresión son auto equilibradas. Se ha procurado que ambas mallas tengan una cierta similitud en cuanto al tamaño del elemento para evitar diferencias inducidas por la calidad de la malla.

Figura 3. Ejemplo de validación. a) aplicación de cargas. b) restricción de movimientos.

En la Figura 4 se muestran los resultados del análisis tridimensional los cuales son usados de referencia. Se observa que tanto el desplazamiento en ${\textstyle x\,}$ como en ${\textstyle \,y\,\,}$ son idénticos y con valores totalmente simétricos. Siendo el desplazamiento máximo de ${\textstyle 1.1406\times {10}^{-5}\,m}$.

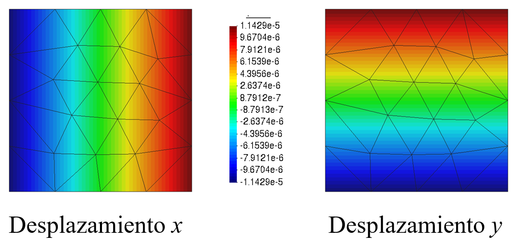
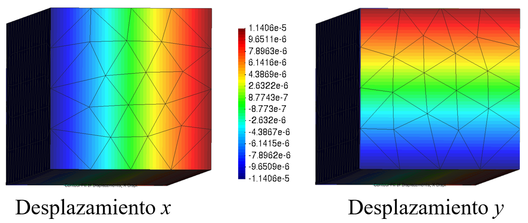
La Figura 5 muestra los resultados de los mismos desplazamientos sobre un dominio bidimensional utilizando la formulación propuesta. En este caso, también los desplazamientos en ${\textstyle x}$ e ${\textstyle y}$ son idénticos y simétricos con un valor máximo de ${\textstyle 1.1429\times {10}^{-5}\,m}$.

Comparando ambos análisis se puede concluir que la formulacion presentada es congruente y correcta ya que el error entre ambas formulaciones es prácticamente nulo ( ${\textstyle 0.20\%}$ ).

Figura 4. Ejemplo de validación. Resultados 3D sobre la superficie de carga de los desplazamientos ${\textstyle x}$ e ${\textstyle y}$.

Figura 5. Ejemplo de validación. Resultados 2D de los desplazamientos ${\textstyle x}$ e ${\textstyle y}$

3.2- Análisis triaxial.

En este ejemplo se reproduce un estado triaxial sobre un cilindro horadado y de material homogéneo por el cual circula un fluido a una presión similar a la exterior. Axialmente el cilindro se encuentra comprimido a ${\textstyle 1.0\times {10}^{7}\,Pa}$ mientras que se aplica una presión sobre la superficie exterior del cilindro de ${\textstyle 5.0\times {10}^{6}\,Pa}$ al tiempo que la presión interna es de ${\textstyle 1.0\times {10}^{7}\,Pa}$. Este ejemplo reproduce una sección de un pozo sin camisa por donde se inyecta un fluido a presión. El análisis clásico es tridimensional, sin embargo, aplicando la formulación presentada es posible atacar el problema mediante un análisis 2D.

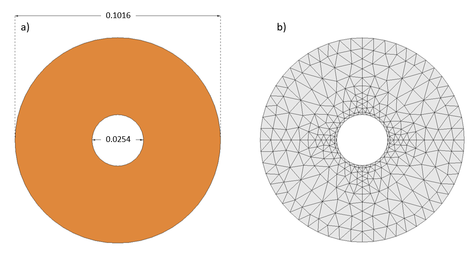
La probeta se encuentra formada por un disco de diámetro exterior de ${\textstyle 0.1016\,m}$. y de diámetro interior de ${\textstyle 0.0254\,m}$ como se muestra en la Figura 6 a). El material a usar tiene un Módulo de elasticidad de ${\textstyle 3.4\times {10}^{9}\,Pa}$ y coeficiente de Poisson de ${\textstyle 0.20}$.

La malla utilizada se muestra en la Figura 6 b) y está formada por 352 nodos y 616 elementos triangulares de tres nodos.

Figura 6. Análisis triaxial. a) Geometría. b) Malla utilizada.

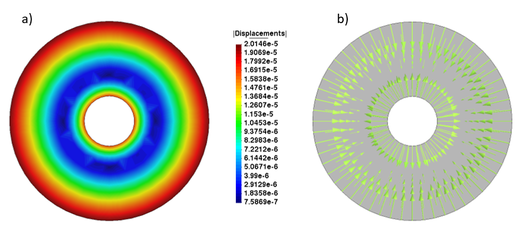
Los resultados obtenidos se muestran en la Figura 7 en donde se puede observar los desplazamientos tanto en áreas de igual color (a) como de forma vectorial (b).

Figura 7. Análisis triaxial. Resultados 2D de los desplazamientos ${\textstyle x}$ e ${\textstyle y}$

La Figura 8 muestra la distribución de todos los esfuerzos involucrados en la formulación y quizás este sea el aspecto más interesante pues se puede describir un comportamiento tridimensional de forma adecuada, sobre todo, en el caso ser necesario un análisis plástico o de daño. La Figura 7 a) y 7 b) representan los esfuerzos ${\textstyle \,{\sigma }_{x}}$ y ${\textstyle \,{\sigma }_{y}}$ respectivamente. La Figura 7 c) corresponde al esfuerzo ${\textstyle \,{\sigma }_{z}\,}$ y finalmente, la figura 7 d) el esfuerzo de corte ${\textstyle \,{\sigma \gamma }_{xy}}$.

Conclusiones

El elemento presentado tiene una buena respuesta y es capaz de evaluar adecuadamente el efecto de tener un esfuerzo normal diferente de cero. Una de las ventajas asociadas a esta formulación es la de poder modelar mediante un problema bidimensional el daño o plasticidad en un estado triaxial sin necesidad de tener que resolver un problema 3D, con el consabido error de tiempo y memoria.

Figura 8. Análisis triaxial. a) esfuerzos ${\textstyle \,{\sigma }_{x}}$ b) esfuerzos ${\textstyle \,{\sigma }_{y}}$ c) esfuerzos ${\textstyle \,{\sigma }_{z}}$ d) esfuerzos ${\textstyle \,{\gamma }_{xy}}$

Referencias

[1] Oñate, E. Cálculo de Estructuras por el Método de los Elementos Finitos. Análisis Estático Lineal. Vol 1. (2016) ISBN: 978-84-945689-7-8 Editorial: CIMNE Barcelona. España

[2] Zárate, F. & Oñate, E. A simple FEM–DEM technique for fracture prediction in materials and structures. Comp. Part. Mech. (2015) 2: 301. doi.org/10.1007/s40571-015-0067-2

[3] Zárate, F., Cornejo, A. & Oñate E., A three-dimensional FEM–DEM technique for predicting the evolution of fracture in geomaterials and concrete. Comp. Part. Mech. (2018) 5: 411. doi.org/10.1007/s40571-017-0178-z

[4] Zárate, F. & Oñate E. Predicción de fracturas en estructuras de hormigón combinando los métodos de elementos finitos y de elementos discretos. Hormigón y Acero. (2018) doi.org/10.1016/j.hya.2018.05.002