Evaluation of monthly rainfall calculated with TRMM for meteorological drought studies

Abstract

Precipitation is considered the main variable for the evaluation of meteorological drought in a basin. Drought is a phenomenon of different spatial scale, so it is convenient to have simultaneous time rainfall series in different locations, in order to analyze its evolution in space, depending on the size and the variability of the characteristics in the basin. In Argentina, specifically in the central region, the availability of information on the spatial variability of rainfall is not usual, so drought studies in this region are limited. Due to this it is convenient to validate the rainfall information obtained through satellite missions. The present work evaluates the validity and applicability of monthly rainfall data estimated through TRMM in ten stations in the basin of the Carcarañá river in the central region of Argentina and its subsequent application to studies on meteorological droughts through a representative index (SPI). Statistical parameters such as the concordance coefficient, the correlation coefficient and the bias were used for this analysis. There was a significant variation of the parameters with respect to the height. In addition, better coefficients in stations located in plain compared with stations located in mountainous areas, were observed.

INTRODUCCIÓN

Para el caso de evaluación y monitoreo del fenómeno extremo de la sequía meteorológica a nivel de cuenca, la precipitación es considerada la variable principal a tener en cuenta para lo cual es conveniente contar con series de datos históricos consecutivos sin datos faltantes y con una longitud de registro considerable. A su vez, como las sequías son consideradas fenómenos de distinta escala espacial, para analizar su evolución en el espacio es conveniente contar con una amplia cobertura de puntos de monitoreo con registros simultáneos en el tiempo y en distintas localizaciones, dependiendo en este caso, del tamaño de la cuenca y de la variabilidad en las características climáticas y topográficas dentro de la misma, entre otras características. En Argentina, los antecedentes relacionados a la sequía tienen, predominantemente, un enfoque climático y agrícola (Scian y Donnari, 1997; Hartmann et al., 2003; Havrylenko et al., 2013) o bien, forman parte de un estudio con otros ejes temáticos (Scarpati y Capriolo, 2013). En la región pampeana de Argentina, es posible observar trabajos de sequías meteorológicas con la finalidad de obtener resultados útiles para la actividad socieconómica (Ravelo, 2000) o principalmente locales, donde se analizan periodos cortos de tiempo (D´Ambrosio et al., 2013) o que finalizan en décadas anteriores (Carbone y Píccolo, 2004). Específicamente en la región central, la disponibilidad de información sobre la variabilidad espacial de las precipitaciones no es habitual, por lo que los estudios de sequías en esta región son limitados. Para avanzar y profundizar el análisis sobre este fenómeno crítico extremo con características complejas de definir y debido a la precariedad de información en el área de interés, existen obstáculos y limitaciones que requieren de un esfuerzo mayor interdisciplinario. Sobre la base de la escasa información disponible, Vicario et al. (2015), desarrolla un análisis regional en el área central de Argentina de la información de estaciones pluviométricas existentes, para identificar zonas hidrometeorológicamente homogéneas e identificar periodos de sequías meteorológicas a través de índices.

Aun así, se destaca la importancia de estudiar y buscar nuevas herramientas de estimación de datos de precipitaciones a nivel de cuenca, ya sea a través de nuevas tecnologías y/o derivados de instrumentos de distintas características. El uso de información remota registrada por satélites es una alternativa que a priori presenta un gran potencial.

En noviembre de 1997 comenzó la misión satelital TRMM (por sus siglas en inglés de la Misión Tropical de Medición de Precipitaciones) desarrollada en forma conjunta entre la NASA y la agencia japonesa de exploración aeroespacial: JAXA, con el fin de estudiar las precipitaciones para investigaciones climatológicas. La misión TRMM finalizó en abril del año 2015, ofreciendo alrededor de 17 años de información para la investigación y mejora del conocimiento sobre el clima y las precipitaciones. Estos datos admiten aplicaciones para la evaluación de la dinámica hidrológica, por ejemplo, en la llanura pampeana (Campos et al., 2014).

En general, los valores de lluvia estimados a través de satélites presentan errores de distinto tipo y por distintas causas (Semiere et al., 2012). Rasmussen et al., (2013) mostró que es necesario examinar el sesgo de los valores obtenidos por TRMM ya que puede afectar la percepción de la climatología y de la hidrología en regiones relativamente áridas. Previamente otros autores, sugirieron y revisaron el algoritmo de estimación de precipitación de la TRMM, ya que observaron incertidumbres en las estimaciones respecto de los valores superficiales de lluvia en tormentas convectivas (Iguchi, et al., 2009) siendo este tipo de tormentas, características en Sudamérica (Zipser, et al., 2006).

A pesar de estas evaluaciones generales, es conveniente que dicha variable se valide según el objetivo de estudio y la metodología que será implementada. Por ejemplo, Ramos Fernández (2013) realizó el estudio sobre la validación de lluvia estimada por satélite para modelación hidrológica, pero los antecedentes sobre su uso para la estimación de índices de sequías en Argentina, tales como los realizados por Naumann et al. (2012) en distintas cuencas de África o Li, et al. (2013) en China, son escasos.

En el presente trabajo se evalúa la validez y aplicabilidad de los datos de precipitaciones mensuales estimadas a través de TRMM, en una cuenca de la región central de la República Argentina y con la finalidad de aplicarlas a estudios que evalúen la evolución temporal de las sequías meteorológicas a través de un índice representativo. Las validaciones de las estimaciones de precipitaciones realizadas con TRMM se realizan sobre los valores de profundidad de precipitación mensual y sobre los índices de sequías SPI.

Cuenca de estudio

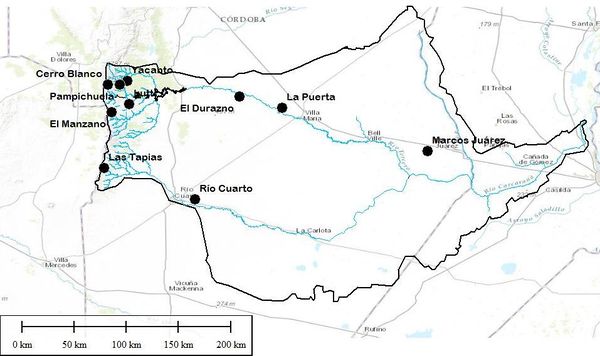
La cuenca del río Carcarañá se ubica en la región pampeana (principalmente ocupada por llanuras) de la Argentina, en el centro-sudeste de la provincia de Córdoba y atraviesa el sur la provincia de Santa Fe para desembocar en el río Paraná. El río Carcarañá, drena un área de aproximadamente 60000 km² (Figura 1) y sus nacientes se desarrollan en zona serrana. Esta cuenca posee tres grandes subcuencas, las mismas pertenecen a los ríos Tercero (o Ctalamochita), Saladillo y el arroyo Tortugas.

Información utilizada

La cuenca del río Carcarañá posee una gran extensión y puede considerarse de macroescala espacial. Esto es importante para que la resolución de TRMM permita caracterizar la variabilidad espacial dentro de la cuenca. Para su cuenca media y baja se analizan en este trabajo dos series de datos pluviométricos de una longitud suficientemente extensa en la zona de llanura, denominadas estación Marcos Juárez y estación Río Cuarto (1980-2009). Además, se analizan en este trabajo ocho estaciones cuyos datos utilizados, a los fines comparativos con el inicio de la TRMM, son desde 1998 hasta el 2014 en la región serrana (cuenca alta) del río Carcarañá. Dichas estaciones se detallan en la Tabla 1 y su ubicación se muestra en la Figura 2.

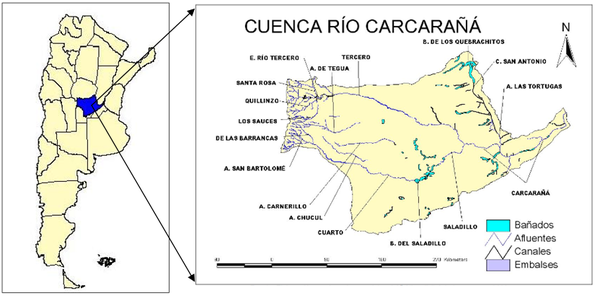Figura 1. Ubicación de la cuenca del río Carcarañá en la República Argentina. (Fuente: Subsecretaría de Recursos Hídricos de la Nación.)

Tabla 1. Coordenadas y altura de las estaciones pluviométricas seleccionadas en la cuenca del río Carcarañá.

Estación	Coordenadas geográficas (en decimales)		Altura (msnm)
	Latitud	Longitud
El Durazno	-32,23	-64,78	1095
Cerro Blanco	-32,13	-64,92	2106
El Manzano	-32,37	-64,88	1813
La Puerta	-32,33	-64,78	1259
Lutti	-32,30	-64,73	1037
Pampichuela	-32,13	-64,82	1185
Yacanto	-32,10	-64,75	1132
Las Tapias	-32,85	-64,95	1455
Marcos Juárez	-32,42	-62,1	114
Río Cuarto	-33,07	-64,1	421

Figura 2. Ubicación de las estaciones pluviométricas en la cuenca del río Carcarañá.

Se utilizaron valores de precipitaciones estimadas a través de la TRMM en las mismas ubicaciones geográficas (definidas por coordenadas) correspondientes a las estaciones con registros en superficie. Se obtiene datos de precipitaciones diarias en cada punto a partir del año 1998 hasta el año 2014, las cuales fueron procesadas y agregadas en paso de tiempo mensual.

Para obtener las series de índices de sequía meteorológica se utiliza el índice estandarizados de precipitaciones, SPI (por sus siglas en inglés: Standarized Precipitation Index) propuesto por McKee et al. (1993). El SPI fue diseñado para mejorar la detección del comienzo de la sequía y para el monitoreo de la misma; el mismo se fundamenta en las probabilidades de ocurrencia de precipitación para un período dado. La Organización Meteorológica Mundial (2012) indica que el cálculo del SPI para una localidad se basa en el registro de precipitaciones a largo plazo para un período deseado, sin considerar otras variables tales como las condiciones del suelo o la evapotranspiración. Dicho registro a largo plazo se ajusta a una distribución de probabilidades y a continuación se transforma en una distribución normal de modo que el SPI medio para la localidad y el período deseado sea cero (Edwards y McKee, 1997). Los valores de clasificación para el SPI se presentan en la Tabla 2. Se define una sequía cuando el SPI es continuamente negativo y alcanza un valor de 1.0 o inferior, y continúa hasta que el SPI se torna positivo. La duración de la sequía es definida por el intervalo entre el comienzo y el final del período.

Tabla 2. Valores característicos del índice estandarizado de precipitación (SPI) (McKee et al., 1993)

Valor SPI Categoría de sequía
>2,00	Extremadamente húmedo
1,99 a 1,50	Muy húmedo
1,49 a 1,00	Moderadamente húmedo
0,99 a -0,99	Normal
-1,00 a -1,49	Sequía moderada
-1,50 a -1,99	Sequía severa
<-2,00	Sequía extrema

Validación de estimaciones de lluvia y de índice SPI realizadas con TRMM

Para la validación de los datos de lluvia y del índice SPI estimados con TRMM se utilizó el coeficiente de concordancia estadística que es un coeficiente que muestra cuán acordes son un grupo de observaciones respecto de otro, siendo que ambos identifican el mismo fenómeno. Uno de los grupos se establece como patrón de referencia. Para el caso de observaciones continuas y para mejorar otras metodologías estadísticas (Vigiak y Bende-Michl, 2013), Lin (1989) determinó el Coeficiente de Correlación Concordancia (CCC) el cual se define como:

${\textstyle CCC={\frac {A2+B2-C2}{A2+B2+D2}}}$

D²: Diferencia del promedio de los dos grupos

Mediante el uso de este coeficiente se califica la concordancia entre los valores de los dos grupos de observaciones como sustancial si CCC es mayor a 0,95; moderada si está entre los valores de 0,90 y 0,95 y pobre si el CCC es inferior a 0,90. Este coeficiente contempla en sí mismo diferentes características del acuerdo entre los dos grupos como son la correlación (precisión) y sesgo (exactitud). Para conocer la contribución a la concordancia de la correlación o el sesgo se determinaron y se detallan ambos por separado. El Coeficiente de Correlación (CC) cuantifica la relación lineal entre dos series de datos, mediante los valores entre los umbrales –1 a +1, y se evalúa en este trabajo a través del método de Pearson. El sesgo, por definición, hace referencia a la valoración de las observaciones de una muestra, respecto de las observaciones de otra muestra, en referencia a las discrepancias entre sus distribuciones marginales. La metodología empleada para evaluar el sesgo es descriptiva pero no informan acerca si es o no significativa. Para el caso del presente trabajo, se determinó el sesgo relativo (Sot) con base en la diferencia entre los promedios de las series de precipitaciones observadas (Xo) y la media de la serie de precipitaciones obtenidas por TRMM (Xt) como S =(Xo – Xt) /Xt. De tal manera que si S es positivo, se visualiza una subestimación en un porcentaje determinado de las precipitaciones obtenidas por TRMM respecto de los valores observados.

RESULTADOS Y DISCUSIÓN

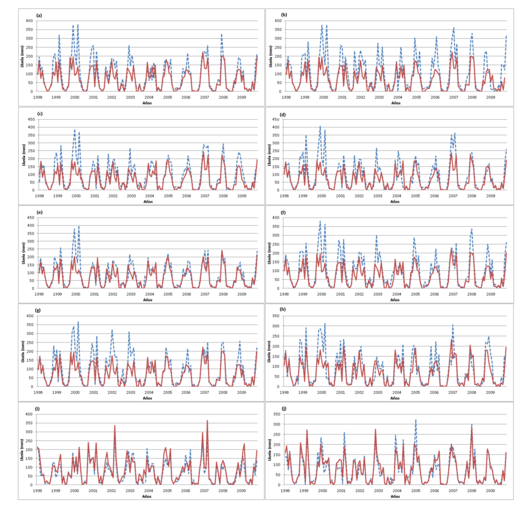
Los principales resultados obtenidos de la validación de estimaciones de precipitaciones realizadas con TRMM respecto de las observadas, se muestran en la Tabla 3. En la Figura 3 se muestran las series temporales de precipitaciones mensuales observadas en superficie y estimadas con TRMM para cada una de las estaciones.

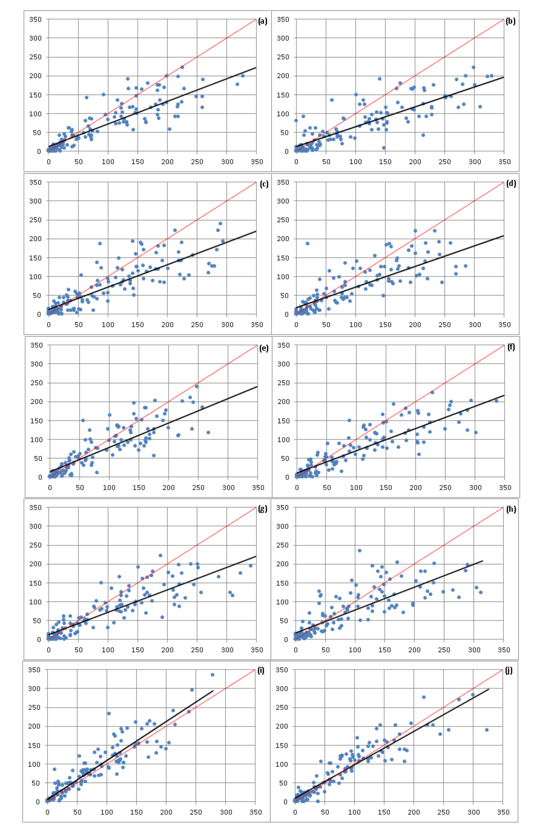
A través de estos parámetros se observa que, en la cuenca media y baja, específicamente para las estaciones de Marcos Juárez y Río Cuarto, los datos obtenidos de TRMM poseen una concordancia moderada respecto de los datos observados, están significativamente correlacionados y sobreestiman las precipitaciones levemente. Mientras que, las estaciones que se encuentran en la región serrana de la cuenca, a pesar que las correlaciones podrían considerarse aceptables, en todos los casos, la concordancia es menor y se observa una subestimación de las precipitaciones del TRMM respecto de las observadas, que varían entre el 16% y 36%, aproximadamente. Lo cual, en zonas serranas no sería recomendable establecer análisis puntuales de precipitaciones con datos obtenidos de la TRMM, no siendo así para los casos de llanuras. En la Figura 4 se muestran los gráficos representativos del índice de concordancia de los dos grupos de datos para las estaciones utilizadas.

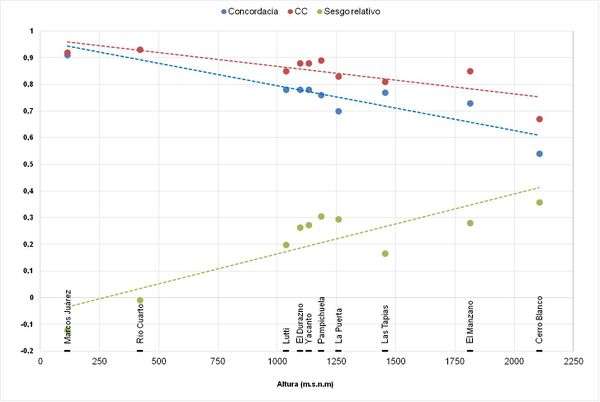
En los resultados reportados se observa una variación significativa de los parámetros de contraste respecto de la altura en la que se encuentran emplazadas las estaciones. Este efecto se muestra claramente en la Figura 5 donde se grafica la evolución de cada uno de los parámetros respecto de dicha característica topográfica.

Tabla 3. Parámetros estadísticos calculados entre las series de precipitaciones observadas y obtenidas a través de TRMM para las localizaciones en la cuenca del río Carcarañá.

	El Durazno	Cerro Blanco	El Manzano	La Puerta	Lutti	Pampi-chuela	Yacanto	Las Tapias	Marcos Juárez	Río Cuarto
Concord.	0,78	0,54	0,73	0,7	0,78	0,76	0,78	0,77	0,91	0,93
CC	0,88	0,67	0,85	0,83	0,85	0,89	0,88	0,81	0,92	0,93
Sesgo (%)	26,26	35,84	28,09	29,38	19,8	30,53	27,2	16,59	-12,22	-0,94

Figura 3. Precipitaciones mensuales observadas (líneas de punto) y obtenidas a través de TRMM (línea continua) para el periodo 1998-2009 en las estaciones: (a) El Durazno, (b) Cerro Blanco, (c) El Manzano, (d) La Puerta, (e) Lutti, (f) Pampichuela, (g) Yacanto, (h) Las Tapias, (i) Marcos Juárez y (j) Río Cuarto.

Figura 4. Concordancia entre los valores de precipitación mensual observada y estimada con TRMM, línea de acuerdo perfecto (45º) y de tendencia lineal para para el periodo 1998-2009 en estaciones: (a) El Durazno, (b) Cerro Blanco, (c) El Manzano, (d) La Puerta, (e) Lutti, (f) Pampichuela, (g) Yacanto, (h) Las Tapias, (i) Marcos Juárez y (j) Río Cuarto.

Figura 5. Coeficientes de concordancia, correlación y sesgo entre las series de precipitaciones observadas y obtenidas de TRMM en las estaciones seleccionadas, ordenadas según su altura topográfica (m.s.n.m)

Para cuantificar los impactos de las diferencias observadas en estudios de sequías meteorológicas, se calcularon las series temporales del índice SPI (12 meses), sobre la base de precipitaciones observadas y estimadas con TRMM. Los gráficos se muestran en las Figuras 6, respectivamente. Debido al índice seleccionado, al estar el valor de la media en el entorno del cero, se observó que el sesgo promedio de la serie tiende a cero y debido a esto los coeficientes de concordancia y de correlación son similares. En la Tabla 4 se muestran los coeficientes de correlación entre las series de los índices SPI calculados a partir de precipitaciones observadas y obtenidas por TRMM en las estaciones analizadas. La mejor correlación se observa para los casos de las estaciones de llanura.

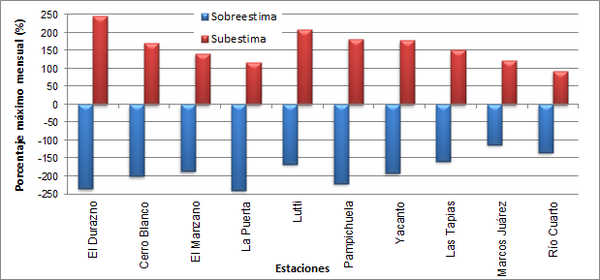
Si bien el sesgo promedio entre las series de SPI tiende a cero, para casos puntuales se observa una marcada diferencia. En la Figura 6 se presentan los valores máximos observados (%) de sobreestimación y de subestimación entre las series de los índices calculados a partir de TRMM respecto de los que fueron calculados con datos observados de precipitaciones, en cada una de las estaciones utilizadas. Se observa que en general, las diferencias máximas son menores en las dos estaciones de llanura (Marcos Juárez y Río Cuarto).

	El Durazno	Cerro Blanco	El Manzano	La Puerta	Lutti	Pampi- chuela	Yacanto	Las Tapias	Marcos Juárez	Río Cuarto
CC	0,49	0,79	0,76	0,73	0,71	0,73	0,62	0,79	0,85	0,85

Tabla4. Coeficientes de Correlación (CC) entre las series de índice SPI calculados a partir de recipitaciones observadas y obtenidas con TRMM en las estaciones utilizadas en la cuenca del río Carcarañá.

Figura 6. Valores máximos de sobreestimación y subestimación (%) de los índices SPI calculados con precipitaciones obtenidas a partir de TRMM, respecto de los SPI calculados con precipitaciones observadas en las estaciones utilizadas de la cuenca del río Carcarañá.

CONCLUSIONES

En la cuenca del río Carcarañá se puede observar que a medida que las estaciones se encuentran en emplazamientos más elevados el sesgo entre las precipitaciones mensuales observadas y las obtenidas con TRMM aumenta; es decir que, las estimaciones mensuales de precipitaciones de TRMM son menos confiables en zonas de altura (o serrana) respecto de las áreas de llanura, con lo cual se debe estudiar detalladamente su validez para casos locales.

Se observó que al calcular el índice SPI por la metodología en sí misma, el sesgo promedio entre las series tiende a cero, aunque para casos puntuales el sesgo es relevante. En general, en las dos estaciones de llanura el sesgo máximo observado está dentro de los valores menores y el coeficiente de correlación mejora respecto de las estaciones ubicadas en la zona serrana.

REFERENCIAS

Campos, A. N, Figueroa Schibber, E. y García, A. G. (2014). Evaluación de la información satelital para el estudio de la dinámica hidrológica de la Llanura Pampeana. 2° Encuentro de Investigadores en Formación en Recursos Hídricos. Instituto Nacional del Agua. Buenos Aires, Argentina.

Edwards, D. C. and McKee T. B. (1997). Characteristics of 20th century drought in the United States at multiple time scales. Climatology Report 97-2, Departamento de Ciencia Atmosférica, Universidad del Estado de Colorado, Fort Collins, Colorado.

Iguchi, T., Kozu, T., Kwiatkowski, J., Meneghini, R., Awaka, J., Okamoto and K. (2009). Uncertainties in the Rain profiling algorithm for the TRMM Precipitation Radar. Journal of the Meteorological Society of Japan, 87A, 1-30.

Rasmussen, K. L., Choi, S. L., Zuluaga, M. D., y and Houze, R. A. Jr. (2013). TRMM precipitation bias in extreme storms in South America. Geophysical Research Letters, 40, 3457–3461, doi:10.1002/grl.50651.

Li, X., Zhang, Q. and Ye, X. (2013). Dry/Wet Conditions Monitoring Based on TRMM Rainfall Data and Its Reliability Validation over Poyang Lake Basin, China. Water 2013, 5, 1848-1864; doi:10.3390/w5041848

Lin, L. (1989). A concordance correlation coefficient to evaluate reproducibility. Biometrics, 45, 255-268.

McKee, T.B., N. J. Doesken, and J. Kliest. (1993). The relationship of drought frequency and duration to time scales. In Proceedings of the 8th Conference of Applied Climatology, 17-22 January, Anaheim, CA. American Meterological Society. Boston, MA. 179-184.

NASA Homepage (2015). Recuperado de: http://trmm.gsfc.nasa.gov/ (consulta: Marzo 2016)

Naumann, G., Barbosa, P. and Carrao, H. (2012). Monitoring drought conditions and their uncertainties in Africa using TRMM data. Journal of Applied Meteorology and Climatology, 51, 1867–1874.

Organización Meteorológica Mundial. (2012). Índice normalizado de precipitación Guía del usuario © OMM-N^o 1090. ISBN 978-92-63-31090-3.

Ramos Fernández, L. (2013). Estudio de la utilidad de la lluvia estimada de satélite en la modelación hidrológica distribuida. Tesis Doctoral. Universidad Politécnica de Valencia. 216 pp.

Semiere F. A., Mohd –Mokhtar R., Ismail W., Mohamad N. and Mandeep, J.S. (2012). Ground validation of space-borne satellite rainfall products in Malasya. Advances In Space Research 50: 1241-1249.

Subsecretaría de Recursos Hídricos de la Nación. Recuperado de: http://www.hidricosargentina.gov.ar. (Consultada hasta agosto 2016)

Vicario, L., García, C.M., Teich, I., Bertoni, J.C., Ravelo, A. y Rodríguez, A. (2015). Caracterización de las sequías meteorológicas en la región central de la Argentina. Revista Tecnología y Ciencias del Agua. ISSN 2007-2422. Instituto Mexicano de Tecnología del Agua, 6 (1), 155-167.

Vigiak, O. and Bende-Michl, U. (2013). Estimating bootstrap and Bayesian prediction intervals for constituent load rating curves. Water Resources Research, 49, 8565–8578, doi:10.1002/2013wr013559

Zipser, E. J., Cecil, D., Liu, C.; Nesbitt, S. and Yorty, D. (2006). Where are the most intense thunderstorms on earth? Bulletin of the American Meteorological Society, 87, 1057–1071.