Approximation to advection equation in plane irregular regions using a Method of Lines and Generalized Finite Differences

Aproximación de la ecuación de advección en regiones irregulares utilizando un Método de Líneas y Diferencias Finitas Generalizadas

Gerardo Tinoco-Guerrero, Francisco Javier Domínguez-Mota, Juan Salvador Lucas-Martínez y José Gerardo Tinoco-Ruiz

Resumen

Uno de los grandes retos en nuestros días continua siendo el diseñar métodos numéricos capaces de aproximar la solución de ecuaciones diferenciales parciales de manera rápida y precisa. Una de las ecuaciones más importantes, debido a las aplicaciones hidráulicas y de transporte con las que cuenta, y a la gran cantidad de dificultades que suele presentar al momento de resolverla numéricamente es la Ecuación de Advección.

En el presente trabajo se presenta un Método de Líneas aplicado a la solución numérica de dicha ecuación en regiones irregulares haciendo uso de un esquema de Diferencias Finitas Generalizadas. Se presentan una serie de pruebas y resultados numéricos, los cuales muestran la precisión del método propuesto.

1 Introducción

Si una sustancia es transportada en un fluido a una velocidad constante ${\textstyle a}$, la función del flujo puede escribirse como

${\begin{array}{l}f(u)=au.\\\end{array}}$

El flujo de materia que pasa por el punto ${\textstyle x}$ puede conocerse multiplicando la densidad local ${\textstyle u(x,t)}$ por la velocidad de transporte. Dado que el total de la masa que pasa entre dos puntos, ${\textstyle x_{1}}$ y ${\textstyle x_{2}}$, cambia únicamente debido al flujo en los puntos límite, puede ser calculada como

${\frac {d}{dt}}\int _{x_{1}}^{x_{2}}u(x,t)dx=f(u(x_{2},t))-f(u(x_{1},t)).$

(1)

Asumiendo suficiente suavidad en ${\textstyle u}$ y ${\textstyle f}$, i.e. son funciones con tantas derivadas como sea necesario, la ecuación (1) puede escribirse como

$\int _{x_{1}}^{x_{2}}\left[{\frac {\partial }{\partial t}}u(x,t)+{\frac {\partial }{\partial x}}f(u(x,t))\right]dx=0,$

(2)

ahora, debido a que la integral debe ser igual a $0$ para cualesquiera valores de $x_{1}$ y $x_{2}$, entonces el integrando es igual a $0$, con esto se obtiene la ecuación diferencial

${\frac {\partial }{\partial t}}u(x,t)+{\frac {\partial }{\partial x}}f(u(x,t))=0.$

(3)

Para el problema del transporte de una sustancia en un fluido a una velocidad constante, se puede escribir $f(u)=au$, donde $a$ es una constante que representa la velocidad del fluido. Utilizando estos valores en la ecuación (3) se puede llegar a

${\frac {\partial }{\partial t}}u(x,t)+a{\frac {\partial }{\partial x}}u(x,t)=0,$

(4)

que es conocida como la ecuación de advección en $(1+1)D$, la cual, por razones de simplicidad, puede ser escrita como

${\frac {\partial u}{\partial t}}+a{\frac {\partial u}{\partial x}}=0.$

(5)

Analogamente, para el problema de transporte en el plano se obtiene la ecuación

${\frac {\partial u}{\partial t}}+a{\frac {\partial u}{\partial x}}+b{\frac {\partial u}{\partial y}}=0.$

(6)

En este trabajo se desea obtener una aproximación en Diferencias Finitas Generalizadas, para la parte espacial, a la solución del problema

${\frac {\partial u}{\partial t}}+a{\frac {\partial u}{\partial x}}+b{\frac {\partial u}{\partial y}}=0\Omega \times [0,T]a,b\in I\!\!R,$

${\begin{array}{l}u(x,y,0)=g(x,y)&&(x,y)\in \Omega ,\\u(x,y,t)|_{S_{1}}=h(x,y,t)&&(x,y)\in \Omega \quad t\in [0,T],\end{array}}$

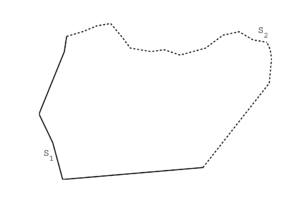
donde ${\textstyle \Omega }$ es un dominio plano simplemente conexo, y su frontera, ${\textstyle \partial \Omega }$, es un polígono de Jordan orientado de manera positiva; además ${\textstyle \partial \Omega =S_{1}\cup S_{2}}$ (como se muestra en la figura 1), ${\textstyle S_{1}}$ corresponde a la frontera con la entrada de flujo. Para la parte temporal se utilizará un Método de Líneas.

El problema de advección es de interés en modelación por las inestabilidades que se presentan al aproximar su solución empleando diferencias finitas.

Figura 1: Dominio $\Omega$ con fronteras $\partial \Omega =S_{1}\cup S_{2}$.

2 Esquema propuesto

Para el caso de la ecuación de advección

${\frac {\partial u}{\partial t}}=-a{\frac {\partial u}{\partial x}}-b{\frac {\partial u}{\partial y}},$

es posible discretizar las derivadas espaciales utilizando el método de Diferencias Finitas Generalizadas; para ello es conveniente considerar la aproximación al operador lineal de segundo orden

$Lu=Au_{xx}+Bu_{xy}+Cu_{yy}+Du_{x}+Eu_{y}+Fu,$

(7)

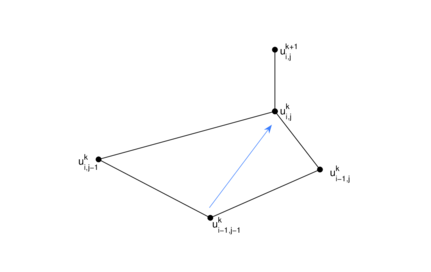
donde ${\textstyle A,B,C,D,E}$ y ${\textstyle F}$ son funciones dadas y su valor en el nodo ${\textstyle p_{0}=(x_{0},y_{0})}$ puede aproximarse usando valores de ${\textstyle u}$ en algunos nodos vecinos ${\textstyle p_{i}=(x_{i},y_{i})}$, ${\textstyle i~=~1,2,\dots ,q}$ (véase figura 2). Para el efecto se utiliza un esquema de diferencias finitas en el nodo ${\textstyle p_{0}}$, el cual puede escribirse como una combinación lineal

$L_{0}=\Gamma _{0}u(p_{0})+\Gamma _{1}u(p_{1})+...+\Gamma _{q}u(p_{q}).$

(8)

donde ${\textstyle \Gamma _{0},\Gamma _{1},\dots ,\Gamma _{q}}$ son pesos adecuados.

Figura 2: Distribución arbitraria de $p_{0}$ y sus vecinos.

Un esquema es consistente si

$[Lu]_{p_{0}}-L_{0}\to 0$

cuando ${\textstyle p_{1},...,p_{q}\to p_{0}}$. Utilizando los primeros seis términos de la expansión en serie de Taylor, hasta segundo orden, de la condición de consistencia se obtiene el sistema

$\left({\begin{array}{lclc}1&1&...&1\\0&\Delta x_{1}&...&\Delta x_{q}\\0&\Delta y_{1}&...&\Delta y_{q}\\0&(\Delta x_{1})^{2}&...&(\Delta x_{q})^{2}\\0&\Delta x_{1}\Delta y_{1}&...&\Delta x_{q}\Delta y_{q}\\0&(\Delta y_{1})^{2}&...&(\Delta y_{q})^{2}\\\end{array}}\right)\left({\begin{array}{l}\Gamma _{0}\\\Gamma _{1}\\\Gamma _{2}\\.\\.\\.\\\Gamma _{q}\\\end{array}}\right)=\left({\begin{array}{l}F(p_{0})\\D(p_{0})\\E(p_{0})\\2A(p_{0})\\B(p_{0})\\2C(p_{0})\\\end{array}}\right),$

(9)

donde ${\textstyle \Delta x_{i}=x_{i}-x_{0}}$ y ${\textstyle \Delta y_{i}=y_{i}-y_{0}}$. Nótese que (9) cuenta con 6 ecuaciones y ${\textstyle q+1}$ incógnitas. En los casos de interés, es un sistema subdeterminado. Sin embargo puede ser resuelto de manera no iterativa en el sentido de cuadrados mínimos, para ello se consideran únicamente las últimas 5 ecuaciones de (9),

$\left({\begin{array}{lcl}\Delta x_{1}&...&\Delta x_{q}\\\Delta y_{1}&...&\Delta y_{q}\\(\Delta x_{1})^{2}&...&(\Delta x_{q})^{2}\\\Delta x_{1}\Delta y_{1}&...&\Delta x_{q}\Delta y_{q}\\(\Delta y_{1})^{2}&...&(\Delta y_{q})^{2}\\\end{array}}\right)\left({\begin{array}{l}\Gamma _{1}\\\Gamma _{2}\\.\\.\\.\\\Gamma _{q}\\\end{array}}\right)=\left({\begin{array}{l}D(p_{0})\\E(p_{0})\\2A(p_{0})\\B(p_{0})\\2C(p_{0})\\\end{array}}\right),$

(10)

cuyas ecuaciones normales pueden resolverse utilizando factorización reducida de Cholesky para obtener los valores de ${\textstyle \Gamma _{1},...,\Gamma _{q}}$. La primera ecuación de (9) determina ${\textstyle \Gamma _{0}}$ como

$\Gamma _{0}=-\Gamma _{1}...-\Gamma _{q}+F(p_{0}).$

(11)

De esta forma se obtiene un conjunto de coeficientes necesarios para definir el esquema (8).

El esquema definido por (8) puede ser aplicado al operador

$-a{\frac {\partial u}{\partial x}}-b{\frac {\partial u}{\partial y}},$

y los coeficientes ${\textstyle \Gamma _{0},...,\Gamma _{q}}$ obtenidos definen el esquema

$L_{0}=\sum _{l=0}^{q}\Gamma _{l}u_{l}.$

(12)

Nótese que el esquema (12) puede ser usado tanto en mallas estructuradas como en mallas no estructuradas. Sin embargo, el uso de mallas lógicamente rectangulares permite aprovechar la estructura dada por el par de índices en la malla ${\textstyle G~=~\{p_{i,j}~|~1\leq i\leq m,1\leq j\leq n\}}$.

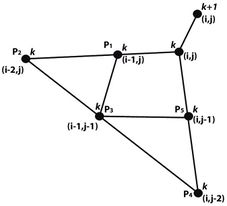
Para este trabajo se proponen dos esquemas diferentes. El primero de ellos utiliza cada nodo de la malla y 3 de sus vecinos, con esta elección de vecinos se obtiene un esténcil como el mostrado en la figura 3; el esquema (12) toma la forma

$L_{0}=\Gamma _{0}u_{0}+\Gamma _{1}u_{1}+\Gamma _{2}u_{2}+\Gamma _{3}u_{3}.$

Figura 3: Esténcil de 4 puntos.

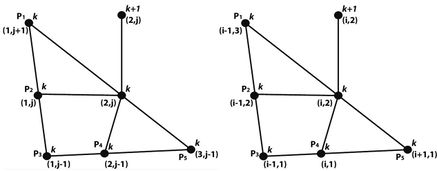
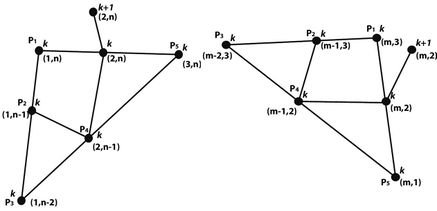
El segundo esquema que se propone utiliza cada nodo de la malla y 5 de sus vecinos. Los esténciles usados varían dependiendo de la localización lógica del nodo correspondiente en términos de su posición en la malla, cada uno de estos esténciles se muestran en la figura 4 y, en todos los casos, se obtiene una expresión de la forma

$L_{0}=\Gamma _{0}u_{0}+\Gamma _{1}u_{1}+\cdots +\Gamma _{5}(i,j)u_{5}.$

(13)

Figura 4: Diferentes esténciles del esquema de 6 puntos.

Una vez que se cuenta con una discretización del operador espacial, el problema de encontrar una aproximación a la solución de la ecuación de advección

${\frac {\partial u}{\partial t}}=L_{0},$

puede resolverse como un sistema lineal de ecuaciones diferenciales ordinarias en el tiempo; el cual puede ser resuelto por medio de un método de Runge-Kutta. En el presente trabajo se propone utilizar Runge-Kutta de orden 2, 3 y 4 de la siguiente manera:

Runge-Kutta de Orden 2

$u^{k}=u^{k-1}+{\frac {\Delta t}{2}}\left(r_{1}+r_{2}\right),$

donde

$r_{1}=L_{0}\left(u^{k-1}\right),$

$r_{2}=L_{0}\left(u^{k-1}+{\frac {\Delta t}{2}}(r_{1})\right).$

Runge-Kutta de Orden 3

$u^{k}=u^{k-1}+{\frac {\Delta t}{6}}\left(r_{1}+4r_{2}+r_{3}\right),$

donde

$r_{1}=L_{0}\left(u^{k-1}\right),$

$r_{2}=L_{0}\left(u^{k-1}+{\frac {\Delta t}{2}}(r_{1})\right),$

$r_{3}=L_{0}\left(u^{k-1}+\Delta t(2r_{2}-r_{1})\right),$

Runge-Kutta de Orden 4

$u^{k}=u^{k-1}+{\frac {\Delta t}{6}}\left(r_{1}+2r_{2}+2r_{3}+r_{4}\right),$

donde

$r_{1}=L_{0}\left(u^{k-1}\right),$

$r_{2}=L_{0}\left(u^{k-1}+{\frac {\Delta t}{2}}(r_{1})\right),$

$r_{3}=L_{0}\left(u^{k-1}+{\frac {\Delta t}{2}}(r_{2})\right),$

$r_{4}=L_{0}\left(u^{k-1}+\Delta t(r_{3})\right),$

en todos los casos, ${\textstyle k}$ representa el nivel de tiempo.

3 Pruebas numéricas

Para medir la precisión de los métodos se planteo el problema de obtener una aproximación a la ecuación

$u(x,y,t)=0.2e^{((-(x-0.5-0.2t)^{2}-(y-0.3-0.2t)^{2})/.01)},$

y se aplicó a dos regiones de prueba denotadas como CAB y MIC, las cuales son regiones planas no rectangulares, como se muestra en la figura 5. Para estas regiones se generaron mallas lógicamente rectangulares con 21, 41 y 81 puntos por lado respectivamente, en la figura 6 se muestran las mallas generadas con 41 puntos por lado.

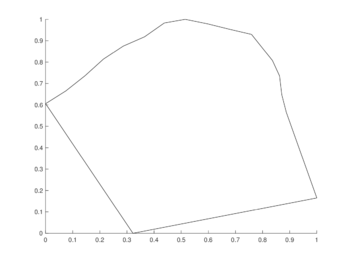
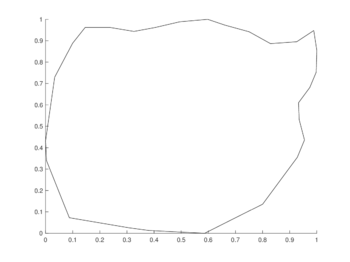
Figura 5: Regiones de prueba.

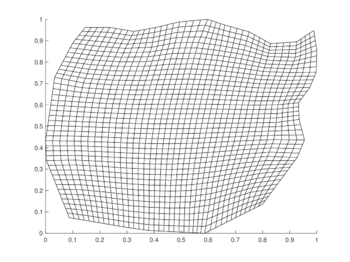
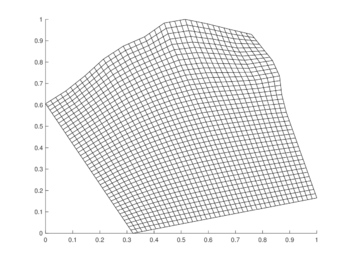
Figura 6: Mallas generadas con 41 puntos por lado.

Las pruebas numéricas se realizaron utilizando una discretizacion uniforme del intervalo de tiempo ${\textstyle [0,1]}$ dividido en 200 subintervalos. En todos los casos se calcularon el error cuadrático medio

$ECM={\hbox{max}}\left({\sqrt {\sum _{i,j}(u_{i,j}^{k}-U_{i,j}^{k})^{2}A_{i,j}}}\right),$

donde ${\textstyle A_{i,j}}$ es el área del cuadrilátero correspondiente; y el error máximo normalizado

$EMN={\frac {{\hbox{max}}\left(u^{k}-U^{k}\right)}{{\hbox{max}}(U^{k})}},$

siendo ${\textstyle u_{i,j}^{k}}$ y ${\textstyle U_{i,j}^{k}}$ la solución aproximada y la exacta, en el nodo ${\textstyle i,j}$ al tiempo ${\textstyle k}$, respectivamente.

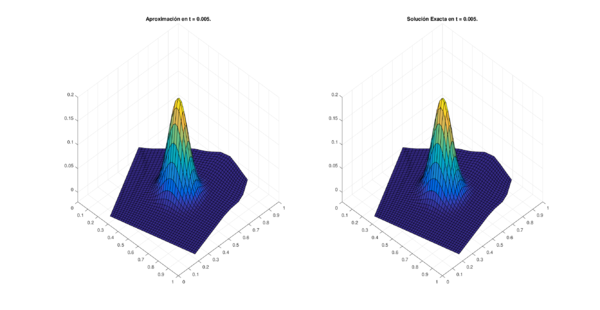
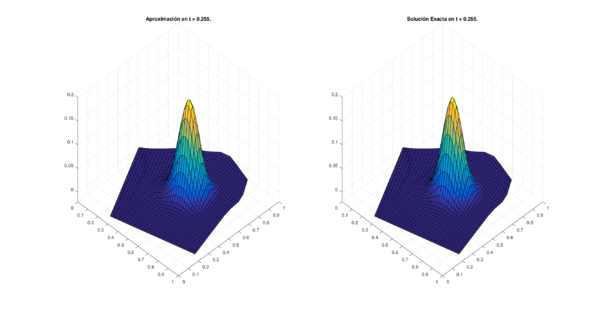
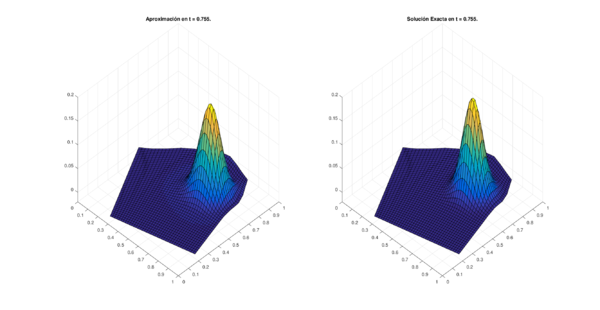
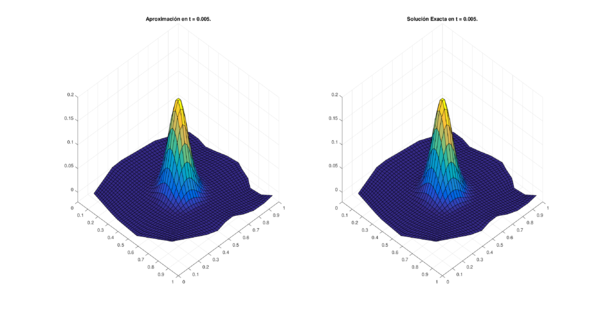
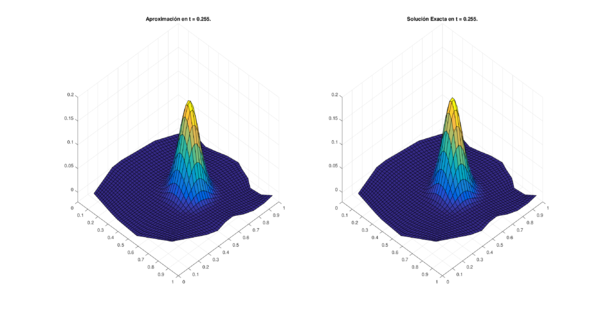
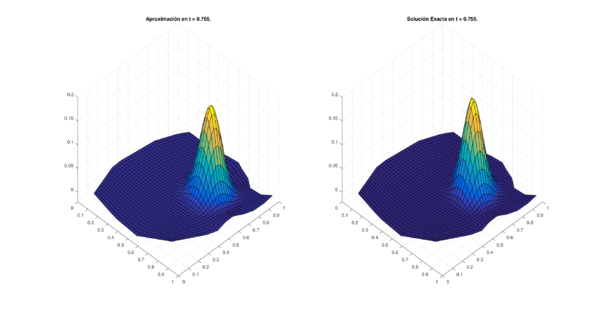
Los conjuntos de figuras 7 y 8 muestran los resultados obtenidos utilizando el método de 6 puntos con Runge-Kutta 4, en la región CAB con ${\textstyle 41\times {41}}$ puntos espaciales en diferentes niveles de tiempo; por su parte los conjuntos de figuras 9 y 10 muestran los resultados correspondientes para la región MIC.

La tabla 1 muestra los errores calculados en todas las pruebas para la región CAB, mientras que la tabla 2 muestra los correspondientes para la región MIC. Los métodos se encuentran abreviados siguiendo la nomenclatura RKN-P, donde N representa el orden utilizado para el método de Runge-Kutta y P el número de nodos utilizados por el esténcil de Diferencias Finitas Generalizadas para la discretización del operador espacial.

Figura 7: Resultados para la región CAB con $[41\times {41}]$ puntos.

Figura 8: Resultados para la región CAB con $[41\times {41}]$ puntos.

Figura 9: Resultados para la región MIC con $[41\times {41}]$ puntos.

Figura 10: Resultados para la región MIC con $[41\times {41}]$ puntos.

Tabla. 1 Errores calculados para la región CAB.

Método	ECM-21	EMN-21	ECM-41	EMN-41	ECM-81	EMN-81
RK2-4	1.4639E-02	5.9141E-01	1.0151E-02	4.2571E-01	6.2021E-03	2.6868E-01
RK3-4	1.4717E-02	5.9386E-01	1.0308E-02	4.3131E-01	6.4582E-03	2.7820E-01
RK4-4	1.4717E-02	5.9386E-01	1.0308E-02	4.3131E-01	6.4581E-03	2.7820E-01
RK2-6	9.7173E-03	3.6234E-01	3.8362E-03	1.4595E-01	1.1686E-03	4.2355E-02
RK3-6	9.7326E-03	3.6546E-01	3.8709E-03	1.5144E-01	1.1113E-03	4.2459E-02
RK4-6	9.7326E-03	3.6546E-01	3.8709E-03	1.5144E-01	1.1113E-03	4.2459E-02

Tabla. 2 Errores calculados para la región MIC.

Método	ECM-21	EMN-21	ECM-41	EMN-41	ECM-81	EMN-81
RK2-4	1.4085E-02	5.9370E-01	9.7196E-03	4.2643E-01	5.9166E-03	2.6669E-01
RK3-4	1.4167E-02	5.9677E-01	9.8742E-03	4.3352E-01	6.1416E-03	2.7784E-01
RK4-4	1.4167E-02	5.9677E-01	9.8742E-03	4.3352E-01	6.1416E-03	2.7784E-01
RK2-6	1.0115E-02	4.0059E-01	4.2626E-03	1.6303E-01	1.2992E-03	4.9904E-02
RK3-6	1.0104E-02	4.0413E-01	4.2624E-03	1.6741E-01	1.2385E-03	5.0770E-02
RK4-6	1.0104E-02	4.0413E-01	4.2624E-03	1.6741E-01	1.2385E-03	5.0770E-02

4 Conclusiones

Puede observarse en los resultados presentados en la sección 3 que el Método de Líneas propuesto para la solución de la ecuación advección produce aproximaciones satisfactorias a la solución de dicha ecuación. En las pruebas realizadas no se perciben oscilaciones espurias ni inestabilidades; además, se muestra que el método es mucho más eficiente si se combina el esquema de Diferencias Finitas Generalizadas que utiliza 6 puntos con un método de Runge-Kutta 4.

Adicionalmente, a pesar de que en principio parece que el método que utiliza 4 puntos para la discretización del operador espacial no produce buenos resultados, los resultados numéricos en las tablas 1 y 2 muestran que una refinación de la malla espacial puede lograr mejorar los resultados del método; como es de esperarse en esta clase de métodos. Vale la pena hacer mención de que, para todas las pruebas, se utilizaron únicamente 200 pasos en la discretización temporal, lo cual hace que el costo computacional de este método resulte bajo, ya que no requiere hacer discretizaciones temporales muy pequeñas, como sucede en otros casos.

5 Agradecimientos

Los autores desean agradecer el apoyo brindado por CIC-UMSNH y Aula CIMNE-Morelia para la realización del presente trabajo; de igual manera se extiende un agradecimiento al Concejo Nacional de Ciencia y Tecnología (CONACyT).

BIBLIOGRAFÍA

[1] M. Celia and W. Gray, Numerical Methods for Differential Equations, Prentice-Hall, (1992).

[2] F. J. Domínguez-Mota, P. M. Fernández-Valdez, E. Ruiz-Díaz, G. Tinoco-Guerrero and J. G. Tinoco-Ruiz, An Heuristic Finite Difference Scheme on Irregular Plane Regions, in Applied Mathematical Sciences, (14), 8, (2014), 671-683.

[3] F. J. Domínguez-Mota, S. Mendoza-Armenta and J. G. Tinoco-Ruiz, Finite Difference Schemes Satisfying an Optimality Condition, in Meeting on Applied Scientific Computation and Tools 2011 Proceedings, IMACS Series, (2011)

[4] R. J. LeVeque, Finite difference methods for ordinary and partial differential equations : steady-state and time-dependent problems, Society for Industrial and Applied Mathematics, 2007.

[5] R. Silhavy, P. Silhavy and Z. Prokopova, Applied Computational Intelligence and Mathematical Methods: Computational Methods in Systems and Software 2017, Volume 2, Springer, (2017)

[6] J. C. Strikwerda, Finite difference schemes and partial differential equations, Society for Industrial and Applied Mathematics, 2004.

[7] J. W. Thomas, Numerical Partial Differential Equations: Finite Difference Methods, Springer, 1998.

[8] G. Tinoco-Guerrero, F. J. Domínguez-Mota, J. G. Tinoco-Ruiz and E. Ruiz-Díaz, Stability aspects of a modified Lax-Wendroff scheme for irregular 2D regions, in Meeting on Applied Scientific Computing and Tools 2015 Proceedings, IMACS Series, 2017.

[9] G. Tinoco-Guerrero, F.J. Domínguez-Mota, A. Gaona-Arias, M.L. Ruiz-Zavala and J.G. Tinoco-Ruiz, A stability analysis for a generalized finite-difference scheme applied to the pure advection equation, in Mathematics and Computers in Simulation, 147, 2018, 293-300.