MOHID platform automaticcalibration employing a stochastic optimization method and realdata from an extreme climate event in Nova Friburgo‐RJ: Part2–sensitivity analysis and hydrological parameters estimation

Resumo

Este é o segundo de 2 artigos complementares que versam sobre a implementação de uma rotina de calibração automática acoplada a um modelo de simulação do escoamento superficial e comportamento hidráulico da rede de drenagem de uma bacia hidrográfica durante eventos de cheias, construído no sistema de modelagem de águas MOdelo HIDrodinâmico (MOHID). Como estudos de caso foram analisadas 2 bacias hidrográficas localizadas na cidade de Nova Friburgo, estado do Rio de Janeiro: bacia do rio Cônego e bacia do rio Santo Antônio. Neste segundo artigo, são discutidos os conceitos de problemas inversos pertinentes e o acoplamento da plataforma MOHID ao método de otimização de Luus‐Jaakola, com intuito de estimar alguns dos principais parâmetros necessários à modelagem de drenagem e escoamento em canais, a saber: coeficiente de rugosidade da bacia e da rede de drenagem, e a altura mínima de água presente em uma célula do modelo digital do terreno (MDT) para que a mesma possa contribuir efetivamente para o escoamento superficial na bacia. A estratégia adotada mostrou‐se bastante eficiente na capacidade de estimar os parâmetros, que conduziram a uma satisfatória concordância entre níveis de água simulados e observados em estações localizadas ao longo dos rios estudados.

Abstract

This is the second of two complementary articles that deal with the implementation of an automatic calibration routine coupled to a simulation model of runoff and hydraulic behavior of the drainage system of a watershed during flood events, built in the water Modeling System MOdelo HIDrodinâmico (MOHID). As a case study two watersheds located in the city of Nova Friburgo, State of Rio de Janeiro were analysed. This second article discusses the pertinent aspects related to the inverse problem technique and the coupling of MOHID platform to Luus‐Jaakola optimization method, aiming to estimate some of the key parameters required for modeling the drainage in watersheds and the flow in channels. The adopted strategy proved very effective in its ability to estimate the parameters which led to a satisfactory agreement between simulated and observed water levels at stations located along the studied rivers.

Palavras‐chave

Bacia hidrográfica;Ondas de cheias;Estimativa de parâmetros;MOHID Land;Luus‐Jaakola

Keywords

Watershed;Flood Waves;Parameter Estimation;MOHID Land;Luus‐Jaakola

1. Introdução

A utilização de modelos matemáticos na previsão e remediação de danos causados por eventos naturais extremos tem sido crescente. Particularmente no âmbito de bacias hidrográficas, tais modelos encontram vasta aplicação.

Na literatura, é possível encontrar diversos estudos envolvendo softwares que têm como base modelos matemáticos que vão desde aplicações em florestas, como o ForestGALES, utilizado na modelagem de risco de ventos [12], àqueles destinados a análise de eventos de precipitações, bem como escoamentos superficiais e nas redes de drenagem. Neste sentido, podem ser citadas, como exemplos recentes, a calibração e validação do software HEC‐HMS 3.4 para a bacia hidrográfica do rio Attanagalu Oya, localizada no Sri Lanka [13]; a utilização da abordagem ASTER GDEM associada ao software HEC‐RAS/HEC‐GeoRAS para a simulação de inundações no rio Tisza, na Hungria [11]; a avaliação do software Simulation Program for River Networks (SPRINT) aplicado aos rios Guadalupe e San Antonio [21]; simulação de interações entre riachos e aquíferos por meio do software MODFLOW [26], dentre outras. Todos esses aplicativos baseiam‐se em modelos matemáticos que, para serem implementados, adotam uma gama de parâmetros, tais como o coeficiente de rugosidade e aqueles que parametrizam os aportes laterais e/ou perdas por infiltração, por exemplo. Estes parâmetros podem ser determinados diretamente através de fórmulas empíricas, ajustados manualmente por confronto com observações [17], implicando em dificuldade de manter o domínio sobre o modelo [7] ou, ainda, estimados por meio de problemas inversos.

O emprego de técnicas alternativas para determinar o coeficiente de rugosidade é encontrado na literatura, como, por exemplo, no trabalho de Lyra et al. [24], onde foi realizado um estudo para estimar o coeficiente de rugosidade de Manning para os períodos de vazão mínima e máxima média mensal, em alguns trechos do rio Paracatu, cuja bacia está localizada no Médio São Francisco, Brasil, baseado em redes neurais artificiais. O modelo construído mostrou desempenho satisfatório, permitindo estimar o coeficiente de rugosidade em função da cota, vazão, declividade do rio e raio hidráulico do mesmo.

Já Srinivasulu e Jain [39] desenvolveram, com bons resultados, um modelo integrado utilizando técnicas de séries temporais e redes neurais artificiais treinadas com algoritmos genéticos (genetic algorithms [GA]) para um modelo de precipitação‐vazão, demonstrando dessa forma a necessidade de se criar modelos híbridos capazes de explorar as melhores vantagens de técnicas individuais, para obter melhores resultados em menor tempo.

A tomada de decisões e, consequentemente, a implementação e execução de medidas preventivas do impacto causado pelas inundações passa por uma melhoria da gestão dos riscos, enfatizada pela importância dos danos causados por esses fenômenos nos últimos anos [30].

Com o objetivo de prever inundações, Tayfur et al. [41] utilizaram GA para obter os valores dos parâmetros ideais do modelo de curva de classificação padrão (standard rating curve model [RCM]), para previsão em tempo real de descarga de fluxos em locais onde há entrada de fluxo lateral significativo. O GA foi utilizado para tratar os parâmetros mais robustos do modelo de curva de classificação, visando empregar o modelo acoplado GA‐RCM em locais onde apenas os níveis de água do rio são medidos e a curva de classificação é desconhecida. O resultado foi uma melhoria do modelo quando comparado ao RCM padrão.

Por outro lado, Wang e Brubaker [44] utilizaram o software Parameter ESTimation (PEST) para realizar um processo de calibração automática do coeficiente de rugosidade do modelo ISWAT, o qual é uma versão melhorada do modelo Soil and Water Assessment Tool (SWAT) 2005 aplicado na bacia do rio Shenandoah, localizado nos Estados Unidos, obtendo, assim, uma maior eficiência no processo de calibração do referido modelo.

Apesar de serem amplamente utilizados na previsão de inundações, apresentando resultados satisfatórios, os programas citados nem sempre estão disponíveis para acesso e/ou download de forma gratuita na internet e/ou outros meios de divulgação. Além disso, quando seus desenvolvedores o disponibilizam, apenas o «executável» pode ser obtido, o que dificulta possíveis melhorias em sua estrutura por meio do código‐fonte. Outro fator negativo é o fato de que nem todos esses softwares apresentam um ambiente GIS e interface numérica integrada, sendo necessária a construção de arquivos de modelos digitais de terreno em outras plataformas.

Nesse aspecto, a plataforma MOdelo HIDrodinâmico (MOHID) Water Modelling System [25] surge como alternativa interessante, por ter seu código‐fonte distribuído abertamente na internet. Tal facilidade permite, por exemplo, o seu acoplamento a rotinas computacionais que agilizem o processo de determinação de coeficientes que controlem a simulação desejada, algo que pode ser conduzido, por exemplo, por técnicas de otimização.

Em trabalho pioneiro nesse sentido, Lima [19] determinou parâmetros hidrodinâmicos do estuário do rio Macaé, utilizando métodos estocásticos acoplados à ferramenta MOHID Water. No entanto, o acoplamento do problema inverso à ferramenta MOHID Land com o intuito de simular o comportamento hidráulico de um rio de montanha ainda não foi encontrado na literatura.

2. Materiais e métodos

2.1. Modelo matemático

Na plataforma MOHID, em sua ferramenta MOHID Land, o escoamento superficial e na rede de drenagem é modelado pelas equações de Saint Venant, as quais podem ser deduzidas a partir das equações da continuidade e conservação da altura de movimento (Momentum) aplicadas a um volume de controle no interior de um fluido em movimento. O escoamento superficial é bidimensional [4] e o escoamento na rede fluvial é 1D, descrito pelas equações [40]:

${\frac {\partial Q}{\partial x}}+{\frac {\partial A}{\partial t}}+$$q=0$

(1)

${\frac {\partial Q}{\partial t}}+{\frac {\partial }{\partial x}}\left(\beta {\frac {Q^{2}}{A}}\right)+$$Ag\left({\frac {\partial h}{\partial x}}-S_{0}+S_{f}+S_{e}\right)-$$\beta qv_{x}+WB=0$

(2)

onde x (m) e t (s) são as variáveis espacial e temporal, respectivamente; Q (m3/s) é a descarga do canal; (m²) é a área da seção transversal; q (m2/s) é a contribuição lateral para a descarga, sendo negativo quando entra no rio e calculado pelo escoamento superficial 2D; β (‐) é o número de Boussinesq; g (m/s²) é a aceleração da gravidade; h (m) é a altura da lâmina d’água; S₀ (m/m) é a declividade do fundo do canal; R_h (m) é o raio hidráulico; n (s/m1/³) é o coeficiente que parametriza a resistência do canal ao fluxo, conhecido também como coeficiente de rugosidade de Manning; S_e (m/m) é a perda de carga devida a vórtices gerados em expansões ou contrações súbitas do canal, proporcional ao quadrado da variação da velocidade; v_x (m/s) é a velocidade da contribuição lateral; W (m2/s2) é a tensão decorte devida ao vento e B (m) é a largura da superfície livre.

Na equação (2), as declividades do fundo do canal (S₀) e da linha de energia (), e a perda de carga por vórtices (S_e) são expressas por:

$S_{0}=-{\frac {\partial z_{f}}{\partial x}}$

(3)

$S_{f}={\frac {Q^{2}n^{2}}{R_{h}^{4/3}A^{2}}}$

(4)

$S_{e}={\frac {k_{e}}{2g}}{\frac {\partial }{\partial x}}{\left({\frac {Q}{A}}\right)}^{2}$

(5)

onde x (m) e t (s) são as variáveis espacial e temporal, respectivamente; Q (m3/s) é a descarga do canal; A (m2) é a área da seção transversal; q (m2/s) é a contribuição lateral para a descarga, sendo negativo quando entra no rio e calculado pelo escoamento superficial 2D; β (‐) é o número de Boussinesq; g (m/s2) é a aceleração da gravidade; h (m) é a altura da lâmina d’água; S₀ (m/m) é a declividade do fundo do canal; R_h (m) é o raio hidráulico; n (s/m1/3) é o coeficiente que parametriza a resistência do canal ao fluxo, conhecido também como coeficiente de rugosidade de Manning; S_e (m/m) é a perda de carga devida a vórtices gerados em expansões ou contrações súbitas do canal, proporcional ao quadrado da variação da velocidade; v_x (m/s) é a velocidade da contribuição lateral; W (m2/s2) é a tensão decorte devida ao vento e B (m) é a largura da superfície livre.

As simulações envolvendo o escoamento superficial em uma bacia hidrográfica e sua rede de drenagem utilizando a ferramenta MOHID Land requerem, necessariamente, um arquivo do modelo digital de terreno, sua rede de drenagem e dados de precipitação da região de interesse. Na Parte 1 deste artigo, foi descrito o processo de construção de cada um desses arquivos, bem como a obtenção dos dados de precipitação para a região de Nova Friburgo.

2.2. Estimativa de parâmetros

Visando a calibração automática do modelo matemático descrito pelas equações (1) e (2), presentes na plataforma MOHID, foi desenvolvida uma metodologia para estimar alguns parâmetros de interesse com base no acoplamento de um método de otimização à referida plataforma.

Em outras palavras, no simulador de calibração automática proposto neste trabalho, busca‐se minimizar a diferença entre os dados experimentais referentes aos níveis de água em 2 cursos fluviais que drenam o município de Nova Friburgo – os quais são obtidos no site do Instituto Estadual do Ambiente (INEA), conforme descrito na Parte 1 deste artigo – e os respectivos dados simulados, obtidos por meio da plataforma MOHID, ferramenta MOHID Land. Assim, o problema inverso apresentado aqui passa a ser formulado implicitamente como um problema de otimização, no qual se busca minimizar a soma dos resíduos quadrados dados pela seguinte equação [34]:

$S({\overset {\rightarrow }{Y}})=\sum _{j=1}^{Nd}{\left[h_{calc_{j}}({\overset {\rightarrow }{Y}})-h_{{exp}_{j}}\right]}^{2}$

(6)

onde, ${\textstyle {\overset {\rightarrow }{Y}}}$ é o vetor das incógnitas, 3 neste caso, Nd   é o número de dados experimentais, ${\textstyle h_{{exp}_{j}}}$ (m) são os níveis de água medidos no rio e ${\textstyle h_{calc_{j}}}$ (m) são os níveis de água no rio calculados através da solução do problema direto, por meio da plataforma MOHID e sua ferramenta MOHID Land.

Para encontrar os parâmetros considerados ótimos em um problema de otimização, usam‐se algumas técnicas numéricas, as quais podem ser divididas em 2 grandes grupos: os métodos determinísticos e os métodos estocásticos.

Uma das principais vantagens dos métodos determinísticos é a rápida convergência para um ponto estacionário. Porém, não há garantias de que o valor encontrado se refere a um ponto de mínimo (ou máximo) global, a não ser que sejam feitas suposições acerca do problema, as quais podem ser, por vezes, difíceis de provar na realidade [6].

Os métodos estocásticos diferem dos determinísticos por possuírem características aleatórias, permitindo que estes forneçam uma garantia, mensurada por uma probabilidade definida, de que o mínimo (ou o máximo) global poderá ser alcançado [5].

Entre as técnicas determinísticas e/ou estocásticas usadas em problemas de otimização, destacam‐se os métodos de Levenberg‐Marquardt [3] ;  [35], gradiente conjugado [31] ;  [46], Quase‐Newton [8] ;  [15], método de regularização de Tikhonov [27] ;  [28], AG [9]; [18] ;  [45], algoritmo de colisão de partículas [10]; [32] ;  [34], Luus‐Jaakola (LJ) [16]; [22]; [29] ;  [37], bem como métodos de regularização híbridos [38].

Neste artigo é utilizado o método estocástico de LJ. Ressalta‐se, porém, que a metodologia descrita neste trabalho permite a escolha de qualquer outro método determinístico ou estocástico.

2.3. Método de Luus‐Jaakola

O método estocástico de LJ foi proposto por R. Luus e T. H. I. Jaakola em 1973 [23], sendo um dos métodos de busca aleatória mais populares [22]. A ideia central desse método é considerar uma região de busca ampla, que englobe os possíveis valores das variáveis, e gerar soluções aleatórias, enquanto a região de busca torna‐se menor ao longo das iterações [20].

Primeiramente são definidos os intervalos de busca para as variáveis que se deseja estimar de acordo com o problema a ser tratado, bem como a amplitude dos referidos intervalos – denominado, onde m corresponde ao número de incógnitas. Deve‐se ainda, escolher o número de vezes (nout) em que o intervalo de busca será reduzido ao longo do processo interativo e o fator (,) pelo qual esse intervalo será contraído. Por fim, estabelece‐se o número de possíveis soluções (nint) que serão geradas nos intervalos a cada redução do mesmo ao longo do processo iterativo.

Com o algoritmo configurado, gera‐se uma primeira estimativa de forma aleatória e atribui‐se a, (=). Assim, tem‐se início ao processo iterativo, no qual são geradas as novas estimativas candidatas à solução do problema (, k = 1,..., n_out e s = 1..., n_int), com base a melhor solução encontrada ao longo das iterações, a qual encontra‐se armazenada em (). Caso o vetor contendo a nova solução, seja melhor que a solução contida em, os vetores são atualizados, ou seja, =. Ao final desse processo iterativo obtém‐se a solução considerada ótima para o problema inverso. Entende‐se como solução ótima para o problema aquela com o menor valor da função objetivo dada pela Eq. (6).

Ao longo dos anos, particular ênfase tem‐se dado aos estudos e análise da contração do intervalo de busca do método de LJ. Alguns autores propuseram novas maneiras de se realizar essa contração, possibilitando a obtenção de ótimos globais com menor número de avaliações da função objetivo e, consequentemente, maior rapidez. O leitor interessado em maiores detalhes sobre essas diferentes abordagens pode consultar [14]. Na figura 1 é descrito o pseudocódigo do método de LJ.

Figura 1. Pseudocódigo do método de Luus‐Jaakola, onde ${\textstyle Fitness({\overset {\rightarrow }{Y}})=S({\overset {\rightarrow }{Y}})}$, dado pela equação (6).

2.4. Simulador de calibração automática

O simulador de calibração automática consiste na implementação, em linguagem de programação Fortran 90, do método de otimização LJ para a estimativa dos parâmetros de interesse contidos no vetor ${\textstyle {\overset {\rightarrow }{Y}}}$ acoplado à plataforma MOHID.

Na plataforma MOHID esses dados são considerados como parâmetros de entrada do modelo, os quais são identificados por uma palavra‐chave dentro dos arquivos de dados. Assim, para modificar esses arquivos, a fim de alterar os parâmetros a serem estimados, necessita‐se saber somente em quais arquivos localizam‐se as palavras‐chave relacionadas a cada parâmetro [19] e desenvolver um processo iterativo onde ocorra a atualização desses arquivos. Ou seja, a cada estimativa gerada pelo método de LJ, os arquivos «.dat» utilizados pela ferramenta MOHID Land para realizar as simulações são atualizados com os valores obtidos pela rotina inversa.

Posteriormente, uma rotina computacional executa a plataforma MOHID sem a necessidade de abertura da interface gráfica. Internamente, a ferramenta MOHID Land «lê» os arquivos atualizados e os utiliza como dados de entrada para o modelo matemático descrito pelas equações (1) e (2). Após a sua execução, obtêm‐se os arquivos contendo as informações sobre os níveis de água na rede de drenagem de interesse. Esses valores são «lidos» por uma função contida no simulador e comparados com os dados experimentais oriundos do site do INEA por meio da equação (6). Se o valor dessa diferença for menor que os valores armazenados, os parâmetros são atualizados, caso contrário, os parâmetros permanecem inalterados. O processo é repetido até que o número de loops externos do método de LJ seja satisfeito.

Neste trabalho, objetiva‐se estimar 3 parâmetros de grande relevância na simulação dos processos que ocorrem em uma bacia hidrográfica, a saber: a altura mínima de água presente em uma célula do modelo digital do terreno, para que a mesma contribua efetivamente para o escoamento superficial durante/após um evento de precipitação, e os coeficientes de rugosidade da bacia e da rede de drenagem.

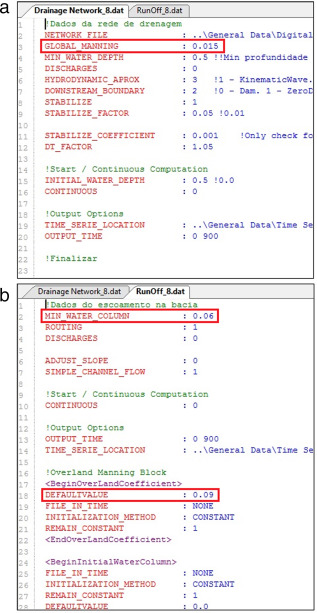
A altura mínima de água na célula não está presente diretamente nas equações (1)‐(5). No entanto, esse parâmetro indica que as águas oriundas das precipitações só começarão a escoar pela bacia após atingirem essa cota estabelecida inicialmente para, posteriormente, serem aplicadas as equações de Saint Venant, na sua forma completa ou simplificada. Já os coeficientes de rugosidade podem ser encontrados implicitamente nas equações de Saint Venant, por meio do parâmetro n (coeficiente de rugosidade de Manning, equação (4)). Nas figuras 2a e 2b são mostrados os arquivos «Drainage Network_8.dat» e «RunOff_8.dat», que contêm os parâmetros a serem alterados pelo problema inverso através do método LJ e suas respectivas palavras‐chave.

Figura 2. Arquivos contendo as palavras‐chave necessárias à execução da plataforma MOHID, ferramenta MOHID Land, onde: (a) «GLOBAL_MANNING» é o coeficiente de rugosidade do canal; (b) «MIN_WATER_COLUMN» é o mínimo de água nas células necessário para iniciar o escoamento e «DEFAULTVALUE» é o coeficiente de rugosidade da bacia hidrográfica.

Assim, é possível sintetizar o processo de calibração automática da plataforma MOHID por meio do método de LJ da seguinte maneira:

• Passo 1: configura‐se a plataforma MOHID com os valores dos parâmetros que são conhecidos a priori.
• Passo 2: configura‐se os parâmetros do método estocástico LJ que serão utilizados para a estimativa dos parâmetros de interesse contidos no vetor (${\textstyle {\overset {\rightarrow }{Y}}}$) e estipula‐se um critério de parada para o processo iterativo. Define‐se ainda a região de busca para os parâmetros que se deseja estimar.
• Passo 3: estimam‐se os valores dos parâmetros de interesse destacados nas figuras 2a e 2c (altura de água mínima na célula para iniciar o escoamento e coeficientes de rugosidade da bacia e do canal), utilizando o método LJ.
• Passo 4: com os parâmetros estimados, realiza‐se a simulação do problema direto (plataforma MOHID) e obtêm‐se os níveis de água na rede de drenagem das bacias de interesse.
• Passo 5: comparam‐se os resultados dos níveis de água (${\textstyle {\overset {\rightarrow }{h}}_{calc}}$) nos canais de drenagem obtidos no Passo 4, por meio da ferramenta numérica MOHID Land com os dados experimentais (${\textstyle {\overset {\rightarrow }{h}}_{exp}}$) utilizando a equação (6). Se o valor obtido satisfizer o critério de parada estabelecido a priori, finaliza‐se o processo. Caso contrário, volta‐se ao Passo 3 e calcule nova estimativa dos parâmetros de interesse.

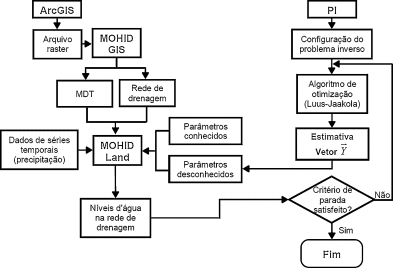
Levando‐se em consideração as etapas preliminares descritas na primeira parte deste artigo, no que se refere à obtenção de um arquivo em formato compatível com a interface MOHID GIS (arquivo ASCII Raster), a construção do modelo digital do terreno (MDT) e a rede de drenagem de uma bacia hidrográfica, até a execução da ferramenta MOHID Land para a obtenção dos níveis de água na rede de drenagem de uma bacia hidrográfica por meio da estimativa dos parâmetros contidos no vetor ${\textstyle {\overset {\rightarrow }{Y}}}$, com base no método LJ, pode‐se representar o simulador descrito aqui através da figura 3.

Figura 3. Fluxograma contendo todas as etapas necessárias para a estimativa dos níveis de água nos canais de drenagem de uma bacia hidrográfica.

Destaca‐se que Telles et al. [43] também utilizaram o método de LJ para estimar os mesmos parâmetros do vetor ${\textstyle {\overset {\rightarrow }{Y}}}$ presentes na bacia do Córrego D’Antas. Porém, no referido trabalho, deu‐se enfoque à busca de um melhor ajuste entre os dados experimentais e simulados pela plataforma MOHID, fazendo uma comparação com os resultados obtidos por Telles [42], não sendo, portanto, descrita a metodologia utilizada para a implementação do simulador de calibração automática, bem como os passos necessários para a estimativa dos parâmetros.

3. Resultados e discussões

3.1. Estudos de caso

Como exemplos de aplicação do simulador de calibração automática descrito neste artigo, foram escolhidas 2 bacias hidrográficas presentes no município de Nova Friburgo, estado do Rio de Janeiro, Brasil, a saber: bacia hidrográfica do rio Cônego e bacia do rio Santo Antônio. Ainda na primeira parte deste artigo, também foi descrito o processo de aquisição dos dados de precipitação e níveis de água da rede de drenagem das bacias hidrográficas do município de Nova Friburgo através do site do INEA. Para essa aplicação, foi escolhido o evento de precipitação ocorrido nas bacias do rio Cônego e rio Santo Antônio, no período de 18:00 horas do dia 11 de janeiro de 2011 às 00:00 horas do dia 13 de janeiro do mesmo ano. Neste período se verificaram as intensas precipitações que resultaram na tragédia que se abateu sobre a região serrana do estado do Rio de Janeiro, noticiada como a maior tragédia ambiental registrada no país.

Nas Figura 4, Figura 5 ;  Figura 6 é apresentada a variação no tempo do nível de precipitação registrado nesse período, tendo como referência as estações hidrológicas Pico do Caledônia e Olaria, localizadas na bacia do rio Cônego, e a estação Ypu, localizada na bacia do rio Santo Antônio.

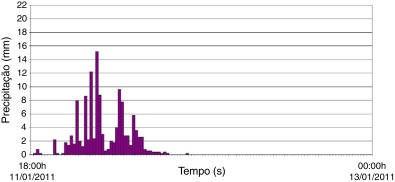
Figura 4. Intensidade das precipitações medidas no evento de 11/01/2011 às 18:00 horas até 13/01/2011 às 00:00 horas na estação Pico do Caledônia.

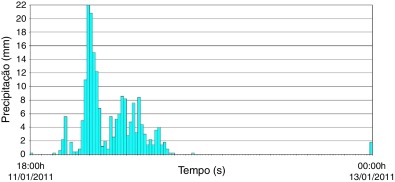
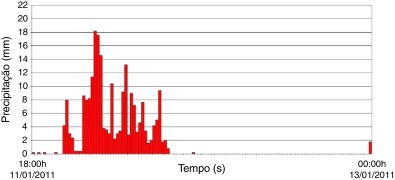
Figura 5. Intensidade das precipitações medidas no evento de 11/01/2011 às 18:00 horas até 13/01/2011 às 00:00 horas na estação Olaria.

Figura 6. Intensidade das precipitações medidas no evento de 11/01/2011 às 18:00 horas até 13/01/2011 às 00:00 horas na estação Ypu.

É possível verificar, com base nas Figura 4, Figura 5 ;  Figura 6, o quão intensas foram as precipitações ocorridas na bacia do rio Cônego durante a tragédia de 2011, onde observa‐se um acumulado de precipitação de 22 milímetros na estação de Olaria em apenas 15 minutos (figura 5).

3.2. Análise de sensibilidade

Em problemas inversos, a análise de sensibilidade tem um importante papel na estimativa dos parâmetros de interesse, uma vez que ela permite estudar, analisar e avaliar o comportamento (variação) da grandeza observável (dados experimentais) frente às variações ocorridas nestes parâmetros [36]. Um coeficiente de sensibilidade pode ser expresso pela primeira derivada parcial de uma variável em relação ao parâmetro desconhecido [1] ;  [2], dado por:

${\chi }_{i}^{j}(t_{j},{\overset {\rightarrow }{\gamma }},{\overset {\rightarrow }{Y}})=$${\frac {\partial \Omega ({\overset {\rightarrow }{t}},{\overset {\rightarrow }{\gamma }},{\overset {\rightarrow }{Y}})}{\partial Y_{i}}},{\mbox{ }}i=$$1,\ldots ,m{\mbox{ }}e{\mbox{ }}j=1,\ldots ,N_{d}$

(7)

onde ${\textstyle \Omega ({\overset {\rightarrow }{t}},{\overset {\rightarrow }{\gamma }},{\overset {\rightarrow }{Y}})}$ é uma variável de estado (variável observável); t_j é o instante de tempo no qual é obtido o dado experimental; ${\textstyle {\overset {\rightarrow }{\gamma }}}$ é o vetor dos parâmetros conhecidos (parâmetros de configuração da plataforma MOHID, ferramenta MOHID Land) e ${\textstyle {\overset {\rightarrow }{Y}}}$ é o vetor dos parâmetros que se busca estimar, que no presente estudo são os coeficientes de rugosidade da bacia hidrográfica e de sua rede de drenagem e o parâmetro que define a altura mínima de água presente nas células do MDT, para que a mesma possa contribuir efetivamente para o escoamento sobre a bacia hidrográfica. Finalmente, ${\textstyle {\chi }_{i}^{j}}$ é o coeficiente de sensibilidade no instante t_j para o parâmetro Y_j.

Como nem sempre as incógnitas que se está interessado em estimar possuem as mesmas unidades ou ordem de grandeza, é conveniente a utilização de um coeficiente de sensibilidade modificado (equação (8)), permitindo a comparação direta da sensibilidade do modelo frente às diferentes incógnitas analisadas, dado por [33]:

${\chi }_{i}^{j}(t_{j},{\overset {\rightarrow }{\gamma }},{\overset {\rightarrow }{Y}})=$$Y_{i}{\frac {\partial \Omega ({\overset {\rightarrow }{t}},{\overset {\rightarrow }{\gamma }},{\overset {\rightarrow }{Y}})}{\partial Y_{i}}},i=$$1,\ldots ,m{\mbox{ }}e{\mbox{ }}j=1,\ldots ,N_{d}$

(8)

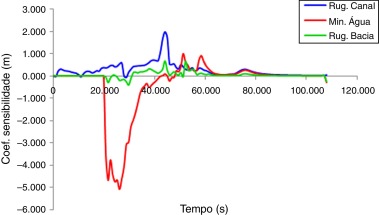
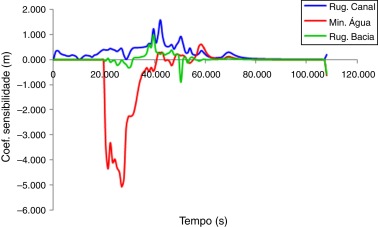
A fim de verificar se os parâmetros a serem estimados neste trabalho possuem dependência entre si, foi realizada a análise de sensibilidade dos mesmos nas estações hidrológicas de Olaria e Ypu, uma vez que a estação do Pico do Caledônia trata‐se apenas de uma estação pluviométrica (não fluviométrica). Nas Figura 7 ;  Figura 8 são apresentados os comportamentos dos coeficientes de sensibilidade descritos pela equação (8) com base no evento ocorrido em janeiro de 2011, onde é possível verificar que o parâmetro de maior sensibilidade é a altura mínima de água presente nas células do MDT.

Figura 7. Perfil dos coeficientes de sensibilidade dos parâmetros de interesse na estação de Olaria.

Figura 8. Perfil dos coeficientes de sensibilidade dos parâmetros de interesse na estação de Ypu.

Além disso, os resultados da análise de sensibilidade mostram que os parâmetros não estão correlacionados e, nesse caso, podem ser estimados de forma simultânea.

3.3. Estimativa de parâmetros

Nesta seção são apresentados os resultados do simulador de calibração automática aplicado às bacias hidrográficas do rio Cônego e rio Santo Antônio de forma isolada, com base no evento de precipitação de janeiro de 2011, cujo processo de obtenção dos dados experimentais foi descrito na Parte 1 deste artigo, assim como a construção dos arquivos base necessários à simulação.

Os resultados foram obtidos em um computador Core 2 Duo, com processador de 1,90 GHz e 2 GB de memória RAM, tendo todo o processo de implementação ocorrido na linguagem Fortran 90/95. No que se refere ao tempo de execução do problema direto, foram necessários aproximadamente 4 minutos para a realização das simulações ocorridas na bacia do rio Cônego, enquanto as simulações na bacia do rio Santo Antônio levaram em torno de 6 minutos. O consumo de tempo nos 2 casos pode ser considerado relativamente baixo, uma vez que a simulação envolvendo o episódio que resultou na tragédia de 2011 tem como base um período de 30 horas. Já o tempo de execução do problema inverso está diretamente relacionado ao número de chamadas da função objetivo, uma vez que esta necessita da execução do problema direto.

Por fim, o método de LJ foi configurado com 20 loops externos (n_out) e 10 loops internos (n_int), enquanto o coeficiente de contração do intervalo de busca foi fixado em 10⁻². Em todos os testes realizados aqui, o intervalo de busca para o coeficiente de rugosidade do canal de drenagem foi [0,0050; 0,0300] (s/m^1/3), para o coeficiente de rugosidade da bacia adotou‐se o intervalo [0,0050; 0,0300] (s/m^1/3) e para a altura mínima de água na célula foi [0,0000; 0,1000] (m). Já para o nível de água inicial da rede de drenagem ao iniciar a simulação, considerado constante em todo o leito, adotou‐se o valor de 0,50 metros para o rio Cônego e um metro para o rio Santo Antônio. Na tabela 1 são apresentados os melhores valores para os parâmetros de interesse para as 2 bacias analisadas.

Tabela 1. Valor dos coeficientes de rugosidade da bacia e sua rede de drenagem e a altura mínima de água presente nas células do MDT para que a mesma possa contribuir efetivamente para o escoamento, estimados por meio do método de Luus‐Jaakola durante o evento de janeiro de 2011

Parâmetros	Rugos. canal (s/m1/3)	Rugos. bacia (s/m1/3)	Altura mín. água (m)
Bacias
Rio Cônego	0,0201	0,0106	0,0010
Rio Santo Antônio	0,0151	0,0103	0,0602

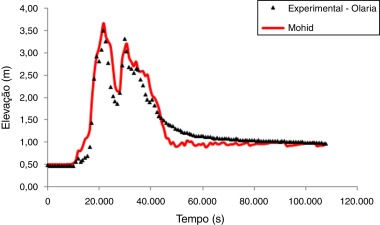
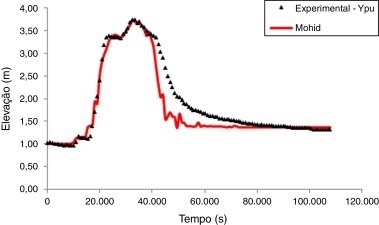
Os perfis da lâmina de água nas respectivas redes de drenagens são mostrados nas Figura 9 ;  Figura 10, onde é possível verificar que houve um bom ajuste entre os dados experimentais e os resultados numéricos obtidos pela plataforma MOHID referente às estações de Olaria e Ypu, apesar de uma pequena discrepância entre os dados ao final da onda de cheia.

Figura 9. Ajuste entre os dados experimentais e os resultados numéricos obtidos com a melhor estimativa do método de Luus‐Jaakola na estação de monitoramento Olaria, localizada no rio Cônego.

Figura 10. Ajuste entre os dados experimentais e os resultados numéricos obtidos com a melhor estimativa do método de Luus‐Jaakola na estação de monitoramento Ypu, localizada no rio Santo Antônio.

4. Conclusões

Este trabalho teve como objetivo descrever a construção de um simulador de calibração automática, utilizando o método estocástico de LJ acoplado à plataforma MOHID, com o intuito de determinar a altura mínima de água presente nas células do MDT para que a mesma contribua efetivamente para o escoamento superficial na bacia hidrográfica, bem como estimar os coeficientes de rugosidade da bacia e do canal e sua influência nos níveis (elevação) da lâmina de água na rede de drenagem. A estratégia foi aplicada em 2 bacias hidrográficas localizadas no município de Nova Friburgo, no Rio de Janeiro, do rio Cônego e rio Santo Antônio.

Os resultados obtidos por meio da metodologia descrita neste trabalho foram comparados com dados experimentais obtidos diretamente do site do INEA, para o evento de precipitação de 18 horas do dia 11 de janeiro de 2011 às 00:00 horas do dia 13 de janeiro do mesmo ano. Com base nesses resultados, apresentados nas Figura 9 ;  Figura 10, conclui‐se que as abordagens envolvendo as técnicas inversas levaram a um bom ajuste entre os dados experimentais e os valores calculados pelo modelo, mostrando‐se uma ferramenta promissora tanto do ponto de vista ambiental – por sua flexibilidade em simular diferentes cenários, contendo, inclusive, módulos de análise de qualidade da água (não contemplado neste trabalho) – como do ponto de vista social – devido à possibilidade de sua utilização no auxílio ao processo de tomada de decisões em eventos de cheias e prognósticos sobre os impactos que a elevação da lâmina d’água possa causar.

Ressalta‐se, ainda, que a metodologia descrita nesse artigo (Partes 1 e 2) poderia ter sido utilizada para a análise de qualquer outra bacia hidrográfica, bem como a escolha de outro método estocástico não alteraria a estrutura do simulador descrita neste trabalho.

Conflito de interesses

Os autores declaram não haver conflito de interesses.

Agradecimentos

Os autores agradecem o suporte financeiro proveniente da CAPES, Coordenação de Aperfeiçoamento de Pessoal de Nível Superior, do CNPq, Conselho Nacional de Desenvolvimento Científico e Tecnológico, e da FAPERJ, Fundação Carlos Chagas Filho de Amparo à Pesquisa do estado do Rio de Janeiro.

Referências

1. [1] J.V. Beck, K.J. Arnold; Parameter Estimation in Engineering and Science; John Wileyand Sons (1977)
2. [2] J.V. Beck, B. Blackwell, C.R. St Clair Jr.; Inverse Heat Conduction. III‐Posed Problems; John Wileyand Sons (1985)
3. [3] M.J. Berrocal Tito, N.C. Roberty, A.J. Silva Neto; Absorption and scattering coefficient estimation in two‐dimensional participating media using the generalized maximal entropy and Levenberg‐Marquardt; 13thInternational Atlantic Nuclear Conference: National Meeting of Reactor Physics and Thermal Hydraulics, Rio de Janeiro (2002)
4. [4] D. Brito, F.J. Campuzano, J. Sobrinho, R. Fernandes, R. Neves; Integrating operational watershed and coastal models for the Iberian Coast: Watershed model implementation – A first approach; Estuarine, Coastal and Shelf Science (2015)
5. [5] R.H. Byrd, C.L. Dert, A.H.G.R. Kan, R.B. Schnabel; Concurrent stochastic methods for global optimization, 46, Mathematical Programming (1990)
6. [6] J.F.M. Caseiro; Estratégias Evolucionárias de Optimização de Parâmetros Reais; Dissertação de Mestrado, Universidade de Aveiro, Aveiro, Portugal (2009)
7. [7] K.A. Chau; Review on integration of artificial intelligence in to water quality modeling; Marine Pollution BulletinV 52 (2006), pp. 726–736
8. [8] B. Combal, F. Baret, M. Weiss, A. Trubuil, D. Mace, A. Pragnere, et al.; Retrieval of canopy biophysical variables from bidirectional reflectance using prior information to solve the ill‐posed inverse problem; Remote Sens Environ., 84 (1) (2003), pp. 1–15
9. [9] H. Fang, S.H. Liang, A. Kuusk; Retrieving leaf area index using a genetic algorithm with canopy radiative transfer model; Remote Sens Environ., 8 (2003), pp. 257–270
10. [10] K.M. Fernandes, R.A. Tenenbaum, A.J. Silva Neto, L.T. Stutz; Comparação e desempenho de métodos estocásticos na identificação de dano estrutural via abordagem de propagação de ondas acústicas in 13^th Encontro de Modelagem Computacional; Nova Friburgo (2010)
11. [11] T.Z. Gichamo, I. Popescu, A. Jonoski, D. Solomatine; River cross‐section extraction from the ASTER global DEM for flood modeling; EMS, 31 (2012), pp. 37–46
12. [12] S.E. Hale, B. Gardiner, A. Peace, B. Nicoll, P. Taylor, S. Pizzirani; Comparison and validation of three versions of a forest wind risk model; EMS, 68 (2015), pp. 27–41
13. [13] D. Halwatura, M.M.M. Najim; Application of the HEC‐HMS model for runoff simulation in a tropical catchment; EMS, 46 (2013), pp. 155–162
14. [14] J. Jezowski, R. Bochenek, G. Ziomek; Random search optimization approach for highly multi‐modal nonlinear problems; Advances in Engineering SoftwareV 36 (2005), pp. 504–517
15. [15] A.D. Klose, A. Hielscher; Quasi‐Newton methods in optical tomographic image reconstruction; Inverse Problems, 19 (2003), pp. 387–409
16. [16] D.C. Knupp, A.J. Silva Neto, W.F. Sacco; Radiative properties estimation with the Luus‐Jaakola and the Particle Collision Algorithm; CMES, 54 (2) (2009), pp. 121–146
17. [17] J.H. Kondageski; Calibração de Modelo de Qualidade da Água para Rio utilizando Algoritmo Genético. Dissertação de Mestrado; Universidade Federal do Paraná (UFP), Curitiba (2008)
18. [18] M. Lahamas; Anatomy‐based three‐dimensional dose optimization in brachytherapy using multiobjective genetic algorithms; Med Phys., 26 (1999), pp. 1904–1918
19. [19] E.B. Lima; Problemas Inversos Aplicados à Identificação de Parâmetros Hidrodinâmicos de um Modelo do Estuário do Rio Macaé. Tese de Doutorado; Universidade do Estado do Rio de Janeiro (UERJ), Nova Friburgo (2012)
20. [20] E.B. Lima, P.P.G.W. Rodrigues, A.J. Silva Neto, M.I. Mesa, O.L. Santiago, J.L. Lugon Junior; Inverse problem for parameter estimation In Model of Estuarine Hydrodynamics. In 9^th Congreso Internacional de Ingeniería Hidráulica y 5^th Seminario Internacional del Uso Integral del Agua; Santiago, Cuba (2009)
21. [21] F. Liu, B.R. Hodges; Applying microprocessor analysis methods to river network modelling; EMS, 52 (2014), pp. 234–252
22. [22] F.S. Lobato, J.R.V. Steffen; Algoritmo de Luus‐Jaakola aplicado a um problema inverso de fermentação batelada alimentada. TEMA Tend; Mat. Apl. Comput., 9 (3) (2008), pp. 417–426
23. [23] R. Luus, T.H.I. Jaakola; Optimization by direct search and systematic reduction of the size of search region; AIChE Journal, 19 (1973), pp. 760–766
24. [24] G.B. Lyra, R.A. Cecílio, S.S. Zanetti; Coeficiente de rugosidade de Manning para o rio Paracatu; RBEAA, 14 (4) (2010), pp. 343–350
25. [25] Maretec. MOHID. Descrição do MOHID. Essentia Editora: Campos dos Goytagazes, 2012.
26. [26] G. Ou, X. Chen, A. Kilic, S. Bartelt-Hunt, Y. Li, A. Samal; Development of a cross‐section based streamflow routing package for MODFLOW; EMS, 50 (2013), pp. 132–143
27. [27] R.P.F. Paz; Estimativa de propriedades radiativas em meios participantes unidimensionais homogêneos como o funcional de Tikhonov e distâncias de Bregman baseadas nos momentos da q‐discrepância. Tese de Doutorado; Universidade do Estado do Rio de Janeiro (UERJ), Nova Friburgo (2005)
28. [28] R.A. Ramlau; New approach for the iterative regularization of nonlinear operator equations. In Applied Inverse Problems; Cirencester, UK (2005)
29. [29] P.P.G.W. Rodrigues, Y.M. Gonzalez, E.P. Sousa, F.D. Moura Neto; Estimativa dos parâmetros de dispersão em rios montanhosos através do algoritmo de Luus‐Jaakola; RBRH, 17 (2012), pp. 87–96
30. [30] H. Roux, D. Dartus; Sensitivity analysis and predictive uncertainty using inundation observations for parameter estimation in open‐channel inverse problem; J Hydrol Eng, 134 (2008), pp. 541–549
31. [31] R. Roy, E. Sevi-Muraca.; Numerical study of gradient‐based nonlinear optimization methods for contrast enhanced optical tomography; Opt Express., 9 (1) (2001), pp. 49–65
32. [32] W.F. Sacco, C.R.E. Oliveira, C.M.N. Pereira; Two stochastic optimization algorithms applied to nuclear reactor core design; In: Nuclear Energy, 48 (6) (2006), pp. 525–539
33. [33] A.J. Silva Neto; Problemas Diretos e Inversos em Transferência Radiativa e Processos Difusivos. Tese de Professor Titular; Universidade do Estado do Rio de Janeiro (UERJ), Nova Friburgo (2012)
34. [34] A.J. Silva Neto, J.C. Becceneri; Técnicas de Inteligência Computacional Inspiradas na Natureza – Aplicação em Problemas Inversos em Transferência Radiativa; Notas em Matemática Aplicada, 41, SBMAC (2012)
35. [35] A.J. Silva Neto; Özisik. An inverse problem of simultaneous estimation of radiation phase function, albedo and optical thickness; J Quant Spectros Rad., 53 (4) (1995), pp. 379–409
36. [36] C.K.F. Silva, Z.E. Silva, M.P. Andrade, M.A.C. Silva, J.P.A. Júnior; Transferência de massa em tomate cereja (Lycopersicon Esculentum Var. Cerasiforme) submetido a desidratação osmótica – modelagem e estimação dos parâmetros. In 11^thBrazilian Congress of Thermal Sciences and Engineering; ABCM, Curitiba (2006)
37. [37] F.M. Silva, A.J. Silva Neto, L.D.T. Câmara; Modelagem da dinâmica de percolação em cromatografia mediante fenomenologia de adsorção e dessorção; 13th Encontro de Modelagem Computacional, Nova Friburgo, Rio de Janeiro (2010)
38. [38] F.J.C.P. Soeiro, P.O. Soares, A.J. Silva Neto; Solution of inverse radiative transfer problems with artificial neural networks and hybrid methods. Inverse Problems in Engineering Seminar, v. 13, Cincinnati, Ohio; Proceedings IPES (2004)
39. [39] S. Srinivasulu, A. Jain; River flow prediction using an integrated approach; J Hydrol Eng, 14 (2009), pp. 75–83
40. [40] R. Szymkiewicz; Numerical modeling in open channel hydraulics; Springer (2010)
41. [41] G. Tayfur, S. Bartetta, T. Moramarco; Genectic Algorithm based dischange estimation at sites receiving lateral inflows; J Hydrol Eng, 14 (2009), pp. 463–474
42. [42] W.R. Telles Previsão do Comportamento Hidráulico de um Rio com Base na Estimativa de Coeficientes que Controlam seu Escoamento. Estudo de Caso: Rio Bengalas, Nova Friburgo‐RJ. Tese de Doutorado, Universidade do Estado do Rio Janeiro (UERJ), 2014.
43. [43] W.R. Telles, P.P.G.W., Rodrigues, A.J. Silva Neto Calibração Automática de um Simulador Aplicado a um Rio de Montanha Empregando Dados Experimentais de Precipitação e Nível–Estudo de Caso: Córrego D’Antas, RJ. Revista Brasileira de Recursos Hídricos. No prelo 2016.
44. [44] Y. Wang, K. Brubaker; Multi‐objective model auto‐calibration and reduced parameterization: Exploiting gradient‐based optimization tool for a hydrologic model; EMS, 70 (2015), pp. 1–15
45. [45] R. Zhang, W. Verkruysse, B. Choi, J.A. Viator, B. Jung, L.O. Svaasand, et al.; Determination of human skin optical properties from spectrophotometric measurements based on optimization by genetic algorithms; J Biomed Optics., 10 (2) (2005), pp. 24–30
46. [46] W. Zhu, Y. Wang, Y. Yao; Iterative total least‐square image reconstruction algorithm for optical tomography by the conjugate gradient method; J Opt Soc Am A., 14 (4) (1997), pp. 799–807