Transpiration effect on stagnation-point flow of a Carreau nanofluid in the presence of thermophoresis and Brownian motion

Abstract

The effect of transpiration on magnetohydrodynamic stagnation-point flow of a Carreau nanofluid toward a stretching/shrinking sheet in the presence of thermophoresis and Brownian motion was investigated numerically. The transformed governing partial differential equations are solved using Runge–Kutta coupled with shooting technique. The effect of pertinent parameters on velocity, temperature and concentration profiles along with the friction factor, local Nusselt and Sherwood numbers is presented graphically and through tables. It is observed that, increasing values of the thermophoresis parameter enhances the heat and mass transfer rate, whereas the Weissenberg number enlarges the momentum boundary layer thickness along with the heat and mass transfer rate. A good agreement of the present results has been observed by comparing with the published results.

Keywords

MHD; Carreau fluid; Thermophoresis; Brownian motion; Stagnation-point flow

1. Introduction

The problem of convective heat and mass transfer past a permeable stretching/shrinking sheet plays a vital role in manufacturing industries in design of reliable equipments. The study of fluid flow through a stretching sheet is a wide area of research, and it has gained the attention of many researchers due to its enormous industrial and engineering applications such as extrusion of plastic and rubber sheets, glass blowing, cooling/drying of papers and textiles, hot rolling polymer processing industries, glass fiber and textile production, petroleum production, crystal growing, wire drawing, fiber spinning, and the cooling of nuclear reactors. In view of these wide varieties of applications Crane [1] has pioneered the work on steady two-dimensional flow over a permeable stretching sheet. Sandeep and Sulochana [2] studied the influence of chemical reaction on MHD mixed convective micropolar fluid flow through a stretching/shrinking surface in the presence of non-uniform heat generation/absorption and observed the dual solutions. Singh and Chamkha [3] observed the dual solutions for viscous fluid flow and heat transfer toward a linearly shrinking plate with second order slip. Nadeem et al. [4] discussed the suction/injection effects on MHD Casson nanofluid flow through a nonlinearly shrinking surface in the presence of convective boundary conditions. This study was further extended by many authors such as Mansur et al. [5], Qasim and Noreen [6], Robert et al. [7], Lok and Pop [8], Mahapatra and Samir Kumar [9], Sharma et al. [10], Makinde et al. [11], Raju et al. [12], Bhattacharyya [13], Prakash et al. [14], Yacob et al. [15], and Wahiduzzaman et al. [16] to investigate several aspects such as suction/blowing, viscous dissipation, thermal radiation, Buoyancy effects, chemical reaction, and heat generation over a stretching/shrinking surface.

In the recent years, the problem of stagnation point flow has received tremendous research interest. Stagnation-point flow is seen in every type of flow whenever the fluid impinges on a solid object. Then, the fluid velocity reduces to zero and the fluid pressure and heat mass transfer rates are highest at the stagnation point area. The studies of stagnation-point flow toward a stretching or shrinking sheet are classic in fluid mechanics because of its enormous practical applications in industry and engineering, such as cooling of nuclear reactors and cooling of electronic devices by fans, in the design of radial diffusers and thrust bearings, drag reduction and many hydrodynamic processes. In view of aforesaid applications Wang [17] studied the stagnation point flow through a shrinking sheet and observed that due to increase in boundary layer thickness the heat transfer rate decreases with the rate of shrinking. The effect of induced magnetic field on MHD stagnation point flow and heat transfer of an viscous incompressible fluid through a stretching surface is studied by Ali et al. [18] and they compared their results in the absence of magnetic field parameters with previously derived results and the results are found to be good. Akbar et al. [19] analyzed the influence of Brownian motion, thermophoresis and radiation effects on steady two-dimensional stagnation point flow of nanofluid past a stretching cylinder in the presence of convective boundary conditions. Rushi Kumar et al. [20] studied the effect of chemical reaction on MHD flow through a vertical cone with variable electrical conductivity. A lot of work on stagnation-point flow is done by the researchers [21], [22], [23], [24], [25], [26], [27], [28], [29], [30], [31], [32], [33] and [34].

Moreover, shear stress is directly proportional to shear rate of both Newtonian and non-Newtonian fluids. Carreau fluid is a type of Newtonian fluid. The study of peristaltic flow of a Carreau fluid attracted the attention of many researchers because of its wide applications in the field of science and technology viz. Physiology, treatment of diagnostic diseases, neurological treatment, cancer treatment. The effect of magnetic field on a Carreau (Newtonian) fluid has been used for treatment of gastronomic pathologies, hypertension, cancer tumor treatment, hyperthermia, blood reduction during surgeries, etc. Although many researchers such as Raju et al. [35] and [36], Akbar et al. [37], Riaz et al. [38], Jasmine Benazir et al. [39] and Nadeem et al. [40] addressed the non-Newtonian fluid through different channels, in all the aforesaid investigations, a less work has been available on the flow of Carreau fluids past a stretching/shrinking sheet. Very recently, the researchers [41], [42], [43] and [44] investigated the heat and mass transfer in magnetohydrodynamic flows by considering the Buongiorno’s model.

In this study, we investigated the influence of transpiration on the flow of a Carreau nanofluid near a stagnation-point toward a stretching/shrinking sheet in the presence of Brownian motion and thermophoresis effects. The governing partial differential equations are transformed into nonlinear ordinary differential equations by using appropriate similarity transformations and then solved numerically. The influence of non-dimensional governing parameters namely magnetic field parameter, power-law index, Weissenberg number, Brownian motion, thermophoresis and stretching/shrinking parameter on velocity, temperature and concentration profiles along with friction factor, local Nusselt and Sherwood numbers is discussed and presented through graphs and tables for both suction and injection cases and obtained the dual solutions.

2. Mathematical formulation

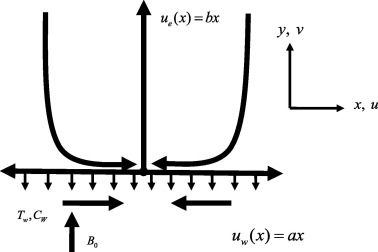
Consider a steady two dimensional stagnation point flow of an incompressible Carreau nanofluid over a wall coinciding with plane y = 0, and the flow is being confined to ${\textstyle y>0}$. A magnetic field of strength ${\textstyle B_{0}}$ is applied along x-direction as displayed in Fig. 1. Induced magnetic field is neglected in this study. Thermophoresis and Brownian motion effects are taken into account. The flow is generated due to the linear stretching. Extra stress tensor for Carreau fluid is [16],

${\overline {\tau }}_{ij}={\eta }_{0}\left[1+{\frac {\left(n-1\right)}{2}}{\left(\Gamma {\overline {\overset {\cdot }{\gamma }}}\right)}^{2}\right]{\overline {\overset {\cdot }{\gamma }}}_{ij}$

(1)

Figure 1. Physical model of the problem.

In which ${\textstyle {\overline {\tau }}_{ij}}$ is the extra stress tensor, ${\textstyle {\eta }_{0}}$ is the zero shear rate viscosity, ${\textstyle \Gamma }$ is the time constant, n   is power law index and ${\textstyle {\overline {\overset {\cdot }{\gamma }}}_{ij}}$ is defined as

${\overline {\overset {\cdot }{\gamma }}}={\sqrt {{\frac {1}{2}}{\sum }_{i}{\sum }_{j}{\overline {\overset {\cdot }{\gamma }}}_{ij}{\overline {\overset {\cdot }{\gamma }}}_{ji}}}=$${\sqrt {\frac {1}{2}}}\prod {\mbox{.}}$

(2)

Here ${\textstyle \prod }$ is the second invariant strain tensor. The physical model of the problem is displayed in Fig. 1.

Flow equation for Carreau fluid model after applying the boundary layer approximations can be defined as follows:

${\frac {\partial u}{\partial x}}+{\frac {\partial v}{\partial y}}=$$0{\mbox{,}}$

(3)

$u{\frac {\partial u}{\partial x}}+v{\frac {\partial u}{\partial y}}=$${\nu }_{f}{\frac {{\partial }^{2}u}{\partial y^{2}}}+{\nu }_{f}{\frac {3(n-1){\Gamma }^{2}}{2}}{\left({\frac {\partial u}{\partial y}}\right)}^{2}{\frac {{\partial }^{2}u}{\partial y^{2}}}+$${\frac {\sigma {\beta }_{0}^{2}}{{\rho }_{f}}}(u_{e}-u)+u_{e}{\frac {\partial u_{e}}{\partial x}}{\mbox{,}}$

(4)

$u{\frac {\partial T}{\partial x}}+v{\frac {\partial T}{\partial y}}=$${\frac {k_{f}}{{\rho }_{f}c_{p}}}{\frac {{\partial }^{2}T}{\partial x^{2}}}+$$\tau \left(D_{B}{\frac {\partial C}{\partial y}}{\frac {\partial T}{\partial y}}+\right.$$\left.{\frac {D_{T}}{T_{\infty }}}{\left({\frac {\partial T}{\partial y}}\right)}^{2}\right){\mbox{,}}$

(5)

$u{\frac {\partial C}{\partial x}}+v{\frac {\partial C}{\partial y}}=$$D_{B}{\frac {{\partial }^{2}C}{\partial y^{2}}}+{\frac {D_{T}}{T_{\infty }}}\left({\frac {{\partial }^{2}T}{\partial y^{2}}}\right){\mbox{,}}$

(6)

Here u and v are velocity components along x and y   directions, respectively, where ${\textstyle {\nu }_{f}}$ is kinematic velocity, ${\textstyle \sigma }$ is the electrical conductivity, ${\textstyle {\rho }_{f}}$ is the density of the base fluid and ${\textstyle D_{B}\quad {\mbox{and}}\quad D_{T}}$ are the Brownian motion and thermophoretic diffusion coefficients. It is noticed that for power law index ${\textstyle \left(n=1\right)}$ our problem reduced to the case of Newtonian fluid while for ${\textstyle n>1}$ phenomena remains for non-Newtonian fluid. The corresponding boundary conditions are

${\begin{array}{c}u=u_{w}(x)=ax{\mbox{,}}\quad v=v_{w}(x){\mbox{,}}\quad T=T_{1}{\mbox{,}}\quad C=C_{1}\quad {\mbox{at}}\quad y=0\\u\rightarrow u_{e}(x)=bx{\mbox{,}}\quad v\rightarrow 0{\mbox{,}}\quad T\rightarrow T_{2}{\mbox{,}}\quad C\rightarrow C_{2}\quad {\mbox{as}}\quad y\rightarrow \infty \end{array}}$

(7)

In which ${\textstyle b>0}$ is constant, we assume that ${\textstyle u_{w}(x)=ax}$ and ${\textstyle u_{e}(x)=bx}$ are the velocities near and away from the wall respectively. Introducing the following similarity transformations

$\eta ={\sqrt {{\frac {b}{\nu }}_{f}}}y{\mbox{,}}\quad \psi =$${\sqrt {b{\nu }_{f}}}xf(\eta ){\mbox{,}}\quad \theta (\eta )=$${\frac {T-T_{\infty }}{T_{w}-T_{\infty }}}{\mbox{,}}\quad \phi (\eta )=$${\frac {C-C_{\infty }}{C_{W}-C_{\infty }}}$

(8)

where η   is the similarity variable and ${\textstyle \psi }$ is the stream function defined in the usual notation as ${\textstyle u=\partial \psi /\partial y}$ and ${\textstyle v=-\partial \psi /\partial x}$.

Which identically satisfy the equation of continuity defined in Eq. (3). By using aforesaid similarity transformation defined in Eq. (7) on Eqs. (2), (3), (4), (5) and (6), we get the following:

$f^{'''}-{\left(f^{'}\right)}^{2}+{ff}^{''}+1+{\frac {3(n-1){We}^{2}}{2}}f^{'''}{\left(f^{''}\right)}^{2}+$$M^{2}(1-f^{'})=0{\mbox{,}}$

(9)

$Pr\quad {\theta }^{''}+f{\theta }^{''}+Nb\quad {\theta }^{'}{\phi }^{'}+$$Nt{\left({\theta }^{'}\right)}^{2}=0{\mbox{,}}$

(10)

${\phi }^{''}+{\frac {Nt}{Nb}}{\theta }^{''}+Scf{\phi }^{'}=$$0{\mbox{,}}$

(11)

The boundary conditions (7) reduce to

${\begin{array}{l}f=s{\mbox{,}}\quad f^{'}=\lambda {\mbox{,}}\quad \theta =1{\mbox{,}}\quad \phi =1\quad {\mbox{at}}\quad \eta =0\\f\rightarrow 0{\mbox{,}}f^{'}\rightarrow 1{\mbox{,}}\quad \theta \rightarrow 0{\mbox{,}}\quad \phi \rightarrow \quad 0\quad {\mbox{as}}\quad \eta \rightarrow \infty \end{array}}$

(12)

where ${\textstyle s=-v_{w}/{\left(av\right)}^{1/2}{\mbox{,}}\quad s>0(i.e.v_{w}<0)}$ corresponding to suction and ${\textstyle s<0(i.e.v_{w}>0)}$ corresponding to blowing case. Here ${\textstyle \lambda =a/b}$ is the stretching/shrinking parameter, ${\textstyle {We}^{2}={\frac {b^{3}x^{2}{\Gamma }^{2}}{\nu }}}$ is the Weissenberg number, ${\textstyle M^{2}={\frac {\sigma B_{0}^{2}}{\rho b}}}$ is the magnetic parameter, ${\textstyle Pr={\frac {k}{\mu c_{p}}}}$ is the Prandtl number, ${\textstyle Nb={\frac {\tau D_{B}(C_{w}-C_{\infty })}{\nu }}}$ is the Brownian motion parameter, ${\textstyle N_{t}={\frac {\tau D_{T}(T_{w}-T_{\infty })}{\nu T_{\infty }}}}$ is the Thermophoresis parameter, and ${\textstyle Sc={\frac {\nu }{D_{B}}}}$ is the Schmidt number. After using boundary layer approximations wall shear stress ${\textstyle {\tau }_{w}}$ is given by

${\tau }_{w}={\frac {\partial u}{\partial x}}+{\frac {(n-1){\Gamma }^{2}}{2}}{\left({\frac {\partial u}{\partial y}}\right)}^{3}$

(13)

The coefficient of skin friction is defined as

$c_{f}={\frac {{\tau }_{w}}{\rho u_{w}^{2}}}$

(14)

In dimensionless form skin friction is defined as

${\sqrt {Re}}c_{f}={\left[f^{''}(\eta )+{\frac {(n-1){We}^{2}}{2}}{\left(f^{''}(\eta )\right)}^{3}\right]}_{\eta =0}$

(15)

The local Nusselt and Sherwood numbers are given by

${Re}_{x}^{-1/2}{Nu}_{x}=-{\theta }^{'}(0){\mbox{,}}$

(16)

${Re}_{x}^{-1/2}{Sh}_{x}=-{\phi }^{'}(0){\mbox{,}}$

(17)

3. Results and discussion

The nonlinear ordinary differential Eqs. (9), (10) and (11) with respect to the boundary conditions (12) are solved numerically using Runge–Kutta based shooting technique (Sandeep and Sulochana [29]). In order to get the clear insight into the problem, the results obtained show the influence of the non-dimensional governing parameters namely Magnetic field parameter M, power-law index n, thermophoresis parameter Nt, Brownian motion parameter Nb  , stretching/shrinking parameter ${\textstyle \lambda }$, Weissenberg number We on velocity, temperature and concentration profiles of the flow. In the present study, for numerical computation we have considered the non-dimensional parameter values such as We = 0.3; M = 1; Nb = 0.1; Nt = 0.1; Pr = .7; Sc = 0.6; ${\textstyle \lambda =2}$. These values are kept as common in the entire study except the varied values as shown in respective figures and tables. In the present study we considered two cases such as suction and injection and obtained dual solutions by keeping S value S > 0 and S < 0 for suction and injection cases respectively.

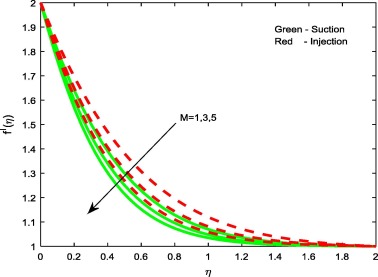
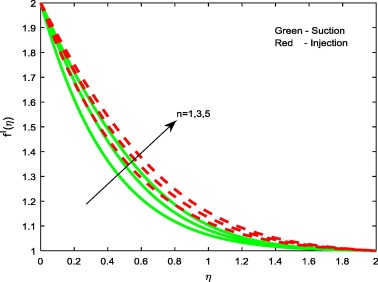
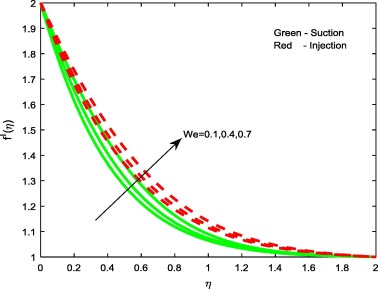
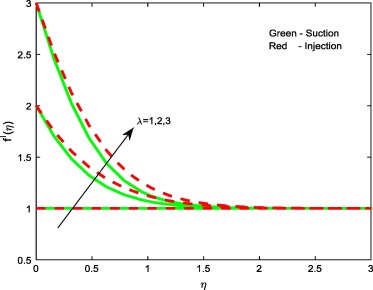
Figure 2, Figure 3, Figure 4 and Figure 9 depict the influence of the non-dimensional parameters such as magnetic field M, power-law index n, Weissenberg number We   and stretching/shrinking parameter ${\textstyle \lambda }$ on velocity profiles of the flow. It is evident from Fig. 2 that rising values of the magnetic field parameter M depreciate the velocity profiles for both suction and injection cases. This is due to the fact that the effect of horizontal magnetic field on electrically conducting fluid creates a drag force and develops the body force known as Lorentz force. This force reduces the motion of the fluid; hence, it causes to reduce in the velocity field. From Figure 3 and Figure 4 it is noticed that increasing values of the power-law index parameter n and Weissenberg number We enhances the velocity profiles for both the cases. Physically, rising values of the power-law index increase the nonlinearity of the sheet, and this helps to reduce the resistive force. In Fig. 9 it is observed that increasing values of ${\textstyle \lambda }$ enhances the velocity profiles for both cases. Physically, rising values of the stretching parameter enhance the stretching velocity of the flow. This leads to increase the momentum boundary layer thickness.

Figure 2. Velocity profiles for different values of M.

Figure 3. Velocity profiles for different values of n.

Figure 4. Velocity profiles for different values of We.

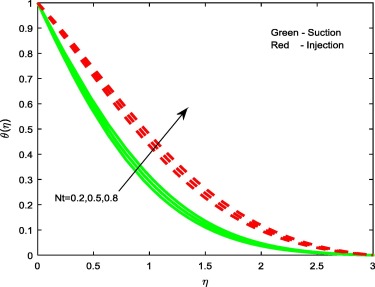
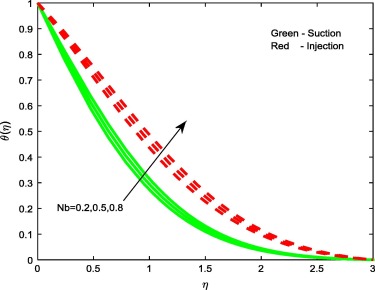
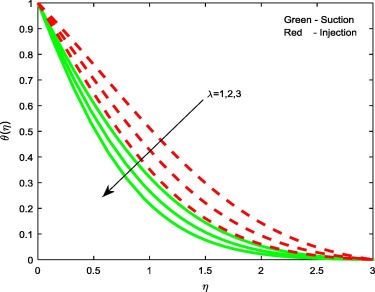
Figure 5, Figure 7 and Figure 10 display the influence of the non-dimensional parameters such as thermophoresis parameter Nt, Brownian motion parameter Nb   and stretching/shrinking parameters ${\textstyle \lambda }$ on temperature profiles of the flow. From Figure 5 and Figure 7 it is evident that increasing values of Nt and Nb enhances the temperature profiles for both the cases. This is due to the fact that, different nanoparticles have different values of Nt and Nb. This leads to different heat transfer rate. These two particles can be used to control the heat transfer rate in a nanofluid. As a result, boundary layer thickness of the thermal field increases with enhancement in the values of Nt and Nb  . But we have noticed opposite trend in case of stretching/shrinking parameter. That is rise in ${\textstyle \lambda }$ declines the temperature profiles for both the cases. This leads to enhance the heat transfer rate.

Figure 5. Temperature profiles for different values of Nt.

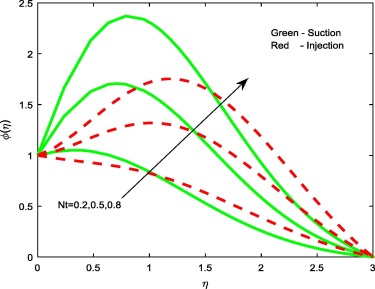
Figure 6. Concentration profiles for different values of Nt.

Figure 7. Temperature profiles for different values of Nb.

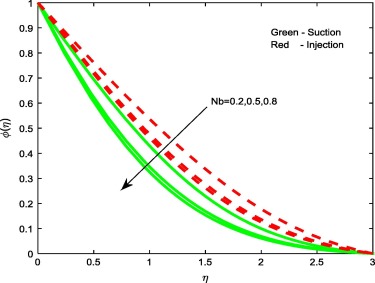
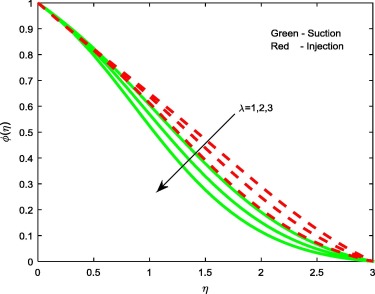
Figure 6, Figure 8 and Figure 11 reveal the effect of thermophoresis parameter Nt, Brownian motion parameter Nb   and Stretching/shrinking parameter ${\textstyle \lambda }$ on concentration profiles of the flow. Brownian motion and thermophoresis parameters have an opposite effect on concentration profiles (see Figure 6 and Figure 8). Fig. 6 portrays that the enhancement in the value of Nt improves the concentration profiles for both the cases, whereas in case of Brownian motion parameter and stretching/shrinking parameter, increase in Nb   and ${\textstyle \lambda }$ depresses concentration profiles for both the cases. The reason behind this is Brownian motion helps to heat the fluid in the boundary layer and simultaneously exacerbates particle deposition away from the fluid regime or onto the surface; thereby, it is seen reduction in the concentration profiles.

Figure 8. Concentration profiles for different values of Nb.

Figure 9. Velocity profiles for different values of ${\textstyle \lambda }$.

Figure 10. Temperature profiles for different values of ${\textstyle \lambda }$.

Figure 11. Concentration profiles for different values of ${\textstyle \lambda }$.

Table 1 and Table 2 depict the effects of non-dimensional governing parameters on friction factor, local Nusselt and Sherwood numbers for both suction and injection cases. It is evident from the tables that rise in the magnetic field and thermophoresis parameters depreciates the heat and mass transfer rate. As we discussed above, the thermophoresis and Brownian motion values are not uniform for all nanoparticles. This leads to decline the heat and mass transfer rate. Increasing values of non-Newtonian parameter and stretching parameter enhances the heat and mass transfer rate but reduces the skin friction coefficient. A similar type of result has been observed with the increase in Weissenberg number. Physically, rising values of the Weissenberg number boost-up the thermal conductivity of the flow, and hence the heat transfer rate. Table 3 depicts the validation of the present study by comparing with the existed studies. We found a good agreement of the present results. This proves the validity of the present results along with the numerical technique used in the present study.

Table 1. Variation in ${\textstyle f^{''}(0)}$, ${\textstyle -{\theta }^{'}(0)}$ and ${\textstyle -{\phi }^{'}(0)}$ at different non-dimensional parameters for suction case.

M	n	We	Nt	Nb	${\textstyle \lambda }$	${\textstyle f^{''}(0)}$	${\textstyle -{\theta }^{'}}$ (0)	${\textstyle -{\phi }^{'}}$ (0)
1						−2.525906	1.013520	0.445605
3						−3.003430	1.005620	0.445503
5						−3.428428	0.999722	0.445533
	1					−2.410951	1.008874	0.445806
	3					−2.740310	1.021423	0.445569
	5					−2.964644	1.028777	0.445835
		0.1				−2.426350	1.009514	0.445770
		0.4				−2.593440	1.016104	0.445561
		0.7				−2.815233	1.023965	0.445684
			0.2			−2.525086	0.962819	−0.284024
			0.5			−2.525087	0.901708	−1.843874
			0.8			−2.525087	0.844223	−3.096175
				0.2		−2.525087	0.951278	0.640987
				0.5		−2.525087	0.857436	0.838972
				0.8		−2.525087	0.770151	0.887667
					1	0.000000	0.860143	0.308584
					2	−2.525086	0.984021	0.309574
					3	−6.100597	1.112523	0.319893

Table 2. Variation in ${\textstyle f^{''}(0)}$, ${\textstyle -{\theta }^{'}(0)}$ and ${\textstyle -{\phi }^{'}(0)}$ at different non-dimensional parameters for injection case.

M	n	We	Nt	Nb	${\textstyle \lambda }$	${\textstyle f^{''}(0)}$	${\textstyle -{\theta }^{'}}$ (0)	${\textstyle -{\phi }^{'}}$ (0)
1						−1.968908	0.615412	0.530400
3						−2.447425	0.606141	0.530317
5						−2.871317	0.599465	0.530344
	1					−1.884604	0.612845	0.530420
	2					−2.146035	0.620488	0.530376
	3					−2.344675	0.625674	0.530468
		0.1				−1.895195	0.613175	0.530414
		0.4				−2.022650	0.617008	0.530374
		0.7				−2.211498	0.622251	0.530399
			0.2			−1.967600	0.550167	0.210043
			0.5			−1.967600	0.509256	−0.157505
			0.8			−1.967600	0.471057	−0.341803
				0.2		−1.967600	0.545343	0.480295
				0.5		−1.967600	0.490702	0.541782
				0.8		−1.967600	0.439984	0.556700
					1	0.000000	0.446399	0.372719
					2	−1.967600	0.564433	0.376997
					3	−4.902551	0.685096	0.384657

Table 3. Comparison of the present results for skin friction coefficient when ${\textstyle M=Pr=Sc=Nt=Nb=We=0{\mbox{,}}\quad n=1}$ .

${\textstyle \lambda }$	Akbar et al. [19]	Mahapatra and Samir Kumar [9]	Present results
0	1.2326	1.2326	1.232612
0.1	1.1466	1.1466	1.146610
0.2	1.0511	1.0511	1.051101
0.3	0.7133	0.7133	0.713311

4. Conclusions

This study presents a numerical solution for analyzing the heat and mass transfer in the Carreau nanofluid near the stagnation-point toward a permeable stretching/shrinking sheet in the presence of Brownian motion and thermophoresis effects. Conclusions of the present study are as follows:

• Rise in non-Newtonian parameter effectively enhances the heat and mass transfer rate.
• Magnetic field parameter has tendency to control the flow field.
• Dual solutions exist only for certain range of suction/injection parameter.
• Momentum, thermal and concentration boundary layers are highly significant in injection case while compared with the suction case.
• Weissenberg number has tendency to enlarge the momentum boundary layer thickness along with the heat and mass transfer rate.

References

1. [1] L.J. Crane; Flow past a stretching plate; Z. Angew. Math. Phys., 21 (1970), pp. 645–647
2. [2] N. Sandeep, C. Sulochana; Dual solutions for unsteady mixed convection flow of MHD micropolar fluid over a stretching/shrinking sheet with non-uniform heat source/sink; Eng. Sci. Technol. Int. J., 18 (2015), pp. 738–745
3. [3] G. Singh, A.J. Chamkha; Dual solutions for second-order slip flow and heat transfer on a vertical permeable shrinking sheet; Ain Shams Eng. J., 4 (2013), pp. 911–917
4. [4] S. Nadeem, Rizwan Ul Haq, C. Lee; MHD flow of a Casson fluid over an exponentially shrinking sheet; Sci. Iranica B, 19 (6) (2012), pp. 1550–1553
5. [5] S. Mansur, A. Ishak, I. Pop; The magnetohydrodynamic stagnation-point flow of a nanofluid over a stretching/shrinking sheet with suction; PLoS ONE, 10 (3) (2015) pone.0117733 http://dx.doi.org/10.1371/journal pone.0117733
6. [6] M. Qasim, S. Noreen; Heat transfer in the boundary layer flow of a Casson fluid over a permeable shrinking sheet with viscous dissipation; Eur. Phys. J. Plus, 129 (7) (2014) http://dx.doi.org/10.1140/epjp/i2014-14007-5
7. [7] Robert A. Van Gorder, K. Vajravelu, I. Pop; Hydromagnetic stagnation-point flow over a stretching or shrinking sheet; Meccanica, 47 (1) (2012), pp. 31–50
8. [8] Y.Y. Lok, I. Pop; Stretching or shrinking sheet problem for unsteady separated stagnation-point flow; Meccanica, 49 (6) (2014), pp. 1479–1492
9. [9] T.R. Mahapatra, N. Samir Kumar; Stability of dual solutions in stagnation-point flow and heat transfer over a porous shrinking sheet with thermal radiation; Meccanica, 48 (1) (2013), pp. 23–32
10. [10] R. Sharma, A. Ishak, I. Pop; Stability analysis of magnetohydrodynamic stagnation-point flow toward a stretching/shrinking sheet; Comput. Fluids, 102 (10) (2014), pp. 94–98
11. [11] O.D. Makinde, W.A. Khan, Z.H. Khan; Buoyancy effects on MHD stagnation point flow and heat transfer of a nanofluid past a convectively heated stretching/shrinking sheet; Int. J. Heat Mass Transf., 62 (2013), pp. 526–533
12. [12] C.S.K. Raju, N. Sandeep, V. Sugunamma; Dual solutions for three-dimensional MHD flow of a nanofluid over a nonlinearly permeable stretching sheet; Alex. Eng. J., 55 (2016), pp. 151–162
13. [13] K. Bhattacharyya; Dual solutions in stagnation-point flow and mass transfer with chemical reaction past a stretching/shrinking sheet; Int. Commun. Heat Mass Transfer, 38 (7) (2011), pp. 917–922
14. [14] J. Prakash, B. Rushi Kumar, R. Sivaraj; Radiation and Dufour effects on unsteady MHD mixed convective flow in an accelerated vertical wavy plate with varying temperature and mass diffusion, Walailak; J. Sci. Technol., 11 (2014), pp. 939–954
15. [15] N.R. Yacob, A. Ishak, I. Pop; Melting heat transfer in boundary layer stagnation point flow towards a stretching/shrinking sheet in a micropolar fluid; Comput. Fluids, 47 (1) (2011), pp. 16–21
16. [16] M. Wahiduzzaman, Md. Shakhaoath Khan, Ifsana Karim; MHD convective stagnation flow of nanofluid over a shrinking surface with thermal radiation, heat generation and chemical reaction; Proc. Eng., 105 (2015), pp. 398–405
17. [17] CY. Wang; Stagnation flow towards a shrinking sheet; Int. J. Non-Linear Mech., 43 (2008), pp. 377–382
18. [18] F.M. Ali, R. Nazar, N.M. Arifin, I. Pop; MHD stagnation-point flow and heat transfer towords stretching sheet with induced magnetic field; Appl. Math. Mech. –Engl. Ed., 32 (4) (2011), pp. 409–418
19. [19] N.S. Akbar, S. Nadeem, R. Ul Haq, Z.H. Khan; Radiation effects on MHD stagnation-point flow of nanofluid towards a stretching surface with convective boundary condition; Chin. J. Aeronaut., 26 (6) (2013), pp. 1389–1397
20. [20] B. Rushi Kumar, R. Sivaraj, A. Jasmine Benazin; Chemically reacting MHD free convective flow over a vertical cone with variable electric conductivity; Int. J. Pure Appl. Math., 101 (2015), pp. 821–828
21. [21] M. Turkyilmazoglu, I. Pop; Exact analytical solutions for the flow and heat transfer near the stagnation point on a stretching/shrinking sheet in a Jeffrey fluid; Int. J. Heat Mass Transf., 57 (1) (2013), pp. 82–88
22. [22] C.S.K. Raju, N. Sandeep, S. Saleem, Effects of induced magnetic field and homogeneous heterogeneous reactions on stagnation flow of a Casson fluid, Eng. Sci. Technol. Int. J., 2016, http://dx.doi.org/10.1016/j.jestch.2015.12.004 (in press).
23. [23] N. Sandeep, C. Sulochana, I.L. Animasaun; Stagnation-point flow of a Jeffrey nano fluid over a stretching surface with induced magnetic field and chemical reaction; Int. J. Eng. Res. Afr., 20 (2016), pp. 93–111
24. [24] Y.Y. Lok, A. Ishak, I. Pop; MHD stagnation-point flow towards a shrinking sheet; Int. J. Num. Meth. Heat Fluid Flow, 21 (1) (2011), pp. 61–72
25. [25] N. Sandeep, C. Sulochana; Effect of induced magneticfield on MHD stagnation point flow of a nano fluid over a stretching cylinder with suction; J. Nano Fluids, 5 (1) (2016), pp. 68–73
26. [26] N. Bachok, Anuar Ishak, Ioan Pop; Stagnation point flow toward a stretching/shrinking sheet with a convective surface boundary condition; J. Franklin Inst., 350 (2) (2013), pp. 2736–2744
27. [27] C. Sulochana, N. Sandeep; Stagnation-point flow and heat transfer behavior of Cu–water nanofluid towards horizontal and exponentially stretching/shrinking cylinders; Appl. Nanosci. (2015) http://dx.doi.org/10.1007/s13204-015-0451-5
28. [28] N. Sandeep, C. Sulochana; Dual solutions for MHD stagnation point flow of a nano fluid over a stretching surface with induced magnetic field; Int. J. Sci. Eng., 9 (1) (2015), pp. 1–8
29. [29] N. Sandeep, C. Sulochana; Dual solutions for unsteady mixed convection flow of MHD micropolar fluid over a stretching/shrinking sheet with non-uniform heat source/sink; Eng. Sci. Technol. Int. J., 18 (2015), pp. 738–745
30. [30] C.S.K. Raju, N. Sandeep; Stagnation point flow of a micro polar fluid over a nonlinear stretching surface with suction; Int. J. Sci. Eng. Res., 6 (9) (2015), pp. 67–73
31. [31] J.V. Ramana Reddy, V. Sugunamma, N. Sandeep, C.S.K. Raju, M. Jayachnadra Babu; Induced magneticfield effect on stagnation point flow of magneto nano fluids towards a stretching sheet; Adv. Sci. Eng. Med., 7 (11) (2015), pp. 968–974
32. [32] M. Mustafa, T. Hayat, I. Pop, S. Asghar, S. Obaidat; Stagnation-point flow of a nanofluid towards a stretching sheet; Int. J. Heat Mass Transf., 54 (25–26) (2011), pp. 5588–5594
33. [33] R. Sivaraj, B. Rushi Kumar; Unsteady MHD dusty viscoelastic fluid Couette flow in an irregular channel with varying mass diffusion; Int. J. Heat Mass Transf., 55 (2012), pp. 3076–3089
34. [34] M.Y. Malik, Iffat Zehra, S. Nadeem; Flows of Carreau fluid with pressure dependent viscosity in a variable porous medium: application of polymer melt; Alex. Eng. J., 53 (2014), pp. 427–435
35. [35] C.S.K. Raju, N. Sandeep; Heat and mass transfer in MHD non-Newtonian bio-convection flow over a rotating cone/plate with cross diffusion; J. Mol. Liq., 215 (2016), pp. 115–126
36. [36] C.S.K. Raju, N. Sandeep, M. Gnaneswar Reddy; Effect of nonlinear thermal radiation on 3D Jeffrey fluid flow in the presence of homogeneous–heterogeneous reactions; Int. J. Eng. Res. Afr., 21 (2016), pp. 52–68
37. [37] N.S. Akbar, S. Nadeem, Zafar Hayat Khan; Numerical simulation of peristaltic flow of a Carreau nanofluid in an asymmetric channel; Alex. Eng. J., 53 (2014), pp. 191–197
38. [38] A. Riaz, R. Ellahi, S. Nadeem; Peristaltic transport of a Carreau fluid in a compliant rectangular duct; Alex. Eng. J., 53 (2014), pp. 475–484
39. [39] A. Jasmine Benazir, R. Sivaraj, O.D. MAkinde; Unsteady MHD Casson fluid flow over a vertical cone and flat plate with non-uniform heat source/sink; Int. J. Eng. Res. Afr., 21 (2015), pp. 69–83
40. [40] S. Nadeem, A. Riaz, R. Ellahi, N.S. Akbar; Series solution of unsteady peristaltic flow of a Carreau fluid in eccentric cylinders; Ain Shams Eng. J., 5 (2014), pp. 293–304
41. [41] S. Malik, A.K. Nayak, Buoyancy driven heat transfer in nanofluids due to wall mounted heat source, Alex. Eng. J. 55 (2) (2016) 797–810.
42. [42] M. Turkyilmazoglu; Analytical solutions of single and multi-phase models for the consideration of nanofluid film flow and heat transfer; Eur. J. Mech. B/Fluids, 53 (2015), pp. 272–277
43. [43] P. Sudarshana Reddy, A.J. Chamka; Influence of size, shape, type of nanoparticles, type and temperature of the base fluid on natural convection MHD of nanofluids; Alex. Eng. J., 55 (2016), pp. 331–341
44. [44] K. Das, P.R. Durai, P.K. Kundu; Nanofluid flow over an unsteady stretching surface in presence of thermal radiation; Alex. Eng. J., 53 (2014), pp. 737–745