1. Introducción
Ahorrar recursos naturales y energía es uno de los retos del siglo XXI, y en el sector del transporte la forma más eficaz para ahorrar energía es disminuir la masa de la estructura, lo que reduce el consumo del vehículo. Por lo tanto, las estructuras sándwich de composites se utilizan sobre todo en las aplicaciones donde es necesario una gran resistencia y una alta relación rigidez-peso, como en el ámbito aeronáutico, automoción, ferrocarril o náutica [1–3]. En las aplicaciones mencionadas, las células fotovoltaicas se suelen pegar sobre los paneles sándwich [4]. En estos diseños, las placas solares suelen añadir peso a la estructura, con una contribución insignificante a las propiedades mecánicas.
Las variables de diseño para mejorar la eficiencia de los paneles sándwich son [5] el material de las pieles, núcleos celulares, espesores relativos entre el núcleo y las pieles, o distribuciones de espesores de láminas simétricas o asimétricas. La función principal del núcleo en el panel sándwich es afrontar las cargas de cizalladura, cargas de compresión fuera de plano y una alta resistencia a perforación. Por lo tanto, la opción de celdas unitarias de alta resistencia axial es una imprescindible [5]. Ha y Lu [6] compararon diferentes estructuras celulares presentes en la naturaleza, y concluyeron que la estructura trabecular del ala del escarabajo es la ceda unitaria más eficaz. En el caso de la compresión y la perforación cuasi-estática, se ha observado en diferentes casos la mejora al utilizar estructura trabecular frente a la estructura hexagonal [7–11].
En cuanto a la inserción de funcionalidades en un panel sándwich, Echsel et al. [12] fabricaron un satélite a base a estructuras sándwich con elementos electrónicos embebidos en el núcleo para disminuir las etapas de ensamblaje y el coste de producción. En la estructura del nucleo, se han generado huecos específicamente diseñados para introducir elementos como los sensores o los conectores para disminuir el espacio necesario total.
Una vez visto la posibilidad de integrar diferentes funcionalidades y mejorar las prestaciones introduciendo paneles sándwich, se analizó el comportamiento de tres placas diferentes a flexo-torsión, a perforación cuasi-estática e impacto. El objetivo de este artículo es analizar el efecto de la célula fotovoltaica en el panel sándwich.
2. Materiales y métodos empleados
2.1. Materiales y proceso de fabricación
Los paneles sándwich empleados en este artículo han sido fabricados mediante infusión de fibra de vidrio con epoxy, para la encapsulación de las células fotovoltaicas y el núcleo del panel sándwich se ha fabricado mediante fabricación de filamento fundido (FFF) en la impresora Raise Pro2®. El material empleado ha sido una poliamida con fibra corta de carbono y poliamida con fibra corta de vidrio para conseguir aislamiento eléctrico en algunas zonas críticas. La geometria de la celda unitaria del núcleo será hexagono trabecular con el tamaño de celda de 6 mm. Las dimensiones del núcleo son de 200 x 200 mm y la altura de 15 mm y para no tener problemas a la hora de realizar la infusión con la fibra de vidrio y el epoxy, se han imprimido 3 capas solidas en la parte inferior y superior del nucleo. Además, se ha fabricado un biselado de 30 mm alrededor del núcleo para facilitar la impregnación en el proceso de infusión (Figura 1). En el núcleo se ha realizado una cajera en la parte inferior para poder insertar la caja de conexionado y proporcionar la salida de los cables.

a) |

b) |
| Figura 1. A) Diseño del núcleo con biselado y ranuras para el cableado; b) Panel sándwich terminado con célula fotovoltaica integrada. | |
La fabricación de los paneles sándwich con y sin células fotovoltaicas ha sido mediante infusión. Cada piel dispone de 3 capas de lámina de 0/90° con un gramaje de 300 g/m2. Para no generar delaminación en el proceso de infusión, se ha realizado un programa de curado lento y con aumento de temperatura gradual. Además, se ha utilizado un epoxy adaptado a estos materiales para mejorar la adhesión entre piel y núcleo. Una vez terminada la infusión, se corta la zona del biselado de los núcleos obteniendo un módulo de 200x200 mm.
2.2. Ensayos experimentales
Se han realizado tres ensayos experimentales; i) ensayo de impacto a baja velocidad; ii) ensayo de perforación cuasi-estática; iii) cargas complejas, ensayo a flexo-torsión. Los ensayos se han realizado a 23°C y 50% de humedad relativa.
El ensayo de impacto se ha realizado en la máquina de ensayos Fractovis-Plus Ceast. El impactor era una cabeza hemisférica de 20 mm de diámetro equipada con una celda de carga de 20 kN, que registró los datos de fuerza-tiempo durante el impacto. Integrando esta curva de fuerza-tiempo basada en la segunda ley de Newton (ecuaciones (1)(2)), se pueden calcular gráficos de desplazamiento-tiempo y energía-tiempo. Las muestras de impacto se sujetaron con un anillo circular de diámetro exterior e interior de 100 mm y 70 mm, respectivamente. El par de apriete de los cuatro tornillos de sujeción fue de 100 Nm. Además, la máquina de ensayos está equipada con un sistema antirrebote para evitar múltiples colisiones que puedan alterar los resultados. La caracterización se ha realizado mediante un impacto de 150 J (15 kg desde 1 m de altura) a cada probeta para obtener una perforación total del panel sándwich.
|
|
|
(1) | ||
|
|
|
(2) |
Donde, F(x) es la fuerza instantánea, l el desplazamiento del indentador y m la masa total de la probeta.
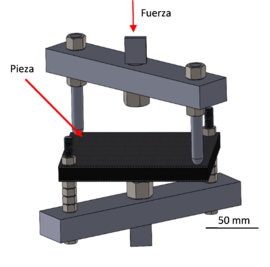
El ensayo de cargas complejas a flexo-torsión, se ha realizado en la máquina de ensayos universal, Hoytom/HM-D equipada con una célula de carga de 100 kN y registra el desplazamiento del cabezal móvil. Dicho ensayo no sigue una norma estandarizada, por lo tanto, se ha tomado como referencia el artículo de Aviles et al. [13]. El utillaje empleado se ha fabricado a medida para este ensayo. Se aplica la fuerza en dos vértices diagonales de la placa cuadrada y en los dos vértices opuestos se amarra con dos tornillos (Figura 2b). La fuerza se aplica mediante dos puntos con punta hemisférica de 10 mm y la fuerza se aplica con el cabezal móvil. En cada punto de aplicación se aplica la mitad de la fuerza total.
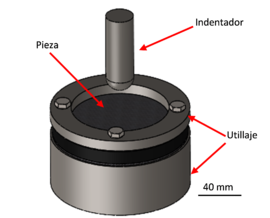
En cuanto al ensayo de perforación cuasi-estática se ha realizado en la máquina de ensayos universal, Hoytom/HM-D, como el ensayo de flexo-torsión. El ensayo se ha realizado de acuerdo con la norma ASTM D6264/D6264M-12. La norma indica que la probeta debe ir amarrado en todo el contorno como se muestra en la Figura 2a, al igual que en el ensayo de impacto. El ensayo se ha llevado a la perforación completa del panel para analizar el comportamiento del conjunto.
|
|
| a) | b) |
| Figura 2.: Descripción de los ensayos realizados; a) ensayo de perforación cuasi-estática e impacto; b) ensayo de flexo-torsión. | |
3. Resultados y discusión
3.1. Resultados de impacto
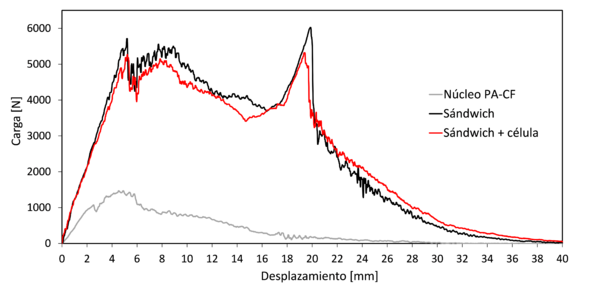
El ensayo de impacto se ha utilizado para medir la fuerza máxima y la cantidad de energía disipada durante el impacto en cada panel. La curva típica de fuerza de contacto – desplazamiento de los impactos en los paneles sándwich, con y sin panel fotovoltaico, presenta tres etapas dependiendo del proceso de fallo. En la primera etapa, la fuerza aumenta hasta alcanzar un pico máximo, donde la piel frontal se daña y se perfora. El primer pico en el caso del sándwich sin la célula alcanza 5876 N mientras que el sándwich con la célula 5324 N. A continuación, en la segunda etapa la carga disminuye hasta alcanzar la carga mínima comprimiendo el núcleo. En el caso del núcleo, sin piel superior ni inferior, se observa un pico máximo de 1494 N a 5 mm de desplazamiento y a partir de ese momento la fuerza desciende constantemente. El modo de fallo del núcleo ha sido una combinación de compresión y cizalla.
Los valores característicos obtenidos a partir de las curvas de impacto se recogen en la Tabla 1. Como se puede observar, la contribución de las pieles mejora considerablemente tanto la fuerza de perforación como la energía máxima disipada aumentan, lo que se debe al aumento de la resistencia en el plano y de perforación aportadas por las pieles. En segundo lugar, se ha constatado que la integración de la célula fotovoltaica disminuye las prestaciones a impacto cerca de un 10%.
| Probeta | Fmax [N] | Energía disipada [J] | SEA [J/g] |
| Núcleo PA-CF | 1494 ± 26 | 14,9 ± 0,6 | 0,05 |
| Sándwich | 5743 ± 278 | 100,5 ± 0,2 | 0,29 |
| Sándwich + célula | 5321 ± 145 | 98,5 ± 0,3 | 0,26 |
3.2. Resultados de Flexo-torsión cuasi-estática
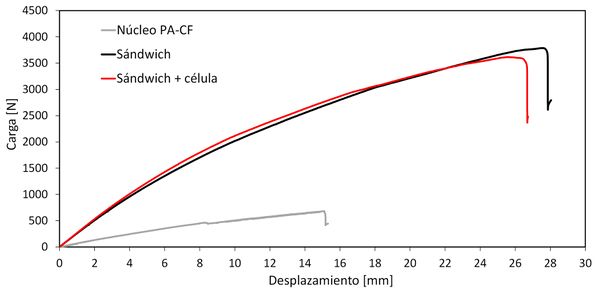
El ensayo de flexo-torsión se realizó para analizar la rigidez del panel y la deformación que puede sufrir antes de perder las propiedades mecánicas y generar rotura. En la Figura 4 se puede observar que la pendiente del núcleo sin pieles ni placas fotovoltaicas es 10 veces inferior. La fibra continua de las pieles aporta gran rigidez al panel. En cuanto a la deformación antes de la rotura, el núcleo se deforma hasta 15 mm antes de generar la primera rotura, pero en el caso de los paneles sándwich, se deforma hasta 26-27 mm, aumentando la resistencia del panel.
El modo de fallo del núcleo y los paneles sándwich no ha sido el mismo. En el primer caso, se ha generado una grieta entre los dos puntos de carga, partiendo la placa desde la mitad. En cambio, en el caso de los paneles sándwich, la resistencia de las placas ha sido superior y se ha perforado el panel en los puntos donde se aplica la carga. El esfuerzo local en esos dos puntos ha sido superior a la resistencia de la placa.
La fuerza máxima del núcleo alcanza 682 N, pero cuando se añaden las fibras de vidrio en las pieles, se obtienen valores de 3615 – 3786 N, 5 veces mayor con las pieles que solamente el núcleo. Pero comparando los paneles sándwich con y sin célula, la diferencia es de 4,5 %. El peso de los paneles sándwich con y sin célula aumenta un 12 %, por lo tanto, se ha calculado la fuerza máxima específica para poder realizar una comparación más ajustada. Se ha observado que la fuerza máxima especifica disminuye 13% insertando la célula.
En la tabla 2 se resumen todos los valores obtenidos de la curva de la Figura 4.
| Probeta | Rigidez [N/mm] | Fmax [N] | Fmax /m [N/g] | Deformación [mm] |
| Núcleo PA-CF | 6,04 | 682 | 2,67 | 15,2 |
| Sándwich | 66,1 | 3786 | 10,9 | 27,6 |
| Sándwich + célula | 62,3 | 3615 | 9,51 | 26,6 |
3.3. Resultados de perforación cuasi-estática
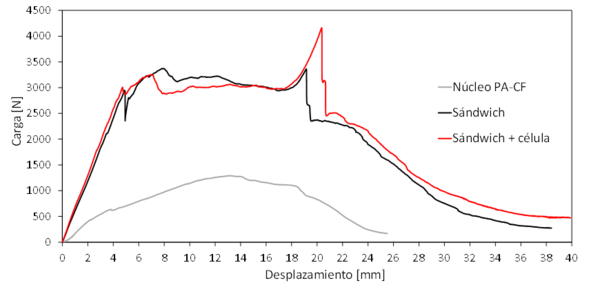
En los ensayos de perforación cuasi-estática se ha analizado la carga máxima y la energía disipada del panel. Se ha observado que el núcleo alcanza la carga máxima de 1288,8 N a 26 mm de desplazamiento. No se observan diferentes etapas a la hora de la perforación, ya que el material empleado y la estructura son iguales en todo el núcleo.
En cuanto a los paneles sándwich con y sin célula, se puede observar cómo hay 3 etapas en cada curva. En primer lugar, la carga aumenta hasta alcanzar un pico máximo, donde se genera el daño en la piel superior y se perfora. A partir del pico, entra la segunda etapa, donde el nucleo se comprime y se daña el núcleo. En la segunda etapa se observa un plato, donde la carga para ambos paneles es igual. Cuando el plato se termina y empieza a incrementar la fuerza, es donde empieza la tercera etapa. En esta última etapa, la piel inferior es el único elemento que queda. En este caso se observan dos comportamientos diferentes para los paneles sándwich. El panel sin la célula alcanza la carga máxima de 3448 N y desciende la carga. En cambio, el panel con la célula alcanza4286 N y desciende hasta obtener la perforación total.
La energía disipada con la célula fotovoltaica es 7% superior a la disipada sin la célula fotovoltaica. Pero si se analiza la energía especifica, los valores con y sin la célula son iguales. El peso que añade la célula es proporcional a la cantidad de energía que disipa. En el caso de la perforación cuasi-estática, incrementar las intercaras con la célula no generan la perdida de propiedades mecánicas y puede llegar a mejorar la capacidad de disipación de energía. En la tabla 3 se resumen los datos obtenidos en la perforación cuasi-estática.
| Probeta | Fmax [N] | Energía disipada [J] | SEA [J/g] |
| Núcleo PA-CF | 1289 | 20,7 | 0,08 |
| Sándwich | 3448 | 74,1 | 0,21 |
| Sándwich + célula | 4286 | 79,7 | 0,21 |
4. Conclusiones
Las estructuras sándwich con y sin células fotovoltaicas fabricadas mediante FFF e infusión se han ensayado en condiciones estáticas y dinámicas. Se ha analizado el efecto que tiene insertar la célula fotovoltaica en las propiedades mecánicas. Las conclusiones que se han obtenido son los siguientes:
- 1. En los tres ensayos realizados se ha observado que la piel del panel sándwich aumenta la rigidez y la capacidad de disipación de energía, en valores absolutos y específicos.
- 2. En el ensayo de impacto, la capacidad de disipación de energía disminuye cuando se inserta la célula fotovoltaica, mientras que en el caso la perforación cuasi-estática aumenta en términos absolutos y se iguala en valores específicos. Por lo tanto, se concluye que la integración de las células fotovoltaicas no lastra al panel sándwich.
- 3. En cuanto al comportamiento a flexo-torsión, la presencia de la célula fotovoltaica reduce tanto la rigidez como la carga máxima, lo que se atribuye a la mayor facilidad de generar delaminaciones en las nuevas intercaras.
Agradecimientos
Los autores quieren agradecer al Gobierno Vasco la financiación recibida para la realización de este trabajo (Nº proyectos: KK-2021/00066, IT1613-22).
Bibliografía
[1] B. Castaine, C. Bouvet, and M. Ginot, “Review of composite sandwich structure in aeronautic applications,” Compos. Part C Open Access, vol. 1, p. 100004, 2020, doi: 10.1016/j.jcomc.2020.100004.
[2] G. Palomba, G. Epasto, and V. Crupi, “Lightweight sandwich structures for marine applications: a review,” Mech. Adv. Mater. Struct., vol. 29, no. 26, pp. 4839–4864, 2022, doi: 10.1080/15376494.2021.1941448.
[3] M. F. Aly, K. T. Hamza, and M. M. Farag, “A materials selection procedure for sandwiched beams via parametric optimization with applications in automotive industry,” Mater. Des., vol. 56, pp. 219–226, 2014, doi: 10.1016/j.matdes.2013.10.075.
[4] X. Meng, D. Zhang, P. Feng, and N. Hu, “Review on mechanical behavior of solar cells for building integrated photovoltaics,” Sustain. Struct., vol. 1, no. 2, 2021, doi: 10.54113/j.sust.2021.000009.
[5] V. Birman and G. A. Kardomateas, “Review of current trends in research and applications of sandwich structures,” Compos. Part B Eng., vol. 142, pp. 221–240, 2018, doi: 10.1016/j.compositesb.2018.01.027.
[6] N. S. Ha and G. Lu, “A review of recent research on bio-inspired structures and materials for energy absorption applications,” Compos. Part B Eng., vol. 181, p. 107496, 2020, doi: 10.1016/j.compositesb.2019.107496.
[7] X. Zhang, J. Xie, J. Chen, Y. Okabe, L. Pan, and M. Xu, “The beetle elytron plate: A lightweight, high-strength and buffering functional-structural bionic material,” Sci. Rep., vol. 7, 2017, doi: 10.1038/s41598-017-03767-w.
[8] J. Chen, X. Zhang, Y. Okabe, K. Saito, Z. Guo, and L. Pan, “The deformation mode and strengthening mechanism of compression in the beetle elytron plate,” Mater. Des., vol. 131, pp. 948–961, 2017, doi: 10.1016/j.matdes.2017.06.014.
[9] J. Chen, X. Yu, M. Xu, Y. Okabe, X. Zhang, and W. Tuo, “The compressive properties and strengthening mechanism of the middle-trabecular beetle elytron plate,” J. Sandw. Struct. Mater., vol. 22, pp. 948–961, 2020, doi: 10.1177/1099636218777188.
[10] X. Zhang, J. Chen, Y. Okabe, P. Zhang, X. Xiong, and X. Yu, “Influence of honeycomb dimensions and forming methods on the compressive properties of beetle elytron plates,” J. Sandw. Struct. Mater., vol. 22, pp. 28–39, 2020, doi: 10.1177/1099636217731993.
[11] I. Sukia, A. Esnaola, U. Morales, L. Aretxabaleta, and J. Aurrekoetxea, “3D printing of bio-inspired cores for out-of-o autoclave sandwich structures,” Rev. Mater. Compuestos, no. Núm. 1-Sostenibilidad y reciclaje-Fabricación, Jul. 2022, doi: 10.23967/R.MATCOMP.2022.07.047.
[12] M. Echsel, P. Springer, and S. Hümbert, “Production and planned in-orbit qualification of a function-integrated, additive manufactured satellite sandwich structure with embedded automotive electronics,” CEAS Sp. J., vol. 13, no. 1, pp. 111–118, 2021, doi: 10.1007/s12567-020-00328-2.
[13] F. Avilés, F. Couoh-Solis, L. A. Carlsson, A. Hernández-Pérez, and A. May-Pat, “Experimental determination of torsion and shear properties of sandwich panels and laminated composites by the plate twist test,” Compos. Struct., vol. 93, no. 7, pp. 1923–1928, 2011, doi: 10.1016/j.compstruct.2011.02.001.
Document information
Published on 15/10/23
Accepted on 15/10/23
Submitted on 18/05/23
Volume 08 - COMUNICACIONES MATCOMP21 (2022) Y MATCOMP23 (2023), Issue Núm. 2 - Fabricación y Aplicaciones Industriales - Sostenibilidad y Reciclaje., 2023
DOI: 10.23967/r.matcomp.2024.02.12
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?