Behaviour of fibre/matrix interface cracks under biaxial stress state caused by edge effect in carbon/epoxy laminates

1. Introducción

La reciente explicación física del fenómeno del efecto escala (París et al. [1]) ha derivado en estudios micromecánicos sobre la aparición del daño a fatiga en laminados cross-ply con láminas ultradelgadas (Sánchez-Carmona et al. [2]). Tras el análisis microscópico realizado en dicho trabajo, se detectaron daños no convencionales en la capa de 90°, tal y como se observa en la Figura 1. Estos daños no convencionales se corresponden con grietas de interfase fibra/matriz que aparecían paralelas a las capas de 0°. Ello implica que dichos despegues longitudinales a la carga aplicada debían estar originados por tensiones interlaminares.

Figura 1. Daño no convencional en la capa de 90°.

Sánchez-Carmona et al. [3] analizaron en detalle el origen de estos daños no convencionales, retomando estudios previos del denominado efecto borde, los cuales se encuentran bien resumidos en Mittelstedt et al. ([4], [5]).

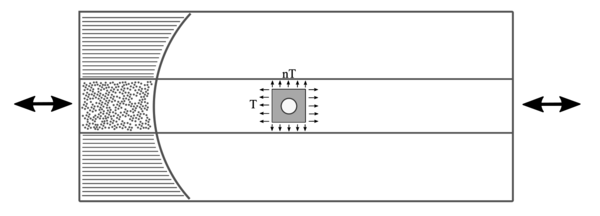
En Sánchez-Carmona et al. [3] se mantiene el mismo número de capas de 0° en el laminado cross-ply, disminuyendo progresivamente el espesor de la capa de 90° usando láminas ultradelgadas con gramajes desde 30 a 150g/m². Debido a ello, las tensiones nominales transversales en el plano en la capa de 90° aumentan considerablemente cuando se disminuye el espesor de dicha capa. Además, aparecen tensiones transversales fuera del plano en la capa de 90° derivadas de dicho fenómeno. La combinación de ambas tensiones en la capa de 90° genera un estado biaxial de tensiones, Figura 2, el cual se acentúa al usar láminas ultradelgadas.

Figura 2. Estado biaxial de tensiones en la capa de 90° derivado del efecto borde.

Dicho fenómeno está generado tanto por tensiones térmicas de curado como por las tensiones cíclicas mecánicas. En otras palabras, únicamente tras el curado del material, se han observado despegues longitudinales en la capa de 90°. Este hecho ha motivado el presente trabajo, en el cual se ha realizado una minuciosa observación microscópica de probetas de laminados cross-ply con el fin de encontrar fibras lo más aisladas posible que tuviesen grieta de interfase originada tras el curado del material en el autoclave. El ángulo de los despegues longitudinales detectados se ha comparado con los crecimientos esperados derivados de los estudios numéricos previos de autores de este trabajo ([6]–[8]).

2. Observación microscópica de grietas de interfase fibra/martriz

El laminado cross-ply analizado en este trabajo es [0₄/90/0₄] que ha sido fabricado con cinta unidireccional preimpregnada carbono/epoxi T700S/TP402 suministrada por North Thin Ply Technology. Los gramajes utilizados han sido 150 g/m² para las capas de 0° y 30 g/m² para las de 90°. La fabricación se ha realizado mediante apilado manual y se ha curado en autoclave siguiendo las recomendaciones suministradas por el proveedor [9].

Únicamente tras el curado del material, las probetas se han lijado y pulido en sus bordes con el fin de observar los despegues longitudinales ocurridos por el efecto borde derivados de las tensiones térmicas residuales de curado. En este caso, el estado biaxial presente es T-1,40T siendo T = 24,34 MPa.

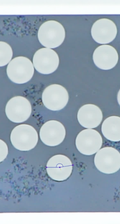
Se presentan varias micrografías (Figura 3) en las que se observa las grietas de interfase fibra/matriz generadas únicamente por el curado del material.

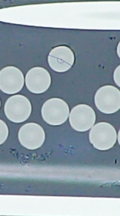
(a)	(b)	(c)

Figura 3. Micrografías de la capa de 90° con grietas de interfase fibra/matriz únicamente tras curado.

En la Tabla 1 se recoge la media, y la estadística correspondiente, del ángulo de los 25 despegues semi-aislados medidos microscópicamente tras el curado del material en 3 probetas distintas.

Tabla 1. Ángulo medio, y correspondiente estadística, de las grietas de interfase fibra/matriz observadas tras curado.

	Ángulo de despegues tras curado
Media (°)	191,22
Desviación estándar (°)	23,50
Coeficiente de variación (%)	12,29

3. Predicción del crecimiento de grietas de interfase

La predicción sobre el crecimiento inestable de una grieta de interfase ante cargas biaxiales de tracción se ha realizado siguiendo la metodología presentada en Correa et al. [6]. Para ello, se emplea un modelo de Elementos de Contorno de fibra única, en el cual una grieta crece a lo largo de la interfase entre una fibra de carbono (de radio r=3,75·10^-6 m) y la matriz epoxi. Dicho sistema bimaterial se somete al estado tensional de carga biaxial producido únicamente por el curado. Al haber observado el ángulo de despegues en casos de fibras semi-aisladas, se ha optado por un modelo de fibra única. Además, los resultados obtenidos en Sandino et al. [8] para cargas biaxiales de tensión demuestran que, conforme aumenta la carga secundaria de tracción, la presencia de fibras cercanas tiene una influencia menor en los resultados obtenidos, en comparación con modelos sometidos a cargas uniaxiales de tracción (Sandino et al. [7]).

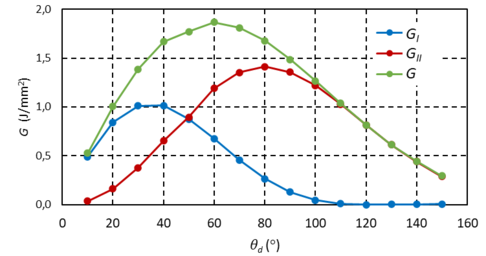
A partir de las tensiones y desplazamientos obtenidos por el modelo en la interfase, se puede calcular el Índice de Liberación de Energía, G, utilizando Irwin [10]. La Figura 4 representa la evolución de dicho índice (también las componentes en Modo I y Modo II) en función del ángulo de despegue considerado θ_d. El modelo de fibra única es un modelo simétrico similar al presentado en Correa et al. [6], lo que implica que el verdadero despegue corresponderá con el doble de θ_d.

Figura 4. Evolución de G vs θ_d para una grieta de interfase sometida al estado biaxial producido únicamente por el curado.

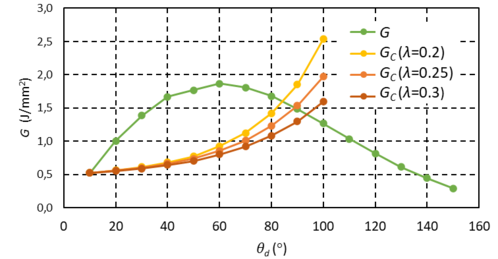
A partir de los valores presentados en la Figura 4, y siguiendo la metodología empleada en Correa et al. [6] y Sandino et al. [8], se calcula el valor crítico de G, G_C (Hutchison and Suo [11]), que permite la predicción del final del crecimiento inestable de la grieta. La evolución de G y G_C se muestra en la Figura 5, tomando distintos valores del parámetro de sensibilidad al modo de fractura λ. La comparación de ambas curvas permite determinar que el final del crecimiento inestable de la grieta de interfase se produce para un despegue de entre 170° y 190°.

Figura 5. Comparación de G y G_C para una grieta de interfase sometida al estado biaxial producido únicamente por el curado.

4. Conclusiones

Los daños no convencionales en la capa de 90°, longitudinales a las capas de 0° de laminados cross-ply, derivados del efecto borde aparecen tanto por las tensiones térmicas residuales de curado como por la carga cíclica mecánica aplicada.

En primer lugar, se han localizado despegues longitudinales suficientemente aislados en probetas de un laminado cross-ply con la capa de 90° de espesor ultradelgado, provenientes exclusivamente del proceso de curado, es decir, aún no han sufrido carga mecánica cíclica.

Tras ello, a partir del estado tensional biaxial derivado del efecto borde existente, se ha evaluado el Índice de Liberación de Energía, G, y se ha calculado el valor crítico de G, G_c, que permite la predicción del final del crecimiento inestable de la grieta, obteniendo que se produce para un despegue de entre 170° y 190°.

Tras el análisis de los resultados mostrados se puede concluir que existe una excelente correlación entre la evidencia experimental y la predicción numérica del ángulo inicial que deben tener las grietas de interfase fibra/matriz cuando existe un estado biaxial de tensiones de tracción.

Agradecimientos

Este trabajo ha sido financiado por la Universidad de Sevilla [subvención VIPPIT-2018-II.2], por la Consejería de Economía y Conocimiento Junta de Andalucía [proyecto P18-FR-3360] correspondiente al Programa Operativo FEDER I+D+I 2014-2020; y por el Ministerio Español de Ciencia, Innovación y Universidades [proyecto PID2021-126279OB-I00]. Los autores quieren agradecer la colaboración de la Dra. María Luisa Velasco López para la puesta a punto del Modelo de Elementos de Contorno.

Bibliografía

[1] F. París, M. L. Velasco, and E. Correa, “The scale effect in composites: An explanation physically based on the different mechanisms of damage involved in failure,” Compos Struct, vol. 257, p. 113089, Feb. 2021, doi: 10.1016/j.compstruct.2020.113089.

[2] S. Sánchez-Carmona, E. Correa, A. Barroso, and F. París, “Experimental observations of fatigue damage in cross-ply laminates using carbon/epoxy ultra-thin plies,” Compos Struct, vol. 306, no. 116564, 2023, doi: 10.1016/j.compstruct.2022.116564.

[3] S. Sánchez-Carmona, A. Barroso, V. Mantic, E. Correa, and F. París, “Non-conventional failures caused by the edge effect in cross-ply laminates made of ultra-thin plies,” Composites Part B, vol. 254, no. 110576, pp. 1–10, 2023, doi: 10.1016/j.compositesb.2023.110576.

[4] C. Mittelstedt and W. Becker, “Free-edge effects in composite laminates,” Appl Mech Rev, vol. 60, no. 1–6, pp. 217–245, 2007, doi: 10.1115/1.2777169.

[5] C. Mittelstedt, W. Becker, A. Kappel, and N. Kharghani, “Free-Edge Effects in Composite Laminates-A Review of Recent Developments 2005-2020,” Appl Mech Rev, vol. 74, no. 1, Jan. 2022, doi: 10.1115/1.4054145.

[6] E. Correa, F. París, and V. Mantič, “Effect of the presence of a secondary transverse load on the inter-fibre failure under tension,” Eng Fract Mech, vol. 103, pp. 174–189, May 2013, doi: 10.1016/j.engfracmech.2013.02.026.

[7] C. Sandino, E. Correa, and F. París, “Numerical analysis of the influence of a nearby fibre on the interface crack growth in composites under transverse tensile load,” Eng Fract Mech, vol. 168, pp. 58–75, 2016, doi: http://dx.doi.org/10.1016/j.engfracmech.2016.01.022.

[8] C. Sandino, E. Correa, F. París, “Composite materials under transverse biaxial loads: Study of the influence of a nearby fibre on the interface crack growth under tension,” in ECCM 2016 - Proceeding of the 17th European Conference on Composite Materials, Munich; Germany, 2016.

[9] North Thin Ply Technology, “NTPT ThinPreg 402 data sheet,” NTPT Product Data Sheet, 2017, [Online]. Available: https://www.thinplytechnology.com/assets/mesimages/NTPT-DS-ThinPreg-402-May2017-v3.pdf

[10] G. Irwin, “Analysis of Stresses and Strains Near the End of a Crack Traversing a Plate,” J Appl Mech, 1957, [Online]. Available: http://asmedigitalcollection.asme.org/appliedmechanics/article-pdf/24/3/361/6750462/361_1.pdf

[11] J. W. Hutchinson and Z. Suo, “Mixed Mode Cracking in Layered Materials,” Advances in Applied Mechanics, vol. 29, no. C, pp. 63–191, Jan. 1991, doi: 10.1016/S0065-2156(08)70164-9.