El papel de los modelos numéricos en la investigación y el diseño de aliviaderos de presas

1 Introducción

El Centro Internacional de Métodos Numéricos en Ingeniería (CIMNE) es un centro de investigación dependiente del Gobierno de Cataluña y de la Universidad Politécnica de Cataluña creado en 1987. Su principal actividad es el desarrollo y aplicación de métodos numéricos innovadores para resolver problemas prácticos en diversos campos de la ingeniería, y se desarrolla fundamentalmente en el marco de proyectos de investigación nacionales e internacionales.

En los últimos años el centro ha participado en diversos proyectos relacionados con la seguridad de presas, fundamentalmente hidráulica, pero también estructural, en cooperación con diversas empresas y organismos públicos de investigación como el CEDEX y la UPM.

La presente comunicación describe brevemente los objetivos principales de los mencionados proyectos, haciendo hincapié en cómo la modelación numérica ha contribuido a alcanzarlos.

2 Métodos numéricos

Si bien la descripción detallada de los métodos numéricos empleados queda fuera del objetivo de la presente comunicación, se considera adecuado hacer una breve reseña de los mismos, aportando las referencias esenciales para que el lector interesado pueda profundizar en ellos. En ambos casos el objetivo final es la resolución de las ecuaciones de Navier-Stokes, que rigen la dinámica de fluidos, y el movimiento del agua en el caso de aliviaderos.

Los primeros esquemas numéricos que se desarrollaron para la modelación de problemas de este tipo utilizan una formulación Euleriana. Esto quiere decir que el dominio de cálculo se discretiza mediante una malla de elementos finitos, que se mantiene constante durante toda la simulación. La evolución de la superficie libre se calcula utilizando una función suave (level-set) [1], o bien mediante un valor escalar que representa la cantidad de fluido que ocupa una región determinada (métodos de volumen de fluido). El principal inconveniente de estos métodos es el tratamiento de los términos convectivos, así como la detección de superficies libres muy irregulares y variables en el tiempo. En CIMNE, se ha desarrollado una herramienta basada en esta técnica e implementada en el entorno Kratos Multi-Physics [2], [3].

La descripción detallada del método (en adelante, Kratos) puede encontrarse en [4]. Sus principales ingredientes son los siguientes:

1. Discretización de las ecuaciones de Navier-Stokes para flujo incompresible usando el enfoque tradicional del Método de los Elementos Finitos.

2. Uso de elementos de bajo orden: triángulos en 2D y tetraedros en 3D.

3. Integración temporal mediante una versión semiexplícita del método de pasos fraccionados.

4. Mejora de la conservación de la masa mediante el uso de una técnica de “recuperación de errores” que permite considerar (y corregir) los errores cometidos en los pasos de tiempo precedentes.

5. Método level-set para la definición de la posición de la superficie libre.

6. Una función de extrapolación que permite calcular los valores de velocidad, presión y gradiente de presión en la zona no ocupada por el fluido adyacente a la superficie libre.

El algoritmo sigue los siguientes pasos:

1. Extrapolación de la velocidad, la presión y el gradiente de presiones al dominio de extrapolación, que es la región adyacente a la superficie libre que en tⁿ no está ocupada por el fluido.

2. Convección de la función level-set que define la posición de la superficie libre a partir del campo de velocidades en los dominios de fluido y de extrapolación. De este modo, se obtiene la posición de la superficie libre en el instante tⁿ⁺¹.

3. Reinicialización de la función distancia en todo el dominio, partiendo de la superficie libre calculada en el paso anterior, que tiene un valor nulo de dicha función.

4. Resolución de las ecuaciones de momento.

5. Imposición de la condición de presión de modo que tiene un valor nulo en la superficie libre antes calculada y que respete la incompresibilidad.

6. Cálculo de la presión.

7. Cálculo de la velocidad.

8. Vuelta al paso 1.

En la actualidad, el método está paralelizado para funcionar en sistemas con memoria compartida.

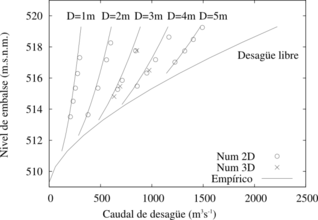
Se ha aplicado Kratos para el cálculo de las curvas de desagüe del aliviadero de la presa de Oliana, que tiene dos vanos de 17 m de longitud regulados por compuertas. Se realizaron cálculos fijando la carga sobre el vertedero y la apertura de compuertas, y registrando el caudal desaguado en cada situación. A partir de los resultados se obtuvieron las curvas de desagüe, como se muestra en la Figura 1.

Figura 1. Izquierda: detalle del modelo del aliviadero de la presa de Oliana. Derecha: curvas de desagüe obtenidas.

Una alternativa a esta formulación es utilizar una descripción Lagrangiana para formular las ecuaciones de gobierno de los dominios del fluido y del contorno. En la formulación Lagrangiana se sigue el movimiento de cada una de las partículas de líquido o del sólido de forma individual y, consecuentemente, pueden considerarse como partículas cuyo movimiento se sigue durante la solución en el tiempo.

En los últimos años, CIMNE ha desarrollado un tipo particular de formulación Lagrangiana para resolver problemas en los que interviene la interacción entre fluidos y sólidos. El método se denomina Método de Partículas y Elementos Finitos (PFEM). El PFEM trata los nodos en la malla, tanto en los dominios del fluido como de la estructura, como partículas que pueden moverse libremente e incluso separarse del dominio principal del fluido representando, por ejemplo, el efecto de gotas o chorreones de agua. Una malla de elementos finitos conecta los nodos que definen el dominio discretizado donde se resuelven las ecuaciones de gobierno de la mecánica de fluidos (para el líquido) y de la mecánica de sólidos (para la estructura) en la forma estándar del MEF [6], [7], [8].

Una ventaja de la formulación Lagrangiana es que los términos convectivos desaparecen de las ecuaciones del fluido. La dificultad, sin embargo, se transfiere al problema de mover adecuadamente (y eficientemente) los nodos de la malla. En general, suele ser necesario remallar a lo largo de la solución en cada paso de tiempo.

En general, el PFEM tiene ventajas frente a los métodos Eulerianos para seguir el movimiento de las partículas del fluido en flujos en donde la superficie libre es muy irregular y variable en el tiempo.

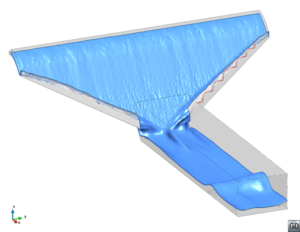
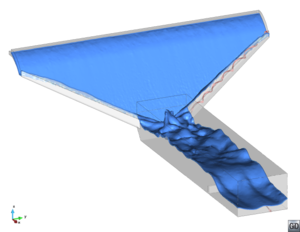
Una de las primeras aplicaciones del PFEM a hidráulica de presas consistió en la simulación del funcionamiento del aliviadero de la presa de Itoiz¹. Se reprodujeron tanto el diseño original como el final, resultado de las modificaciones realizadas tras la campaña de ensayos en modelo físico. En el diseño inicial, se observa la formación de ondas de choque junto a los cajeros, que confluyen justo a la entrada del cuenco, y pequeños sobrevertidos en el canal de descarga. En el diseño final se mantienen las ondas de choque, pero no llegan a confluir, con lo que el reparto del caudal es más uniforme en el cuenco y el comportamiento de éste más adecuado. Además, no hay sobrevertido. Estos mismos patrones se observaron en los modelos físicos [9].

Figura 2. Vista en alzado del modelo numérico del aliviadero de la presa de Itoiz. Izquierda: diseño original. Derecha: diseño final.

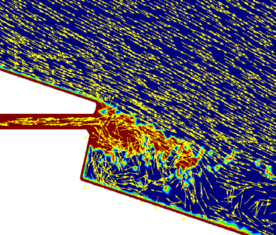
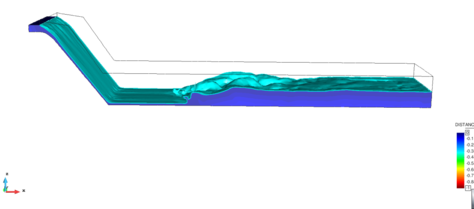
El mismo método PFEM permite modelar la erosión producida en el lecho por el movimiento del agua. El modelo implementado considera el medio erosionable como un continuo, y evalúa la capacidad erosiva del agua en base a su velocidad [8]. El algoritmo puede resumirse en los siguientes pasos:

1. Cálculo de la tensión tangencial generada por la partícula de fluido en movimiento sobre cada punto de la superficie del medio erosionable.

2. Cálculo del trabajo de fricción generado por la tensión tangencial.

3. La erosión se inicia en el momento en que el trabajo excede un umbral crítico función de las características del material del lecho.

4. Cuando dicho umbral se sobrepasa, el nodo en cuestión se separa del medio erosionable, pasando a ser transportado por el fluido, aunque conserva su densidad.

5. Si alguno de esos nodos desprendidos y transportados por el fluido llegan a una zona donde la velocidad es inferior a un umbral determinado, se deposita, volviendo a formar parte del lecho.

La Figura 3 muestra un ejemplo de la modelación de la erosión en la zona de caída de un aliviadero en trampolín.

Figura 3. Erosión y sedimentación al pie de un trampolín de lanzamiento.

(¹) La información necesaria para la modelación del aliviadero de la presa de Itoiz fue facilitada por D. Raimundo Lafuente Dios, Director Técnico de la Confederación Hidrográfica del Ebro.

3 Proyectos de investigación

En esta sección se describen someramente los proyectos de investigación relacionados con la hidráulica de presas, con indicación de los participantes, los objetivos generales, y cómo los modelos numéricos han contribuido a alcanzarlos.

3.1 Rotura de presas de materiales sueltos por sobrevertido. Proyectos XPRES y EDAMS

El proyecto XPRES y su continuación (el proyecto EDAMS) tienen como objetivo principal el estudio de las consecuencias de un sobrevertido sobre presas de materiales sueltos para mejorar el conocimiento de este fenómeno tan complejo y poder entonces optimizar las inversiones económicas sobre estas estructuras.

En ambos proyecto participan la UPM, el Centro de Estudios Hidrográficos del CEDEX y CIMNE. Los dos primeros se centran en el estudio experimental y CIMNE en el desarrollo y aplicación de un modelo numérico.

UPM y CEDEX han realizado varias campañas experimentales para entender cuáles son los factores clave en la rotura de presas de escollera por sobrevertido. Se han analizado, entre otros, el efecto de la geometría del talud aguas abajo, el tipo de protección usada, la dimensión del material y el caudal unitario. Los detalles sobre el estudio experimental se pueden encontrar en otras ponencias de esta misma jornada.

El primer objetivo desde el punto de vista numérico ha sido poder simular la evolución del flujo en lámina libre fuera y dentro de la escollera al variar el caudal de filtración.

Para modelar numéricamente la filtración se ha desarrollado un código Euleriano de elementos finitos para el cálculo de flujo en lámina libre, y se ha modificado la formulación para que pueda tener en cuenta de forma automática la presencia de una región porosa en el dominio de análisis. Se ha considerado el hecho de que la filtración dentro la escollera no se rige por la ley de Darcy, sino por una la ley no lineal. Se ha elegido entonces una ley de resistencia cuadrática e inicialmente se han adoptado los coeficientes de Ergun. Durante el EDAMS se ha generalizado la formulación para dejar al usuario la elección de los coeficientes de la ley de resistencia más adecuados al problema estudiado.

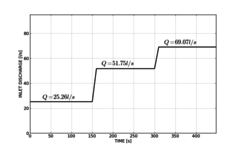
Este código permite imponer un hidrograma o una condición de entrada de caudal variable aguas arriba y estudia tanto el régimen transitorio como el estacionario (Figura 4). Durante el proyecto EDAMS se ha modificado este algoritmo para calcular la filtración, no solamente en la escollera, sino también en núcleos arcillosos.

(a) Hidrograma usado.

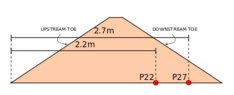
(b) Geometría de la presa y posición de los sensores.

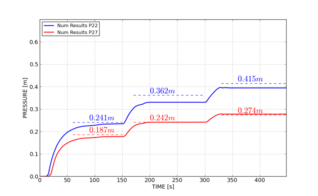
(c) Evolución de la altura de presión en los puntos P22 (línea azul) y P27 (línea roja) en comparación con los resultados experimentales (líneas discontinuas).

Figura 4. Estudio de la filtración con un caudal variable aguas arriba.

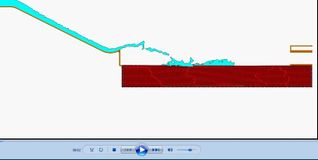
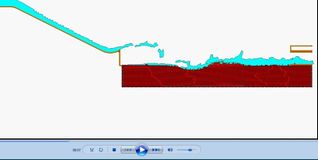
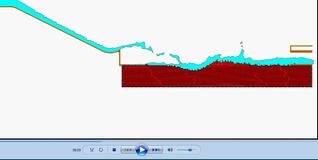
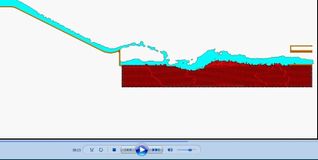
El segundo objetivo ha sido la simulación de la rotura del espaldón de aguas abajo de las presas de escollera debido al sobrevertido. Se ha utilizado el método PFEM anteriormente presentado, para el desarrollo de un algoritmo Lagrangiano que permite seguir las grandes deformaciones a que se ve sometida la escollera en caso de rotura. Se ha adoptado un modelo visco plástico para describir el comportamiento del material y un criterio de fallo de Mohr Coulomb [10].

Finalmente estos dos códigos de cálculo (CFD y estructural) se han acoplado para poder simular la rotura de la presa debido a los efectos hidrodinámicos en régimen transitorio [11]. El modelo desarrollado se ha validado con los resultados de las campañas experimentales de UPM y CEDEX (Figura 5) [12], [13].

Figura 5. Comparación numérico-experimental del avance de la rotura. En la imagen de arriba (numérico) se aprecia el material deformado por el efecto de la filtración. La rotura alcanza la coronación tanto en la simulación como en el experimento.

Cabe destacar que el modelo desarrollado simula siempre a escala real la presa (sea esta una ensayo, un prototipo o real). Esto quiere decir que, a diferencia de los ensayos experimentales, por su propia naturaleza no sufre del efecto de escala y puede ser una herramienta útil para calibrar de forma efectiva ensayos que reproduzcan a escala presas reales.

3.2 Modelación numérica de la aireación en desagües de fondo. Proyecto VADIVAP

Este proyecto se planteó para estudiar con detalle las válvulas de asiento plano y paso circular, diseñadas y comercializadas por la empresa INHISA. Se analizaron diversos aspectos relacionados con el comportamiento de estas válvulas, como el fenómeno del downpull, las pérdidas de carga, y en especial la aireación. Se pretendía utilizar la modelación numérica para sortear las dificultades que plantea la modelación física en válvulas de este tipo, generalmente de grandes dimensiones y que trabajan bajo una elevada carga hidráulica.

En este caso, se utilizó principalmente el método PFEM para modelar la interacción entre el agua pasando a gran velocidad bajo la compuerta y el aire que es arrastrado por ella. No obstante, se utilizó también Kratos para analizar algunos aspectos concretos, como las pérdidas de carga con aperturas parciales.

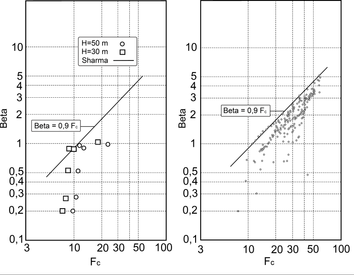
En primer lugar se realizó la validación del método de forma cualitativa y cuantitativa, a partir de estudios teóricos y experimentales de otros autores [14]. La Figura 6 muestra los resultados en comparación con los experimentos de Sharma [15], de referencia en este campo.

Se reprodujo además el desagüe de fondo de la presa de Susqueda, cuya válvula se estaba reemplazando, y pudo ser sometida a pruebas. Aunque no fue posible medir con precisión suficiente el caudal de aire demandado en función de la apertura de compuerta, sí se pudo comprobar que el conducto de aireación se pone en carga para aperturas superiores al 90 %, resultado que coincide con lo observado en el modelo numérico.

Figura 6. Modelación del desagüe de fondo de la presa de Susqueda con PFEM. Izquierda: detalle de la malla de elementos finitos. Se observa el conducto de desagüe, la válvula, y el aireador, que tiene un codo de 90º y conecta con el paramento de aguas abajo de la presa. Centro: Resultados de la campaña de modelación numérica, en cuanto al cociente entre el caudal de demanda de aire y el de agua (β), en función del número de Froude bajo la compuerta (F_C) Derecha: resultados experimentales de Sharma.

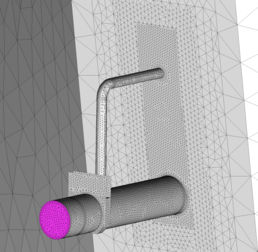
A continuación se realizó una campaña de ensayos numéricos tomando un modelo de base y haciendo variar los principales parámetros que pueden influir en el funcionamiento de un desagüe de fondo: la longitud del conducto de desagüe, la carga de agua sobre la compuerta, el grado de apertura de la compuerta y el diámetro y la longitud del conducto aireador. Este modelo es tridimensional y está basado en la geometría de la compuerta de asiento plano y paso circular de INHISA, instalada en un conducto de desagüe de 1,5 m de diámetro.

Entre los resultados más relevantes puede destacarse que la demanda máxima de aire no siempre se da con una apertura del 60%, sino que depende de otros factores, entre los que se encuentra el diámetro del aireador.

El método utilizado no permite modelar la formación de las burbujas de aire y su movimiento en la masa de agua, por lo que los resultados en cuanto a las propiedades de la mezcla agua-aire no son totalmente fiables. Sin embargo, se llega a reproducir el efecto de arrastre del aire por el cortante generado por el agua en la interfase entre ambos fluidos y ello se traduce en que el caudal de aire demandado, que en principio depende de la caída de presión en la cara de aguas abajo de la compuerta, parece adaptarse adecuadamente a la realidad, lo que permite su aplicación para el dimensionamiento del sistema de aireación.

3.3 Modelación de aliviaderos de bloques en forma de cuña. Proyecto ACUÑA

El proyecto ACUÑA tiene como objetivo fundamental el desarrollo de criterios de diseño de aliviaderos formados por bloques en forma de cuña, dispuestos sobre el paramento de aguas abajo de presas o balsas de materiales sueltos. Esta solución puede reducir de manera importante el coste del aliviadero en este tipo de estructuras, que en general es elevado en términos relativos. En el proyecto, además de CIMNE participan la empresa de prefabricados de hormigón PREHORQUISA, la consultora ALATEC y la UPM, que lleva a cabo la campaña de modelación física. También está involucrado indirectamente el CEDEX, que a través de un convenio de colaboración con la UPM, ha cedido un espacio en el laboratorio del Centro de Estudios hidrográficos para la ejecución de una parte de los ensayos. El planteamiento del proyecto y la selección de los participantes responden al objetivo de profundizar en el conocimiento del fenómeno mediante la combinación de la modelación física y numérica.

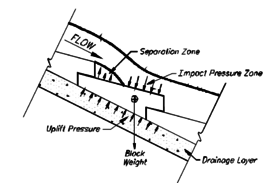
Una de las claves para el dimensionamiento de este tipo de aliviaderos es la estabilidad de los bloques en cualquier situación de vertido, ya que el desprendimiento de una de las piezas generaría una inestabilidad del flujo que podría provocar la erosión del material de apoyo. El fenómeno físico en cuestión es complejo, ya que debe considerarse la disminución de presión que produce el paso del agua sobre el vértice de las piezas en forma de cuña, y cómo se transmite a la base del bloque a través de los orificios de que dispone. Este efecto es positivo para la estabilidad del bloque, ya que la transmisión de esta depresión genera una fuerza de succión que contribuye a evitar que el bloque se desprenda (Figura 7).

Figura 7. Fundamento del funcionamiento de los aliviaderos de bloques en forma de cuña.

En la primera fase del proyecto, la modelación numérica se ha centrado en la comprobación de la aparición de dichas depresiones en la zona de separación del flujo, con el objetivo de hacer una preselección de alternativas de diseño a ensayar en modelo físico. Se trata de optimizar los recursos a emplear en la modelación física. Para ello, se han utilizado los códigos numéricos descritos.

Con PFEM se ha considerado la existencia de aire previo al paso del agua, de modo que se observa si existe o no arrastre de aire con diferentes combinaciones de calados y velocidades. Por otra parte, Kratos se ha utilizado para comprobar el valor de la presión dinámica en esa zona. La primera variante que se está comenzando a estudiar de cara a optimizar el diseño del bloque es la disposición de los orificios de succión y drenaje en la zona superior de la contrahuella.

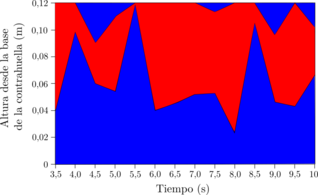
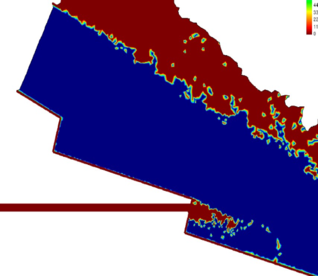
La Figura 8 muestra que la caída de presión es mayor en la zona superior de la contrahuella. En la Figura 9 se muestra un ejemplo de unos de los casos modelados con el orificio partiendo de la zona superior. Se observa cómo en la situación estudiada se produce efectivamente la succión deseada, y el agua (en azul) arrastra el aire (en rojo) que ocupa inicialmente el conducto en el modelo numérico.

Figura 8. Ejemplo de evolución temporal de la zona de presiones negativas (en rojo) de la contrahuella. El eje vertical es la distancia a la base de la contrahuella. Se observa que la presión negativa se registra en la parte superior de la contrahuella, mientras que en la base es siempre positiva.

Figura 9. Funcionamiento esperado del orificio. La depresión que se produce tras el vértice del bloque por el paso del agua (en azul) succiona el aire (en rojo) y por tanto transmite la presión negativa a la base, mejorando la estabilidad del bloque.

3.4 Aliviaderos con cajeros altamente convergentes. Proyecto ALCON

Los aliviaderos con cajeros altamente convergentes son especialmente adecuados para el aumento de la capacidad de desagüe de presas de gravedad existentes. Tienen la particularidad de que la longitud del vertedero es sensiblemente mayor que el ancho del cuenco amortiguador. Para conducir el caudal vertido al cuenco, se disponen unos cajeros con fuerte convergencia.

Los aliviaderos con cajeros altamente convergentes ya han sido utilizados en varias presas tanto en España como en el resto del mundo. Sin embargo no existen referencias sobre criterios de diseño de carácter general para esta tipología, resulta complejo realizar un dimensionamiento inicial y se hace necesario realizar ensayos en modelo físico específicos en cada caso a la hora de proyectar un aliviadero de este tipo.

Con el objetivo de desarrollar criterios generales para establecer una metodología para el cálculo hidráulico y proyecto de este tipo de aliviaderos se está llevando a cabo el proyecto ALCON incluido en el Plan Nacional de Investigación Científica del Ministerio de Economía y Competitividad, en el que participan ALATEC, UPM Y CIMNE.

Como en otros proyectos, la planificación del proyecto ALCON prevé la ejecución en paralelo de ensayos en modelo físico y numérico, a cargo de la UPM y CIMNE respectivamente. Los objetivos de la campaña de modelación numérica son: a) validar el modelo numérico, b) completar la información obtenida de los modelos físicos y c) comprobar el funcionamiento de diseños diferentes de los ensayados en laboratorio. El código de cálculo utilizado en este caso es Kratos.

3.4.1 Calibración

En una primera fase se ha calibrado el modelo mediante la reproducción de un ensayo en modelo físico sencillo. Se trata de un vertido sobre un vertedero con la forma de típica del aliviadero de una presa de gravedad, dispuesto sobre un canal rectangular de 30 cm de ancho. El calado aguas abajo se controla mediante la variación de la apertura de una compuerta, de modo que se fuerza la formación de un resalto hidráulico. Se registra el valor del calado aguas abajo que produce dicho resalto.

El procedimiento seguido es el siguiente:

1. Se ajusta la apertura de compuerta en el ensayo en laboratorio para forzar la formación de un resalto claro.

2. Se registra el calado aguas abajo producido por dicha apertura de compuerta.

3. Se impone el calado en el modelo numérico, y se observa el régimen de funcionamiento.

Figura 10. Resalto forzado en el modelo físico. El calado medio aguas abajo es de 8,0 cm (con fluctuaciones entre 7 y 9 cm).

La Figura 10 muestra una imagen del resalto hidráulico formado en el canal del laboratorio de la UPM. Para la formación del resalto de la imagen fue necesario un calado medio aguas abajo de 8,0 cm, con variación entre 7,0 y 9,0 aproximadamente. Las fluctuaciones y el hecho de que pequeñas variaciones de la apertura de compuerta hicieran modificar sensiblemente el régimen dan idea de la inestabilidad del fenómeno con las condiciones hidráulicas de entrada al cuenco disponibles en el canal de ensayo.

Al imponer en el modelo numérico un calado de 8,0 cm se produce un resalto desplazado hacia el pie de presa. Se tantearon por tanto valores más pequeños, registrándose un comportamiento similar al del laboratorio con un calado de 7,5 cm, como se muestra en la Figura 11.

Figura 11. Resalto bien definido. Calado aguas abajo = 7,5 cm.

3.4.2 Campaña de modelación numérica

Se ha realizado una campaña de modelación numérica sobre un modelo base de aliviadero con cajeros altamente convergentes y diversas configuraciones del cuenco amortiguador, con los objetivos siguientes:

• Estudio del comportamiento del flujo de agua en las proximidades de los cajeros altamente convergentes y estudio del patrón de movimiento, con la posible formación de un flujo helicoidal.

• Estudio de los efectos del ángulo de convergencia de los cajeros en la disipación de energía producida en el cuenco amortiguador.

• Estudio de las dimensiones óptimas para un cuenco amortiguador alimentado por un aliviadero con cajeros altamente convergentes y su relación con las correspondientes en un aliviadero convencional.

En la actualidad, se están analizando los resultados y comparándolos con los obtenidos en los modelos físicos. A modo de ejemplo, la Figura 12 muestra una comparación entre dos configuraciones del cuenco. En una de ellas (izquierda) el bordillo dispuesto a la salida es insuficiente para conseguir la disipación de la energía, mientras que en la otra (derecha) se consigue una mayor disipación.

Figura 12. Funcionamiento del cuenco amortiguador de un aliviadero con cajeros altamente convergentes. Izquierda: el bordillo no tiene altura suficiente para crear el calado necesario para disipar suficientemente la energía. Derecha: caso contrario, con un bordillo de mayor altura. En ambos casos se observa la trayectoria helicoidal del movimiento en los cajeros laterales.

3.4.3 Herramienta de predimensionamiento

Uno de los objetivos del proyecto consiste en el desarrollo de una herramienta de cálculo numérico que permita un predimensionamiento del cuenco de este tipo de aliviaderos. El criterio fundamental para su elaboración es la sencillez de manejo por parte del usuario, de modo que pueda ser utilizado sin necesidad de formación específica en métodos numéricos.

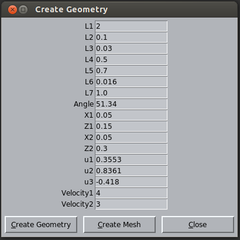
Se ha implementado un módulo de cálculo dentro del programa de pre y post proceso GiD [17]. Permite generar un modelo del cuenco introduciendo únicamente los parámetros geométricos que lo definen. El software impone automáticamente las condiciones de contorno e iniciales, ajusta un tamaño de malla conveniente en la mayoría de los casos, y fija el resto de parámetros del cálculo a valores adecuados. Se genera la malla de elementos finitos automáticamente, y se lanza el cálculo en Kratos (Figura 13). De este modo, se pueden tantear diferentes geometrías con agilidad. No obstante, el usuario interesado puede hacer uso de las opciones de personalización de GiD en lo que se refiere a la generación de la malla o modificación de la geometría, así como de otras opciones de Kratos.

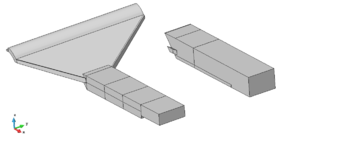
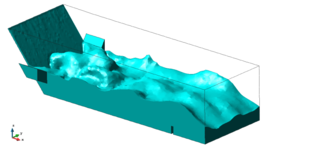
Para permitir la generación automática del modelo, ha sido necesario simplificar la geometría del aliviadero, como se muestra en la Figura 14. Así, se considera únicamente el cuenco amortiguador y las entradas de caudal provenientes de las zonas central y laterales. El objetivo es el predimensionamiento del cuenco: ancho, longitud y calado conjugado necesario. La Figura 15 muestra una imagen del comportamiento del cuenco modelado con la geometría simplificada.

Figura 13. Ventana de entrada de datos de la herramienta de predimensionamiento. Los campos contienen las dimensiones del cuenco, el ángulo del canal de descarga, y los datos que definen las entradas de caudal (calado, módulo y dirección de la velocidad de entrada en los cajeros laterales).

Figura 14. Comparación entre el modelo completo del aliviadero y el simplificado que genera la herramienta de predimensionamiento.

Figura 15. Caso de ejemplo calculado con la herramienta de predimensionamiento.

En la actualidad, se está elaborando un breve manual de usuario que describe el proceso de instalación e indica el significado de cada una de las variables de entrada. Además, se está trabajando en la elaboración de criterios para aproximar la velocidad de entrada del agua en los canales laterales en función de las características del aliviadero.

Cabe resaltar que la herramienta permite comprobar el funcionamiento de un cuenco de resalto convencional (recto), simplemente asignando un valor nulo a la velocidad de entrada de los cajeros laterales, de modo que la totalidad del caudal vertido entre en el cuenco por la zona frontal.

4 Resumen y conclusiones

Se han descrito brevemente algunas aplicaciones de los métodos numéricos en el ámbito de la seguridad de presas, tanto en el diseño como especialmente en proyectos de investigación. Actualmente, presentan limitaciones, como la dificultad para modelar completamente la interacción agua-aire, o el elevado coste computacional en casos complejos. Otros inconvenientes, como la necesidad de formación específica para su aplicación, se están intentando salvar con el desarrollo de herramientas sencillas como la descrita en el proyecto ALCON. No obstante lo anterior, los métodos numéricos son útiles como complemento a los ensayos en modelo físico, ya que:

• Permiten comprobar el funcionamiento de gran variedad de soluciones, previamente a su ensayo en laboratorio, de modo que se pueden descartar a priori las menos adecuadas.

• Aportan más información sobre el funcionamiento de las estructuras hidráulicas, por la posibilidad de registrar las variables relevantes (presión, velocidad) en cualquier punto del dominio. Con ello se puede completar lo observado en laboratorio, donde la instrumentación generalmente es limitada.

• Soslayan el problema del efecto de escala inherente a todos los modelos físicos a escala reducida.

Con ello se optimizan los recursos a emplear, tanto en el marco de proyectos de investigación como en el diseño de estructuras hidráulicas.

Agradecimientos

Los autores desean expresar su agradecimiento a Raimundo Lafuente, Director Técnico de la Confederación Hidrográfica del Ebro (CHE), por facilitar la información necesaria para la modelación del aliviadero de Itoiz; a Gonzalo Rabasa (CHE) y Francisco Riquelme (INHISA), por promover la modelación numérica del aliviadero de Oliana; a Luis Ruano, de PREHORQUISA, y Javier Caballero por su disposición a participar en proyectos de I+D.

Al Ministerio de Ciencia e Innovación por su apoyo en la financiación de los siguientes proyectos de investigación:

“ROTURA DEL ELEMENTO IMPERMEABLE DE PRESAS DE MATERIALES SUELTOS EN SITUACION DE SOBREVERTIDO Y ANÁLISIS DE PROTECCIONES COMBINANDO MODELACIÓN FÍSICA E INTELIGENCIA ARTIFICIAL” de código BIA2010-21350-C03-03, perteneciente a la convocatoria de 2010 del Plan Nacional de I+D+i 2008-2011, dentro del Subprograma de Proyectos de Investigación Fundamental No Orientada.

“DESARROLLO DE UN PROTOTIPO DE BLOQUE EN FORMA DE CUÑA Y DE LA METODOLOGÍA PARA SU USO COMO PROTECCIÓN FRENTE A LA EROSIÓN EN PRESAS O BALSAS DE MATERIALES SUELTOS” de código IPT-2011-0997-020000, perteneciente a la convocatoria de 2011 del Plan

Nacional de I+D+i 2008-2011, dentro del Subprograma INNPACTO.

“DESARROLLO DE CRITERIOS DE DISEÑO PARA EL INCREMENTO EN LA CAPACIDAD DE DESAGÜE EN PRESAS DE FÁBRICA MEDIANTE ALIVIADEROS CON CAJEROS ALTAMENTE CONVERGENTES” de código IPT-310000-2010-11, perteneciente a la convocatoria de 2010 del Plan Nacional de I+D+i 2008-2011, dentro del Subprograma INNPACTO.

“ESTUDIO DE LAS PRINCIPALES VARIABLES DE LAS VÁLVULAS DE ASIENTO PLANO Y PASO CIRCULAR” de código CIT-460000-2009-5, perteneciente a la convocatoria de 2009 del Programa Nacional de Investigación Aplicada, Subprograma de Investigación Aplicada Colaborativa.

Referencias

[1] Osher, S. y Fedkiw, R. (2001), Level set methods: an overview and some recent results, Journal of Computational Physics, Vol. 169, pp. 463-502.

[2] Kratos, Multiphysics opensource fem code. http://www.cimne.com/kratos.

[3] Dadvand, P., Rossi, R. y Oñate, E. (2010). An object-oriented environment for developing finite element codes for multi-disciplinary applications. Archives of Computational Methods in Engineering. 2010. Vol. 17, 253-297.

[4] Rossi, R., Larese, A., Dadvand, P., & Oñate, E. (2013). An efficient edge-based level set finite element method for free surface flow problems. Int. J. Numer. Meth. Fluids, 71:687-716.

[5] Salazar, F., Morán, R., Rossi, R., & Oñate, E. (2013). Analysis of the discharge capacity of radial-gated spillways using CFD and ANN - Oliana Dam case study. Journal of Hydraulic Research, (ahead-of-print), 1-9. DOI: 10.1080/00221686.2012.755714

[6] Idelsohn, S.R., Oñate, E., Del Pin, F. y Calvo, N. (2006) Fluid-structure interaction using the particle finite element method. Computer Methods in Applied Mechanics and Engineering, 195, pp. 2100-2123.

[7] Oñate, E., Idelsohn, S.R., Del Pin, F. y Aubry, R. (2004). The particle finite element method: an overview. International Journal on Computational Methods. 1:267-307.

[8] Oñate, E., Idelsohn, S.R, Celigueta, M.A., y Rossi, R. (2008). Advances in the particle finite element method for the analysis of fluid-multibody interaction and bed erosion in free surface flows. Comp. Methods in Apll. Mech. And Eng., Vol. 197, 1777-1800

[9] CEDEX. Ensayo en modelo reducido de la presa de Itoiz (1994). Informe final.

[10] Larese, A. A coupled Eulerian-PFEM model for the simulation of overtopping in rockfill dams. Phd thesis: Universitat Politècnica de Catalunya. UPC BarcelonaTech, 2012. http://hdl.handle.net/10803/108502.

[11] Larese, A.; Rossi, R.; Oñate, E. & Idelsohn, S. A coupled PFEM- Eulerian approach for the solution of porous FSI problems. Computational Mechanics, DOI: 10.1007/s00466-012-0768-9, 2012, 50 (6), 805-819

[12] Larese, A.; Rossi, R. & Oñate, E. Theme B: simulation of the behavior of prototypes of rockfill dams during overtopping scenarios: seepage evolution and beginning of failure Proceeding of the XI ICOLD Benchmark Workshop on Numerical Analysis of Dams, 2011, ISBN: 978-84-695-1816-8

[13] Larese, A.; Rossi, R. & Oñate, E. Coupling Eulerian and Lagrangian models to simulate seepage and evolution of failure in prototype rockfill damsProceeding of the XI ICOLD Benchmark Workshop on Numerical Analysis of Dams, 2011, ISBN: 978-84-695-1816-8

[14] Pozo, D., Salazar, F. y Toledo, M.Á. Modelación del funcionamiento hidráulico de los dispositivos de aireación de desagües de fondo de presas mediante el Método de Partículas y Elementos Finitos (PFEM). Revista Internacional de Métodos Numéricos en Ingeniería (aceptado).

[15] Sharma, H.R. (1976). Air-Entrainment in High-Head Gated Conduits. Journal of the Hydraulics Division, 102(11), 1629-1646.

[16] Frizell, K. H. (1997). Protecting embankment dams with concrete stepped overlays. Hydro Review, 16(5), 36-45.

[17] GiD. The personal pre and post processor. www.gidhome.com