1 Introducción
La combinación de dos pieles de material compuesto entre las que se interpone un núcleo de baja densidad, proporciona a las estructuras sándwich de material compuesto altos valores de rigidez y resistencia a flexión, bajo peso, buena tolerancia al daño y alta capacidad de absorción de energía. Todas estas características hacen que estas estructuras sean ampliamente utilizadas en la industria aeronáutica y del transporte.
A pesar de las ventajas mencionadas, las pieles de tipo laminado muestran cierta vulnerabilidad ante cargas impulsivas, ya sean de alta o baja velocidad, siendo las cargas de impacto balístico una de las condiciones más críticas al que este tipo de estructuras pueden estar sometidas [1]. Muchos autores han centrado sus investigaciones en el análisis de la respuesta estructural de estructuras sándwich sometidas a impacto normal [2-3], en el que la dirección de impacto es perpendicular a la superficie de la estructura; sin embargo, este tipo de impactos no son los más frecuentes durante la vida en servicio de los componentes estructurales, existiendo un cierto ángulo de oblicuidad entre proyectil y componente. Es por ello que es necesario analizar su respuesta estructural frente a estas condiciones de impacto.
Un estudio experimental exhaustivo resulta muy costoso desde el punto de vista temporal y económico, por lo que para reducir los costes de desarrollo y de certificación, las industrias suelen recurrir al uso de métodos computacionales que permitan predecir la integridad estructural de las estructuras de material compuesto cuando éstas se encuentran sometidas a diferentes condiciones de carga.
El objetivo de este trabajo es analizar la respuesta estructural de placas sándwich con pieles de material compuesto sometidas a impactos oblicuos de alta velocidad. Para ello se han desarrollado tres modelos mediante el código de elementos finitos Abaqus/Explicit, que han sido validados mediante ensayos experimentales disponibles en literatura. A partir de los mismos se ha modificado la oblicuidad del ángulo de impacto, de manera que la variación permita analizar su influencia sobre los resultados obtenidos.
2 Descripción del modelo numérico
Para analizar el comportamiento de la estructura sándwich ante diferentes ángulos de impacto, se han implementado tres modelos de elementos finitos en el código comercial Abaqus/Explicit: modelo de una placa de laminado, de dos placas de laminado separadas una distancia igual al espesor del núcleo (también llamadas spaced-plates) y de una placa sándwich con pieles del mismo laminado y nucleo de nido de abeja de aluminio.
Para el modelo de la placa sándwich, se han representado dos elementos: un proyectil esférico y una placa sándwich (de dimensiones 120 x 120 mm) formada por dos pieles de material compuesto y un núcleo tipo panal de abeja de aluminio.
Los laminados que conforman las pieles de esta estructura sandwich, así como los modelos de la placa de laminado y de las placas espaciadas, de 2 mm de espesor, están compuestas por tejido plano formado por fibras de carbono en resina epoxi, AS4/8552. El comportamiento del tejido fue definido a través de la subrutina abq_ply_fabric, disponible en el programa de elementos finitos Abaqus/Explicit [4].
En el caso de la estructura sándwich, el núcleo, de 20 mm de espesor, estaba formado por una aleación de aluminio 3003 con un tamaño de celda de 4,8 mm y un espesor de lámina de aluminio de 60 µm. En el modelo de elementos finitos el comportamiento del aluminio se definió como elástico-plástico y la iniciación del daño se modelizó a través del criterio de Johnson-Cook (criterio de iniciación del daño para metales dúctiles). La supresión de elementos fue activada en ambos casos, pieles y núcleo.
Para poder llevar a cabo el proceso de impacto, se modelizó un proyectil de acero (E=210 GPa, Ʋ=0,3) de 7,5 mm de diámetro y 1,7 g de peso. Este proyectil fue definido como un elemento completamente rígido, sobre el que se aplicó la velocidad de impacto.
La estructura se encontraba empotrada en todos sus bordes exteriores, al igual que en el caso de los ensayos experimentales que se utilizaron para la validación. Se definió un contacto de tipo general en Abaqus/Explicit para toda la estructura, de modo que todos los componentes pudieran interactuar entre sí durante el proceso de impacto.
La sensibilidad de los resultados a la malla empleada se evaluó realizando sucesivas discretizaciones espaciales. Los resultados presentados en este estudio se basan en la malla optimizada, en concreto, los laminados que componen las caras delantera y trasera de la estructura sándwich se modelaron usando 11664 elementos lineales de cuatro nodos tipo S4R en Abaqus. También este tipo de elementos se utilizó para el núcleo de nido de abeja, en el que se emplearon 28930 elementos. El proyectil quedo definido medinate 896 elementos hexaédricos de ocho nodos con un punto de integración (C3D8R en Abaqus/Explicit).
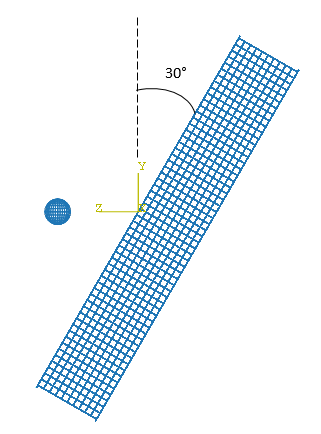
En la Figura 1 se puede observar la malla correspondiente al modelo de elementos finitos de la estructura sándwich junto con el proyectil.
Para evaluar la contribución del núcleo en la respuesta del impacto oblicuo en estructuras sándwich se implementó un modelo adicional (Figura 2): de una estructura formada por dos placas espaciadas de material compuesto sin núcleo.
Ambas placas están separadas una distancia de 20 mm, equivalente a la anchura del núcleo de nido de abeja.
No se definió ningún tipo de interacción entre las placas. También se desarrolló un modelo de una placa de laminado, que representa una de las pieles de la estructura sándwich, para validar el modelo.
3 Validación del modelo numérico
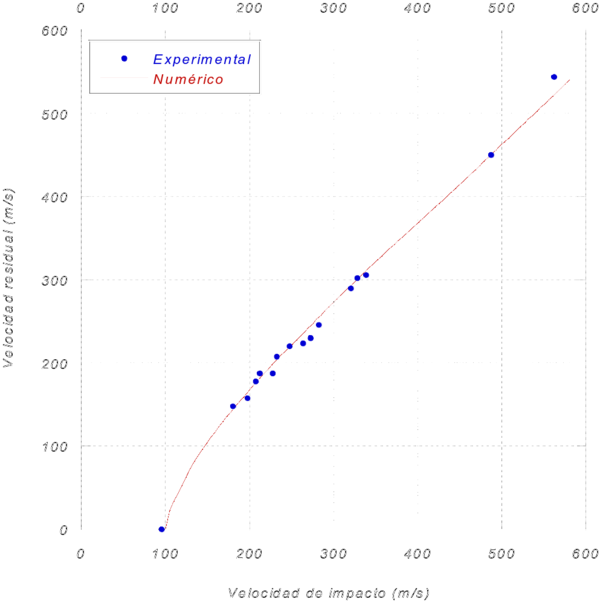
Los modelos numéricos del laminado, las placas espaciadas y la estructura sándwich fueron validados comparando los resultados obtenidos con datos experimentales disponibles en la literatura: laminado [5], placas espaciadas [6] y estructura sándwich [7], respectivamente.
La variable utilizada en la validación de los modelos numéricos fue la velocidad residual de un impacto normal en función de la velocidad de impacto del proyectil.
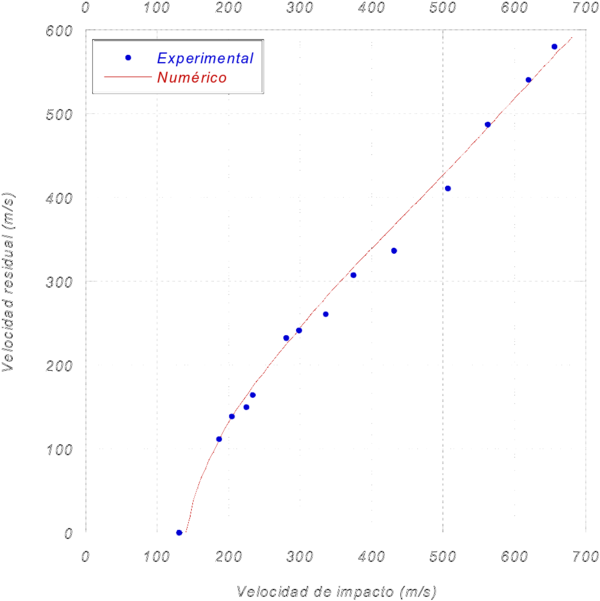
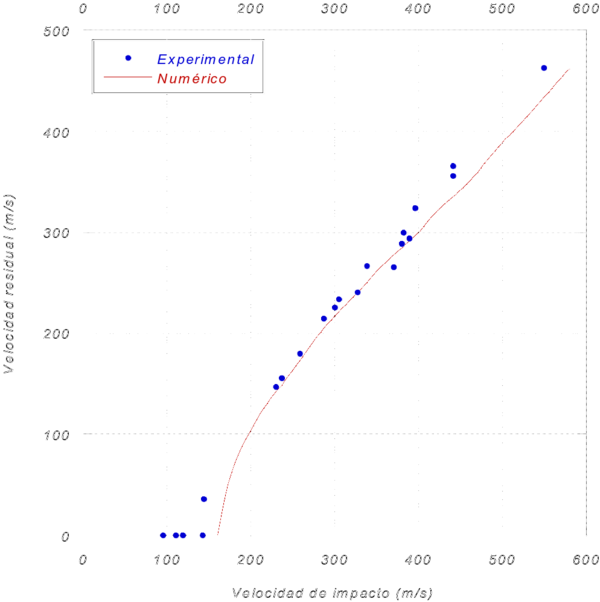
Las figuras que se muestran a continuación representan la comparación entre los resultados experimentales y numéricos del laminado (Figura 3), las placas espaciadas (Figura 4) y la estructura sándwich (Figura 5).
Se puede observar una buena correlación entre los datos experimentales y numéricos para los tres modelos implementados. La mayor diferencia existente entre dichos datos se da para la estructura tipo sándwich, con un valor del 9%, para una velocidad de impacto de 396 m/s.
En ningún caso, las diferencias en velocidad residual entre modelo numérico y resultados experimentales superan el 10%, como resultado, los tres modelos numéricos se pueden considerar validados.
4 Estudio numérico: efecto del ángulo de impacto
El efecto del ángulo de impacto sobre el comportamiento de las estructuras sándwich con núcleo tipo panal de abeja y pieles de laminados de material compuesto, se analizó a través de dos variables: límite balístico y velocidad residual.
La oblicuidad del impacto viene dada por el ángulo que forma el eje del impactador y la normal a la estructura sándwich, tal y como se aprecia en el ejemplo de la Figura 6.
Para analizar la influencia del núcleo en la respuesta del impacto oblicuo sobre las estructuras sándwich, los resultados obtenidos se compararán con los obtenidos para el modelo de placas espaciadas.
4.1 Límite balístico
El límite balístico se define como la mínima velocidad de impacto requerida para que el proyectil penetre completamente la estructura en este caso, cuando ha atravesado la piel posterior del sándwich y de las placas espaciadas.
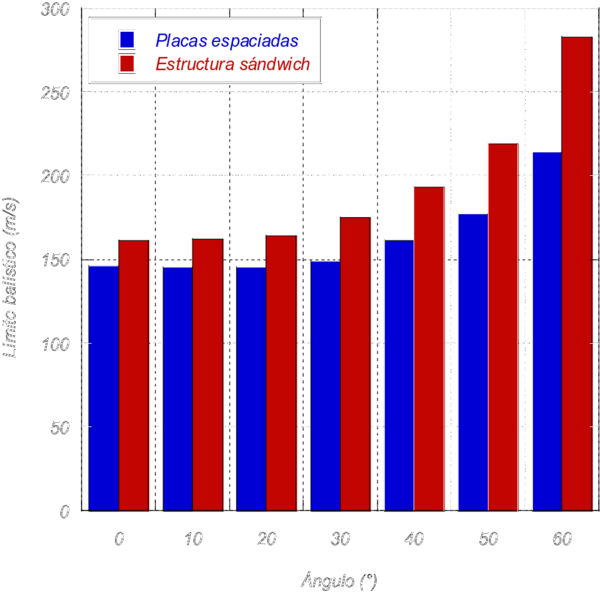
En la figura 7 aparecen representados los límites balísticos de ambas estructuras estudiadas (placas espaciadas y estructura sándwich) para diferentes ángulos de impacto en un rango de 0 a 60°. Los resultados obtenidos muestran que la variación de este parámetro con el ángulo de oblicuidad no es exactamente lineal.
En ambos modelos el valor del límite balístico no varía prácticamente para ángulos de impacto comprendidos entre 0 y 20°. Las diferencias máximas en este rango de ángulos de impacto son de 0,7% para el modelo de placas espaciadas y 1,9% en la estructura sándwich.
Sin embargo, es a partir de una oblicuidad de 30º cuando el límite balístico y las diferencias observadas aumentan de manera pronunciada. Para un ángulo de impacto de 60º, el límite balístico de las placas espaciadas aumenta un 43,6%, en referencia a un ángulo de impacto de 30º. Para el caso de la estructura sándwich, el límite balístico aumenta un 61,7% entre ángulos de impacto de 30º y 60º.
El aumento del límite balístico es más pronunciado en la estructura sandwich. Esto puede ser debido a que en los impactos con mayor oblicuidad, el proyectil debe recorrer una distancia mayor para llegar a la placa posterior, en comparación con los casos más parecidos al impacto normal, donde la trayectoria del proyectil es prácticamente una línea recta. La disminución de velocidad en ese trayecto es ligeramente mayor, aumentando el valor necesario de velocidad de impacto inicial para que sea capaz de atravesar la estructura entera.
Como se ha observado, para ángulos de valor 0, 10 y 20°, las diferencias de límite balístico para un mismo ángulo entre las placas espaciadas y la estructura sándwich no son tan significativas como lo son para ángulos mayores (la mayor diferencia en el rango entre 0 y 20º es de 13%). Esto es debido a la presencia del núcleo en la estructura sándwich. Al ser un núcleo de nido de abeja, que no tiene una estructura isotropa y está compuesto por celdas, el proyectil al impactar con un ángulo determinado debe atravesar multitud de paredes pertenecientes a las celdas del núcleo que no estaban presentes en el caso del impacto normal, por lo que la resistencia al proyectil es menor, disminuyendo la velocidad al alcanzar el laminado posterior.
4.2 Velocidad residual
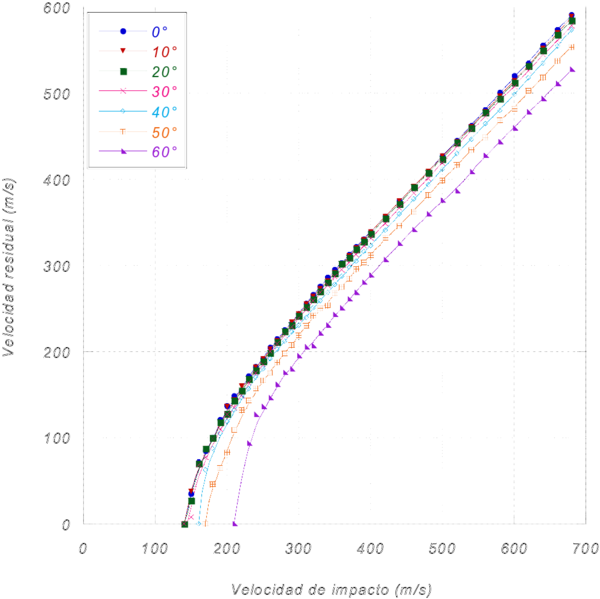
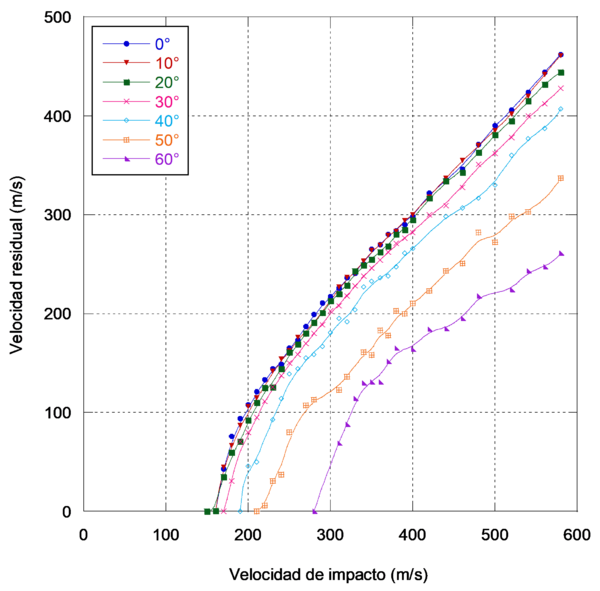
Las Figuras 8 y 9 muestran la velocidad residual en función de la velocidad de impacto de ambas estructuras estudiadas para diferentes ángulos de impacto.
Las curvas anteriores presentan una tendencia lineal a velocidades de impacto alejadas del límite balístico. Sin embargo, en zonas cercanas a éste, las curvas no son lineales ya que el límite balístico se caracteriza por ser una velocidad crítica de impacto a la que la estructura va a ser penetrada con una probabilidad del 50%. Por tanto, existe un intervalo de velocidades de impacto en el cual la estructura puede o no puede ser perforada completamente.
Por otra parte, dichas curvas muestran un comportamiento bastante similar para ángulos comprendidos entre 0 y 40° en el caso de placas espaciadas, empezandose a notar cambios a partir de un ángulo de 30° en el caso de la estructura sándwich
Para ángulos superiores, las curvas se desplazan hacia la derecha, indicativo de la mayor dificultad del proyectil para atravesar las estructuras debido a la gran oblicuidad de las mismas y a la geometría del núcleo tipo panal de abeja, tal y como se explicó en el apartado 4.1.
Los datos de velocidad residual son también un indicativo de la energía que ambas estructuras absorben en cada impacto. Para analizar este fenómeno con más detalle, la Figura 10 representa la energía absorbida en función de la energía de impacto en un impacto normal y en uno con una oblicuidad de 30°.
En zonas cercanas al límite balístico, el porcentaje de energía absorbida por la estructura se encuentra en un rango comprendido entre 80 y 100%, ya que el proyectil se mueve con la energía justa para atravesar la estructura.
A medida que las curvas se distancian del límite balístico, el porcentaje de energía absorbida por ambos modelos disminuye debido a que el proyectil se mueve con una energía de impacto superior y por tanto la estructura opone menor resistencia al paso del mismo. La absorción de energía en este caso es menor y el daño observado es más localizado.
Es destacable la aportación del núcleo en la estructura sándwich en comparación con las placas espaciadas, ya que la absorción de energía es mucho mayor.
Como ya se comprobó en las gráficas de velocidad, el aumento del ángulo de oblicuidad en el impacto produce un aumento de la energía absorbida en ambos modelos, siendo mayor este incremento en el caso de la estructura sándwich.
5 Conclusiones
En este trabajo se ha estudiado la influencia de la oblicuidad de ángulo de impacto sobre el límite balístico y la velocidad residual obtenida para placas sándwich sometidas a impacto de alta velocidad. La estructura sándwich estaba compuesta por pieles de tejido carbono/epoxi y núcleo de nido de abeja de aluminio. Para llevar a cabo este análisis, se ha implementado un modelo numérico utilizando el código de elementos finitos Abaqus/Explicit.
Este modelo ha sido validado mediante resultados tomados de la literatura. Asimismo, para poder evaluar la contribución del núcleo al proceso de impacto, se ha implementado un modelo adicional de placas espaciadas, cuya separación era la misma que la altura del núcleo de la estructura sándwich.
Los resultados muestran el incremento del límite balístico y de la velocidad residual (y por tanto de la energía absorbida) con el ángulo de oblicuidad, tanto en el modelo de la estructura sándwich como en el de placas espaciadas. Para ángulos de impacto por debajo de 30º, los resultados de ambas estructuras prácticamente no presentaban variación, siendo sus resultados muy similares a los obtenidos para impacto normal.
En cuanto a la contribución del núcleo, en todos los casos estudiados la estructura sándwich mostraba mayores resultados tanto de límite balístico como de velocidad residual en comparación con el modelo de placas espaciadas, evidenciando su intervención durante el proceso de impacto.
Referencias
[1] M.M. Ansari, A. Chakrabarti, Composite Science and Technology, 142, pág.107-116 (2017).
https://doi.org/10.1016/j.compscitech.2016.12.033
[2] I. Iváñez, C. Santiuste, E. Barbero, S. Sanchez-Saez, Composite Structures, 93, 9, pág. 2392–2399 (2011).
https://doi.org/10.1016/j.compstruct.2011.03.028
[3] L, Aktay, A.F Johnson, M. Holzapfel, Computer Material Science, 32, pág. 252–260 (2005)
https://doi.org/10.1016/j.commatsci.2004.09.044
[4] Abaqus/Standard version 6.13. User´s manual. Hibbit, Karlsson: 2013.
[5] B. L. Buitrago, S. K. García-Castillo, E. Barbero, Composites Part B: Engineering, 49, pág. 86-92 (2013).
https://doi.org/10.1016/j.compositesb.2013.01.005
[6] B.L. Buitrago, Tesis doctoral, Universidad Carlos III de Madrid (2012).
[7] B.L. Buitrago, C. Santiuste, S. Sánchez-Sáez, E. Barbero, C. Navarro, Composite Structures. 92, 9, pág. 2090–2096 (2010).
Document information
Published on 19/10/17
Accepted on 19/10/17
Submitted on 19/10/17
Volume 01 - Comunicaciones Matcomp17 (2017), Issue Núm. 1 - Comportamiento en Servicio de los Materiales Compuestos, 2017
DOI: 10.23967/r.matcomp.2017.10.003
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?