Bat algorithm optimized fuzzy PD based speed controller for brushless direct current motor

Abstract

In this paper, design of fuzzy proportional derivative controller and fuzzy proportional derivative integral controller for speed control of brushless direct current drive has been presented. Optimization of the above controllers design is carried out using nature inspired optimization algorithms such as particle swarm, cuckoo search, and bat algorithms. Time domain specifications such as overshoot, undershoot, settling time, recovery time, and steady state error and performance indices such as root mean squared error, integral of absolute error, integral of time multiplied absolute error and integral of squared error are measured and compared for the above controllers under different operating conditions such as varying set speed and load disturbance conditions. The precise investigation through simulation is performed using simulink toolbox. From the simulation test results, it is evident that bat optimized fuzzy proportional derivative controller has superior performance than the other controllers considered. Experimental test results have also been taken and analyzed for the optimal controller identified through simulation.

Keywords

Bat algorithm ; Brushless direct current motor ; Cuckoo search ; Fuzzy proportional derivative controller ; Fuzzy proportional derivative integral controller

1. Introduction

Brushless Direct Current (BLDC) motors are widely used in servo robotic positioning actuators, traction, fans, and blowers due to their high reliability, high efficiency, low maintenance, and many other advantages [1] . In the last decade, many number for speed controllers have been developed for the speed control of brushless dc motor. They are classified as proportional integral derivative controller, fuzzy logic based controller, Neuro fuzzy controller, etc [2] , [3] , [4] , [5] , [6] , [7] , [8] , [9] , [10] , [11] , [12] , [13] , [14] , [15] , [16] , [17] , [18] , [19] , [20] , [21]  and [22] .

Normally, Proportional Integral derivative controller is an optimum choice for controlling the speed of the BLDC motor. However, it has uncertainty problem due to load as well as in set speed variations. Also, tuning of the proportional integral and derivative (PID) controller leads to uncertainty in the control system parameters [2] . In order to overcome the above problems, precise method of control can be provided with help of intelligent system based on fuzzy logic and neural network approach. But most of the time, fuzzy logic based controller provides better results than the conventional and neural network.

Conventional proportional integral (PI) controller has been implemented for BLDC motor in [3] . Direct self control was designed for brushless dc motor with PI speed controller in [4] . Three phase brushless dc motor with proportional integral based speed controller has been presented for four quadrant operation in [5] . From the literatures [3] , [4]  and [5] , the proportional controller is the most preferable speed controller for BLDC motor, but PI controller produces sluggish response in the system, and also it produces uncertainty problem in some operating conditions of the BLDC motor. To avoid these shortcomings, the fuzzy logic controller has been developed [6] , [7] , [8]  and [9] . In [6] , adaptive fuzzy logic based speed controller has been designed for brushless dc motor. In [7] , comparative analysis for PI controller, fuzzy tuned PID controller, fuzzy variable structure controller, and ANFIS controller has been developed for Brushless DC motor. In [8] , adaptive fuzzy PID controller has been developed for the dc motor. In [9] , fuzzy like Proportional Derivative (PD) controller was developed for non linear plant. But the non linearity of the system depends on the scaling factor of the fuzzy Proportional Derivative controller.

From [6] , [7] , [8]  and [9] , all parameters were in favor of the fuzzy logic based controller. Even though, performance of the fuzzy logic controller depends on the scaling factor of the input and output of the fuzzy logic controller, it also affects the control system performance. In order to overcome these problems, the tuning of scaling factor of the PID and fuzzy logic controller with naturally inspired algorithm such as genetic algorithm, particle swarm optimization, and cuckoo search algorithm was developed for the optimization of constant parameter in [10] , [11] , [12]  and [13] . The design and the tuning of PID controller through the genetic algorithm approach have been presented for robotic manipulator in [10] . From the simulation result, torque of the manipulator has larger overshoot and larger error. In [11] , tuning of PID controller gain by particle swarm optimization (PSO) was implemented for brushless dc motor, but the electromagnetic torque has high overshoot and undershoots in the starting period.

In [12] , genetic algorithm has been used for tuning the scaling factor of fuzzy logic based PID controller, and it was applied for the speed control of brushless dc motor. From the experimental results it was pointed out that speed response has uncertainty problem due to load variations. In [13] , the survey has been presented explaining the nature-inspired optimization algorithms for tuning the scaling factor of the fuzzy logic control. The importance of particle swarm optimization for large scale optimization was explained in [14] . In [15] , comparison of particle swarm optimization and genetic algorithm for FACTS-based controller design has been explained. In [16] , the comparison of Cuckoo search with standard versions of PSO and GA has been discussed. Cuckoo search algorithm was applied for tuning the parameter of two degrees of freedom controller in the automatic generation control of multi area system which has been presented in [17] . But with this algorithm also, only steady state response of the system has improved without significant transient response improvement. The comparative analysis of swarm intelligent techniques (cuckoo search, firefly algorithm, and glowworm swarm optimization) with population based algorithm (genetic algorithm) was presented in [18] . The superiority of each swarm intelligent techniques has been noticed with population based algorithm. The scaling factor of fractional order fuzzy PID controller tuning by cuckoo search algorithm has been presented in [16] . In [19]  and [20] , bat algorithm was used for tuning the parameters of the power system stabilizers, and its effectiveness was also reported. Most of the researchers only concentrated on the GA, PSO, and Cuckoo algorithm for tuning fuzzy logic controller scaling factors.

The operation of the system under fuzzy logic control not only depends on the input and output scaling factors of the fuzzy logic controller but it also depends on the position of the membership function of the input and outputs of the comptroller. Tuning of membership function of Fuzzy PWM based on Genetic Algorithm for battery charging has been outlined in [21] . Genetic fuzzy self-tuning PID controllers for antilock braking systems have been presented in [22] . Genetic algorithm has been used for tuning the antecedent part of the input membership function, and coefficients of the consequent parts of the Takagi and Sugeno fuzzy inference system. Totally, 93 parameters have been tuned for the fuzzy inference system. From this, genetic algorithm takes large computation time for getting optimal parameter for the fuzzy logic control. Although, overshoot, performance indices, i.e., integral of absolute error and integral of time multiplied absolute error was not favored for the fuzzy self tuned PID controller. There is no significant literature based on bat algorithm optimized tuning of parameters in fuzzy logic controller. Flexible job shop scheduling problem using an estimation of distribution algorithm (EDA) has been explained, and effectiveness of EDA has been addressed in [23] . But EDA has some disadvantages that are loss of diversity, insufficient use of local information of solution, and it traps into local optima.

The objective of this paper is to design the fuzzy PD and fuzzy PID controller for the speed control of brushless dc motor and optimize the input and output scaling factor, antecedent part of the input membership function, and coefficients of the consequent parts of the fuzzy inference system of the fuzzy PD controller and fuzzy PID controller with bat, PSO, and cuckoo search algorithms. The purpose of optimization is to minimize the objective function in order to improve the time domain specifications and performance indices under different operating conditions. Parameters such as overshoot, undershoot, settling time, recovery time, steady state error, root mean squared error, integral of absolute error, integral of time multiplied absolute error and integral of squared error are measured and compared for the above controllers with different operating conditions of the brushless dc motor drive. Based on the simulation results, best controller is suggested and validated. An attempt has also been made to prove experimentally the results of the optimal controller pointed out through simulation study.

The paper is organized as follows: Speed control of BLDC motor is given in brief in section 2 , and design of Fuzzy PD and Fuzzy PID type speed controller is explained in section 3 . Formulation of the objective function for the fuzzy PD and fuzzy PID controller is presented in the section 4 . Review of nature-inspired optimization algorithms for tuning of fuzzy PD and fuzzy PID controller has been provided in section 5 . Section 6 discusses the simulation results, and section 7 provides experimental verification and discussion on results. Concluding remarks are outlined in section 8 .

2. The speed control of the brushless dc motor

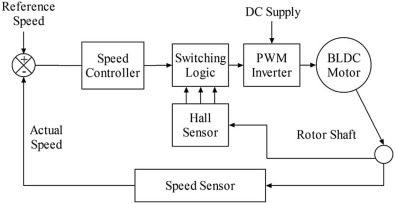
Speed control system for BLDC motor is represented in Fig. 1 . Three phase star connected brushless dc motor can be described by the following five equations (1) , (2) , (3) , (4)  and (5) as,

$v_{ab}=R\left(i_{a}-i_{b}\right)+L{\frac {d}{dt}}\left(i_{a}-\right.$$\left.i_{b}\right)+e_{a}-e_{b}$

( 1)

$v_{bc}=R\left(i_{b}-i_{c}\right)+L{\frac {d}{dt}}\left(i_{b}-\right.$$\left.i_{c}\right)+e_{b}-e_{c}$

( 2)

$v_{ca}=R\left(i_{c}-i_{a}\right)+L{\frac {d}{dt}}\left(i_{c}-\right.$$\left.i_{a}\right)+e_{c}-e_{a}$

( 3)

$T_{e}=k_{f}{\omega }_{m}+J{\frac {d{\omega }_{m}}{dt}}+T_{L}$

( 4)

${\omega }_{m}={\frac {d{\theta }_{m}}{dt}}$

( 5)

Fig. 1. Speed control system of brushless dc motor.

Where V_ab , V_bc , and V_ca are the phase to phase voltage in volts. Phase currents of the stator winding represents by i_a , i_b , and i_c in amperes. L denotes the self inductance of the motor in Henry. Back electromagnetic force is represented by e_a , e_b , and e_c in volts. T_e and T_L are the electromagnetic torque and Load torque of the motor in N-m. J is the rotor inertia, k_f is a friction constant, ω_m is the rotor speed of the motor in rad/s, and θ_m is the rotor position of the motor in rad. Fig. 1 shows the speed control system of the brushless dc motor. The system consists of two loops, such as the inner loop and the outer loop. Inner loop is used for synchronizing the inverting gate signal with back electro motive force or rotor position of the motor. The outer loop is used to sense the actual speed of the motor, and then it is compared with the reference speed to produce speed error. The speed error is then processed via controller thus provide the controlling signal to the switching logic and PWM inverter and control the dc bus voltage thus by controlling the speed of the motor [7] .

3. Design of fuzzy PD and fuzzy PID type speed controller for the brushless DC motor

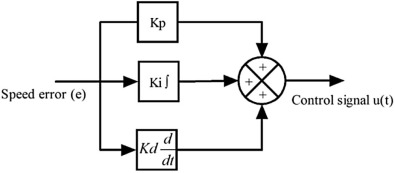
Structure of conventional PID controller is shown in Fig. 2 . The control output of the PID controller in time-domain is expressed in equation (6) as,

$u\left(t\right)=K_{p}e\left(t\right)+K_{i}\int e\left(t\right)dt+$$K_{d}{\frac {de}{dt}}$

( 6)

Fig. 2. Structure of conventional PID controller.

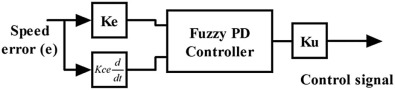
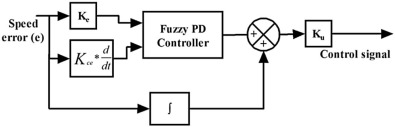
Where, e (t) represents the tracking speed error, the difference between the desired input value (ω_ref ), and the actual output (ω_act ), u(t) is the control signal to the plant, K_p is the proportional gain, K_i is the integral gain, and K_d is derivative gain of the PID controller. The design of fuzzy PD controller and fuzzy PID controller is given below, and their structures are shown in Fig. 3  and Fig. 4 .

Fig. 3. Structure of fuzzy PD type controller.

Fig. 4. Structure of fuzzy PID type controller.

The proportional derivative controller uses the derivative action to improve closed-loop stability. The basic description of a PD controller is expressed in the equation (7) as,

$u\left(t\right)=K_{p}e\left(t\right)+K_{d}{\frac {de\left(t\right)}{dt}}$

( 7)

The input to the fuzzy PD controller is the error and rate of change of error, the control output is the nonlinear function of error and rate of change of error and given in the equation (8) as,

$u\left(t\right)=f\left(K_{e}{_{\ast }}e\left(t\right),{\mbox{ }}K_{ce}{_{\ast }}{\frac {de\left(t\right)}{dt}}\right){_{\ast }}K_{u}$

( 8)

The function f is the input–output map of the fuzzy controller. Using the linear approximation, the equation (8) rewrite as,

$u\left(t\right)=\left(K_{e}{_{\ast }}e\left(t\right)+K_{ce}{_{\ast }}{\frac {de\left(t\right)}{dt}}\right){_{\ast }}K_{u}$

( 9)

$u\left(t\right)=K_{e}{_{\ast }}K_{u}{_{\ast }}e\left(t\right)+$$K_{ce}{_{\ast }}K_{u}{_{\ast }}{\frac {de\left(t\right)}{dt}}$

( 10)

By comparing, the gains in (7) and (10) are related in the following equation (11) and (12) as,

$K_{p}=K_{e}{_{\ast }}K_{u}$

( 11)

$K_{d}=K_{ce}{_{\ast }}K_{u}$

( 12)

Where, K_e and K_ce are input scaling factor of the fuzzy PD controller. K_u is the output scaling factor of the fuzzy PD controller. It has simple control structure which gives better sensitivity and increases the overall stability of the closed loop system. Also this structure provides reduced overshoot and enhanced damping to the overall closed loop system. The nonlinearity of the system can be handled by appropriate choice of input and output membership functions [9] .

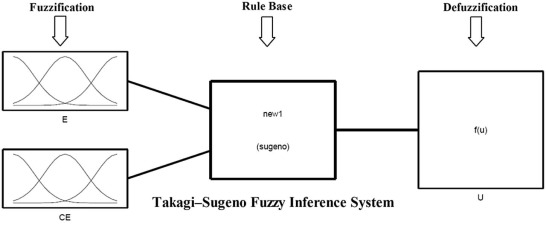
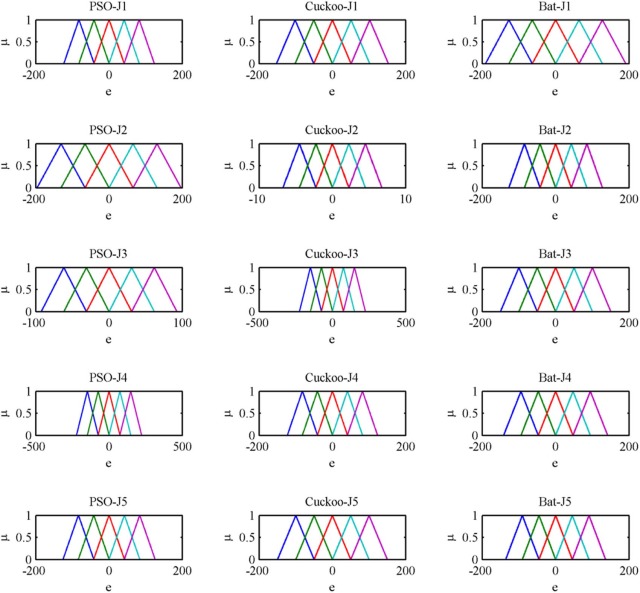
The internal structure of Fuzzy PD controller has two inputs that are error (e) and rate of change of error (Δe) and one output (U), and it is shown in Fig. 5 . The inputs are distributed with five triangular membership functions.

Fig. 5. Internal structure of fuzzy PD controller.

Fuzzy inference system is modeled by zero order Takagi-Sugeno fuzzy inference system. The triangular membership function is described by the equation (13) as,

$f\left(x,{\mbox{ }}a,{\mbox{ }}b,{\mbox{ }}c\right)=$$\lbrace {\begin{array}{cc}0,&x\leq 0\\{\frac {x-a_{j}}{b_{j}-a_{j}}},&a_{j}\leq x\leq b_{j}\\{\frac {c_{j}-x}{c_{j}-b_{j}}},&b_{j}\leq x\leq c_{j}\\0,&c_{j}\leq x\end{array}}$

( 13)

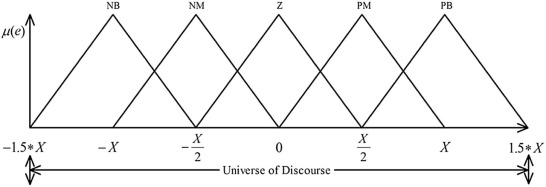
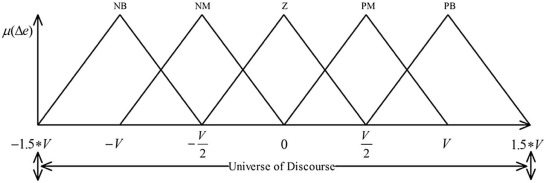
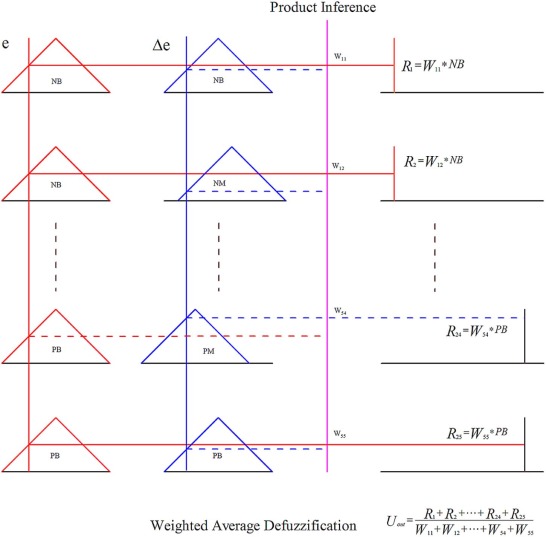
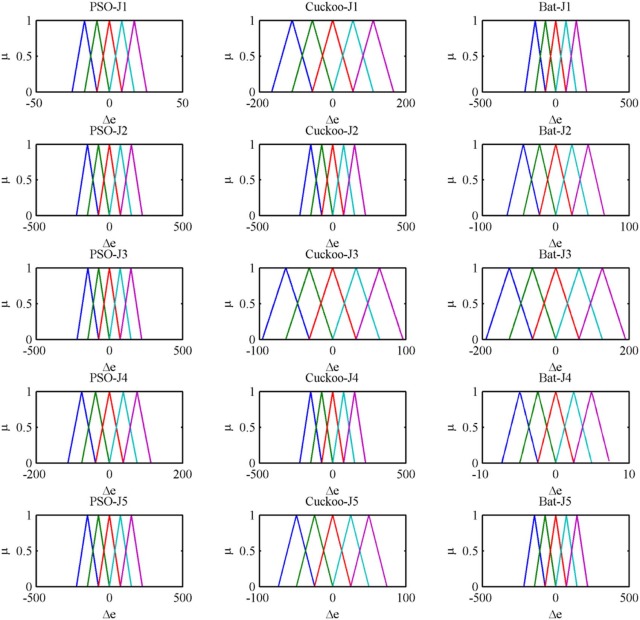
Where a and c locate the feet of the triangle and the parameter b locates the peak. The distribution of membership functions for the error and the rate of change of error are shown in Fig. 6  and Fig. 7 . Two inputs has range from −1.5*X to 1.5*X and −1.5*V to 1.5*V, respectively, membership function denote by Negative Big (NB), Negative Medium (NM), Zero (Z), Positive Medium (PM), and Positive Big (PB). The range of output is from –H to H. The distribution of output is shown in Fig. 8 . Initially, 25 rules created for fuzzy PD controller and, the overall fuzzy rule is shown in Table 1 . Fig. 9 shows the fuzzy reasoning procedure for a zero order Takagi-Sugeno fuzzy inference system. The fuzzy part is only in its antecedent. Each rule has a crisp output, and the overall output is obtained via weighted average. This fuzzy procedure avoids the time consuming process of defuzzification required in a Mamdani fuzzy model.

Fig. 6. Distribution of Membership Function of Error.

Fig. 7. Distribution of Membership Function of Rate of Change of Error.

Fig. 8. Distribution of coefficient of consequent part of output.

Table 1. Initial rule base for fuzzy PD controller.

e/Δe	NB	NM	Z	PM	PB
NB	NB	NB	PM	NM	NM
NM	NB	NM	Z	Z	Z
Z	NB	NM	Z	PM	PB
PM	Z	Z	Z	PM	PB
PB	PM	PM	PM	PB	PB

Fig. 9. Fuzzy reasoning of a zero order Takagi-Sugeno fuzzy inference system.

The fuzzy PD controller has three scaling parameters, i.e., K_e , K_ce , and K_u , and it has three adjustable parameters for the input membership function and coefficient of consequent part, i.e., X, V, and H. By varying this parameter, the optimal solution for the speed control of the brushless dc motor is obtained. This parameter is tuned by using particle swarm optimization, cuckoo search and bat algorithm, and it has been outlined in section V.

Regarding the design of fuzzy PID controller, it is straightforward to imagine a fuzzy PID with three input terms: error, integral error, and derivative error. A rule base with three inputs and output will increase the fuzzy rules as mentioned in literature survey, and also, rules concerning the integral action are troublesome [12] . Therefore, it is common to separate the integral action as in the Fuzzy PD plus Integral controller (also known as fuzzy PID controller) in Fig. 4 . The control output is computed and expressed in equation (14) as,

$u\left(t\right)=\left(K_{e}e\left(t\right)+K_{ce}{\frac {de\left(t\right)}{dt}}+\right.$$\left.\int e\left(t\right)dt\right){_{\ast }}K_{u}$

( 14)

By comparing, the gains in (14) and (6) are related in the following equation (15) , (16) and (17) as,

$K_{p}=K_{e}{_{\ast }}K_{u}$

( 15)

$K_{d}=K_{ce}{_{\ast }}K_{u}$

( 16)

$K_{i}=K_{u}$

( 17)

This controller provides all the benefits of PID control. The input and output scaling factors of the Fuzzy PID controller are K_e , K_ce , and K_u , and it also has three adjustable parameters for the input membership function and coefficient of consequent part, i.e., X, V, and H. By adjusting this scaling factor and adjustable parameters, optimal results for the speed control of the brushless dc motor can be obtained. The fuzzy PID controller scaling factor is also tuned by using particle swarm optimization, cuckoo search and bat algorithm, and it is discussed in the section V.

4. Formulation of the objective functions for tuning of fuzzy PD and fuzzy PID controller

A system is considered an optimum control system when the system parameters are adjusted so that the index reaches a minimum value. To be useful, a performance index must be a number that is always positive or zero. Then the best system is delineated as the system that minimizes this index.

Four commonly used performance indices for designing single-loop control algorithm are explained as follows.

The root-mean-square error (RMSE) is a frequently used measure of the differences between reference value of the closed loop system and actual output of the system, and it is expressed in equation (18) as,

$J_{1}={\sqrt {\frac {{{\sum }_{i=0}^{T}\left(\omega {\left(t\right)}_{ref_{i}}-\omega {\left(t\right)}_{act_{i}})\right)}^{2}}{T}}}$

( 18)

Where ω(t)_refi is the reference speed in rad/sec, ω(t)_acti actual speed of the motor in rad/sec at each sample and T is the total simulation time for the optimization. Essentially, the RMSE represents the sample standard deviation of the differences between reference input and actual output of the system. RMSE is a good measure of the system accuracy.

A fairly useful performance index is the integral of absolute error (IAE), and it is expressed in the equation (19) as,

$J_{2}=\int _{0}^{T}\vert \omega {\left(t\right)}_{ref}-\omega {\left(t\right)}_{act}\vert dt$

( 19)

IAE integrates the absolute error over time. It doesn't add weight to any of the errors in a systems response. It tends to produce a slower response in the system but results in a fairly good under damped system.

A very useful criterion that penalizes long duration transient is known as the integral of time multiplied absolute error (ITAE). It is expressed in equation (20) as,

$J_{3}=\int _{0}^{T}t{_{\ast }}\left(\vert \omega {\left(t\right)}_{ref}-\right.$$\left.\omega {\left(t\right)}_{act}\vert \right)dt$

( 20)

The ITAE criterion tries to minimize time multiplied absolute error of the control system. The time multiplication term penalizes the error more at the later stages than at the start and therefore effectively reduces the settling time.

Another useful performance index is the integral of the square of the error (ISE) criterion, and it is expressed in equation (21) as,

$J_{4}=\int _{0}^{T}{\left(\omega {\left(t\right)}_{ref}-\omega {\left(t\right)}_{act}\right)}^{2}dt$

( 21)

By focusing on the square of the error function. It penalizes positive and negative values of the error.

In addition, in order to improve the system performance, one more performance indices is introduced in this paper, i.e., addition of the four performance indices (RMSE + IAE + ITAE + ISE), and it is expressed in equation (22) as,

$J_{5}=J_{1}+J_{2}+J_{3}+J_{4}$

( 22)

The five performance indices are considered as the objective function used for fuzzy PD and fuzzy PID controller tuning to ensure stability and attain superior damping to sudden load disturbance and set speed change.

5. Review of nature-inspired optimization algorithms for tuning of fuzzy PD and fuzzy PID controller

Optimization methods are extensively applied in numerous domain fields' areas such as electrical engineering, electronics engineering, and mechanical engineering, etc. During the last couple of years, many optimization algorithms have been created based on the nature inspired resemblance. However, these algorithms are not always able to solve some problems in the best way. Although it has been shown that these are good methods to solve complex problems, there are no methods yet to know the optimal parameters to solve problems that can be set at the beginning when using the algorithms. In this section, we briefly described the optimization algorithms used in this paper, i.e., particle swarm optimization, cuckoo search algorithm, and bat search algorithm for tuning of the input and output scaling factor and parameter of antecedent and consequent part of the fuzzy PD and fuzzy PID controller. The following subsections briefly describe the basic theory of each algorithm in its original form. This description is considered necessary to grasp the ideas behind the use of fuzzy PD and Fuzzy PID logic in enhancing the original Meta-heuristic methods by providing them with dynamic parameter adaptation capabilities.

5.1. Particle swarm optimization

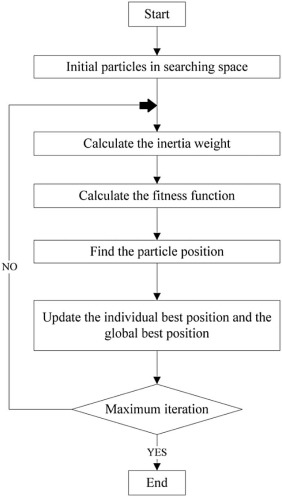
Particle Swarm Optimization (PSO) is a population based stochastic optimization technique developed by Kennedy and Eberhart in 1995 inspired by the social behavior of bird flocking or fish schooling. The particle swarm concept was motivated from the simulation of social behavior. PSO requires only primitive mathematical operators, and is computationally inexpensive in terms of both memory requirements and time. A swarm in PSO consists of a number of particles. Each particle represents a potential solution to the optimization task. Each particle represents a candidate solution. Each particle moves to a new position according to the new velocity which includes its previous velocity and the moving vectors according to the past best solution and global best solution. The best solution is then kept; each particle accelerates in the directions of not only the local best solution but also the global best position. If a particle discovers a new probable solution, other particles will move closer to it in order to explore the region. The basic steps for PSO are given in the flowchart as shown in Fig. 10 .

Fig. 10. Flowchart for Particle Swarm optimization.

A swarm is composed of m particles flying in the D-dimension in a certain speed. Every particle changes its position on the basis of considering its own historical best position and other particles' historical best position. The position for the ith particle is ${\textstyle {\overline {x}}_{i}=\left(x_{i1}{\mbox{​}},{\mbox{ }}x_{i2}{\mbox{​}},{\mbox{ }}\ldots {\mbox{ }}x_{iD}\right)}$ , where 1 ≤ i ≤ m and m is the size of the particle swarm. The speed for the ith particle is ${\textstyle {\overline {v}}_{i}=\left(v_{i1}{\mbox{​}},{\mbox{ }}v_{i2}{\mbox{​}},{\mbox{ }}\ldots {\mbox{ }}v_{iD}\right)}$ , where 1 ≤ i ≤ D and D is the dimension of search space. The historical best position for the ith particle (p_best ) is ${\textstyle {\overline {p}}_{i}=\left(p_{i1}{\mbox{​}},{\mbox{ }}p_{i2}{\mbox{​}},{\mbox{ }}\ldots {\mbox{ }}p_{iD}\right)}$ . The best position for the whole swarm (g_best ) is ${\textstyle {\overline {p}}_{g}=\left(p_{g1}{\mbox{​}},{\mbox{ }}p_{g2}{\mbox{​}},{\mbox{ }}\ldots {\mbox{ }}p_{gm}\right)g\in \left\{1,{\mbox{ }}2,{\mbox{ }}\ldots {\mbox{ }}m\right\}}$ .

The speed and the position of the particle can be updated by the following formulations:

$v_{id}{\mbox{ }}\left(t+1\right)=v_{id}{\mbox{ }}\left(t\right)+$$c_{1}r_{1}{\mbox{ }}\left(p_{id}{\mbox{ }}\left(t\right)-\right.$$\left.x_{id}{\mbox{ }}\left(t\right)\right)+c_{2}r_{2}{\mbox{ }}\left(p_{gd}{\mbox{ }}\left(t\right)-\right.$$\left.x_{id}{\mbox{ }}\left(t\right)\right)$

( 23)

$x_{id}{\mbox{ }}\left(t+1\right)=x_{id}{\mbox{ }}\left(t\right)+$$v_{id}{\mbox{ }}\left(t+1\right)$

( 24)

Where c₁ and c₂ are learning factors and are positive constant, ${\textstyle x_{id}{\mbox{ }}\left(t\right)}$ is the position vector for the ith particle, ${\textstyle v_{id}{\mbox{ }}\left(t\right)}$ is the associated speed vector. Due to the learning factor, the particles have the capability of self-summing up and learning from the excellent individual of the group, the particle could be close to its own historical best position as well as to the historical best position of the group. The learning factors c₁ and c₂ are usually set as 2. The values of r₁ and r₂ are randomly distributed in [0,1]. The speed of particles is restricted within the maximum speed V_max . Shi and Eberhart introduced the idea of inertia weight to improve an algorithms astringency, and the revised formulation of the speed is shown in following equation,

$v_{id}{\mbox{ }}\left(t+1\right)=\omega v_{id}{\mbox{ }}\left(t\right)+$$c_{1}r_{1}{\mbox{ }}\left(p_{id}{\mbox{ }}\left(t\right)-\right.$$\left.x_{id}{\mbox{ }}\left(t\right)\right)+c_{2}r_{2}{\mbox{ }}\left(p_{gd}{\mbox{ }}\left(t\right)-\right.$$\left.x_{id}{\mbox{ }}\left(t\right)\right)$

( 25)

Where ω is the inertia weight, the value of which decides the quantity inherited from the current speed of the particle. If it is chosen properly, then the particle will have the balanced ability of exploitation and development.

5.2. Cuckoo search algorithm

In 2009, Xin-She Yang and Suash Deb proposed a new metaheuristic optimization technique named Cuckoo search algorithm. It is based on the brood parasitic breeding behavior of some species of cuckoos. It follows the cuckoos strategy of finding other birds nest where they would lay eggs. Cuckoos try to find a nest in which host has just laid its eggs so that their eggs would hatch before the host because of this fact that cuckoo eggs hatch earlier than their host eggs. Other interesting feature of cuckoo birds is the mimicry in color and pattern of eggs of some of the host species. It would help in their ability to reproduce and survival of eggs or their chick. The cuckoos chick forced out the egg or young of the host from the nest. It would increase its share in food by frequent calling and by mimic the call of hosts chick. Some host birds are able to detect the contamination of their nest by cuckoos or they can distinguish between their eggs and cuckoos eggs, then they will either throw these foreigner eggs or vacate their nest and develop a new shelter or nest. The main theme of this algorithm is to choose the best nest with potentially good solutions or eggs. Each nest is a representative of a potential candidate [16]  and [17] . The three significant rules that are used for implementing CSA algorithm are discussed as follow:

• Each cuckoo lays single egg and places it in an arbitrarily chosen nest.
• The best nests carry the potential solution which will move onto next generation.
• The available host nests are limited and a host bird can find the foreign eggs by a probability ‘p’ which ranges [0, 1].

For generating a new nest for cuckoos, a law named Levy flight is used which is as follows:

$x_{c}{\mbox{ }}\left(t+1\right)=x_{c}{\mbox{ }}\left(t\right)+$${\alpha }_{0}\oplus Levy\left({\lambda }_{0}\right)$

( 26)

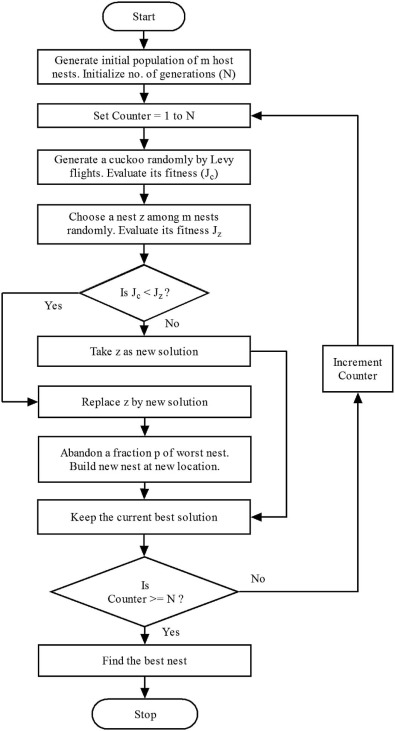
Where α₀ (α₀  > 0) is step size and is related to the problem specified in the equation (26) represents a random walk which is a Markov chain which means its next step depends on the current location and the transition probability. The random walk proves to be more promising in exploring the search space due to its longer step length in long run. The Levy flight is characterized by random walk which is derived from the Levy distribution with an infinite variance and infinite mean. The Levy distribution in the proposed CSA is developed using the exponential law proposed by Mantegna. In this, the step size should be taken as λ₀ /100, where λ₀ is the search space size as Levy distribution may be too strong for larger step size that new solutions may be opted out from the searched space [24] . The basic steps for CSA are given in the flowchart as shown in Fig. 11 .

Fig. 11. Flowchart for Cuckoo search algorithm.

5.3. BAT algorithm

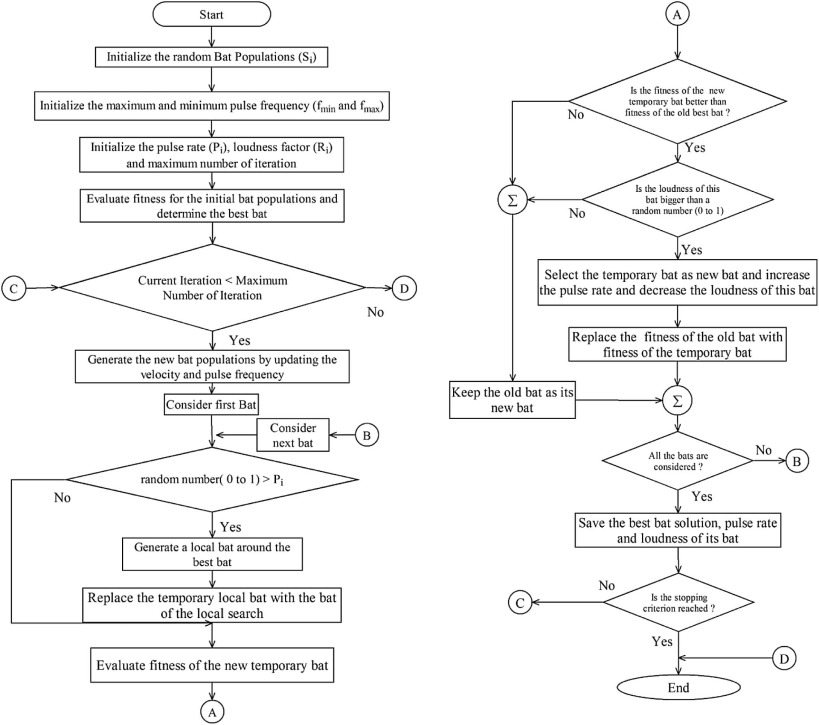
The bat algorithm uses the echolocation behavior of bats. These bats emit a very loud sound pulse (echolocation) and listens for the echo that bounces back from the surrounding objects. Their signal bandwidth varies depending on the species. Each sound pulse includes frequency, loudness, and pulse emission rate. Most bats use signals with tuning frequencies while the rest use fixed-frequency signals. The frequency range used by these creatures is between 25 KHz to 150 KHz. Bat algorithms are based on the following aspects; all bats use echolocation and distinguish the difference between victim and obstruction. Bats are flying with a random velocity, in a random location, with a variable frequency, loudness, and the pulse emission rate [19] , [20]  and [25] . Bat algorithm is bad at exploration and exploitation. In order to tackle with the problem mentioned above, distribution of the population modification structure has been proposed for the original algorithm. The flowchart for the proposed bat algorithm is shown in Fig. 12 . Bat algorithm for optimization of tuning of the adjustable parameter in fuzzy PD and fuzzy PID controller as follows:

• Step1:

Formulation of Objective function J(S) for optimization with S = (S1… S_d ), where d is the number of tuning parameter.

The fitness function can be defined as a particular type of objective function that is used to summarize, as a single figure of merit. In general, the fitness function should be a measure of how closely the model prediction matches the observed or expected data for a given set of model parameters. The notion of fitness is fundamental to the application of evolutionary algorithms; the degree of success in their application may depend critically on the definition of a fitness that changes neither too rapidly nor too slowly with the design parameters of the optimization problem. The fitness function must guarantee that individuals can be differentiated according to their suitability for solving the optimization problem.

In evolutionary algorithms, the performance of the individual run is measured by a fitness function. After each iteration, the members are given a performance measure derived from the fitness function, and the “fittest” members of the population will propagate for the next iteration. In this paper, to assure stability and attain superior damping to sudden load disturbance and set speed variations, the parameters of the controllers may be chosen to minimize the objective function described by the equations ((18) , (19) , (20) , (21)  and (22) ) is considered as a fitness function for the optimization,

For fuzzy PD and fuzzy PID controller: d = 6, S1 = Ke, S2 = Kce, S3 = Ku, S4 = H, S5 = X, and S6 = V.

The range for tuning parameter in fuzzy PD controller and fuzzy PID controller is given in equation (27) as,

${\begin{array}{c}0<Ke,{\mbox{ }}Kce,{\mbox{ }}Ku,{\mbox{ }}H,{\mbox{ }}X,{\mbox{ }}and{\mbox{ }}V\leq 150\end{array}}$

( 27)

Fig. 12. Flowchart for the Bat algorithm.

• Sep 2: Initialize the bat population S_i and initial velocity L_i for (i = 1, 2… n), where n is the number of bat populations.
• Step 3: Define pulse frequency f_i at S_i . Initialize pulse rates P_i , maximum number of iterations and the loudness factor R_i
• Step 4: Loop:
• Start;
• t=0;
• While (t <Maximum number of iterations)
• t=t+1; iteration count.
• Generate new solutions by adjusting frequency and updating velocities and locations/solutions by the equation ((28) , (29)  and (30) )

$f_{i}=f_{min}+\left(f_{max}-f_{min}\right)\gamma$

( 28)

$L_{i}^{t}=L_{i}^{t-1}+\left(S_{i}^{t-1}-S_{b}\right)f_{i}$

( 29)

$S_{i}^{t}=S_{i}^{t-1}+L_{i}^{t}$

( 30)

• Where, γ is a random vector drawn from a uniform distribution and frequency range f_min  = 0 and f_max  = 100. S_b is a global best for every iteration or generation.
• The second term of the Equation (29) provides local search with guidance of the best solution in the standard algorithm. Exclusive usage of this term may cause premature convergence problem, thus solutions get stuck at a local minimum. When the best solution is near a local minimum toward the end of optimization process, the i^th solution can have no chance to get away from that undesired local minimum as the movement of the i^th particle depends on such best solution toward the end of the optimization process [26] . For this purpose, the velocity equation has been modified to perform the situation that the k^th solution could also affect the i^th solution. The equation (29) modified as,

$L_{i}^{t}=L_{i}^{t-1}+\left(S_{i}^{t}-S_{b}\right)f_{i}{\xi }_{1}+$$\left(S_{i}^{t}-S_{k}^{t}\right)f_{i}{\xi }_{2}$

${\xi }_{1}+{\xi }_{2}=1$

• Where S_k is one of the best solutions randomly chosen among the population${\textstyle \left(i\not =k\right)}$ , ${\textstyle {\xi }_{1}}$ is learning factor ranging from ${\textstyle {\omega }_{min}}$ to ${\textstyle {\omega }_{max}}$ . As the value of ${\textstyle {\xi }_{1}}$ increases, the effect of the best solution (S_b ) is higher than the k^th solution and vice versa. The ${\textstyle {\xi }_{1}}$ value has to be updated as iterations proceed in order that the solution can switch from global to local search.

${\textstyle {\xi }_{1}={\omega }_{max}{\mbox{ }}\left(1-e^{-iter}\right)+}$${\omega }_{min}$

• Where, “iter” is the current iteration number, ${\textstyle {\omega }_{max}}$ and ${\textstyle {\omega }_{min}}$ are maximum and minimum inertia weight. The inertia weights of the optimization are chosen as 0.9 and 0.1 respectively. This procedure called as distribution of the population modification structure.
• If (random number (0 to 1) > P_i )
• Select a solution among the best solutions and generate a local solution around the selected best solution using the equation (31) ,

$S_{i}^{t}=S_{b}+\epsilon R^{t}$

( 31)

• Where, ε is a random number. While R_t = < R_tⁱ  > is the average loudness of all the bats at this time step (t).
• End if
• Generate a new solution by flying randomly
• If (random number (0 to 1) < R_i & J(S_i ) < J(S_b ))
• Accept the new solutions,
• Increase P_i and reduce R_i using equation (32) and (33) .

$R_{i}^{t+1}=\beta R_{i}^{t}{\mbox{​}},{\mbox{ }}P_{i}^{t+1}=$$P_{i}^{0}{\mbox{ }}\left(1-e^{\left(-\sigma t\right)}\right)$

( 32)

• Where, β and σ are constants. For any 0 < β < 1 and σ > 0, we have

$R_{i}^{t}\rightarrow 0,{\mbox{ }}P_{i}^{t}=P_{i}^{0}{\mbox{​}},{\mbox{ }}{\mbox{as}}{\mbox{ }}t\rightarrow \infty$

( 33)

• For simplicity, β = σ can be used, and for this work, β = σ = 0.9 is considered.
• End if
• Rank the bats and find the current best (S_b )
• End while
• Loop end
• Step 5: Display the optimum solutions.

Bat algorithm has many advantages, and one of the key advantages is that it can provide very quick convergence at a very initial stage by switching from exploration to exploitation. This makes it an efficient algorithm for applications such as classifications and others when a quick solution is needed. There are many reasons for the success of bat-based algorithms. By analyzing the key features and updating equations, we can summarize the following three key points/features:

• Frequency tuning: Bat algorithm uses echolocation and frequency tuning to solve problems. Though echolocation is not directly used to mimic the true function in reality, frequency variations are used. This capability can provide some functionality that may be similar to the key feature used in particle swarm optimization and harmony search. Therefore, bat algorithm possesses the advantages of other swarm-intelligence-based algorithms.
• Automatic zooming: Bat algorithm has a distinct advantage over other metaheuristic algorithms. That is, Bat algorithm has a capability of automatically zooming into a region where promising solutions have been found. This zooming is accompanied by the automatic switch from explorative moves to local intensive exploitation. As a result, bat algorithm has a quick convergence rate, at least at early stages of the iterations, compared with other algorithms.
• Parameter control: Many metaheuristic algorithms used fixed parameters by using some, pre-tuned algorithm-dependent parameters. In contrast, bat algorithm uses parameter control, which can vary the values of parameters (P and R) as the iterations proceed. This provides a way to automatically switch from exploration to exploitation when the optimal solution is approaching. This gives another advantage of bat algorithm over other metaheuristic algorithms.

Likely many metaheuristic algorithms, bat algorithm has the advantage of simplicity and flexibility. Bat algorithm is easy to implement, and such a simple algorithm can be very flexible to solve a wide range of problems as we have seen in the above review. In addition, preliminary theoretical analysis by Huang suggested that Bat algorithm has guaranteed global convergence properties under the right condition, and bat algorithm can also solve large-scale problems effectively [27]  and [28] .

6. Simulation results and discussions

In this section, the superiority of particle swarm, cuckoo search, and bat algorithms optimized fuzzy PD controller over particle swarm, cuckoo search, and bat algorithms optimized fuzzy PID controller is proved through simulation for the speed control of BLDC motor. The parameters of the considered algorithms are given in Table 2 . PSO, Cuckoo and bat algorithm progressively minimize the objective functions (18) to (22) over the iterations while finding optimal set of parameters for the fuzzy PD and fuzzy PID controller. The program stops if the value of the objective function does not change appreciably over consecutive iterations (i.e. the change is less than the pre-specified tolerance level) or the maximum number of iterations is exceeded. The maximum number of iterations is kept as 10 and the tolerance level is kept at 10⁻⁶ . With a population of P = 10 individuals for G = 10 generations, the fitness function in Equation (18) , (19) , (20) , (21)  and (22) are evaluated 100 times. Indeed, this number (E = P x G) represents the act of evaluating points inside the search space. The optimization procedure is performed using Matlab-R2010a, M-file under Windows 7 on a PC Pentium dual core processor CPU, and 2.1 GHz speed system. Totally, 50 trials have been performed, in order to be definite that convergence has taken place and 5000 function has been evaluated for 50 trails.

Table 2. Parameters of the PSO, Cuckoo, and Bat algorithm.

PSO		Cuckoo search		Bat algorithm
Generation	10	Generation	10	Generation	10
Population size	10	Number of nests	10	Population size	10
Cognitive parameter (c1)	2	Discovery rate (pa)	0.25	β = σ	0.9
Social parameter (c2)	2			P10	0.9
Initial weight (Wmin )	0.9			R10	0.9
Final weight (Wmax )	0.4			fmin	0
				fmax	100
Trial	50	Trial	50	Trial	50

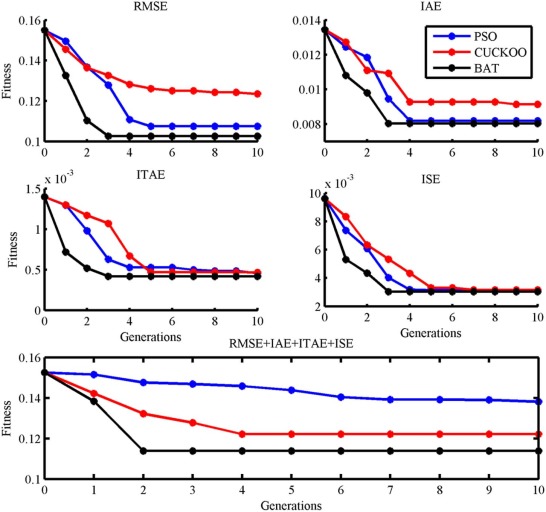
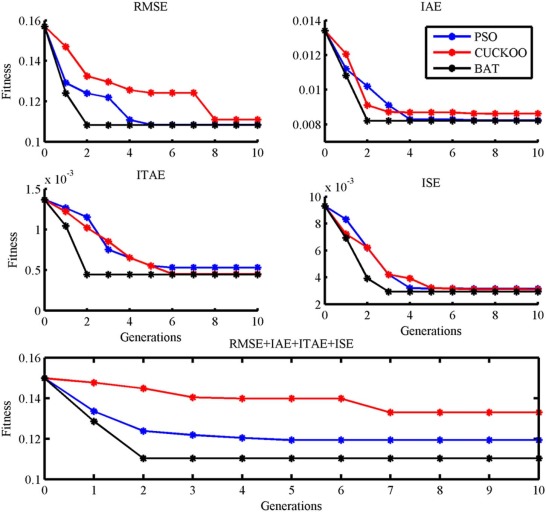
Fig. 13 (a) shows the optimization of the fuzzy PD, fuzzy PID controller using PSO, Cuckoo search and Bat algorithm.

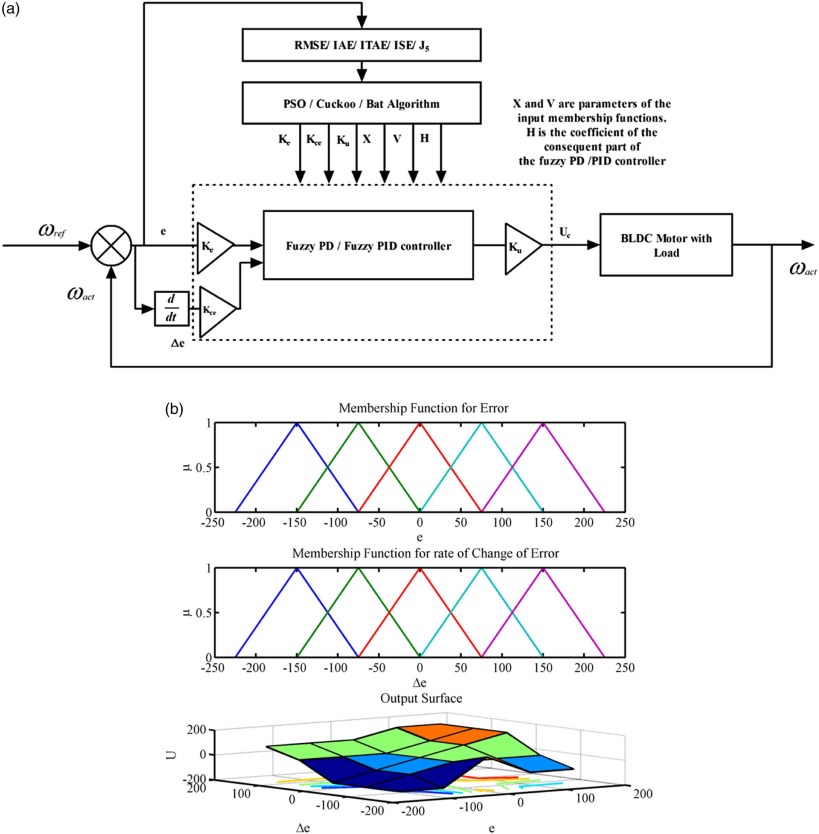
Fig. 13. (a). Optimization of the fuzzy PD, fuzzy PID controller using PSO, Cuckoo search and Bat algorithm. (b). Initial membership function for error, rate of change of error and output surface of fuzzy PD and fuzzy PID controller.

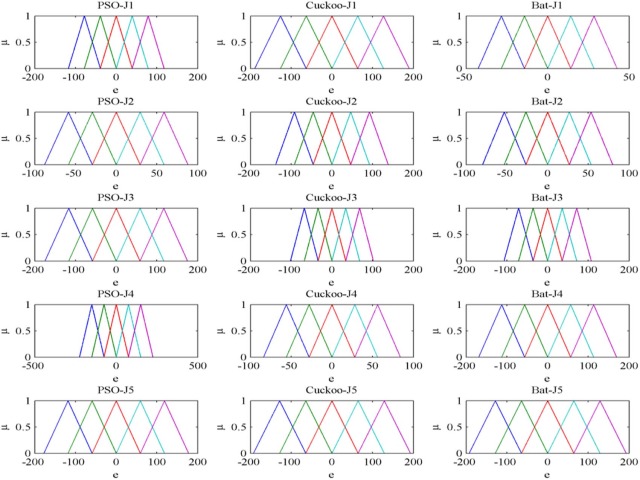
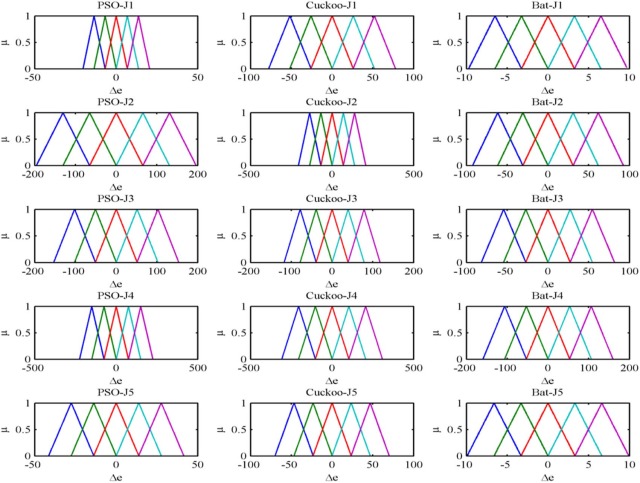
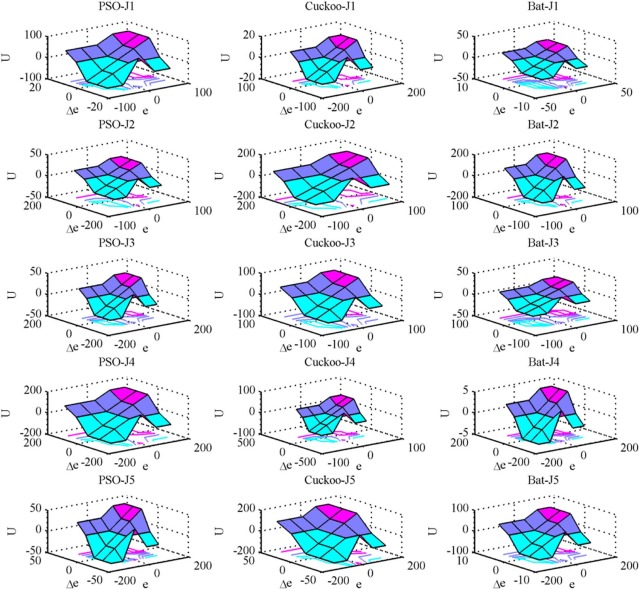
Fig. 13 (b) shows the initial guess for the error and rate of change error membership functions and output surface of the fuzzy PD and fuzzy PID controller. Initial values for input and output scaling factor of the fuzzy PD and fuzzy PID controller are K_e  = 150, K_ce  = 150 and K_u  = 150. Initial values of antecedent and consequent part of the fuzzy PD and fuzzy PID controller are X = V = H = 150.

Fig. 14 shows the convergence graph of above stated algorithms for tuning of fuzzy PD controller. The tuning parameter of the fuzzy PD controller with considered algorithms are shown in Table 3 . The objective function value for final best population is best only for bat algorithm over PSO and Cuckoo search, and also, the average computation time taken by the bat algorithm is less than PSO and Cuckoo search. From the convergence graph and Table 3 , bat algorithm has superior objective function value and less average computation time than other two algorithms.

Fig. 14. Convergence graph for tuning parameter of the fuzzy PD controller.

Table 3. Optimal value of tuning parameter of the Fuzzy PD controller with PSO, Cuckoo search and Bat algorithm.

RMSE (J1)
Algorithm	Ke	Kce	Ku	H	X	V	Best	Worst	Mean	Standard deviation	Average computation time (sec)
PSO	66.7792	139.0034	14.3992	56.4864	82.2190	16.9855	0.1074	0.1550	0.1204	0.0186	429.7240
Cuckoo	36.0998	111.5952	58.1305	36.9542	101.9201	110.7451	0.1235	0.1554	0.1315	0.0104	642.5300
Bat	118.8531	143.9291	98.3967	5.4544	127.3857	140.1068	0.1026	0.1557	0.1074	0.0160	248.7020

IAE (J2)
Algorithm	Ke	Kce	Ku	H	X	V	Best	Worst	Mean	Standard deviation	Average computation time (sec)
PSO	150.0000	0.1000	19.9640	82.3017	131.0437	150.0000	0.0082	0.0134	0.0095	0.0020	387.4590
Cuckoo	0.4399	0.9269	137.4575	97.3321	4.5031	149.5709	0.0091	0.0133	0.0102	0.0015	909.3230
Bat	66.1901	8.6379	42.3185	64.3631	85.0581	44.1775	0.0080	0.0134	0.0085	0.0016	252.8630

ITAE (J3)
Algorithm	Ke	Kce	Ku	H	X	V	Best	Worst	Mean	Standard deviation	Average computation time (sec)
PSO	48.5968	147.0557	50.4469	48.6462	61.7448	147.1379	0.0005	0.0014	0.0007	0.0003	384.1950
Cuckoo	82.2899	94.4075	24.8378	149.7029	150.0000	63.9726	0.0005	0.0014	0.0008	0.0004	603.4860
Bat	104.3006	10.2912	38.2921	33.6826	100.2072	126.6734	0.0004	0.0009	0.0005	0.0002	271.4610

ISE (J4)
Algorithm	Ke	Kce	Ku	H	X	V	Best	Worst	Mean	Standard deviation	Average computation time (sec)
PSO	26.2795	81.5246	26.6294	125.1210	148.0905	75.6607	0.0031	0.0096	0.0045	0.0022	426.7350
Cuckoo	4.7749	89.7148	61.6997	113.4746	81.9585	149.9967	0.0032	0.0093	0.0048	0.0023	540.2730
Bat	72.6903	126.7381	31.4841	82.8827	94.5138	4.8897	0.0030	0.0094	0.0036	0.0019	263.7860

RMSE + IAE + ITAE + ISE (J5)
Algorithm	Ke	Kce	Ku	H	X	V	Best	Worst	Mean	Standard deviation	Average Computation Time (sec)
PSO	10.3533	19.7405	50.7451	99.9594	83.7049	150.0000	0.1381	0.1525	0.1440	0.0052	405.4830
Cuckoo	36.5949	79.8609	24.5980	78.3844	99.9910	49.4134	0.1221	0.1521	0.1281	0.0102	483.2470
Bat	16.0324	17.1473	117.9016	44.0223	90.7856	144.8829	0.1138	0.1538	0.1175	0.0121	305.2550

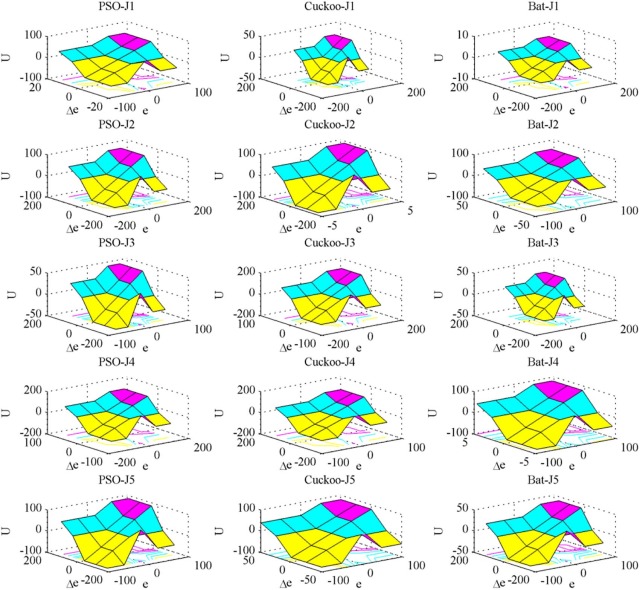
Fig. 15 shows the after optimization of the error membership function of the fuzzy PD controller using PSO, Cuckoo search and bat algorithm with five objective functions. Fig. 16 shows the after optimization of the rate of change of membership function for the fuzzy PD controller using PSO, Cuckoo search and bat algorithm with five objective functions. Fig. 17 shows the after optimization of the output surface of the fuzzy PD controller with five objective functions.

Fig. 15. Error membership function of fuzzy PD controller after optimization using PSO, Cuckoo search and bat algorithm.

Fig. 16. Rate of change of error membership function of fuzzy PD controller after optimization using PSO, Cuckoo search and bat algorithm.

Fig. 17. Output surface of the fuzzy PD controller after optimization using PSO, Cuckoo search and bat algorithm.

Fig. 18 shows the convergence graph for the tuning parameters of the fuzzy PID controller. Optimization results for the fuzzy PID controller are shown in Table 4 . The objective function value is only best for the bat algorithm over PSO and cuckoo search. And also the average computation time is less for bat algorithm than PSO and cuckoo search. Again, bat algorithm has outperformed the other two algorithms since minimum objective function value and less computation time is obtained than other two algorithms. Fig. 19 shows the after optimization of the error membership function of the fuzzy PID controller using PSO, Cuckoo search and bat algorithm with five objective functions. Fig. 20 shows the after optimization of the rate of change of membership function for the fuzzy PID controller using PSO, Cuckoo search and bat algorithm with five objective functions. Fig. 21 shows the after optimization of the output surface of the fuzzy PID controller with five objective functions.

Fig. 18. Convergence graph for tuning parameter of the fuzzy PID controller.

Table 4. Optimal value of tuning parameter of the Fuzzy PID controller with PSO, Cuckoo search and Bat algorithm.

RMSE (J1)
Algorithm	Ke	Kce	Ku	H	X	V	Best	Worst	Mean	Standard deviation	Average computation time (sec)
PSO	88.2954	144.5239	12.9768	75.1248	78.2863	13.6159	0.1084	0.1391	0.1159	0.0108	384.4700
Cuckoo	90.3794	125.3976	101.0240	13.9376	126.4255	51.8392	0.1109	0.1570	0.1270	0.0146	516.1440
Bat	28.9570	18.5499	30.9032	22.0622	28.4416	6.4933	0.1082	0.1240	0.1097	0.0048	257.8630

IAE (J2)
Algorithm	Ke	Kce	Ku	H	X	V	Best	Worst	Mean	Standard deviation	Average computation time (sec)
PSO	57.0861	150.0000	68.6791	25.0706	58.6882	130.6920	0.0082	0.0120	0.0091	0.0014	373.5650
Cuckoo	33.3408	135.1884	51.7629	122.8613	92.1014	137.6761	0.0086	0.0146	0.0093	0.0018	603.7420
Bat	6.3802	16.1419	92.5163	140.9666	53.2443	61.6647	0.0082	0.0134	0.0087	0.0016	342.8120

ITAE (J3)
Algorithm	Ke	Kce	Ku	H	X	V	Best	Worst	Mean	Standard deviation	Average computation time (sec)
PSO	66.9731	37.7918	85.3110	33.2685	116.7263	102.1748	0.0005	0.0014	0.0008	0.0003	407.5620
Cuckoo	31.2468	71.9042	65.6869	63.1240	67.8707	78.4008	0.0005	0.0013	0.0007	0.0003	521.6800
Bat	75.6367	97.0607	46.2350	20.8988	71.3923	54.4366	0.0004	0.0007	0.0005	0.0001	289.6610

ISE (J4)
Algorithm	Ke	Kce	Ku	H	X	V	Best	Worst	Mean	Standard deviation	Average computation time (sec)
PSO	100.834	65.0621	4.8456	141.1888	150.0000	150.0000	0.0031	0.0093	0.0046	0.0023	393.6480
Cuckoo	39.0057	147.9450	16.2927	56.4042	56.0387	205.6135	0.0031	0.0092	0.0045	0.0021	558.8910
Bat	111.072	69.2280	95.1338	4.5961	112.9094	106.1842	0.0029	0.0042	0.0030	0.0004	262.9670

RMSE + IAE + ITAE + ISE (J5)
Algorithm	Ke	Kce	Ku	H	X	V	Best	Worst	Mean	Standard deviation	Average computation time (sec)
PSO	13.1549	118.2739	150.0000	47.2018	118.4169	27.6085	0.1193	0.1498	0.1241	0.0095	419.4700
Cuckoo	80.3004	88.3897	24.7887	144.4952	128.5186	46.6502	0.1329	0.1498	0.1394	0.0061	518.0000
Bat	66.2040	143.4404	18.6981	70.6740	128.5554	6.6109	0.1103	0.1437	0.1133	0.0101	290.3320

Fig. 19. Error membership function of fuzzy PID controller after optimization using PSO, Cuckoo search and bat algorithm.

Fig. 20. Rate of change of error membership function of fuzzy PID controller after optimization using PSO, Cuckoo search and bat algorithm.

Fig. 21. Output surface of the fuzzy PID controller after optimization using PSO, Cuckoo search and bat algorithm.

When compared with the objective values and average computation times in Table 3  and Table 4 , bat algorithm optimized fuzzy PD controller has minimum objective function value and less computation time than the others. In order to validate effectiveness of the bat algorithm tuned fuzzy PD controller, it is compared with bat, PSO, and cuckoo search algorithm tuned fuzzy PID controller. The BLDC motor is operated for different operating conditions with above controller. Also, the time domain specification such as overshoot, undershoot, recovery time, and steady state error, settling time and performance indices such RMSE, IAE, ITAE, ISE are compared with for the above considered controllers.

Three operating conditions are considered for proving the effectiveness of the controller.

Condition 1.

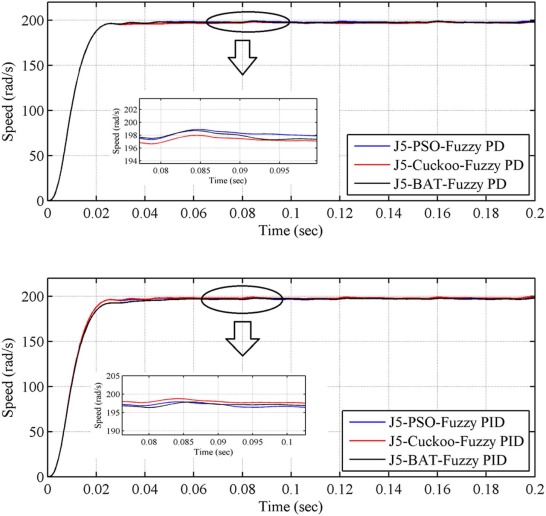
The reference speed is set to 200 rad/s with no load conditions. The time domain specification and performance indices for the speed response under fuzzy PD and fuzzy PID controllers are provided in Table 5 . From these results, optimization with objective function J5 (PSO, Cuckoo, and Bat algorithm) produces better results than other objective function (J1, J2, J3 and J4). The simulation result for the condition 1 with objective function J5 is shown in the Fig. 22 . From these results, bat optimized fuzzy PD; fuzzy PID controller (objective function J5) has better time domain specification and performance indices than other algorithms. Therefore, these two are compared. Bat algorithm optimized fuzzy PD controller (objective function J5) shows better performance than bat optimized fuzzy PID controller (objective function J5). Because steady state error of speed of the motor has 0.0472 for bat optimized fuzzy PD controller (objective function J5) but 0.0535 for bat optimized fuzzy PID controller(objective function J5), total indices is 0.2825 for bat optimized fuzzy PD controller(objective function J5) but 0.2840 for bat optimized fuzzy PID controller(objective function J5). From the results, it is clear that bat optimized fuzzy PD controller (objective function J5) has superior performance in all aspects.

Table 5. Performance parameters for condition 1.

PSO
Objective function	Controller	Time domain specifications				Performance indices				Total indices
		Rise time	Overshoot	Settling time	Steady state error	RMSE	IAE	ITAE	ISE
J1	Fuzzy PD	0.0119	4.0271	0.0331	0.0585	0.1837	0.0092	0.0001	0.0047	4.3284
	Fuzzy PID	0.0123	2.1769	0.0286	0.0564	0.1837	0.0086	0.0001	0.0045	2.4712
J2	Fuzzy PD	0.0118	4.4244	0.0362	0.0656	0.2017	0.0080	0.0001	0.0037	4.7516
	Fuzzy PID	0.0118	4.4244	0.0351	0.0615	0.1964	0.0081	0.0001	0.0037	4.7410
J3	Fuzzy PD	0.0118	4.4244	0.0352	0.0668	0.2039	0.0080	0.0001	0.0037	4.7538
	Fuzzy PID	0.0118	4.4244	0.0351	0.0630	0.1984	0.0081	0.0001	0.0037	4.7445
J4	Fuzzy PD	0.0135	0.0000	0.0308	0.0589	0.1876	0.0071	0.0001	0.0032	0.3014
	Fuzzy PID	0.0135	0.0000	0.0329	0.0617	0.1875	0.0074	0.0001	0.0032	0.3064
J5	Fuzzy PD	0.0135	0.0000	0.0310	0.0590	0.1976	0.0086	0.0001	0.0032	0.313
	Fuzzy PID	0.0123	0.0000	0.0295	0.0557	0.1935	0.0097	0.0001	0.0045	0.3053

Cuckoo search
Objective function	Controller	Time domain specifications				Performance indices				Total Indices
		Rise time	Overshoot	Settling time	Steady state error	RMSE	IAE	ITAE	ISE
J1	Fuzzy PD	0.0135	0.0000	0.0297	0.0570	0.1977	0.0069	0.0001	0.0047	0.3097
	Fuzzy PID	0.0123	2.4594	0.0295	0.0578	0.1852	0.0087	0.0001	0.0045	2.7576
J2	Fuzzy PD	0.0118	4.4244	0.0344	0.0601	0.1938	0.0081	0.0001	0.0037	4.7364
	Fuzzy PID	0.0118	4.4244	0.0352	0.0635	0.2004	0.0081	0.0001	0.0037	4.7471
J3	Fuzzy PD	0.0118	4.4244	0.0352	0.0629	0.1997	0.0080	0.0001	0.0037	4.7458
	Fuzzy PID	0.0118	4.4244	0.0352	0.0660	0.2035	0.0080	0.0001	0.0037	4.7527
J4	Fuzzy PD	0.0135	0.0000	0.0480	0.0626	0.1880	0.0075	0.0001	0.0032	0.3230
	Fuzzy PID	0.0135	0.0000	0.0308	0.0583	0.1974	0.0097	0.0001	0.0043	0.3143
J5	Fuzzy PD	0.0126	0.0000	0.0219	0.0565	0.1951	0.0086	0.0001	0.0035	0.2984
	Fuzzy PID	0.0118	0.0000	0.0263	0.0514	0.1924	0.0091	0.0001	0.0047	0.3059

Bat algorithm
Objective function	Controller	Time domain specifications				Performance indices				Total Indices
		Rise time	Overshoot	Settling time	Steady state error	RMSE	IAE	ITAE	ISE
J1	Fuzzy PD	0.0135	0.0000	0.0310	0.0604	0.1878	0.0072	0.0001	0.0032	0.3034
	Fuzzy PID	0.0126	1.1161	0.0219	0.0566	0.1806	0.0086	0.0001	0.0044	1.4011
J2	Fuzzy PD	0.0118	4.4244	0.0352	0.0634	0.1993	0.0081	0.0001	0.0037	4.7460
	Fuzzy PID	0.0118	4.4244	0.0351	0.0638	0.1992	0.0081	0.0001	0.0037	4.7462
J3	Fuzzy PD	0.0118	4.4244	0.0344	0.0609	0.1947	0.0081	0.0001	0.0037	4.7381
	Fuzzy PID	0.0123	2.4594	0.0295	0.0569	0.1843	0.0087	0.0001	0.0045	2.7558
J4	Fuzzy PD	0.0142	1.6364	0.0298	0.0615	0.1907	0.0078	0.0001	0.0042	1.9447
	Fuzzy PID	0.0144	0.0000	0.0487	0.0601	0.1852	0.0071	0.0001	0.0031	0.3187
J5	Fuzzy PD	0.0138	0.0000	0.0304	0.0472	0.1810	0.0067	0.0001	0.0032	0.2825
	Fuzzy PID	0.0137	0.0000	0.0205	0.0535	0.1863	0.0067	0.0001	0.0032	0.2840

Fig. 22. Simulation result for the condition 1.

Condition 2.

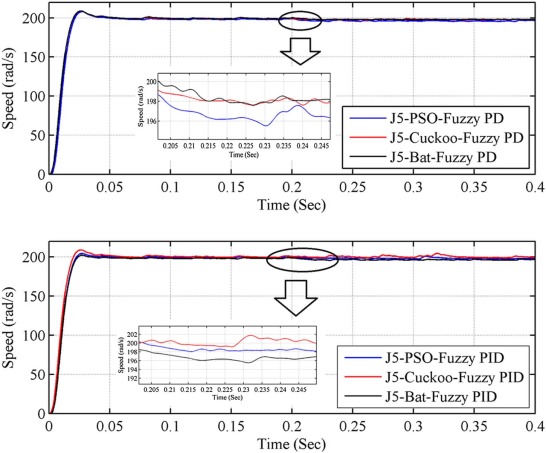
In order to validate the effectiveness of the controller for realistic working conditions, load disturbance is introduced and performance is checked. The reference speed is set to 200 rad/s, and load is varied from no load to full load condition at 0.2s. The time domain specification and performance indices for the speed response are presented in Table 6 . From these results, optimization with objective function J5 (PSO, Cuckoo, and Bat algorithm) produces better results than other objective function (J1, J2, J3 and J4). The simulation result for the conditions 2 with objective function J5 is shown in the Fig. 23 . From the results, it is ascertained that bat optimized fuzzy PD controller (objective function J5) has clear edge over other algorithms. Bat algorithm optimized fuzzy PD controller (objective function J5) shows better performance in overshoot (0.2458), undershoot (0.3992), recovery time (0.3992 s), steady state error (0.0345 rad/s), and it has high quality of performance indices compared to other considered controllers.

Table 6.

Performance parameters for condition 2.

PSO
Objective function	Controller	Time domain specification			Performance indices				Total indices
		Overshoot	Recovery time	Steady state error	RMSE	IAE	ITAE	ISE
J1	Fuzzy PD	0.7314	0.3997	0.0383	0.1276	0.0109	0.0005	0.0048	1.3131
	Fuzzy PID	1.4342	0.3988	0.0329	0.1269	0.0098	0.0003	0.0046	2.0075
J2	Fuzzy PD	0.7136	0.3978	0.0353	0.1377	0.0093	0.0003	0.0038	1.2977
	Fuzzy PID	1.0748	0.3998	0.0348	0.1359	0.0092	0.0003	0.0038	1.6587
J3	Fuzzy PD	2.3419	0.3977	0.0372	0.1402	0.0094	0.0003	0.0038	2.9305
	Fuzzy PID	1.7930	0.3988	0.0360	0.1375	0.0093	0.0003	0.0038	2.3788
J4	Fuzzy PD	0.8293	0.3992	0.0400	0.1309	0.0090	0.0005	0.0033	1.4123
	Fuzzy PID	0.8258	0.3997	0.0450	0.1318	0.0098	0.0006	0.0033	1.4160
J5	Fuzzy PD	0.7266	0.3992	0.0323	0.1230	0.0090	0.0003	0.0033	1.2937
	Fuzzy PID	0.7266	0.3995	0.0329	0.1265	0.0099	0.0003	0.0033	1.2991

Cuckoo search
Objective function	Controller	Time domain specification			Performance indices				Total indices
		Overshoot	Recovery time	Steady state error	RMSE	IAE	ITAE	ISE
J1	Fuzzy PD	0.7030	0.3996	0.0369	0.1304	0.0085	0.0004	0.0033	1.2821
	Fuzzy PID	0.8227	0.3995	0.0339	0.1270	0.0101	0.0004	0.0046	1.3981
J2	Fuzzy PD	0.6234	0.3971	0.0348	0.1341	0.0093	0.0003	0.0038	1.2029
	Fuzzy PID	2.6484	0.3995	0.0363	0.1395	0.0093	0.0003	0.0038	3.2371
J3	Fuzzy PD	3.1059	0.3964	0.0342	0.1367	0.0091	0.0003	0.0038	3.6864
	Fuzzy PID	2.0813	0.3990	0.0373	0.1401	0.0094	0.0003	0.0038	2.6712
Fuzzy PD	0.5360	0.3997	0.0469	0.1323	0.0100	0.0007	0.0034	1.1290	J4
Fuzzy PID	1.2565	0.3986	0.0395	0.1309	0.0089	0.0005	0.0033	1.8381
J5	Fuzzy PD	0.4501	0.3942	0.0331	0.1259	0.0089	0.0003	0.0032	1.0157
	Fuzzy PID	0.4763	0.3952	0.0339	0.1265	0.0089	0.0003	0.0033	1.0444

Full-size table

Bat algorithm
Objective function	Controller	Time domain specification			Performance indices				Total indices
		Overshoot	Recovery time	Steady state error	RMSE	IAE	ITAE	ISE
J1	Fuzzy PD	0.4284	0.3992	0.0439	0.1318	0.0095	0.0006	0.0033	1.0168
	Fuzzy PID	0.2491	0.3997	0.0372	0.1256	0.0103	0.0005	0.0045	0.8270
J2	Fuzzy PD	1.4090	0.3998	0.0356	0.1384	0.0093	0.0003	0.0038	1.9962
	Fuzzy PID	0.9302	0.3980	0.0352	0.1366	0.0093	0.0003	0.0038	1.5133
J3	Fuzzy PD	0.6756	0.3980	0.0350	0.1344	0.0093	0.0003	0.0038	1.2564
	Fuzzy PID	0.3392	0.3997	0.0345	0.1274	0.0101	0.0004	0.0046	0.9159
J4	Fuzzy PD	2.3568	0.3996	0.0373	0.1401	0.0090	0.0003	0.0043	2.9475
	Fuzzy PID	0.6992	0.3998	0.0447	0.1309	0.0095	0.0006	0.0032	1.2878
J5	Fuzzy PD	0.2458	0.3992	0.0345	0.1308	0.0092	0.0003	0.0032	0.8230
	Fuzzy PID	0.2459	0.3999	0.0361	0.1294	0.0094	0.0003	0.0032	0.8244

Fig. 23. Simulation result for the condition 2.

Condition 3.

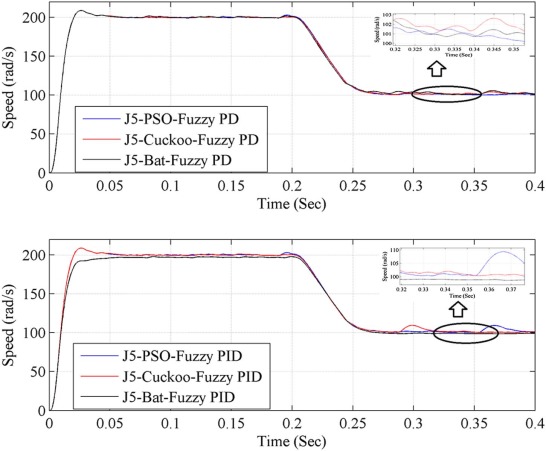
In order to ascertain the efficiency of the controller for realistic working conditions, change in set speed condition is introduced and performance is checked. Initially the reference speed set as 200 rad/s at no load condition. At 0.2 s, the reference speed is changed to 100 rad/s. For this set speed change condition, the time domain specifications such as undershoot, recovery time and steady state error and performance indices are presented in Table 7 . From these results, optimization with objective function J5 (PSO, Cuckoo, and Bat algorithm) produces better results than other objective function (J1, J2, J3 and J4). The simulation results are shown in Fig. 24 .

Table 7. Performance parameters for condition 3

PSO
Objective function	Controller	Time domain specification			Performance indices				Total indices
		Overshoot	Recovery time	Steady state error	RMSE	IAE	ITAE	ISE
J1	Fuzzy PD	0.5384	0.3074	0.0640	0.1892	0.0178	0.0019	0.0097	1.1285
	Fuzzy PID	0.1118	0.3737	0.0684	0.2016	0.0178	0.0020	0.0103	0.7857
J2	Fuzzy PD	0.0000	0.2965	0.0746	0.2117	0.0172	0.0020	0.0093	0.6113
	Fuzzy PID	0.1786	0.3711	0.0707	0.2058	0.0166	0.0019	0.0088	0.8536
J3	Fuzzy PD	0.0000	0.2672	0.0782	0.2173	0.0175	0.0021	0.0096	0.5918
	Fuzzy PID	0.1028	0.2994	0.0712	0.2057	0.0166	0.0019	0.0088	0.7063
J4	Fuzzy PD	0.7100	0.2624	0.0659	0.1971	0.0162	0.0020	0.0088	1.2625
	Fuzzy PID	0.8691	0.2619	0.0661	0.1931	0.0167	0.0021	0.0086	1.4176
J5	Fuzzy PD	0.0000	0.2612	0.0640	0.1890	0.0161	0.0019	0.0088	0.5411
	Fuzzy PID	0.0000	0.2992	0.0640	0.1891	0.0162	0.0019	0.0087	0.5792

Cuckoo search
Objective function	Controller	Time domain specification			Performance indices				Total indices
		Overshoot	Recovery time	Steady state error	RMSE	IAE	ITAE	ISE
J1	Fuzzy PD	0.4859	0.2629	0.0664	0.1998	0.0157	0.0019	0.0086	1.0413
	Fuzzy PID	0.5047	0.2634	0.0652	0.1936	0.0174	0.0019	0.0097	1.0557
J2	Fuzzy PD	0.0680	0.2895	0.0692	0.2040	0.0166	0.0019	0.0088	0.6580
	Fuzzy PID	0.0000	0.3691	0.0738	0.2082	0.0166	0.0019	0.0087	0.6782
J3	Fuzzy PD	0.0000	0.3975	0.0792	0.2161	0.0171	0.0020	0.0092	0.7211
	Fuzzy PID	0.0000	0.2993	0.0737	0.2097	0.0169	0.0019	0.0089	0.6105
J4	Fuzzy PD	1.0513	0.2624	0.0679	0.1956	0.0170	0.0021	0.0088	1.6051
	Fuzzy PID	0.7338	0.2627	0.0663	0.1984	0.0163	0.0020	0.0089	1.2884
J5	Fuzzy PD	0.0000	0.2612	0.0636	0.1809	0.0156	0.0019	0.0086	0.5319
	Fuzzy PID	0.0000	0.2988	0.0643	0.1892	0.0157	0.0019	0.0086	0.5786

Bat algorithm
Objective function	Controller	Time domain specification			Performance indices				Total indices
		Overshoot	Recovery time	Steady state error	RMSE	IAE	ITAE	ISE
J1	Fuzzy PD	0.9233	0.2628	0.0680	0.1990	0.0167	0.0021	0.0090	1.4809
	Fuzzy PID	0.7197	0.2627	0.0636	0.1913	0.0177	0.0020	0.0100	1.2670
J2	Fuzzy PD	0.0000	0.3964	0.0790	0.2103	0.0172	0.0020	0.0089	0.7138
	Fuzzy PID	0.0853	0.3792	0.0733	0.2067	0.0167	0.0019	0.0087	0.7719
J3	Fuzzy PD	0.2271	0.3728	0.0691	0.2031	0.0167	0.0019	0.0089	0.8996
	Fuzzy PID	0.4014	0.2625	0.0637	0.1913	0.0172	0.0019	0.0096	0.9476
J4	Fuzzy PD	0.0000	0.3728	0.0890	0.2172	0.0183	0.0024	0.0102	0.7099
	Fuzzy PID	1.3469	0.2618	0.0675	0.1944	0.0166	0.0021	0.0087	1.8981
J5	Fuzzy PD	0.0000	0.2617	0.0628	0.1810	0.0156	0.0019	0.0085	0.5316
	Fuzzy PID	0.0000	0.2631	0.0641	0.1928	0.0167	0.0019	0.0085	0.5472

Fig. 24. Simulation result for the condition 3.

Similar to the previous two conditions, for this condition 3 also, bat algorithm optimized fuzzy PD controller (objective function J5) has shown superior performance than the other controllers, and it is evident from the test results of time domain specifications and performance indices considered. The parameters value obtained are very much enhanced than the other controllers. All the values are in favor of bat optimized fuzzy PD controller (objective function J5).

7. Experimental set up and results discussion

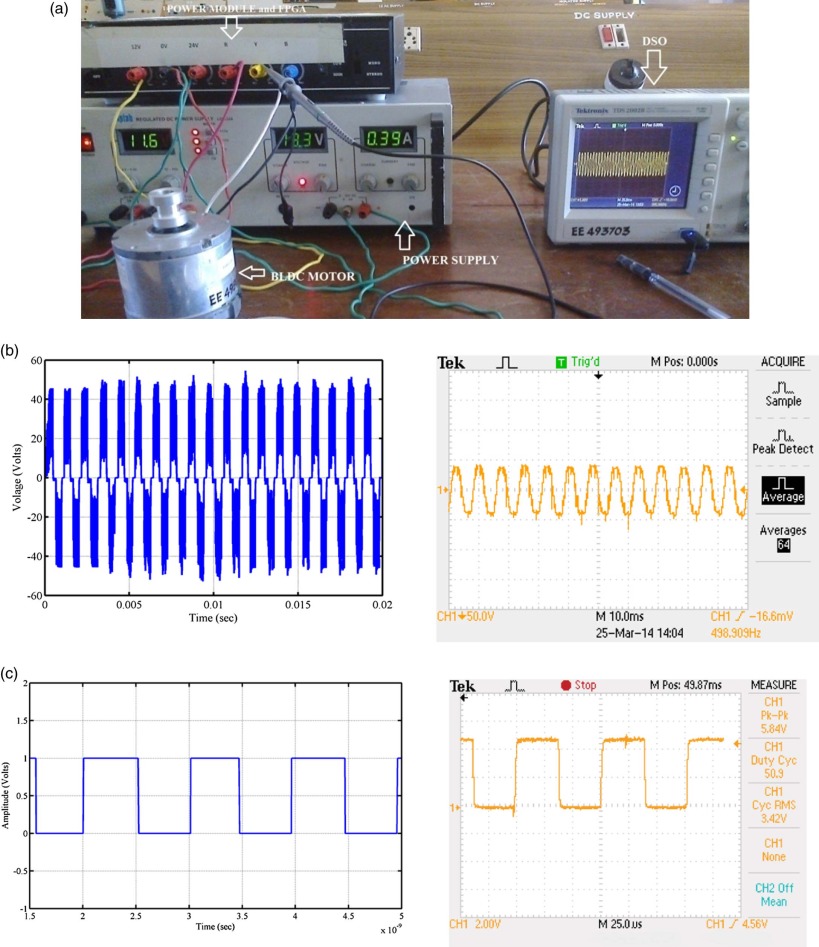
Since bat algorithm optimized fuzzy PD controller (objective function J5) is having clear edge over the other controllers considered, an attempt is made to implement for BLDC motor by using Spartan-3E FPGA starter kit. The rotor position of the brushless dc motor is measured by means of Hall sensor, and it is given as input to analog to digital converter (ADC). Rotor position is then converted into actual speed by derivative algorithm used in the FPGA kit. The set speed is assigned to motor by toggle switches according to the requirement, and load requirement is assigned by eddy current loading arrangement. The following Fig. 25 (a) shows the experimental set up for Spartan-3E FPGA based fuzzy PD based Speed controller for BLDC motor drive.

Fig. 25. (a). Experimental set up of FPGA based fuzzy PD speed controller for BLDC motor. (b) Experimental setup – Voltage across phases of motor, left side: simulated output and right side: experimental output. (c) Experiential setup – Hall sensor output of the motor, left side: simulated output and right side: experimental output.

Once this is performed, the ADC data are sent in FPGA kit and this develops an output value based on a fuzzy PD control algorithm stored in FPGA kit. And the output of controller in turn varies the duty cycle of a PWM signal to increase, decrease or maintain a constant speed of the motor [29]  and [30] . Power Module consists of switching power converters which are used in brushless dc motor drives to deliver the required energy to the motor. The energy that a switching power converter delivers to a brushless dc motor which is controlled by Pulse Width Modulated (PWM) signal applied to the gate of a power IGBT coming from PWM module of FPGA kit. In order to change the set speed of the drive, the toggle switch position is properly changed, and for changing the loading conditions as per the requirement, eddy current loading arrangement is suitably varied.

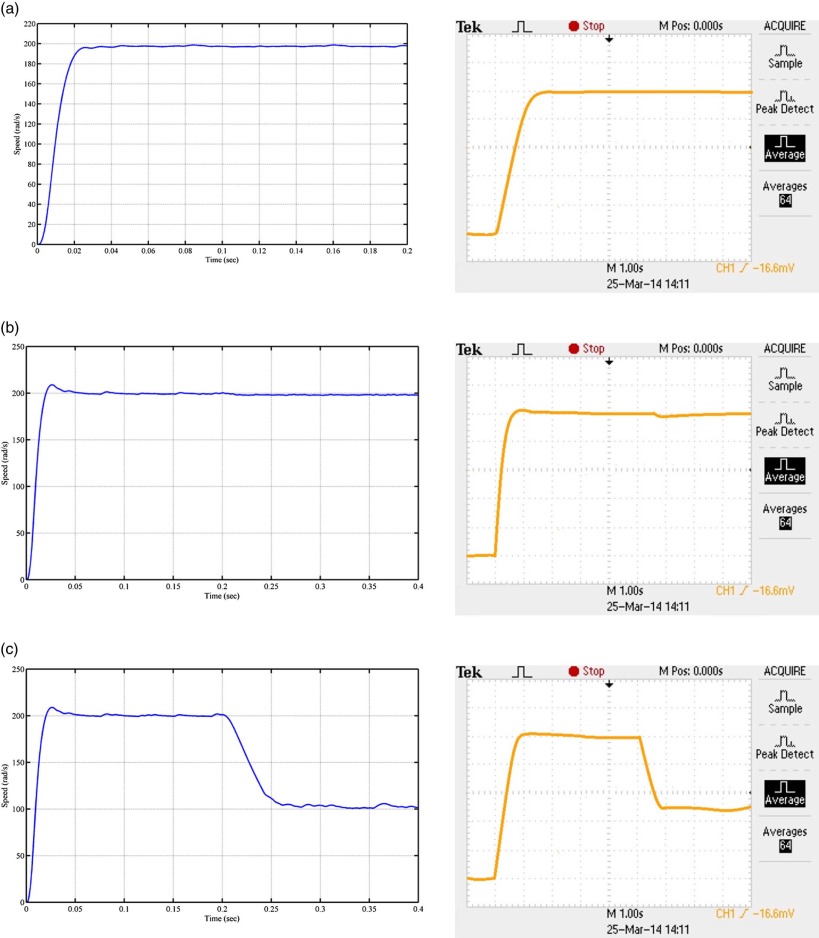
Fig. 25 (b) shows the voltage across the phases of the brushless dc motor. Fig. 25 (c) shows the hall sensor output of the brushless dc motor. From Fig. 23 , it is clear that the simulated output and experimental output are identical. Fig. 26 (a) to (c) shows the experimental results for three operating conditions of the brushless dc motor. It is clear that the response is same as that of the simulated output of the bat optimized fuzzy PD speed controller (objective function J5) of the brushless dc motor. From the simulated and experimental testing, bat optimized fuzzy PD speed controller (objective function J5) outperforms the other controller in all operating conditions.

Fig. 26. (a) Simulated and experimental speed response of the brushless dc motor with fuzzy PD controller for condition 1. (b) Simulated and experimental speed response of the brushless dc motor with fuzzy PD controller for condition 2. (c) Simulated and experimental speed response of the brushless dc motor with fuzzy PD controller for condition 3.

8. Conclusion

Bat algorithm optimized fuzzy proportional derivative based speed controller for Brushless DC motor has been presented. The overall control system has been created and simulated using MATLAB/Simulink and Sim power system tools to confirm the validity and development of the proposed system. Effectiveness of the proposed controller is analyzed and compared with PSO, Cuckoo search algorithm optimized fuzzy PD, fuzzy PID controller and bat algorithm optimized fuzzy PID controller. In order to test the effectiveness of the proposed controllers under realistic operating environment, various operating conditions such as constant load, varying load and varying set speed conditions are considered, and the performances are observed. In order to make a reasonable comparison, several performance measures are used such as rise time, settling time, recovery time maximum overshoot, steady state error, root mean square error, integral absolute error, integral of squared error, and integral time multiplied absolute error. The results obtained from the simulations clearly show the drastic improvements on performance measures and proved that the disturbances are also compensated much more effectively with the use of the proposed controller. To validate the performance of the proposed controller under real time operating conditions, the experimental realization for the control of Brushless DC motor has been fabricated and tested. From the results of the simulation and experimental set up, it is made clear that the proposed controller is able to eliminate the uncertainty problem occurring due to load variations and set speed variations. Since the controller exhibits unmatched performance, it is ideal for application in process industries.

References

1. [1] T.J. Sokira, W. Jaffe; Brushless DC Motors Electronic Commutation and Controls; Tab Books, Inc., Blue Ridge Summit, PA (1990), pp. 1–20
2. [2] R.A. Krohling, J.P. Rey; Design of optimal disturbance rejection PID controllers using genetic algorithms; IEEE Trans. Evolut. Comput, 5 (1) (2001), pp. 78–82
3. [3] B. Singh, S. Singh; Single-phase power factor controller topologies for permanent magnet brushless DC motor drives; IET Power Electron, 3 (2) (2010), pp. 147–175
4. [4] J. Gao, Y. Hu; Direct self-control for BLDC motor drives based on three-dimensional coordinate system; IEEE Trans. Ind. Electron, 57 (8) (2010), pp. 2836–2844
5. [5] C.S. Joice, S.R. Paranjothi, V.J.S. Kumar; Digital control strategy for four quadrant operation of three phase BLDC motor with load variations; IEEE Trans. Ind. Inform, 9 (2) (2013), pp. 974–982
6. [6] K. Premkumar, B.V. Manikandan; Adaptive fuzzy logic speed controller for brushless DC motor; Power, Energy and Control (ICPEC), 2013 International Conference on, pp. 290, 295; 6–8 Feb.  (2013) http://dx.doi.org/10.1109/ICPEC.2013.6527668
7. [7] K. Premkumar, B.V. Manikandan; Adaptive neuro-fuzzy inference system based speed controller for brushless DC motor; Neurocomputing, 138 (2014), pp. 260–270
8. [8] G.G. Rigatos; Adaptive fuzzy control of DC motors using state and output feedback; Electr. Pow. Syst. Res, 79 (11) (2009), pp. 1579–1592
9. [9] P.S. Londhe, B.M. Patre, A.P. Tiwari; Fuzzy-like PD controller for spatial control of advanced heavy water reactor; Nucl. Eng. Des, 274 (2014), pp. 77–89
10. [10] H.V.H. Ayala, L. Coelho; Tuning of PID controller based on a multiobjective genetic algorithm applied to a robotic manipulator; Expert Syst. Appl, 39 (10) (2012), pp. 8968–8974
11. [11] S.A.K.H. Mozaffari Niapour, S. Danyali, M.B.B. Sharifian, M.R. Feyzi; Brushless DC motor drives supplied by PV power system based on Z-source inverter and FL-IC MPPT controller; Energy Convers. Manag, 52 (8–9) (2011), pp. 3043–3059
12. [12] A. Rubaai, M.J. Castro-Sitiriche, A.R. Ofoli; DSP-based laboratory implementation of hybrid fuzzy-PID controller using genetic optimization for high-performance motor drives; IEEE Trans. Ind. Appl, 44 (6) (2008), pp. 1977–1986
13. [13] F. Valdez, P. Melin, O. Castillo; A survey on nature-inspired optimization algorithms with fuzzy logic for dynamic parameter adaptation; Expert Syst. Appl, 41 (14) (2014), pp. 6459–6466
14. [14] X. Li, X. Yao; Cooperatively coevolving particle swarms for large scale optimization; IEEE Trans. Evolut. Comput, 16 (2) (2012), pp. 210–224
15. [15] S. Panda, N.P. Padhy; Comparison of particle swarm optimization and genetic algorithm for FACTS-based controller design; Appl. Soft Comput, 8 (4) (2008), pp. 1418–1427
16. [16] R. Sharma, K.P.S. Rana, V. Kumar; Performance analysis of fractional order fuzzy PID controllers applied to a robotic manipulator; Expert Syst. Appl, 41 (9) (2014), pp. 4274–4289
17. [17] P. Dash, L.C. Saikia, N. Sinha; Comparison of performances of several Cuckoo search algorithm based 2DOF controllers in AGC of multi-area thermal system; Int. J. Electr. Power Energy Syst, 55 (2014), pp. 429–436
18. [18] S. Chetty, A.O. Adewumi; Comparison study of swarm intelligence techniques for the annual crop planning problem; IEEE Trans. Evolut. Comput, 18 (2) (2014), pp. 258–268
19. [19] D.K. Sambariya, R. Prasad; Robust tuning of power system stabilizer for small signal stability enhancement using metaheuristic bat algorithm; Int. J. Electr. Power Energy Syst, 61 (2014), pp. 229–238
20. [20] E.S. Ali; Optimization of power system stabilizers using BAT search algorithm; Int. J. Electr. Power Energy Syst, 61 (2014), pp. 683–690
21. [21] C.-S. Shieh; Fuzzy PWM based on Genetic Algorithm for battery charging; Appl. Soft Comput, 21 (2014), pp. 607–616
22. [22] A.B. Sharkawy; Genetic fuzzy self-tuning PID controllers for antilock braking systems; Eng. Appl. Artif. Intell, 23 (7) (2010), pp. 1041–1052
23. [23] R. Pérez-Rodríguez, S. Jöns, A. Hernández-Aguirre, C. Alberto-Ochoa; Simulation optimization for a flexible job shop scheduling problem using an estimation of distribution algorithm; Int. J. Adv. Manuf. Tech, 73 (1) (2014), pp. 3–21
24. [24] A. Ochoa-Zezzatti, O. Castillo, P. Melín, N. Castillo, S. Bustillos, J. Arreola; Shipwrecked on fear: selection of electives in school minorities in a university using cuckoo search algorithm; Recent Advances on Hybrid Approaches for Designing Intelligent Systems, vol. 547 (2014), pp. 139–150
25. [25] I. Fister Jr., D. Fister, X.-S. Yang; A hybrid bat algorithm; Elektroteh. Vestn, 80 (1–2) (2013), pp. 1–7 http://arxiv.org/abs/1303.6310
26. [26] S. Yılmaz, E.U. Küçüksille; A new modification approach on bat algorithm for solving optimization problems; Appl. Soft Comput, 28 (2015), pp. 259–275
27. [27] A. Ochoa, L. Margain, A. Hernandez, J. Ponce, A. De Luna, A. Hernandez, et al.; Bat algorithm to improve a Financial Trust Forest; in Nature and Biologically Inspired Computing (NaBIC), 2013 World Congress on, pp. 58–62; 12–14 Aug.  (2013)
28. [28] A. Ochoa, L. Margain, J. Arreola, A. De Luna, G. Garcia, E. Soto, et al.; Improved solution based on Bat Algorithm to Vehicle Routing Problem in a Caravan Range Community; in Hybrid Intelligent Systems (HIS), 2013 13th International Conference on, pp. 18–22; 4–6 Dec.  (2013)
29. [29] H.M. Hasanien; FPGA implementation of adaptive ANN controller for speed regulation of permanent magnet stepper motor drives; Energy Convers. Manag, 52 (2) (2011), pp. 1252–1257
30. [30] C.-F. Hsu, B.-K. Lee; FPGA-based adaptive PID control of a DC motor driver via sliding-mode approach; Expert Syst. Appl, 38 (9) (2011), pp. 11866–11872