Modeling and analysis of hybrid energy absorption devices for aircraft structures

1 Introducción

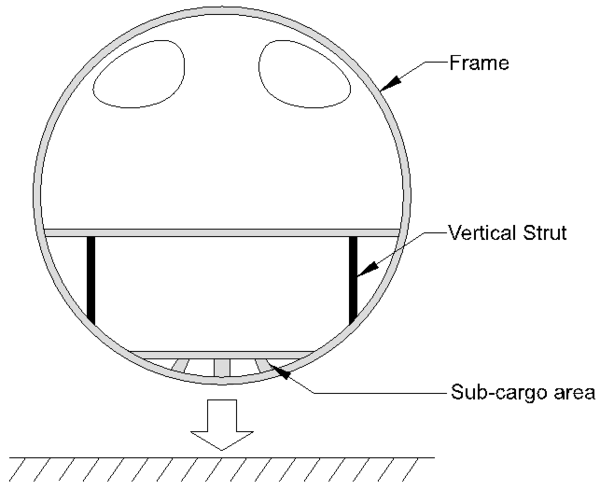
La mejora de la capacidad de protección frente a impacto de un fuselaje requiere modificar el comportamiento de sus estructuras, monitorizar y acotar las aceleraciones experimentadas por los ocupantes, y mejorar las capacidades de disipar energía de los componentes [1]. En la figura 1 se muestran los elementos estructurales encargados de disipar la mayor parte de la energía cinética previa al impacto: el cajón multicelular bajo el suelo de la bodega (sub-cargo area), la piel del fuelaje con su rigidización mediante cuadernas (frame) y los pilares de arriostramiento vertical (vertical strut) [2].

Figura 1. Esquema estructural de los principales conjuntos involucrados en la disipación de energía de impacto en un fuselaje.

Los pilares están sometidos a cargas dominadas por la componente axial y han demostrado poseer un efecto crucial en las aptitudes ante impacto del avión [3,4]. Así, el uso de riostras rígidas aumenta el área habitable tras el accidente y mejora la absorción de energía en las partes inferiores del fuselaje, mientras que unas riostras más flexibles reducen los picos de aceleración transmitidos a los pasajeros [5]. También se ha estudiado con ayuda de simulaciones numéricas los efectos de variar su configuración y posición [6,7] y la evolución de su colapso [8], confirmando la sensibilidad del comportamiento global de la aeronave al diseño de estos componentes [9].

Los pilares de arriostramiento pueden ser mejorados añadiendo refuerzos internos que complementen la estructura original. Este núcleo de refuerzo, que puede poseer diversas formas y materiales, constriñe el mecanismo de colapso dúctil del pilar aumentando el número de pliegues que forma el tubo exterior y su energía disipada [10]. El diseño de los refuerzos empleados abarca desde núcleos compactos hasta estructuras complejas como nidos de abeja o conjuntos de laminados. Aunque todos son susceptibles de aportar mejoras al comportamiento global, los nidos de abeja de celdas tanto regulares como irregulares han demostrado buenas cualidades para mejorar la absorción específica de energía del componente [11].

Considerando todo lo anterior, esta investigación aborda el diseño, análisis y optimización de forma y tamaño de absorbedores híbridos de energía formados por un tubo de pared delgada y sección cuadrada relleno de una estructura de nido de abeja de material compuesto de fibra de vidrio y extrusiones de espuma polimérica.

2 Materiales

Los absorbedores metálicos ofrecen altos niveles de disipación de energía por plasticidad; mientras que los núcleos de refuerzo de materiales compuestos y espuma han demostrado suplementar significativamente la respuesta de los tubos de pared delgada. En este caso, el tubo confinante se diseña con la aleación de aluminio AA7075-T651, usada habitualmente en estructuras aeronáuticas. Por su parte, la estructura interna de nido de abeja se configura con Ultramid A3WG10 BK00564, un polímero reforzado con fibra de vidrio (GFRP) de BASF; mientras que las celdas se rellenan de la espuma polimérica ArmaFORM PET/W AC 135 de Armacell.

Las curvas de tensión-deformación de la aleación de aluminio siguen una versión modificada del modelo de plasticidad de Johnson-Cook dependiente de la velocidad de deformación, propuesto por Børvik et al [12]. Al despreciar el término de temperatura, la ecuación constitutiva para la rama plástica queda definida como

${\begin{matrix}\,EQ\,{\sigma }_{y}=\left(A+B{p}^{n}\right){\left(1+{\frac {\overset {\cdot }{p}}{{\overset {\cdot }{p}}_{0}}}\right)}^{C}\#\left(1\right)\end{matrix}}$

donde A es el límite elástico del material, B es el modificador de la amplitud de la ley de endurecimiento, p es la deformación plástica equivalente, ${\textstyle {\frac {\overset {\cdot }{p}}{{\overset {\cdot }{p}}_{0}}}}$ es el ratio adimensional de deformación plástica y C el modificador de la dependencia de la velocidad de deformación (tabla 1).

Tabla 1. Propiedades mecánicas del aluminio AA7075-T651.

E	ν	ρ	A	B	n	C	${\overset {\cdot }{\mathit {\boldsymbol {p}}}}_{\mathit {\boldsymbol {0}}}$
70 MPa	0,30	27,70 kN/m3	520,0 MPa	477,0 MPa	0,52	0,001	0,0005

En el caso del material compuesto de fibra de vidrio (GFRP), la calibración de su respuesta se ha realizado a partir de los datos obtenidos de los ensayos de Costas et al. [13] (tabla 2). El modelo constitutivo se presenta de la siguiente forma:

${\begin{matrix}{\sigma }_{y}=\,{\sigma }_{0}+\left[\sum _{j=1}^{k}{Q}_{j}\left(1-{e}^{-{b}_{j}p}\right)\right],\#\left(2\right)\end{matrix}}$

donde Q_j, b_j y σ₀ son constantes del material y k es el número de términos usados para aproximar la respuesta del material. Para este material, se toma un valor de k = 2 y una deformación máxima antes de rotura de 2.38%.

Tabla 2. Propiedades mecánicas de Ultramid A3WG10 BK00564.

E	ν	Ρ	σ0	Q1	Q2	b1	b2
15,48 MPa	0,40	15,15 kN/m3	25,00 MPa	124,86 MPa	44,46 MPa	315,89	5748,46

La espuma también ha sido ajustada a partir de los resultados de los ensayos de Costas et al. [13] para obtener su respuesta a cargas de compresión. Aunque el material es ortótropo, se considera que la espuma se carga paralelamente a la dirección de la extrusión, la más rígida de ellas. Para capturar los procesos de endurecimiento durante su solicitación, se usa el modelo de Desphande y Fleck [14] para espumas metálicas. La superficie de plastificación f, que incluye dependencia de la presión, se modela con un círculo de Mises en el plano de tensión desviadora y una elipse centrada en el plano de tensión meridional de la forma

${\begin{matrix}f=\,{\sqrt {{{\sigma }_{eq}}^{2}+{\alpha }^{2}{{\sigma }_{H}}^{2}}}-D=0,\#\left(3\right)\end{matrix}}$

donde la tensión de von Mises está representada por σ_eq, la tensión hidrostática corresponde a σ_H, α es el factor de forma de la elipse que define la magnitud relativa de los ejes, y D es el tamaño del eje vertical de la elipse. Además, se incluye un potencial de flujo g para representar el flujo no-asociado, tomando la forma

${\begin{matrix}g=\,{\sqrt {{{\sigma }_{eq}}^{2}+{\beta }^{2}{{\sigma }_{H}}^{2}}}=0,\#\left(4\right)\end{matrix}}$

siendo β la forma de la elipse del potencial de flujo en el plano meridional, dependiente del coeficiente de Poisson plástico ν_p.

Tabla 3. Propiedades de la espuma ArmaFORM PET/W AC 125.

E	ν	ρ	α	β	νp
59,01 MPa	0,10	1,35 kN/m3	0,729	1,76	0,111

3 Geometría de los absorbedores

En esta investigación se estudian dos configuraciones de absorbedores híbridos de energía, cuyas diferencias principales residen en el uso o no de espuma de relleno y en las dimensiones del tubo exterior. El espécimen A posee una sección cuadrada con menor inercia y prescinde de la espuma (figura 2), mientras que el espécimen B cuenta con celdas rellenas de espuma y mayor inercia seccional.

Figura 2. Corte tridimensional y mallado del espécimen A.

3.1 Espécimen A

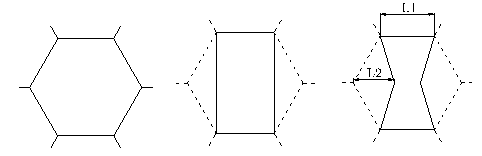
Este componente está definido geométricamente por tres parámetros y cuatro variables de diseño. Los primeros son la altura del tubo (500 mm), la longitud de la arista (100 mm) y la altura del refuerzo interior (480 mm). El decalaje de 20 mm existente entre el tubo y el núcleo se ha implementado buscando reducir el pico de fuerza durante los primeros instantes del colapso del tubo [15]. Por otro lado, las cuatro variables de diseño para el proceso de optimización incluyen el espesor de las chapas de aluminio (T₁), el espesor del composite (T₂), el tamaño de las celdas del nido de abeja (L₁) y la forma de la celda (S). Esta última variable es la responsable de variar la forma de las celdas, estando definida como

${\begin{matrix}S=\,{\frac {L1}{L2}}\#\left(5\right)\end{matrix}}$

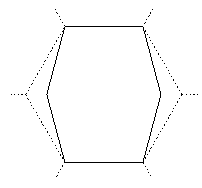
El efecto de esta variable sobre el diseño de la celda se muestra en la figura 3. Cuando S=0, la celda toma forma de un hexágono regular. Según el valor aumenta, la celda tiende hacia un rectángulo con una proporción del lado largo entre lado corto de 1,73:1 (S=0.5). Cuando el valor de S supera 0.5, las celdas se asemejan a un reloj de arena.

Figura 3. Diferentes configuraciones de la forma de las celdas del nido de abeja. De izquierda a derecha, S=0, S=0,5 y S=0,75.

Las funciones objetivo consideradas incluyen tanto métricas simples como ratios, siendo las cuatro elegidas la energía absorbida (E_a), la masa de los absorbedores (m), el pico de fuerza máximo (P_peak) y la absorción específica de energía (SEA). Todas ellas, con excepción de la masa, se obtienen de las curvas fuerza-desplazamiento resultantes de la simulación numérica del aplastamiento del componente.

La razón por la que se han elegido estas funciones objetivo reside en la necesidad de formular una optimización fiable del crashworthiness de los componentes. Como en cualquier optimización multi-objetivo, las métricas estudiadas deben ser contrapuestas y estar asociadas a diferentes capacidades del modelo. Al maximizar E_a, las riostras disiparían mayor energía aliviando así los esfuerzos que recibirían otras estructuras del fuselaje. Además, una reducción de la masa del componente conlleva menores costes para manufacturarlo y una mejor eficiencia del aeronave. Considerando lo anterior, la optimización mono-objetivo de la SEA del espécimen supone maximizar E_a y minimizar la masa simultáneamente. Sin embargo, y aunque esta optimización proporciona información relevante de la respuesta del espécimen y la sensibilidad de las variables de diseño, las métricas originadas a partir de ratios tienden a mostrar una naturaleza más ruidosa que las métricas simples. Además, la optimización de la SEA no permite tener control sobre la energía absorbida ni la masa por separado. Por último, al considerar P_peak como función objetivo se considera la parte de protección de los ocupantes.

3.2 Espécimen B

El segundo de los absorbedores estudiados también se define con tres parámetros de diseño y cuatro variables. El espécimen se compone de un tubo cuadrado hueco de aluminio de 500 mm de longitud y una arista de 150 mm, reforzado con un núcleo de composites y espuma de 450 mm de altura. Las variables de diseño son homólogas a las del espécimen A: espesor de aluminio y GFRP, y forma y tamaño de las celdas.

En este diseño, las extrusiones de espuma se adaptan a la forma del nido de abeja, dejando una holgura de 1 mm entre la espuma y el GFRP para facilitar la convergencia de la simulación numérica y facilitar un hipotético proceso de manufacturado, sin que ello suponga un efecto representativo sobre las capacidades del componente. Otro de los aspectos característicos de este modelo que se puede percibir en las figuras 4a – 4d es la ausencia de espuma entre el nido de abeja y el tubo cuando no cabe una extrusión completa de espuma. Esto facilita el proceso de construcción y ensamblaje, ya que no se requiere el corte de rellenos ad hoc para cada una de las celdas limítrofes con el tubo. Al igual que con el espécimen A, se toman cuatro funciones objetivo, tanto para la optimización mono- como para la multi-objetivo.

Figura 4. Formas representativas de diversas configuraciones del espécimen B.

4 Condiciones del análisis

Considerando el gran número de simulaciones necesarias para el proceso de optimización y su eficacia en problemas con altas no-linealidades, se opta por el uso de técnicas de optimización con modelos subrogados [15]. Para ello, primero se realiza un muestreo en todo el espacio de diseño llevando a cabo simulaciones por elementos finitos en paralelo que permitirán construir un metamodelo con las respuestas de cada absorbedor.

Para la elección de los tamaños de malla usados, se considera el comportamiento que presentará la estructura y las propiedades de los materiales. Tras el estudio de sensibilidad de la malla, se procede a usar elementos lámina rectangulares de 4 mm de arista con integración reducida para el tubo y el nido de abeja. Este tamaño de malla permite capturar el colapso plástico del tubo, obteniendo el mismo número de pliegues y niveles de absorción de energía similares que con mallas más finas. Se descarta el uso de elementos sólidos para estas partes dado el alto coste computacional que conllevaría. Sin embargo, la espuma sí se modela con elemento sólidos, siendo estos de ocho nodos con integración reducida y control de inestabilidades de tipo hourglass, también con una dimensión de arista de 4 mm. La figura 2 muestra un corte tridimensional del componente mallado.

La simulación con elementos finitos busca replicar las condiciones con las que la estructura será aplastada en un fuselaje. En primer lugar, se procede a añadir un trigger en las aristas superiores de los tubos con el fin de obtener un mecanismo de colapso más estable y reducir las fuerzas pico. Las imágenes de la figura 5 muestran la deformada final de dos tubos idénticos, habiéndose aplicado el trigger solo a uno de ellos. Los resultados muestran una reducción de P_peak de más del 30%, sin afectar representativamente a la absorción de energía del espécimen.

Figura 5. Comparativa de los especímenes colapsados. Modelo sin trigger (izquierda) y con trigger (derecha).

La velocidad de impacto elegida varía según el componente: el espécimen A se colapsa a una velocidad constante de 10 m/s, mientras que el B se ve sometido a un aplastamiento a 15 m/s dada su mayor capacidad de disipación de energía con el uso de espuma.

Para la construcción del modelo subrogado, primero se realiza un muestreo por cada uno de los especímenes con el método latin hypercube sampling (LHS), calculando 500 y 600 muestras para los componentes A y B, respectivamente. Cada muestra ha sido calculada y postprocesada con el software Abaqus 6.13 en su versión Explicit, necesitando aproximadamente seis horas de simulación con una paralelización en ocho núcleos. Posteriormente, se usa la técnica de moving least squares (MLS) para construir ambos metamodelos, que son sometidos a escrutinio mediante validación cruzada, calculando el error medio cuadrático y la bondad de ajuste de los subrogados, que permanece dentro de niveles aceptables.

5 Resultados

5.1 Espécimen A

5.1.1 Optimización mono-objetivo

La primera de las estrategias seguidas es la optimización mono-objetivo de la SEA del espécimen. Inicialmente se realiza sin aplicar ninguna restricción, y posteriormente se impone un límite de fuerza pico de 250 kN. En el primero de los casos, el diseño óptimo tiende configuraciones con los valores de las variables próximos o incluso tomando el valor del límite superior especificado, con una ligera variación de la forma regular de la celda. La tabla 4 compara este diseño con el inicial, mostrando un aumento de la SEA de un 136%, aunque el pico de fuerza también se incrementa en un 46%.

Tabla 4. Optimización mono-objetivo del espécimen A.

Modelo	Variable de diseño (mm)				Función objetivo	Condición
	L1	T1	T2	S	SEA (kJ/kg)	Ppeak (kN)
Inicial	6,50	1,35	1,00	0,00	15,58	307,77
Incondicionado	14,27	2,99	2,55	0,07	36,88	449,76
Condicionado	14,24	2,17	1,43	0,27	25,76	248,89
	14,27	1,98	1,46	0,00	22,15	241,95

Considerando la importancia de la función P_peak, se establece un límite de fuerza de 250 kN. El resultado de este procedimiento ofrece un componente que mejora la SEA inicial en más del 65% y una reducción de P_peak de 19% como consecuencia de la restricción. La forma de la celda óptima resultante toma un valor de S = 0,27, lo que origina la forma irregular mostrada en la figura 6. A la vista de este resultado, y como comprobación del aporte de la optimización de forma de la celda, se realiza el mismo proceso de optimización fijando la forma de la celda como hexágono regular. Los resultados, presentados en la tabla 4, muestran un incremento de la SEA del 17% como consecuencia de la optimización de tamaño del nido de abeja.

Figura 6. Forma óptima de la celda del espécimen A tras la optimización mono-objetivo condicionada.

5.1.2 Optimización multi-objetivo

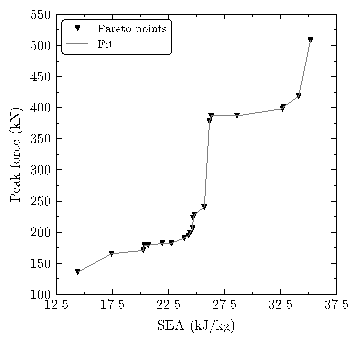
Este espécimen se ve sometido a dos procedimientos de optimización multi-objetivo con combinaciones de dos funciones objetivo cada una. Los resultados en la figura 7 muestran valores bajos de espesores y celdas grandes e irregulares para valores bajos de SEA y P_peak. La tendencia observada al incrementar progresivamente los valores de las funciones objetivo es la de reducir el tamaño de la celda, variar su forma hacia el hexágono regular, e incrementar el espesor del aluminio. Esto mejora la eficiencia del componente hasta valores de SEA de 26 kJ/kg, manteniendo el valor de P_peak por debajo de 250 kN. Sin embargo, para superar al superar los 26 kJ/kg de SEA, cuando aumentan los espesores del composite y los valores de P_peak aumentan hasta más de 400 kN. Aún así, el diseño inicial está claramente dominado por el frente obtenido, pudiendo reducir P_peak en un 55% manteniendo el mismo valor de SEA, o incrementar ésta en un 65% para diseños con un pico de fuerza similar al inicial.

Figura 7. Frente de Pareto SEA - P_peak para el espécimen A.

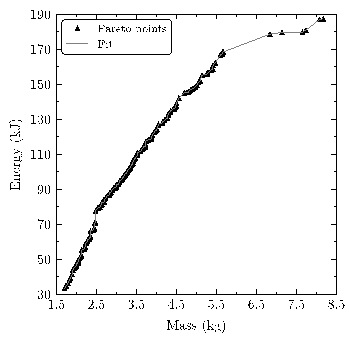
La segunda optimización incluye masa y energía absorbida como métricas objetivo. La evolución de las variables de diseño en el frente de Pareto en la figura 8 muestra como se incrementan la masa y la energía absorbida a medida que se reduce el tamaño de celda y aumentan los espesores. La forma de las celdas, siempre irregulares, presentan valores de S entre 0,15 y 0,40 en la mayor parte del espacio de diseño. Para valores de masa inferiores a 5,5 kg, la frontera de Pareto sigue una tendencia pseudo-lineal, manteniendo una proporción constante entre los incrementos de masa y energía absorbida. Sin embargo, para superar estos valores la pendiente de la curva cambia reduciendo en consecuencia la eficiencia de los diseños en términos de SEA, ya que los especímenes resultantes tienden a formas de celda de reloj de arena, menos eficientes para este propósito. Con todo ello, se obtiene que los valores más altos de SEA, cercanos a 31 kJ/kg, se corresponden con diseños con S ≈ 0,35, mostrando que la forma regular de nido de abeja no es la más ventajosa en los diseños estudiados.

Figura 8. Frente de Pareto masa - E_a para el espécimen A.

5.2 Espécimen B

5.2.1 Optimización mono-objetivo

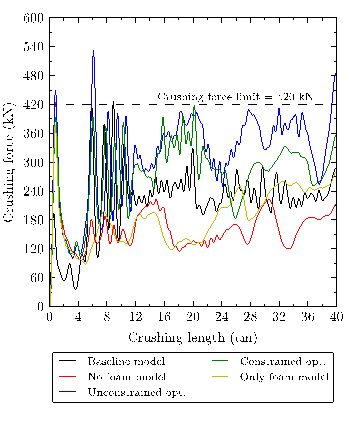
El procedimiento de optimización seguido para el espécimen B es homólogo al realizado con el diseño previo. Tras la optimización no condicionada de la SEA se obtiene una mejora del 26% de esta métrica con respecto al diseño inicial, aumentando para ello el espesor de aluminio y tendiendo hacia celdas pseudo-rectangulares. Esta forma es la más eficiente para el componente propuesto, ya que resulta en una menor cantidad de GFRP y, consecuentemente, aumenta la masa de espuma que rellena el absorbedor. Como consecuencia, también aumenta el pico de fuerza en más de un 25%, por lo que se procede a imponer una condición de límite de P_peak a 420 kN. Los resultados, mostrados en la tabla 5 y representados en la figura 9, cumplen con el límite establecido mejorando también la SEA un 22%, resultando en diseños con menor espesor de materiales y celdas más pequeñas entre el hexágono regular y el rectángulo (S ≈ 0,20).

Además, se realizan otras dos optimizaciones con componentes modificados para estudiar ciertas características de los absorbedores. Uno de los modelos prescinde de las extrusiones de espuma, pudiendo cuantificar así el aporte de estas estructuras a la respuesta del espécimen. Los resultados muestran que tras la optimización no condicionada, la SEA obtenida es un 28% menor que el modelo óptimo homólogo con espuma rellenando las celdas. También se analiza un modelo relleno exclusivamente de un bloque macizo de espuma. La absorción específica de energía de este componente llega a los 27,8 kJ/kg, un 16% superior a lo obtenido con las configuraciones propuestas. Sin embargo, la absorción de energía de este diseño estaría limitada a 75 kJ, resultando en modelos eficientes pero sin margen de mejora con los procesos de optimización propuestos.

Figura 9. Curvas fuerza-desplazamiento del diseño inicial del componente B comparadas con modelos óptimos y modelos con y sin espuma.

5.2.2 Optimización multi-objetivo

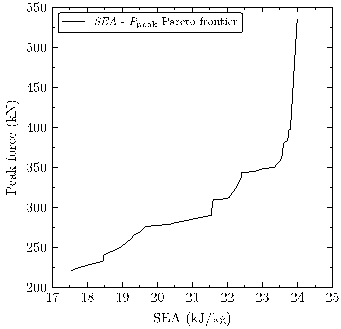
Similarmente a lo realizado con el espécimen A, se siguen dos procedimientos de optimización multi-objetivo que enfrentan SEA - P_peak y m - E_a. El frente de Pareto originado del primer proceso se muestra en la figura 10, en la que se aprecia una no-linealidad significativa de la respuesta. Esto sucede por la variación de los espesores de aluminio a lo largo de la frontera obtenida, ya que según se incrementa este espesor el aumento en la fuerza pico es significativamente mayor que la mejora obtenida en la SEA. Nuevamente, el tamaño de las celdas se reduce para obtener valores altos de SEA, aunque sin bajar de los 11,5 mm. Además, el espesor del composite se mantiene cercano al límite inferior de diseño ya que la contribución aportada por el aumento de espesor del aluminio es más beneficiosa en términos de SEA y P_peak que hacer lo propio con el GFRP, hecho que se puede atribuir al diferenciado mecanismo de colapso de ambas estructuras. Finalmente, los resultados muestran que las celdas con formas próximas al rectángulo ofrecen los valores más altos de SEA.

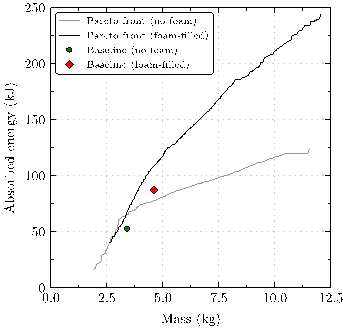
Para la optimización de masa y energía absorbida, se consideran dos configuraciones distintas con el fin de estudiar el aporte de la espuma al modelo, incluyendo o descartando su uso según el espécimen. Las gráficas de la figura 11 muestran ambos frentes obtenidos, así como los modelos iniciales de los que parte la optimización. Para el caso sin espuma, la energía absorbida se incrementa rápidamente entre los 25 kJ y 75 kJ, alcanzando valores de SEA de 20 kJ/kg.

Tabla 5. Resultados de la optimización mono-objetivo del espécimen B.

Modelo	Variable de diseño (mm)				Función objetivo	Condición	Métrica
	L1	T1	T2	S	SEA (kJ/kg)	Ppeak (kN)	Ea (kJ)
Inicial	10,00	1,50	1,50	0,00	19,04	425,97	87,60
Incondicionado	11,72	2,47	1,28	0,48	24,04	532,25	125,99
Condicionado	9,63	2,49	1,01	0,20	23,17	418,78	109,44
Sin espuma	14,73	2,50	1,10	0,28	18,76	424,30	64,93
Sólo espuma	-	2,50	-	-	27,82	377,50	74,36

Figura 10. Frente de Pareto SEA - Ppeak para el espécimen B

Sin embargo, esta eficiencia se ve reducida para modelos con mayor masa, traducida en una pendiente más tendida en la frontera de Pareto, que culmina con especímenes de 11 kg con SEA inferior a 12 kJ/kg. Este comportamiento puede ser explicado entendiendo la contribución de cada una de las partes del absorbedor. En la primera región del frente, la ganancia obtenida en la E_a se atribuye al constreñimiento del mecanismo de colapso del tubo a causa del relleno interior usado. Sin embargo, alcanzado un cierto nivel de rigidez del material de refuerzo, para aumentar la absorción de energía es necesario incrementar el espesor del tubo exterior, con la consecuente pérdida de eficiencia estructural.

Como respuesta a esta limitación, se realiza la optimización del componente que incluye las extrusiones de espuma como relleno de las celdas. En la figura 11 se aprecia como hasta los 3 kg, ambos frentes de Pareto ofrecen un comportamiento muy similar, aunque una vez superado ese valor, el componente con espuma domina claramente al que no la tiene. Analizando comportamiento de las variables de diseño a lo largo del frente de Pareto, se observa como a medida que E_a aumenta el tamaño de la celda se reduce gradualmente y el aluminio y el GFRP se engruesan. Para componentes con masas superiores a 4.5 kg el espesor del aluminio toma el valor del límite superior, lo que indica la importancia del diseño del tubo al buscar valores altos de SEA. Las celdas varían progresivamente del hexágono regular hasta que finalmente alcanzan la forma de reloj de arena, que maximiza la cantidad de GFRP del espécimen. Sin embargo, esta configuración de celda se obtiene sólo si se buscan valores elevados de E_a, pero no se corresponde con los diseños con la SEA más alta.

Por lo que respecta a la SEA, su valor varía desde los 15 kJ/kg hasta un máximo de 24 kJ/kg para componentes de masas cercanas a los 5 kg. Después de este punto, la SEA se reduce progresivamente hasta los 20 kJ/kg. Además, los resultados concuerdan con lo obtenido en la optimización mono-objetivo de la SEA, consiguiendo su valor máximo para configuraciones con espesores altos de aluminio y bajos de GFRP, y celdas rectangular de 10-12 milímetros.

Figura 11. Frentes de Pareto masa - E_a para el espécimen B con y sin espuma.

6 Conclusiones

Esta investigación se centra en el análisis del comportamiento ante impacto y la optimización de dos diseños de absorbedores de energía híbridos diseñados para trabajar como arriostramiento en la mitad inferior del fuselaje de un avión. Los tubos metálicos huecos y de pared delgada se complementan con refuerzos interiores de materiales compuestos en forma de nido de abeja y extrusiones de espuma de alta densidad, pudiendo variar los espesores de los materiales y el tamaño y forma de las celdas. Los resultados muestran que, a nivel de componente, el uso de refuerzos internos puede modificar los patrones de colapso y mejorar la absorción específica de energía, principalmente debido al efecto de interacción entre el núcleo de refuerzo y la estructura confinante. De este trabajo se concluye que:

• El uso de triggers en las aristas del tubo que reciben el impacto reduce en más de un 30% el pico de fuerza inicial, además de producir mecanismos de colapso más estables.

• La optimización mono-objetivo de la forma de las celdas del espécimen A revela que los diseños no regulares ofrecen una absorción de energía específica hasta un 10% superior a los hexágonos regulares, sin detrimento en el pico de fuerza máximo.

• El uso de extrusiones de espuma también incrementa la absorción de energía específica en un 28%, sin que ello suponga un aumento de la fuerza pico.

• La optimización de la forma de las celdas del espécimen B resultó en diseños con valores de SEA de hasta 24 kJ/kg para celdas pseudo-rectangulares, mientras que el diseño inicial con hexágonos regulares solo alcanzaba 19 kJ/kg.

• Diferentes optimizaciones multi-objetivo de ambos especímenes muestran que los diseños con un comportamiento más eficaz y eficiente en términos de masa, absorción de energía y fuerza pico, son aquellos con celdas grandes, no regulares y de pared delgada en el nido de abeja, y un espesor grueso del tubo confinante.

En consecuencia, puede establecerse que la aplicación de absorbedores híbridos supone un incremento significativo de la capacidad estructural para absorber cargas dinámicas de impacto y de mejora de la protección de los ocupantes con respecto a los absorbedores convencionales metálicos. Por último, cabe mencionar que la optimización estructural es una estrategia crucial durante el diseño de componentes para aeronaves. El uso de estas metodologías permite obtener diseños de componentes más seguros y robustos sin despreciar la ligereza y la eficiencia energética de estos, permitiendo así reducir el consumo de combustible e incrementar la fiabilidad y la capacidad de carga útil.

Agradecimientos

La investigación presentada ha sido financiada a cargo del proyecto “OPTISAFE. Optimización probabilista de estructuras aeronáuticas intactas y dañadas frente a cargas dinámicas y de impacto”, concedido por el Ministerio de Economía y Competitividad con referencia DPI2016-76934- R.

Referencias

[1] S. Heimbs, “Energy Absorption in Aircraft Structures,” International Workshop on Hydraulic Equipment and Support Systems for Mining (IWHEM 2012), Huludao, China, (2012).

[2] E. L. Fasanella, K. E. Jackson, K. H. Lyle, C. E. Sparks, and A. K. Sareen, “Multi-Terrain Impact Tests and Simulations of an Energy Absorbing Fuselage Section,” Journal of the American Helicopter Society, 52, 2, pp. 159–168 (2007).

[3] J. F. M. Wiggenraad, A. Michielsen, D. Santoro, F. Le Page, C. Kindervater, F. Beltran and M. Alkhalil, “Finite Element Methodologies Development to Simulate the Behaviour of Composite Fuselage Structure and Correlation with Drop Test,” Air & Space Europe, 3, 3, pp. 228–233 (2001).

[4] M. B. Woodson, E. R. Johnson and R. T. Haftka, “Optimal Design of Composite Fuselage Frames for Crashworthiness,” International Journal of Crashworthiness, 1, 4, pp. 369–380 (1996).

[5] H. Shoji, M. Minegishi, and T. Aoki, “Impact Characteristics Estimation of Channel Section Short Column Under Axial Impact Load,” 48th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, 4, pp. 3967–3976, Honolulu, Hawaii (2007).

[6] Y. Ren and J. Xiang, “A Comparative Study of the Crashworthiness of Civil Aircraft with Different Strut Configurations,” International Journal of Crashworthiness, 15, 3, pp. 321–330 (2010).

[7] Y. Ren and J. Xiang, “The Crashworthiness of Civil Aircraft Using Different Quadrangular Tubes as Cabin-Floor Struts,” International Journal of Crashworthiness, 16, 3, pp. 253–262 (2011).

[8] X. Jia, G. Chen, Y. Yu, G. Li, J. Zhu, X. Luo, C. Duan, X. Yang and D. Hui, “Effect of Geometric Factor, Winding Angle and Pre-Crack Angle on Quasi-Static Crushing Behavior of Filament Wound CFRP Cylinder,” Composites, Part B: Engineering, 45, 1, pp. 1336–1343 (2013).

[9] T. Zou, H. Mou and Z. Feng, “Research on Effects of Oblique Struts on Crashworthiness of Composite Fuselage Sections,” Journal of Aircraft, 49, 6, pp. 2059–2063 (2012).

[10] J. Paz, J. Díaz, L. Romera and M. Costas, “Crushing Analysis and Multi-Objective Crashworthiness Optimization of GFRP Honeycomb- Filled Energy Absorption Devices,” Finite Elements in Analysis and Design, 91, pp. 30–39 (2014).

[11] J. Schultz, D. Griese, J. Ju, P. Shankar, J. Summers and L. Thompson, “Design of Honeycomb Mesostructures for Crushing Energy Absorption,” Journal of Mechanical Design, 134, 7, (2012).

[12] T. Børvik, O. Hopperstad, T. Berstad and M. Langseth, “A Computational Model of Viscoplasticity and Ductile Damage for Impact and Penetration,” European Journal of Mechanics, A/Solids, 20, 5, pp. 685–712 (2001).

[13] M. Costas, D. Morin, M. Langseth, L. Romera and J. Díaz, “Axial Crushing of Aluminum Extrusions Filled with PET Foam and GFRP. An Experimental Investigation,” Thin-Walled Structures, 99, pp. 45–57 (2016).

[14] V. Deshpande and N. Fleck, “Isotropic Constitutive Models for Metallic Foams,” Journal of the Mechanics and Physics of Solids, 48, 6, pp. 1253–1283 (2000).

[15] J. Paz, J. Díaz, L. Romera and M. Costas, “Size and Shape Optimization of Aluminum Tubes with GFRP Honeycomb Reinforcements for Crashworthy Aircraft Structures,” Composite Structures, 133, pp. 499–507 (2015).