Zener fractional order determination and biomechanical blood flow characterization

Resumen

El propósito principal de la presente publicación consiste en la determinación adecuada del orden fraccional en el modelo viscoelástico de Zener y el análisis de las implicaciones que se derivan de la precisión en la obtención del mismo. Esto se realiza empleando el método numérico de Levenberg-Marquardt a partir de valores reportados en la literatura. Los parámetros utilizados son obtenidos para un segmento de arteria empleando un experimento de relajación a los esfuerzos. Una vez determinado el orden fraccional se procede a determinar la solución del modelo empleando la función de dos parámetros de Mittag-Leffler y la operación de convolución, con la finalidad de comparar el comportamiento del modelo de orden fraccional con el de orden entero e identificar sus principales diferencias. Se obtienen además las deformaciones que experimenta la arteria bajo el estímulo de un pulso sanguíneo normal y otros disímiles, simulando el efecto provocado en el flujo sanguíneo por una arritmia y el ocasionado por el proceso de ventilación mecánica. Por último se analiza la respuesta dinámica del material bajo una serie de pulsos, utilizando la operación de convolución y el método numérico de Gauss-Kronrod, identificando la precisión en la reproducción de los mismos en el modelo de orden fraccional comparado con el de orden entero.

Abstract

The main purpose of this publication is the proper determination of the fractional order at the Zener viscoelastic models and the analysis of the implications derived from the accuracy in obtaining this. The procedure is performed using the numerical method of Levenberg-Marquardt from values reported in the literature. The parameters used are obtained from an artery segment using a stress relaxation test. After determining the fractional order is proceeded to find the model solution using, the function of Mittag-Leffler with two parameters and the convolution operation in order to compare the behavior of the fractional model vs the integer order and identify their key differences. The displacements present on the artery are obtained, under the stimulus of a normal blood pulse and two dissimilar, simulating the effect in blood flow caused by an arrhythmia and by mechanical ventilation process. Finally the dynamic response from the pulses is analyzed using the convolution operation and Gauss Kronrod numeric method, where the solutions accuracy obtained by the fractional model is observed, an compared with the integer order model.

Palabras clave

Biomecánica ; Cálculo fraccional ; Viscoelasticidad ; Arteria ; Tejidos blandos

Keywords

Biomechanics ; Fractional calculus ; Viscoelasticity ; Artery ; Soft tissues

1. Introducción

Determinar los fenómenos mecánicos que ocurren en las arterias resulta de suma importancia debido a su influencia en la fisiología arterial y en el tratamiento-seguimiento de los principales padecimientos arteriales ocasionados por los efectos del flujo sanguíneo [1] . Estos padecimientos se deben generalmente a: la calcificación de las paredes arteriales, los aneurismas [2] , la obstrucción de las arterias por acumulación de placas de colesterol, padecimiento comúnmente conocido como aterosclerosis, [3] y por los efectos perjudiciales de la hipertensión [4] , por citar algunos de los principales.

Los materiales que forman el cuerpo humano se dividen principalmente en dos grandes ramas, los tejidos blandos y los mineralizados. En la primera rama se encuentran las arterias, venas, músculos, piel, tendones, entre otros. La segunda se compone principalmente de los huesos y los dientes. Aunque en algunos casos suelen presentarse, tejidos blandos con formaciones calcificadas, estos no son habituales.

Las arterias a su vez se componen principalmente de redes de colágeno y elastina, además de tejido muscular liso lo que les proporciona un tipo de comportamiento material sumamente complejo.

Generalmente en la mayoría de los estudios biomecánicos de los tejidos blandos, estos han sido caracterizados bajo los modelos de comportamiento material viscoelástico [5] . Debido a que poseen características propias de los materiales elásticos, generalmente sólidos, y a su vez también se comportan como un fluido viscoso.

Una de las principales características de los materiales elásticos consiste en su capacidad de almacenar energía cuando son deformados bajo cargas, y en devolver toda esta energía cuando la carga se deja de aplicar. De forma contraria en el fluido viscoso la energía mecánica es continuamente disipada en forma de calor. Sin embargo existen materiales, como el caso de este estudio, que simultáneamente almacenan y disipan energía mecánica cuando se sujetan a un proceso de cargas, este tipo de materiales se conocen como viscoelásticos. Por lo que en estos no solamente se relaciona la tensión mecánica con la deformación, sino que además involucra su razón de cambio con respecto al tiempo.

Los materiales viscoelásticos suelen ser modelados a través de arreglos consistentes de resortes y amortiguadores, como lo son los modelos reológicos de Maxwell y de Kelvin-Voigt. Los modelos mencionados anteriormente son propuestos inicialmente por Fung [6] para su aplicación en la modelación de tejidos blandos. Sin embargo sólo se consideraban como aproximaciones teóricas, ya que estos modelos tradicionales presentan únicamente una caracterización parcial o descriptiva del fenómeno. Los mismos han sido modificados usualmente a partir de los modelos clásicos agregando más elementos en serie o paralelo al original, logrando una mejor caracterización del comportamiento mecánico.

El problema derivado de realizar esta adición de elementos es que se aumenta considerablemente la complejidad del modelo haciendo poco conveniente su uso.

Sin embargo en los últimos años un antiguo concepto con novedosas aplicaciones, el cálculo fraccional, ha sido utilizado en la modelación y caracterización de materiales viscoelásticos, principalmente los polímeros.

Al parecer la viscoelasticidad es el campo de mayor aplicación de los operadores diferenciales e integrales fraccionales... se demuestra que el uso de derivadas fraccionales para el modelado matemático de materiales viscoelásticos resulta natural... Podlubny [7]

También existen una serie de investigaciones orientadas a la caracterización de los efectos mecánicos en los tejidos biológicos blandos empleando modelos fraccionales viscoelásticos como lo son: el utilizado en tejido extraído del hígado [8] , la determinación del comportamiento mecánico del tejido graso empleando núcleos derivativos [9] o el del tejido cerebral [10] a partir de los modelos clásicos agregando un nuevo elemento fraccional conocido como spring-pot , cuya derivada es de orden no entero y se encuentra para dichos modelos entre cero y uno [11] .

A su vez los modelos viscoelásticos de orden fraccional son empleados en la obtención de los cambios de las propiedades mecánicas de tejidos blandos para la detección temprana de diversas situaciones patológicas, principalmente el cáncer de próstata [12] , donde el papel de la determinación del orden fraccional en el modelo juega un rol sumamente importante debido a que la exactitud del mismo está directamente asociado con la certeza del procedimiento. Por lo que en diversas investigaciones se desarrollan metodologías en función de su adecuada obtención [13]  ;  [14] .

2. Cálculo fraccional

El origen del cálculo fraccional data desde el mismo fundamento del cálculo diferencial [7] cuando en una carta enviada a Leibniz el 30 de Septiembre de 1695 en la que L’Höpital le cuestiona el significado que tendría su notación desarrollada para la n-ésima derivada ${\textstyle {\frac {d^{n}y}{dx^{n}}}}$ , el qué sucedería en el caso ${\textstyle n={\frac {1}{2}}}$ , a lo que Leibniz le responde:

“Usted puede ver por eso señor que uno puede expresar por una serie infinita una cantidad como ${\textstyle {\frac {d^{1/2}y}{dx^{1/2}}}}$ . Aunque las series infinitas y geométricas son relaciones distantes, las series infinitas admiten sólo el uso de exponentes que son enteros, no hace todavía el uso de exponentes fraccionarios... esto conduciría a una paradoja, de la que algún día se extraerán consecuencias útiles”

2.1. La derivada fraccional definida en ${\textstyle {\mathbb {R} }^{+}}$2.1. La derivada fraccional definida en R + {\textstyle {\mathbb {R} }^{+}}

El operador diferencial local de la derivada de orden n para una variable independiente t   , ${\textstyle D_{t}^{n}={\frac {d^{n}}{dt^{n}}}}$ es solamente el operador inverso por la izquierda del operador integral no local del n   -campo integral ${\textstyle {}_{a}I_{t}^{n}}$ teniendo como punto de inicio cualquier valor a  < t   . De hecho, para cualquier función continua con derivada continua, es decir, ${\textstyle f(t)\in {\mbox{   }}C^{2}}$ se reconoce:

$D_{t}^{n}{\mbox{   }}\circ {\mbox{   }}{}_{a}I_{t}^{n}{\mbox{   }}f(t)=$$f(t),\quad t>a,$

( 1)

y

${}_{a}I_{t}^{n}{\mbox{   }}\circ {\mbox{   }}D_{t}^{n}{\mbox{   }}f(t)=$$f(t)-\sum _{k=0}^{n-1}f^{\left(k\right)}(a^{+}){\frac {{\left(t-a\right)}^{k}}{k!}},\quad t>a.$

( 2)

donde f^{(k )} (a⁺ ) es la k -ésima derivada de la función f evaluada en a por la derecha. Como consecuencia de esto, tomando a  = 0 se requiere que ${\textstyle {}_{0}D_{t}^{\alpha }}$ sea definida como inversa por la izquierda   de ${\textstyle {}_{0}I_{t}^{\alpha }}$ . Para dicho propósito primero se introduce el número entero:

$m\in \mathbb {N} \quad tal{\mbox{   }}que\quad m-$$1<\alpha <m$

y entonces se define la derivada fraccional de Riemann-Liouville de orden α  > 0:

${}_{0}D_{t}^{\alpha }f(t)=D_{t}^{m}{\mbox{   }}\circ {\mbox{   }}{}_{0}I_{t}^{m-\alpha }{\mbox{   }}f(t),{\mbox{   }}con,{\mbox{   }}m-$$1<\alpha <m,$

( 3)

como:

${}_{0}D_{t}^{\alpha }f(t)={\frac {1}{\Gamma \left(m-\alpha \right)}}{\frac {d^{m}}{dt^{m}}}{\int }_{0}^{t}{\frac {f(\tau )d\tau }{{\left(t-\tau \right)}^{\alpha +1-m}}},$

( 4)

$si\quad m-1<\alpha <m\quad y\quad {\frac {d^{m}}{dt^{m}}}f(t),\quad si\quad \alpha =$$m$

para complementar la definición de la derivada se tiene que ${\textstyle {}_{0}D_{t}^{0}=I.}$ Donde Γ(x ) es la función Gamma la cual se emplea como una generalización del factorial para el caso donde x no es un número entero.

Intercambiando en la ecuación (3) el proceso de derivación e integración, se llega a la conocida definición de la derivada fraccional de Caputo , tratada de forma extensa en [15] , de orden α  > 0 definida como:

${}_{0}^{\ast }D_{t}^{\alpha }f(t)={}_{0}I_{t}^{m-\alpha }\circ {\mbox{   }}D_{t}^{m}{\mbox{   }}{\mbox{   }}f(t),{\mbox{   }}con,{\mbox{   }}{\mbox{   }}m-$$1<\alpha <m,$

( 5)

donde:

${}_{0}^{\ast }D_{t}^{\alpha }f(t)={\frac {1}{\Gamma \left(m-\alpha \right)}}{\int }_{0}^{t}{\frac {f^{\left(m\right)}(\tau )}{{\left(t-\tau \right)}^{\alpha -m+1}}}d\tau ,$

( 6)

$si\quad m-1<\alpha <m\quad y\quad {\frac {d^{m}}{dt^{m}}}f(t),\quad si\quad \alpha =$$m$

Para ${\textstyle \alpha \not \in \mathbb {Z} }$ la definición de Caputo, ecuación (5) , se requiere que la m -ésima derivada de f (t ) sea absolutamente integrable y no solamente por partes.

2.2. La transformada de Laplace para derivadas fraccionales

Cabe señalar que resulta de mayor utilidad la definición de derivada fraccional de Caputo en aquellos problemas propios de la física y la ingeniería donde se utilizan condiciones iniciales las cuales se encuentran expresadas en términos de derivadas de orden entero. Esto puede ser visualizado fácilmente mediante el uso de la transformada de Laplace, misma que requiere en su definición de transformada de una derivada, de las condiciones iniciales las cuales están dadas en términos de derivadas de orden entero. De hecho, análogamente a la definición para la transformada de una derivada de orden entero, para la derivada de Caputo de orden α con m  − 1 < α  ≤ m , se tiene:

$L\lbrace {}_{0}^{\ast }D_{t}^{\alpha }{\mbox{   }}f(t);s\rbrace =$$s^{\alpha }{\tilde {f}}(s)-\sum _{k=0}^{m-1}s^{\alpha -1-k}f^{\left(k\right)}(0^{+}),$

( 7)

donde

$f^{\left(k\right)}(0^{+})={\underset {t\rightarrow 0^{+}}{lim}}{\mbox{   }}D_{t}^{k}f(t)$

para la cual ${\textstyle L\left\{;s\right\}}$ es el operador de Laplace, y ${\textstyle {\tilde {f}}(s)}$ es la transformación de la función f (t ) del dominio del tiempo al de la frecuencia. Sin embargo cuando las condiciones iniciales son cero, la ecuación (7) , se reduce a:

$L\lbrace {}_{0}^{\ast }D_{t}^{\alpha }{\mbox{   }}f(t);s\rbrace =$$s^{\alpha }{\tilde {f}}(s),\quad m-1<\alpha <m$

( 8)

La transformada de Laplace puede ser expresada en términos de las funciones de Mittag-Leffler, en particular

$L\left\{t^{\beta -1}E_{\alpha ,\beta }(-\lambda t^{\alpha });s\right\}=$${\frac {s^{\alpha -\beta }}{s^{\alpha }+\lambda }}$

( 9)

donde

$E_{\alpha ,\beta }(-\lambda t^{\alpha })=\sum _{n=0}^{\infty }{\frac {{\left(-\lambda t^{\alpha }\right)}^{n}}{\Gamma (\alpha n+\beta )}}$

( 10)

con ${\textstyle \alpha ,\beta \in {\mathbb {R} }^{+}}$ y ${\textstyle \lambda \in \mathbb {R} }$ . E_{α ,β} (− λt^α ) es la función de dos parámetros de Mittag-Leffler, la cual surge como una generalización de la función exponencial.

3. Modelo viscoelástico de Zener

El modelo viscoelástico de Zener consiste en una adecuación fraccional del sólido lineal estándar (SLS por sus siglas en inglés) [16] . Para lograr obtener la versión fraccional es necesario que se reemplace la derivada de primer orden por la derivada fraccional de orden α  ∈ (0, 1) en su ecuación constitutiva. De aquí se obtienen las siguientes relaciones de esfuerzo deformación:

$\left[1+a_{1}{\mbox{   }}{}_{0}^{\ast }D_{t}^{\alpha }\right]\sigma (t)=$$\left[m+b_{1}{\mbox{   }}{}_{0}^{\ast }D_{t}^{\alpha }\right]\epsilon (t)$

( 11)

donde σ (t ) es el esfuerzo, ϵ (t ) es la deformación y a₁ , b₁ , m son constantes del modelo relacionadas con los coeficientes de elasticidad y viscosidad.

La teoría de la viscoelasticidad establece una relación entre el esfuerzo y la deformación a través del módulo de relajación a los esfuerzos G (t ) y el de fluencia J (t ) de la siguiente manera:

$\sigma (t)={\int }_{-\infty }^{t}G(t-\xi ){\frac {d\epsilon (\xi )}{d\xi }}d\xi$

( 12)

y

$\epsilon (t)={\int }_{-\infty }^{t}J(t-\xi ){\frac {d\sigma (\xi )}{d\xi }}d\xi$

( 13)

donde ξ es una variable de convolución. En el caso del modelo de Zener el módulo de fluencia tiene la forma:

$J(t)={\frac {a_{1}}{b_{1}}}+\left({\frac {1}{m}}-{\frac {a_{1}}{b_{1}}}\right)\left[1-\right.$$\left.E_{\alpha ,1}\left[-{\left(m{\mbox{   }}t/b_{1}\right)}^{\alpha }\right]\right]$

( 14)

y el módulo de relajación a los esfuerzos se define como:

$G(t)=m+\left({\frac {b_{1}}{a_{1}}}-m\right)E_{\alpha ,1}\left[-\right.$$\left.{\left(t/a_{1}\right)}^{\alpha }\right]$

( 15)

además sustituyendo en la ecuación (12) , es posible obtener el módulo complejo en el dominio de la frecuencia

$E^{\ast }(s)={\frac {{\tilde {\sigma }}(s)}{{\tilde {\epsilon }}(s)}}=$${\frac {m+b_{1}s^{\alpha }}{1+a_{1}s^{\alpha }}}$

donde E^* (s ) es el módulo complejo y se compone de las contribuciones de la parte elástica y la parte viscosa a la deformación.

4. Resultados

Utilizando la definición de la transformada de Laplace para derivadas fraccionales, ecuación (7) y la de la función de dos parámetros de Mittag-Leffler, ecuación (9) , se obtiene:

$\epsilon (t)=\left[{\frac {t^{\alpha -1}}{b_{1}}}E_{\alpha ,\alpha }\left(-\right.\right.$$\left.\left.\lambda t^{\alpha }\right)+{\frac {a_{1}}{b_{1}t}}E_{\alpha ,0}\left(-\right.\right.$$\left.\left.\lambda t^{\alpha }\right)\right]\ast \sigma (t)$

( 16)

donde ${\textstyle \lambda ={\frac {m}{b_{1}}}}$ .

Desarrollando los tres primeros términos de las sumatorias para la definición de las funciones de Mittag-Leffler, ecuación (10) , se obtiene:

$E_{\alpha ,\alpha }\left(-{\frac {m}{b_{1}}}t^{\alpha }\right)=$${\frac {1}{\Gamma (\alpha )}}-{\frac {mt^{\alpha }}{b_{1}\Gamma (2\alpha )}}+$${\frac {m^{2}t^{2\alpha }}{b_{1}^{2}\Gamma (3\alpha )}}$

y

$E_{\alpha ,0}\left(-{\frac {m}{b_{1}}}t^{\alpha }\right)=$$t\delta (t)-{\frac {mt^{\alpha }}{b_{1}\Gamma (\alpha )}}+$${\frac {m^{2}t^{2\alpha }}{b_{1}^{2}\Gamma (2\alpha )}}$

donde δ (t ) es la función delta de Dirac y la introducción de la misma permite evadir la singularidad ocasionada por el segundo parámetro en la función de Mittag-Leffler. Aplicando la transformada de Laplace para la operación de convolución,

$L\left\{f(t)\ast g(t);s\right\}={\tilde {f}}(s)\cdot {\tilde {g}}(s)$

Es posible obtener una solución analítica de la deformación experimentada, bajo la aplicación de una función de tensión temporal [17] .

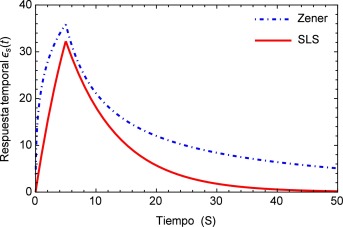
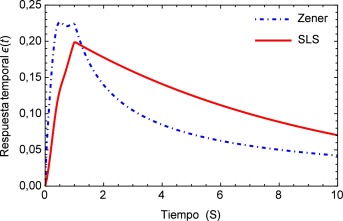
Sea ϵ_s (t ) la respuesta temporal correspondiente a una función escalón unitario σ_s (t ) utilizada como la fuerza aplicada de manera temporal a la que está sometida la arteria, es posible obtener para el modelo de Zener, ecuación (16) , la respuesta de deformación. La misma se muestra en la figura 1 para los valores de los parámetros a₁ =5.4871, b₁ =5.8712, m =0.68 y α =0.408.

Figura 1. Modelo fraccional viscoelástico de Zener comparado con el modelo clásico del sólido lineal estándar.

Como es de esperarse, la solución del modelo de Zener exhibe el clásico comportamiento material que presentan los tejidos blandos, al ser estos materiales viscoelásticos. Donde la deformación en relación con la aplicación de la carga se presenta de manera no lineal mostrando una tendencia hacia los materiales considerados como fluidos viscosos. Sin embargo en la segunda etapa cuando la fuerza cesa en su aplicación, se muestra un estado de relajación, el cual es propio de los materiales viscoelásticos. Comparado con el modelo SLS el cual presenta a partir del momento donde se aplica inicialmente la carga un comportamiento elástico clásico es decir casi lineal y un tiempo de relajación más breve que el presentado por el modelo de Zener. Estas características del modelo de Zener, resultan sumamente favorables dado que el mismo se utilizará para simular los efectos mecánicos en un tejido blando, particularmente un segmento de arteria.

Los parámetros mecánicos que se utilizan en la presente investigación son los mismos que los obtenidos por Craiem et al [18] empleando un experimento de relajación a los esfuerzos, este se realiza sobre segmentos de arteria extraídos de cuatro pacientes. El mismo consiste en aplicar una carga cíclica periódica sobre el segmento de arteria y al cesar su aplicación se miden los tiempos que tarda en regresar a su estado tensorial original.

Se elige al primer paciente en el nivel de esfuerzo mecánico bajo debido a que la geometría de la arteria con la que se cuenta se construyó a partir de imágenes médicas obtenidas mediante un TAC para un paciente de 37 años de edad y estos parámetros son los que más se aproximan a las condiciones reales.

Como señalan los autores, estos no encontraron variaciones significativas entre los valores de las constantes mecánicas para los pacientes entre los dos modelos que emplearon, sin embargo si identificaron variaciones entre los valores de α[19] , este último valor representa el orden de la derivada fraccional. Por esta razón se decidió realizar un ajuste sobre el valor de α , para determinar si este resultado es aquel que mejor se aproxima al conjunto de datos o si se debía considerar un nuevo valor del orden fraccionario y que implicaciones se derivan de realizar dicho ajuste.

La determinación del orden fraccional se realiza mediante la implementación de un algoritmo basado en el método numérico de Levenberg-Marquardt para ajuste de curvas mediante mínimos cuadrados para modelos no lineales, aproximando la función de relajación a los esfuerzos G (t ) a un conjunto de puntos experimentales obtenidos en [19] .

Los resultados obtenidos se muestran en el tabla (1 ) donde es posible observar que incrementando el número de datos utilizados en el método numérico se obtienen valores cercanos a 0.4, mismo que se encuentra dentro de los rangos adecuados para tejidos blandos como se muestra en diversos estudios, por ejemplo los de Craiem et al [20] que oscilan alrededor de 0.2 para el caso de un segmento de arteria, pero más cercanos a los presentados por Nagehan y Ergin [21] para otros tejidos blandos. Este valor de α indica que el material tiene características predominantes del tipo elástico al estar por debajo de 0.5, pero con una etapa de fluido viscoso al identificarse claramente el fenómeno de relajación a los esfuerzos, cuando la carga es retirada.

Tabla 1. Relación entre el número de puntos de control utilizados al momento de implementar el método numérico, el valor que se obtiene para α y la calidad de la aproximación en términos de la desviación estándar de la curva obtenida contra la experimental.

Cantidad de datos utilizados	Valor obtenido de α	Desviación estándar
450	0.2132	0.0048
900	0.2336	0.0034
1,800	0.2542	0.0015
4,500	0.2813	0.0004
4,500,000	0.4026	0.0001
45,000,000	0.4081	0.00003

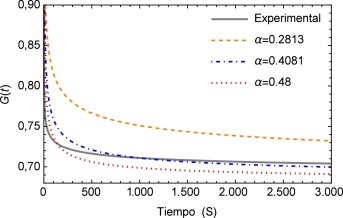
A continuación en la figura 2 se muestra un gráfico en el cual se presentan los distintos valores de α para el ajuste del modelo de Zener, resulta conveniente mencionar que a partir del valor α =0.4081 la aproximación aumenta su desviación estándar, es decir comienza a alejarse del mínimo absoluto en la regresión. Además se observa que a pesar de que el rango en el que se mueve la función es relativamente pequeño (0.72 ∼ 0.77), el ajuste propuesto inicialmente en la investigación de la cual se obtuvieron los parámetros dista considerablemente del nuevo valor de α propuesto. Y al estar trabajando con un sistema dinámico, es necesario tener en consideración el como se afecta la precisión del mismo, ya que el sistema puede tener un respuesta sensible a las condiciones iniciales, como se muestra adelante en este estudio.

Figura 2. Aproximación de la función de relajación a los esfuerzos G (t ) para diversos valores de α y la curva obtenida de manera experimental.

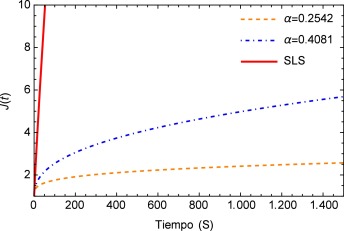
Por otra parte el módulo de fluencia J (t ) es comúnmente utilizado en experimentos donde se mantiene de forma constante el esfuerzo y se registran los diferenciales de la deformación en función del tiempo.

Los materiales viscoelásticos presentan un comportamiento variado, el mismo debe ser cuadrático en pequeños intervalos de tiempo y lineal en tiempos mayores, esta función se muestra en la figura 3 . Aquí se puede apreciar inicialmente el comportamiento lineal que proporciona el modelo de orden entero y la notable diferencia entre los valores de α donde se puede apreciar como para el valor de α =0.2542 el módulo de fluencia entra rápidamente en el estado lineal lo cual no sucede para el valor de α =0.4081.

Figura 3. Representación gráfica del módulo de fluencia.

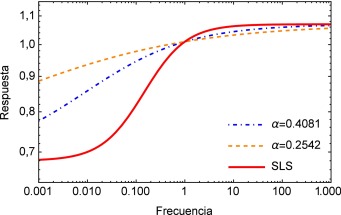
Como se mencionó anteriormente, el módulo complejo es el vector obtenido como suma de las contribuciones de los módulos elástico (parte real) y viscoso (parte imaginaria), en la figura 4 se muestra el módulo complejo en el dominio de la frecuencia s . Una vez más se puede apreciar la diferencia entre la respuesta obtenida para el modelo de orden entero y los de orden fraccional donde para estos últimos también es posible apreciar una considerable diferencia para bajas frecuencias.

Figura 4. Se muestra el módulo complejo E* (s ) para dos valores α del modelo de Zener y él obtenido para el SLS.

Es importante mencionar que es a partir del módulo complejo que se obtienen los parámetros en el dominio de la frecuencia, los cuales son introducidos en un software especializado para el cálculo mediante elementos finitos, para la obtención de la distribución de esfuerzos en el segmento de arteria.

Por último se desea determinar cuál es la respuesta temporal de deformación para la arteria a partir de la aplicación de una serie de pulsos sanguíneos tal como sucede en la realidad. Primeramente se construye una función que asemeje el pulso con las fases de sístole (contracción) y diástole (relajación), descripciones del flujo arterial pueden ser consultadas en [22] .

La función que simula el efecto del pulso sanguineo se describe a continuación:

$p(t)={\begin{array}{l}12.6cos(3.79t)-3.4cos(10.82t)+\\20.1sin(1.97t)+1.3sin(12.11t)\end{array}}$

( 17)

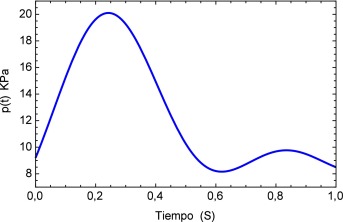
y la forma del pulso se muestra en la figura 5 .

Figura 5. Se muestra la representación gráfica de la función de pulso de 120/80 mmHg convertida a pascales y compuesta básicamente de las dos etapas del mismo.

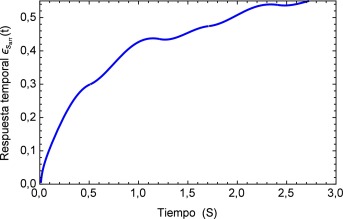
Para este pulso unitario se obtiene la respuesta temporal del segmento de arteria, el mismo se muestra en la figura 6 . Aquí es posible apreciar la precisión que presenta el modelo fraccional en comparación con el del SLS, en el tiempo inicial se observa el efecto del pulso con sus etapas para el modelo de Zener y en cambio para el SLS esta etapa se refleja en dos estados casi lineales, para después caer en un estado de relajación nuevamente lineal. A diferencia del fraccional donde existe una caída no lineal y un estado pronunciado de relajación.

Figura 6. Respuesta temporal del pulso unitario.

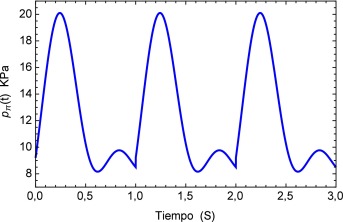
Sin embargo es de sumo interés determinar los efectos del pulso como una sucesión de los mismos por lo que se genera una función periódica p_π (t ), la cual se muestra en la figura 7 para los tres primeros períodos.

Figura 7. Representación gráfica del tren de pulsos, que simulan el pulso sanguíneo presente habitualmente en la arteria.

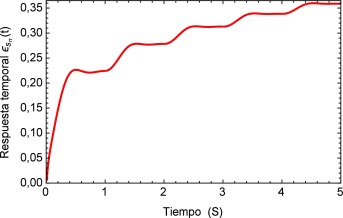
Aplicando el método numérico de Gauss-Kronrod en la solución de las integrales presentes en el proceso de convolución es posible obtener la respuesta temporal de la aplicación del tren de impulsos, la misma que se muestra en la figura 8 para su estado inicial, y para tiempos prolongados en la figura 9 . Se puede observar en principio una zona de inestabilidad, pero alrededor de los cinco segundos se presenta una zona de oscilación que muestra básicamente la relación de tensión y deformación de interés en la investigación. Se debe tener en cuenta, como se mencionó anteriormente, que debido al uso de la definición de la transformada de Laplace para la derivada fraccional de Caputo, se requiere que las condiciones iniciales del sistema sean definidas para órdenes enteros de las derivadas. Con la finalidad de simplificar el sistema, las condiciones iniciales se toman como nulas. De aquí se concluye que la dinámica del sistema entra en un estado estable y este permanecería así de no retirar el estímulo sobre el mismo, figura 10 .

Figura 8. Representación gráfica de la respuesta temporal en su estado inicial.

Figura 9. Representación gráfica de la respuesta temporal al tren de pulsos que simulan el flujo sanguíneo presente en el segmento de arteria.

Figura 10. Representación gráfica de la respuesta temporal en la zona estable.

Ahora el segmento de arteria será sometido a una carga “inusual” simulando un proceso de arritmia [23]  ;  [24] el cual se compone de un pulso inicial en el que antes de haber terminado su período se presenta un nuevo pulso lo cual genera un traslape entre los dos. Este se define como p_aπ (t ) donde los pulsos tienen una misma frecuencia pero distinta amplitud. La simulación del fenómeno se muestra en la figura 11

Figura 11. Tren de pulsos simulando el efecto de una arritmia

A diferencia de la estabilidad mostrada en el caso anterior, para el presente tren de impulsos con diferente amplitud se tiene una zona de inestabilidad que tiende aumentar a lo largo del tiempo, esto se muestra en la figura 12 .

Figura 12. Respuesta temporal inicial al tren de pulsos con diferentes amplitudes.

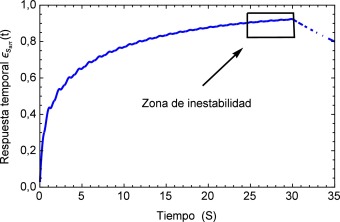
Inicialmente se muestra una zona de inestabilidad, la cual sobrepasa el estado de deformaciones del pulso regular en menos de tres segundos, sin embargo a partir del tiempo t  = 5 el sistema debería comenzar a estabilizarse, cosa que no sucede. Después del tiempo inicial continuá un estado creciente donde al cabo de 20 segundos prácticamente se duplica la magnitud de la deformación. Es claro que este fenómeno fisiológicamente no es posible, debido a que de presentarse esta condición por un período de tiempo similar se hubiese producido un infarto. Ver figura 13 .

Figura 13. Respuesta temporal al tren de pulsos con diferentes amplitudes, se puede observar como a diferencia del primer estado, aquí no se presenta una zona de estabilidad del sistema dinámico.

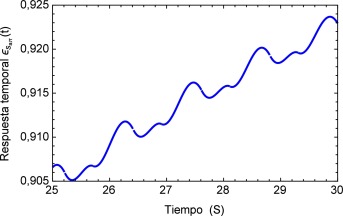
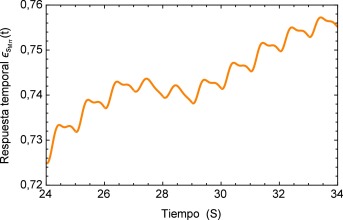
Realizando un acercamiento a la zona de inestabilidad señalada en la figura 13 , se genera la figura 14 donde se puede observar el comportamiento repetitivo de la respuesta temporal al flujo que simula el proceso de arritmia y nuevamente es posible visualizar la sensibilidad que presenta el modelo fraccional al reproducir este efecto.

Figura 14. Acercamiento a la zona de inestabilidad.

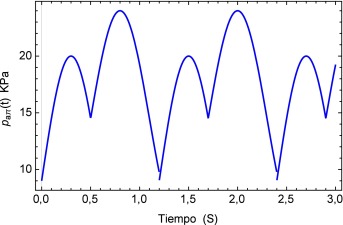
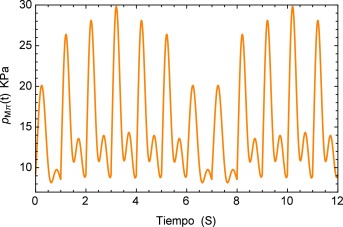
Para concluir se analiza el cambio en el flujo común provocado por un dispositivo de ventilación mecánica descrito en [25] donde se detectan picos de presión en conjunto con un desplazamiento oscilatorio de la señal en la aorta. La representación del flujo sanguíneo de la presión se describe en la figura 15 .

Figura 15. Cambio en la presión sanguínea ocasionado por la asistencia de un respirador mecánico.

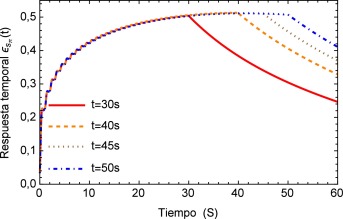
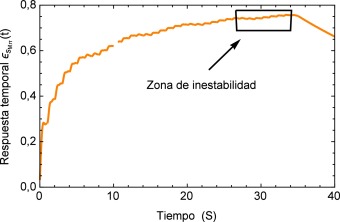
La respuesta del sistema es similar a la presentada por el efecto de arritmia donde al igual que esta última se tiene una respuesta temporal que sobrepasa los límites presentados por el flujo normal de 120/80 mmHg y donde también se observa un efecto no transitorio de oscilaciones con una pendiente creciente. Para fines de la investigación este efecto se prolonga en un tiempo t  = 40s , sin embargo en la realidad este fenómeno sólo se presenta durante breves intervalos de tiempo en el proceso de ventilación mecánica. La respuesta a este comportamiento se describe en la figura 16 .

Figura 16. Respuesta temporal al flujo ocasionado por un respirador mecánico.

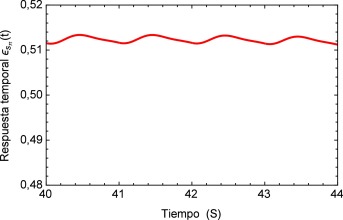
Realizando un acercamiento a la zona de interés, figura 17 , se observa nuevamente el comportamiento creciente y oscilatorio que se presenta en la respuesta del sistema dinámico, donde también se logra apreciar la sensibilidad que presenta el modelo fraccional en lo concerniente a la precisión que se tiene en la caracterización de la respuesta al lograr reproducir los efectos más mínimos oscilatorios.

Figura 17. Acercamiento a la zona de interés.

5. Conclusiones

Se comprobó la utilidad del modelo de Zener y por añadidura el del cálculo fraccional en la modelación de tejidos blandos particularmente en un segmento de arteria, los cuales se caracterizaron a través de un modelo constitutivo que obedece las leyes del material viscoelástico.

Se determinó el orden de la derivada fraccionaria que mejor ajusta el modelo aquí aplicado al conjunto de datos, obteniendo un valor que si bien se aproxima a las investigaciones realizadas actualmente por Craiem [18] para las arterias, este es aún más cercano al reportado por Magin y Nagehan [21]  ;  [26] para otros tipos de tejidos blandos. Se comprobó la importancia de la precisión en la determinación del orden fraccional debido a las diferencias que se presentan entre ambos valores de α a pesar de la cercanía de los valores del orden fraccional.

Se aplicaron una serie de pulsos de entrada al modelo, obteniéndose respuestas que dejan ver una dinámica compleja del sistema de ecuaciones diferenciales y una sensibilidad en los cambios en las condiciones iniciales. Esto lleva a pensar en un análisis propio de la dinámica del sistema y explorar en esta dimensión fractal la viabilidad del caos, como se hace referencia en los artículos de Magin y Awrejcewicz [26]  ;  [27] . Si bien el modelo de Zener presenta ventajas sobre el de orden entero, este aún resulta limitado ya que en el mismo no se consideran los efectos metabólicos presentes en el cuerpo humano, lo que genera una reconstitución y modificación mecánica del material. De igual manera es necesario escalar este sistema unidimensional a un sistema tridimensional que permita caracterizar los efectos de anisotropía presente en la mayor parte de los materiales biológicos, así como la posibilidad de generar una subrutina de elementos finitos que incluya la formulación fraccional como la desarrollada por Agrawal [28] y no solamente se incluya a partir de la obtención de parámetros del dominio de la frecuencia como en el caso de esta investigación.

Agradecimientos

Los autores agradecen el apoyo otorgado por el Tecnológico Nacional de México, el Instituto Tecnológico Superior de Cajeme. Al grupo de biomecánica perteneciente al Instituto Superior Politécnico José Antonio Echeverría de la Habana, Cuba.

References

1. [1] A. Ikbal; Viscoelastic blood flow through arterial stenoses - effect of various viscosity; International Journal of Nonlinear Mechanics, 47 (2012), pp. 888–894
2. [2] C. Martin, W. Sun, T. Pham, J. Elefteriades; Predictive biomechanical analysis of ascending aortic aneurysm rupture potential; Acta biomaterialia, 9 (12) (2013), pp. 9392–9400
3. [3] J. Córdova, J. Barriguete, A. Lara, S. Barquera, et al.; Las enfermedades crónicas no transmisibles en méxico: sinopsis epidemiológica y prevención integral; salud pública de méxico, 50 (5) (2008), pp. 419–427
4. [4] F. Pérez, E. Rodilla, J. Costa, J. Pascual; Presión arterial central y lesión vascular; Medicina Clínica (10) (2014), pp. 534–570
5. [5] W. Maurel, Y. Wu, N. Magnenat, D. Thalmann; Biomechanical Models for Soft Tissue Simulation (ESPRIT Basic Research Series), 1998 Edition; Springer (2013)
6. [6] Y. Fung; Biomechanics: mechanical properties of living tissues; Springer (1981)
7. [7] I. Podlubny; Fractional differential equations, Vol. 198 of Mathematics in Science and Engineering; Academic Press (1999)
8. [8] C. Wex, C. Bruns, A. Stoll; Fractional kelvin-voight model for liver tissue in the frequency and time domain; Scottish Journal of Arts, Social Sciences and Scientific Studies, 21 (1) (2014), pp. 69–78
9. [9] A. Freed, K. Diethelm; Fractional calculus in biomechanics: a 3d viscoelastic model using regularized fractional derivative kernels with application to the human calcaneal fat pad; Biomechanics and modeling in mechanobiology, 5 (4) (2006), pp. 203–215
10. [10] G. Davis, M. Kohandel, S. Sivaloganathan, G. Tenti; The constitutive properties of the brain paraenchyma: Part 2. fractional derivative approach; Medical engineering & physics, 28 (5) (2006), pp. 455–459
11. [11] M. Bulíček, P. Kaplick`y, M. Steinhauer; On existence of a classical solution to a generalized kelvin-voigt model; Pacific Journal of Mathematics, 262 (1) (2013), pp. 11–33
12. [12] J. Palacio, S. Hammer, D. Good, S. McNeill, et al.; Quantitative diagnostic soft tissue through viscoelastic characterization using time-based instrumented palpation; Journal of the Mechanical Behavior of Biomedical Materials, 12 (41) (2015), pp. 149–160
13. [13] C. Ingo, R. Magin, T. Parrish; New insights into the fractional order diffusion equation using entropy and kurtosis; Entropy, 12 (16) (2014), pp. 5838–5852
14. [14] F. Meral, T. Royston, R. Magin; Fractional calculus in viscoelasticity: An experimental study; Commun. Nonlinear Sci. Numer. Simulat., 4 (15) (2010), pp. 939–945
15. [15] M. Caputo; Diffusion with space memory modelled with distributed order space fractional differential equations; Annals of Geophysics, 46 (2) (2003), pp. 121–130
16. [16] S. Bentil, R. Dupaix; Exploring the mechanical behavior of degrading swine neural tissue at low strain rates via the fractional zener constitutive model; Journal of the Mechanical Behavior of Biomedical Materials, 30 (2014), pp. 83–90
17. [17] J. Palomares-Ruiz, M. Rodriguez-Madrigal, J. Castro-Lugo, A. Rodriguez-Soto; Fractional viscoelastic models applied to biomechanical constitutive equations; Revista Mexicana de Física, 12 (58) (2015), pp. 348–352
18. [18] D.O. Craiem, F.J. Rojo, J.M. Atienza, G.V. Guinea, et al.; Fractional calculus applied to model arterial viscoelasticity; Latin American Applied Research (38) (2008), pp. 141–145
19. [19] D.O. Craiem, F.J. Rojo, J.M. Atienza, R.L. Armentano, et al.; Fractional-order viscoelasticity applied to describe uniaxial stress relaxation of human arteries; Physics in Medicine and Biology (53) (2008), pp. 4543–4554
20. [20] D.O. Craiem, R.L. Armentano; A fractional derivative model to describe arterial viscoelasticity; Biorheology (44) (2007), pp. 251–263
21. [21] D. Nagehan, T. Ergin; Non-integer viscoelastic constitutive law to model soft biological tissues to in-vivo indentation; Acta of Bioengineering and Biomechanics (4) (2014), pp. 13–21
22. [22] D. Jodko, D. Obidowski, P. Reorowicz, K. Jóźwik; Simulations of the blood flow in the arterio-venous fistula for haemodialysis; Acta of Bioengineering and Biomechanics, 16 (1) (2014), pp. 69–74
23. [23] S. Kumar, H. Inbarani; Modified soft rough set based ecg signal classification for cardiac arrhythmias; A.E. Hassanien, A.T. Azar, V. Snasael, J. Kacprzyk, J.H. Abawajy (Eds.), Big Data in Complex Systems, Vol. 9 of Studies in Big Data, Springer International Publishing (2015), pp. 445–470
24. [24] A. Caillard, E. Gayat, A. Tantot, G. Dubreuil, et al.; Comparison of cardiac output measured by oesophageal doppler ultrasonography or pulse pressure contour wave analysis; British Journal of Anaesthesia, 114 (6) (2015), pp. 893–900
25. [25] F. Michard; Changes in arterial pressure during mechanical ventilation; Anesthesiology, 103 (2) (2005), pp. 419–428
26. [26] R. Magin; Fractional calculus models of complex dynamics in biological tissues; Computers and mathematics with applications (59) (2010), pp. 1586–1593
27. [27] J. Awrejcewicz, V. Krysko, I. Papkova, A. Krysko; Routes to chaos in continuous mechanical systems. part 1: Mathematical models and solution methods; Chaos, Solitons & Fractals (45) (2012), pp. 687–708
28. [28] O. Agrawal; A general finite element formulation for fractional variational problems; Journal of Mathematical Analysis and Applications, 12 (337) (2008), pp. 1–12