State estimation of electrical power systems based on optimal deployment of PMU considering contingencies

Resumen

El presente trabajo propone diseñar y aplicar un algoritmo de Estimador de Estado en los Sistemas Eléctricos, aplicando la metodología de los Mínimos Cuadrados Ponderados, mediante un proceso denominado estimador hibrido no lineal el mismo que utiliza las mediciones provenientes de las PMU y las mediciones convencionales, además, de encontrar las ubicaciones óptimas de PMU respetando las restricciones de observabilidad y redundancia para los Sistemas Eléctricos de Potencia, a través de la programación lineal entera mixta, considerando las contingencias N-1 en el SEP. El estimador de estado propuesto se ajusta a las mediciones obtenidas, ante la presencia de contingencias en el SEP. Las simulaciones que se obtienen como resultado de la implementación del estimador de estado hibrido, muestran que la propuesta mejoran la precisión del estimador y la velocidad de convergencia, considerando el mínimo error de mediciones del sistema y número de PMU colocadas en el Sistema de Potencia, luego de presentarse una contingencia, que pueden ser la salida de una PMU o la pérdida de una de las línea de transmisión del SEP.

Palabras Clave: Estimador de estado, PMU, mínimos cuadrados, ubicación óptima de PMU, sistemas eléctricos de potencia

Abstract

The present research proposes to design and apply a state estimator algorithm in electrical power systems, applying the Weighted Least Squares methodology, through a process called non-linear hybrid estimator, the same one that uses measurements from PMUs and conventional measurements. in addition, to find the optimal PMU locations respecting the observability and redundancy restrictions for the Electric Power Systems, through mixed integer linear programming, considering the N-1 contingencies in the SEP. The proposed state estimator is adjusted to the measurements obtained, in the presence of contingencies in the SEP. The simulations obtained as a result of the implementation of the hybrid state estimator show that the proposal improves the precision of the estimator and the speed of convergence, considering the minimum error of system measurements and the number of PMUs placed in the Power System, after a contingency occurs, which may be the departure of a PMU or the loss of one of the transmission lines of the SEP.

Keywords: State estimator, PMU, least squares, optimal PMU location, electrical power system

1. Introducción

El estimador de estado tiene como objetivo principal detectar, identificar y eliminar las mediciones y/o parámetros erróneos de los Sistemas Eléctricos de Potencia (SEP) y proporcionar el estado más probable del mismo [1], mediante un proceso que toma como entrada las mediciones del SEP y obtiene como salida las variables de estado (voltaje) del SEP. Hoy en día, la estimación del estado dinámico es una tarea crucial para el monitoreo y control de los sistemas eléctricos, particularmente después de una desconexión o pérdida de una línea de trasmisión, para realizar una operación restaurativa adecuada del sistema eléctrico [2]. En la actualidad se pueden encontrar varias investigaciones enfocadas en aspectos y metodologías de diferentes estimadores de estado, que van desde su formulación matemática, hasta los problemas para su implementación [3].

Los Estimadores de Estado (EE) requieren de toda la topología de red, parámetros de las líneas de transmisión, así como las mediciones provenientes de los sistemas de medición convencional SCADA, y de la Unidad de Medición Fasorial (PMU) [4] y se proponen la condición de estimar todos los fasores de voltaje de cada nodo del SEP, estas funciones se realizan en los centros de control modernos [5].

Los EE tradicionales utilizan las mediciones provenientes de los flujos de potencia e inyecciones de potencia real y reactiva, tomando en cuenta las mediciones de los fasores de las corrientes proveniente de las PMUs en la red; se puede plantear un esquema de Estimador de Estado Híbrido (EEH) con mediciones provenientes de las PMU y SCADA, debido a que no hay la cantidad suficiente de PMU instaladas en el sistema eléctrico [6].

Una de las formulaciones efectivas para solución de los EE tradicionales y EEH [7], es la metodología de los Mínimos Cuadrados Ponderados (WLS), el EEH considera las mediciones convencionales y fasoriales, los resultados demuestran que las simulaciones del algoritmo de EEH mejora en gran medida la precisión y obtienen un mejor comportamiento en comparación con el estimador de estado tradicional [8].

La determinación del comportamiento del SEP en tiempo real, basados en la medición de los diferentes parámetros eléctricos, es uno de los retos actuales que tienen los operadores del sistema de potencia [9], para lo cual se han desarrollado diferentes técnicas que usan la información obtenida por las PMU [10]. La presencia de contingencias genera dificultades en la velocidad de respuesta de los algoritmos estimadores de estado y errores por el cambio en la topología del sistema de eléctrico [11].

El trabajo de la PMU permite realizar, con gran precisión y velocidad, el análisis dinámico del estado del SEP, utilizando la técnica de estimación de fasores, este mecanismo es esencial para análisis e interpretación de los datos recopilados de manera correcta [12]. Por lo tanto, un proceso de estimación de fasores tiene mucha importancia en diseño de mecanismos de control y diversos sistemas de protección [13].

La tecnología de medición de sincrofasores tiende a convertirse en una tecnología madura con el despliegue de una gran cantidad de PMU en muchos sistemas eléctricos importantes en todo el mundo, en las últimas dos décadas [14] con las adecuadas redes de comunicaciones las mediciones recopiladas por las PMU, en diferentes ubicaciones del sistema, se sincronizan y se ajustan en el tiempo, para después combinarse y proporcionar una fotografía completa y precisa del SEP, en diferentes puntos y a grandes distancias logrando que se interconecten en tiempo real. Lo cual permite reaccionar, determinar y tomar acciones a los operadores del SEP, para mantener la continuidad y calidad del servicio [15], existen algunos obstáculos para utilizar los datos de la PMU en aplicaciones en tiempo real, de los cuales podemos mencionar: la necesidad de un software compatible con el Concentrador de datos Phasor Data Concentrator (PDC), para organizar los datos de las PMUs [16], además, la comunicación de ancho de banda para transmitir una gran cantidad de datos generados por las PMU ubicadas en diferentes sitios del sistema eléctrico. Las PMUs no se limitan solo a recolectar datos, además, tienen las funciones para la desconexión automática de elementos del SEP, considerando ciertas condiciones. Así mismo, los PDC permiten al Sistema de Monitores de Control y Protección (WAMPC), acoplarse a diferentes sistemas de control para mejorar la detección y resolución de fallas [17].

La PMU mide directamente los fasores de voltaje y corriente del nodo donde está instalado y los fasores actuales de las líneas que inciden en ese nodo. Por lo tanto, no es exigente instalar PMU en todos los nodos del SEP, para logar que el sistema sea completamente observable. Existen varios algoritmos para la ubicación óptima de PMU [18,19], para su selección de ubicación e instalación estratégicas y para que se realicen de manera inteligente, con un número máximo de mediciones disponibles que aumentan la observabilidad del sistema [20].

Desde los últimos años, algunas herramientas matemáticas directas como la programación lineal entera mixta (MILP), el algoritmo codicioso (voraz), así como varias técnicas no deterministas como algoritmo genético (GA), optimización de enjambre de partículas (PSO), etc. han sido utilizados ampliamente, para obtener una solución al problema de ubicación óptima de PMU [21].

La observabilidad de una o varias PMUs se refiere a la región en la cual se puede estimar confiablemente la capacidad de observación del sistema eléctrico [22,23], la cual puede reducirse si algunas PMUs dejan de estar disponibles, por lo cual se requiere maximizar la utilización de diferentes PMUs para mantener la observabilidad del sistema y la precisión bajo cualquier escenario de medición incompleto [24,25]. Debido a que los costos asociados (gestión, compilación de gran cantidad de datos de los sincrofasores) para la adquisición e instalación de PMU es elevado, la ubicación óptima de las PMUs es un papel crítico, la programación lineal entera mixta, es la más utilizada, para encontrar ubicaciones óptimas de PMU, para la completa observabilidad del sistema ante las contingencias que pueden presentarse en los sistemas eléctricos [26,27].

La presente investigación propone un modelo de Estimador de Estado, que utilice las mediciones tanto de los PMU y SCADA, con el cual, se pueda determinar el comportamiento del Sistema de Potencia con el menor error luego de una contingencia N-1 que pueden ser la salida de PMUs o pérdida de líneas de transmisión del SEP y mantener el número adecuado de PMU en el SEP. Con el objeto de verificar la precisión del EE ante la pérdida de las mediciones provenientes de las líneas de transmisión y las PMUs del SEP, se utilizó los modelos de prueba de la IEEE de 14, 30 y 118 barras.

El trabajo consta de cinco secciones, que se detallan a continuación. Sección 1: introducción, Sección 2: metodología para la ubicación óptima de PMU, Sección 3: Estimador de Estado, tomando en cuenta las mediciones convencionales y las provenientes de los PMU, la Sección 4 presenta las gráficas obtenidas de las simulaciones, ante las contingencias que pueden presentarse en el SEP y los beneficion de la implementación del estimador de estado híbrido y para finalizar en la sección 5 se detallan las conclusiones obtenidas del presente trabajo.

2. Ubicación óptima de PMU

La observabilidad de los SEP se fundamentan en las Leyes de Ohm y Kirchhoff, mediante tres reglas, directa, indirecta y la calculada, con las cuales se puede obtener los fasores de corriente y voltaje en todos los nodos del sistema [27].

Para el despliegue óptimo de PMU en el SEP, se debe construir como paso inicial, la matriz cuadrada $nxn$ de conectividad (CM), la misma que varía según la topología de la red, para cada SEP [26,27]

$CM_{nxn}=\left\lbrace {\begin{matrix}{0}&{\hbox{si}}~i=~j\\1&{\hbox{si nodos estan conectados}}\\0&{\hbox{otro caso}}\end{matrix}}\right.$

(1)

donde $i$ son los nodos de salida, y $j$ los nodos de llegada.

2.1 Ubicación óptima de PMU considerando la observabilidad del SEP

Con el fin de minimizar el número de PMU a ser ubicadas, se describe la función objetivo en la ec.(2), tomando en cuenta las restricciones de redundancia y observabilidad, descritas en las restricciones; la ec.(3) indica que al menos una PMU se encuentra instalada en el SEP; la ec.(4) mantiene al máximo la redundancia del SEP y la ec.(5) restringe al 100 % la observabilidad del sistema.

FO:

$\min _{nPMU}\sum _{i=1}^{n}W_{i}X_{i};\,\vee i\,\varepsilon \,\,{\hbox{nodos}}$

(2)

Restricciones:

$f(x)\geq 1$

(3)

$\max R=(n_{PMU},U_{PMU})$

(4)

$X_{i}+\sum _{j=1}^{n}X_{j}\geq \alpha _{i};\,\vee j\,\varepsilon \,\,{\hbox{nodos}}$

(5)

donde ${\textstyle n_{PMU}}$ son los números de PMU, ${\textstyle U_{PMU}}$ los nodos de ubicación de PMU, $n$ los nodos del sistema, ${\textstyle \alpha _{i}}$ es una variable de observabilidad (1 si es observable, caso contrario 0) y ${\textstyle X_{i}}$ es una variable de selección (1 si se requiere una PMU en el nodo i, caso contrario 0).

2.2 Ubicación óptima de PMU considerando las contingencias del SEP

Ubicación óptima de PMU considerando las contingencias del SEP Las contingencias se definen como eventos muy frecuentes presentes en los sistemas eléctricos, por lo cual, los instrumentos de medición deben mantener los registros de los parámetros eléctricos, aún cuando las contingencias N-1 continúen presentes en el sistema. Para ubicar las PMUs de manera óptima, se debe considerar las contingencias como la pérdida de una PMU o la salida de una línea de transmisión [27].

2.2.1 Pérdida de PMU

Ante la salida de una PMU, se pretende que el sistema sea observable completamente, por lo cual, cada nodo debería ser observado por 2 PMU, la función objetivo se define en la ec.(6); restringida por: la ec.(7) indica que al menos una PMU se encuentra instalada en el SEP, la ec.(8) mantiene al máximo la redundancia del SEP y la ec.(9) restringe al 100 % la observabilidad del sistema.

FO:

$\min _{nPMU}=\sum _{i=1}^{n}W_{i}X_{i};\,\forall i\,\varepsilon \,\,{\hbox{nodos}}$

(6)

Restricciones:

$f(x)\geq 1$

(7)

$\max R=(n_{PMU},U_{PMU})$

(8)

$X_{i}+\sum _{j=1}^{n}X_{j}\geq 2~x~\alpha _{i};\,\forall i\,\varepsilon \,\,{\hbox{nodos}}$

(9)

2.2.2 Pérdida de línea de transmisión

Cuando se presenta en el sistema la salida de una línea de transmisión, la misma debe estar asociada a una PMU o a su vez cada nodo debe ser observado por 2 PMU; con la seguridad de no perder la observabilidad del sistema, se aplica la función objetivo (ec.(10)); restringida por: ec.(11) que indica que al menos una PMU se encuentra instalada en el SEP, la ec.(12) mantiene al máximo la redundancia del sistema y las ecs.(13) y (14) restringen al 100 % la observabilidad del sistema.

FO:

$\min _{nPMU}=\sum _{i=1}^{n}W_{i}X_{i};\,\forall i\,\varepsilon \,\,{\hbox{nodos}}$

(10)

Restricciones:

$f(x)\geq 1$

(11)

$\max R=(n_{PMU},U_{PMU})$

(12)

$X_{i}+\alpha _{i}\geq 1;\,\forall i\,\varepsilon ~~{\hbox{nodos}}$

(13)

$\sum _{j=1}^{n}X_{j}\geq 2~x~\alpha _{i};\,\forall j\,\varepsilon \,\,{\hbox{nodos}}$

(14)

3. Estimador de estado

Esta sección describe la metodología propuesta para la elaboración del EEH que integra las mediciones fasoriales ($I_{ij,r}$ y $I_{ij,i}$) al proceso de EE convencional ($P_{inyec}$, $P_{flujo}$, $Q_{inyec}$ y $Q_{flujo}$), obteniendo como resultado un EE que genera la óptima estimación de las variables de estado (voltaje en magnitud y ángulo) del sistema, con el menor número de iteraciones, manteniendo la redundancia de las mediciones, cuando se presentan contingencias.

3.1 Estimador de estado convencional WLS

El EE convencional se basa en la metodología de WLS cuya función objetivo es minimizar la suma ponderada de los cuadrados de las desviaciones, resulado de la diferencia de las mediciones estimadas ${\hat {z}}$ y las mediciones reales $z$ [8] y utiliza el grupo de mediciones, convencionales ($P_{inyec}$, $P_{flujo}$, $Q_{inyec}$ y $Q_{flujo}$), además, de las magnitudes de tensiones nodales, la ecuación no lineal que relaciona las medidas y el vector del estado se define:

$z=h(x)+e$

(15)

donde $z$ es el vector de mediciones ($P_{inyec}$, $P_{flujo}$, $Q_{inyec}$ y $Q_{flujo}$), $h(x)$ el vector de las funciones no lineales y $e$ el vector de error de medición y número de mediciones.

También podemos escribir la ec.(15) de la siguiente manera:

$e=z-z_{verdadero}$

(16)

Las cantidades con sombrero son los valores estimados de las cantidades sin sombrero correspondientes, los errores estimados se lo pueden obtener mediante:

${\hat {e}}=z-{\hat {z}}=z-h{\hat {x}}=e-h({\hat {x}}-x)$

(17)

La matriz jacobiana del sistema se obtiene a partir de las derivadas parciales con respeto al vector de estado $x$, la cual se desea minimizar y se define en la ec.(18)

$J(x)=[z-h(x)]^{T}R^{-1}[z-h(x)]=0$

(18)

El vector $h(x)$ relaciona a las mediciones con las variables de estado, se encuentra integrado por funciones no lineales, las cuales, calculan el valor verdadero de las mediciones del sistema, permitiendo linealizar el problema de estimación alrededor de un valor dado para todos los componentes del vector de estado, tenemos la matriz de ganancia G definida para los valores de $k=0,1,2.\cdots$ hasta una apropiada convergencia, definida de la siguiente manera:

$G=[H(x^{k})]^{T}R^{-1}H(x)=0$

(19)

Como se desea minimizar la función, mediante la deducción de WLS, remplazando la ec.(19) en la ec.(18), resulta:

$\Delta (x)=[H^{T}R^{-1}H]^{-1}*H^{T}R^{-1}[z-h(x)]=0$

(20)

Para resolver la ecuación de estimador de estado ${\hat {x}}_{n}$, se sigue el mismo procedimiento que el de flujos de potencia por Newton Raphson, los valores en módulo y ángulo de las variables de estado (fasor voltaje) ingresan como datos iniciales de entrada, para la segunda iteración y el proceso continua hasta obtener el menor error al cual converge el sistema. De forma alternativa, podemos escribir la ec.(20) de la siguiente manera:

$x_{n}^{(1)}=x_{n}^{(0)}+G_{x}^{\left(0\right)-1}H_{x}^{\left(0\right)T}R^{-1}\ast e_{n}^{(0)}$

(21)

La matriz de errores medidos se denomina, matriz de covarianza (R), los valores de cada elemento fuera de la diagonal son cero porque los errores se han supuesto independientes, los valores esperados de la diagonal corresponden a $\sigma _{1}^{2}$ las varianzas de $e_{n}$, obtenemos una matriz $R^{-1}$a partir de:

$R^{-1}=\left[{\begin{matrix}\displaystyle {\frac {1}{\sigma _{1}^{2}}}&.&.\\.&\displaystyle {\frac {1}{\sigma _{2}^{2}}}&.\\.&.&\displaystyle {\frac {1}{\sigma _{n}^{2}}}\\\end{matrix}}\right]$

(22)

Además, definimos los términos de las derivadas parciales dependientes de $x$, de la siguiente manera:

$H={\frac {dh}{dx}}(x)=\left[{\begin{matrix}\displaystyle {\frac {\partial \left|V\right|}{\partial \left|V\right|}}&0\\\displaystyle {\frac {{\partial P}_{flujo}}{\partial \left|V\right|}}&\displaystyle {\frac {{\partial P}_{flujo}}{\partial \theta }}\\{\begin{matrix}\displaystyle {\frac {{\partial Q}_{flujo}}{\partial \left|V\right|}}\\{\begin{matrix}\displaystyle {\frac {{\partial P}_{inye}}{\partial \left|V\right|}}\\\displaystyle {\frac {{\partial Q}_{inyec}}{\partial \left|V\right|}}\\\end{matrix}}\\\end{matrix}}&{\begin{matrix}\displaystyle {\frac {{\partial Q}_{flujo}}{\partial \theta }}\\{\begin{matrix}\displaystyle {\frac {{\partial P}_{inyec}}{\partial \theta }}\\\displaystyle {\frac {{\partial Q}_{inyec}}{\partial \theta }}\\\end{matrix}}\\\end{matrix}}\\\end{matrix}}\right]$

(23)

3.2 Estimador de estado híbrido EEH con PMU

Para realizar la estimación de estado utilizando las corrientes medidas por las PMUs se procede de manera similar para el caso del EE que utiliza las mediciones convencionales ($P_{inyec}$, $P_{flujo}$, $Q_{inyec}$ y $Q_{flujo}$), al vector de estado se lo expresa en parte real e imaginaria, las funciones se las obtienen a partir del modelo $\pi$ generalizado, estas funciones relacionan al vector de estado con las mediciones de corriente fasoriales [6,8], que se expresan de la siguiente manera:

$\left[{\begin{matrix}{\begin{matrix}I_{ij,r}=\left(g_{ij}+g_{io}\right)V_{i}\cos {\theta _{i}-g_{ij}V_{j}}\cos \theta _{j}\\-\left(b_{ij}+b_{io}\right)V_{i}\sin {\theta _{i}-b_{ij}V_{j}}\sin {\theta _{j}}\\\end{matrix}}\\{\begin{matrix}I_{ij,i}=(g_{ij}+g_{io})V_{i}\sin {\theta _{i}-g_{ij}V_{j}\sin \theta _{j}}\\-(b_{ij}+b_{io})V_{i}\cos {\theta _{i}-b_{ij}V_{j}}\cos {\theta _{j}}\end{matrix}}\end{matrix}}\right.$

(24)

donde $I_{ij,r}$ es la parte real de corriente $I_{ij}$, $I_{ij,i}$ la parte imaginaria de corriente $I_{ij}$, $y_{ij}=g_{ij}+i{g}_{ij}$ el enlace del elemento conectado entre $i$ y $j$, $V_{i},V_{j}$ la magnitud de voltajes de los nodos $i$ y $j$ y $\theta _{i},\theta _{j}$ el ángulo de voltajes de los nodos $i$ y $j$.

La matriz jacobiana la podemos definir de la siguiente manera:

$HI={\frac {dh}{dx}}(x)=\left[{\begin{matrix}\displaystyle {\frac {\partial \left|V\right|}{\partial \left|V\right|}}&0\\\displaystyle {\frac {{\partial I}_{ij,r}}{\partial \left|V\right|}}&\displaystyle {\frac {{\partial I}_{ij,r}}{\partial \theta }}\\{\begin{matrix}\displaystyle {\frac {{\partial I}_{ij,i}}{\partial \left|V\right|}}\\\end{matrix}}&{\begin{matrix}\displaystyle {\frac {{\partial I}_{ij,i}}{\partial \theta }}\\\end{matrix}}\\\end{matrix}}\right]$

(25)

El modelo híbrido de EE, que considera las mediciones de $P_{inyec}$, $P_{flujo}$, $Q_{inyec}$, $Q_{flujo}$ y $I_{ij,r}$, $I_{ij,i}$, es definido mediante:

$H_{t}=\left[{\begin{matrix}\displaystyle {\frac {\partial V}{\partial |V|}}&0\\\displaystyle {\frac {{\partial P}_{flujo}}{\partial |V|}}&\displaystyle {\frac {{\partial P}_{flujo}}{\partial \theta }}\\{\begin{matrix}{\begin{matrix}{\begin{matrix}\displaystyle {\frac {{\partial Q}_{flujo}}{\partial |V|}}\\{\begin{matrix}\displaystyle {\frac {{\partial P}_{inye}}{\partial |V|}}\\\displaystyle {\frac {{\partial Q}_{inyec}}{\partial |V|}}\\\end{matrix}}\\\end{matrix}}\\{\begin{matrix}\displaystyle {\frac {{\partial I}_{ij,r}}{\partial |V|}}\\\displaystyle {\frac {{\partial I}_{ij,i}}{\partial |V|}}\\\end{matrix}}\\\end{matrix}}\\\end{matrix}}&{\begin{matrix}{\begin{matrix}{\begin{matrix}\displaystyle {\frac {{\partial Q}_{flujo}}{\partial \theta }}\\{\begin{matrix}\displaystyle {\frac {{\partial P}_{inyec}}{\partial \theta }}\\\displaystyle {\frac {{\partial Q}_{inyec}}{\partial \theta }}\\\end{matrix}}\\\end{matrix}}\\{\begin{matrix}\displaystyle {\frac {{\partial I}_{ij,r}}{\partial \theta }}\\\displaystyle {\frac {{\partial I}_{ij,i}}{\partial \theta }}\\\end{matrix}}\\\end{matrix}}\\\end{matrix}}\\\end{matrix}}\right]\left[{\begin{matrix}\Delta V\\\Delta \theta \\\end{matrix}}\right]=\left[{\begin{matrix}H\\H1\\\end{matrix}}\right]\left[{\begin{matrix}\Delta V\\\Delta \theta \\\end{matrix}}\right]$

(26)

La matriz de covarianzas híbrida está constituida de las matrices de covarianza del EE convencional e Híbrido, la matriz $R_{I}$ se define como la de covarianza de las mediciones provenientes de las mediciones real e imaginaria de las corrientes, la matriz de covarianzas híbrida se define de la siguiente manera:

$R_{T}=\left[{\begin{matrix}R&0\\0&R_{I}\\\end{matrix}}\right]$

(27)

Una vez definida la matriz de covarianzas y la matriz jacobiana para el EEH, podemos rescribir la ecuación (20), con lo cual obtenemos:

$\Delta (x)=[H_{t}^{T}R_{T}^{-1}H_{t}]^{-1}*H_{t}^{T}R_{T}^{-1}[z_{t}-h(x)_{t}]=0$

(28)

donde $z_{t}$ son las mediciones provenientes del EE tradicional y las provenientes de los PMU parte real e imaginaria, y $h(x)_{t}$ es el vector de las funciones no lineales, que calcula los fujos de potencia, inyecciones de potencia activa y reactiva; corrientes real e imaginaria del SEP.

En el siguiente diagrama de flujo se muestra el procedimiento para la resolución del EEH, mediante el método WLS, como primer paso se ingresa los datos de las mediciones del SEP tanto las convencionales ($P_{inyec}$, $P_{flujo}$, $Q_{inyec}$, $Q_{flujo}$) como las provenientes de las PMUs ($I_{ij,r}$ y $I_{ij,i}$) y las características de las líneas de transmisión ($X_{l}$,$R_{l}$) y topología del SEP. Si se excede el número de iteraciones permitidas, el algoritmo despliega un mensaje mencionando que el sistema no converge, si el ${e}_{max}$ es menor al fijado en las condiciones iniciales y la solución encontrada se encuentra dentro del número adecuado de iteraciones, el algoritmo despliega los valores de los vectores de estado.

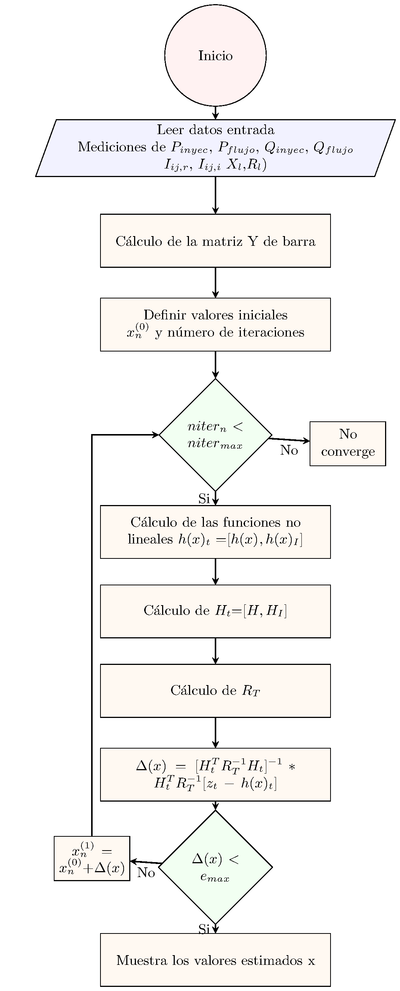
4. Análisis de resultados

4.1 Ubicación óptima de PMU

La Tabla 1 muestra el contraste de número de PMU en el SEP, ante la presencia de contingencias y sin contingencias, cuando se consideran las contingencias aumenta el número de PMU a ser colocadas en el SEP, con la ventaja que ante la pérdida de algún elemento del SEP se conserva la observabilidad del todo el sistema.

Tabla 1. Número de PMU con y sin contingencias

Ubicación de PMU
Modelo IEEE	Sin contingencia	Con contingencia
14 nodos	2, 6, 7, 9	1, 3, 6, 8, 9, 10, 13
30 nodos	1, 2, 6, 10, 11, 12, 15, 19, 25, 29	2, 3, 7, 8, 10, 11, 12, 13, 15, 16, 19, 21, 24, 26, 27, 29
118 nodos	1, 5, 9, 12, 15, 17, 21, 25, 28, 34, 37, 40, 45, 49, 52, 56, 62, 64, 68, 70, 71, 76, 77, 80, 85, 87, 91, 94, 101, 105, 110, 114	1, 5, 6, 8, 10, 11, 12, 15, 17, 19, 21, 23, 26, 27, 29, 32, 34, 36, 37, 38, 40, 42, 44, 46, 49, 50, 51, 53, 56, 59, 61, 64, 67, 68, 72, 73, 74, 75, 76, 78, 80, 83, 85, 87, 89, 91, 92, 94, 92, 100, 102, 105, 106, 109, 111, 112, 114, 116, 117

4.2 Estimador de estado hibrido EEH

El EEH muestra un mejor desempeño, debido a que toma en cuenta mediciones de $P_{inyec}$, $P_{flujo}$, $Q_{inyec}$, $Q_{flujo}$, $I_{ij,r}$ y $I_{ij,i}$, que logran que el número de iteraciones disminuya y aumente su precisión, en contraste con el EEC y el EE PMU. Las mediciones del EE PMU son incluidas en el proceso de EEC para lograr una matriz $H$, como se muestra en la ec.(26), que ante la pérdida de las mediciones provenientes de las líneas de transmisión en el SEP o de las PMUs, mantengan la precisión y calidad del vector de estado resultante, como se puede corroborar en los siguientes escenarios de contingencias analizados.

4.2.1 Primer escenario

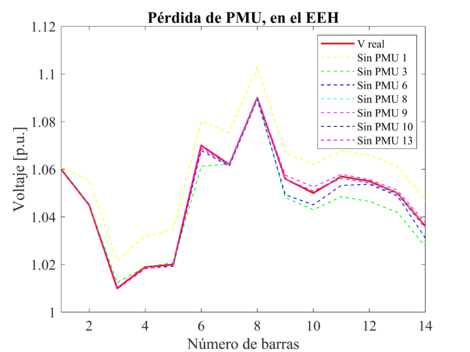
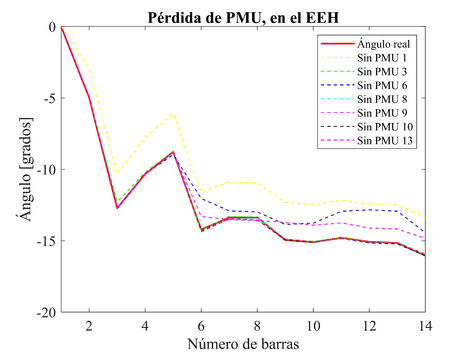
Para el siguiente análisis se llevó a cabo la disminución de las PMU del SEP, con el objeto de observar la variación del vector de estado estimado, tanto en magnitud y ángulo para los EEH y EE-PMU, como se puede apreciar en las Figuras 1 y 2, respectivamente. Para el EEH, se evidencia que su precisión se mantiene, a pesar de la pérdida de PMU en el sistema eléctrico, ya que el número de mediciones convencionales que proporciona el EEC al sistema equivalen aproximadamente al número de mediciones fasoriales de las PMU que se pierden, el aporte de las mediciones convencionales mantiene la precisión del EEH, siendo la pérdida del PMU 1 la más severa para el sistema, obteniendo el valor máximo de voltaje en p.u. de 1.103 y la máxima diferencia angular de 2.709 grados, entre los valores estimados y reales.

Figura 1. Variación de voltaje en p.u. debido a la disminución de PMU, para el EEH

Figura 2. Variación de ángulo en grados, debido a la disminución de PMU, para el EEH

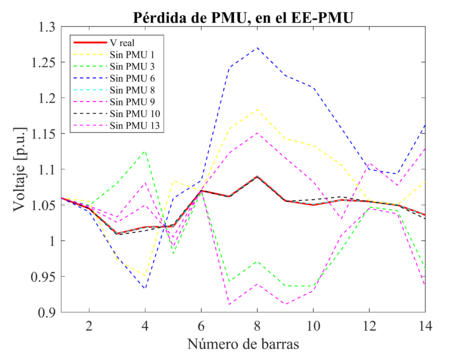
Para el EE-PMU, en las Figuras 3 y 4 se puede observar que, ante la salida de la PMU 1, se presenta el peor escenario para el sistema eléctrico, debido a que la pérdida de la PMU causa distorsiones y la pérdida de la precisión el estimador debido a que la salida de las PMUs disminuye la cantidad de mediciones del estimador de estado. Siendo la pérdida de la PMU 1, la más severa para el sistema, obteniendo el valor máximo de voltaje en p.u. de 1.269 y la máxima diferencia angular de 9.060 grados, entre los valores reales y los estimados.

Figura 3. Variación de voltaje en p.u. debido a la disminución de PMU, para el EE-PMU

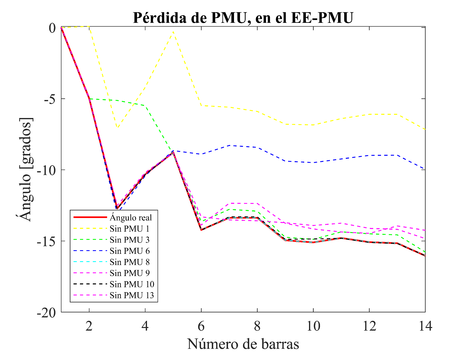
Figura 4. Variación de ángulo en grados, debido a la disminución de PMU, para el EE-PMU

4.2.2 Segundo escenario

Para este análisis se ha considerado la pérdida de elementos del SEP, como líneas de transmisión del sistema eléctrico y su contraste con las variaciones del vector de estado estimado para los EEC, EE PMU y EEH.

Para el EEH, en las Figuras 5 y 6 se puede observar que, ante la salida de las mediciones asociadas a las líneas de transmisión, el estimador de estado mantiene su precisión, ya que las mediciones convencionales mantienen la precisión del estimador, el peor escenario para el sistema eléctrico, se presenta ante la pérdida de la línea de Transmision 4-7, obteniendo el valor máximo de voltaje en p.u. de 1.121 y la máxima diferencia angular de 3.947 grados, entre los valores reales y los estimados.

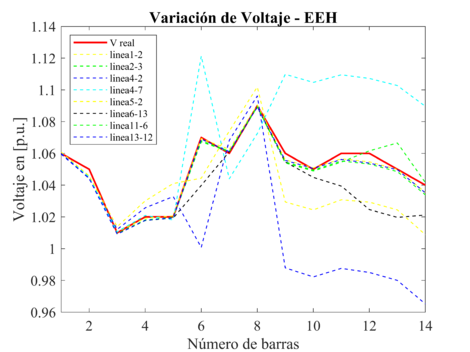
Figura 5. Variación de voltaje en p.u., debido a la pérdida de líneas de transmisión, para el EEH

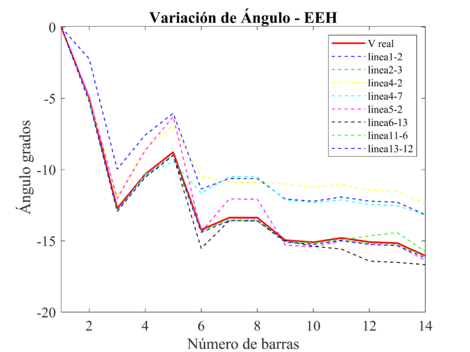
Figura 6. Variación del ángulo, debido a la pérdida de líneas de transmisión, para el EEH

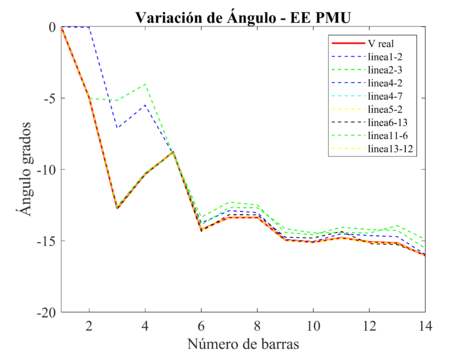
Para el EE PMU, en las Figuras 7 y 8 se puede observar que, ante la salida de las PMUs, el estimador de estado presenta valores excesivos en los valores estimados, ya que las pérdidas de mediciones disminuye la precisión del estimador, el peor escenario para el sistema eléctrico, se presenta ante la pérdida de la línea de Transmision 2-3, obteniendo el valor máximo de voltaje en p.u. de 1.178 y la máxima diferencia angular de 8.386 grados, entre los valores reales y los estimados.

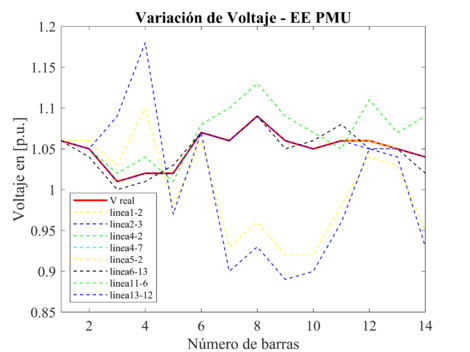
Figura 7. Variación de voltaje en p.u., debido a la pérdida de líneas de transmisión, para el EE PMU

Figura 8. Variación del ángulo, debido a la pérdida de líneas de transmisión, para el EE PMU

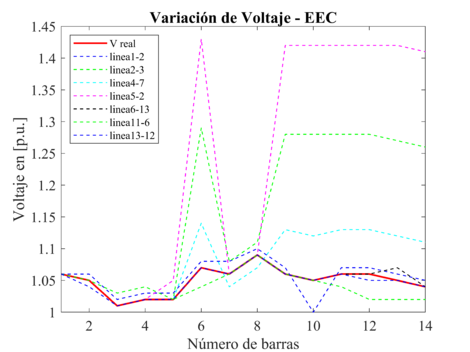
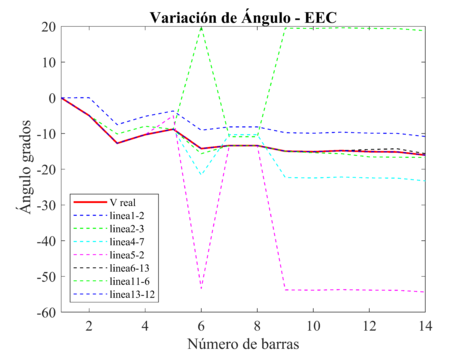
Para el EEC, en las Figuras 9 y 10 se puede observar que, ante la salida de las mediciones asociadas a las líneas de transmisión, el estimador de estado presenta valores excesivos en los valores estimados, ya que la pérdida de mediciones disminuye la precisión del estimador, el peor escenario para el sistema eléctrico, se presenta ante la pérdida de la línea de Transmision 5-2, obteniendo el valor máximo de voltaje en p.u. de 1.43 y la máxima diferencia angular de 39.14 grados, entre los valores reales y los estimados. Además ante la pérdida de la línea de Transmision 4-2 el sistema no converge, es decir no tiene una solución óptima.

Figura 9. Variación de voltaje en p.u., debido a la pérdida de líneas de transmisión, pare el EEC

Figura 10. Variación del ángulo, debido a la pérdida de líneas de transmisión, para el EEC

Ante la pérdida de las líneas de transmisión del SEP, se evidencia la disminución de precisión del vector de estado, resultado de los estimadores de estado, como se puede apreciar en las figuras. Obteniendo los peores escenarios para el EEC, ya que debido a la pérdida de las mediciones relacionada con las líneas de transmisión, el estimador de estado pierde su precisión y calidad en los valores estimados; el EE PMU presenta mejor precisión en comparación del EEC, ya que la pérdida de mediciones asociadas a las líneas de Transmision son compensadas con el resto de las mediciones provenientes de las PMU y el EEH mantiene su precisión y robustez ante la perdida de mediciones, siendo para el EEH, el que presenta los mejores resultados para el vector de estado estimado y la mejor opción de estimación de estado para el SEP, debido a que existen mediciones convencionales y fasoriales, que se complementan para mantener la precisión del mismo.

En la Tabla 2, se visualiza el número de iteraciones y el tiempo en segundos que tarda el código para los EEH y EE PMU, debido a la pérdida de PMU en el sistema eléctrico, que generan los peores escenarios del vector de estado. Para los sistemas de la IEEE de prueba de 14, 30 y 118 nodos. El EEH presenta los mejores tiempo de respuesta y número de iteraciones en contraste con el EE PMU.

Tabla 2. Pérdida de PMU en el SEP

PMU
Tipo de Estimador	Modelo IEEE	Tiempo (seg)	No. de iteraciones
EEH	14 nodos	0.0044, 0.0264, 0.0047	9, 31, 9
	30 nodos	0.0313, 0.1201, 0.0213	13, 15, 14
	118 nodos	0.2381, 0.3012, 0.2582	14, 15, 14
EE PMU	14 nodos	0.001, 0.0328, 0.0025	8, 6, 7
	30 nodos	0.0327, 0.0457, 0.0311	12, 11, 13
	118 nodos	0.2471, 0.2842, 0.3584	15, 15, 18

5. Conclusiones

Es eminente el aumento en la cantidad de PMU en el sistema eléctrico de potencia que considera contingencias en contraste con el sistema que no considera contingencias, como la salida de una PMU o la pérdida de una línea de transmisión, sin embargo, esto ayuda a mejorar la precisión y calidad del estimador de estado. Las mediciones provenientes de las PMUs mantienen la observabilidad y redundancia del SEP.

Ante la pérdida de PMU en el sistema eléctrico, se evidencia una reducción en la precisión de los EEH y EE PMU, siendo el EEH, el cual presenta una mejor respuesta con respecto al EE PMU, ya que el aporte de las mediciones convencionales mantiene la calidad del vector de estado tanto en magnitud y ángulo. Las mediciones convencionales, equivalen aproximadamente al número de mediciones fasoriales de las PMUs que se pierden ante una contingencia, motivo por el cual no deben ser desechadas en el proceso de estimación de estado híbrido. Ante este escenario de pérdida de PMUs en el SEP, el EEH presenta la mejor respuesta y calidad del vector de estado.

Con la perdida de las líneas de Transmision del SEP, se evidencia disminución considerable en la precisión de los EEH, EEPMU y EEC, siendo este último el que mayor número de iteraciones y tiempos de solución del algoritmo presenta, seguido del EE PMU, el EEH la mejor opción de estimación de estado para el SEP debido a que existen mediciones convencionales y fasoriales, que se complementan y mantienen la calidad y precisión del vector de estado estimado, además, su implementación en los actuales estimadores de estado convencionales, no requiere grandes cambios en el software existente.

El objetivo de los SEP a largo plazo es contar con el mayor número posible de PMU, sin embargo, los costos asociados (gestión, compilación de gran cantidad de datos de los sincrofasores) para la instalación de PMU son elevados, motivo por el cual ante las contingencias que pueden presentarse en los SEP, como la pérdida de una PMU o la salida de una línea de transmisión, el papel de las mediciones convencionales es de gran importancia para el proceso de estimación de estado, ya que las mismas mantienen la precisión del estimador sin incrementar el número de iteraciones y el tiempo de respuesta del estimador de estado.

Referencias

[1] Venugopal S., Sunitha R. Robust dynamic state estimationDuring missing of PMU data. 4th International Conference for Convergence in Technology (I2CT) SDMIT Ujire, Mangalore, India, pp. 1–6, Oct 27-28, 2018. Doi: 10.1109/i2ct42659.2018.9058140.

[2] Kumar L.U., and Devi R. Power system dynamic state estimation using Kalman filtering technique. Proceedings of the International Conference on Inventive Research in Computing Applications, ICIRCA 2018, pp. 1173–1178, 2018. Doi: 10.1109/ICIRCA.2018.8597367.

[3] Shabaninia F., Sadeghi H., Vaziri M., Vadhva S. PMU-based recursive state estimation and its performance with neural network. IEEE Power and Energy Society General Meeting, pp. 1–5, 2012. Doi: 10.1109/PESGM.2012.6345075.

[4] Habiballah I., Sahito M. Heuristic placement of PMU in power system state estimation. 2017 9th IEEE-GCC Conference and Exhibition (GCCCE), pp 1–5, 2017. Doi: 10.1109/ieeegcc.2017.8448263.

[5] Singh R.S., Hooshyar H., Vanfretti L. Experimental real-time testing of a decentralized PMU data-based power systems mode estimator. IEEE Power and Energy Society General Meeting, pp. 1–4, Januray 2018. Doi: 10.1109/PESGM.2017.8274269.

[6] Noopura S.P., Jayan M.V. A hybrid state estimator using current based estimator and PMU measurements. Energy Procedia, 117:1117–1124, 2017. Doi: 10.1016/j.egypro.2017.05.236.

[7] Zhang Y., Liu J., Li Y., Liu R., Ma X. A method of state estimation with variable weights iteration based on piece wise linear weight function. China International Conference on Electricity Distribution, CICED, pp. 10–13, September 2016. Doi: 10.1109/CICED.2016.7576165.

[8] Lin J., Su Y., Cheng Y., Lu C., Zhu L., Huang H., Liu Y. A robust complex-domain state estimator using synchrophasor measurements. International Journal of Electrical Power and Energy Systems, 96:412–421, 2018. Doi: 10.1016/j.ijepes.2017.10.020.

[9] Ganjkhani M., Fallah S.N., Badakhshan S., Shamshirband S., Chau K.-w. A novel detection algorithm to identify false data injection attacks on power system state estimation. Energies, 12(11):2209, MDPI, 2019. Doi: 10.3390/en12112209.

[10] Nanda P., Panigrahi C.K., Dasgupta A. Phasor estimation and modelling techniques of PMU - A review. Energy Procedia, 109:64–77, 2017. Doi: 10.1016/j.egypro.2017.03.052.

[11] Raposo A.A., Rodrigues A.B., da Silva M.d.G. Optimalmeter placement algorithm for state estimation in power distribution networks. Electric Power Systems Research, 147:22–30, 2017. Doi: 10.1016/j.epsr.2017.02.015.

[12] Israel Akingeneye J.W. PMU-assisted bad data dection in power systems. In 2018 IEEE/PES Transmission and Distribution Conference and Exposition (TD), pp. 5–9, 2018. Doi: 10.1109/TDC.2018.8440235.

[13] Shrivastava D.R., Siddiqui S.A., Verma K. Optimal PMU placement for complete power system observability under (P-1) contingency. 2017 IEEE InternationalWIE Conference on Electrical and Computer Engineering (WIECON-ECE), pp. 129–132, 2017. Doi: 10.1109/WIECON-ECE.2017.8468924.

[14] Bundoc P., Orillaza J. PMU-based distribution system state estimation. IEEE Region 10 Annual International Conference, Proceedings/TENCON, pp. 993–998, October 2018. Doi: 10.1109/TENCON.2018.8650416.

[15] Almasabi S., Mitra J. Multistage optimal PMU placement considering substation infrastructure. IEEE Transactions on Industry Applications, 54(6):6519–6528, 2018. Doi: 10.1109/TIA.2018.2862401.

[16] Bi T., Yuan D., Chen L., Liu H., Yang Q. Synchrophasor measurements based power system distributed dynamic state estimation. IEEE Power and Energy Society General Meeting, pp. 1–5, 2015. Doi: 10.1109/PESGM.2015.7286338.

[17] Patil G.C., Thosar A.G. Application of synchrophasor measurements using PMU for modern power systems monitoring and control. 6th International Conference on Computationof Power, Energy, Information and Communication (ICCPEIC), pp. 754–760, 2017. Doi: 10.1109/ICCPEIC.2017.8290464.

[18] Aminifar F., Fotuhi-Firuzabad M., Safdarian A. Optimal PMU placement based on probabilistic cost/benefit analysis. IEEE Transactions on Power Systems, 28(1):566–567, 2013. Doi: 10.1109/TPWRS.2012.2198312.

[19] Aminifar F., Shahidehpour M., Fotuhi-Firuzabad M., Kamalinia S. Power system dynamic state estimation with synchronized phasor measurements. IEEE Transactions on Instrumentation andMeasurement, 63(2):352–363, 2014. Doi: 10.1109/TIM.2013.2278595.

[20] Ghosh P.K. Complete and incomplete PMU observablity for hybridstate estimation. 6th International Conference on Computationof Power, Energy, Information and Communication (ICCPEIC), pp. 867–870, 2017. [Online]. Available:doi:10.1109/ICCPEIC.2017.8290487.

[21] Tawfik A.S., Abdallah E.N., Youssef K.H. Optimal placementof phasor measurement units using binary bat algorithm. 2017 Nineteenth International Middle East Power Systems Conference (MEPCON), pp. 559-564, 2017. Doi: 10.1109/MEPCON.2017.8301236.

[22] Hyacinth L.R., Gomathi V. Optimal PMU placement techniqueto maximize measurement redundancy based on closed neighbourhood search. Energies, 14(16):1–15, 2021. Doi: 10.3390/en14164782.

[23] Shahriar M.S., Habiballah I.O., Hussein H. Optimization of phasor measurement unit (PMU) placement in supervisory control and data acquisition (SCADA)-based power system for better state-estimation performance. Energies, 11(3):1-15, 2018. Doi: 10.3390/en11030570.

[24] Zhang Y., Xu Y., Dong Z.Y. Robust ensemble data analytics for incomplete PMU measurements-Based power system stability assessment. IEEE Transactions on Power Systems, 33(1):1124–1126, 2017. Doi: 10.1109/tpwrs.2017.2698239.

[25] Tarif T., Ladjici A.A., Chabane Y. Optimal PMU placement for small-signal stability assessment using genetic algorithm. Proceedings of 2018 3rd International Conference on Electrical Sciences and Technologies in Maghreb (CISTEM), pp. 1–6, 2018. Doi: 10.1109/CISTEM.2018.8613597.

[26] Ahmed M.M., Imran K. An optimal PMU placement against N-1 contingency of PMU using integer linear programming approach. 2019 International Conference on Applied and Engineering Mathematics (ICAEM), pp. 127–132, 2019. Doi: 10.1109/ICAEM.2019.8853656.

[27] Carrión Galarza D.F., González Sánchez J.W. Ubicación óptima de PMU considerando restricciones de contingencias N-1 en sistemas eléctricos de potencia. Enfoque UTE, 10(1):1–12, 2019. Doi: 10.29019/enfoqueute.v10n1.437.