Analytical formulation of the stiffness method for 2D reticular structures using Green functions

Resumen

Las funciones de Green (F.G.) se definen como la respuesta de un medio ante una carga puntual unitaria y son usadas ampliamente para la solución de problemas de valores en la frontera. Desafortunadamente, en el análisis estructural su uso es limitado y solo se emplean de forma indirecta y con otro nombre en el cálculo de líneas de influencia y en algunos casos esporádicos en la formulación del método del trabajo virtual. En este artículo se presenta el método de rigidez con funciones de Green (Green functions stiffness method) el cual es una metodología novedosa para obtener la respuesta analítica o exacta de estructuras reticulares planas, y como su nombre lo indica mezcla al método de rigidez con las funciones de Green. En particular se realizará la formulación para elementos tipo barra (sometidos a fuerza axial), viga (sometidos a fuerza cortante y momento flector), viga sobre fundación flexible (sometidos a fuerza cortante y momento flector) y pórtico plano (sometidos a fuerza axial, fuerza cortante y momento flector). Esta formulación tiene como propiedad principal que puede ser empleada para obtener la respuesta analítica ante cualquier distribución de carga externa y minimiza el número de elementos a emplear en las discretizaciones. Además se presenta la equivalencia de esta formulación con aquella obtenida mediante una implementación “exacta” del método de elementos finitos.

Palabras clave: Método de rigidez con funciones de Green, Funciones de Green, Método de rigidez, Método de elementos finitos, Vigas de Bernoulli, Pórticos planos, Vigas sobre fundación flexible, Funciones de forma

Abstract

Green functions (F.G.) are defined as the response of a medium to a unit point load and are widely used to solve boundary value problems. Unfortunately, in structural analysis, its use is limited and they are only used indirectly and with another name in the calculation of influence lines and in the formulation of the virtual work method. This article presents the Green functions stiffness method, which is a novel methodology to obtain the analytical or exact response of two dimensional frames, which mixes the stiffnes method and the Green functions, the latter used for the calculation of displacement fields. In particular, the formulation will be carried out for bar elements (subjected to axial force), beam elements (subjected to shear force and bending moment), beam over flexible foundation elements (subjected to shear force and bending moment) and two dimensional frames (subjected to axial force, cutting force and bending moment). This formulation has as its main property that it can be used to compute the analytic reponse for any external load distribution and minimizes the number of elements to be used in discretizations. In addition, the equivalence of this formulation with that obtained by an “exact” implementation of the finite element method is presented.

Keywords: Green function stiffness method, Green functions, stiffness method, finite element method, Bernoulli beam, plane frames, beams on elastic foundations, shape functions

1. Introducción

Las funciones de Green (F.G.) son la respuesta de un medio o elemento ante la acción de una fuente o fuerza puntual unitaria y son muy importantes en la solución de problemas de valor en la frontera (P.V.F.) de fenómenos físicos e ingenieriles, cuyas ecuaciones diferenciales (E.D.) gobernantes sean lineales [1]. Esto es debido a que ellas por sí solas son solución de problemas fundamentales, pueden ser empleadas para resolver problemas con fuentes o fuerzas distribuidas [2] o de forma indirecta se emplean en métodos numéricos de frontera o contorno, como el método directo de elementos de frontera [3], el método indirecto de elementos de frontera [4] o el método de las soluciones fundamentales [5]. En geotecnia las principales F.G. son: la respuesta de un espacio completo o infinito [6], la respuesta de un semi-espacio ante la acción de un fuerza en superficie [7,8] y en el interior [9]. En sismología las principales F.G. son: la respuesta de un espacio completo [10], la respuesta de un semi-espacio debida a la acción de una fuerza normal [11] y tangencial [12], para el lector interesado en este tema se le recomiendan los libros [13,14]. Pese a lo anteriormente mencionado, es desafortunado el poco uso que se les da a las F.G. en el análisis estructural, donde su uso (con otro nombre) se limita al cálculo de líneas de influencia y en algunos casos esporádicos a la formulación del método del trabajo virtual.

Para el caso particular de la elasticidad y análisis estructural, las funciones de Green se expresan como ${\textstyle G_{ij}(\mathbf {x} ,{\boldsymbol {\xi }})}$, la cual corresponde al desplazamiento en dirección ${\textstyle i}$ del punto ${\textstyle \mathbf {x} }$, debido a una fuerza puntual unitaria en dirección ${\textstyle j}$ aplicada en el punto ${\textstyle {\boldsymbol {\xi }}}$.

En la actualidad los métodos matriciales son los más empleados para la solución de problemas de análisis estructural, entre estos destacan el método de rigidez y el método de elementos finitos (M.E.F.). El primero de estos es más complejo de implementar y busca la solución exacta del modelo estructural en estudio, mientras que el segundo es más general y simple de implementar y busca una solución aproximada. Por esta razón es usual emplear el método de rigidez para solucionar problemas “sencillos” que involucran modelos lineales con elementos de sección transversal constante y cargas de geometrías simples, como puntuales o distribuidas con variación lineal. Mientras que el M.E.F. suele emplearse para el análisis de estructuras de sección transversal constante o variable pero sometidas a cargas cuya definición es compleja, o para problemas no lineales. Pese a lo anterior, ambos métodos tienen pequeñas falencias intrínsecas, en el método de rigidez hay gran dificultad para manejo de cargas genéricas y no es usual el cálculo del campo de desplazamientos ([15,16,17], mientras que en el M.E.F. la solución es aproximada, lo cual lleva contradicciones a la hora de calcular las fuerzas internas a partir de los campos de desplazamientos [18,19].

En este artículo se presenta una formulación particular del método de rigidez para obtener la respuesta analítica de problemas de análisis estructural formados por estructuras reticulares planas (pudiendo estar formadas por elementos tipo barra, viga, viga sobre fundación flexible o pórtico plano), la cual se llamará el método de rigidez con funciones de Green (Green functions stiffness method), y emplea a las funciones de Green para realizar el cálculo de los desplazamientos al interior de los elementos. Esta metodología busca combinar las principales fortalezas del método de rigidez (obtención de soluciones analíticas) y del M.E.F. (posibilidad de manejar cargas complejas), para la solución total de estas estructuras, es decir, para el cálculo de sus reacciones, campos de desplazamiento y campos de fuerzas internas. Al final de este artículo se presentan tres apéndices donde se presenta la equivalencia de la actual metodología (la cual parte de las ecuaciones diferenciales gobernantes de cada tipo de elemento) y una “exacta” por el M.E.F. (la cual parte de la forma débil de las ecuaciones diferenciales en lugar de estas).

A continuación se comenzarán presentando las ecuaciones diferenciales gobernantes de cada uno de los cuatro tipos de elementos a analizar (barra, viga, pórtico plano y viga sobre fundación flexible), luego se describirá en detalle la metodología de análisis propuesta en este artículo, seguido a esto se realizará la formulación “exacta” del método de rigidez para cada uno de los tipos de elemento estudiados y se concluirá con la realización tres ejemplos ilustrativos (para una viga, una viga sobre fundación flexible y un pórtico plano respectivamente).

2. Ecuaciones diferenciales gobernantes

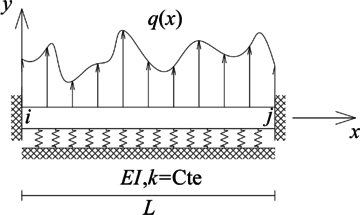
A continuación se definirán las propiedades de los elementos tipo barra, viga, pórtico plano y viga sobre fundación flexible a estudiar en este documento, al igual que sus ecuaciones diferenciales gobernantes. Como generalidad, para todos estos tipos elementos se empleará la convención de fuerzas internas positiva presentada en la Figura 1, la cual se inspira en aquella usada para la definición de los esfuerzos positivos en la mecánica del medio continuo o de sólidos.

Figura 1. Convención positiva para las fuerzas internas. $P(x)$ es la fuerza axial (dirección eje local $x$), $V(x)$ es la fuerza cortante (dirección eje local $y$) y $M(x)$ es el momento flector (dirección eje local $z$, perpendicular tanto a $x$ como a $y$)

2.1 Elemento tipo barra

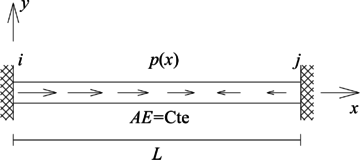
Se define como elemento tipo barra, a aquel cuya única fuerza interna es axial y se encuentra sometido a una fuerza externa distribuida por unidad de longitud (${\textstyle p(x)}$), la cual actúa en dirección del eje ${\textstyle x}$, y su valor es positivo si se dirige en la dirección de dicho eje local (Figura 2). Para el caso que el elemento sea de sección transversal constante con área de la sección transversal ${\textstyle A}$, material elástico lineal con módulo de elasticidad ${\textstyle E}$, su ecuación diferencial gobernante es:

$AE{\dfrac {d^{2}u}{dx^{2}}}(x)=-p(x)$

(1)

donde ${\textstyle u(x)}$ es el desplazamiento en dirección axial del elemento (eje local ${\textstyle x}$).

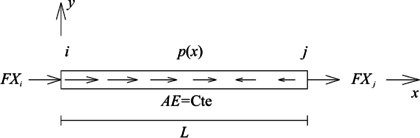
Figura 2. Elemento tipo barra y el sistema coordenado local empleado para la definición de su E.D. gobernante

Mientras que a partir de la ley de Hooke unidimensional su fuerza interna axial ${\textstyle (P)}$ se calcula como:

$P(x)=A\sigma (x)=AE\epsilon (x)=AE{\dfrac {du}{dx}}(x)$

(2)

donde ${\textstyle \sigma (x)}$ es el esfuerzo axial y ${\textstyle \epsilon (x)}$ es la deformación unitaria axial.

2.2 Elemento tipo viga (viga de Euler)

El elemento tipo viga está sometido tanto a fuerza cortante en dirección del eje local ${\textstyle y}$, como a momento flector alrededor del eje local ${\textstyle z}$ (perpendicular a los ejes ${\textstyle x}$ y ${\textstyle y}$, Figura 3). Sus cargas externas se definen en términos de la carga por unidad de longitud en dirección del eje local ${\textstyle y}$ (${\textstyle q(x)}$), la cual es positiva en la dirección de este eje (Figura 3). Si el elemento es de sección transversal constante, con momento de inercia ${\textstyle I}$ y material elástico lineal con módulo de elasticidad ${\textstyle E}$, su ecuación diferencial gobernante es:

$EI{\dfrac {d^{4}v}{dx^{4}}}(x)=q(x)$

(3)

donde ${\textstyle v(x)}$ es el desplazamiento en dirección del eje local ${\textstyle y}$, es decir, perpendicular al eje longitudinal del elemento.

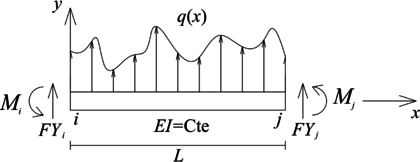
Figura 3. Elemento tipo viga y el sistema coordenado local empleado para la definición de su E.D. gobernante

Mientras que las fuerzas internas cortante y momento flector se calculan a partir del campo de desplazamiento ${\textstyle v(x)}$, respectivamente como:

$V(x)=-EI{\dfrac {d^{3}v}{dx^{3}}}(x)$	(4.a)
$M(x)=EI{\dfrac {d^{2}v}{dx^{2}}}(x)$	(4.b)

2.3 Elemento tipo viga sobre fundación flexible

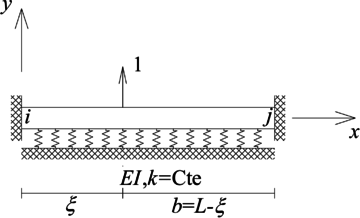
El elemento viga sobre fundación flexible se define como un elemento tipo viga que esta apoyado sobre un medio elástico, el cual tiene una rigidez por unidad de longitud ${\textstyle k}$ y genera una fuerza por unidad de longitud sobre la viga igual a ${\textstyle -kv(x)}$ (Figura 4). Sus fuerzas internas son iguales a las de la viga, es decir, fuerza cortante y momento flector, y su ecuación diferencial gobernante es [20]:

$EI{\dfrac {d^{4}v}{dx^{4}}}(x)+kv(x)=q(x)$

(5)

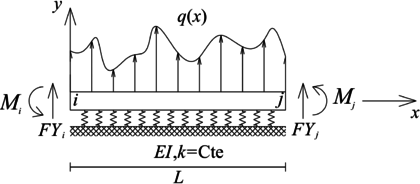
Figura 4. Elemento tipo viga sobre fundación flexible y el sistema coordenado local empleado para la definición de su E.D. gobernante

Al igual que para los elementos tipo viga, para este elemento las fuerzas internas se calculan a partir del campo de desplazamientos empleando (4).

2.4 Elemento tipo pórtico plano

El elemento tipo pórtico plano se define como la superposición de un elemento tipo barra y uno tipo viga, por lo cual sus fuerzas internas son la fuerza axial, la fuerza cortante y el momento flector respecto al eje local ${\textstyle z}$. Sus ecuaciones diferenciales gobernantes son (1) para el desplazamiento axial y (3) para el desplazamiento perpendicular al eje longitudinal del elemento (eje ${\textstyle y}$) y sus fuerzas internas se calculan a partir de los campos de desplazamiento empleando (2) y (4).

3. Metodología

En la formulación del método de rigidez para elementos prismáticos se expresan las fuerzas y momentos en los extremos de estos en función de los desplazamiento y rotaciones en esos mismos puntos (lo cual comúnmente se conoce como grados de libertad). Esta formulación se expresa matricialmente en un sistema local de coordenadas como:

$\{{F'}_{E}\}{=[K'}_{E}]\{\Delta '_{E}\}+\{\left.{F'}_{E}\right.^{f}\}$

(6)

donde ${\textstyle \{{F'}_{E}\}}$ es el vector de fuerzas en los extremos del elemento en coordenadas locales, ${\textstyle {[K'}_{E}]}$ es la matriz de rigidez en coordenadas locales, ${\textstyle \{\Delta '_{E}\}}$ es el vector de desplazamientos en los extremos del elemento en coordenadas locales y ${\textstyle \{\left.{F'}_{E}\right.^{f}\}}$ es el vector de fuerzas de empotramiento en coordenadas locales.

De analizar los dos términos del lado derecho de (6) es evidente que el problema se puede descomponer como la superposición o suma de dos problemas fundamentales. El primero se llamará problema homogéneo (la justificación de esto se presentará mas adelante) y es el encargado de la aparición del término que incluye a la matriz de rigidez, este problema solo depende de los desplazamientos de los nodos (nodales) y no de las cargas externas. El segundo problema se llamará problema empotrado (la justificación para su nombre también se dará mas adelante) y es el encargado de la aparición del vector de fuerzas de empotramiento y no depende de los desplazamientos nodales, pero si de las fuerzas externas. A partir de esta idea, las componentes de los campos de desplazamientos para los elementos estudiados se expresan como:

$d(x)=d_{h}(x)+d_{f}(x)$

(7)

donde ${\textstyle d(x)}$ es el componente del campo de desplazamiento, ${\textstyle d_{h}(x)}$ el omponente del campo homogéneo de desplazamiento y ${\textstyle d_{f}(x)}$ el omponente del campo empotrado de desplazamiento.

A continuación, a partir de (7), se definirán y solucionarán los problemas de valor en la frontera (P.V.F.) empleados para la formulación del método de rigidez con funciones de Green de cada uno de los cuatro tipos de elementos a analizar, así como los P.V.F. que dan lugar a los campos homogéneos y empotrados de estos mismos.

4. Formulación analítica del método de rigidez con funciones de Green para elementos tipo barra

El P.V.F. que gobierna la formulación del método de rigidez para elementos tipo barra de sección transversal constante y longitud ${\textstyle L}$ es (Figura (2)):

$AE{\frac {d^{2}u}{dx^{2}}}(x)=-p(x)$ (8.a) $u(0)=u_{i}$ (8.b) $u(L)=u_{j}$ (8.c)

donde ${\textstyle u(0)=u_{i}}$ es el desplazamiento en dirección axial (eje local ${\textstyle x}$) en el extremo inicial del elemento y ${\textstyle u(L)=u_{j}}$ es el desplazamiento en la misma dirección pero en el extremo final del elemento.

Para este caso la particularización de (7) es:

$u(x)=u_{h}(x)+u_{f}(x)$

(9)

donde ${\textstyle u_{h}(x)}$ es el campo de desplazamiento homogéneo (sección 4.1), mientras que ${\textstyle u_{f}(x)}$ es el campo empotrado (sección 4.2).

4.1 Solución del P.V.F. homogéneo

El P.V.F. que gobierna al campo homogéneo se presenta en (10) y su nombre se debe a que (10.a) es una ecuación diferencial homogénea.

$AE{\frac {d^{2}u_{h}}{dx^{2}}}(x)=0$ (10.a) $u_{h}(0)=u_{i}$ (10.b) $u_{h}(L)=u_{j}$ (10.c)

Es fácil probar que la solución de (10) es el siguiente polinomio de primer grado:

$u_{h}(x)=\psi _{1}(x)u_{i}+\psi _{4}(x)u_{j}$

(11)

donde:

$\psi _{1}(x)=1-{\dfrac {x}{L}}$ (12.a) $\psi _{4}(x)={\dfrac {x}{L}}$ (12.b)

${\textstyle \psi _{1}(x)}$ y ${\textstyle \psi _{4}(x)}$ son conocidas como las funciones de forma “exactas” de este problema y en este caso son iguales a aquellas que suelen emplearse en el M.E.F. para interpolar el campo de desplazamientos en un elemento tipo barra. Un par de propiedades muy importantes de ${\textstyle \psi _{1}(x)}$ y ${\textstyle \psi _{4}(x)}$, las cuales nos permitirán expresar de forma compacta algunos cálculos posteriores, son:

$\psi _{1}(x)=\psi _{4}(L-x)$ (13.a) $\psi _{4}(x)=\psi _{1}(L-x)$ (13.b)

En este punto es importante resaltar que en el M.E.F. es usual emplear (11) para aproximar el campo total de desplazamientos, lo cual, a partir de (9), se observa que es inexacto pues no incluye al campo empotrado.

Por su parte, empleando la ley de Hooke uniaxial, se tiene que la fuerza axial homogénea se puede calcular como:

$P_{h}(x)=AE{\dfrac {du_{h}}{dx}}(x)={\dfrac {AE}{L}}\left(-u_{i}+u_{j}\right)$

(14)

Mientras que las fuerzas en dirección del eje local ${\textstyle x}$ en los extremos de la barra son:

$FX_{i}^{h}=-P_{h}(0)={\dfrac {AE}{L}}\left(u_{i}-u_{j}\right)$ (15.a) $FX_{j}^{h}=P_{h}(L)={\dfrac {AE}{L}}\left(-u_{i}+u_{j}\right)$ (15.b)

4.2 Solución del P.V.F. empotrado

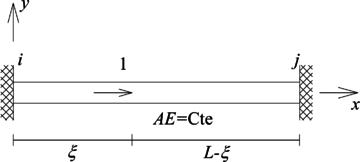
El problema de P.V.F. que gobierna al campo empotrado se presenta en (16). Su nombre se debe a que representa la respuesta de una barra doblemente empotrada sometida a una carga externa por unidad de longitud igual a la del elemento en estudio (Figura 5a)

$AE{\frac {d^{2}u_{f}}{dx^{2}}}(x)=-p(x)$ (16.a) $u_{f}(0)=0$ (16.b) $u_{f}(L)=0$ (16.c)

(a) Carga distribuida arbitraria.	(b) Fuerza puntual unitaria.
Figura 5. Barras de sección transversal constante doblemente empotradas, sometidas a una carga distribuida arbitraria y una carga puntual unitaria

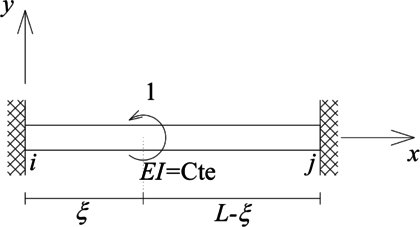
Para la solución del P.V.F. (16) se empleará la función de Green de un elemento tipo barra doblemente empotrada, que es de sección transversal constante y material elástico lineal (Figura 5b). Esta corresponde a la respuesta (campo de desplazamiento axial) debido a la aplicación de una carga puntual unitaria ubicada a una distancia ${\textstyle \xi }$ del origen de coordenadas y está gobernada por el siguiente P.V.F (notar que las dos últimas ecuaciones corresponden a la continuidad de desplazamiento y equilibrio en el punto de aplicación de la fuerza puntual unitaria ${\textstyle (x=\xi )}$):

$AE{\frac {\partial ^{2}G_{xx}}{\partial x^{2}}}(x,\xi )=-\delta (x-\xi )$ (17.a) $G_{xx}(0,\xi )=0$ (17.b) $G_{xx}(L,\xi )=0$ (17.c) $G_{xx}(\xi ^{-},\xi )-G_{xx}(\xi ^{+},\xi )=0$ (17.d) $-AE{\dfrac {\partial G_{xx}}{\partial x}}(\xi ^{-},\xi )+AE{\dfrac {\partial G_{xx}}{\partial x}}(\xi ^{+},\xi )=-1$ (17.e)

donde ${\textstyle \delta (x)}$ es la función delta de Dirac y lo superíndices - y + significan a la izquierda y a la derecha del punto en cuestión.

La solución de (17) expresada en términos de las funciones de forma (12), se puede escribir de forma compacta como:

$G_{xx}(x,\xi )={\begin{cases}G_{xx}^{I}(x,\xi )={\dfrac {L}{AE}}\psi _{4}(x)\psi _{1}(\xi )&0<x\leq \xi \\[0.3cm]G_{xx}^{II}(x,\xi )={\dfrac {L}{AE}}\psi _{1}(x)\psi _{4}(\xi )\qquad &\xi \leq x<L\end{cases}}$

(18)

donde, para su escritura se han explotado las propiedades de simetría de las funciones de forma presentadas en (13), así como las siguientes propiedades de simetría la función de Green:

$G_{xx}^{I}(x,\xi )=G_{xx}^{II}(\xi ,x)=G_{xx}^{II}(L-x,L-\xi )$ (19.a) $G_{xx}^{II}(x,\xi )=G_{xx}^{I}(\xi ,x)=G_{xx}^{I}(L-x,L-\xi )$ (19.b)

Como se verá más adelante, es importante reescribir a ${\textstyle G_{xx}(x,\xi )}$ en los intervalos ${\textstyle 0<\xi \leq x}$ y ${\textstyle x\leq \xi <L}$, lo cual da como resultado:

$G_{xx}(x,\xi )={\begin{cases}G_{xx}^{II}(x,\xi )&0<\xi \leq x\\[0.3cm]G_{xx}^{I}(x,\xi )\qquad &x\leq \xi <L\end{cases}}$

(20)

Multiplicando a ambos lados de (17.a) por ${\textstyle p(\xi )}$ e integrando respecto a ${\textstyle \xi }$ entre 0 y ${\textstyle L}$ se obtiene:

$AE\int _{0}^{L}{\dfrac {\partial ^{2}G_{xx}}{\partial x^{2}}}(x,\xi )p(\xi )d\xi =-\int _{0}^{L}\delta (x-\xi )p(\xi )d\xi$ $AE{\dfrac {\partial ^{2}}{\partial x^{2}}}\left[\int _{0}^{L}G_{xx}(x,\xi )p(\xi )d\xi \right]=-p(x)$

(21)

donde se empleó la siguiente propiedad de la función delta de Dirac: ${\textstyle p(x)=\int _{0}^{L}\delta (x-\xi )p(\xi )d\xi }$ (${\textstyle 0<\xi {<}L}$).

De comparar (21) y (16.a), así como empleando (20) se concluye que:

$u_{f}(x)=\int _{0}^{L}G_{xx}(x,\xi )p(\xi )d\xi =\int _{0}^{x}G_{xx}^{II}(x,\xi )p(\xi )d\xi {+\int }_{x}^{L}G_{xx}^{I}(x,\xi )p(\xi )d\xi$

(22)

La cual también puede interpretarse mediante el principio de superposición pues el desplazamiento en cada punto ${\textstyle x}$ de la barra doblemente empotrada es la suma de los desplazamientos causados en ese mismo punto por infinitas cargas puntuales ubicadas en ${\textstyle \xi }$ desde 0 hasta ${\textstyle L}$ y cuyo valor es ${\textstyle q(\xi )d\xi }$, donde los limites de ambas integrales se explican por (20).

Empleando la ley de Hooke uniaxial, a partir de (22) el campo de fuerza axial empotrado se calcula como:

$P_{f}(x)=AE{\dfrac {du_{f}}{dx}}(x)$ $=AE\int _{0}^{L}{\dfrac {\partial G_{xx}}{\partial x}}(x,\xi )p(\xi )d\xi$ $=AE\left[\int _{0}^{x}{\dfrac {\partial G_{xx}^{II}}{\partial x}}(x,\xi )p(\xi )d\xi +\int _{x}^{L}{\dfrac {\partial G_{xx}^{I}}{\partial x}}(x,\xi )p(\xi )d\xi \right]$ $=-\int _{0}^{x}\psi _{4}(\xi )p(\xi )d\xi {+\int }_{x}^{L}\psi _{1}(\xi )p(\xi )d\xi$

(23)

Y las reacciones o fuerzas de empotramiento en dirección del eje local ${\textstyle x}$ son:

$FX_{i}^{f}=-P_{f}(0)=-\int _{0}^{L}\psi _{1}(\xi )p(\xi )d\xi =-\int _{0}^{L}\psi _{1}(x)p(x)dx$ (24.a) $FX_{j}^{f}=P_{f}(L)=-\int _{0}^{L}\psi _{4}(\xi )p(\xi )d\xi =-\int _{0}^{L}\psi _{4}(x)p(x)dx$ (24.b)

Es de destacar que la anterior forma de expresar las fuerzas de empotramiento en función de la funciones de forma es coherente con aquella presentada para la formulación “exacta” del M.E.F., la cual se encuentra en el Apéndice A.

4.3 Superposición del campo homogéneo y el campo empotrado

Reemplazando (11) y (22) en (9) se tiene que el campo de desplazamiento en el elemento, expresado en función de los desplazamientos nodales y las cargas externas es:

$u(x)=\psi _{1}(x)u_{i}+\psi _{4}(x)u_{j}+\int _{0}^{x}G_{xx}^{II}(x,\xi )p(\xi )d\xi +\int _{x}^{L}G_{xx}^{I}(x,\xi )p(\xi )d\xi$

(25)

Mientras que a partir de sumar (15) y (24), se tiene que las fuerzas en dirección del eje local ${\textstyle x}$ en los extremos del elemento, se expresan en términos de los desplazamientos en esos mismos puntos y en la misma dirección axial:

${\begin{Bmatrix}FX_{i}\\FX_{j}\end{Bmatrix}}={\begin{Bmatrix}FX_{i}^{h}\\FX_{j}^{h}\end{Bmatrix}}+{\begin{Bmatrix}FX_{i}^{f}\\FX_{j}^{f}\end{Bmatrix}}={\dfrac {AE}{L}}{\begin{bmatrix}1&-1\\-1&1\end{bmatrix}}{\begin{Bmatrix}u_{i}\\u_{j}\end{Bmatrix}}-{\begin{Bmatrix}\int _{0}^{L}\psi _{1}(x)p(x)dx\\\int _{0}^{L}\psi _{4}(x)p(x)dx\end{Bmatrix}}$

(26)

La cual es la formulación en coordenadas locales del método de rigidez con funciones de Green para un elemento tipo barra y es equivalente a la presentada en el Apéndice A para el caso de la formulación “exacta” por el método de elementos finitos.

Para finalizar es importante resaltar que las definiciones de los P.V.F. (10) y (16) no han sido arbitrarias y son totalmente coherentes con (8) y (9). Por ejemplo si se reemplaza (9) en (8) y se emplean (16), se obtiene directamente el P.V.F. (10), lo cual también ocurre para los demás tipos de elementos analizados en este artículo.

5. Formulación analítica del método de rigidez con funciones de Green para elementos tipo viga

El P.V.F. que gobierna la formulación del método de rigidez de un elemento tipo viga de sección transversal constante con momento de inercia ${\textstyle I}$, material elástico lineal homogéneo con módulo de elasticidad ${\textstyle E}$ y longitud ${\textstyle L}$ es (Figura 3):

$EI{\frac {d^{4}v}{dx^{4}}}(x)=q(x)$ (27.a) $v(0)=v_{i}$ (27.b) ${\dfrac {dv}{dx}}(0)=\theta _{i}$ (27.c) $v(L)=v_{j}$ (27.d) ${\dfrac {dv}{dx}}(L)=\theta _{j}$ (27.e)

donde ${\textstyle v(0)=v_{i}}$ es el desplazamiento en dirección del eje local ${\textstyle y}$ en extremo inicial del elemento, ${\textstyle {\dfrac {dv}{dx}}(0)=\theta _{i}}$ es la pendiente en ese mismo punto, ${\textstyle v(L)=v_{j}}$ es el desplazamiento en dirección del eje local ${\textstyle y}$ en extremo final del elemento y ${\textstyle {\dfrac {dv}{dx}}(L)=\theta _{j}}$ es la rotación en ese último punto.

Para este caso la particularización de (7) es:

$v(x)=v_{h}(x)+v_{f}(x)$

(28)

donde ${\textstyle v_{h}(x)}$ es el campo de desplazamiento homogéneo (sección 5.1), mientras que ${\textstyle v_{f}(x)}$ es el campo empotrado (sección 5.2).

5.1 Solución del P.V.F. homogéneo

Para este caso el P.V.F. gobernante es:

$EI{\frac {d^{4}v_{h}}{dx^{4}}}(x)=0$ (29.a) $v_{h}(0)=v_{i}$ (29.b) ${\dfrac {dv_{h}}{dx}}(0)=\theta _{i}$ (29.c) $v_{h}(L)=v_{j}$ (29.d) ${\dfrac {dv_{h}}{dx}}(L)=\theta _{j}$ (29.e)

Cuya solución, es el siguiente polinomio de orden tres:

$v_{h}(x)=\psi _{2}(x)v_{i}+\psi _{3}(x)\theta _{i}+\psi _{5}(x)v_{j}+\psi _{6}(x)\theta _{j}$

(30)

donde ${\textstyle \psi _{2}(x)}$, ${\textstyle \psi _{3}(x)}$, ${\textstyle \psi _{5}(x)}$ y ${\textstyle \psi _{6}(x)}$ se conocen coma las funciones de forma “exactas” de este problema y tienen el siguiente valor:

$\psi _{2}(x)=1-3\left({\dfrac {x}{L}}\right)^{2}+2\left({\dfrac {x}{L}}\right)^{3}$ (31.a) $\psi _{3}(x)=\left[{\dfrac {x}{L}}-2\left({\dfrac {x}{L}}\right)^{2}+\left({\dfrac {x}{L}}\right)^{3}\right]L$ (31.b) $\psi _{5}(x)=3\left({\dfrac {x}{L}}\right)^{2}-2\left({\dfrac {x}{L}}\right)^{3}$ (31.c) $\psi _{6}(x)=\left[-\left({\dfrac {x}{L}}\right)^{2}+\left({\dfrac {x}{L}}\right)^{3}\right]L$ (31.d)

Fuera de lo anterior, las siguientes propiedades de simetría de las funciones de forma ${\textstyle \psi _{2}(x)}$, ${\textstyle \psi _{3}(x)}$, ${\textstyle \psi _{5}(x)}$ y ${\textstyle \psi _{2}(x)}$ son muy importantes de resaltar:

$\psi _{2}(x)=\psi _{5}(L-x)$ (32.a) $\psi _{5}(x)=\psi _{2}(L-x)$ (32.b) $\psi _{3}(x)=-\psi _{6}(L-x)$ (32.c) $\psi _{6}(x)=-\psi _{3}(L-x)$ (32.d)

Al igual que para el caso de las barras, las funciones de forma “exactas” presentadas en (31) son iguales a las empleadas en el M.E.F. para aproximar o interpolar el campo total de desplazamiento, lo cual de nuevo es inexacto pues se omite el campo empotrado (28).

A partir de (30) y (4), las fuerzas internas homogéneas son:

$M_{h}(x)=EI{\frac {d^{2}v_{h}}{dx^{2}}}(x)={\frac {EI}{L^{2}}}\left[\left(-6+12{\frac {x}{L}}\right)v_{i}+\left(-4+6{\frac {x}{L}}\right)\theta _{i}L+\left(6-12{\frac {x}{L}}\right)v_{j}+\left(-2+6{\frac {x}{L}}\right)\theta _{j}L\right]$ (33.a) $V_{h}(x)=-EI{\frac {d^{3}v_{h}}{dx^{3}}}(x)={\frac {EI}{L^{3}}}(-12v_{i}-6\theta _{i}L+12v_{j}-6\theta _{j}L)$ (33.b)

Mientras que las fuerzas homogéneas en los extremos del elemento en dirección de los ejes locales ${\textstyle y}$, ${\textstyle z}$ son:

$FY_{i}^{h}=-V_{h}(0)={\dfrac {12EI}{L^{3}}}v_{i}+{\dfrac {6EI}{L^{2}}}\theta _{i}-{\dfrac {12EI}{L^{3}}}v_{j}+{\dfrac {6EI}{L^{2}}}\theta _{j}$ (34.a) $M_{i}^{h}=-M_{h}(0)={\dfrac {6EI}{L^{2}}}v_{i}+{\dfrac {4EI}{L}}\theta _{i}-{\dfrac {6EI}{L^{2}}}v_{j}+{\dfrac {2EI}{L}}\theta _{j}$ (34.b) $FY_{j}^{h}=V_{h}(L)=-{\dfrac {12EI}{L^{3}}}v_{i}-{\dfrac {6EI}{L^{2}}}\theta _{i}+{\dfrac {12EI}{L^{3}}}v_{j}-{\dfrac {6EI}{L^{2}}}\theta _{j}$ (34.c) $M_{j}^{h}=M_{h}(0)={\dfrac {6EI}{L^{2}}}v_{i}+{\dfrac {2EI}{L}}\theta _{i}-{\dfrac {6EI}{L^{2}}}v_{j}+{\dfrac {4EI}{L}}\theta _{j}$ (34.d)

5.2 Solución del P.V.F. empotrado

El problema de P.V.F. que gobierna al campo empotrado se presenta en (35) y corresponde a la respuesta de una viga doblemente empotrada sometida a una carga externa genérica definida por la función ${\textstyle q(x)}$ (Figura 6a)

$EI{\frac {d^{4}v_{f}}{dx^{4}}}(x)=q(x)$ (35.a) $v_{f}(0)=0$ (35.b) ${\dfrac {dv_{f}}{dx}}(0)=0$ (35.c) $v_{f}(L)=0$ (35.d) ${\dfrac {dv_{f}}{dx}}(L)=0$ (35.e)

(a) Carga distribuida arbitraria.	(b) Fuerza puntual unitaria.
Figura 6. Vigas de sección transversal constante doblemente empotradas, sometidas a una carga distribuida arbitraria y una carga puntual unitaria

Para solucionar el P.V.F. (35) se definirá la función de Green asociada con este problema, es decir, la respuesta de una viga doblemente empotrada de sección transversal constante y material elástico lineal, sometida a una fuerza puntual unitaria ubicada a una distancia ${\textstyle \xi }$ del extremo izquierdo del elemento (Figura 6b). Esta función de Green está gobernada por el P.V.F. (36), el cual comprende el cumplimiento de la ecuación diferencial gobernante, condiciones de frontera, condiciones de continuidad de desplazamientos y rotaciones en (${\textstyle x=\xi }$) y equilibrio vertical y rotacional en este mismo punto:

$EI{\frac {\partial ^{4}G_{yy}}{\partial x^{4}}}(x,\xi )=\delta (x-\xi )$ (36.a) $G_{yy}(0,\xi )=0$ (36.b) ${\dfrac {\partial G_{yy}}{\partial x}}(0,\xi )=0$ (36.c) $G_{yy}(L,\xi )=0$ (36.d) ${\dfrac {\partial G_{yy}}{\partial x}}(L,\xi )=0$ (36.e) $G_{yy}(\xi ^{-},\xi )-G_{yy}(\xi ^{+},\xi )=0$ (36.f) ${\dfrac {\partial G_{yy}}{\partial x}}(\xi ^{-},\xi )-{\dfrac {\partial G_{yy}}{\partial x}}(\xi ^{+},\xi )=0$ (36.g) $EI{\dfrac {\partial ^{3}G_{yy}}{\partial x^{3}}}(\xi ^{-},\xi )-EI{\dfrac {\partial ^{3}G_{yy}}{\partial x^{3}}}(\xi ^{+},\xi )=-1$ (36.h) $-EI{\dfrac {\partial ^{2}G_{yy}}{\partial x^{2}}}(\xi ^{-},\xi )+EI{\dfrac {\partial ^{2}G_{yy}}{\partial x^{2}}}(\xi ^{+},\xi )=0$ (36.i)

La solución de (36), es decir, la función de Green para la viga doblemente empotrada presentada en la Figura 6b es:

$G_{yy}(x,\xi )={\begin{cases}{\dfrac {L^{3}}{6EI}}\left[-\left({\dfrac {x}{L}}\right)^{3}\psi _{2}(\xi )+3\left({\dfrac {x}{L}}\right)^{2}{\dfrac {\psi _{3}(\xi )}{L}}\right]&0<x\leq \xi \\[0.3cm]{\dfrac {L^{3}}{6EI}}\left[-\left(1-{\dfrac {x}{L}}\right)^{3}\psi _{5}(\xi )-3\left(1-{\dfrac {x}{L}}\right)^{2}{\dfrac {\psi _{6}(\xi )}{L}}\right]\qquad &\xi \leq x<L\end{cases}}$

(37)

La cual se ha podido expresar de forma tan compacta empleando las propiedades se simetría de las funciones de forma presentadas en (32) y las siguientes propiedades de simetría de la función de Green:

$G_{yy}^{I}(x,\xi )=G_{yy}^{II}(\xi ,x)=G_{yy}^{II}(L-x,L-\xi )$ (38.a) $G_{yy}^{II}(x,\xi )=G_{yy}^{I}(\xi ,x)=G_{yy}^{I}(L-x,L-\xi )$ (38.b)

La cual, por simplicidad en los próximos cálculos se reescribirá de forma compacta como:

$G_{yy}(x,\xi )={\begin{cases}G_{yy}^{I}(x,\xi )&0<x\leq \xi \\G_{yy}^{II}(x,\xi )\qquad &\xi \leq x<L\end{cases}}$

(39)

O de forma alternativa como:

$G_{yy}(x,\xi )={\begin{cases}G_{yy}^{II}(x,\xi )&0<\xi \leq x\\G_{yy}^{I}(x,\xi )\qquad &x\leq \xi <L\end{cases}}$

(40)

Multiplicando a ambos lados de (36.a) por ${\textstyle q(\xi )}$ e integrando respecto a ${\textstyle \xi }$ entre 0 y ${\textstyle L}$ se obtiene:

$EI\int _{0}^{L}{\dfrac {\partial ^{4}G_{yy}}{\partial x^{4}}}(x,\xi )q(\xi )d\xi =\int _{0}^{L}\delta (x-\xi )q(\xi )d\xi$ $EI{\dfrac {\partial ^{4}}{\partial x^{4}}}\left[\int _{0}^{L}G_{yy}(x,\xi )q(\xi )d\xi \right]=q(x)$

(41)

donde se empleó que ${\textstyle q(x)=\int _{0}^{L}\delta (x-\xi )q(\xi )d\xi }$ ${\textstyle (0<\xi {<}L)}$.

De comparar (21) y (35.a), así como empleando (40), se concluye que:

$v_{f}(x)=\int _{0}^{L}G_{yy}(x,\xi )q(\xi )d\xi =\int _{0}^{x}G_{yy}^{II}(x,\xi )q(\xi )d\xi {+\int }_{x}^{L}G_{yy}^{I}(x,\xi )q(\xi )d\xi$

(42)

Al igual que para el caso de la barra, el campo empotrado presentado en (42) puede interpretarse a partir del principio de superposición como la respuesta en un punto ${\textstyle x}$ debido a la suma de los aportes de los diferenciales de fuerza ${\textstyle q(\xi )d\xi }$ ubicados a lo largo de toda la viga, para lo cual se emplea (40).

Mientras que los campos de fuerzas internas se calculan como:

$M_{f}(x)=EI{\dfrac {d^{2}v_{f}}{dx^{2}}}(x)$ $=EI\int _{0}^{L}{\dfrac {\partial ^{2}G_{yy}}{\partial x^{2}}}(x,\xi )q(\xi )d\xi$ $=EI\int _{0}^{x}{\dfrac {\partial ^{2}G_{yy}^{II}}{\partial x^{2}}}(x,\xi )q(\xi )d\xi +EI\int _{x}^{L}{\dfrac {\partial ^{2}G_{yy}^{I}}{\partial x^{2}}}(x,\xi )q(\xi )d\xi$ $=\int _{0}^{x}\left[-\psi _{6}(\xi )-\psi _{5}(\xi )(L-x)\right]q(\xi )d\xi +\int _{x}^{L}\left[\psi _{3}(\xi )-\psi _{2}(\xi )x\right]q(\xi )d\xi$

(43)

$V_{f}(x)=-EI{\dfrac {d^{3}v_{f}}{dx^{3}}}(x)$ $=-EI\int _{0}^{L}{\dfrac {\partial ^{3}G_{yy}}{\partial x^{3}}}(x,\xi )q(\xi )d\xi$ $=-EI\int _{0}^{x}{\dfrac {\partial ^{3}G_{yy}^{II}}{\partial x^{3}}}(x,\xi )q(\xi )d\xi -EI\int _{x}^{L}{\dfrac {\partial ^{3}G_{yy}^{I}}{\partial x^{3}}}(x,\xi )q(\xi )d\xi$ $=-\int _{0}^{x}\psi _{5}(\xi )q(\xi )d\xi {+\int }_{x}^{L}\psi _{2}(\xi )q(\xi )d\xi$

(44)

Y las reacciones o fuerzas de empotramiento en dirección de los ejes locales ${\textstyle y}$ y ${\textstyle z}$ son:

$FY_{i}^{f}=-V_{f}(0)=-\int _{0}^{L}\psi _{2}(\xi )q(\xi )d\xi =-\int _{0}^{L}\psi _{2}(x)q(x)dx$ (45.a) $M_{i}^{f}=-M_{f}(0)=-\int _{0}^{L}\psi _{3}(\xi )q(\xi )d\xi =-\int _{0}^{L}\psi _{3}(x)q(x)dx$ (45.b) $FY_{j}^{f}=V_{f}(L)=-\int _{0}^{L}\psi _{5}(\xi )q(\xi )d\xi =-\int _{0}^{L}\psi _{5}(x)q(x)dx$ (45.c) $M_{j}^{f}=M_{f}(L)=-\int _{0}^{L}\psi _{6}(\xi )q(\xi )d\xi =-\int _{0}^{L}\psi _{6}(x)q(x)dx$ (45.d)

Por su parte para el caso en que se presente un momento puntual, pese a que este se puede expresar como una función ${\textstyle q(x)}$ empleando el límite de dos funciones delta de Dirac, por comodidad a continuación se presenta la función de Green para este caso (Figura 7):

$G_{y\theta }(x,\xi )=\lim _{\Delta \xi \to 0}{\dfrac {G_{yy}(x,\xi {+\Delta }\xi )-G_{yy}(x,\xi )}{\Delta \xi }}={\dfrac {\partial G_{yy}}{\partial \xi }}(x,\xi )$

(46)

con lo cual:

$G_{y\theta }(x,\xi )={\begin{cases}{\dfrac {L^{3}}{6EI}}\left[-\left({\dfrac {x}{L}}\right)^{3}{\dfrac {d\psi _{2}}{d\xi }}(\xi )+{\dfrac {3}{L}}\left({\dfrac {x}{L}}\right)^{2}{\dfrac {d\psi _{3}}{d\xi }}(\xi )\right]&0<x\leq \xi \\[0.3cm]{\dfrac {L^{3}}{6EI}}\left[-\left(1-{\dfrac {x}{L}}\right)^{3}{\dfrac {d\psi _{5}}{d\xi }}(\xi )-{\dfrac {3}{L}}\left(1-{\dfrac {x}{L}}\right)^{2}{\dfrac {d\psi _{6}}{d\xi }}(\xi )\right]\qquad &\xi \leq x<L\end{cases}}$

(47)

Mientras que los campos de fuerzas internas debidas al momento puntual son:

$M_{f}(x,\xi )=EI{\dfrac {\partial ^{2}G_{y\theta }}{\partial x^{2}}}(x,\xi )={\begin{cases}{\dfrac {d\psi _{3}}{d\xi }}(\xi )-{\dfrac {d\psi _{2}}{d\xi }}(\xi )x&0<x<\xi \\[0.3cm]-{\dfrac {d\psi _{6}}{d\xi }}(\xi )+{\dfrac {d\psi _{5}}{d\xi }}(\xi )(x-L)&\xi <x<L\end{cases}}$

(48)

$V_{f}(x,\xi )=-EI{\dfrac {\partial ^{3}G_{y\theta }}{\partial x^{3}}}(x,\xi )={\begin{cases}{\dfrac {d\psi _{2}}{d\xi }}(\xi )&0<x\leq \xi \\[0.3cm]-{\dfrac {d\psi _{5}}{d\xi }}(\xi )\qquad &\xi \leq x<L\end{cases}}$

(49)

con lo cual las fuerzas de empotramiento para este caso son:

$FY_{i}^{f}=-{\dfrac {\psi _{2}}{\partial \xi }}(\xi )$ (50.a) $M_{i}^{f}=-{\dfrac {\psi _{3}}{\partial \xi }}(\xi )$ (50.b) $FY_{j}^{f}=-{\dfrac {\psi _{5}}{\partial \xi }}(\xi )$ (50.c) $M_{j}^{f}=-{\dfrac {\psi _{6}}{\partial \xi }}(\xi )$ (50.d)

Figura 7. Viga de sección transversal constante doblemente empotrada, sometidas a un momento puntual unitario

Debido a que el problema estudiado es lineal, en caso de que el momento aplicado no sea unitario sinó de valor ${\textstyle M}$, los resultados anteriores se deberán simplemente multiplicar por ${\textstyle M}$, y en caso de que sea un momento por unidad de longitud distribuido, este se deberá integrar de forma similar a como se realizó con la carga ${\textstyle q(\xi )}$ pero ahora empleando ${\textstyle G_{y\theta }(x,\xi )}$ en lugar de ${\textstyle G_{yy}(x,\xi )}$.

5.3 Superposición del campo homogéneo y el campo empotrado

Reemplazando (30) y (42) en (28) se obtiene que el campo de desplazamientos puede expresarse en función de los desplazamientos nodales y las fuerzas externas como:

$v(x)=\psi _{2}(x)v_{i}+\psi _{3}(x)\theta _{i}+\psi _{5}(x)v_{j}+\psi _{6}(x)\theta _{j}+\int _{0}^{x}G_{yy}^{II}(x,\xi )q(\xi )d\xi +\int _{x}^{L}G_{yy}^{I}(x,\xi )q(\xi )d\xi$

(51)

Mientras que las fuerzas en los extremos del elemento se expresan en términos de los desplazamiento y rotaciones en esos mismos puntos a partir de la suma de (34) y (45):

${\begin{Bmatrix}FY_{i}\\M_{i}\\FY_{j}\\M_{j}\end{Bmatrix}}={\begin{Bmatrix}FY_{i}^{h}\\M_{i}^{h}\\FY_{j}^{h}\\M_{j}^{h}\end{Bmatrix}}+{\begin{Bmatrix}FY_{i}^{f}\\M_{i}^{f}\\FY_{j}^{f}\\M_{j}^{f}\end{Bmatrix}}={\begin{bmatrix}{\dfrac {12EI}{L^{3}}}&{\dfrac {6EI}{L^{2}}}&-{\dfrac {12EI}{L^{3}}}&{\dfrac {6EI}{L^{2}}}\\{\dfrac {6EI}{L^{2}}}&{\dfrac {4EI}{L}}&-{\dfrac {6EI}{L^{2}}}&{\dfrac {2EI}{L}}\\-{\dfrac {12EI}{L^{3}}}&-{\dfrac {6EI}{L^{2}}}&{\dfrac {12EI}{L^{3}}}&-{\dfrac {6EI}{L^{2}}}\\{\dfrac {6EI}{L^{2}}}&{\dfrac {2EI}{L}}&-{\dfrac {6EI}{L^{2}}}&{\dfrac {4EI}{L}}\end{bmatrix}}{\begin{Bmatrix}v_{i}\\\theta _{i}\\v_{j}\\\theta _{j}\end{Bmatrix}}-{\begin{Bmatrix}\int _{0}^{L}\psi _{2}(x)q(x)dx\\\int _{0}^{L}\psi _{3}(x)q(x)dx\\\int _{0}^{L}\psi _{5}(x)q(x)dx\\\int _{0}^{L}\psi _{6}(x)q(x)dx\end{Bmatrix}}$

(52)

La cual es la formulación en coordenadas locales del método de rigidez con funciones de Green para un elemento tipo viga y es equivalente a la formulación “exacta” del M.E.F. presentada en el Apéndice B.

6. Formulación analítica del método de rigidez con funciones de Green para elementos tipo viga sobre fundación flexible

El P.V.F. que gobierna la formulación del método de rigidez en coordenadas locales de un elemento tipo viga sobre fundación flexible de sección transversal constante, material elástico lineal, rigidez del suelo por unidad de longitud constante e igual ${\textstyle k}$ y longitud ${\textstyle L}$ es (Figura 4):

${\frac {d^{4}v}{dx^{4}}}(x)+4\lambda ^{4}v(x)={\frac {q(x)}{EI}}$ (53.a) $v(0)=v_{i}$ (53.b) ${\dfrac {dv}{dx}}(0)=\theta _{i}$ (53.c) $v(L)=v_{j}$ (53.d) ${\dfrac {dv}{dx}}(L)=\theta _{j}$ (53.e)

donde se ha empleado como ecuación diferencial una versión equivalente de (5), en la cual se define ${\textstyle \lambda ={\sqrt[{4}]{\dfrac {k}{4EI}}}}$ y ${\textstyle v_{i}}$, ${\textstyle \theta _{i}}$, ${\textstyle v_{j}}$ y ${\textstyle \theta _{j}}$ tienen el mismo significado que para la viga (sección 5)

Para este caso la particularización de (7) es:

$v(x)=v_{h}(x)+v_{f}(x)$

(54)

donde ${\textstyle v_{h}(x)}$ es el campo de desplazamiento homogéneo (sección 6.1), mientras que ${\textstyle v_{f}(x)}$ es el campo empotrado (sección 6.2).

6.1 Solución del P.V.F. homogéneo

Para este caso el P.V.F. gobernante es:

${\frac {d^{4}v_{h}}{dx^{4}}}(x)+4\lambda ^{4}v_{h}(x)=0$ (55.a) $v_{h}(0)=v_{i}$ (55.b) ${\dfrac {dv_{h}}{dx}}(0)=\theta _{i}$ (55.c) $v_{h}(L)=v_{j}$ (55.d) ${\dfrac {dv_{h}}{dx}}(L)=\theta _{j}$ (55.e)

cuya solución se expresa como:

$v_{h}(x)=\Psi _{2}(x)v_{i}+\Psi _{3}(x)\theta _{i}+\Psi _{5}(x)v_{j}+\Psi _{6}(x)\theta _{j}$

(56)

donde ${\textstyle \Psi _{2}(x)}$, ${\textstyle \Psi _{3}(x)}$, ${\textstyle \Psi _{5}(x)}$ y ${\textstyle \Psi _{6}(x)}$ son las funciones de forma “exactas” de este problema y tienen el siguiente valor:

$\Psi _{2}(x)={\frac {-({\hbox{s}}^{2}\cdot {\hbox{ch}}^{2}+{\hbox{c}}^{2}\cdot {\hbox{sh}}^{2})\sin(\lambda x)\sinh(\lambda x)+({\hbox{s}}\cdot {\hbox{c}}+{\hbox{sh}}\cdot {\hbox{ch}})\sin(\lambda x)\cosh(\lambda x)}{{\hbox{sh}}^{2}-{\hbox{s}}^{2}}}$ $+{\frac {-({\hbox{s}}\cdot {\hbox{c}}+{\hbox{sh}}\cdot {\hbox{ch}})\cos(\lambda x)\sinh(\lambda x)+({\hbox{sh}}^{2}-{\hbox{s}}^{2})\cos(\lambda x)\cosh(\lambda x)}{{\hbox{sh}}^{2}-{\hbox{s}}^{2}}}$

(57)

$\Psi _{3}(x)={\frac {1}{\lambda }}{\frac {({\hbox{s}}\cdot {\hbox{c}}-{\hbox{sh}}\cdot {\hbox{ch}})\sin(\lambda x)\sinh(\lambda x)+{\hbox{sh}}^{2}\sin(\lambda x)\cosh(\lambda x)-{\hbox{s}}^{2}\cos(\lambda x)\sinh(\lambda x)}{{\hbox{sh}}^{2}-{\hbox{s}}^{2}}}$

(58)

$\Psi _{5}(x)={\frac {2{\hbox{s}}\cdot {\hbox{sh}}\cdot \sin(\lambda x)\sinh(\lambda x)-({\hbox{s}}\cdot {\hbox{ch}}+{\hbox{c}}\cdot {\hbox{sh}})\sin(\lambda x)\cosh(\lambda x)+({\hbox{s}}\cdot {\hbox{ch}}+{\hbox{c}}\cdot {\hbox{sh}})\cos(\lambda x)\sinh(\lambda x)}{{\hbox{sh}}^{2}-{\hbox{s}}^{2}}}$

(59)

$\Psi _{6}(x)={\frac {1}{\lambda }}{\frac {({\hbox{c}}\cdot {\hbox{sh}}-{\hbox{s}}\cdot {\hbox{ch}})\sin(\lambda x)\sinh(\lambda x)+{\hbox{s}}\cdot {\hbox{sh}}\cdot \sin(\lambda x)\cosh(\lambda x)-{\hbox{s}}\cdot {\hbox{sh}}\cdot \cos(\lambda x)\sinh(\lambda x)}{{\hbox{sh}}^{2}-{\hbox{s}}^{2}}}$

(60)

Y para simplificar la escritura, se ha definido ${\textstyle {\hbox{s}}=\sin(\lambda L)}$, ${\textstyle {\hbox{c}}=\cos(\lambda L)}$, ${\textstyle {\hbox{sh}}=\sinh(\lambda L)}$ y ${\textstyle {\hbox{ch}}=\cosh(\lambda L)}$.

Al igual que para el caso de la viga, las funciones de forma para la viga sobre fundación flexible también poseen las siguientes propiedades de simetría:

$\Psi _{2}(x)=\Psi _{5}(L-x)$ (61.a) $\Psi _{5}(x)=\Psi _{2}(L-x)$ (61.b) $\Psi _{3}(x)=-\Psi _{6}(L-x)$ (61.c) $\Psi _{6}(x)=-\Psi _{3}(L-x)$ (61.d)

A diferencia de lo que ocurre para el caso la barra y la viga, las funciones de forma “exactas” presentadas en (57) a (60) no son aquellas que suelen emplearse en la formulación del M.E.F. para vigas sobre fundación flexible, en el cual se emplean las mismas funciones de forma que en este artículo se definieron para la viga (ecuaciones (31)). Como se presentará en el apéndice C, si en la formulación del M.E.F. para una viga sobre fundación flexible se emplean las funciones de forma (57) a (60), se obtiene una formulación matricial “exacta” y una matriz de rigidez y fuerzas de empotramientos iguales a los obtenidos en el método presentado en este artículo (método de rigidez con funciones de Green), siempre y cuando se sumen tanto el campo de desplazamiento homogéneo como el empotrado.

6.2 Solución del P.V.F. empotrado

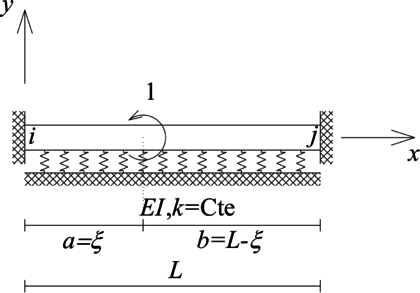
Para este caso el P.V.F. que define al problema empotrado es (Figura 8a):

${\frac {d^{4}v_{f}}{dx^{4}}}(x)+4\lambda ^{4}v_{f}(x)={\dfrac {q(x)}{EI}}$ (62.a) $v_{f}(0)=0$ (62.b) ${\dfrac {dv_{f}}{dx}}(0)=0$ (62.c) $v_{f}(L)=0$ (62.d) ${\dfrac {dv_{f}}{dx}}(L)=0$ (62.e)

(a) Carga distribuida arbitraria	(b) Fuerza puntual unitaria
Figura 8. Vigas sobre fundación flexible de sección transversal constante doblemente empotradas, sometidas a una carga distribuida arbitraria y una carga puntual unitaria

Mientras que la función de Green se define por medio del siguiente P.V.F (Figura 8b):

${\frac {\partial ^{4}{\bar {G}}_{yy}}{\partial x^{4}}}(x)+4\lambda ^{4}{\bar {G}}_{yy}(x)={\dfrac {\delta (x-\xi )}{EI}}$ (63.a) ${\bar {G}}_{yy}(0,\xi )=0$ (63.b) ${\dfrac {\partial {\bar {G}}_{yy}}{\partial x}}(0,\xi )=0$ (63.c) ${\bar {G}}_{yy}(L,\xi )=0$ (63.d) ${\dfrac {\partial {\bar {G}}_{yy}}{\partial x}}(L,\xi )=0$ (63.e) ${\bar {G}}_{yy}(\xi ^{-},\xi )-{\bar {G}}_{yy}(\xi ^{+},\xi )=0$ (63.f) ${\dfrac {\partial {\bar {G}}_{yy}}{\partial x}}(\xi ^{-},\xi )-{\dfrac {\partial {\bar {G}}_{yy}}{\partial x}}(\xi ^{+},\xi )=0$ (63.g) $EI{\dfrac {\partial ^{3}{\bar {G}}_{yy}}{\partial x^{3}}}(\xi ^{-},\xi )-EI{\dfrac {\partial ^{3}{\bar {G}}_{yy}}{\partial x^{3}}}(\xi ^{+},\xi )=-1$ (63.h) $-EI{\dfrac {\partial ^{2}{\bar {G}}_{yy}}{\partial x^{2}}}(\xi ^{-},\xi )+EI{\dfrac {\partial ^{2}{\bar {G}}_{yy}}{\partial x^{2}}}(\xi ^{+},\xi )=0$ (63.i)

donde se ha usado como convención emplear una linea horizontal encima de la letra ${\textstyle G}$ para diferenciar esta función de Green de aquella de las vigas.

La solución de (63) se expresa en forma compacta empleando las funciones de forma (57) a (60), como:

${\bar {G}}_{yy}(x,\xi )={\begin{cases}{\bar {G}}_{yy}^{I}(x,\xi )&0<x\leq \xi \\{\bar {G}}_{yy}^{II}(x,\xi )\qquad &\xi \leq x<L\end{cases}}$

(64)

donde:

${\bar {G}}_{yy}^{I}(x,\xi )={\dfrac {1}{EI}}\left[-{\dfrac {\sin(\lambda x)\cosh(\lambda x)-\sinh(\lambda x)\cos(\lambda x)}{4\lambda ^{3}}}\Psi _{2}(\xi )+{\dfrac {\sin(\lambda x)\sinh(\lambda x)}{2\lambda ^{2}}}\Psi _{3}(\xi )\right]$

(65)

${\bar {G}}_{yy}^{II}(x,\xi )={\dfrac {1}{EI}}\left\{-{\dfrac {\sin =\lambda (L-x)\cosh =\lambda (L-x)\cos =\lambda (L-x)}{4\lambda ^{3}}}\Psi _{5}(\xi )\right.$ $\left.-{\dfrac {\sin =\lambda (L-x)\sinh =\lambda (L-x)}{2\lambda ^{2}}}\Psi _{6}(\xi )\right\}$

(66)

La cual se ha podido expresar de forma tan compacta empleando las propiedades se simetría de las funciones de forma presentadas en (61) y las siguientes propiedades de simetría de la misma función de Green:

${\bar {G}}_{yy}^{I}(x,\xi )={\bar {G}}_{yy}^{II}(\xi ,x)={\bar {G}}_{yy}^{II}(L-x,L-\xi )$ (67.a) ${\bar {G}}_{yy}^{II}(x,\xi )={\bar {G}}_{yy}^{I}(\xi ,x)={\bar {G}}_{yy}^{I}(L-x,L-\xi )$ (67.b)

Multiplicando a ambos lados de (63.a) por ${\textstyle q(\xi )}$ e integrando respecto a ${\textstyle \xi }$ entre 0 y ${\textstyle L}$ se obtiene:

$\int _{0}^{L}{\dfrac {\partial ^{4}{\bar {G}}_{yy}}{\partial x^{4}}}(x,\xi )q(\xi )d\xi {+4}\lambda ^{4}\int _{0}^{L}{\bar {G}}_{yy}(x,\xi )q(\xi )d\xi ={\dfrac {1}{EI}}\int _{0}^{L}\delta (x-\xi )q(\xi )d\xi$ ${\dfrac {\partial ^{4}}{\partial x^{4}}}\left[\int _{0}^{L}{\bar {G}}_{yy}(x,\xi )q(\xi )d\xi \right]+4\lambda ^{4}\int _{0}^{L}{\bar {G}}_{yy}(x,\xi )q(\xi )d\xi ={\dfrac {q(x)}{EI}}$

(68)

donde se empleó que ${\textstyle q(x)=\int _{0}^{L}\delta (x-\xi )q(\xi )d\xi }$.

De comparar (21) y (62.a) se concluye que:

$v_{f}(x)=\int _{0}^{L}{\bar {G}}_{yy}(x,\xi )q(\xi )d\xi =\int _{0}^{x}{\bar {G}}_{yy}^{II}(x,\xi )q(\xi )d\xi {+\int }_{x}^{L}{\bar {G}}_{yy}^{I}(x,\xi )q(\xi )d\xi$

(69)

A partir de (69) y (4), se obtiene que las fuerzas internas se pueden calcular como:

$M_{f}(x)=\int _{0}^{x}\left\{-{\dfrac {\sin =\lambda (L-x)\cosh =\lambda (L-x)\sinh =\lambda (L-x)}{2\lambda }}\Psi _{5}(\xi )-\cos =\lambda (L-x)\cosh =\lambda (L-x)\Psi _{6}(\xi )\right\}q(\xi )d\xi$ $+\int _{x}^{L}\left\{-{\dfrac {\sin(\lambda x)\cosh(\lambda x)+\cos(\lambda x)\sinh(\lambda x)}{2\lambda }}\Psi _{2}(\xi )+\cos(\lambda x)\cosh(\lambda x)\Psi _{3}(\xi )\right\}q(\xi )d\xi$

(70)

$V_{f}(x)=\int _{0}^{x}\left\{-\cos =\lambda (L-x)\cosh =\lambda (L-x)\Psi _{5}(\xi )+\lambda \left\{\sin =\lambda (L-x)\cosh =\lambda (L-x)\sinh =\lambda (L-x)\right\}\Psi _{6}(\xi )\right\}q(\xi )d\xi$ $+\int _{x}^{L}\left\{\cos(\lambda x)\cosh(\lambda x)\Psi _{2}(\xi )+\lambda \left[\sin(\lambda x)\cosh(\lambda x)-\cos(\lambda x)\sinh(\lambda x)\right]\Psi _{3}(\xi )\right\}q(\xi )d\xi$

(71)

Y las reacciones o fuerzas de empotramiento en dirección de los ejes locales se calculan como:

$FY_{i}^{f}=-V_{f}(0)=-\int _{0}^{L}\Psi _{2}(\xi )q(\xi )d\xi =-\int _{0}^{L}\Psi _{2}(x)q(x)dx$ (72.a) $M_{i}^{f}=-M_{f}(0)=-\int _{0}^{L}\Psi _{3}(\xi )q(\xi )d\xi =-\int _{0}^{L}\Psi _{3}(x)q(x)dx$ (72.b) $FY_{j}^{f}=V_{f}(L)=-\int _{0}^{L}\Psi _{5}(\xi )q(\xi )d\xi =-\int _{0}^{L}\Psi _{5}(x)q(x)dx$ (72.c) $M_{j}^{f}=M_{f}(L)=-\int _{0}^{L}\Psi _{6}(\xi )q(\xi )d\xi =-\int _{0}^{L}\Psi _{6}(x)q(x)dx$ (72.d)

De forma similar a como se realizó para el caso de la viga, la función de Green debida a un momento puntual unitario se puede obtener directamente de aquella debida a una fuerza puntual mediante la derivada de la misma respecto a ${\textstyle \xi }$ (Figura 9), es decir:

${\bar {G}}_{y\theta }(x,\xi )={\begin{cases}{\bar {G}}_{y\theta }^{I}(x,\xi )&0\leq x\leq \xi \\{\bar {G}}_{y\theta }^{II}(x,\xi )\qquad &\xi \leq x\leq L\end{cases}}$

(73)

donde:

${\bar {G}}_{y\theta }^{I}(x,\xi )={\dfrac {1}{EI}}\left[-{\dfrac {\sin(\lambda x)\cosh(\lambda x)-\sinh(\lambda x)\cos(\lambda x)}{4\lambda ^{3}}}{\dfrac {d\Psi _{2}}{d\xi }}(\xi )+{\dfrac {\sin(\lambda x)\sinh(\lambda x)}{2\lambda ^{2}}}{\dfrac {d\Psi _{3}}{d\xi }}(\xi )\right]$

(74)

${\bar {G}}_{y\theta }^{II}(x,\xi )={\dfrac {1}{EI}}\left\{-{\dfrac {\sin =\lambda (L-x)\cosh =\lambda (L-x)\cos =\lambda (L-x)}{4\lambda ^{3}}}{\dfrac {d\Psi _{5}}{d\xi }}(\xi )\right.$ $\left.-{\dfrac {\sin =\lambda (L-x)\sinh =\lambda (L-x)}{2\lambda ^{2}}}{\dfrac {d\Psi _{6}}{d\xi }}(\xi )\right\}$

(75)

Mientras que el campo de momento flector es:

$M_{f}(x,\xi )=EI{\dfrac {\partial ^{2}G_{y\theta }}{\partial x^{2}}}(x,\xi )={\begin{cases}M_{f}^{I}(x,\xi )&0<x<\xi \\M_{f}^{II}(x,\xi )&\xi <x<L\end{cases}}$

(76)

donde:

$M_{f}^{I}(x,\xi )=-{\dfrac {\sin(\lambda x)\cosh(\lambda x)+\cos(\lambda x)\sinh(\lambda x)}{2\lambda }}{\dfrac {\partial \Psi _{2}}{\partial \xi }}(\xi )+\cos(\lambda x)\cosh(\lambda x){\dfrac {\partial \Psi _{3}}{\partial \xi }}(\xi )$

(77)

$M_{f}^{II}(x,\xi )=-{\dfrac {\sin =\lambda (L-x)\cosh =\lambda (L-x)\sinh =\lambda (L-x)}{2\lambda }}{\dfrac {\partial \Psi _{5}}{\partial \xi }}(\xi )$ $-\cos =\lambda (L-x)\cosh =\lambda (L-x){\dfrac {\partial \Psi _{6}}{\partial \xi }}(\xi )$

(78)

Y el campo de fuerza cortante es:

$V_{f}(x,\xi )=-EI{\dfrac {\partial ^{3}G_{y\theta }}{\partial x^{3}}}(x,\xi )={\begin{cases}V_{f}^{I}(x,\xi )&0<x\leq \xi \\V_{f}^{II}(x,\xi )&\xi \leq x<L\end{cases}}$

(79)

donde:

$V_{f}^{I}(x,\xi )=\cos(\lambda x)\cosh(\lambda x){\dfrac {\partial \Psi _{2}}{\partial \xi }}(\xi )+\lambda \left[\sin(\lambda x)\cosh(\lambda x)-\cos(\lambda x)\sinh(\lambda x))\right]{\dfrac {\partial \Psi _{3}}{\partial \xi }}(\xi )$

(80)

$V_{f}^{II}(x,\xi )=-\cos =\lambda (L-x)\cosh =\lambda (L-x){\dfrac {\partial \Psi _{5}}{\partial \xi }}(\xi )$ $+\lambda \left\{\sin =\lambda (L-x)\cosh =\lambda (L-x)\sinh =\lambda (L-x)\right\}{\dfrac {\partial \Psi _{6}}{\partial \xi }}(\xi )$

(81)

Con lo cual, a partir de (76) y (79) se tiene que las fuerzas de empotramiento son:

$FY_{i}^{f}=-V_{f}(0)=-{\dfrac {\Psi _{2}}{\partial \xi }}(\xi )$ (82.a) $M_{i}^{f}=-M_{f}(0)=-{\dfrac {\Psi _{3}}{\partial \xi }}(\xi )$ (82.b) $FY_{j}^{f}=V_{f}(L)=-{\dfrac {\Psi _{5}}{\partial \xi }}(\xi )$ (82.c) $M_{j}^{f}=M_{f}(L)=-{\dfrac {\Psi _{6}}{\partial \xi }}(\xi )$ (82.d)

Debido a que el problema estudiado es lineal, en caso de que el momento aplicado no sea unitario sino de valor ${\textstyle M}$, los resultados anteriores se deberán simplemente multiplicar por ${\textstyle M}$. Mientras que si se trata de un momento distruido, debe realizarse la integración del campo debido al momento puntual multiplicado por la función que define al momento distribuido.

Figura 9. Viga sobre funcdación flexible doblemente empotrada y de de sección transversal constante, sometidas a un momento puntual unitario

6.3 Superposición del campo homogéneo y el campo empotrado

Reemplazando (56) y (69) en (54), el campo de desplazamiento total se expresa en función de los desplazamientos de los extremos del elemento y de la carga externa como:

$v(x)=\Psi _{2}(x)v_{i}+\Psi _{3}(x)\theta _{i}+\Psi _{5}(x)v_{j}+\Psi _{6}(x)\theta _{j}+\int _{0}^{x}{\bar {G}}_{yy}^{II}(x,\xi )q(\xi )d\xi +\int _{x}^{L}{\bar {G}}_{yy}^{I}(x,\xi )q(\xi )d\xi$

(83)

Mientras que las fuerzas en los extremos del elemento se expresan en función de los desplazamientos en estos mismos puntos y de las cargas externas como:

${\begin{Bmatrix}FY_{i}\\M_{i}\\FY_{j}\\M_{j}\end{Bmatrix}}={\begin{Bmatrix}FY_{i}^{h}\\M_{i}^{h}\\FY_{j}^{h}\\M_{j}^{h}\end{Bmatrix}}+{\begin{Bmatrix}FY_{i}^{f}\\M_{i}^{f}\\FY_{j}^{f}\\M_{j}^{f}\end{Bmatrix}}={\begin{bmatrix}k_{22}&k_{23}&k_{25}&k_{26}\\k_{32}&k_{33}&k_{35}&k_{36}\\k_{52}&k_{53}&k_{55}&k_{56}\\k_{62}&k_{63}&k_{65}&k_{66}\end{bmatrix}}{\begin{Bmatrix}v_{i}\\\theta _{i}\\v_{j}\\\theta _{j}\end{Bmatrix}}-{\begin{Bmatrix}\displaystyle \int _{0}^{L}\Psi _{2}(x)q(x)dx\\\displaystyle \int _{0}^{L}\Psi _{3}(x)q(x)dx\\\displaystyle \int _{0}^{L}\Psi _{5}(x)q(x)dx\\\displaystyle \int _{0}^{L}\Psi _{6}(x)q(x)dx\end{Bmatrix}}$

(84)

donde los términos de la matriz de rigidez son ([21]):

$k_{22}=k_{55}=4EI\lambda ^{3}{\frac {{\hbox{s}}\cdot {\hbox{c}}+{\hbox{sh}}\cdot {\hbox{ch}}}{{\hbox{sh}}^{2}-{\hbox{s}}^{2}}}$ (85.a) $k_{23}=k_{32}=-k_{56}=-k_{65}=2EI\lambda ^{2}{\frac {{\hbox{s}}^{2}+{\hbox{sh}}^{2}}{{\hbox{sh}}^{2}-{\hbox{s}}^{2}}}$ (85.b) $k_{25}=k_{52}=-4EI\lambda ^{3}{\frac {{\hbox{s}}\cdot {\hbox{ch}}+{\hbox{c}}\cdot {\hbox{sh}}}{{\hbox{sh}}^{2}-{\hbox{s}}^{2}}}$ (85.c) $k_{26}=k_{62}=-k_{35}=-k_{53}=4EI\lambda ^{2}{\frac {{\hbox{s}}\cdot {\hbox{sh}}}{{\hbox{sh}}^{2}-{\hbox{s}}^{2}}}$ (85.d) $k_{33}=k_{66}=2EI\lambda {\frac {{\hbox{sh}}\cdot {\hbox{ch}}-{\hbox{s}}\cdot {\hbox{c}}}{{\hbox{sh}}^{2}-{\hbox{s}}^{2}}}$ (85.e) $k_{36}=k_{63}=2EI\lambda {\frac {{\hbox{s}}\cdot {\hbox{ch}}-{\hbox{c}}\cdot {\hbox{sh}}}{{\hbox{sh}}^{2}-{\hbox{s}}^{2}}}$ (85.f)

Es importante resaltar que (84) corresponde a la formulación analítica del método de rigidez en coordenadas locales para una viga sobre fundación flexible y es equivalente a aquella formulación “exacta” del M.F.F. que se presenta en el Apéndice C.

7. Formulación analítica del método de rigidez con funciones de Green para elementos tipo pórtico plano

Como se mencionó en la sección 2.4 el elemento tipo pórtico plano es simplemente la superposición de un elemento tipo barra y uno tipo viga, con lo cual a partir de lo presentado en (26) y (52) se tiene que la formulación del método de rigidez con funciones de Green en coordenadas locales para un elemento tipo pórtico plano es:

${\begin{Bmatrix}FX_{i}\\FY_{i}\\M_{i}\\FX_{j}\\FY_{j}\\M_{j}\end{Bmatrix}}={\begin{bmatrix}{\dfrac {AE}{L}}&0&0&-{\dfrac {AE}{L}}&0&0\\0&{\dfrac {12EI}{L^{3}}}&{\dfrac {6EI}{L^{2}}}&0&-{\dfrac {12EI}{L^{3}}}&{\dfrac {6EI}{L^{2}}}\\0&{\dfrac {6EI}{L^{2}}}&{\dfrac {4EI}{L}}&0&-{\dfrac {6EI}{L^{2}}}&{\dfrac {2EI}{L}}\\-{\dfrac {AE}{L}}&0&0&{\dfrac {AE}{L}}&0&0\\0&-{\dfrac {12EI}{L^{3}}}&-{\dfrac {6EI}{L^{2}}}&0&{\dfrac {12EI}{L^{3}}}&-{\dfrac {6EI}{L^{2}}}\\0&{\dfrac {6EI}{L^{2}}}&{\dfrac {2EI}{L}}&0&-{\dfrac {6EI}{L^{2}}}&{\dfrac {4EI}{L}}\end{bmatrix}}{\begin{Bmatrix}u_{i}\\v_{i}\\\theta _{i}\\u_{j}\\v_{j}\\\theta _{j}\end{Bmatrix}}-\left\{{\begin{matrix}\displaystyle \int _{0}^{L}\psi _{1}(x)p(x)dx\\\displaystyle \int _{0}^{L}\psi _{2}(x)q(x)dx\\\displaystyle \int _{0}^{L}\psi _{3}(x)q(x)dx\\\displaystyle \int _{0}^{L}\psi _{4}(x)p(x)dx\\\displaystyle \int _{0}^{L}\psi _{5}(x)q(x)dx\\\displaystyle \int _{0}^{L}\psi _{6}(x)q(x)dx\end{matrix}}\right\}$

(86)

Mientras que los campos de desplazamiento en dirección de los ejes locales ${\textstyle x}$ y ${\textstyle y}$, se calculan a partir de las ecuaciones (25) y (51) respectivamente.

8. Ejemplos

8.1 Viga

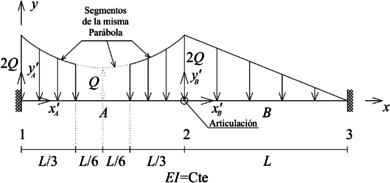
Calcular la respuesta (reacciones, campos de desplazamientos y campos de fuerzas internas) de la viga presentada en la Figura 10a.

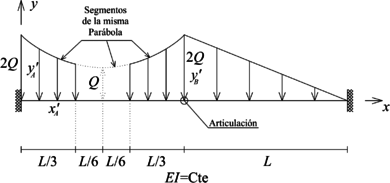
(a) Problema a resolver	(b) Discretización
Figura 10. Viga con articulación interior y discretización empleada para su solución

Discretización

La discretización a emplear en la solución de este problema se presenta en la Figura 10b y consta de solo dos elementos. El elemento ${\textstyle A}$ tiene una carga externa definida en tres tramos, mientras que el elemento ${\textstyle B}$ tiene una carga externa lineal sobre toda su longitud.

Definición de las funciones de carga externa

Para el elemento ${\textstyle A}$ su carga externa se define como:

${q_{A}(x'}_{A})={\begin{cases}Q\left[-2+4{\dfrac {{x'}_{A}}{L}}-4\left({\dfrac {{x'}_{A}}{L}}\right)^{2}\right]\qquad &0\leq {x'}_{<}<{\dfrac {L}{3}}\\0&{\dfrac {L}{3}}{<x'}_{A}<{\dfrac {2L}{3}}\\Q\left[-2+4{\dfrac {{x'}_{A}}{L}}-4\left({\dfrac {{x'}_{A}}{L}}\right)^{2}\right]&{\dfrac {2L}{3}}{<x'}_{A}\leq L\end{cases}}$

(87)

O en forma compacta como:

${q_{A}(x'}_{A})={\begin{cases}q_{A}^{I}{(x'}A)\qquad &{0<x'}_{A}<{\dfrac {L}{3}}\\[0.3cm]q_{A}^{II}{(x'}A)&{\dfrac {L}{3}}{<x'}_{A}<{\dfrac {2L}{3}}\\[0.3cm]q_{A}^{III}{(x'}A)&{\dfrac {2L}{3}}{<x'}_{A}<L\end{cases}}$

(88)

Por su parte la carga externa en el elemento ${\textstyle B}$ es:

${q_{B}(x'}_{B})=Q\left(-2+2{\frac {{x'}_{B}}{L}}\right)\qquad {0<x'}_{B}<L$

(89)

Cálculo de las fuerzas de empotramiento

Según lo presentado en (45), las fuerzas de empotramiento del elemento ${\textstyle A}$ se calculan como:

$FY_{1}^{Af}=-\int _{0}^{L}\psi _{2}(x'_{A})q_{A}(x'_{A})dx'_{A}={\dfrac {40}{81}}QL$ (90.a) $M_{1}^{Af}=-\int _{0}^{L}\psi _{3}(x'_{A})q_{A}(x'_{A})dx'_{A}={\dfrac {71}{1215}}QL^{2}$ (90.b) $FY_{2}^{Af}=-\int _{0}^{L}\psi _{5}(x'_{A})q_{A}(x'_{A})dx'_{A}={\dfrac {40}{81}}QL$ (90.c) $M_{2}^{Af}=-\int _{0}^{L}\psi _{6}(x'_{A})q_{A}(x'_{A})dx'_{A}=-{\dfrac {71}{1215}}QL^{2}$ (90.d)

Mientras que las del elemento ${\textstyle B}$ como:

$FY_{2}^{Bf}=-\int _{0}^{L}\psi _{2}(x'_{B})q_{B}(x'_{B})dx'_{B}={\dfrac {7}{10}}QL$ (91.a) $M_{2}^{Bf}=-\int _{0}^{L}\psi _{3}(x'_{B})q_{B}(x'_{B})dx'_{B}={\dfrac {1}{10}}QL^{2}$ (91.b) $FY_{3}^{Bf}=-\int _{0}^{L}\psi _{5}(x'_{B})q_{B}(x'_{B})dx'_{B}={\dfrac {3}{10}}QL$ (91.c) $M_{3}^{Bf}=-\int _{0}^{L}\psi _{6}(x'_{B})q_{B}(x'_{B})dx'_{B}=-{\dfrac {1}{15}}QL^{2}$ (91.d)

Sistema matricial de ecuaciones de cada elemento

A partir de lo presentado en (52), la formulación del método de rigidez para el elemento ${\textstyle A}$ es:

${\begin{Bmatrix}FY_{1}\\M_{1}\\FY_{2}^{A}\\M_{2}^{A}\end{Bmatrix}}={\begin{bmatrix}{\dfrac {12EI}{L^{3}}}&{\dfrac {6EI}{L^{2}}}&-{\dfrac {12EI}{L^{3}}}&{\dfrac {6EI}{L^{2}}}\\{\dfrac {6EI}{L^{2}}}&{\dfrac {4EI}{L}}&-{\dfrac {6EI}{L^{2}}}&{\dfrac {2EI}{L}}\\-{\dfrac {12EI}{L^{3}}}&-{\dfrac {6EI}{L^{2}}}&{\dfrac {12EI}{L^{3}}}&-{\dfrac {6EI}{L^{2}}}\\{\dfrac {6EI}{L^{2}}}&{\dfrac {2EI}{L}}&-{\dfrac {6EI}{L^{2}}}&{\dfrac {4EI}{L}}\end{bmatrix}}{\begin{Bmatrix}v_{1}\\\theta _{1}\\v_{2}^{A}\\\theta _{2}^{A}\end{Bmatrix}}+{\begin{Bmatrix}{\dfrac {40}{81}}QL\\{\dfrac {71}{1215}}QL^{2}\\{\dfrac {40}{81}}QL\\-{\dfrac {71}{1215}}QL^{2}\end{Bmatrix}}$

(92)

Mientras que para elemento ${\textstyle B}$ este es:

${\begin{Bmatrix}FY_{2}^{B}\\M_{2}^{B}\\FY_{3}\\M_{3}\end{Bmatrix}}={\begin{bmatrix}{\dfrac {12EI}{L^{3}}}&{\dfrac {6EI}{L^{2}}}&-{\dfrac {12EI}{L^{3}}}&{\dfrac {6EI}{L^{2}}}\\{\dfrac {6EI}{L^{2}}}&{\dfrac {4EI}{L}}&-{\dfrac {6EI}{L^{2}}}&{\dfrac {2EI}{L}}\\-{\dfrac {12EI}{L^{3}}}&-{\dfrac {6EI}{L^{2}}}&{\dfrac {12EI}{L^{3}}}&-{\dfrac {6EI}{L^{2}}}\\{\dfrac {6EI}{L^{2}}}&{\dfrac {2EI}{L}}&-{\dfrac {6EI}{L^{2}}}&{\dfrac {4EI}{L}}\end{bmatrix}}{\begin{Bmatrix}v_{2}\\\theta _{2}^{B}\\v_{3}\\\theta _{3}\end{Bmatrix}}+{\begin{Bmatrix}{\dfrac {7}{10}}QL\\{\dfrac {1}{10}}QL^{2}\\{\dfrac {3}{10}}QL\\-{\dfrac {1}{15}}QL^{2}\end{Bmatrix}}$

(93)

Cálculo de los desplazamientos nodales desconocidos

A partir de las fuerzas externas e internas conocidas en los nodos, y empleando continuidad de desplazamientos y equilibrio en estos, se obtiene el siguiente sistema lineal de tres ecuaciones con igual número de incógnitas:

${\begin{Bmatrix}FY_{2}\\M_{2}^{A}\\M_{2}^{B}\end{Bmatrix}}={\begin{Bmatrix}FY_{2}^{A}+FY_{2}^{B}\\M_{2}^{A}\\M_{2}^{B}\end{Bmatrix}}={\begin{Bmatrix}0\\0\\0\end{Bmatrix}}={\begin{bmatrix}{\dfrac {24EI}{L^{3}}}&-{\dfrac {6EI}{L^{2}}}&{\dfrac {6EI}{L^{2}}}\\-{\dfrac {6EI}{L^{2}}}&{\dfrac {4EI}{L}}&0\\{\dfrac {6EI}{L^{2}}}&0&{\dfrac {4EI}{L}}\end{bmatrix}}{\begin{Bmatrix}v_{2}\\\theta _{2}^{A}\\\theta _{2}^{B}\end{Bmatrix}}+{\begin{Bmatrix}{\dfrac {967}{810}}QL\\-{\dfrac {71}{1215}}QL^{2}\\{\dfrac {1}{10}}QL^{2}\end{Bmatrix}}$

(94)

Cuya solución es:

${\begin{Bmatrix}v_{2}\\\theta _{2}^{A}\\\theta _{2}^{B}\end{Bmatrix}}={\begin{Bmatrix}-{\dfrac {1549}{9720}}{\dfrac {QL^{4}}{EI}}\\-{\dfrac {4363}{19440}}{\dfrac {QL^{3}}{EI}}\\{\dfrac {1387}{6480}}{\dfrac {QL^{3}}{EI}}\\\end{Bmatrix}}$

(95)

Cálculo del campo de desplazamiento del elemento $A$

Reemplazando los desplazamientos nodales del elemento ${\textstyle A}$ en (30), se obtiene que el campo de desplazamiento homogéneo para este elemento es:

${v_{A}^{h}(x'}_{A})={\dfrac {QL^{4}}{EI}}\left[-{\dfrac {4931}{19440}}\left({\dfrac {{x'}_{A}}{L}}\right)^{2}+{\dfrac {611}{6480}}\left({\dfrac {{x'}_{A}}{L}}\right)^{3}\right]$

(96)

Mientras que debido a que la carga externa en el elemento ${\textstyle A}$ tiene tres tramos, el campo de desplazamientos empotrado también los tendrá, es decir:

${v_{A}^{f}(x'}_{A})={\begin{cases}v_{A}^{f-1}{(x'}A)\qquad &{0<x'}_{A}\leq {\dfrac {L}{3}}\\[0.3cm]v_{A}^{f-2}{(x'}A)\qquad &{\dfrac {L}{3}}\leq {x'}_{A}\leq {\dfrac {2L}{3}}\\[0.3cm]v_{A}^{f-3}{(x'}A)&{\dfrac {2L}{3}}\leq {x'}<L\end{cases}}$

(97)

donde, a partir de (42), el campo de desplazamiento empotrado en cada uno de los tres tramos se calcula como:

$v_{A}^{f-1}{(x'}_{A})=\int _{0}^{{x'}_{A}}q_{A}^{I}(\xi _{A})G_{yy}^{II}{(x'}_{A},\xi _{A})d\xi +\int _{{x'}_{A}}^{L/3}q_{A}^{I}(\xi )G_{yy}^{I}{(x'}_{A},\xi _{A})d\xi _{A}+\int _{2L/3}^{L}q_{A}^{III}(\xi _{A})G_{yy}^{I}{(x'}_{A},\xi _{A})d\xi _{A}$ $={\dfrac {QL^{4}}{EI}}\left[-{\dfrac {71}{2430}}\left({\dfrac {{x'}_{A}}{L}}\right)^{2}+{\dfrac {20}{243}}\left({\dfrac {{x'}_{A}}{L}}\right)^{3}-{\dfrac {1}{12}}\left({\dfrac {{x'}_{A}}{L}}\right)^{4}+{\dfrac {1}{30}}\left({\frac {{x'}_{A}}{L}}\right)^{5}-{\dfrac {1}{90}}\left({\frac {{x'}_{A}}{L}}\right)^{6}\right]$

(98)

$v_{A}^{f-2}{(x'}_{A})=\int _{0}^{L/3}q_{A}^{I}(\xi _{A})G_{yy}^{II}{(x'}_{A},\xi _{A})d\xi _{A}+\int _{2L/3}^{L}q_{A}^{III}(\xi )G_{yy}^{I}{(x'}_{A},\xi _{A})d\xi _{A}$ $={\dfrac {QL^{4}}{EI}}\left[{\dfrac {83}{131220}}-{\dfrac {19}{2430}}{\dfrac {{x'}_{A}}{L}}+{\dfrac {19}{2430}}\left({\dfrac {{x'}_{A}}{L}}\right)^{2}\right]$

(99)

$v_{A}^{f-3}{(x'}_{A})=\int _{0}^{L/3}q_{A}^{I}(\xi _{A})G_{yy}^{II}{(x'}_{A},\xi _{A})d\xi _{A}+\int _{2L/3}^{{x'}_{A}}q_{A}^{III}(\xi _{A})G_{yy}^{II}{(x'}_{A},\xi _{A})d\xi _{A}+\int _{{x'}_{A}}^{L}q_{A}^{III}(\xi _{A})G_{yy}^{I}{(x'}_{A},\xi _{A})d\xi _{A}$ $={\dfrac {QL^{4}}{EI}}\left[-{\dfrac {13}{1620}}+{\dfrac {109}{2430}}{\dfrac {{x'}_{A}}{L}}-{\dfrac {281}{2430}}\left({\dfrac {{x'}_{A}}{L}}\right)^{2}+{\dfrac {34}{243}}\left({\dfrac {{x'}_{A}}{L}}\right)^{3}-{\dfrac {1}{12}}\left({\dfrac {{x'}_{A}}{L}}\right)^{4}+{\dfrac {1}{30}}\left({\dfrac {{x'}_{A}}{L}}\right)^{5}-{\dfrac {1}{90}}\left({\dfrac {{x'}_{A}}{L}}\right)^{6}\right]$

(100)

Ahora sumando (96) y (97) se obtiene que el campo de desplazamiento total en el elemento es:

${v_{A}(x'}_{A})={\begin{cases}{v_{A}^{I}(x'}_{A})&{0<x'}_{A}\leq {\dfrac {L}{3}}\\[0.5cm]v_{A}^{II}{(x'}A)&{\dfrac {L}{3}}\leq {x'}_{A}\leq {\dfrac {2}{3}}L\\[0.5cm]v_{A}^{III}{(x'}A)\qquad &{\dfrac {2}{3}}L\leq {x'}_{<}L\end{cases}}$

(101)

donde:

${v_{A}^{I}(x'}_{A})={\dfrac {QL^{4}}{EI}}\left[-{\dfrac {611}{2160}}\left({\dfrac {{x'}_{A}}{L}}\right)^{2}+{\dfrac {3433}{19440}}\left({\dfrac {{x'}_{A}}{L}}\right)^{3}-{\dfrac {1}{12}}\left({\dfrac {{x'}_{A}}{L}}\right)^{4}+{\dfrac {1}{30}}\left({\dfrac {{x'}_{A}}{L}}\right)^{5}-{\dfrac {1}{90}}\left({\dfrac {{x'}_{A}}{L}}\right)^{6}\right]$

(102)

$v_{A}^{II}{(x'}=A)={\dfrac {QL^{4}}{EI}}\left[{\dfrac {83}{131220}}-{\dfrac {19}{2430}}{\dfrac {{x'}_{A}}{L}}-{\dfrac {59}{240}}\left({\dfrac {{x'}_{A}}{L}}\right)^{2}+{\dfrac {611}{6480}}\left({\dfrac {{x'}_{A}}{L}}\right)^{3}\right]$

(103)

$v_{A}^{III}{(x'}=A)={\dfrac {QL^{4}}{EI}}\left[-{\dfrac {13}{1620}}+{\dfrac {109}{2430}}{\dfrac {{x'}_{A}}{L}}-{\dfrac {2393}{6480}}\left({\dfrac {{x'}_{A}}{L}}\right)^{2}+{\dfrac {4553}{19440}}\left({\dfrac {{x'}_{A}}{L}}\right)^{3}-{\dfrac {1}{12}}\left({\dfrac {{x'}_{A}}{L}}\right)^{4}\right.$ $\left.+{\dfrac {1}{30}}\left({\dfrac {{x'}_{A}}{L}}\right)^{5}-{\dfrac {1}{90}}\left({\dfrac {{x'}_{A}}{L}}\right)^{6}\right]$

(104)

Cálculo del campo de desplazamiento del elemento $B$

Procediendo de igual manera a como se hizo para el elemento ${\textstyle A}$, se calculan los campos de desplazamiento homogéneo, empotrado y total del elemento ${\textstyle B}$:

${v_{B}^{h}(x'}_{B})={\frac {QL^{4}}{EI}}\left[-{\frac {1549}{9720}}+{\frac {1387}{6480}}{\frac {{x'}_{B}}{L}}+{\frac {1}{20}}\left({\frac {{x'}_{B}}{L}}\right)^{2}-{\frac {407}{3888}}\left({\frac {{x'}_{B}}{L}}\right)^{3}\right]$ (105.a) ${v_{B}^{f}(x'}_{B})={\frac {QL^{4}}{EI}}\left[-{\frac {1}{20}}\left({\frac {{x'}_{B}}{L}}\right)^{2}+{\frac {7}{60}}\left({\frac {{x'}_{B}}{L}}\right)^{3}-{\frac {1}{12}}\left({\frac {{x'}_{B}}{L}}\right)^{4}+{\frac {1}{60}}\left({\frac {{x'}_{B}}{L}}\right)^{5}\right]$ (105.b)

${v_{B}(x'}_{B})={\frac {QL^{4}}{EI}}\left[-{\frac {1549}{9720}}+{\frac {1387}{6480}}{\frac {{x'}_{B}}{L}}+{\frac {233}{19440}}\left({\frac {{x'}_{B}}{L}}\right)^{3}-{\frac {1}{12}}\left({\frac {{x'}_{B}}{L}}\right)^{4}+{\frac {1}{60}}\left({\frac {{x'}_{B}}{L}}\right)^{5}\right]$

(106)

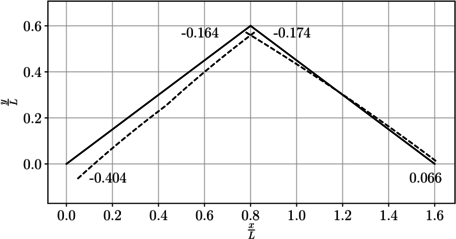
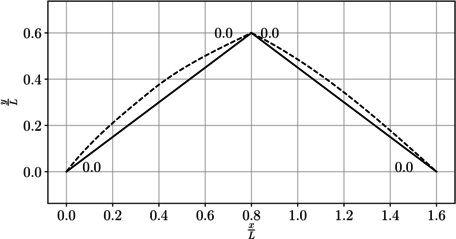
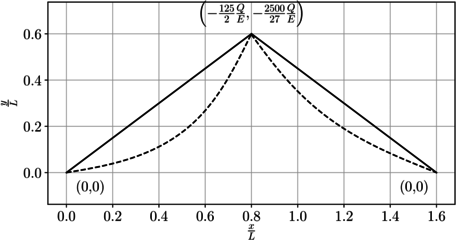
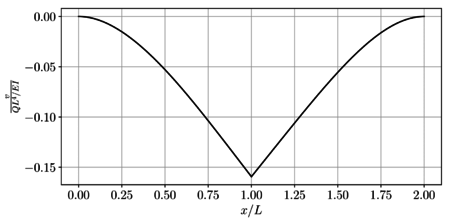
Como resumen, en la Figura 11 se presenta el campo de desplazamientos en toda la viga.

Figura 11. Diagrama del campo de desplazamientos

Cálculos de los campos de fuerzas internas

A partir de (101) y empleando (4), se obtiene que las fuerzas internas para el elemento ${\textstyle A}$ son:

${V_{A}(x'}_{A})={\begin{cases}QL\left[-{\dfrac {3433}{3240}}+2{\dfrac {{x'}_{A}}{L}}-2\left({\dfrac {{x'}_{A}}{L}}\right)^{2}+{\dfrac {4}{3}}\left({\dfrac {{x'}_{A}}{L}}\right)^{3}\right]\qquad &{0<x'}_{A}\leq {\dfrac {L}{3}}\\[0.5cm]-{\dfrac {611}{1080}}QL&{\dfrac {L}{3}}\leq {x'}_{A}\leq {\dfrac {2}{3}}L\\[0.5cm]QL\left[-{\dfrac {4553}{3240}}+2{\dfrac {{x'}_{A}}{L}}-2\left({\dfrac {{x'}_{A}}{L}}\right)^{2}+{\dfrac {4}{3}}\left({\dfrac {{x'}_{A}}{L}}\right)^{3}\right]&{\dfrac {2}{3}}L\leq {x'}_{<}L\end{cases}}$

(107)

${M_{A}(x'}_{A})={\begin{cases}QL^{2}\left[-{\dfrac {611}{1080}}+{\dfrac {3433}{3240}}{\dfrac {{x'}_{A}}{L}}-\left({\dfrac {{x'}_{A}}{L}}\right)^{2}+{\dfrac {2}{3}}\left({\dfrac {{x'}_{A}}{L}}\right)^{3}-{\dfrac {1}{3}}\left({\dfrac {{x'}_{A}}{L}}\right)^{4}\right]&0\leq {x'}_{A}\leq {\dfrac {L}{3}}\\[0.5cm]QL^{2}\left[-{\dfrac {59}{120}}+{\dfrac {611}{1080}}{\dfrac {{x'}_{A}}{L}}\right]&{\dfrac {L}{3}}\leq {x'}_{A}\leq {\dfrac {2}{3}}L\\[0.5cm]QL^{2}\left[-{\dfrac {2393}{3240}}+{\dfrac {4553}{3240}}{\dfrac {{x'}_{A}}{L}}-\left({\dfrac {{x'}_{A}}{L}}\right)^{2}+{\dfrac {2}{3}}\left({\dfrac {{x'}_{A}}{L}}\right)^{3}-{\dfrac {1}{3}}\left({\dfrac {{x'}_{A}}{L}}\right)^{4}\right]\qquad &{\dfrac {2}{3}}L\leq {x'}_{A}\leq L\end{cases}}$

(108)

De forma similar, a partir de (106), se tiene que los campos de fuerzas internas en el elemento ${\textstyle B}$ son:

${V_{B}(x'}_{B})=QL\left[-{\dfrac {233}{3240}}+2{\dfrac {{x'}_{B}}{L}}-\left({\dfrac {{x'}_{B}}{L}}\right)^{2}\right]{0<x'}_{B}<L$ (109.a) ${M_{B}(x'}_{B})=QL^{2}\left[{\frac {233}{3240}}{x'}_{B}-\left({\frac {{x'}_{B}}{L}}\right)^{2}+{\frac {1}{3}}\left({\frac {{x'}_{B}}{L}}\right)^{3}\right]{0<x'}_{B}<L$ (109.b)

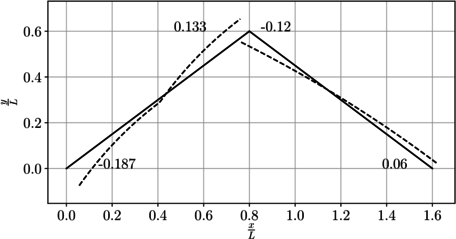
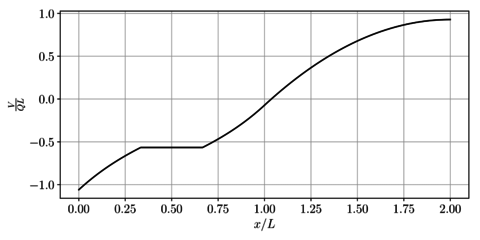
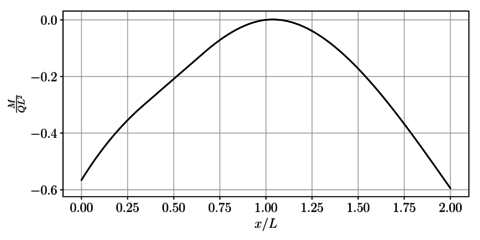
Como resumen de los anteriores resultados, en la Figura 12 se presentan las fuerzas internas en toda la viga.

(a) Fuerza cortante	(b) Momento flector
Figura 12. Diagramas de fuerzas internas

Cálculo de las reacciones

Aunque es posible calcular las reacciones mediante un sistema lineal de ecuaciones, donde las incógnitas sean las cuatro reacciones, a continuación se calcularán a partir de los campo de fuerzas internas calculados anteriormente:

$FY_{1}=-V_{A}(0)={\dfrac {3433}{3240}}QL$ (110.a) $M_{1}=-M_{A}(0)={\dfrac {611}{1080}}QL^{2}$ (110.b) $FY_{3}=V_{B}(L)={\dfrac {3007}{3240}}QL$ (110.c) $M_{3}=M_{B}(L)=-{\dfrac {1927}{3240}}QL^{2}$ (110.d)

Para revisar la validez de los resultados anteriores, a continuación se realizará el equilibrio vertical y rotacional respecto al nudo 1 de toda la viga:

$\sum FY=FY_{1}+FY_{3}+\int _{0}^{L/3}Q\left[-2+4{\frac {{x'}_{A}}{L}}-4\left({\frac {{x'}_{A}}{L}}\right)^{2}\right]{dx'}_{A}+\int _{2L/3}^{L}Q\left[-2+4{\frac {{x'}_{A}}{L}}-4\left({\frac {{x'}_{A}}{L}}\right)^{2}\right]{dx'}_{A}$ $+\int _{0}^{L}Q\left(-2+2{\frac {{x'}_{B}}{L}}\right){dx'}_{B}=0$

(111)

$\sum M_{1}=M_{1}+M_{3}+2FY_{3}+\int _{0}^{L/3}Q\left[-2+4{\frac {{x'}_{A}}{L}}-4\left({\frac {{x'}_{A}}{L}}\right)^{2}\right]{x'}_{A}{dx'}_{A}+\int _{2L/3}^{L}Q\left[-2+4{\frac {{x'}_{A}}{L}}-4\left({\frac {{x'}_{A}}{L}}\right)^{2}\right]{x'}_{A}{dx'}_{A}$ $+\int _{0}^{L}Q\left(-2+2{\frac {{x'}_{B}}{L}}\right){(L+x'}_{B})dx'_{B}=0$

(112)

En el siguiente enlace se encuentra el código de Python empleado para la solución de este ejemplo:

https://drive.google.com/open?id=1-rqbQquE5YmvSKxRtQW2z7Lpm1O8C8-Y

8.2 Viga sobre fundación flexible

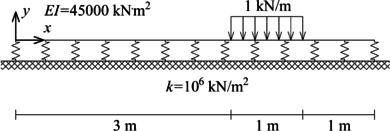
Resolver la viga sobre fundación flexible presentada en la Figura 13a.

(a) Problema a resolver	(b) Discretización
Figura 13. Viga sobre fundación flexible y discretización empleada para su solución

Discretización

Para este problema se empleará la discretización de un solo elemento presentada en la Figura 13b, la cual muestra una de las principales bondades de la presente metodología. Consistente en minimizar el número de elementos a emplear, pues usualmente en la solución de este problema se emplearía una discretización con tres elementos para obtener la respuesta analítica.

Preliminares

El coeficiente ${\textstyle \lambda }$ para este problema es:

$\lambda ={\sqrt[{4}]{\dfrac {k}{4EI}}}=1.535260$

(113)

Mientras que las funciones de forma son:

$\Psi _{2}(x)=-1.0000017\sin(\lambda x)\sinh(\lambda x)+1.0000014\sin(\lambda x)\cosh(\lambda x)-1.0000014\cos(\lambda x)\sinh(\lambda x)$ $+1.0\cos(\lambda x)\cosh(\lambda x)$

(114)

$\Psi _{3}(x)=-0.6513563\sin(\lambda x)\sinh(\lambda x)+0.6513561\sin(\lambda x)\cosh(\lambda x)-5.426830x10^{-7}\cos(\lambda x)\sinh(\lambda x)$

(115)

$\Psi _{5}(x)=1.825552x10^{-3}\sin(\lambda x)\sinh(\lambda x)-1.076690x10^{-3}\sin(\lambda x)\cosh(\lambda x)$ $+1.076690x10^{-3}\cos(\lambda x)\sinh(\lambda x)$

(116)

$\Psi _{6}(x)=-4.877763x10^{-4}\sin(\lambda x)\sinh(\lambda x)+5.945417x10^{-4}\sin(\lambda x)\cosh(\lambda x)$ $-5.945417x10^{-3}\cos(\lambda x)\sinh(\lambda x)$

(117)

Por su parte la función de Green de la viga doblemente empotrada asociada con este problema se obtiene a partir de (65) y (66):

${\bar {G}}_{yy}(x,\xi )={\begin{cases}{\bar {G}}_{yy}^{I}(x,\xi )&0<x\leq \xi \\{\bar {G}}_{yy}^{II}(x,\xi )&\xi \leq x<10{\hbox{ m}}\end{cases}}={\begin{cases}C(x)\Psi _{2}(\xi )+D(x)\Psi _{3}(\xi )&0<x\leq \xi \\A(x)\Psi _{5}(\xi )+B(x)\Psi _{6}(\xi )&\xi \leq x<10{\hbox{ m}}\end{cases}}$

(118)

donde:

$A(x)=-1.535260x10^{-6}\sin =\lambda (5-x)\cosh =\lambda (5-x)+1.535260x10^{-6}\cos =\lambda (5-x)\sinh =\lambda (5-x)$ (119.a) $B(x)=-4.714045x10^{-6}\sin =\lambda (5-x)\sinh =\lambda (5-x)$ (119.b) $C(x)=-1.535260x10^{-6}\sin(\lambda x)\cosh(\lambda x)+1.535260x10^{-6}\cos(\lambda x)\sinh(\lambda x)$ (119.c) $D(x)=4.714045x10^{-6}\sin(\lambda x)\sinh(\lambda x)$ (119.d)

Cálculo de las fuerzas de empotramiento

Para este problema la carga externa se expresa por la siguiente función que posee tres tramos:

$q(x)={\begin{cases}0&0<x<3{\hbox{ m}}\\-1{\hbox{ kN}}&3{\hbox{ m}}<x<4{\hbox{ m}}\\0&4{\hbox{ m}}<x<5{\hbox{ m}}\end{cases}}$

(120)

Con lo cual las fuerzas de empotramiento se calculan a partir de las funciones de forma presentadas en (114) a (117), como:

$FY_{i}^{f}=-\int _{0}^{L}q(x)\Psi _{2}(x)dx=\int _{3}^{4}\Psi _{2}(x)dx=-0.00217865$ (121.a) $M_{i}^{f}=-\int _{0}^{L}q(x)\Psi _{3}(x)dx=\int _{3}^{4}\Psi _{3}(x)dx=-0.0027525$ (121.b) $FY_{j}^{f}=-\int _{0}^{L}q(x)\Psi _{4}(x)dx=\int _{3}^{4}\Psi _{5}(x)dx=0.0351345$ (121.c) $M_{j}^{f}=-\int _{0}^{L}q(x)\Psi _{5}(x)dx=\int _{3}^{4}\Psi _{6}(x)dx=-0.05640796$ (121.d)

Formulación del sistema de ecuaciones de cada elemento

A partir de (84) se tiene que la formulación del método de rigidez para el único elemento de la discretización es:

${\begin{Bmatrix}FY_{1}\\M_{1}\\FY_{2}\\M_{2}\end{Bmatrix}}={\begin{bmatrix}651356&212132&-701&387\\212132&138173&-387&103\\-701&-387&651356&-212132\\387&103&-212132&138173\end{bmatrix}}{\begin{Bmatrix}v_{1}^{A}\\\theta _{1}^{A}\\v_{2}^{A}\\\theta _{2}^{A}\end{Bmatrix}}+{\begin{Bmatrix}-0.00217865\\-0.0027525\\0.0351345\\-0.05640796\end{Bmatrix}}$

(122)

Obtención de los desplazamientos nodales

La solución de (122) es:

${\begin{Bmatrix}v_{1}\\\theta _{1}\\v_{2}\\\theta _{2}\end{Bmatrix}}={\begin{Bmatrix}-6.690465x10^{-9}\,{\hbox{m}}\\3.014775x10^{-8}\,{\hbox{rad}}\\1.580475x10^{-7}\,{\hbox{m}}\\6.508803x10^{-7}\,{\hbox{rad}}\end{Bmatrix}}$

(123)

Cálculo del campo de desplazamientos

Para el cálculo del campo de desplazamientos se realizará la siguiente superposición o descomposición:

$v(x)=v_{h}(x)+v_{f}(x)$

(124)

donde ${\textstyle v_{h}(x)}$ es el campo de desplazamientos homogéneo y ${\textstyle v_{f}(x)}$ es el campo de desplazamientos empotrado. A partir de (56) y empleando los desplazamientos y rotaciones nodales, se obtiene que el campo de desplazamiento homogéneo es:

$v_{h}(x)=-1.297541x10^{-8}\sin(\lambda x)\sinh(\lambda x)+1.316325x10^{-8}\sin(\lambda x)\cosh(\lambda x)$ $+6.473651x10^{-9}\cos(\lambda x)\sinh(\lambda x)-6.690466x10^{-9}\cos(\lambda x)\cosh(\lambda x)$

(125)

Mientras que el campo de desplazamiento empotrado se calcula a partir de (69) y se expresa como:

$v_{f}(x)={\begin{cases}v_{f}^{I}(x)&0<x\leq 3{\hbox{ m}}\\v_{f}^{II}(x)&3{\hbox{ m}}\leq x\leq 4{\hbox{ m}}\\v_{f}^{III}(x)&4{\hbox{ m}}\leq x<5{\hbox{ m}}\end{cases}}$

(126)

donde:

$v_{f}^{I}(x)=\int _{3}^{4}{\bar {G}}_{yy}^{I}(x,\xi )q(\xi )d\xi$ $=1.297541x10^{-8}\sin(\lambda x)\sinh(\lambda x)-3.344800x10^{-9}\sin(\lambda x)\cosh(\lambda x)+3.344800x10^{-9}\cos(\lambda x)\sinh(\lambda x)$

(127)

$v_{f}^{II}(x)=\int _{3}^{x}{\bar {G}}_{yy}^{II}(x,\xi )q(\xi )d\xi {+\int }_{x}^{4}{\bar {G}}_{yy}^{I}(x,\xi )d\xi$ $=-3.779091x10^{-7}\sin =\lambda (x-3)\sinh =\lambda (x-3)+7.449378x10^{-7}\sin =\lambda (x-3)\cosh =\lambda (x-3)$ $\quad -7.449378x10^{-7}\cos =\lambda (x-3)\sinh =\lambda (x-3)+1.0x10^{-6}\cos =\lambda (x-3)\cosh =\lambda (x-3)-1.0x10^{-6}$

(128)

$v_{f}^{III}(x)=\int _{3}^{4}{\bar {G}}_{yy}^{II}(x,\xi )q(\xi )d\xi$ $=1.684965x10^{-5}\sin(\lambda x)\sinh(\lambda x)-1.684965x10^{-5}\sin(\lambda x)\cosh(\lambda x)$ $\quad +2.352508x10^{-4}\cos(\lambda x)\sinh(\lambda x)-2.352506x10^{-4}\cos(\lambda x)\cosh(\lambda x)$

(129)

Con lo cual el campo de desplazamiento total es:

$v(x)={\begin{cases}v^{I}(x)&0<x\leq 3{\hbox{ m}}\\v^{II}(x)&3{\hbox{ m}}\leq x\leq 4{\hbox{ m}}\\v^{III}(x)&4{\hbox{ m}}\leq x<5{\hbox{ m}}\end{cases}}$

(130)

$v^{I}(x)=9.818452x10^{-9}\sin(\lambda x)\cosh(\lambda x)+9.818452x10^{-9}\cos(\lambda x)\sinh(\lambda x)$ $-6.690465x10^{-9}\cos(\lambda x)\cosh(\lambda x)$

(131)

$v^{II}(x)=1.034235x10^{-7}\sin(\lambda (x-3)]\sinh(\lambda (x-3)]$ $+1.032491x10^{-7}\sin(\lambda (x-3)]\cosh =\lambda (x-3)$ $-5.050451x10^{-7}\cos(\lambda (x-3)]\sinh =\lambda (x-3)$ $+4.948749x10^{-7}\cos(\lambda (x-3)]\cosh =\lambda (x-3)-1.0x10^{-6}$

(132)

$v^{III}(x)=1.683667x10^{-5}\sin(\lambda x)\sinh(\lambda x)-1.683648x10^{-5}\sin(\lambda x)\cosh(\lambda x)$ $+2.352573x10^{-4}\cos(\lambda x)\sinh(\lambda x)-2.352573x10^{-4}\cos(\lambda x)\cosh(\lambda x)$

(133)

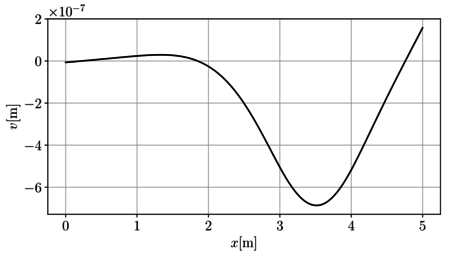
En la Figura 11 se presenta de forma gráfica el campo de desplazamiento vertical en toda la viga.

Cálculo de las fuerzas que el suelo le hace a la viga

La fuerza que el suelo ejerce sobre la viga se calcula a partir del campo de desplazamientos de la siguiente forma:

$f_{S}(x)=-kv(x)={\begin{cases}f_{S}^{I}(x)&0<x\leq 3{\hbox{ m}}\\f_{S}^{II}(x)&3{\hbox{ m}}\leq x\leq 4{\hbox{ m}}\\f_{S}^{III}(x)&4{\hbox{ m}}\leq x<5{\hbox{ m}}\end{cases}}$

(134)

donde:

$f_{S}^{I}(x)=-kv^{I}(x)=-9.818452x10^{-3}\sin(\lambda x)\cosh(\lambda x)$ $-9.818452x10^{-3}\cos(\lambda x)\sinh(\lambda x)+6.690465x10^{-3}\cos(\lambda x)\cosh(\lambda x)$

(135)

$f_{S}^{II}(x)=-kv^{II}(x)=-0.1034235\sin =\lambda (x-3)\sinh =\lambda (x-3)$ $-0.1032491\sin =\lambda (x-3)\cosh =\lambda (x-3)$ $+0.5050450\cos =\lambda (x-3)\sinh =\lambda (x-3)$ $-0.4948749\cos =\lambda (x-3)\cosh =\lambda (x-3)+1$

(136)

$f_{S}^{III}(x)=-kv^{III}(x)=1.684965x10^{-5}\sin(\lambda x)\sinh(\lambda x)$ $-1.684965x10^{-5}\sin(\lambda x)\cosh(\lambda x)$ $+2.352508x10^{-4}\cos(\lambda x)\sinh(\lambda x)-2.352506x10^{-4}\cos(\lambda x)\cosh(\lambda x)$

(137)

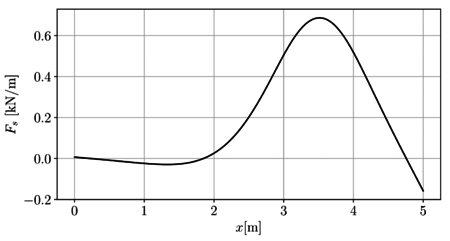
Como resumen de las anteriores tres ecuaciones, en la Figura 14b se presenta la fuerza el suelo ejerce sobre la viga.

(a) Campo de desplazamientos	(b) Campo de la fuerza que el suelo ejerce sobre la viga
Figura 14. Campos de desplazamiento en la viga y fuerza que el suelo ejerce sobre esta

Como revisión de las fuerzas que el suelo realiza sobre la viga y por ende del campo de desplazamientos, a continuación se revisará el equilibrio vertical y rotacional al rededor del punto 1 para toda la viga:

$\sum FY=-1-k\int {_{0}^{3}v^{I}(x)dx'}_{A}-k\int _{3}^{4}v^{II}(x)dx-k\int _{4}^{5}v^{III}(x)dx=0$ (138.a) $\sum M_{1}=-3.5-k\int _{0}^{3}v^{I}(x)xdx-k\int _{3}^{4}v^{II}(x)xdx-k\int _{4}^{5}v^{III}(x)xdx=0$ (138.b)

Cálculo de las fuerzas internas

A partir del campo de desplazamientos es posible obtener el campo de momento flector como:

$M(x)=EI{\frac {d^{2}v}{dx^{2}}}(x)={\begin{cases}M^{I}(x)&0<x\leq 3{\hbox{ m}}\\M^{II}(x)&3{\hbox{ m}}\leq x\leq 4{\hbox{ m}}\\M^{III}(x)&4{\hbox{ m}}\leq x<5{\hbox{ m}}\end{cases}}$

(139)

donde:

$M^{I}(x)=EI{\frac {d^{2}v^{I}}{dx}}(x)=1.419262x10^{-3}\sin(\lambda x)\sinh(\lambda x)$ $-2.082808x10^{-3}\sin(\lambda x)\cosh(\lambda x)+2.082808x10^{-3}\cos(\lambda x)\sinh(\lambda x)$

(140)

$M^{II}(x)=EI{\frac {d^{2}v^{II}}{dx^{2}}}(x)=-0.104979\sin =1.535260(x-3)\sinh =1.535260(x-3)$ $+0.107136\sin =1.535260(x-3)\cosh =1.535260(x-3)$ $+0.0219024\cos =1.535260(x-3)\sinh =1.535260(x-3)$ $+0.0219394\cos =1.535260(x-3)\cosh =1.535260(x-3)$

(141)

$M^{III}(x)=EI{\frac {d^{2}v^{III}}{dx^{2}}}(x)=49.905617\sin(\lambda x)\sinh(\lambda x)$ $-49.905603\sin(\lambda x)\cosh(\lambda x)$ $-3.571557\cos(\lambda x)\sinh(\lambda x)+3.571597\cos(\lambda x)\cosh(\lambda x)$

(142)

Mientras que el campo de fuerza cortante se calcula como:

$V(x)=-EI{\frac {d^{3}v}{dx^{3}}}(x)={\begin{cases}V^{I}(x)&0<x\leq 3{\hbox{ m}}\\V^{II}(x)&3{\hbox{ m}}\leq x\leq 4{\hbox{ m}}\\V^{III}(x)&4{\hbox{ m}}\leq x<5{\hbox{ m}}\end{cases}}$

(143)

donde:

$V^{I}(x)=-EI{\frac {d^{3}v^{I}}{dx^{3}}}{(x'}_{6}.395303x10x10^{-3}\sin(\lambda x)\sinh(\lambda x)$ $-2.178936x10^{-3}\sin(\lambda x)\cosh(\lambda x)-2.178936x10^{-3}\cos(\lambda x)\sinh(\lambda x)$

(144)

$V^{II}(x)=-EI{\frac {d^{3}v^{II}}{dx}}(x)=-0.1308560\sin =1.535260(x-3)\sinh =1.535260(x-3)$ $+0.1948525\sin =1.535260(x-3)\cosh =1.535260(x-3)$ $+0.1274870\cos =1.535260(x-3)\sinh =1.535260(x-3)$ $-0.1981079\cos =1.535260(x-3)\cosh =1.535260(x-3)$

(145)

$V^{III}(x)=-EI{\frac {d^{3}v^{III}}{dx^{3}}}(x)=71.134797\sin(\lambda x)\sinh(\lambda x)$ $-71.134758\sin(\lambda x)\cosh(\lambda x)-82.101417\cos(\lambda x)\sinh(\lambda x)$ $+82.101334\cos(\lambda x)\cosh(\lambda x)$

(146)

En las Figuras 12a y 12b se presentan respectivamente los campos de fuerza cortante y momento flector para toda la viga.

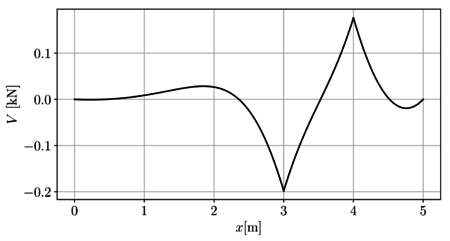
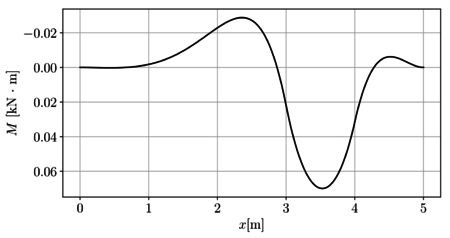
(a) Fuerza cortante	(b) Momento flector
Figura 15. Campos de fuerzas internas

En el siguiente enlace se encuentra el código de Python empleado para la solución de este ejemplo:

https://drive.google.com/open?id=1yq_G2WYO3X6oUW3Nnlq4jb9ATUd_WvlP

8.3 Pórtico plano

Resolver el pórtico plano presentado en la Figura 16a cuyos elementos son rectangulares de base y altura iguales a ${\textstyle L/20}$ y cuyo módulo de elasticidad es ${\textstyle E}$.

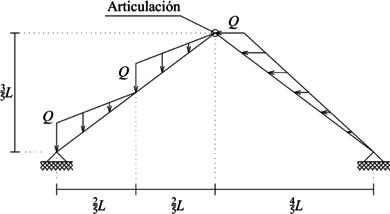
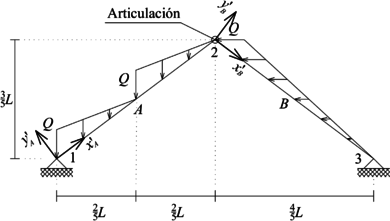
(a) Problema a resolver	(b) Discretización
Figura 16. Pórtico plano sometido a cargas externas oblicuas y discretización empleada para su solución

Discretización

En la Figura 16b se presenta la discretización y ejes locales a emplear en la solución de este ejercicio.

Definición de la carga externa en coordenadas locales

A partir de la Figura 16a, es posible obtener el valor de la carga externa en dirección ${\textstyle {x'}_{A}}$ del elemento ${\textstyle A}$:

${p_{A}(x'}_{A})={\begin{cases}{\dfrac {24}{25}}Q\left(-{\dfrac {1}{2}}+{\dfrac {{x'}_{A}}{L}}\right)\qquad &{0<x'}_{A}<{\dfrac {L}{2}}\\[0.3cm]{\dfrac {24}{25}}Q\left(-1+{\dfrac {{x'}_{A}}{L}}\right)&{\dfrac {L}{2}}{<x'}_{A}<L\end{cases}}$

(147)

Mientras que la carga externa en dirección del eje ${\textstyle {y'}_{A}}$ en el elemento ${\textstyle A}$ es:

${q_{A}(x'}_{A})={\begin{cases}{\dfrac {32}{25}}Q\left(-{\dfrac {1}{2}}+{\dfrac {{x'}_{A}}{L}}\right)\qquad &{0<x'}_{A}<{\dfrac {L}{2}}\\[0.3cm]{\dfrac {32}{25}}Q\left(-1+{\dfrac {{x'}_{A}}{L}}\right)&{\dfrac {L}{2}}{<x'}_{A}<L\end{cases}}$

(148)

De forma similar, se tiene que las cargas externas en dirección de los ejes ${\textstyle {x'}_{B}}$ y ${\textstyle {y'}_{B}}$ en el elemento ${\textstyle B}$ son respectivamente:

${p_{B}(x'}_{B})={\dfrac {12}{25}}Q\left(-1+{\dfrac {{x'}_{B}}{L}}\right)$ (149.a) ${q_{B}(x'}_{B})={\dfrac {9}{25}}Q\left(-1+{\dfrac {{x'}_{B}}{L}}\right)$ (149.b)

Cálculo del sistema de ecuaciones de cada elemento en coordenadas locales

A partir de lo presentado en (86) se tiene que las ecuaciones del método de rigidez en coordenadas locales para los elementos ${\textstyle A}$ y ${\textstyle B}$ son respectivamente:

${\begin{Bmatrix}\left.{FX'}_{1}\right.^{A}\\\left.{FY'}_{1}\right.^{A}\\\left.{M'}_{1}\right.^{A}\\\left.{FX'}_{2}\right.^{A}\\\left.{FY'}_{2}\right.^{A}\\\left.{M'}_{2}\right.^{A}\end{Bmatrix}}=E{\begin{bmatrix}{\dfrac {L}{400}}&0&0&-{\dfrac {L}{400}}&0&0\\0&{\dfrac {L}{160000}}&{\dfrac {L^{2}}{320000}}&0&-{\dfrac {L}{160000}}&{\dfrac {L^{2}}{320000}}\\0&{\dfrac {L^{2}}{320000}}&{\dfrac {L^{3}}{480000}}&0&-{\dfrac {L^{2}}{320000}}&{\dfrac {L^{3}}{960000}}\\-{\dfrac {L}{400}}&0&0&{\dfrac {L}{400}}&0&0\\0&-{\dfrac {L}{160000}}&-{\dfrac {L^{2}}{320000}}&0&{\dfrac {L}{160000}}&-{\dfrac {L^{2}}{320000}}\\0&{\dfrac {L^{2}}{320000}}&{\dfrac {L^{3}}{960000}}&0&-{\dfrac {L^{2}}{320000}}&{\dfrac {L^{3}}{480000}}\end{bmatrix}}{\begin{Bmatrix}\left.{u'}_{1}\right.^{A}\\\left.{v'}_{1}\right.^{A}\\\left.\theta '_{1}\right.^{A}\\\left.{u'}_{2}\right.^{A}\\\left.{v'}_{2}\right.^{A}\\\left.\theta '_{2}\right.^{A}\end{Bmatrix}}+Q{\begin{Bmatrix}{\dfrac {7}{50}}L\\{\dfrac {47}{250}}L\\{\dfrac {41}{1500}}L^{2}\\{\dfrac {1}{10}}L\\{\dfrac {33}{250}}L\\-{\dfrac {13}{500}}L^{2}\end{Bmatrix}}$

(150)

${\begin{Bmatrix}\left.{FX'}_{2}\right.^{B}\\\left.{FY'}_{2}\right.^{B}\\\left.{M'}_{2}\right.^{B}\\\left.{FX'}_{3}\right.^{B}\\\left.{FY'}_{3}\right.^{B}\\\left.{M'}_{3}\right.^{B}\end{Bmatrix}}=E{\begin{bmatrix}{\dfrac {L}{400}}&0&0&-{\dfrac {L}{400}}&0&0]\\0&{\dfrac {L}{160000}}&{\dfrac {L^{2}}{320000}}&0&-{\dfrac {L}{160000}}&{\dfrac {L^{2}}{320000}}\\0&{\dfrac {L^{2}}{320000}}&{\dfrac {L^{3}}{480000}}&0&-{\dfrac {L^{2}}{320000}}&{\dfrac {L^{3}}{960000}}\\-{\dfrac {L}{400}}&0&0&{\dfrac {L}{400}}&0&0\\0&-{\dfrac {L}{160000}}&-{\dfrac {L^{2}}{320000}}&0&{\dfrac {L}{160000}}&-{\dfrac {L^{2}}{320000}}\\0&{\dfrac {L^{2}}{320000}}&{\dfrac {L^{3}}{960000}}&0&-{\dfrac {L^{2}}{320000}}&{\dfrac {L^{3}}{480000}}\end{bmatrix}}{\begin{Bmatrix}\left.{u'}_{2}\right.^{B}\\\left.{v'}_{2}\right.^{B}\\\left.\theta '_{2}\right.^{B}\\\left.{u'}_{3}\right.^{B}\\\left.{v'}_{3}\right.^{B}\\\left.\theta '_{3}\right.^{B}\end{Bmatrix}}+Q{\begin{Bmatrix}{\dfrac {4}{25}}L\\{\dfrac {63}{500}}L\\{\dfrac {9}{500}}L^{2}\\{\dfrac {2}{25}}L\\{\dfrac {27}{500}}L\\-{\dfrac {3}{250}}L^{2}\end{Bmatrix}}$

(151)

Cálculo del sistema de ecuaciones de cada elemento en coordenadas globales

Las ecuaciones (150) y (151) se transforman a coordenadas globales como:

${\begin{Bmatrix}FX_{1}^{A}\\FY_{1}^{A}\\M_{1}^{A}\\FX_{2}^{A}\\FY_{2}^{A}\\M_{2}^{A}\end{Bmatrix}}=E{\begin{bmatrix}{\dfrac {6409}{4000000}}L&{\dfrac {1197}{1000000}}L&-{\dfrac {3}{1600000}}L^{2}&-{\dfrac {6409}{4000000}}L&-{\dfrac {1197}{1000000}}L&-{\dfrac {3}{1600000}}L^{2}\\{\dfrac {1197}{1000000}}L&{\dfrac {113}{125000}}L&{\dfrac {1}{400000}}L^{2}&-{\dfrac {1197}{1000000}}L&-{\dfrac {113}{125000}}L&{\dfrac {1}{400000}}L^{2}\\-{\dfrac {3}{1600000}}L^{2}&{\dfrac {1}{400000}}L^{2}&{\dfrac {1}{480000}}L^{3}&{\dfrac {3}{1600000}}L^{2}&-{\dfrac {1}{400000}}L^{2}&{\dfrac {1}{960000}}L^{3}\\-{\dfrac {6409}{4000000}}L&-{\dfrac {1197}{1000000}}L&{\dfrac {3}{1600000}}L^{2}&{\dfrac {6409}{4000000}}L&{\dfrac {1197}{1000000}}L&{\dfrac {3}{1600000}}L^{2}\\-{\dfrac {1197}{1000000}}L&-{\dfrac {113}{125000}}L&-{\dfrac {1}{400000}}L^{2}&{\dfrac {1197}{1000000}}L&{\dfrac {113}{125000}}L&-{\dfrac {1}{400000}}L^{2}\\-{\dfrac {3}{1600000}}L^{2}&{\dfrac {1}{400000}}L^{2}&{\dfrac {1}{960000}}L^{3}&{\dfrac {3}{1600000}}L^{2}&-{\dfrac {1}{400000}}L^{2}&{\dfrac {1}{480000}}L^{3}\end{bmatrix}}{\begin{Bmatrix}u_{1}\\v_{1}\\\theta _{1}\\u_{2}\\v_{2}\\\theta _{2}^{A}\end{Bmatrix}}+Q{\begin{Bmatrix}-{\dfrac {1}{1250}}L\\{\dfrac {293}{1250}}L\\{\dfrac {41}{1500}}L^{2}\\{\dfrac {1}{1250}}L\\{\dfrac {207}{1250}}L\\-{\dfrac {13}{500}}L^{2}\end{Bmatrix}}$

(152)

${\begin{Bmatrix}FX_{2}^{B}\\FY_{2}^{B}\\M_{2}^{B}\\FX_{3}^{B}\\FY_{3}^{B}\\M_{3}^{B}\end{Bmatrix}}=E{\begin{bmatrix}{\dfrac {6409}{4000000}}L&-{\dfrac {1197}{1000000}}L&{\dfrac {3}{1600000}}L^{2}&-{\dfrac {6409}{4000000}}L&{\dfrac {1197}{1000000}}L&{\dfrac {3}{1600000}}L^{2}\\-{\dfrac {1197}{1000000}}L&{\dfrac {113}{125000}}L&{\dfrac {1}{400000}}L^{2}&{\dfrac {1197}{1000000}}L&-{\dfrac {113}{125000}}L&{\dfrac {1}{400000}}L^{2}\\{\dfrac {3}{1600000}}L^{2}&{\dfrac {1}{400000}}L^{2}&{\dfrac {1}{480000}}L^{3}&-{\dfrac {3}{1600000}}L^{2}&-{\dfrac {1}{400000}}L^{2}&{\dfrac {1}{960000}}L^{3}\\-{\dfrac {6409}{4000000}}L&{\dfrac {1197}{1000000}}L&-{\dfrac {3}{1600000}}L^{2}&{\dfrac {6409}{4000000}}L&-{\dfrac {1197}{1000000}}L&-{\dfrac {3}{1600000}}L^{2}\\{\dfrac {1197}{1000000}}L&-{\dfrac {113}{125000}}L&-{\dfrac {1}{400000}}L^{2}&-{\dfrac {1197}{1000000}}L&{\dfrac {113}{125000}}L&-{\dfrac {1}{400000}}L^{2}\\{\dfrac {3}{1600000}}L^{2}&{\dfrac {1}{400000}}L^{2}&{\dfrac {1}{960000}}L^{3}&-{\dfrac {3}{1600000}}L^{2}&-{\dfrac {1}{400000}}L^{2}&{\dfrac {1}{480000}}L^{3}\end{bmatrix}}{\begin{Bmatrix}u_{2}\\v_{2}\\\theta _{2}^{B}\\u_{3}\\v_{3}\\\theta _{3}\end{Bmatrix}}+Q{\begin{Bmatrix}{\dfrac {509}{2500}}L\\{\dfrac {3}{625}}L\\{\dfrac {9}{500}}L^{2}\\{\dfrac {241}{2500}}L\\-{\dfrac {3}{625}}L\\-{\dfrac {3}{250}}L^{2}\end{Bmatrix}}$

(153)

Cálculo de los desplazamientos nodales desconocidos

A partir del equilibrio de los nudos en las direcciones donde las fuerzas externas o internas son conocidas, se obtiene el siguiente sistema lineal de cinco ecuaciones con igual número de incógnitas:

${\begin{Bmatrix}M_{1}\\FX_{2}\\FY_{2}\\M_{2}^{A}\\M_{2}^{B}\\M_{3}\end{Bmatrix}}={\begin{Bmatrix}0\\0\\0\\0\\0\\0\end{Bmatrix}}=E{\begin{bmatrix}{\dfrac {1}{480000}}L^{3}&{\dfrac {3}{1600000}}L^{2}&-{\dfrac {1}{400000}}L^{2}&{\dfrac {1}{960000}}L^{3}&0&0\\{\dfrac {3}{1600000}}L^{2}&{\dfrac {6409}{2000000}}L&0&{\dfrac {3}{1600000}}L^{2}&{\dfrac {3}{1600000}}L^{2}&{\dfrac {3}{1600000}}L^{2}\\-{\dfrac {1}{400000}}L^{2}&0&{\dfrac {113}{62500}}L&-{\dfrac {1}{400000}}L^{2}&{\dfrac {1}{400000}}L^{2}&{\dfrac {1}{400000}}L^{2}\\{\dfrac {1}{960000}}L^{3}&{\dfrac {3}{1600000}}L^{2}&-{\dfrac {1}{400000}}L^{2}&{\dfrac {1}{480000}}L^{3}&0&0\\0&{\dfrac {3}{1600000}}L^{2}&{\dfrac {1}{400000}}L^{2}&0&{\dfrac {1}{480000}}L^{3}&{\dfrac {1}{960000}}L^{3}\\0&{\dfrac {3}{1600000}}L^{2}&{\dfrac {1}{400000}}L^{2}&0&{\dfrac {1}{960000}}L^{3}&{\dfrac {1}{480000}}L^{3}\end{bmatrix}}{\begin{Bmatrix}\theta _{1}\\u_{2}\\v_{2}\\\theta _{2}^{A}\\\theta _{2}^{B}\\\theta _{3}\end{Bmatrix}}+Q{\begin{Bmatrix}{\dfrac {41}{1500}}L^{2}\\{\dfrac {511}{2500}}L\\{\dfrac {213}{1250}}L\\-{\dfrac {13}{500}}L^{2}\\{\dfrac {9}{500}}L^{2}\\-{\dfrac {3}{250}}L^{2}\end{Bmatrix}}$

(154)

Cuya solución es:

${\begin{Bmatrix}\theta _{1}\\u_{2}\\v_{2}\\\theta _{2}^{A}\\\theta _{2}^{B}\\\theta _{3}\end{Bmatrix}}={\dfrac {Q}{EL}}{\begin{Bmatrix}-{\dfrac {1395895}{54}}\\-{\dfrac {125}{2}}L\\-{\dfrac {2500}{27}}L\\{\dfrac {1368905}{54}}\\-{\dfrac {823415}{54}}\\{\dfrac {731785}{54}}\end{Bmatrix}}$

(155)

Cálculo de las reacciones

Del equilibrio de los nodos en las direcciones donde se desconocen las reacciones se obtiene el siguiente sistema lineal de cuatro ecuaciones:

${\begin{Bmatrix}FX_{1}\\FY_{1}\\FX_{3}\\FY_{3}\end{Bmatrix}}=E{\begin{bmatrix}-{\dfrac {3}{1600000}}L^{2}&-{\dfrac {6409}{4000000}}L&-{\dfrac {1197}{1000000}}L&-{\dfrac {3}{1600000}}L^{2}&0&0\\{\dfrac {1}{400000}}L^{2}&-{\dfrac {1197}{1000000}}L&-{\dfrac {113}{125000}}L&{\dfrac {1}{400000}}L^{2}&0&0\\0&-{\dfrac {6409}{4000000}}L&{\dfrac {1197}{1000000}}L&0&-{\dfrac {3}{1600000}}L^{2}&-{\dfrac {3}{1600000}}L^{2}\\0&{\dfrac {1197}{1000000}}L&-{\dfrac {113}{125000}}L&0&-{\dfrac {1}{400000}}L^{2}&-{\dfrac {1}{400000}}L^{2}\end{bmatrix}}{\begin{Bmatrix}\theta _{1}\\u_{2}\\v_{2}\\\theta _{2}^{A}\\\theta _{2}^{B}\\\theta _{3}\end{Bmatrix}}+QL{\begin{Bmatrix}-{\dfrac {1}{1250}}\\{\dfrac {293}{1250}}\\{\dfrac {241}{2500}}\\-{\dfrac {3}{625}}\end{Bmatrix}}=QL{\begin{Bmatrix}{\dfrac {19}{90}}\\{\dfrac {47}{120}}\\{\dfrac {4}{45}}\\{\dfrac {1}{120}}\end{Bmatrix}}$

(156)

donde se emplearon los valores de los desplazamientos nodales presentados en (155).

Como revisión de las reacciones obtenidas anteriormente se realizará el equilibrio de toda la estructura:

$\sum FX=FX_{1}+FX_{3}-{\frac {3}{10}}QL=0$ (157.a) $\sum FY=FY_{1}+FY_{3}-{\frac {1}{5}}QL-{\frac {1}{5}}QL=0$ (157.b) $\sum M_{1}=FY_{3}\cdot {\frac {8}{5}}L-{\frac {1}{5}}QL\cdot {\frac {2}{15}}L-{\frac {1}{5}}QL\cdot {\frac {8}{15}}L+{\frac {3}{10}}QL\cdot {\frac {2}{5}}L=0$ (157.c)

Cálculo del campo de desplazamiento del elemento $A$

Para poder calcular el campo de desplazamiento homogéneo del elemento ${\textstyle A}$ es necesario haber transformado los desplazamientos en los extremos de este elemento de coordenadas globales a locales. Una vez realizado esto, se tiene que el campo de desplazamiento homogéneo en dirección ${\textstyle {x'}_{A}}$ del elemento ${\textstyle A}$ es:

${u_{A}^{h}(x'}_{A})=-{\frac {950Q}{9E}}{\frac {{x'}_{A}}{L}}$

(158)

Mientras que a partir de lo presentado en (22) y (147), se tiene que el campo de desplazamiento empotrado en dirección ${\textstyle {x'}_{A}}$ del elemento ${\textstyle A}$ es:

${u_{A}^{f}(x'}_{A})={\begin{cases}{\dfrac {Q}{E}}\left[-56{\dfrac {{x'}_{A}}{L}}+96\left({\dfrac {{x'}_{A}}{L}}\right)^{2}-64\left({\dfrac {{x'}_{A}}{L}}\right)^{3}\right]&{0<x'}_{A}\leq {\dfrac {L}{2}}\\[0.5cm]{\dfrac {Q}{E}}\left[24-152{\dfrac {{x'}_{A}}{L}}+192\left({\dfrac {{x'}_{A}}{L}}\right)^{2}-64\left({\dfrac {{x'}_{A}}{L}}\right)^{3}\right]&{\dfrac {L}{2}}\leq {x'}<L\end{cases}}$

(159)

Con lo cual el campo total de desplazamiento en dirección ${\textstyle {x'}_{A}}$ del elemento ${\textstyle A}$ es:

${u_{A}(x'}_{A})={\begin{cases}{\dfrac {Q}{E}}\left[-{\dfrac {1454}{9}}{\dfrac {{x'}_{A}}{L}}+96\left({\dfrac {{x'}_{A}}{L}}\right)^{2}-64\left({\dfrac {{x'}_{A}}{L}}\right)^{3}\right]&{0<x'}_{A}\leq {\dfrac {L}{2}}\\[0.4cm]{\dfrac {Q}{E}}\left[24-{\dfrac {2318}{9}}{\dfrac {{x'}_{A}}{L}}+192\left({\dfrac {{x'}_{A}}{L}}\right)^{2}-64\left({\dfrac {{x'}_{A}}{L}}\right)^{3}\right]&{\dfrac {L}{2}}\leq {x'}<L\end{cases}}$

(160)

Procediendo de forma similar a como se realizó en el ejemplo 8.1, se tiene que los campos homogéneo, empotrado y total en dirección ${\textstyle {y'}_{A}}$ del elemento ${\textstyle A}$ son respectivamente:

${v_{A}^{h}(x'}_{A})={\dfrac {Q}{L}}\left[-{\dfrac {1395895}{54}}{\frac {{x'}_{A}}{L}}+26240\left({\frac {{x'}_{A}}{L}}\right)^{2}-{\frac {1280}{3}}\left({\frac {{x'}_{A}}{L}}\right)^{3}\right]$

(161)

${v_{A}^{f}(x'}_{A})={\begin{cases}{\dfrac {Q}{E}}\left[-26240\left({\dfrac {{x'}_{A}}{L}}\right)^{2}+60160\left({\dfrac {{x'}_{A}}{L}}\right)^{3}-51200\left({\dfrac {{x'}_{A}}{L}}\right)^{4}+20480\left({\dfrac {{x'}_{A}}{L}}\right)^{5}\right]&{0<x'}_{A}\leq {\dfrac {L}{2}}\\[0.3cm]{\dfrac {Q}{E}}\left[-3200+25600{\dfrac {{x'}_{A}}{L}}-103040\left({\dfrac {{x'}_{A}}{L}}\right)^{2}+162560\left({\dfrac {{x'}_{A}}{L}}\right)^{3}-102400\left({\dfrac {{x'}_{A}}{L}}\right)^{4}+20480\left({\dfrac {{x'}_{A}}{L}}\right)^{5}\right]&{\dfrac {L}{2}}\leq {x'}<L\end{cases}}$

(162)

${v_{A}(x'}_{A})={\begin{cases}{\dfrac {Q}{E}}\left[-{\dfrac {1395895}{54}}{\dfrac {{x'}_{A}}{L}}+{\dfrac {179200}{3}}\left({\dfrac {{x'}_{A}}{L}}\right)^{3}-51200\left({\dfrac {{x'}_{A}}{L}}\right)^{4}+20480\left({\dfrac {{x'}_{A}}{L}}\right)^{5}\right]&0\leq {x'}_{A}\leq {\dfrac {L}{2}}\\[0.3cm]{\dfrac {Q}{E}}\left[-3200-{\dfrac {13495}{54}}{\dfrac {{x'}_{A}}{L}}-76800\left({\dfrac {{x'}_{A}}{L}}\right)^{2}+{\dfrac {486400}{3}}\left({\dfrac {{x'}_{A}}{L}}\right)^{3}-102400\left({\dfrac {{x'}_{A}}{L}}\right)^{4}+20480\left({\dfrac {{x'}_{A}}{L}}\right)^{5}\right]&{\dfrac {L}{2}}\leq {x'}_{A}\leq L\end{cases}}$

(163)

Cálculo del campo de desplazamiento del elemento $B$

De igual forma a como se realizó con el elemento ${\textstyle A}$, se tiene que los campos de desplazamiento homogéneo, empotrado y total en dirección ${\textstyle {x'}_{B}}$ del elemento ${\textstyle B}$ son respectivamente:

${u_{B}^{h}(x'}_{B})={\frac {Q}{E}}\left({\frac {50}{9}}-{\frac {50}{9}}{\frac {{x'}_{B}}{L}}\right)$

(164)

${u_{B}^{f}(x'}_{B})={\frac {Q}{E}}\left[-64{\frac {{x'}_{B}}{L}}+96\left({\frac {{x'}_{B}}{L}}\right)^{2}-32\left({\frac {{x'}_{B}}{L}}\right)^{3}\right]$

(165)

${u_{B}(x'}_{B})={\frac {Q}{E}}\left[{\frac {50}{9}}-{\frac {626}{9}}{\dfrac {{x'}_{B}}{L}}+96\left({\dfrac {{x'}_{B}}{L}}\right)^{2}-32\left({\dfrac {{x'}_{B}}{L}}\right)^{3}\right]$

(166)

Mientras que los campos de desplazamiento homogéneo, empotrado y total en dirección ${\textstyle {y'}_{B}}$ del elemento ${\textstyle B}$ son respectivamente:

${v_{B}^{h}(x'}_{B})={\frac {Q}{E}}\left[-{\frac {6025}{54}}-{\frac {823415}{54}}{\frac {{x'}_{B}}{L}}+17280\left({\frac {{x'}_{B}}{L}}\right)^{2}-1920\left({\frac {{x'}_{B}}{L}}\right)^{3}\right]$

(167)

${v_{B}^{f}(x'}_{B})={\frac {Q}{E}}\left[-17280\left({\frac {{x'}_{B}}{L}}\right)^{2}+40320\left({\frac {{x'}_{B}}{L}}\right)^{3}-28800\left({\frac {{x'}_{B}}{L}}\right)^{4}+5760\left({\frac {{x'}_{B}}{L}}\right)^{5}\right]$

(168)

${v_{B}(x'}_{B})={\frac {Q}{E}}\left[-{\frac {6025}{54}}-{\frac {823415}{54}}{\frac {{x'}_{B}}{L}}+38400\left({\frac {{x'}_{B}}{L}}\right)^{3}-28800\left({\frac {{x'}_{B}}{L}}\right)^{4}+5760\left({\frac {{x'}_{B}}{L}}\right)^{5}\right]$

(169)

Como síntesis de los campos de desplazamiento calculados anteriormente en la Figura 17d se presenta la configuración deformada de la estructura.

Cálculo de las fuerzas internas

A partir de la derivación de los campos de desplazamientos en coordenadas locales de ambos elementos se obtiene las fuerzas internas en estos (ecuaciones (2) y (4)):

${P_{A}(x'}_{A})=AE{\dfrac {{du'}_{A}}{{dx'}_{A}}}{(x'}_{A})={\begin{cases}QL\left[-{\dfrac {727}{1800}}+{\dfrac {12}{25}}{\dfrac {{x'}_{A}}{L}}-{\dfrac {12}{25}}\left({\dfrac {{x'}_{A}}{L}}\right)^{2}\right]\qquad &{0<x'}_{A}<{\dfrac {L}{2}}\\[0.4cm]QL\left[-{\dfrac {1159}{1800}}+{\dfrac {24}{25}}{\dfrac {{x'}_{A}}{L}}-{\dfrac {12}{25}}\left({\dfrac {{x'}_{A}}{L}}\right)^{2}\right]&{\dfrac {L}{2}}{<x'}L<L\end{cases}}$

(170)

${V_{A}(x'}I)=-EI{\dfrac {{d^{3}v'}_{A}}{\left.{dx'}_{A}\right.^{3}}}{(x'}_{A})={\begin{cases}QL\left[-{\dfrac {14}{75}}+{\dfrac {16}{25}}{\dfrac {{x'}_{A}}{L}}-{\dfrac {16}{25}}\left({\dfrac {{x'}_{A}}{L}}\right)^{2}\right]\qquad &{0<x'}_{A}\leq {\dfrac {L}{2}}\\[0.4cm]QL\left[-{\dfrac {38}{75}}+{\dfrac {32}{25}}{\dfrac {{x'}_{A}}{L}}-{\dfrac {16}{25}}\left({\dfrac {{x'}_{A}}{L}}\right)^{2}\right]&{\dfrac {L}{2}}\leq {x'}<L\end{cases}}$

(171)

${M_{A}(x'}_{A})=EI{\dfrac {{d^{2}v'}_{A}}{\left.{dx'}_{A}\right.^{2}}}{(x'}_{A}){\begin{cases}QL^{2}\left[{\dfrac {14}{75}}{\dfrac {{x'}_{A}}{L}}-{\dfrac {8}{25}}\left({\dfrac {{x'}_{A}}{L}}\right)^{2}+{\dfrac {16}{75}}\left({\dfrac {{x'}_{A}}{L}}\right)^{3}\right]\qquad &{0<x'}_{A}\leq {\dfrac {L}{2}}\\[0.3cm]QL^{2}\left[-{\dfrac {2}{25}}+{\dfrac {38}{75}}{\dfrac {{x'}_{A}}{L}}-{\dfrac {16}{25}}\left({\dfrac {{x'}_{A}}{L}}\right)^{2}+{\dfrac {16}{75}}\left({\dfrac {{x'}_{A}}{L}}\right)^{3}\right]&{\dfrac {L}{2}}\leq {x'}<L\end{cases}}$

(172)

${P_{B}(x'}_{B})=AE{\dfrac {{du'}_{B}}{{x'}_{B}}}{(x'}=QLL\left[-{\frac {313}{1800}}+{\frac {12}{25}}{\frac {{x'}_{B}}{L}}-{\frac {6}{25}}\left({\frac {{x'}_{B}}{L}}\right)^{2}\right]$ (173.a) ${V_{B}(x'}_{B})=EI{\dfrac {{d^{3}v'}_{B}}{\left.{dx'}_{B}\right.^{3}}}{(x'}_{B})=QL\left[-{\frac {3}{25}}+{\frac {9}{25}}{\frac {{x'}_{B}}{L}}-{\frac {9}{50}}\left({\frac {{x'}_{B}}{L}}\right)^{2}\right]$ (173.b) ${M_{B}(x'}_{B})=EI{\dfrac {{d^{2}v'}_{B}}{\left.{dx'}_{B}\right.^{2}}}{(x'}_{Q}L^{2}L^{2}\left[{\frac {3}{25}}{\frac {{x'}_{B}}{L}}-{\frac {9}{50}}\left({\frac {{x'}_{B}}{L}}\right)^{2}+{\frac {3}{50}}\left({\frac {{x'}_{B}}{L}}\right)^{3}\right]$ (173.c)

Como resumen en las Figuras 17a a 17c se presentan los diagramas de fuerzas internas en los dos elementos que componen la estructura.

(a) Fuerza axial dividida ${\textstyle QL}$, ${\textstyle \left({\dfrac {P}{QL}}\right)}$	(b) Fuerza cortante dividida ${\textstyle QL}$, ${\textstyle \left({\dfrac {V}{QL}}\right)}$
(c) Momento flector dividido ${\textstyle QL^{2}}$, ${\textstyle \left({\dfrac {M}{QL^{2}}}\right)}$	(d) Configuración deformada de la estructura, los desplazamientos adimensionalizados han sido escalados 0.00002 veces
Figura 17. Diagramas de fuerza internas adimensionalizadas y configuración deformada de la estructura

En el siguiente enlace se encuentra el código de Python empleado para la solución de este ejemplo:

https://drive.google.com/open?id=1WNnbqC-09Odkh3GajgONgi8Al1sKhRz_

9. Conclusiones

1. Se ha presentado una extensión del método de rigidez para estructuras reticulares planas, la cual puede ser aplicable para obtener la respuesta total de este tipo de estructural ante cualquier carga externa. Esta metodología ha sido nombrada el método de rigidez con funciones de Green (Green function stiffness method) y a partir de sus ideas básicas, esta metodología puede expandirse a otras configuraciones estructurales.
2. La metodología presentada, al ser definida de forma explícita para cualquier carga externa, permite minimizar el número de elementos que se emplearían respecto a aquellos usando el método de rigidez o el M.E.F. Como caso particular se tiene que en los textos clásicos de análisis matricial de estructuras [15,16,17] es usual subdividir los elementos si las cargas externas son complejas y estas no aparecen en sus tablas de fuerzas de empotramiento, lo cual no es necesario con la presente metodología.
3. Se extiende el concepto de fuerzas de empotramiento típico del método de rigidez al concepto de campo de desplazamientos empotrado, el cual, al emplear las funciones de Green permite el cálculo de los campos de desplazamientos incluso cuando las fuerzas externas son complejas.
4. En la metodología presentada se da una gran importancia al cálculo de los campos de desplazamientos. Esto se debe a que los desplazamientos son las variables dependientes principales de los problemas de análisis estructural e incluso a partir de estos es posible calcular los campos de fuerzas internas.
5. Se presenta una forma novedosa de expresar a las funciones de Green en términos de las funciones de forma “exactas” para los diferentes tipos de elementos estructurales estudiados. Esta se base propiedades de simetría observadas tanto en las funciones de forma como en las funciones de Green.
6. Se hace explícita la gran importancia que tienen las funciones de forma “exactas” en la respuesta estructural, ya que estas no solo son la base para el cálculo del campo de desplazamiento homogéneo sinó también del empotrado pues aparecen de forma natural en las funciones de Green y en las fuerzas de empotramiento.
7. En los apéndices se presenta la equivalencia entre la metodología presentada en este artículo, la cual parte de las ecuaciones diferenciales gobernantes para cuatro tipos de elementos diferentes y aquella obtenida por medio de una formulación “exacta” del M.E.F. (la cual parte de la forma débil de dichas ecuaciones diferenciales).

10. Agradecimientos

Las ideas fundamentales de este artículo han nacido del los cursos de análisis estructural y mecánica estructural que el autor Juan Camilo Molina-Villegas ha dictado en lo últimos años en la Universidad de Medellín y en la Universidad Nacional de Colombia - Sede Medellín, y de los cuales han sido estudiantes los otros dos autores. Los comentarios de muchos de los estudiantes de dichos cursos han contribuido al nivel actual de maduración de las ideas presentadas en este artículo, por lo cual los autores les agradecen infinitamente.

Apéndices

A. Formulación exacta del M.E.F. para un elemento tipo barra

A continuación se presentará una formulación “exacta” del M.E.F. la cual es equivalente a la presentada en la sección 4, la cual también se basa en la solución del P.V.F (8) pero ahora a partir de la llamada forma débil de (8.a) en lugar de esta directamente. De forma similar a como se indicó para el método de rigidez con funciones de Green, el campo de desplazamientos se expresará como:

$u(x)=u_{h}(x)+u_{f}(x)=\psi _{1}(x)u_{i}+\psi _{4}(x)u_{j}+u_{f}(x)$

(174)

donde ${\textstyle \psi _{1}(x)}$ y ${\textstyle \psi _{4}(x)}$ son las funciones de forma presentadas en (12) y ${\textstyle u_{f}(x)}$ se calcula según lo presentado en (22).

Además, es fácil probar que las funciones de forma ${\textstyle \psi _{1}(x)}$ y ${\textstyle \psi _{4}(x)}$ cumplen la siguiente propiedad asociada con (10.a) (ecuación diferencial del campo homogeneo):

${\dfrac {d^{2}\psi _{i}}{dx^{2}}}(x)=0\quad i=1,4$

(175)

Multiplicando a ambos lados de (8.a) por una función de peso o ponderación ${\textstyle w(x)}$ se obtiene:

$AE{\dfrac {d^{2}u}{dx^{2}}}(x)w(x)=-p(x)w(x)$

(176)

Ahora, integrando a ambos lados de (176) con respecto a ${\textstyle x}$ entre 0 y ${\textstyle L}$ se obtiene:

$AE\int _{0}^{L}\left[{\dfrac {d^{2}u_{h}}{dx^{2}}}(x)+{\dfrac {d^{2}u_{f}}{dx^{2}}}(x)\right]w(x)dx=-\int _{0}^{L}p(x)w(x)dx$

(177)

E integrando por partes en el lado izquierdo de la anterior ecuación el resultado es:

$AE\left[{\dfrac {du_{h}}{dx}}(x)w(x)+{\dfrac {du_{f}}{dx}}(x)w(x)\right]_{x=0}^{x=L}-AE\int _{0}^{L}\left[{\dfrac {du_{h}}{dx}}(x)+{\dfrac {du_{f}}{dx}}(x)\right]{\dfrac {dw}{dx}}(x)dx=-\int _{0}^{L}p(x)w(x)dx$

(178)

La cual luego de evaluar el primer y reordenarse, da lugar a:

$FX_{i}w(0)+FX_{j}w(L)=AE\int _{0}^{L}\left[{\dfrac {du_{h}}{dx}}(x)+{\dfrac {du_{f}}{dx}}(x)\right]{\dfrac {dw}{dx}}(x)dx-\int _{0}^{L}p(x)w(x)dx$

(179)

Ahora si se emplean como las funciones de ponderación o peso (${\textstyle w(x)}$) a las funciones de forma (${\textstyle \psi _{1}(x)}$ y ${\textstyle \psi _{4}(x)}$) se tiene que:

$\int _{0}^{L}{\dfrac {du_{f}}{dx}}(x){\dfrac {dw}{dx}}(x)dx=\left.{\dfrac {dw}{dx}}(x)u_{f}(x)\right|_{x=0}^{x=L}-\int _{0}^{L}u_{f}(x){\dfrac {d^{2}w}{dx^{2}}}(x)dx=0-0=0$

(180)

Lo anterior debido a que ${\textstyle u_{f}(0)=u_{f}(L)=0}$ y a (175).

Con lo cual (179) se puede reescribir como:

$FX_{i}w(0)+FX_{j}w(L)=AE\int _{0}^{L}{\dfrac {du_{h}}{dx}}(x){\dfrac {dw}{dx}}(x)dx-\int _{0}^{L}p(x)w(x)dx$

(181)

Ahora, si como caso particular primero se emplea ${\textstyle \psi _{1}(x)}$ en lugar de ${\textstyle w(x)}$ y luego ${\textstyle \psi _{4}(x)}$, a partir de (181) se obtiene respectivamente:

$FX_{i}={\dfrac {AE}{L}}\left(u_{i}-u_{j}\right)-\int _{0}^{L}\psi _{1}(x)p(x)dx$ (182.a) $FX_{j}={\dfrac {AE}{L}}\left(-u_{i}+u_{j}\right)-\int _{0}^{L}\psi _{4}(x)p(x)dx$ (182.b)

La cual es equivalente a la formulación del método de rigidez para elementos tipo barra de sección constante y material elástico lineal presentada en (26).

B. Formulación exacta del M.E.F. para un elemento tipo viga

Ahora, de forma similar a como se realizó en el apéndice A para el elemento tipo barra, se procederá a realizar la formulación “exacta” del M.E.F. para un elemento tipo viga de sección transversal constante. Al igual que lo presentado en la sección 5, el objetivo es realizar esta formulación mediante la solución del P.V.F. (27) pero ahora empleando la forma de débil de la E.D. (27.a) en lugar de esta directamente. A diferencial de la formulación tradicional del M.E.F., en esta alternativa el campo de desplazamientos no solo dependerá de los desplazamientos y rotaciones de los extremos del elemento (campo homogéneo) sino también de la carga externa (campo empotrado), es decir:

$v(x)=v_{h}(x)+v_{f}(x)=\psi _{2}(x)v_{i}+\psi _{3}(x)\theta _{i}+\psi _{5}(x)v_{j}+\psi _{6}(x)\theta _{j}+v_{f}(x)$

(183)

donde una propiedad importante de las funciones de forma ${\textstyle \psi _{2}(x)}$, ${\textstyle \psi _{3}(x)}$, ${\textstyle \psi _{5}(x)}$ y ${\textstyle \psi _{6}(x)}$ es que estas cumplen la siguiente ecuación diferencial:

${\dfrac {d^{4}\psi _{i}}{dx^{4}}}(x)=0i=2,3,5,6$

(184)

Multiplicando por una función de peso o ponderación ${\textstyle w(x)}$ a ambos lados de (27.a) se obtiene:

$EI{\frac {d^{4}v}{dx^{4}}}(x)w(x)=q(x)w(x)$

(185)

E integrando con respecto a ${\textstyle x}$ entre 0 y ${\textstyle L}$ a ambos lados de (185) se obtiene:

$EI\int _{0}^{L}{\frac {d^{4}v}{dx^{4}}}(x)w(x)dx=\int _{0}^{L}q(x)w(x)dx$

(186)

Resolviendo con integración por partes la integral del lado izquierdo de la anterior ecuación se obtiene:

$EI\left[\left.{\frac {d^{3}v}{dx^{3}}}(x)w(x)\right|_{x=0}^{x=L}-\int _{0}^{L}{\frac {d^{3}v}{dx^{3}}}(x){\frac {dw}{dx}}(x)dx\right]=\int _{0}^{L}q(x)w(x)dx$

(187)

Ahora, teniendo en cuenta que la fuerza cortante se obtiene a partir del campo de desplazamiento vertical como ${\textstyle V(x)=-EI{\dfrac {d^{3}v}{dx^{3}}}(x)}$, se obtiene:

$-V(L)w(L)+V(0)w(0)-EI\int _{0}^{L}{\frac {d^{3}v}{dx^{3}}}(x){\frac {dw}{dx}}(x)dx=\int _{0}^{L}q(x)w(x)dx$

(188)

Mientras que debido a que ${\textstyle FY_{i}=-V(0)}$ y ${\textstyle FY_{j}=V(L)}$, la anterior ecuación se reescribe como:

$-FY_{i}w(0)-FY_{j}w(L)-EI\int _{0}^{L}{\dfrac {d^{3}v}{dx^{3}}}(x){\frac {dw}{dx}}(x)dx=\int _{0}^{L}q(x)w(x)dx$

(189)

Integrando por partes de nuevo, ahora en el tercer término del lado izquierdo de la ecuación anterior, se obtiene:

$-FY_{i}w(0)-FY_{j}w(L)-EI\left[\left.{\frac {d^{2}v}{dx^{2}}}(x){\frac {dw}{dx}}(x)\right|_{x=0}^{x=L}-\int _{0}^{L}{\frac {d^{2}v}{dx^{2}}}(x){\frac {d^{2}w}{dx^{2}}}(x)dx\right]=\int _{0}^{L}q(x)w(x)dx$

(190)

Por último, teniendo en cuenta que el campo de momentos interno se calcula como ${\textstyle M(x)=EI{\dfrac {d^{2}v}{dx^{2}}}(x)}$ y que ${\textstyle M_{i}=-M(0)}$ y ${\textstyle M_{j}=M(L)}$, la ecuación anterior se reescribe como:

$FY_{i}w(0)+FY_{j}w(L)+M_{i}{\frac {dw}{dx}}(0)+M_{j}{\frac {dw}{dx}}(L)=EI\int _{0}^{L}{\frac {d^{2}v}{dx^{2}}}(x){\frac {d^{2}w}{dx^{2}}}(x)dx-\int _{0}^{L}q(x)w(x)dx$

(191)

Reemplazando (183) en el lado derecho de (191), se obtiene:

$FY_{i}w(0)+FY_{j}w(L)+M_{i}{\frac {dw}{dx}}(0)+M_{j}{\frac {dw}{dx}}(L)=$ $EI\int _{0}^{L}\left[{\frac {d^{2}\psi _{2}}{dx^{2}}}(x)v_{i}+{\frac {d^{2}\psi _{3}}{dx^{2}}}(x)\theta _{i}+{\frac {d^{2}\psi _{5}}{dx^{2}}}(x)v_{j}+{\frac {d^{2}\psi _{6}}{dx^{2}}}(x)\theta _{j}+{\frac {d^{2}v_{f}}{dx^{2}}}(x)\right]{\frac {d^{2}w}{dx^{2}}}(x)dx-\int _{0}^{L}q(x)w(x)dx$

(192)

Ahora, si como funciones de ponderación se emplean las funciones de forma, empleando integración por partes se prueba lo siguiente:

$\int _{0}^{L}{\frac {d^{2}v_{f}}{dx^{2}}}(x){\frac {d^{2}w}{dx^{2}}}(x)dx=\int _{0}^{L}{\frac {d^{2}v_{f}}{dx^{2}}}(x){\frac {d^{2}\psi _{i}}{dx^{2}}}(x)dxi=2,3,5,6$ $=\left.{\dfrac {dv_{f}}{dx}}(x){\dfrac {d^{2}\psi _{i}}{dx^{2}}}(x)\right|_{x=0}^{x=L}-\int _{0}^{L}{\dfrac {dv_{f}}{dx}}(x){\dfrac {d^{3}\psi _{i}}{dx^{3}}}(x)dx$ $=-\int _{0}^{L}{\dfrac {dv_{f}}{dx}}(x){\dfrac {d^{3}\psi _{i}}{dx^{3}}}(x)dx$ $=-\left.v_{f}(x){\dfrac {d^{3}\psi _{i}}{dx^{3}}}(x)\right|_{x=0}^{x=L}+\int _{0}^{L}v_{f}(x){\dfrac {d^{4}\psi _{i}}{dx^{4}}}(x)dx$ $=0$

(193)

donde se ha empleado (184) y que los valores de ${\textstyle v_{f}(x)}$ y ${\textstyle {\dfrac {dv_{f}}{dx}}(x)}$ son iguales a cero en ${\textstyle x=0}$ y ${\textstyle x=L}$.

Con lo cual, a partir de (193), la ecuación (192) se puede reescribir como:

$FY_{i}w(0)+FY_{j}w(L)+M_{i}{\frac {dw}{dx}}(0)+M_{j}{\frac {dw}{dx}}(L)=$ $EI\int _{0}^{L}\left[{\frac {d^{2}\psi _{2}}{dx^{2}}}(x)v_{i}+{\frac {d^{2}\psi _{3}}{dx^{2}}}(x)\theta _{i}+{\frac {d^{2}\psi _{5}}{dx^{2}}}(x)v_{j}+{\frac {d^{2}\psi _{6}}{dx^{2}}}(x)\theta _{j}\right]{\frac {d^{2}w}{dx^{2}}}(x)dx-\int _{0}^{L}q(x)w(x)dx$

(194)

Si como caso particular primero se emplea ${\textstyle \psi _{2}(x)}$, luego ${\textstyle \psi _{3}(x)}$, ${\textstyle \psi _{5}(x)}$ y ${\textstyle \psi _{6}(x)}$, a partir de (194) se obtienen las siguientes cuatro ecuaciones:

$FY_{i}={\dfrac {12EI}{L^{3}}}v_{i}+{\dfrac {6EI}{L^{2}}}\theta _{i}-{\dfrac {12EI}{L^{3}}}v_{j}+{\dfrac {6EI}{L^{2}}}\theta _{j}-\int _{0}^{L}\psi _{2}(x)q(x)dx$ (195.a) $M_{i}={\dfrac {6EI}{L^{2}}}v_{i}+{\dfrac {4EI}{L}}\theta _{i}-{\dfrac {6EI}{L^{2}}}v_{j}+{\dfrac {2EI}{L}}\theta _{j}-\int _{0}^{L}\psi _{3}(x)q(x)dx$ (195.b) $FY_{j}=-{\dfrac {12EI}{L^{3}}}v_{i}-{\dfrac {6EI}{L^{2}}}\theta _{i}+{\dfrac {12EI}{L^{3}}}v_{j}-{\dfrac {6EI}{L^{2}}}\theta _{j}-\int _{0}^{L}\psi _{5}(x)q(x)dx$ (195.c) $M_{j}={\dfrac {6EI}{L^{2}}}v_{i}+{\dfrac {2EI}{L}}\theta _{i}-{\dfrac {6EI}{L^{2}}}v_{j}+{\dfrac {4EI}{L}}\theta _{j}-\int _{0}^{L}\psi _{6}(x)q(x)dx$ (195.d)

Que son equivalentes al sistema de ecuaciones presentado en (52).

C. Formulación exacta del M.E.F. para un elemento tipo viga sobre fundación flexible

Para este caso el objetivo es resolver el P.V.F. (53) pero ahora empleando la forma débil de (53.a) en lugar de esta directamente.

Como se presentó en (83), la solución de (53.a) se expresa como la suma de un campo homogéneo (${\textstyle v_{h}(x)}$) y un campo empotrado (${\textstyle v_{f}(x)}$), es decir:

$v(x)=v_{h}(x)+v_{f}(x)$

(196)

donde el campo homogéneo se expresa en función de los desplazamientos y rotaciones en los extremos del elemento y de las funciones de forma ${\textstyle \Psi _{2}(x)}$, ${\textstyle \Psi _{3}(x)}$, ${\textstyle \Psi _{5}(x)}$ y ${\textstyle \Psi _{6}(x)}$ de la siguiente manera:

$v_{h}(x)=\Psi _{2}(x)v_{i}+\Psi _{3}(x)\theta _{i}+\Psi _{5}(x)v_{j}+\Psi _{6}(x)\theta _{j}$

(197)

Mientras que el campo empotrado se calcula solo empleando la carga externa y las funciones de Green.

Con lo cual, el campo de desplazamiento total, se expresa ahora como:

$v(x)=\Psi _{2}(x)v_{i}+\Psi _{3}(x)\theta _{i}+\Psi _{5}(x)v_{j}+\Psi _{6}(x)\theta _{j}+v_{f}(x)$

(198)

Es importante resaltar que debido a que ${\textstyle v_{h}(x)}$ es una combinación lineal de las funciones de forma ${\textstyle \Psi _{2}(x)}$, ${\textstyle \Psi _{3}(x)}$, ${\textstyle \Psi _{5}(x)}$ y ${\textstyle \Psi _{6}(x)}$, estas últimas cumplen la propiedad de ser solución de la ecuación diferencial homogénea asociada con (53.a), es decir:

$EI{\dfrac {d^{4}\Psi _{i}}{dx^{4}}}(x)+k\Psi _{i}(x)=0\quad i=2,3,5,6$

(199)

Multiplicando por una función de peso o ponderación ${\textstyle w(x)}$ a ambos lados de (5) (o (53.a)) se obtiene:

$EI{\frac {d^{4}v}{dx^{4}}}(x)w(x)+kv(x)w(x)=q(x)w(x)$

(200)

E integrando con respecto a ${\textstyle x}$ entre 0 y ${\textstyle L}$ a ambos lados de (200) se obtiene:

$EI\int _{0}^{L}{\frac {d^{4}v}{dx^{4}}}(x)w(x)dx=-k\int _{0}^{L}v(x)w(x)dx+\int _{0}^{L}q(x)w(x)dx$

(201)

Resolviendo con integración por partes la integral del lado izquierdo de la anterior ecuación, da como resultado:

$EI\left[\left.{\frac {d^{3}v}{dx^{3}}}(x)w(x)\right|_{x=0}^{x=L}-\int _{0}^{L}{\frac {d^{3}v}{dx^{3}}}(x){\frac {dw}{dx}}(x)dx\right]=-k\int _{0}^{L}v(x)w(x)dx+\int _{0}^{L}q(x)w(x)dx$

(202)

Ahora teniendo en cuenta que la fuerza cortante se obtiene a partir del campo de desplazamiento vertical como ${\textstyle V(x)=-EI{\dfrac {d^{3}v}{dx^{3}}}(x)}$, se obtiene:

$-V(L)w(L)+V(0)w(0)-EI\int _{0}^{L}{\frac {d^{3}v}{dx^{3}}}(x){\frac {dw}{dx}}(x)dx=-k\int _{0}^{L}v(x)w(x)dx+\int _{0}^{L}q(x)w(x)dx$

(203)

Teniendo en cuenta que ${\textstyle FY_{i}=-V(0)}$ y ${\textstyle FY_{j}=V(L)}$, la anterior ecuación toma la siguiente forma:

$-FY_{i}w(0)-FY_{j}w(L)-EI\int _{0}^{L}{\dfrac {d^{3}v}{dx^{3}}}(x){\frac {dw}{dx}}(x)dx=-k\int _{0}^{L}v(x)w(x)dx+\int _{0}^{L}q(x)w(x)dx$

(204)

Integrando por partes de nuevo, ahora en el tercer término del lado izquierdo de la ecuación anterior, se obtiene:

$-FY_{i}w(0)-FY_{j}w(L)-EI\left[\left.{\frac {d^{2}v}{dx^{2}}}(x){\frac {dw}{dx}}(x)\right|_{x=0}^{x=L}-\int _{0}^{L}{\frac {d^{2}v}{dx^{2}}}(x){\frac {d^{2}w}{dx^{2}}}(x)dx\right]=$ $-k\int _{0}^{L}v(x)w(x)dx+\int _{0}^{L}q(x)w(x)dx$

(205)

Por último, teniendo en cuenta que el campo de momentos interno se calcula como ${\textstyle M(x)=EI{\dfrac {d^{2}v}{dx^{2}}}(x)}$ y que ${\textstyle M_{i}=-M(0)}$ y ${\textstyle M_{j}=M(L)}$, la ecuación anterior se reescribe como:

$FY_{i}w(0)+FY_{j}w(L)+M_{i}{\frac {dw}{dx}}(0)+M_{j}{\frac {dw}{dx}}(L)=$ $EI\int _{0}^{L}{\frac {d^{2}v}{dx^{2}}}(x){\frac {d^{2}w}{dx^{2}}}(x)dx+k\int _{0}^{L}v(x)w(x)dx-\int _{0}^{L}q(x)w(x)dx$

(206)

Reemplazando (198) en el lado derecho de (206), se obtiene:

$FY_{i}w(0)+FY_{j}w(L)+M_{i}{\frac {dw}{dx}}(0)+M_{j}{\frac {dw}{dx}}(L)=$ $EI\int _{0}^{L}\left[{\frac {d^{2}\Psi _{2}}{dx^{2}}}(x)v_{i}+{\frac {d^{2}\Psi _{3}}{dx^{2}}}(x)\theta _{i}+{\frac {d^{2}\Psi _{5}}{dx^{2}}}(x)v_{j}+{\frac {d^{2}\Psi _{6}}{dx^{2}}}(x)\theta _{j}+{\frac {d^{2}v_{f}}{dx^{2}}}(x)\right]{\frac {d^{2}w}{dx^{2}}}(x)dx$ $+k\int _{0}^{L}\left[\Psi _{2}(x)v_{i}+\Psi _{3}(x)\theta _{i}+\Psi _{5}(x)v_{j}+\Psi _{6}(x)\theta _{j}+v_{f}(x)\right]w(x)dx-\int _{0}^{L}q(x)w(x)dx$

(207)

Ahora, si como funciones de ponderación se emplean las funciones de forma, empleando integración por partes se prueba lo siguiente:

$EI\int _{0}^{L}{\frac {d^{2}v_{f}}{dx^{2}}}(x){\frac {d^{2}w}{dx^{2}}}(x)dx+k\int _{0}^{L}v_{f}(x)w(x)dx=$ $EI\int _{0}^{L}{\frac {d^{2}v_{f}}{dx^{2}}}(x){\frac {d^{2}\Psi _{i}}{dx^{2}}}(x)dx+k\int _{0}^{L}v_{f}(x)\Psi _{i}(x)dx=$ $EI\left.{\dfrac {dv_{f}}{dx}}(x){\dfrac {d^{2}\Psi _{i}}{dx^{2}}}(x)\right|_{x=0}^{x=L}-EI\int _{0}^{L}{\dfrac {dv_{f}}{dx}}(x){\dfrac {d^{3}\psi _{i}}{dx^{3}}}(x)dx+k\int _{0}^{L}v_{f}(x)\Psi _{i}(x)dx=$ $-EI\int _{0}^{L}{\dfrac {dv_{f}}{dx}}(x){\dfrac {d^{3}\psi _{i}}{dx^{3}}}(x)dx+k\int _{0}^{L}v_{f}(x)\Psi _{i}(x)dx=$ $-EI\left.v_{f}(x){\dfrac {d^{3}\Psi _{i}}{dx^{3}}}(x)\right|_{x=0}^{x=L}+\int _{0}^{L}v_{f}(x){\dfrac {d^{4}\Psi _{i}}{\partial x^{4}}}(x)dx+k\int _{0}^{L}v_{f}(x)\Psi _{i}(x)dx=$ $\int _{0}^{L}v_{f}(x)\left[{\dfrac {d^{4}\Psi _{i}}{dx^{4}}}(x)+k\psi _{i}(x)\right]dx=0$

(208)

donde se ha empleado (199) y que los valores de ${\textstyle v_{f}(x)}$ y ${\textstyle {\dfrac {dv_{f}}{dx}}(x)}$ son iguales a cero en ${\textstyle x=0}$ y ${\textstyle x=L}$.

Empleando (208) en (207) esta última toma la siguiente forma (donde para ser coherentes con (208), se ha tomado que ${\textstyle w(x)=\Psi _{l}(x)}$):

$FY_{i}\Psi _{l}(0)+FY_{j}\Psi _{l}(L)+M_{i}{\frac {d\Psi _{l}}{dx}}(0)+M_{j}{\frac {d\Psi _{l}}{dx}}(L)=$ $EI\int _{0}^{L}\left[{\frac {d^{2}\Psi _{2}}{dx^{2}}}(x)v_{i}+{\frac {d^{2}\Psi _{3}}{dx^{2}}}(x)\theta _{i}+{\frac {d^{2}\Psi _{5}}{dx^{2}}}(x)v_{j}+{\frac {d^{2}\Psi _{6}}{dx^{2}}}(x)\theta _{j}\right]{\frac {d^{2}\Psi _{l}}{dx^{2}}}(x)dx$ $+k\int _{0}^{L}\Psi _{l}(x)\left[\Psi _{2}(x)v_{i}+\Psi _{3}(x)\theta _{i}+\Psi _{5}(x)v_{j}+\Psi _{6}(x)\theta _{j}\right]dx-\int _{0}^{L}q(x)\Psi _{l}(x)dx$

(209)

Reemplazando ${\textstyle l}$ por 2,3,5 y 6 en (209) se obtienen cuatro ecuaciones, las cuales se expresan en forma matricial como:

${\begin{Bmatrix}FY_{i}\\M_{i}\\FY_{j}\\M_{j}\end{Bmatrix}}={\begin{bmatrix}k_{22}&k_{23}&k_{25}&k_{26}\\k_{32}&k_{33}&k_{35}&k_{36}\\k_{52}&k_{53}&k_{55}&k_{56}\\k_{62}&k_{63}&k_{65}&k_{66}\end{bmatrix}}{\begin{Bmatrix}v_{i}\\\theta _{i}\\v_{j}\\\theta _{j}\end{Bmatrix}}-{\begin{Bmatrix}\int _{0}^{L}\Psi _{2}(x)q(x)dx\\\int _{0}^{L}\Psi _{3}(x)q(x)dx\\\int _{0}^{L}\Psi _{5}(x)q(x)dx\\\int _{0}^{L}\Psi _{6}(x)q(x)dx\end{Bmatrix}}$

(210)

donde:

$k_{ij}=\int _{0}^{L}\left[EI{\dfrac {d^{2}\Psi _{i}}{dx^{2}}}(x){\dfrac {d^{2}\Psi _{j}}{dx^{2}}}(x)+k\Psi _{i}(x)\Psi _{j}(x)\right]dx$

(211)

Lo cual es equivalente a lo presentado en (84).

Referencias

[1] Challis L., Sheard F. The green of Green functions. American Institute of Physics, Physics Today, 56(12):41-46, 2003.

[2] Duffy D.G. Green’s functions with applications. Chapman and Hall/CRC, 2015.

[3] Banerjee P.K., Butterfield R. Boundary element methods in engineering science. McGraw-Hill, New York, 1981.

[4] Sánchez-Sesma F.J., Ramos-Martínez J., Campillo M. An indirect boundary element method applied to simulate the seismic response of alluvial valleys for incident P, S and Rayleigh waves. Earthquake Engineering & Structural Dynamics, 22(4):279-295, 1993.

[5] Fairweather G., Karageorghis A., Martin P.A. The method of fundamental solutions for scattering and radiation problems. Engineering Analysis with Boundary Elements, 27(7):759-769, 2003.

[6] Thomson W.T. Transmission of elastic waves through a stratified solid medium. Journal of Applied Physics, 21(2):89-93, 1950.

[7] Boussinesq J. Application des potentiels a l'étude de l'équilibre et du mouvement des solides élastiques. Gauthier-Villars, Imprimeur-Libraire, 1885.

[8] Cerruti V. Ricerche intorno all'equilibrio de'corpi elastici isotropi: memoria. Coi tipi del Salviucci, 1882.

[9] Mindlin R.D. Force at a point in the interior of a semi-infinite solid. AIP Physics, 7(5):195-202, 19336.

[10] Stokes G.G. On dynamical theory of diffraction. Transactions of the Cambridge Philosophical Society, 9:1-48, 1849.

[11] Lamb H. On the propagation of tremors over the surface of an elastic solid. Philosophical Transactions of the Royal Society of London, 203:1-42, 1904.

[12] Chao C.C. Dynamical response of an elastic half-space to tangential surface loadings. Journal of Applied Mechanics, 27:559, 1960.

[13] Kausel E. Fundamental solutions in elastodynamics: a compendium. Cambridge University Press, 2006.

[14] Aki K., Richards P.G. Quantitative seismology. Univ. Science Books, 700 pp., 2002.

[15] Colunga A.T. Análisis de estructuras con métodos matriciales. Limusa, 560 pp., 2007.

[16] McCormac J.C. Structural Analysis: using classical and matrix methods. Wiley Hoboken, NJ, 2007.

[17] Kassimali A. Matrix analysis of structures SI version. Cengage Learning, 640 pp., 2012.

[18] Reddy J.N. An introduction to the finite element method. McGraw-Hill, 2006.

[19] Bathe K.J. Finite element procedures. McGraw-Hill, 2006.

[20] Hetényi M. Beams on elastic foundation: theory with applications in the fields of civil and mechanical engineering. University of Michigan, 1971.

[21] Eisemberger M., Yankelevsky D.Z. Exact stiffness matrix for beams on elastic foundation. Computer & Structures, 21(6):1355-1359, 1985.