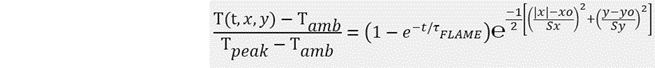Pruebas de fuego virtuales de paneles compuestos termoplásticos

ACKNOWLEDGEMENTS

The authors acknowledge funding support from the CleanSky2 program: H2020, Call: H2020-CS2-CFP09-2018-02, Project ID: 864713; title: HITCOMP; High Temperature Characterization and Modelling of Thermoplastic Composites. This project belongs to the AIRFRAME ITD part and has been led by AIRBUS DS as Topic Manager.

The research work by INTA was performed as a part of a cooperative research with UNIVERSIDAD CARLOS III DE MADRID - UC3M and SENSIA SOLUTIONS SL – SENSIA. Special thanks and acknowledgement are granted to the Airbus DS Fire Test Laboratory where all experimental tasks of the project where performed.

INTRODUCTION

Composite materials are progressively taking an increasing portion of aerospace structures material. Recently, there has been increasing interest in applying these material to structures with fire protection requirements. This has been enabled by the commercial availability of high temperature thermoplastic carbon composites which shall be capable to withstand fire events demands at least until extinctors actuate. Modification of structures from metal, i.e. isotropic, to composites which, in general, are non-isotropic, requires a large amount of tests for sustentation and validation of the updated designs. This is particularly tough when considering structures that have fire protection requirements where tests are particularly demanding and especial facilities and equipment are required.

The key reference for fire protection test methods is the Federal Aviation Administration Advisory Circular AC-20-135 ref [1] which established test requirements to show fireproof and fire resistant capabilities required to show fire protection requirement compliance for engine and auxiliary power units (APU) areas.

The objective of this paper is to describe an approach to numerically simulate fire tests and thus to be able to predict test results which, after validation of the simulation tool, will save further test effort. This ambitious objective has been faced with an engineering approach to avoid including all possibly affecting physical and chemical phenomena and to focus only on the most relevant ones. Within them, basic and condensed simulation is selected to be able to get simulated test results based on limited data. These starting data have been obtained from conventional and normalized coupons and detail tests for the material under investigation.

LITERATURE REVIEW

A full compendium of the available knowledge on fire structural modeling of composites can be found in the paper by Mouritz at all Ref [2] is. It covers most of the aspects and physical phenomena involved in a fire event of composites. The paper includes thermal analysis techniques, material damage techniques and mechanical modeling techniques to simulate the fire events. The paper explores all relevant phases of the fire event including material degradation, pore and gas formation and chemical reactions issues occurring on the resin at high temperatures.

Insight on time to failure are provided for some loading schemes which show tendencies and provide baseline for any fire test analysis. Finally the paper includes a large list of references where any aspect of the fire structural modeling can be further studied more deeply. This turns the paper in a must as a “starting point” for fire on composites.

Ref [3] to Ref [5] collect thermoplastic modeling approaches. Most of them advise to use viscoplastic constitutive models to include creep and plasticity effects simultaneously. All three references coincide in selecting the off axis test, either tension or compression, as the one to identify parameters of the viscoplastic model.

Ref [3] focuses on fire events and provides experimental data for glass/vinyl-ester composite, for naval applications. Ref [4] and Ref [5] illustrate development of a viscoplastic model for AS4_PEEK which is a thermoplastic resin composite similar to the one on our project.

Last, but the most interesting regarding simulation and modeling aspects, is the work by Vogler Ref [6] in which an elastic viscoplastic constitutive model for thermoplastic composite simulation on FEM is presented. A formal development of the constitutive model is provided including elastic, plastic and creep strains along with the implicit and explicit kinematics to include them on FEM codes. Additionally, model results are compared with off axis measurements for coupons tests to show correlation. Unfortunately only unidirectional and short fiber application has been derived thus it is not directly applicable to our case.

SIMULATION APROACH

Objective of the work described here is not to fully integrate all physical and chemical phenomena taking place on a fire event affecting a composite structure but rather to include the minima effects that still yield results correlating with results from mechanical tests in presence of fire. The former approach would be quite ambitious and will require far more hypotheses and/or estimations of simulation parameters at the only advantage of better accuracy.

In the approach selected, the simplest phenomena and modeling option of the problem will be selected. However an insight of further more complicated or elaborated simulation alternatives will be explored to be able to incorporate it if the simpler model is not capable to match the test results.

FIRE TEST MODEL

Flame Effects Simulation on Panel

Fire resistance requirements apply to multiple areas and types of structures. Additionally fire demand may be due to direct flame exposure or to non-flaming hot exhaust gas jets.

A detailed model to simulate a flame or hot gas jet impacting on a structure panel has not been considered for the moment. These type of simulation model shall include, among others, features to take into account flame temperature, distance, orientation, fuel type, burn rate, etc. This simulation model is complex and requires a detailed study, correlation and validation tests on its own which exceed the initial approach on this study.

To take the flame into account, an indirect approach has been selected. It consisting on simulating the temperatures on the panel caused by the flame. This approach is simple but still allows to simulate most of the key features of the burn test under consideration. Temperatures will be selected varying both with time and space but in a separated form. An exponential ramp versus time will be used for time variation and a Gaussian distribution on the structural panel will be used for space variation.

Time variation will be controlled with only one parameter, the exponential time constant which will be selected based on initial test measurements. Space variation will be controlled by two pairs of values, one been the flame vertex or hottest point for any time and the other pair being diffusions or deviations of the Gaussian curve along each direction.

Last, but possible most relevant, is the temperature scale factor. This will be modeled by the temperature increment approaching a peak temperature increment. The expression below summarizes flame effects used in the simulation.

It can be seen that isothermal contours are ellipses centered on cords (xo, yo) and with constant eccentricity Sx/Sy, figure 1. The absolute value used on the x variable has been included to ensure the plane x=0 has a symmetry regardless the value of xo. This is merely a numerical aid to be able to simulate half of the panel and it will not be difficult to avoid it for cases where symmetry cannot be ensured.

Following a list of control parameters for the flame effects along with values selected for initial trials for simulation purposes.

Tamb; Reference temperature from which increments are measured.

Tpeak; Maximum temperature at which the flame/exhaust approaches with time.

τ_FLAME; Time constant of vertex temperature increment. At a time equal to τ_FLAME, temperature increment reaches 63.2% of peak increment. Values has been derived from initial test correlations.

x₀ y₀; Flame vertex location on panel.

S_x S_y; Temperatures standard deviations along x and y direction. Values are selected to correlate measured temps distributions on initial test.

Figure 1 Flame side temperature distribution and vertex relative temperature increment vs t/τ

Flame Effects Simulation on Fitting

On the standard flame test, it is common practice to include a fitting or metal bracket through which load can be applied to the panel while flaming conditions take place. These metal bracket is frequently stainless steel to withstand test conditions. For simulating purposes the fitting will be assumed as both, a perfect conductor and a rigid body. This simplifies the analysis and focuses the simulation on the panel. Once more it will not be difficult to simulate the fitting with its thermal, structural or both properties if deemed necessary.

The perfect conductor assumption involves that only one temperature is present on the fitting at any given time and avoids the need to simulate conduction and other heat exchange phenomena within the fitting itself. However, the fitting temperature will not be assumed equal to the panel temperature to allow for fitting to panel heat exchange. This way of simulating the fitting effects has been selected based on initial trials and although simple and quite limited it still captures the main effect of the fitting presence on the flame test.

Fitting temperature variation with time will be simulated with an exponential function and both reference and peak temperatures will be separated from panel ones in case different values provide better correlation.

Following expression and parameters are used along the simulation:

${\frac {{T}_{fitt}\left(t\right)-Tfittref}{Tfittpeak-Tfittref}}=\left(1-{e}^{-t/\tau FITT}\right)$

Equation 1 Metal Fitting Imposed Temperature

T_fittref; Fitting reference temperature from which increments are measured.

T_fittpeak; Maximum temperature at which the fitting approaches with time.

τ_FITT; fitting time constant. A faster fitting temperature rise is foreseen when flame impacts directly on the fitting.

Panel Fitting Heat Exchange

This heat exchange will be considered only where panel and fitting are in close contact. In these areas a contact conduction will be used yielding a flux q proportional to the temperature difference at the point.

q=H_TC (T_F-T_P)

H_TC; Thermal contact Coefficient.

The selected FEM package can include more elaborated thermal contact heat exchange formulation mainly dependent on the distance found between the two bodies. However, for the intended purposes this simple heat exchange is deemed sufficient. Notice, the model neglects any heat exchange when bodies are not in close contact.

Panel Heat Evacuation on Outer Face

In the most general configuration the engine or APU compartment will be surrounded by the outside air of the airplane. This conforms a heat sink where flame heat energy is dissipated. Following the simplification approach, a convective and uniform radiation (with no form factor effects) will be used. The heat power per unit area exchanged q will be modeled by

q = h (Tp-Ts) + εκf (Tpa⁴ –Tsa⁴)

h; Convection coefficient. When forced convection is applied a higher value of h will be used based on the air velocity.

Ts; Sink temperature. Notice it can be selected differently than the reference flame effects temperature to incorporate possible outer side temperature differences.

ε; panel emissivity

κ; Stefan Boltzmann coefficient: 5.671E-8 W/m² K⁴

f; View factor. Will be assumed uniform radiation and thus f=1

Tpa; Panel absolute Temperature

Tsa; Sink absolute Temperature

THERMOPLASTIC COMPOSITE MATERIAL MODEL

In this part a description of the material constitutive models used for the numerical simulation is provided. The thermoplastic composite material will be mechanically simulated as an Elastic-Viscoplastic solid. Thermally it will be simulated as an anisotropic conductor with thermal capacity. Any parameter on the constitutive models will be varied with temperature since the problem involves a large temperature range.

Elasticity Model

Ply Elasticity

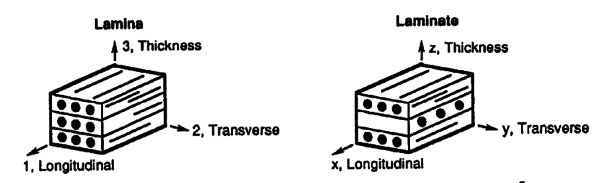
A procedure to find laminates stiffness properties based on single ply measured properties is well stabilized for 2D thin laminates. There is also an extension to 3D developed to simulate thick laminates or significant normal forces. This procedures, which are named laminate theory, provide stiffness data for any combination of materials, angles and thickness of individual plies, figure 2.

Figure 2 Lamina vs laminate orientations

Material selected for this project is TC1225 LMPAEK/T700 unidirectional tape with 194 g/m2 from Toray. According to the supplier and the common orthotropic assumptions lamina stiffness data in [GPa] are:

E1	E2	E3	ν12	ν23	ν31	G12	G23	G31
143.3	8.8	8.8	0.1	0.3	0.3	4.24	4	4.24

Orthotropic Elastic Model

Laminate selected for the fire tests panels are quasi-isotropic (QI) in the laminate plane with the ply sequence: [45, 0, +45, 90]s. Each ply has 0.184mm nominal thickness and thus panels with only one of the 8 plies block will be 1.47mm thick. Some of the thick flame panels are formed by three blocks i.e. they have 4.42mm. In some cases this may be referred to 4.5mm in a rounded form.

Using an extended lamination theory the corresponding engineering properties for the full laminate become [GPa]:

Ex	Ey	Ez	νxy	νyz	νzx	Gxy	Gyz	Gzx
49.69	49.69	9.55	0.32	0.5	0.5	18.8	5	5

The laminate properties constitute a transversely orthotropic model in 3D. Thanks to the quasi-isotropic laminate properties in the xy plane, the overall 3D behavior is transversely orthotropic with the singular axis been z and equal properties in the other two. Unlike in the ply orthotropy, in this case the singular axis is the less rigid one i.e. along the laminate thickness.

Laminate elastic properties will be used for simulating in the most general form of an anisotropic material stiffness matrix. Each term of the stiffness matrix will be varied with temperature using the same elasticity temperature dependency. This simplification of the stiffness variation with temperature does not significantly impact the objective of accounting the time to detachment since the elastic deformation at detachment is low compared with plastic and creep deformations. The simplification allows to retain at least one parameter in case correlation adjustment require to trim elastic deformation. The simplification can easily be avoided if other results become relevant and enough data are available to include different temperature variations along different directions.

From the above engineering properties, the resulting transversely isotropic stiffness matrix at room temperature becomes [GPa];

$\left\{{\begin{matrix}{\sigma }_{x}\\{\sigma }_{y}\\{\sigma }_{z}\\{\tau }_{yz}\\{\tau }_{xz}\\{\tau }_{xy}\end{matrix}}\right\}=$$\left|{\begin{matrix}{\begin{matrix}61.4&23.7&8.2\\&61.4&8.2\\&&11.1\end{matrix}}&0\\sym&{\begin{matrix}5&0&0\\&5&0\\&&19\end{matrix}}\end{matrix}}\right|\left\{{\begin{matrix}{\epsilon }_{x}\\{\epsilon }_{y}\\{\epsilon }_{z}\\{\gamma }_{yz}\\{\gamma }_{xz}\\{\gamma }_{xy}\end{matrix}}\right\}$

Viscoplasticity Model

Unlike to thermosetting resins, the selected thermoplastic matrix will show plastic behavior which is relevant for the simulation purposes. This matrix plasticity will transfer to a plastic behavior on the smeared properties of the full composite. Initially a basic isotropic plastic behavior will be used avoiding the use of anisotropic plasticity which will require deeper characterization of the material.

At high temperature, thermoplastic matrix show viscoplastic response i.e. the response upon an applied stress is not just a static deformation (elastic, plastic or both) and includes a time varying additional deformation. The term Creep is used when the time dependency deformations are analyzed separately and the term Viscoplasticity is used when plastic and time varying deformation are treated in a unified way.

These phenomena explain the observed increasing strain at constant stress (flow) or stress reduction at constant deformation (relaxation). It is generally less relevant for conventional engineering materials mainly in short duration evets. However, at high temperatures this is the mechanism explaining the observed large deformations of thermoplastic and thus the selected one to be included in the virtual test tool.

In the selected non-linear FEM package a formulation is available which includes a power law definition of the viscoplastic strain rate. Including this type of deformation requires an integration on time for each non-linear step of the overall solution in the so called creep analysis type.

ε̅̊^vp = A (σ̅) ^m (ε̅^vp)ⁿ (T_a)^p (qt^q-1)

The formulation allows multiples parameters to simulate different materials. Here a basic selection of the most relevant is used to keep relevant effects while maintaining simplicity on the simulation:

ε̅̊^vp; viscoplastic equivalent strain rate.

ε̅^vp; viscoplastic equivalent strain

σ̅; equivalent stress

A; Viscoplastic scale parameter. Dimensions vary with exponents used.

t; time

T_a; Absolute temperature (K)

m; equivalent stress exponent. m=1 will be selected to retain linear stress dependency.

n; equivalent viscoplastic strain exponent. n=0 will be used neglecting strain rate dependency on strain itself.

p; Temperature exponent. p=3 has been selected to increase strain rate at high temperatures.

q; Time exponent. q=1 will be used neglecting direct time dependency of creep strain rate.

Values for A have initially been selected correlating previous pull through and bearing test at 300ºC. However final viscoplastic scale factor A will be selected for proper correlation of selected fire test. A refined temperature exponent value may be required if the purpose is to fully match a deformation curve but the first rough estimation of p=3 has been sufficient to study overall time to failure.

Additionally to the ε̅̊^vp expression, the constitutive model requires two stress levels from which to activate the plasticity effects and the creep effects. These values are called yield and back stress; σ_yld and σ_bck respectively.

This study will consider creep to take place at any stress level and thus σ_bck=0. For plasticity, its effects will be considered for stresses exceeding a room temperature σ_yld value based on lamina strength data and laminate strength model. This value will be varied with temperature to account for the softening of the composite at high temperature.

Properties Variation with Temperature

A large temperature range is foreseen for the simulation. For any material property used in this analysis, its variation with temperature will be required. It has been selected to impose the shape for variations with temperature and to use only a few scalar parameters to adjust to experimental data or to correlate simple tests at different temperatures.

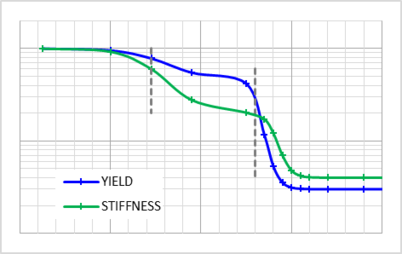
For the shape of the properties variation with temperature, the double hyperbolic tangent steps has been selected, figure 3. In a first step the glass transition transformation is simulated and in a second step the melting approach transformation is simulated. Later in the analysis it was found that the glass transition transformation has almost no impact on the results since the Tg temperature is quickly exceeded and the relevant zones are most of the time at higher temperatures.

On the other hand, the value assigned for yield and stiffness at temperatures close to the melting point demonstrated to have direct influence on time and deformation to failure. These values have been estimated initially to adjust with performed coupon test of the material for temperatures from 20ºC to 300ºC. These data need to be measured in further characterization tests since they greatly influence the results.

${\frac {P(T)}{{P}_{R}}}=\left\{1-{\frac {1}{2}}\left(1-{\frac {{P}_{M}}{{P}_{R}}}\right)\left[1+\right.\right.$$\left.\left.\mathrm {tanh} \,{\xi }_{M}\left(T-{T}_{tM}\right)\right]-{\frac {1}{2}}\left({\frac {{P}_{M}}{{P}_{R}}}-\right.\right.$$\left.\left.{\frac {{P}_{H}}{{P}_{R}}}\right)\left[1+\mathrm {tanh} \,{\xi }_{H}\left(T-{T}_{tH}\right)\right]\right\}$

Equation 2 Property Variation with Temperature P(T) Model

P_R; Property reference value at room temperature. This parameter is a scale factor and provides dimensions to the model. Its value shall be provided for each property from material test at reference temperature i.e. room temperature.

P_M/P_R; Property reduction factor at Middle temperature transformation. Along the study this will be used for glass transition transformation.

P_H/P_R; Property reduction factor at High temperature transformation. In this study resin approaching melting will be this second transition.

ξ_I; shape factor for the slope of the transition; Two data are required for mid and high transitions.

T_tI; Temperature at which the transition occurs, at this temperature and with this model, property takes the mid value of the property below and above the transition. Mid value will be used for the resin glass transition and High value for the resin melting. This last value is also used to adjust the melting of resin effect on properties.

For stiffness, a moderate reduction from its initial value has been used at Tg. A larger reduction of the room temperature stiffness has been selected for temperatures approaching resin melting. For plasticity a light reduction has been used at Tg, and a significant reduction from the room temperature yield stress is used for temperatures above resin melting. This plasticity stress at high temperature has been found to have large influence on simulating results.

Thermal Properties

On previous studies the PEEK carbon material was thermally characterized and a model for conductivity and capacity was developed to match observed test result for diffusivity and thermal degradation test.

It can be seen that at temperatures approaching resin melting, conductivity K(T) shows a significant reduction from its value at room temperature, figure 4. Thermal capacity ρCp(T) has a much lower reduction at resin melting temperatures.

Additionally, and based on better correlating temperature measurements on panels when tested in fire conditions, an anisotropy was introduced on the conductivity model. It was observed that the conductivity along the thickness of the panel was correctly simulated but higher values where required on the in-plane directions to improve temperatures correlation.

SIMULATING RESULTS

Geometry and Load

A case has been selected for which flame test results are available in order to adjust the model for correlation. The thermoplastic composite panel is 600x400mm in size and 3x8 plies QI laminate in thickness (≈4.5mm thick), figure 5. The fitting used for the test is stainless steel but only the fitting geometry is used since it will be simulated to be non-deformable and with uniform temperature.

Load is parallel to panel and applied at a given z offset of 22mm from the panel surface. A value of 7800N constant over time is applied as per the correlation test selected. Panel is clamped at the upper side and pinned along its contour.

Flame burner is applied 100mm from the lower edge of the panel matching the lower fitting edge. However, temperature measurements show peak temperature to be located somehow higher than flame burner and thus the flame temperatures model has been centered on (xo, yo) = (0, 0) where measurements show the highest temperature regardless the burner position.

FEM model

Only half the model has been simulated thanks to symmetry along x=0 plane. The FEM model for the panel has been prepared with Tetra10 elements using an automatic mesh generator. Refinement has been defined on holes where detail is required for load transfer, figure 6.

Fitting has been modeled as a “geometry with nodes” body to be able to introduce the load on a fitting node. For the geometry, only the fitting base and fasteners surfaces have been used since they are the only surfaces contacting the panel. As a geometric body, the fitting is considered with uniform temperature neglecting temperature differences within the fitting. The fitting temperature has been imposed as a boundary condition provided by the flame.

Thermal boundary condition are:

• The imposed temperatures on the flame side which vary with time and location.

• The imposed temperature on the fitting.

• The heat evacuation to the environment on the outer side (opposite to flame side) including a convection and a radiation as previously described.

• A symmetry condition enforcing no heat flow on x=0 symmetry plane.

Additionally to these boundary conditions the panel and the fitting are allowed to exchange heat where in contact and neglecting any heat exchange where separated.

The overall model is slightly above 70 000 DOF but still runs a 300 seconds simulation in about 3h on a conventional PC even being coupled thermo-mechanical and creep analysis type.

FEM Analysis and Results

Simulation has been run for multiple cases to adjust the model and to identify how parameters affect the results. In general, the overall deformation history after flame application is correctly modelled. However, the simulation model is too simple to reproduce the divergence observed just prior to the fitting detachment as can be seen on the test curve on figure 7 where displacement slope jumps advancing the detachment of the fitting. Mesh refinements and element deactivation has been tried to reproduce the observed divergence at detachment with no results. This can be seen on the three other curves of figure 7.

To solve this, a detachment criteria will be used assuming detachment takes place when displacement reaches a value of one fastener diameter, 3.6mm in this case, which agrees with the test displacement jump observed at 4mm displacement. (See Figure 7).

Figure 7 shows fitting vertical displacement for three simulated cases against the fire test measured displacement. Variation of the thermal contact conduction parameter H_TC and the residual yield stress above 300ºC σ_yld.

In most cases simulation is capable to progress until the mesh deformation is so large that the stiffness matrix is no more positive defined and thus causing numerical errors. In any case this is generally past the detachment time observed during the tests.

Both, test and simulation results, show that the fitting displacement is initially very small, less than 1mm in the first 60sec of flame, see figure 8. At about 50sec, temperature on the fitting side of the panel reaches values at which the conductivity is drastically reduced that increases the slope at which temperature builds up and the temperature quickly approaches 600ºC at this location. This lowers the yield stress and material flows increasing displacement quickly. Flow of the hot material around the fasteners is the failure mode both in the tests and in the model.

CONCLUSIONS

A numerical simulation procedure has been established to simulate fire test of mechanically loaded carbon thermoplastic composite panels. A representative aeronautical fitting is included in the model allowing load introduction and local heating of the panel via thermal contact.

A complete set of parameters has been identified which, along with the FEM package, conform the simulation model. A set of values for these parameters have been assigned to simulate a correlation case for which fire test results are available. Simulation has been trimmed to match detachment time observed in the correlation test.

Most relevant is the sensitivity of simulation results to critical parameters which have been identified and which shall be experimentally validated to improve the simulation validity.

Specifically material yield behavior at temperatures exceeding the formal resin melt has shown to significantly affect the time to detachment of the loading fitting.

References

[1] Federal Aviation Administration Advisory Circular AC-20-135

[2] A.P. Mouritz, S. Feih, E. Kandare, Z. Mathys, A.G. Gibson, P.E. Des Jardin, S.W. Case, B.Y. Lattimer. Review of Fire Structural Modelling of Polymer Composites. Composites Part A: Applied Science and Manufacturing 2009

[3] S. W. Kwon, W. L. Smith and S. W. Lee. Thermo-viscoplastic Modeling of Composites Exposed to Fire or High Temperature. Journal of composite materials, Vol. 40, No. 18/2006

[4] T. S. Gates and C. T. Sun. Elastic/Viscoplastic Constitutive Model for Fiber Reinforced Thermoplastic Composites. American Institute of Aeronautics and Astronautics Journal 1990

[5] K. J. Yoon and C. T. Sun. Characterization of Elastic-Viscoplastic Properties of an AS4/PEEK Thermoplastic Composite. Journal of Composite Materials Vol. 25- October 1991

[6] Matthias Vogler. New Material Modeling Approaches for Thermoplastic, Composites and Organic Sheet. 9^th European LS-DYNA Conference 2013

Abbreviations

Tg Glass Transition Temperature

σ_yl Yield Stress above which a permanent deformation remains on the material

QI Quasi-Isotropic

FEM Finite Element Method/Model

q Heat flux; exchanged power per unit area

APU Auxiliary Power Unit

H_TC Thermal contact conduction parameter

σ_yld Stress from which material yields. Will vary with temperature

σ_bck Stress from which material creeps. Will be set to zero to allow creep at any stress.