Systematic study of aqueous monoethanolamine-based CO2 capture process: model development and process improvement

Abstract

In this paper, we present improvements to postcombustion capture (PCC) processes based on aqueous monoethanolamine (MEA). First, a rigorous, rate-based model of the carbon dioxide (CO₂) capture process from flue gas by aqueous MEA was developed using Aspen Plus, and validated against results from the PCC pilot plant trials located at the coal-fired Tarong power station in Queensland, Australia. The model satisfactorily predicted the comprehensive experimental results from CO₂ absorption and CO₂ stripping process. The model was then employed to guide the systematic study of the MEA-based CO₂ capture process for the reduction in regeneration energy penalty through parameter optimization and process modification. Important process parameters such as MEA concentration, lean CO₂ loading, lean temperature, and stripper pressure were optimized. The process modifications were investigated, which included the absorber intercooling, rich-split, and stripper interheating processes. The minimum regeneration energy obtained from the combined parameter optimization and process modification was 3.1 MJ/kg CO₂. This study suggests that the combination of a validated rate-based model and process simulation can be used as an effective tool to guide sophisticated process plant, equipment design and process improvement.

Introduction

Global climate change caused by the increasing atmospheric concentration of greenhouse gases such as carbon dioxide (CO₂), has led to great interest in the development of CO₂ capture and storage (CCS) technologies [1-5]. Among them, the amine-based postcombustion CO₂ capture technique is likely to be the first technology applied on a large scale for CO₂ capture from fossil fuel combustion and energy-related processes [6]. One of the major challenges of the amine-based postcombustion capture (PCC) technology in commercial use is the substantial energy penalty involved in the CO₂ capture process, especially the regeneration energy that accounts for more than 50% total energy consumption [7, 8]. While significant efforts have been devoted to the development of novel solvents [9, 10] that have outstanding performance in terms of high CO₂ absorption rates or capacities and low energy consumption of solvent regeneration, the commercial application of these advanced solvents is still immature and requires more efforts to test their technical and economic feasibility on a large scale. In comparison, aqueous monoethanolamine (MEA), a simple and cheap amine, is still widely recognized as a first choice or at least the benchmark solvent for PCC technology, due to the fast CO₂ absorption rate and mature technology commercially applied in the gas processing industry [11].

Considerable efforts around the world have been made toward the commercialization of the MEA-based CO₂ capture technology in coal-fired power stations. Experimentally, plenty of academic research work including laboratory- and pilot-scale experiments have been carried out to deeply understand the chemical reaction mechanism and to evaluate the technical, economic, and environmental feasibility of this technology [12, 13]. Parallel to the experimental activities, several process simulators such as Aspen Plus [14-16], Aspen HYSYS [17], gProms [18], Fortran [19, 20] etc. were used to thermodynamically or kinetically simulate the absorption/stripping process in order to guide process optimization and development for energy efficiency. The research findings, however, suggest that commercial application for large-scale CO₂ reduction using aqueous MEA will still require significant technology advancements with respect to (1) the energy consumption, (2) solvent degradation, (3) absorption capacity, and (4) equipment corrosion. Among them, the large energy penalty associated with solvent regeneration constitutes a major obstacle for this technology in commercial use. The specific heat requirement of solvent regeneration in the MEA process is generally around 3.6–3.8 MJ/kg CO₂ [17, 21-23], which will lead to a significant drop of net power plant efficiency. For example in Australia, the energy consumption for solvent regeneration and operation of the PCC plant will lead to typically 10%-points decrease in net power generation efficiency if a PCC plant with 90% capture efficiency is integrated into a new black coal-fired power station, consequently resulting in more than doubling the cost of electricity generation across the board [24]. Reducing the energy requirement of solvent regeneration is therefore imperative in order to push forward MEA-based capture technology.

The optimization of the PCC plant including parameter optimization and process modification seems to be an effective method to reduce the energy penalty involved in the CO₂ capture process. Salkuyeh et al. [25] and Abu-Zahra et al. [26] carried out a parametric study and showed that the process operating conditions have a great impact on the stripper reboiler duty. These studies highlighted that the parameters of the CO₂ capture process should be optimized to determine the best conditions that minimize the energy demand. Cousins et al. [27, 28] evaluated sixteen different process configurations aiming at reducing the energy consumption of amine processes, while Karimi et al. [29] studied five different stripper configurations with respect to savings in capital cost and energy consumption. Their results show that the advanced process configurations such as the absorber intercooling, rich solvent split, stripper interheating, etc. play an important role in the energy saving of stripper reboiler duty. Moreover, Freguia et al. [30] and Leonard et al. [31] investigated both the parameter optimization and process modification, and indicated that the energy consumption had a great potential to be significantly reduced by the combination of these two process improvements.

Since large-scale PCC plants are very expensive to be built for research purposes, the rigorous process and equipment modeling is an efficient and economic tool for evaluating the performance of these process improvements. A rigorous rate-based model enables an accurate description and characterization of CO₂ absorption/stripping processes taking place along the packed column, such as mass and heat transfer across the gas and liquid phases, chemical reactions, material and energy balance, and hydraulic properties, etc. [32]. Aspen Plus^®, a commercial software, has been widely used as an effective simulator to study the CO₂ capture process and evaluate the energy demands involved in PCC, specifically the stripper reboiler heat requirement [14-16, 33]. However, process modeling cannot always ensure sufficient confidence in the process performance in a commercial sense and sometimes even generates unpractical results due to a lack of necessary experimental validation from pilot plant results. Therefore, the combined work of pilot plant trials and process simulation would be the most appropriate way to develop the PCC plant economically and effectively.

In 2010, CSIRO in collaboration with Stanwell Corporation Limited based in Queensland, Australia, constructed a PCC pilot plant with a designed CO₂ capture rate of ~100 kg/h using aqueous MEA and real flue gas containing 11.0–13.5% CO₂ from Tarong power station [27, 34]. Using the pilot plant results, a rigorous, rate-based model was developed in Aspen Plus^® V7.3 and used to evaluate the MEA-based CO₂ capture process. The model was validated against the experimental data from Tarong pilot plant trials in terms of the key parameters of both the absorber column and stripper column. Systematic studies including process parameter optimization and flow sheet modifications were investigated to significantly reduce the regeneration energy consumption.

Rate-based Model Development

Model description

The commercially available Aspen Plus^® software was used to simulate the MEA-based CO₂ capture process. The process model consists of a thermodynamic model, a transport model, and a rate-based model. To simplify the process modeling, the absorber simulation and stripper simulation were conducted independently. In the stripping modeling, the inlet stream was copied from the outlet stream from the CO₂ absorber, and vice versa. It should be noted that although this simple method would slightly deviate the material balance of the absorption-desorption system, the marginal deviation has little effect on the technical and energy performance of the MEA process.

Physical and chemical properties

Rigorous physical and chemical properties are fundamentally essential for the model to accurately evaluate the performance and characteristics of the CO₂ capture process by aqueous MEA. In this simulation, the electrolyte non-random two-liquid (NRTL) method and the RK (Redlich–Kwong) equation of state were used to compute liquid properties (activity coefficient, Gibbs energy, enthalpy, and entropy) and vapor properties (fugacity coefficients) of the model MEA-CO₂-H₂O system, respectively. This electrolyte NRTL model has been validated to accurately predict the vapor–liquid equilibrium, aqueous speciation, heat capacity, and CO₂ absorption enthalpy of the MEA–H₂O–CO₂ system with a wide application range: MEA concentration up to 40wt.%, CO₂ loading up to 1.33, temperature up to 443 K and pressure up to 20 MPa [35]. These conditions cover all the conditions used in the pilot plant and simulations studied. The gases CO₂, N_2, and O₂ were selected as Henry-components to which Henrys law was applied. The Henrys constants, transport and thermal properties of the MEA-CO₂-H₂O system were retrieved from the Aspen Plus databanks, which have been proved to accurately describe the physical and transport characteristics based on experimental data [35].

The electrolyte solution chemistry of the MEA-CO₂-H₂O system was modeled taking into account the equilibrium and kinetic reactions shown in Table 1. The equilibrium constants for reactions (1)–(4) were calculated from the standard Gibbs-free energy change and the rate constants for reactions (5)–(8) were taken from the work of Pinsent et al. [36] and Hikita et al. [37]. The equilibrium and kinetic parameters have been built and updated in Aspen Plus databases and are described in more details elsewhere [14-16].

Table 1. Chemical reactions in the MEA-CO₂-H₂O system

No.	Type	Reactions
1	Equilibrium	2H2O ↔ H3O+ + OH−
2	Equilibrium	CO2 + 2H2O ↔ H3O+ + HCO3−
3	Equilibrium	HCO3− + H2O ↔ CO32− + H3O+
4	Equilibrium	MEAH+ + H2O ↔ MEA + H3O+
5	Kinetic	CO2 + OH− → HCO3−
6	Kinetic	HCO3− → CO2 + OH−
7	Kinetic	MEA + CO2 + H2O → MEACOO− + H3O+
8	Kinetic	MEACOO− + H3O+ → MEA + CO2 + H2O

Rate-based modeling

The rate-based model validation of the CO₂ capture process using aqueous MEA was carried out based on the Tarong pilot plant configuration as shown in Figure 1. The RateSep simulator embedded in Aspen Plus was used to simulate the aqueous MEA-based CO₂ capture process. This simulator allows the user to divide the tray column or packed column into different stages and provides more accurate and detailed description of CO₂ absorption behavior at each stage based on the material and energy balance. In order to reflect the actual pilot MEA process, the rate-based model used the same column parameters as the pilot plant, such as packing material, column diameters, and packed heights. Table 2 lists the column parameters of both the CO₂ absorber and CO₂ stripper together with the primary correlations and settings of the rate-based absorber/stripper model. The interfacial area factor was varied from 1.0 to 2.0 to provide a good agreement between experimental and simulation results. The value 1.8 was chosen due to the excellent agreement between the experimental and simulation results. This was shown by the average relative error deviations between experimental and simulation results of 2.7% for CO_2-rich loading, 5.8% for CO₂ absorption rate, 1.3% for reboiler temperature, 0.3% for CO₂ purity, and 4.0% for the regeneration energy. Given the 10% uncertainty associated with the comparison between predicted and pilot results [14], the proposed rate-based model enabled a reasonable prediction of the CO₂ absorption and desorption process. Details are discussed further in the next section.

Figure 1. Process flow-sheet of Tarong CO2 capture pilot plant cited from Cousins et al. [34].

Table 2. Summary of model parameters and column settings used in the rate-based model

Model and column properties	Absorber	Desorber
Number of stages	20	20
Packing material	Mellapak M250X	Mellapak M350X
Total packed height	7.136 m (4 × 1.784 m)	7.168 m (2 × 3.584 m)
Column diameter	350 mm	250 mm
Flow model	Mixed model	Mixed model
Interfacial area factor	1.8	1.8
Initial liquid holdup	0.03 L	0.03 L
Film resistance	Discrxn for liquid; Film for vapor	Discrxn for liquid; Film for vapor
Discretization points for liquid film	5	5
Mass transfer correlation method	Bravo et al. [38]	Bravo et al. [38]
Heat transfer correlation method	Chilton-Colburn	Chilton-Colburn
Interfacial area method	Bravo et al. [38]	Bravo et al. [38]
Liquid holdup correlation method	Bravo et al. [39]	Bravo et al. [39]

Model validation against Tarong pilot plant results

The CO₂ capture process using aqueous MEA in the Tarong PCC pilot plant consisted of two major parts: the absorption and desorption processes. Accordingly, the rate-based modeling for the MEA process was carried out through the validation of the packed absorber column and stripper column, respectively. Table 3 summarizes the operating conditions and pilot results of both the CO₂ absorber and CO₂ stripper, together with the simulation results based on the conditions of the 22 pilot plant trials.

Table 3. Comparison between pilot plant trials and rate-based model simulation results under a variety of experimental conditions

Test date (2011)	1 Feb	3 Feb	7 Feb	11 Feb	22 Mar	24 Mar	25 Mar	30 Mar	4 Apr	5 Apr	13 Apr
Test conditions of CO2 absorption
Lean temp. °C	31.7	31.4	31.3	35.5	33.9	34.8	35.3	33.5	32.4	37.5	35.6
Lean flow rate, L/min	31.7	32.0	27.0	31.3	26.9	33.0	35.8	32.0	24.0	24.4	32.0
Lean MEA conc., wt.%	25.1	24	27.9	25.5	31.6	29.6	29.2	30.3	33.5	34.0	29.3
Lean CO2 loading, mol/mol	0.279	0.294	0.284	0.280	0.314	0.333	0.347	0.316	0.254	0.278	0.414
Inlet flue gas temp. °C	51.7	50.5	48.1	51.3	53.6	54.2	55.8	65.5	66.1	63.9	49.8
Inlet gas pressure, kPa-a	106.1	105.6	106.3	106.6	107.5	107.3	107.3	107.3	108.7	108.3	107.2
Inlet flue gas flow rate, kg/h	489.6	491.1	488.6	489.4	482.8	483.9	484.8	483.2	646.1	644.4	487.5
Inlet flue gas CO2 vol%	11.9	11.8	11.8	12.1	13.4	13.5	13.5	12.8	12.9	13.2	12.7
Inlet flue gas H2O vol%	4.2	5.0	3.8	3.9	4.3	4.0	3.9	3.6	4.3	4.1	3.8
Test conditions of CO2 desorption
Condenser Temp. °C	30.2	29	26.2	29.6	32.0	29.9	29.4	25.4	26.9	24.8	28.8
Stripper top pressure, kPa-a	181.9	180.4	177.5	189.9	189.2	195.0	195.5	191.5	223.3	222.1	151.8
Temp. differencea, K	16.7	16.9	18.5	17.4	21.0	20.0	19.8	19.0	23.8	25.6	17.6
CO2 desorption rate, kg/h	71.6	71.0	70.6	73.6	72.6	76.8	76.7	76.0	93.9	94.2	49.3
Results comparison of pilot plant and simulation
Expt. rich CO2 loading, mol/mol	0.466 ± 0.007	0.480 ± 0.005	0.469 ± 0.004	0.471 ± 0.001	0.481 ± 0.001	0.486 ± 0.004	0.488 ± 0.002	0.494 ± 0.007	0.494 ± 0.001	0.489 ± 0.003	0.525 ± 0.003
Simu. rich CO2 loading, mol/mol	0.491	0.497	0.493	0.493	0.509	0.499	0.496	0.490	0.504	0.505	0.502
Expt. CO2 abs rate, kg/hb	73.5 ± 1.4	74.2 ± 1.6	72.3 ± 1.6	74.4 ± 1.6	74.2 ± 1.7	77.8 ± 1.8	77.4 ± 1.4	75.5 ± 1.5	96.9 ± 1.8	94.1 ± 1.4	49.2 ± 1.9
Simu. CO2 abs rate, kg/h	80.6	75.3	80.2	81.0	68.8	80.8	80.4	83.5	96.3	91.1	45.2
Expt. reboiler temp., °C	116.9 ± 0.3	116.4 ± 0.2	117.0 ± 0.2	117.6 ± 0.2	117.2 ± 0.4	117.1 ± 0.2	115.9 ± 0.2	117.5 ± 0.2	125.3 ± 0.3	125.8 ± 0.4	104.7 ± 0.6
Simu. reboiler temp., °C	118.6	117.9	118.4	119.1	119.2	119.6	119.3	119.5	126.7	126.5	110.0
Expt. regen. energy, MJ/kg CO2	4.48	4.45	4.35	4.50	4.33	4.51	4.60	4.49	4.01	4.04	4.55
Simu. regen. energy, MJ/kg CO2	4.60	4.56	4.57	4.65	4.66	4.68	4.83	4.66	4.01	4.11	5.20
Expt. CO2 product purity, vol%	97.7	97.7	97.8	97.7	97.6	97.8	97.8	98.0	98.9	99.0	98.1
Simu. CO2 product purity, vol%	97.6	97.7	98.0	97.7	97.4	97.8	97.8	98.2	98.3	98.5	97.3

Test date	19 Apr	20 Apr	11 May	12 May	13 May	18 May	20 May	24 May	25 May	26 May	27 May
a Temperature difference of solvent in and out of stripper. b The difference of CO2 mass flow rate across the CO2 absorber. c Experiment regeneration was calculated by sum of three heat components.
Test conditions of CO2 absorption
Lean temp. °C	38.7	38.7	39.4	39.3	39.2	39.7	40.5	39.6	39.4	39.6	39.5
Lean flow rate, L/min	21.1	21.1	27.1	27.0	27.0	32.1	27.0	27.0	26.9	27.2	27.0
Lean MEA conc., wt.%	32.3	32.8	29.2	29.2	28.9	26.2	27.4	28.1	28.3	28.5	28.5
Lean CO2 loading, mol/mol	0.285	0.291	0.285	0.285	0.280	0.314	0.288	0.295	0.297	0.283	0.283
Inlet flue gas temp. °C	48.3	48.8	58.3	59.4	56.7	61.8	60.7	60.0	56.1	58.2	57.9
Inlet gas pressure, kPa-a	106.7	106.6	108.9	108.7	108.8	108.3	108.5	109.0	108.8	108.9	109.0
Inlet flue gas flow rate, kg/h	485.5	487.5	598.7	598.4	597.2	598.0	597.2	596.8	596.0	598.5	597.8
Inlet flue gas CO2, vol%	12.2	12.2	11.1	11.2	11.2	11.1	11.0	11.6	11.6	11.6	11.1
Inlet flue gas H2O, vol%	3.9	3.9	5.2	5.3	5.0	5.5	5.4	5.5	5.1	5.2	5.2
Test conditions of CO2 desorption
Condenser Temp. °C	24.7	23.9	19.2	20.4	18.2	20.7	19.8	19.4	17.6	18.6	17.0
Stripper top pressure, kPa-a	186.9	182.0	202.7	200.0	202.2	200.5	202.2	203.1	202.0	203.3	202.2
Temp. differencea, K	18.6	18.5	18.3	18.8	18.8	17.4	19.6	18.9	19.4	19.2	18.7
CO2 desorption rate, kg/h	73.3	71.1	84.3	83.6	84.0	82.4	84.2	84.6	84.1	84.7	84.2
Results comparison of pilot plant and simulation
Expt. rich CO2 loading, mol/mol	0.486 ± 0.001	0.500 ± 0.001	0.488 ± 0.001	0.488 ± 0.001	0.491 ± 0.002	0.499 ± 0.005	0.503 ± 0.001	0.511 ± 0.006	0.512 ± 0.001	0.492 ± 0.001	0.492 ± 0.006
Simu. rich CO2 loading, mol/mol	0.506	0.506	0.500	0.500	0.501	0.499	0.501	0.503	0.504	0.502	0.503
Expt. CO2 abs rate, kg/hb	76.0 ± 2.1	72.0 ± 1.7	85.3 ± 1.5	83.3 ± 1.6	83.4 ± 2.0	82.8 ± 1.7	84.3 ± 1.6	83.9 ± 2.0	83.8 ± 1.8	85.7 ± 1.5	85.0 ± 1.4
Simu. CO2 abs rate, kg/h	72.9	72.3	81.8	81.7	82.5	75.6	75.6	76.0	75.8	81.4	80.9
Expt. reboiler temp., °C	119.9 ± 0.3	118.7 ± 0.3	121.5 ± 0.2	121.1 ± 0.4	121.2 ± 0.3	119.9 ± 0.1	121.7 ± 0.3	121.3 ± 0.3	121.1 ± 0.2	121.4 ± 0.3	121.6 ± 0.2
Simu. reboiler temp., °C	120.6	119.7	122.4	122.0	122.3	121.0	122.3	122.4	122.2	121.8	122.3
Expt. Regenerationc, MJ/kg CO2	3.86	3.88	4.10	4.12	4.15	4.28	4.18	4.10	4.11	4.12	4.11
Simu. regeneration, MJ/kg CO2	4.01	4.02	4.21	4.23	4.23	4.46	4.29	4.23	4.24	4.19	4.22
Expt. CO2 product purity, vol%	98.5	98.8	99.4	98.7	99.4	99.2	99.4	99.0	99.1	99.3	99.5
Simu. CO2 product purity, vol%	98.3	98.3	98.8	98.7	98.9	98.7	98.8	98.8	99.0	98.9	99.0

Performance of CO₂ absorber

The CO₂ absorption rate is considered one of the most significant indicators for developing a reliable rate-based model, as it closely represents the reaction properties such as equilibrium and kinetic constants. Figure 2A shows the excellent match between model results and pilot plant data for a wide range of CO₂ absorption rates 40–100 kg/h. The average relative error deviation for the 22 tests was 5.6%.

Figure 2. Results of comparison between simulation and Tarong pilot plant measurements: (A) CO2 absorption rate in absorber; (B) CO2 loading of rich solvent leaving absorber; (C) temperature of rich solvent leaving absorber and (D) temperature profiles along absorber column (01 Feb).

Figure 2B shows the parity plot of CO₂ loading (mole ratios of CO₂/MEA) in the rich solvent after absorption between experimental and pilot results. It can be seen that the model gave a 2.7% overestimation on the rich CO₂ loading compared to the experimental data. This overestimation is likely caused by the samples being analyzed offline. A small portion of the absorbed CO₂ was most likely lost during sample collection and measurement due to the high CO₂ partial pressure of the rich solvent samples. Overall, the predictions of CO₂ loading were considered satisfactory.

Figure 2C and D suggest that the experimental temperature has a good agreement with the simulation results, implying that the rate-based model is able to predict the temperature profile along the absorber column. However, it should be noted that the experimental temperatures along the column in Figure 2D were always lower than the model data and the deviation was even greater at the high temperature sections at a packed height of 4–6 m. This is most likely due to heat loss along the column wall during the CO₂ absorption process. Another possibility is that the solvent lost heat through the uninsulated pipe, whilst the solvent was removed from the column between the packed sections.

Performance of CO₂ stripper

Figure 3A shows the parity plot of stripper reboiler temperature between simulation results and pilot plant data. It is found that the experimental values were consistently lower than those of the simulation because of the drastic heat loss in the high temperature stripper (90–130°C). This is demonstrated by the temperature profiles indicated in Figure 3B. Heat loss was always occurring along the stripper column, which is reflected by the temperature deviation from the model results. It is worthwhile to mention that the temperature deviation at the packed height 0–3.584 m (bottom section) was much greater than that at the height 3.584–7.168 m (top section), and that some temperatures in the bottom stage were surprisingly lower than that in the top stage. Two possible reasons can account for this phenomenon. One is the higher temperature in the bottom stage resulted in higher heat loss. The second is that heat loss took place from the solvent when being transported through pipelines between packed sections which are installed outside the stripper column (Fig. 1). This resulted in greater heat loss to the environment.

Figure 3. Results of comparison between simulation and Tarong pilot trials: (A) reboiler temperatures; (B) temperature profiles in packed desorber (Test 01 Feb); (C) CO2 purity in the CO2 product; (D) H2O concentration in the CO2 product; (E) solvent regeneration duty.

Due to water vaporization at high temperatures in the stripper, the CO₂ stream generated in the stripper may require further purification. Condensation was considered as the the effective approach to separate most of the water vapor from the CO₂ stream. In the pilot plant trials, the condenser temperature was controlled in the range of 17–30°C. This ensured a high purity of CO₂ product ranging from 97.5 to 99.5 vol.%, which meets the requirement for CO₂ compression. The simulation results in Figure 3C and 3D are in excellent agreement with the experimental results in terms of H₂O content and CO₂ concentration in the CO₂ product, which proves that the rate-based stripper model has the capability to predict the condensation process.

The experimental regeneration energy was calculated by summing three key components: heat for stripping CO₂ from the solvent, sensible heat for heating up solvent to the required desorption temperature, and the water vapor leaving the stripper in the overhead gas stream. Due to the heat loss along the stripping column, the measured reboiler temperature in pilot trials would be always lower than the actual temperature (Fig. 3A), which resulted in the underestimation of sensible heat and the subsequent regeneration duty. While the model does not take the heat loss into account and take the high modeling reboiler temperature to calculate the regeneration duty. As a result, the simulated results of solvent regeneration duty had an average 4.0% overestimation over the pilot plant results as shown in Figure 3E.

In conclusion, the good agreement between the experimental results and the modeling results for both CO₂ absorber and CO₂ stripper suggests that the established rate-based model can satisfactorily predict the CO₂ capture process by aqueous MEA.

Process Improvement of MEA-Based CO₂ Capture Process

The process improvement was proposed to reduce the energy requirement of the MEA process by using the validated rate-based model to investigate parameter optimization and process modifications. The typical flue gas with 900 kg/h flow rate in the Tarong pilot trials was used and it contained 11.9% CO₂, 7.3% O₂, 4.3% H₂O, and 76.5% N₂. The gas pressure and temperature (at inlet to absorber) were 106 kPa (absolute pressure) and 50°C, respectively. The CO₂ removal efficiency of the MEA process was designed at 85%.

Heat requirement of a typical Tarong pilot case

During the process optimization, the regeneration duty was considered as the most important factor to optimize and improve the MEA process, as it is the main contributor to the total energy required for the CO₂ capture process. In order to understand how the three heat requirements are distributed, the representative Tarong pilot trial (Test 01 Feb) with a regeneration duty of 4596 KJ/kg CO₂ was investigated as shown in Figure 4. Analyzing the individual heat requirement was based on the following equations.

Figure 4. The distribution of three heat requirements: heat of CO2 desorption, sensible heat, heat of water vaporization.

1. ${\textstyle Q_{des,{CO}_{2}}=n_{{CO}_{2}}\quad H_{{CO}_{2}},}$ where ${\textstyle n_{{CO}_{2}}}$ is the mole of regenerated CO₂, mol; ${\textstyle H_{{CO}_{2}}}$ the enthalpy per mole CO₂ desorbed from the solution and the calculation method is taken from Que [40], kJ/mol. The heat of CO₂ desorption required to break the chemical bond between MEA and CO₂, accounts for the largest energy consumption. The higher the MEA concentration and rich CO₂ loading, the lower the heat of CO₂ desorption.
2. ${\textstyle Q_{sens}={\overline {m}}_{solv}{\overline {c}}_{P}\left(T_{in}-\right.}$$\left.T_{out}\right)$, where m_solv is the mass flow rate of the solvent flowing through the stripper, kg/h; C_P specific heat capacity of the solvent, kJ/kg·K; T_in − T_out solvent temperature difference in and out of the stripper, K. Narrowing the temperature difference and lowering the solvent mass flow rate are the primary approaches to reducing the sensible heat.
3. ${\textstyle Q_{vap,\quad \quad H_{2}O}=n_{vap,\quad \quad H_{2}O}\quad H_{vap,\quad \quad H_{2}p}}$, where ${\textstyle n_{vap,\quad \quad H_{2}O}}$ is the moles of excess steam leaving the stripping column, mol; ${\textstyle H_{vap,\quad \quad H_{2}O}}$ latent heat of steam generation. An amount of stripping vapor is needed to maintain the driving force for CO₂ desorption in the stripper. However, if the amount of stripping vapor is high, large amounts of water vapor will leave the stripper and the energy is lost in the condenser. The heat of water vaporization is dependent on the temperature at the top of the stripper before the vapor enters the condenser. The best scenario is to make the temperature of the stripper exit as low as possible, whilst the CO₂ desorption process is maintained by a certain amount of water vapor leaving the stripper.

Parameter optimization

Important process parameters were studied, including MEA concentration, lean CO₂ loading, lean solvent temperature, and stripper pressure. The temperature difference of lean/rich cross heat exchangers was set as 15°C on the hot side.

MEA concentration

As shown in Figure 5A, the energy consumption for solvent regeneration decreased substantially with increasing MEA concentration. This is because high MEA concentration allowed for better CO₂ absorption performance including the improvement of CO₂ reaction rate and the CO₂ absorption capacity per kilogram solvent. The increasing MEA concentration also led to a decrease in the solution circulation rate which resulted in a decrease in sensible heat and a subsequent reduction in regeneration duty. Upon an increase in MEA concentration from 25 to 40 wt.%, the reboiler duty decreased by 14%. However, the use of high concentration MEA will considerably increase the degradation rate due to a higher O₂ mass transfer at higher MEA concentrations in the absorber [41]. Moreover, the higher solvent concentration causes an increase in viscosities and diffusion coefficient, thus increasing the operational difficulty in real practice. For balancing the energy saving and adverse effects, a MEA concentration of 35 wt.% was chosen in this study, which is a compromise concentration between 30% MEA used by Notz et al. [23] and 40% MEA by Abu-Zahra et al. [26]

Figure 5. Effect of (A) MEA concentration, (B) lean CO2 loading, (C) Lean solvent temperature, (D) stripper top pressure on the regeneration energy based on single factor analysis.

Lean CO₂ loading

Figure 5B shows the influence of lean CO₂ loading on the regeneration duty and solvent flow rate. The lean CO₂ loading between 0.25 and 0.275 was the optimal with the energy ranging between 3.59 and 3.61 MJ/kg CO₂. At lean CO₂ loadings below 0.25, although the solution provided more free MEA for faster CO₂ absorption and a lower solvent flow rate, the regeneration duty increases. This is because an increasing amount of stripping steam is required to regenerate such a low loading solvent. At high lean CO₂ loadings, the solvent circulation flow rate increased substantially resulting in an increase in sensible heat and risk of column flooding.

Lean solvent temperature

As shown in Figure 5C, increasing the lean solvent temperature from 30 to 55°C slightly increased the regeneration duty. This is because higher temperatures result in the increase of CO₂ equilibrium pressure and hence decreased the CO₂ absorption capacity of the MEA solvent. However, at high lean temperatures, less cooling duty is required for solvent cooling resulting in lower cooling water consumption. Moreover, from the viewpoint of practical operation, high lean solvent temperature led to the increase in the water vaporization rate from the absorption column, which is beneficial, in that the water condensing in the wash section would make it more effective for removing other trace constituents in the exiting flue gas. After water condensation, it is then periodically recycled back to the lean solvent to maintain the water balance of the system.

Stripper pressure

Elevating the stripper pressure has some benefits. One is to suppress the water vaporization and subsequently a reduction in heat of water vaporization; the second is to increase the stripper temperature to facilitate the CO₂ stripping process. As shown in Figure 5D, increasing stripper pressure from 150 to 275 kPa (absolute pressure) led to an 8.3% reduction in the heat requirement of solvent regeneration. However, the elevated pressure also brings the drawbacks: (1) the high temperature would enhance amine degradation rates and corrosion problems and subsequently increase the material and maintenance cost during operation [42]; (2) the high reboiler temperature would require extraction of higher quality steam which may results in a higher net efficiency penalty on the power station; (3) high pressure would place a burden on the capital cost of stripper design and construction. Thus, the suitable stripper pressure should be determined by considering the energy saving, material saving, construction cost, etc. In this simulation, a compromise stripper pressure of 200 kPa (absolute pressure) was chosen with condenser duty 1.2 MJ/kg CO₂, reboiler temperature 123°C, and regeneration duty 3.6 MJ/kg CO₂, in which heat of CO₂ desorption accounts for 59%, heat of water vaporization 22% and sensible heat 19%. The regeneration duty of 3.6 MJ/kg CO₂ agrees well with the numbers reported in the literature ranging 3.6–3.8 MJ/kg CO₂ [17, 21-23]. It is worth mentioning that the optimal operating conditions are likely to vary depending on flue gas composition, column size, and process configuration. A case by case study is recommended to obtain the best operating conditions for the individual process.

Process modification

Based on the optimized parameters, process modifications were proposed to further reduce the energy consumption of solvent regeneration via the absorber intercooling process, rich-split process and stripper interheating process. The corresponding process configurations are shown in Figure 6.

Figure 6. Process configurations of (A) absorber intercooling, (B) rich-split and (C) stripper interheating (HeatX represents heat-exchanger).

Intercooling process

The exothermic reactions of CO₂ absorption by MEA increase the solvent temperature along the absorber column. This, on the one hand, favors the reaction kinetics due to the improved mass transfer coefficients; on the other hand, limits the solvent absorption capacity due to the increased CO₂ partial pressure at a given loading. The intercooling process modification (Fig. 6A), however, is able to overcome the drawback of absorption capacity caused by the increasing temperature, because this process modification enables the increase of CO₂ loading in the rich solvent owing to the low equilibrium CO₂ partial pressure at low temperature. Knudsen et al. [21] evaluated absorber intercooling at pilot scale and revealed that intercooling enabled a higher CO₂ cyclic carrying capacity thereby reducing regeneration energy.

Table 4 lists the results of different cases with the intercooling process applied to the absorber. All the solvent went through the intercooler to maximize the benefits of the intercooling process. It can be seen that if the intercooler was installed at a low position near the bottom of the absorber, the intercooling process was able to improve the CO₂ loading in the rich solvent and subsequently reduced the reboiler duty, a 1.8% energy saving at intercooling temperature 25°C. In addition to the energy reduction, the intercooling process also had the potential to reduce the column height while maintaining the CO₂ removal efficiency at 85% and similar solvent regeneration duty. When intercooling to 25°C was applied to the absorber, the packed height can be reduced from 7.136 m to 5.325 m. This is a 25% reduction in column height and allows for a great reduction in the capital cost of column design and construction. It also can be seen that the lower the temperature of the intercooling process, the better the performance in terms of regeneration duty. If lower temperature cooling water is available for the PCC plant, the regeneration energy and/or column height could be further reduced by the intercooling process. Furthermore, for scrubbing solvents that have a higher CO₂ absorption capacity than MEA, better benefits of energy decrease and column reduction could be obtained from the intercooling process.

Table 4. Results of intercooling process at different scenarios with L/G ratio 2.3

	Rich CO2 loading, mol/mol	Regeneration energy, MJ/kg CO2	Energy saving,%	Specification
Reference case	0.5007	3.600	−0.0	Total packed height 7.136 m
Intercooler position: height from bottom
3.568 m	0.4989	3.626	+0.72	Cooling to 30°C
1.586 m	0.5026	3.567	−0.92
0.792 m	0.5039	3.545	−1.53
Cooling temperature
40°C	0.5015	3.578	−0.61	Height 0.792 m
35°C	0.5027	3.561	−1.08
25°C	0.5046	3.535	−1.80
Total height of absorber column
5.325 m	0.5013	3.585	−0.41	Cooling to 25°C; height 0.6 m
5.325 m	0.4962	3.660	+1.66	No intercooling

Rich-split process

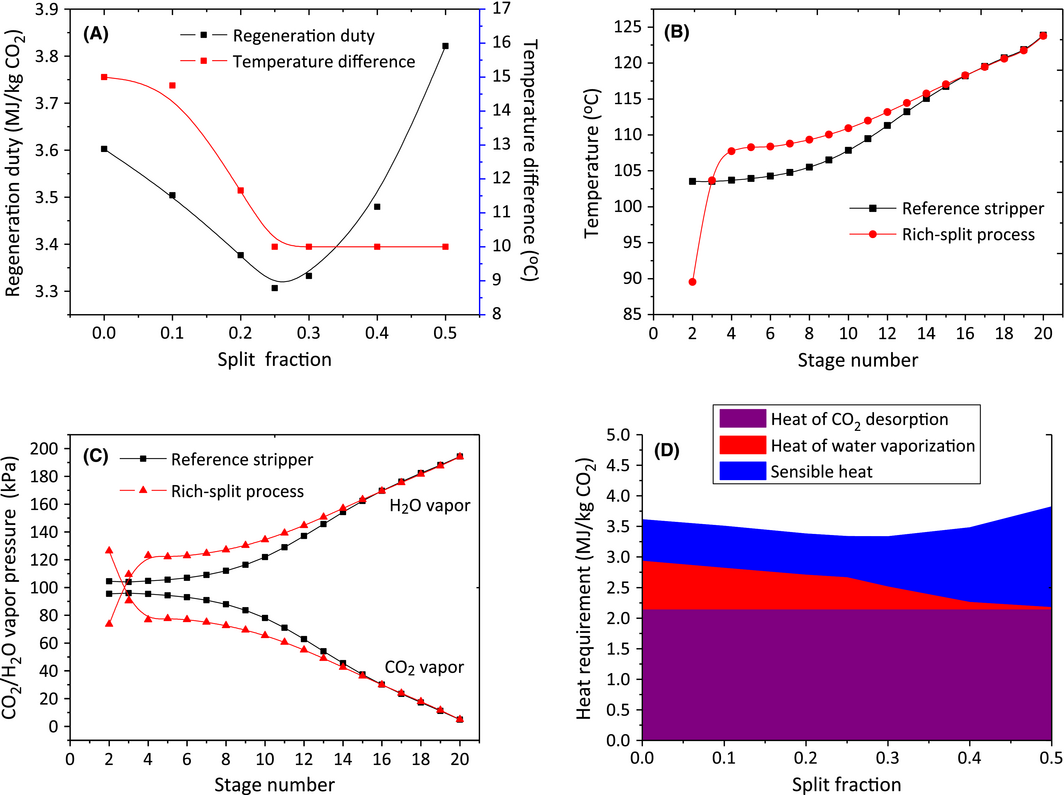
The rich-split process modification shown in Figure 6B is an efficient method to reduce the reboiler duty via the recovery of the steam generated in the stripper. The cold rich stream was split to recover the energy contained in the upcoming high temperature water vapor; meanwhile the rich solvent was heated to release part of the CO₂. This process has proven to be effective in process simulations [43-45] as well as in the Tarong pilot plant trials [34]. In this study, the unsplit stream was introduced at the stage 5 (20 stages in total) after crossing the heat exchanger while the split stream was fed to the top of the stripper. Figure 7A shows the effect of split fraction (the ratio of split stream to the total rich solvent) on the regeneration duty. It can be seen that the rich split has a notable reduction on the reboiler energy consumption when the split fraction was up to 0.45. The temperature difference of the heat exchanger on the hot side decreased but was limited to 10°C with increasing split ratio. A minimum was achieved when 25% of the cold rich solvent was split to the top of the column. This minimum regeneration duty was 3.31 MJ/kg CO₂ together with 0.67 MJ/kg CO₂ condenser duty. This is an 8.06% reduction in reboiler duty and 45.1% reduction in condenser duty compared with the reference case without rich-split process.

Figure 7. (A) Effect of rich split fraction on the total solvent regeneration duty and temperature difference of heat exchanger on the hot side; (B) temperature profile and (C) H2O/CO2 vapor pressure profile along the stripper column between reference stripper and rich-split stripper with 0.25 split ratio (condenser is at stage1; reboiler at stage 20); and (D) the distribution of three heat components: heat of CO2 desorption, heat of water vaporization, sensible heat at different split fractions.

In order to figure out why this saving occurs, the temperature profiles and H₂O/CO₂ vapor pressure along the stripper column were investigated. As shown in Figure 7B, the split cold rich solvent decreased the temperature at the top stage of the stripper (stage 2) in the rich-split process, which was beneficial because it could recover the steam and subsequently reduce the reboiler duty and condenser duty. Meanwhile the temperatures along the column after stage 3 were elevated. This temperature lift came from the heat exchanger where the unsplit rich solvent was heated to a higher temperature as a result of the decreasing solvent flow rate. So the effectiveness of this rich-split modification will be significantly influenced by the efficiency of the lean/rich heat exchanger. The increased temperature along the stripper column resulted in a higher H₂O vapor pressure and subsequently a lower CO₂ vapor pressure after stage 3 (Fig. 7C). This indicated that the driving force of the CO₂ desorption process was enhanced, which has the potential to accelerate the CO₂ desorption rate and reduce the energy consumption of solvent regeneration in practice.

To further specify how the energy was saved by the rich-split process, the distribution of the three heat requirements – heat of CO₂ desorption, heat of water vaporization, sensible heat – was determined. The heat of CO₂ desorption as an inherent property of solvent, was considered to be unchanged since the same rich solvent entering the stripper and the same CO₂ desorption rate were used for all the different split cases. As shown in the Figure 7D, the rich-split configuration led to a significant decrease in the heat of water vaporization with increasing split fraction, which was favorable for lowering condenser duty and the subsequent regeneration duty. However, at higher split fractions, the cold split stream started to cool down the stripper and more sensible heat was required to heat up the split solvent to the required temperature, which led to an increase in reboiler duty. So the heat of water vaporization and sensible heat in the rich-split process were competing with each other, resulting in an appropriate split fraction in which the saving of reboiler duty was maximized. It is worth mentioning that the optimal split fraction was also affected by the temperature approach of heat exchanger on the hot side. The smaller the temperature approach means the higher the temperature of the unsplit rich solvent, which then required more split solvent to recover the stripper steam.

Interheating process

The interheating process shown in Figure 6C exchanges heat between the hot lean stream leaving from the bottom of the stripper and the semi-lean solvent extracted from the middle of the stripper (interheating HeatX) before the hot lean stream goes to the main cross-exchanger (HeatX), thus making better use of the heat in the hot lean stream. This concept has been proposed by Leites et al. [46]. Paul et al. [47] patented this process and suggested using a heat-integrated stripping column to reduce the energy penalty associated with regenerating amine solutions and the modeling results revealed that the heat requirement of solvent regeneration can be reduced with the interheating process [48, 49]. This process design was aimed at reducing reboiler duty and condenser duty by means of (1) recycling the high-quality and high-temperature heat in the hot lean stream, which elevated the overall temperature along the stripper column; (2) reducing the energy loss associated with steam generation by lowering the temperature of the rich solvent entering the top of the stripper column. As shown in Figure 8A and B, like the rich-split process, the interheating process lowers the CO₂ partial pressure by increasing the temperature profiles and H₂O vapor pressure along the stripper column. Meanwhile the interheating process reallocated the heat distribution which elevated the temperature profiles along the bottom of the column whilst decreasing the temperature in the top section of the stripper. This accordingly reduced the energy requirement of sensible heat and heat of water vaporization (Fig. 8C). The regeneration duty with interheating process was reduced to 3.38 MJ/kg CO₂, a 6.1% reduction compared to the reference case.

Figure 8. (A) temperature profiles, (B) H2O/CO2 partial pressure profiles along the stripper column and (C) heat requirement between reference stripper and interheated stripper with interheating at stage 8 (condenser is at stage1; reboiler at stage 20).

It is interesting to find in Table 5 that the flow rate of the interheating stream extracted from the stripper had only a slight effect on the energy saving of the reboiler and condenser. Low flow rates mean that less solvent participated in the heat exchange during the interheating process, but this enabled a higher temperature and higher quality interheated stream entering the middle of the stripper. In contrast, high flow rates mean that more solvent can directly benefit from the interheating process, but results in a relatively lower temperature of the interheated stream. As a result, the extracted solvent obtained similar energy from the interheating process, leading to the results of unchanged energy saving. This can be accounted for by the heat duties of the two heat exchangers, the total of which remained the same with increasing solvent flow rate. This phenomenon suggests that the interheating process would be very flexible in practical application with respect to the amount of solvent extracted from the middle of the stripper. Low interheated solvent flow rates would have the potential of reducing the size of the interheating heat exchanger and energy saving of solvent pumping. It is also found that the total heat duties in the cross exchangers were very close between the reference stripper (135.7 kW) and interheated stripper (135.6–135.8 kW). This indicates that the role of interheating process was to make better utilization of heat contained in the hot lean stream, that is, extracting the high quality and high temperature stream to heat up the stripper column.

Table 5. Effect of interheated solvent flow rate on the duty of two heat exchangers and condenser/reboiler

Interheating solvent flow ratea, kg/h	Reference	500	1000	1500	1900
a The total flow rate of lean solvent was 1961.3 kg/h.
Temperature profiles in the interheating heat exchanger, °C
Cold inlet	–	110.2	110.2	110.2	110.3
Cold outlet	–	119.6	118.1	117.4	117.1
Hot inlet	–	123.9	123.9	123.9	123.9
Hot outlet	–	116.1	116.1	116.1	116.1
Temperature profiles in the main heat exchanger, °C
Cold inlet	39.2	39.2	39.2	39.2	39.2
Cold outlet	108.9	105.3	105.3	105.3	105.3
Hot inlet	123.9	116.1	116.1	116.1	116.1
Hot outlet	48.0	48.0	48.0	48.0	48.0
Heat duties of heat exchangers, kW
Interheating HeatX	–	14.2	14.1	14.1	14.2
Main HeatX	135.7	121.6	121.6	121.5	121.5
Total	135.7	135.8	135.7	135.6	135.7
Energy requirement, MJ/kg CO2
Condenser duty	1.22	0.99	0.99	0.99	0.99
Reboiler duty	3.60	3.38	3.38	3.38	3.38

Combined intercooling, rich-split, and interheating process

The combined process modifications were proposed to make better use of the advantages of the intercooling process, rich-split process, and interheating process. Table 6 summarizes the main design specifications and simulation results of this combined process modification. It should be highlighted that the temperature difference of the main heat exchanger on the cold side was set as 8.8°C to be consistent with the reference case and make a reasonable comparison. Although the combined process increased the cooling duty by 0.14 MJ/kg CO₂ due to the intercooling process, the 25% reduction in absorber size can significantly reduce the capital investment of absorber column and thus compensate the increased cooling duty. More importantly, upon combining the benefits of the three process modifications, the regeneration duty was reduced to 3.11 MJ/kg CO₂, which is a 13.6% reduction in reboiler duty compared to the reference case.

Table 6. Simulation conditions of combined absorber intercooling, rich split, stripper interheating

Simulation conditions	Reference	Combined process
Intercooling temperature, °C	–	30
Intercooling stage (20 stages in total)	–	17
Feed stage of split stream (Split fraction 0.25)	–	2
Feed stage of unsplit stream	–	6
Interheated solvent flow rate, kg/h	–	500
Interheating stage (20 stages in total)	–	8
Temperature difference of main heat exchanger on cold side	8.8	8.8
Condenser temperature, °C	30	30
CO2 desorption rate, kg/h	134.5	134.5
Results
CO2 mass purity, %	99.1	99.1
Intercooling duty, MJ/kg CO2	0	0.61
Condenser duty, MJ/kg CO2	1.20	0.73
Reboiler temperature, °C	123.7	123.7
Reboiler duty, MJ/kg CO2	3.6	3.1

Conclusion

In this study, the combination of pilot-plant trials and process modeling has demonstrated that a validated rate-based model was an effective and reliable tool to evaluate and improve the MEA-based CO₂ capture process. The rate-based model for the absorber and stripper has been successfully validated against the Tarong pilot plant results. The simulation results of the absorber model were in excellent agreement with the experimental results in terms of CO₂ loading in the rich solvent, temperature profiles along the column and CO₂ absorption rate, while the stripper model provided a very good predication of stripper parameters including temperature profiles along the stripper column, CO₂ product composition, and solvent regeneration duty. The rate-based model can be used as a good guide for modeling the MEA-based CO₂ capture process and used as a starting point for more sophisticated models for process development, debottlenecking, plant, and equipment design.

Process improvements including parameter optimization and process modification were carried out to reduce the energy consumption involved in solvent regeneration. After a sensitivity analysis, the optimal operating conditions selected were 35% MEA, 0.25 lean CO₂ loading, 40°C lean solvent temperature and 200 kPa stripper pressure which resulted in a regeneration duty of 3.6 MJ/kg CO₂. The intercooling process alone on the absorber was able to reduce the regeneration duty by 0.6–1.8% or reduce the column height by 25%. The rich-split process alone can reduce the energy by 8.5% with the reboiler duty reduced to 3.3 MJ/kg CO₂. The interheating process alone can also reduce the regeneration duty to 3.3 MJ/kg CO₂. The combination of the three process modifications showed the best energy reduction with the regeneration duty of 3.1 MJ/kg CO₂, which is a 13.6% reduction in reboiler duty compared to the reference case.

Acknowledgments

Kangkang Li thanks the Australian IPRS-APA scholarship and CSIRO Top-up scholarship that supported his research. Weiliang Luo and Jian Chen thank the support from the National Natural Science Foundation of China (key project no. 51134017).

Conflict of Interest

None declared.

Reference

1. International Energy Agency. 2013. 21st Century coal – advanced technology and global energy solution. IEA, Paris, France.
2. Li, K. K., H. Yu, M. Tade, and P. Feron. 2014. Theoretical and experimental study of NH₃ suppression by addition of Me(II) ions (Ni, Cu and Zn) in an ammonia-based CO₂ capture process. Int. J. Greenh. Gas Con.24:54–63.
3. Li, H., J. Yan, J. Yan, and M. Anheden. 2009. Impurity impacts on the purification process in oxy-fuel combustion based CO₂ capture and storage system. Appl. Energy86:202–213.
4. Kunze, C., and H. Spliethoff. 2012. Assessment of oxy-fuel, pre- and post-combustion based carbon capture for future IGCC plants. Appl. Energy94:109–116.
5. Li, K., H. Yu, G. Qi, P. Feron, M. Tade, J. Yu, and S. Wang. 2015. Rate-based modelling of combined SO₂ removal and NH₃ recycling integrated with an aqueous NH₃-based CO₂ capture process. Appl. Energy148:66–77.
6. Rochelle, G. T.2009. Amine scrubbing for CO₂ capture. Science325:1652–1654.
7. Herzog, H., J. Meldon, and A. Hatton. 2009. Advanced post-combustion CO₂ capture. Prepared for Clean Air Task Force. https://mitei.mit.edu/system/files/herzog-meldon-hatton.pdf. Accessed on May 2014.
8. Aaron, D., and C. Tsouris. 2005. Separation of CO₂ from flue gas: a review. Sep. Sci. Technol.40:321–348.
9. Puxty, G., R. Rowland, A. Allport, Q. Yang, M. Bown, R. Burns, et al. 2009. Carbon dioxide postcombustion capture: a novel screening study of the carbon dioxide absorption performance of 76 amines. Environ. Sci. Technol.43:6427–6433.
10. Porcheron, F., A. Gibert, P. Mougin, and A. Wender. 2011. High throughput screening of CO₂ solubility in aqueous monoamine solutions. Environ. Sci. Technol.45:2486–2492.
11. DECC ScottishPower CCS Consortium. 2011. UK Carbon capture and storage demonstration competition. SP-SP 6.0–RT015 FEED Close Out Report.
12. Reynolds, A. J., T. V. Verheyen, S. B. Adeloju, E. Meuleman, A. Chaffee, A. J. Cottrell, et al. 2013. Chemical characterization of MEA degradation in PCC pilot plants operating in Australia. Energy Procedia37:877–882.
13. Manzolini, G., E. S. Fernandez, S. Rezvani, E. Macchi, E. L. V. Goetheer, and T. J. H. Vlugt. 2015. Economic assessment of novel amine based CO₂ capture technologies integrated in power plants based on European Benchmarking Task Force methodology. Appl. Energy138:546–558.
14. Zhang, Y., H. Chen, C. C. Chen, J. M. Plaza, R. Dugas, and G. T. Rochelle. 2009. Rate-based processXmodeling study of CO₂ capture with aqueous monoethanolamine solution. Ind. Eng. Chem.Res.48:9233–9246.
15. Zhang, Y., and C. C. Chen. 2013. Modeling CO₂ absorption and desorption by aqueous monoethanolamine solution with Aspen rate-based model. Energy Procedia37:1584–1596.
16. Zhang, Y., H. Que, and C. C. Chen. 2011. Thermodynamic modeling for CO₂ absorption in aqueous MEA solution with electrolyte NRTL model. Fluid Phase Equilibr.311:67–75.
17. Øi, L. 2007. Aspen HYSYS simulation of CO₂ removal by amine absorption from a gas-based power plant. In: SIMS Conference, Gøteborg.
18. Lawal, A., M. Wang, P. Stephenson, and H. Yeung. 2009. Dynamic modelling of CO₂ absorption for post combustion capture in coal-fired power plants. Fuel88:2455–2462.
19. Tobiesen, F. A., O. Juliussen, and H. F. Svendsen. 2008. Experimental validation of a rigorous desorber model for CO₂ post-combustion capture. Chem. Eng. Sci.63:2641–2656.
20. Tobiesen, F. A., H. F. Svendsen, and O. Juliussen. 2007. Experimental validation of a rigorous absorber model for CO₂ postcombustion capture. AIChE J.53:846–865.
21. Knudsen, J. N., J. Andersen, J. N. Jensen, and O. Biede. 2011. Evaluation of process upgrades and novel solvents for the post combustion CO₂ capture process in pilot-scale. Energy Procedia4:1558–1565.
22. Knudsen, J. N., J. N. Jensen, P.-J. Vilhelmsen, and O. Biede. 2009. Experience with CO₂ capture from coal flue gas in pilot-scale: testing of different amine solvents. Energy Procedia1:783–790.
23. Notz, R., H. P. Mangalapally, and H. Hasse. 2012. Post combustion CO₂ capture by reactive absorption: pilot plant description and results of systematic studies with MEA. Int. J. Greenh. Gas Con.6:84–112.
24. Dave, N., T. Do, D. Palfreyman, P. H. M. Feron, S. Xu, S. Gao, et al. 2011. Post-combustion capture of CO₂ from coal-fired power plants in China and Australia: an experience based cost comparison. Energy Procedia4:1869–1877.
25. Salkuyeh, Y. K., and M. Mofarahi. 2012. Reduction of CO₂ capture plant energy requirement by selecting a suitable solvent and analyzing the operating parameters. Int. J. Energy Res.37:973–981.
26. Abu-Zahra, M. R. M., L. H. J. Schneiders, J. P. M. Niederer, P. H. M. Feron, and G. F. Versteeg. 2007. CO₂ capture from power plants part I. A parametric study of the technical performance based on monoethanolamine. Int. J. Greenh. Gas Con.1: 37–46.
27. Cousins, A., L. T. Wardhaugh, and P. H. M. Feron. 2011. Preliminary analysis of process flow sheet modifications for energy efficient CO₂ capture from flue gases using chemical absorption. Chem. Eng. Res. Des.89:1237–1251.
28. Cousins, A., L. T. Wardhaugh, and P. H. M. Feron. 2011. A survey of process flow sheet modifications for energy efficient CO₂ capture from flue gases using chemical absorption. Int. J. Greenh. Gas Con.5:605–619.
29. Karimi, M., M. Hillestad, and H. F. Svendsen. 2011. Capital costs and energy considerations of different alternative stripper configurations for post combustion CO₂ capture. Chem. Eng. Res. Des.89:1229–1236.
30. Freguia, S., and G. Rochelle. 2003. Modeling of CO₂ capture by aqueous monoethanolamine. AIChE J.49:1676–1686.
31. Leonard, G., and G. Heyen. 2011. Modelling post-combustion CO₂ capture with amine solvents. Comput. Aided Chem. Eng.29:1768–1772.
32. Li, K., H. Yu, M. Tade, P. Feron, J. Yu, and S. Wang. 2014. Process modeling of an advanced NH₃ abatementand recycling technology in the ammonia-based CO₂ capture process. Environ. Sci. Technol.48:7179–7186.
33. Lee, A. S., J. C. Eslick, D. C. Miller, and J. R. Kitchin. 2013. Comparisons of amine solvents for post-combustion CO₂ capture: a multi-objective analysis approach. Int. J. Greenh. Gas Con.18:68–74.
34. Cousins, A., A. Cottrell, A. Lawson, S. Huang, and P. Feron. 2012. Model verification and evaluation of the rich-split process modification at an Australian-based post combustion CO₂ capture pilot plant. Greenh Gas: Sci. Technol.2:329–345.
35. Aspen Technology. 2011. Rate-Based Model of the CO2 Capture Process by MEA using Aspen Plus. Aspen Technology, Burlington, MA.
36. Pinsent, B. R., L. Pearson, and F. J. W. Roughton. 1956. The kinetics of combination of carbon dioxide with hydroxide ions. Trans. Faraday Soc.52:1512–1520.
37. Hikita, H., S. Asai, H. Ishikawa, and M. Honda. 1977. The kinetics of reactions of carbon dioxide with monoethanolamine, diethanolamine, and triethanolamine by a rapid mixing method. Chem. Eng. J.13:7–12.
38. Bravo, J. L., J. A. Rocha, and J. R. Fair. 1985. Mass transfer in gauze packings. Hydrocaborn Process64:91–95.
39. Bravo, J. L., J. A. Rocha, and J. R. Fair. 1993. A comprehensive model for the performance of columns containing structured packings. I. ChemE. Symp. Ser.32:641–651.
40. Que, H., and C. Chen. 2011. Thermodynamic modeling of the NH₃-CO₂-H₂O system with electrolyte NRTL model. Ind. Eng. Chem. Res.50:11406–11421.
41. Léonard, G., C. Crosset, D. Toye, and G. Heyen. 2015. Influence of process operating conditions on solvent thermal and oxidative degradation in post-combustion CO₂ capture. Comput. Chem. Eng. J.83:121–130.
42. Bailey, D., and P. Feron. 2005. Post-combustion decarbonisation processes. Oil. Gas. Sci. Technol.60:461–474.
43. Van Wagener, D.H. 2011. Stripper modeling for CO₂ removal using monoethanolamine and piperazine solvents. Ph.D. Dissertation, The University of Texas at Austin, Austin, TX.
44. Lin, Y. J., T. Madan, and G. T. Rochelle. 2014. Regeneration with rich bypass of aqueous piperazine and monoethanolamine for CO₂ capture. Ind. Eng. Chem. Res.53:4067–4074.
45. Li, K. K., H. Yu, P. Feron, M. Tade, and L. Wardhaugh. 2015. Technical and energy performance of an advanced, aqueous ammonia-based CO₂ capture technology for a 500-MW coal-fired power station. Environ. Sci. Technol.49:10243–10252.
46. Leites, I. L., D. A. Sama, and N. Lior. 2003. The theory and practice of energy saving in the chemical industry: some methods for reducing thermodynamic irreversibility in chemical technology processes. Energy28:55–97.
47. Paul, S., and K. Lance. 2002. Improved aqua-ammonia absorption system generator utilizing structured packing. World Intellectual Property, Patent WO 02/12803 A1, 2002.
48. Karimi, M., M. Hillestad, and H. Svendsen. 2012. Positive and negative effects on energy consumption by interheating of stripper in CO₂ capture plant. Energy Procedia23:15–22.
49. Frailie, P., T. Madan, B. Sherman, and G. Rochelle. 2013. Energy performance of advanced stripper configurations. Energy Procedia37:1696–1705.