Applying 2D numerical model to calculate the scour at the Cua Dai bridge, Quang Nam province

Abstract

When the Cua Dai bridge is built across the Thu Bon River, it causes a narrowing of the flow leading to scour, which seriously threatens the pier and endangers the structure. In order to limit the influence of scour the bridge, it is necessary to ensure that the scour under the bridge is within the allowable range. At the same time, it is necessary to take measures to limit and overcome the causes of scour. Therefore, the study and prediction of locations that are likely to cause scour are of great significance in choosing effective and versatile prevention solutions for works on this river section. Most of the scour formulas for bridge use the 1D average velocity to calculate; The calculated results are much different from the real distribution of flow velocity in the river. Therefore, the results of scour calculation often have big deviations from reality, especially when the river cross-section has no flats or curved rivers... The article focuses on researching scour at the bridge pier based on the two-dimensional horizontal velocity in front of the pier by using RIVER 2D model, built from the mathematical model of two horizontal flows and solved by the finite element method. The results of the paper show that the scour depth of pier by the one-dimensional (1D) average velocity gives much larger than when applying the two-dimensional horizontal velocity to calculate the scour.

Keywords: Scour, 2D average velocity, RIVER 2D model, scour depth

1. Introduction

There are three types of erosion that can be dangerous to structures (bridge piers, abutments, roadbeds, embankments) including: natural erosion: caused by natural deformation (erosion or accretion) of river bed, does not depend on the presence of structures on the river but depends on many other factors such as hydrological regime, geological conditions, exploitation of water resources, etc... of the designed river section. General scour: or narrowing scour due to a small drainage aperture that is less than the calculated flood width, is scour occurring along the bottom line of the cross-section under the bridge. Scour is caused by an increase in the flow rate under the bridge when the river is narrowed. In this area, there is a redistribution of water flow, sediment flow, and flow rate redistribution. Local scour: Local scour is in the form of deep scour holes, it occurs because the works on the river block the flow, causing the local speed to increase; the flow around the work changes suddenly. Local scours occur at the foot of the abutment, the foot of the bridge pier, scour at the head of the regulating dike, the head of the protective embankment. The total scour depth measured at the bridge works is a combination of the above three types of erosion, the first type usually must be based on the riverbed elevation monitoring data for many years to determine, the latter two types can be used theoretical or empirical formula for prediction.

Cua Dai bridge across the Thu Bon River in Quang Nam province, which be an important and inseparable part of the national coastal road system; it connects the eastern coastal areas of Quang Nam province, Da Nang city - Chu Lai Open Economic Zone - Dung Quat Industrial Park and links the coastal of the central region. It is not only meaningful in terms of tourism, timely serving rescue work, preventing, and mitigating damage when there are natural disasters, but also has the effect of ensuring national security and defense in coastal areas in general and Quang Nam province in particular.

The Bridge often causes narrowing of the flow because the bridge length is often smaller than the calculated flood width. The minimum allowable foundation depth of abutments and piers is determined based on the calculation of scour occurring when narrowing the flow due to changes in riverbed behavior and local scour at the bridge piers. Some authors have also studied the problems of pier scour such as: Laursen and Toch [1], Shen et al. [2], Richardson and Davis [3], and Chiew and Melville [4].

In recent years, on the basis of conducting a series of hydraulic experiments combined with systematic calculations on computers based on measurement data in natural rivers and conducting analysis for the old bridges. The authors have been carried out by hydraulic and hydrological scientists in the country such as: Dung [5], Nguyen et al. [6], who have developed the theoretical formula for calculating local scour depth at bridge piers based on energy balance method.

2. Methods of calculating bridge pier scour

2.1 Calculation of pier scour by the method of using 1D average velocity

2.1.1 General scour

Andreev [7] proposed a method to calculate the maximum general scour under the bridge (lower limit of scour) based on the analysis of the movement of alluvium particles in the mainstream and the river beach below the bridge. In the river beach part under the bridge, scour only starts when the velocity of water flowing under the bridge is greater than the allowed non-scour velocity ($V_{ox}$) of the geological soil layer forming the river beach ($V_{bc}>V_{ox}$) and the scour will stop when the flow rate decreases to the allowed non-scour rate. In the mainstream, the flow rate is always greater than the allowable rate of non- scour of the riverbed’s geological layer and therefore the topsoil layer of the riverbed is always in a state of motion, but the river is not deeply eroded because there is a balance of alluvium along the river. Thus, the flow rate under the bridge is greater than the allowable rate without erosion, which is not the cause of scour in the mainstream and the deformation of the river under the bridge can only be explained by the imbalance of alluvium along the river. The overall scour under the bridge is calculated according to the principle of balance of sediment limit for the mainstream and the flow part with alluvium transport of Andreev [7]. The flow depth after scouring is determined according to Eq. (1)

$h'_{ch}=h_{ch}(Q_{2}/Q_{1})^{8/9}(B_{ch}/B'_{ch})^{2/3}$

(1)

where:

$Q_{1}=Q_{ch},Q_{2}=Q'_{ch}$ are the water flow before and after bridge construction at the mainstream.

$h_{ch}$, $h'_{ch}$ are the water depth at mainstream before (natural time) and after scouring.

$h_{ch}=\blacktriangledown h_{hm}-\blacktriangledown h_{tbs}$

$\blacktriangledown h_{hm}$ is the elevation of flow rate at natural time (taken according to design frequency)

$\blacktriangledown h_{tbs}$ is the average elevation of the riverbed.

$B_{ch}$, $B'_{ch}$ are the mainstream width before and after bridge construction.

$B_{ch}=L_{0}=1657.34$m.

$B'_{ch}=L=1401.5$ m.

Calculation results of general scour depth are shown in Table 1.

Table 1. Results for calculating the general scour depth of piers located on the main stream according to the 1D average velocity method

Bridge Piers	Bottom elevation (m)	Surface elevation (m)	Water Depth before scour $h_{ch}$ (m)	Water Depth after scour $h'_{ch}$ (m)	Rising water (m)	General depth scour (m)	Bottom elevation after local scour (m)
T3	-0.500	2.830	3.330	3.504	0.061	0.235	-0.735
T4	-1.250	2.830	4.080	4.293	0.061	0.274	-1.524
T5	-1.240	2.830	4.070	4.283	0.061	0.274	-1.514
T6	-1.210	2.830	4.040	4.251	0.061	0.272	-1.482
T7	-0.960	2.830	3.790	3.988	0.061	0.259	-1.219
T8	-1.420	2.830	4.250	4.472	0.061	0.283	-1.703
T9	-1.720	2.830	4.550	4.788	0.061	0.299	-2.019
T10	-1.900	2.830	4.730	4.977	0.061	0.308	-2.208
T11	-2.050	2.830	4.880	5.135	0.061	0.316	-2.366
T12	-2.540	2.830	5.370	5.651	0.061	0.342	-2.882
T13	-2.630	2.830	5.460	5.745	0.061	0.346	-2.976
T14	-3.400	2.830	6.230	6.556	0.061	0.387	-3.787
T15	-8.150	2.830	10.980	11.554	0.061	0.635	-8.785
T16	-11.600	2.830	14.430	15.184	0.061	0.815	-12.415
T17	1.260	2.830	1.570	1.652	0.061	0.143	1.117
T18	0.000	2.830	2.830	2.978	0.061	0.209	-0.209
T19	-0.050	2.830	2.880	3.031	0.061	0.212	-0.262
T20	0.040	2.830	2.790	2.936	0.061	0.207	-0.167
T21	-0.040	2.830	2.870	3.020	0.061	0.211	-0.251

2.1.2 Caculating local Scour (${\textstyle p=1}$%)2.1.2 Caculating local Scour ( p = 1 {\textstyle p=1} %)

Truc [8] introduced the formula for determining the largest local scour value at the bridge pier. Based on the research results on the causes and development process of local scour on pier scour models in the hydraulic laboratory and the research results of foreign authors, a reasonable structural form of the local scour calculation formula has been selected. When ${\textstyle V=V_{ox}}$ (for mainstream piers), Eq. (2) has the following simple form:

$h_{cb}=0,52.k_{d}.b^{0,88}.h^{0,12}.(V/V_{ox})^{1,16}$

(2)

Where:

-$h_{cb}$ is the maximum local scour depth at bridge pier, m.

- $k_{d}$: the factor taking into account the influence of cylinder shape, taken as 0,1$k_{\zeta }$.

- $k_{\zeta }$: the Iaratslaxev's shape coefficient.

- $h$: the depth of water flow at bridge pier before local scour, m.

- $V$: the water velocity at bridge pier before local scour, m/s.

- $V_{ox}$: the allowable no- scour velocity of the soil layer at the location where scour development.

- $b$: the calculated width of the cylinder, m.

The results of local scour calculation are obtained from Table 2.

Table 2. Table of results of calculation of local scour depth of piers located on the main stream according to the average 1D velocity method

Bridge Piers	Shape factor $K_{d}$	Width'of' pier $b$ (m)	Depth of water flow $h$ (m)	Water Depth after scour $h'_{ch}$ (m)	Velocity $V$ (m/s)	No-scour velocity $V_{ox}$ (m/s)	Maximum local scour depth $h_{cb}$ (m)
T3	0.97	1.8	3.565	1.484	0.720	2.061	2.280
T4	0.97	1.8	4.354	1.484	0.790	1.878	2.097
T5	0.97	1.8	4.344	1.484	0.780	1.903	2.128
T6	0.97	1.8	4.312	1.484	0.770	1.927	2.158
T7	0.97	1.8	4.049	1.484	0.740	2.005	2.243
T8	0.97	1.8	4.533	1.484	0.805	1.843	2.062
T9	0.97	1.8	4.849	1.484	0.815	1.821	2.049
T10	0.97	1.8	5.038	1.484	0.820	1.810	2.044
T11	0.97	2	5.196	1.484	0.825	1.799	2.235
T12	0.97	4	5.712	1.484	0.835	1.777	4.103
T13	0.97	5	5.806	1.484	0.840	1.767	4.969
T14	0.97	5	6.617	1.484	0.860	1.726	4.911
T15	0.97	5	11.615	1.484	0.910	1.631	4.921
T16	0.97	5	15.245	1.484	0.950	1.562	4.837
T17	0.97	4	1.713	1.484	0.650	2.283	4.748
T18	0.97	2	3.039	1.484	0.705	2.105	2.515
T19	0.97	1.8	3.092	1.484	0.705	2.015	2.297
T20	0.97	1.8	2.997	1.484	0.690	2.151	2.346
T21	0.97	1.8	3.081	1.484	0.700	2.120	2.315

2.2 Applying 2D River model to calculate scour at Cua Dai bridge pier

Applying the program RIVER_2D to calculate the velocity field in Cua Dai bridge area:

Upstream margin for flow: ${\textstyle Q=13200}$m³/h

Downstream margin for water level: ${\textstyle Z=2.8}$3m

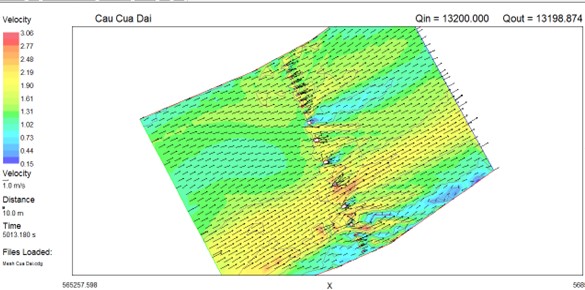
Figure 1 shows the topography at the construction site of Cua Dai bridge in the R2D Bed module. Figure 2 shows the topography at the construction site of Cua Dai bridge in the R2D Mesh module. The result of velocity field at Cua Dai bridge area is showed in Figure 3.

Figure 1. Topography at the construction site of Cua Dai bridge in the R2D bed module

Figure 2. Topography at the construction site of Cua Dai bridge in the R2D mesh module

Figure 3. Velocity field at Cua Dai bridge area

After synthesizing the velocity tables taken from the River 2D program, we get the average velocity table at the bridge piers as in Table 3.

Table 3. Velocity table taken from river_2D program used to calculate local scour depth

Piers	Bottom elevation (m)	Surface elevation (m)	Average velocity  (m/s)
T3	0.500	2.830	1.546
T4	1.250	2.830	1.173
T5	1.240	2.830	1.583
T6	1.210	2.830	1.391
T7	0.960	2.830	1.321
T8	1.420	2.830	1.595
T9	1.720	2.830	1.44
T10	1.900	2.830	1.593
T11	2.050	2.830	1.251
T12	2.540	2.830	1.011
T13	2.630	2.830	1.426
T14	3.400	2.830	1.175
T15	8.150	2.830	1.73
T16	11.600	2.830	1.542
T17	1.260	2.830	1.45
T18	0.000	2.830	0.655
T19	0.050	2.830	1.41
T20	0.040	2.830	0.957
T21	0.040	2.830	0.867

2.3. Applying velocity from River 2D model to calculate scours for Cua Dai bridge pier

The RIVER 2D program uses the main equations to calculate the two shallow water equations, including the equation of continuity and the equation of motion; consider the direction of wind appearing on the surface of the stream, the rotational velocity of the earth. Therefore, it is easy to add these effects to the flow velocity at the pier.

Determination of local scour depth at bridge piers: 

Based on the calculation results of the average flow velocity field extracted from the 2D River model. The flow velocity at the bottom of the river is determined by Eq. (3):  

$U_{d}=U_{bq}((0.5C-4.1)/(C-2))^{0.5}$

(3)

where $U_{bq}$ is the average flow velocity calculated from the RIVER 2D model, and $C$ is the Chezy coefficient. According to Maninh: $n$ is the coefficient of roughness. The local scour depth for each pier is determined and presented in Table 4.

Table 4. Results of local scour calculation with velocity field from River 2D

Piers	Shape factor $K_{d}$	Width of pier $b$ (m)	Depth of water flow $h$ (m)	Velocity $V$ (m/s)	No-scour velocity $V_{ox}$ (m/s)	Rate $V$/$V_{ox}$	Maximum local scour depth $h_{cb}$ (m)
T3	0.970	1.800	3.565	1.546	1.019	0.720	1.475
T4	0.970	1.800	4.354	1.173	0.775	0.790	0.988
T5	0.970	1.800	4.344	1.583	1.046	0.780	1.419
T6	0.970	1.800	4.312	1.391	0.919	0.770	1.238
T7	0.970	1.800	4.049	1.321	0.872	0.740	1.211
T8	0.970	1.800	4.533	1.595	1.055	0.805	1.388
T9	0.970	1.800	4.849	1.440	0.953	0.815	1.226
T10	0.970	1.800	5.038	1.593	1.055	0.820	1.376
T11	0.970	2.000	5.196	1.251	0.829	0.825	1.137
T12	0.970	4.000	5.712	1.011	0.670	0.835	1.632
T13	0.970	5.000	5.806	1.426	0.946	0.840	2.947
T14	0.970	5.000	6.617	1.175	0.781	0.860	2.331
T15	0.970	5.000	11.615	1.730	1.156	0.910	3.684
T16	0.970	5.000	15.245	1.542	1.033	0.950	3.179
T17	0.970	4.000	1.713	1.450	0.946	0.650	2.817
T18	0.970	2.000	3.039	0.655	0.431	0.705	0.599
T19	0.970	1.800	3.092	1.410	0.928	0.705	1.332
T20	0.970	1.800	2.997	0.957	0.629	0.690	0.868
T21	0.970	1.800	3.081	0.867	0.570	0.700	0.764

3. Results and discussions

The results of the combined scour calculation for the 1D average velocity use case and the velocity use case obtained from the River 2D model are presented in Table 5.

Table 5. Comparison table of calculation results by two methods

Piers	Flow velocity (m/s)		Scour depth (m)
	1D average velocity method	Velocity from River 2D model	1D average velocity method	Velocity from River 2D model
T3	1.484	1.019	2.516	1.710
T4	1.484	0.775	2.372	1.262
T5	1.484	1.046	2.402	1.693
T6	1.484	0.919	2.431	1.511
T7	1.484	0.872	2.502	1.470
T8	1.484	1.055	2.345	1.671
T9	1.484	0.953	2.348	1.525
T10	1.484	1.055	2.353	1.684
T11	1.484	0.829	2.551	1.453
T12	1.484	0.670	4.445	1.974
T13	1.484	0.946	5.315	3.293
T14	1.484	0.781	5.298	2.718
T15	1.484	1.156	5.556	4.319
T16	1.484	1.033	5.652	3.994
T17	1.484	0.946	4.891	2.960
T18	1.484	0.431	2.724	0.808
T19	1.484	0.928	2.509	1.544
T20	1.484	0.629	2.553	1.075
T21	1.484	0.570	2.526	0.975

Through the calculation results of general and local scour depth by thinking that the pier scouring velocity is the 1D average or the 2D horizontal velocity (obtained from the application of the RIVER 2D model) shows that: The depth of pier scour by the 1D average velocity gives much larger results than when applying the 2D horizontal velocity to calculate the scour; Theoretically, the calculation results can be reliable and reflect relatively clearly the process of changing surface velocity of the river flow; where the flow velocity is an important parameter in the formula for calculating local scour at the bridge pier. However, the RIVER 2D model also has limitations such as: The RIVER2D model can only determine the 2D velocities on the surface, while the river flow is usually 3D. The vertical flow formed when encountering obstacles such as bridge piers is quite dangerous flow direction. This is one of the main causes of local scour at bridge piers. 

4.  Conclusions

River flow is a complex physical phenomenon, influenced by factors. The main factors affecting the flow formation process include external conditions such as topography, geomorphology, climate, precipitation, evaporation, wind, tides... and internal conditions such as conduction roughness, fluid viscosity, flow obstructions....

The construction of river crossing works often narrows the flow cross-section leading to changes in elevation and slope of the water surface and flow velocity, causing riverbed erosion, especially local scour at bridge piers. Most of the calculation methods given are experimental and semi-empirical formulas built based on actual measurement data or measured data in the laboratory under ideal topographical and geological conditions and 1D flow model. Therefore, the formulas give quite different results and deviate much from reality. In a calculation formula itself, if applied in one condition, it is correct, but in other conditions, the error is too large.

Due to the inability to accurately analyze the causes of scour, scour values, location of scour holes, depth of scour holes, area of scour holes and especially the formation process, development prospects of scour holes, etc., the solutions given to prevent or limit scour development are sometimes very costly but still ineffective.

The use of two-dimensional average velocity, from RIVER 2D model, in the scour calculation formula has overcome the disadvantage compared to using one-dimensional velocity. Calculation results of local scour of Cua Dai bridge piers show that the depth of general and local scour at the construction site, when newly built, is reduced compared to the calculation method using 1D average velocity; even on the entire riverbed section, there are positions where it is accreted but not eroded. From there, appropriate anti-erosion solutions can be devised.

Acknowledgments

The authors thank the University of Danang, University of Science and Technology for supporting for this work.

References

[1] Laursen E.M.,  Toch A. Scour around bridge piers and abutments. Iowa Institute of Hydraulic Research, Bulletin No. 4, 1956.

[2] Shen H., Schneider V.R., Karaki S. Local scour around bridge piers. Journal of the Hydraulics Division, 95:1919-1940, 1969.

[3] Richardson E.V., Davis S.R. Evaluating scour at bridges. 4th Edition, Federal Highway Administration Hydraulic Engineering Circular, No. 18, FHWA NHI 01-001, 2001.

[4] Chiew Y.M.,   Melville B.W. Local scour around bridge piers. Journal of Hydraulic Research, 25(1):15-26, 1987.

[5] Dung D.V. Research and develop a method to calculate local scour at bridge piers (in Vietnamese). PhD Thesis, University of Danang, 2011.

[6] Hung N.T., Truc N.X., Dung D.V.  Applying energy balance conditions for estimating local scour depths at bridge piers. The 14th Asia Congress of Fluid Mechanics - 14ACFM, October 15-19, Hanoi and Ha Long, Vietnam, 2013.

[7] Andreev O.V. Principles of designing regulating structures (in Russian). VNIIZhSi P, Moscow, 1954.

[8] Truc N.X. Design of highways and river crossing projects (In Vietnamese). Volume 3, Educational Publishing House, Hanoi, 2001.