Efficient combined SSIM- and landmark-driven image registration in a variational framework

Abstract

Image registration methods are used to establish geometrical correspondences between different datasets. Various characteristics of image data can be exploited to drive image registration algorithms. Thus, the currently available schemes can be roughly divided into two classes: intensity-based and feature-based registration schemes. In this paper, we present a mathematical framework, based on the calculus of variations, for combining these two classes in order to benefit from the advantages of both strategies. The goal is to obtain a registration algorithm which achieves a good matching of datasets near landmark locations but also away from them (by matching the corresponding intensities). The proposed approach includes the novel formulation of a disparity term which simultaneously takes into account the structural similarity index (a similarity measure which considers spatial dependencies in the images) and the location of outstanding points. Since the iteration which results of the variational formulation is translated into the frequency domain, the implementation of the proposed algorithm offers a good speed-performance trade-off when compared to other state-of-the-art image registration implementations. Experimental results show the advantages, in the medical setting, of the combined SSIM- and landmark-based approach over well-established registration techniques which use either landmark or intensity information alone. In particular, the registration of triple-phase 3D computed tomographies of the liver under injection of a contrast agent has been chosen for such a comparison. The datasets are acquired at different times depending on the arrival time of the contrast agent in arteries, portal and hepatic veins, so they have to be registered in order to show the liver structures acquired at each phase in a common framework. These multi-phase studies provide tumor enhancement on the arterial and portal venous phases that support differential diagnosis of lesions in the liver.

Keywords: Image registration, variational methods, Fourier domain, structural similarity index, landmark-driven registration, contrast-enhanced liver CT

1. Introduction

Image registration is the process of finding the spatial correspondence between two different datasets (images or volumes), which typically represent different views of the same object or similar ones; in other words, register is equivalent to align in this context. Particularly, in medical imaging there are several applications that require a registration step (e.g. image fusion, atlas matching, pathological diagnosis). Classical reviews of image registration can be found, for example, in the references [6], [28], [47] or [29]. More recent comprehensive overviews about image registration methods can be found in [37] and [36], where the state-of-the-art advances in this field are described in a systematic fashion, and the techniques applied to medical datasets are emphasized as well. When classified according to the image characteristics used to estimate the transformation which geometrically relates the involved datasets, registration algorithms are usually divided into three groups: geometric feature-based, which rely on the segmentation, done generally before the registration process itself, of part or all of the images, therefore obtaining objects that are registered by minimizing some geometrical distance between them; intensity-based, which maximize a intensity similarity measure computed between points lying at the same spatial position; and iconic feature-based, which can be understood as intermediate between the two previous categories, since they use explicitly some type of geometrical distance in addition to the intensity similarity measure, see [8]. The performance of intensity-based image registration methods is highly influenced by the choice of the similarity measure. This measure can be defined directly on image intensities as, e.g., sum of squared differences (SSD), correlation coefficient (CC), correlation ratio (CR), or mutual information (MI). A complete analysis of all these metrics can be found in [27]. These measures often rely on the assumption of independence and stationarity of the intensities from pixel to pixel without considering their spatial dependencies. Alternative metrics have been proposed in order to consider intensity nonstationarities and complex spatially-varying intensity distortions. For instance, in [31] a similarity measure based on the residual complexity is described. Another example is the structural similarity index (SSIM), introduced by [43], which achieves a good trade-off between speed and performance and is able to cope with complex relationships between image intensity values. Due to the mathematical properties of SSIM [7] and its potentials in both theoretical development and practical applications, it is being incorporated into optimization frameworks in order to improve perceived image/video quality in a number of image processing problems, as e.g. [17] or [34]. This similarity measure has been previously used in image registration in [1], [4], [41], [42], [45], or [19], but its use is still not widespread —for example, the evaluation addressed in [33] does not include SSIM and the review in [36] does not deal with similarity measures based on the SSIM—.

Intensity-based approaches are in general fully automatic and usually yield good registration results. However, they may perform poorly for specific, important locations such as anatomical landmarks. On the other hand, geometric feature-based registration techniques are designed to accurately match user specified landmarks, see e.g. [35]. Recent examples of landmark-based registration methods in medical imaging scenarios can be found in [44] or [21]. A common drawback of most landmark-driven registration methods is the fact that the intensities of the datasets are completely neglected. Consequently, the registration outcome away from the landmarks may be very poor. In the literature, the registration results are typically obtained by interpolating the transformation with a thin-plate spline (TPS) model [5] or by combining iterative closest point (ICP) registration and parametric relaxation [38], among other techniques. Although these approaches produce a smooth transformation from one dataset to another, they do not define a consistent correspondence between the two datasets except at the landmark points. Some previous attempts to combine the sparse correspondences with a intensity-based registration method can be found in [18] or [39]. However, to the authors knowledge, there has been no attempt to formulate a registration method which combines in the distance term both a SSIM-based term and a landmark-based term. In recent works, such as [32] or [26], the authors of this paper dealt with intensity-based registration approaches within the variational framework first presented in [25], whose formulation in the frequency domain allowed for implementations of high efficiency [40]. Please refer to [2] or [46] for further details regarding variational image registration. The aforementioned approaches involved similarity terms derived from SSD- or CR-based measures, so none of them included a SSIM-based nor a landmark-based distance term. Regardless, the method presented in [26] achieved better results than publicly available state-of-the art approaches such as Elastix [20] and ANTs (${\textstyle http://stnava.github.io/ANTs/}$).

The paper is organized as follows: Section 2 addresses the formulation, within the variational framework, of a novel registration method which combines in the distance term both a SSIM-based term and a landmark-based term. Section 3 shows the results of applying the proposed registration algorithm to a medical imaging scenario; in particular, the image registration of triple-phase 3D computed tomography datasets of the liver under injection of a contrast agent has been chosen; the suitability of our approach in such a scenario is also proved in this section through the comparison of the results it provides and the outcome obtained with the CR-based version of the algorithm, which was recently reported to outperform other well-known approaches in the medical setting [26]. The conclusions of the paper as well as the future lines of research are discussed in Section 4. Finally, an appendix closes the paper with the detailed derivation of the external forces field related to the proposed SSIM-based distance term (i.e., the first addend of the corresponding Euler-Lagrange equation).

2. Mathematical framework

Let ${\textstyle R}$ and ${\textstyle T}$ be two datasets, a reference and a template respectively, which represent the same object (or similar ones) by using the same or different imaging modalities. These ${\textstyle d}$-dimensional datasets are defined as ${\textstyle R,T:\mathbf {\Psi } \rightarrow {\mathcal {I}}}$, with ${\textstyle \mathbf {\Psi } \subset \mathbb {R} ^{d}}$ being the domain where they are supported, and ${\textstyle {\mathcal {I}}\subset \mathbb {R} }$ representing the intensity level in each spatial coordinate ${\textstyle \mathbf {x} =(x_{1},\ldots ,x_{d})}$. We search for a displacement field ${\textstyle \mathbf {u} :\mathbf {\Psi } \rightarrow \mathbb {R} ^{d}}$ that makes the transformed template ${\textstyle T_{\mathbf {u} }:\mathbf {\Psi } \rightarrow {\mathcal {I}}}$ similar to the reference dataset in the geometrical sense, i.e., ${\textstyle \mathbf {x} _{T_{\mathbf {u} }}=\mathbf {x} _{T}+\mathbf {u} (\mathbf {x} _{T})\approx \mathbf {x} _{R}}$, where ${\textstyle \mathbf {u} (\mathbf {x} )=\left(u_{1}(\mathbf {x} ),\ldots ,u_{d}(\mathbf {x} )\right)^{\top }}$. This problem can be approached in terms of the variational calculus by defining a joint energy functional to be minimized:

${\mathcal {J}}[\mathbf {u} ]={\mathcal {D}}[R,T;\mathbf {u} ]+\alpha \,{\mathcal {S}}[\mathbf {u} ]\,,$

(1)

where ${\textstyle {\mathcal {D}}}$ is an energy term which quantifies the disparity between the datasets, ${\textstyle {\mathcal {S}}}$ is a penalty term which measures the roughness of the solution ${\textstyle \mathbf {u} (\mathbf {x} )}$, and ${\textstyle \alpha {>0}}$ is a scalar parameter, usually referred to as the regularization parameter, which is used to control and weight the influence of the penalty term versus the distance term. It should be noted that the present formulation considers the different functions to be continuous in the domain ${\textstyle \mathbf {\Psi } }$ where they are supported; the natural spatial (and temporal) discretization is tackled later in this section.

In the literature, several choices for the dissimilarity measure ${\textstyle {\mathcal {D}}}$ can be found. Depending on the particular datasets to be compared, statistical measures derived from the MI or the CR are usually the most appropriate candidates. As an alternative, in this work we propose the novel approach of incorporating both the SSIM [43] and the Euclidean distance between identifiable corresponding points (i.e., landmarks) into the variational framework which is being presented. The resulting disparity term is the following:

${\mathcal {D}}[R,T;\mathbf {u} ]={\frac {-(2\,\mu _{R}\,\mu _{T}+C_{1})(2\,\sigma _{RT}+C_{2})}{(\mu _{R}^{2}+\mu _{T}^{2}+C_{1})(\sigma _{RR}+\sigma _{TT}+C_{2})}}+{\frac {\beta }{2}}\int _{\mathbf {\Psi } }\sum _{j=1}^{N}\left\|\mathbf {x} _{R_{j}}-\mathbf {x} _{T_{j}}-\mathbf {u} (\mathbf {x} _{T_{j}})\right\|^{2}d\mathbf {x} \,,$

(2)

where ${\textstyle \mu _{R}}$, ${\textstyle \mu _{T}}$, ${\textstyle \sigma _{RR}}$ and ${\textstyle \sigma _{TT}}$ denote the mathematical expectations and variances of the intensity levels of ${\textstyle R}$ and ${\textstyle T_{\mathbf {u} }}$, respectively; ${\textstyle \sigma _{RT}}$ represents the covariance; ${\textstyle C_{1}}$ and ${\textstyle C_{2}}$ are small constants which aim to characterize the saturation effects of the visual system at low luminance and contrast regions and which assure numerical stability when the expectations or variances are very close to zero; ${\textstyle \beta {>0}}$ is a scalar used to weight the influence of the landmark-based term versus the SSIM-based term; ${\textstyle N}$ is the number of identified landmarks; and ${\textstyle \mathbf {x} _{R_{j}}}$ and ${\textstyle \mathbf {x} _{T_{j}}}$ denote the spatial position of the ${\textstyle j}$-th landmark in ${\textstyle R}$ and ${\textstyle T}$, respectively.

The regularization term ${\textstyle {\mathcal {S}}}$ is used to add some prior knowledge on the displacement field, thus preferentially obtaining more likely solutions and giving the smoothness characteristics to ${\textstyle \mathbf {u} (\mathbf {x} )}$. In this work, the regularizer is defined by

${\mathcal {S}}[\mathbf {u} ]={\frac {1}{2}}\sum _{l=1}^{d}\int _{\mathbf {\Psi } }\left\|\nabla ^{\lambda }u_{l}\right\|^{2}\,d\mathbf {x} \,,$

(3)

where ${\textstyle \nabla }$ denotes the ${\textstyle d}$-dimensional gradient operator, and ${\textstyle \lambda \in \{{}1,2\}{}}$ is the regularization order: if ${\textstyle \lambda =1}$, the resulting term is the diffusion smoother [14]; if ${\textstyle \lambda =2}$, the regularizer is the curvature smoother [15].

According to the variational calculus, a necessary condition for a minimizer ${\textstyle \mathbf {u} }$ of the joint energy functional (1) is that the first variation of ${\textstyle {\mathcal {J}}[\mathbf {u} ]}$ in any direction (also known as the Gateaux derivative) vanishes for all possible perturbations ${\textstyle \mathbf {z} \in \mathbb {R} ^{d}}$:

$\mathrm {d} {\mathcal {J}}[\mathbf {u} ;\mathbf {z} ]={\frac {\partial }{\partial \epsilon }}{\Bigl .}{\mathcal {J}}[\mathbf {u} +\epsilon \mathbf {z} ]{\Bigr |}_{\epsilon =0}=0\,,\quad \forall \mathbf {z} \in \mathbb {R} ^{d}\,.$

(4)

The computation of the previous Gateaux derivative leads to the following Euler-Lagrange (E-L) equation:

${\frac {1}{{\mathcal {V}}_{\mathbf {\Psi } }}}\left({\hat {G}}_{\rho }\ast {\frac {\partial L_{\mathbf {u} }^{\mbox{SSIM}}}{\partial i_{t}}}\right)\nabla T_{\mathbf {u} }+\beta \sum _{j=1}^{N}\left(\mathbf {x} _{T_{\mathbf {u} j}}-\mathbf {x} _{R_{j}}\right)+\alpha \,(-\Delta )^{\lambda }\mathbf {u} =\mathbf {0} \,,$

(5)

where ${\textstyle {\mathcal {V}}_{\mathbf {\Psi } }}$ represents the hypervolume of ${\textstyle \mathbf {\Psi } }$; ${\textstyle {\hat {G}}_{\rho }:{\mathcal {I}}^{2}\rightarrow \mathbb {R} }$ is a Gaussian kernel (strictly positive and differentiable); ${\textstyle \ast }$ denotes the ${\textstyle d}$-dimensional convolution operator; ${\textstyle \Delta }$ is the Laplacian operator; finally, we find the term

${\frac {\partial L_{\mathbf {u} }^{\mbox{SSIM}}}{\partial i_{t}}}={\frac {\gamma _{0}+C_{1}\,\gamma _{1}+C_{2}\,\gamma _{2}+C_{1}C_{2}\,\gamma _{3}}{(\mu _{R}^{2}+\mu _{T}^{2}+C_{1})^{2}(\sigma _{RR}+\sigma _{TT}+C_{2})^{2}}}\,,$

(6)

where the variables ${\textstyle \gamma _{0}}$, ${\textstyle \gamma _{1}}$, ${\textstyle \gamma _{2}}$ and ${\textstyle \gamma _{3}}$ are defined as

$\gamma _{0}=4\,\mu _{R}{\Big (}\mu _{R}^{2}(\sigma _{RR}\,\sigma _{RT}+\sigma _{TT}\,\sigma _{RT}-\mu _{R}\,\mu _{T}\,\sigma _{RR}-\mu _{R}\,\mu _{T}\,\sigma _{TT}+2\,\mu _{T}^{2}\,\sigma _{RT}+\mu _{T}\,\sigma _{RR}\,i_{r}+\mu _{T}\,\sigma _{TT}\,i_{r}-2\,\mu _{T}\,\sigma _{RT}\,i_{t})$ $-\mu _{T}^{2}(\sigma _{RR}\,\sigma _{RT}+\sigma _{TT}\,\sigma _{RT}+\mu _{R}\,\mu _{T}\,\sigma _{RR}+\mu _{R}\,\mu _{T}\,\sigma _{TT}-2\,\mu _{T}^{2}\,\sigma _{RT}-\mu _{T}\,\sigma _{RR}\,i_{r}-\mu _{T}\,\sigma _{TT}\,i_{r}+2\,\mu _{T}\,\sigma _{RT}\,i_{t}){\Big )}\,,$

(7)

$\gamma _{1}=2{\Big (}\mu _{R}(-\mu _{R}^{2}\,\sigma _{RR}-\mu _{R}^{2}\,\sigma _{TT}+2\,\sigma _{RR}\,\sigma _{RT}+2\,\sigma _{TT}\,\sigma _{RT}+\mu _{R}\,\sigma _{RR}\,i_{r}+\mu _{R}\,\sigma _{TT}\,i_{r}-\sigma _{RR}\,C_{1}-\sigma _{TT}\,C_{1})$ $-\mu _{T}(2\,\mu _{R}^{2}\,\sigma _{RR}+2\,\mu _{R}^{2}\,\sigma _{TT}+\mu _{R}\,\mu _{T}\,\sigma _{RR}+\mu _{R}\,\mu _{T}\,\sigma _{TT}-2\,\mu _{R}\,\sigma _{RR}\,i_{r}-2\,\mu _{R}\,\sigma _{TT}\,i_{r}-\mu _{T}\,\sigma _{RR}\,i_{r}-\mu _{T}\,\sigma _{TT}\,i_{r})$ $+2\,\mu _{T}\,\sigma _{RT}(\mu _{R}^{2}+\mu _{T}^{2}-\sigma _{RR}-\sigma _{TT}+2\,\mu _{R}\,\mu _{T}-2\,\mu _{R}\,i_{t}-\mu _{T}\,i_{t}+C_{1})+C_{1}\,i_{r}(\sigma _{RR}+\sigma _{TT})-2\,\sigma _{RT}\,i_{t}(\mu _{R}^{2}+C_{1}){\Big )}\,,$

(8)

$\gamma _{2}=2\,\mu _{R}{\Big (}\mu _{R}^{2}(\sigma _{RR}+\sigma _{TT}+2\,\sigma _{RT}-2\,\mu _{R}\,\mu _{T}+2\,\mu _{T}^{2}+2\,\mu _{T}\,i_{r}-2\,\mu _{T}\,i_{t}+C_{2})$ $-\mu _{T}^{2}(\sigma _{RR}+\sigma _{TT}+2\,\sigma _{RT}+2\,\mu _{R}\,\mu _{T}-2\,\mu _{T}^{2}-2\,\mu _{T}\,i_{r}+2\,\mu _{T}\,i_{t}+C_{2}){\Big )}\,,$

(9)

$\gamma _{3}=2{\Big (}\mu _{R}(\sigma _{RR}+\sigma _{TT}-2\,\sigma _{RT}-\mu _{R}^{2}+\mu _{T}^{2}+\mu _{R}\,i_{r}-\mu _{R}\,i_{t}+2\,\mu _{T}\,i_{r}+C_{2})$ $-\mu _{T}(\sigma _{RR}+\sigma _{TT}+2\,\sigma _{RT}+\mu _{R}^{2}-\mu _{T}^{2}+2\,\mu _{R}\,i_{t}-\mu _{T}\,i_{r}+\mu _{T}\,i_{t}-C_{1}+C_{2})-C_{1}\,i_{t}{\Big )}\,,$

(10)

with ${\textstyle i_{r}\,,i_{t}\in {\mathcal {I}}\subset \mathbb {R} }$ being the intensities of ${\textstyle R}$ and ${\textstyle T_{\mathbf {u} }}$, respectively.

In 5, the first addend in equation (5) is deduced. The proof of the internal forces field of the Euler-Lagrange equation (i.e., the last addend in Eq.(5)) can be found in [24]. Finally, the addend which corresponds to the landmark-based term can be easily obtained by applying the definition of the Gateaux derivative to the last addend in Eq.(2):

$\mathrm {d} {\mathcal {D}}^{\mbox{LM}}[R,T;\mathbf {u} ;\mathbf {z} ]={\frac {\partial }{\partial \epsilon }}{\Bigl .}{\frac {\beta }{2}}\int _{\mathbf {\Psi } }\sum _{j=1}^{N}\left\|\mathbf {x} _{R_{j}}-\mathbf {x} _{T_{j}}-\mathbf {u} (\mathbf {x} _{T_{j}})-\epsilon \mathbf {z} (\mathbf {x} _{T_{j}})\right\|^{2}d\mathbf {x} {\Bigr |}_{\epsilon =0}$ $={\Bigl .}\int _{\mathbf {\Psi } }{\Bigl \langle }\beta \sum _{j=1}^{N}\mathbf {x} _{R_{j}}-\mathbf {x} _{T_{j}}-\mathbf {u} (\mathbf {x} _{T_{j}})-\epsilon \mathbf {z} (\mathbf {x} _{T_{j}}),-\mathbf {z} (\mathbf {x} _{T_{j}}){\Bigr \rangle }_{\mathbb {R} ^{d}}d\mathbf {x} {\Bigr |}_{\epsilon =0}=\int _{\mathbf {\Psi } }{\Bigl \langle }\beta \sum _{j=1}^{N}\left(\mathbf {x} _{T_{\mathbf {u} j}}-\mathbf {x} _{R_{j}}\right),\mathbf {z} (\mathbf {x} _{T_{j}}){\Bigr \rangle }_{\mathbb {R} ^{d}}d\mathbf {x} \,,$

(11)

where ${\textstyle \langle \cdot ,\cdot \rangle _{\mathbb {R} ^{d}}}$ denotes the inner (or dot) product in ${\textstyle \mathbb {R} ^{d}}$.

In order to solve the Euler-Lagrange equation (5), an iterative time-marching scheme can be used. For doing so, an artificial time ${\textstyle t}$ has to be added to the E-L equation and then the steady-state solution has to be computed, i.e., ${\textstyle {\frac {\partial }{\partial t}}\mathbf {u} +\mathbf {f} +\alpha \,(-\Delta )^{\lambda }\mathbf {u} =\mathbf {0} }$ (where ${\textstyle \mathbf {f} }$ gathers the first two addends in Eq.(5)). In the steady-state, the displacement field ${\textstyle \mathbf {u} }$ converges and hence ${\textstyle {\frac {\partial }{\partial t}}\mathbf {u} =\mathbf {0} }$. The time ${\textstyle t}$ is discretized, ${\textstyle t=\xi \,\tau }$ (with ${\textstyle \xi \in \mathbb {N} }$ being the iteration index and where ${\textstyle \tau {>0}}$ is the time-step), and finally the temporal derivative is replaced with its discrete approximation (first backward difference). Due to the fact that digital datasets are usually encoded by uniformly distributed spatial elements in each dimension (e.g. pixels if ${\textstyle d=2}$ or voxels if ${\textstyle d=3}$), the discretization of the spatial variable becomes a natural approach too. Therefore in the following the notation ${\textstyle \mathbf {u} ^{(\xi )}[\mathbf {n} ]=\mathbf {u} [\mathbf {n} ,\xi \,\tau ]}$ is used, where ${\textstyle \mathbf {n} =(n_{1},\ldots ,n_{d})}$ is the index of the discrete spatial position, with ${\textstyle n_{i}=0,\ldots \,N_{i}-1}$, and ${\textstyle N_{i}}$ being the number of discrete spatial elements in the ${\textstyle i}$-th dimension. Using this notation, the resulting semi-implicit iteration for the ${\textstyle l}$-th component of the displacement field is the following:

$u_{l}^{(\xi )}[\mathbf {n} ]=u_{l}^{(\xi {-1)}}[\mathbf {n} ]-\tau \,f_{l}^{(\xi {-1)}}[\mathbf {n} ]-\tau \,\alpha \,q[\mathbf {n} ]\ast u_{l}^{(\xi )}[\mathbf {n} ]\,,$

(12)

where the discrete operator ${\textstyle q[\mathbf {n} ]}$ stands for a kernel which performs the discrete approximation of the spatial derivatives of ${\textstyle (-\Delta )^{\lambda }}$.

As an alternative to the spatial approach, solving the iteration (12) in the frequency domain provides a stable implementation for the computation of a numerical solution for the displacement field ${\textstyle \mathbf {u} [\mathbf {n} ]}$, and in a more efficient way than other existing approaches if the ${\textstyle d}$-dimensional fast Fourier transform (FFT) is taken into account [40]. Translating the semi-implicit iteration (12) into the frequency domain results in

$U_{l}^{(\xi )}({\boldsymbol {\omega }})=U_{l}^{(\xi {-1)}}({\boldsymbol {\omega }})-\tau \,F_{l}^{(\xi {-1)}}({\boldsymbol {\omega }})-\tau \,\alpha \,Q({\boldsymbol {\omega }})\,U_{l}^{(\xi )}({\boldsymbol {\omega }})\,,$

(13)

where ${\textstyle U_{l}^{(\xi )}}$, ${\textstyle U_{l}^{(\xi {-1)}}}$ and ${\textstyle F_{l}^{(\xi {-1)}}}$ are the ${\textstyle d}$-dimensional Fourier transforms of ${\textstyle u_{l}^{(\xi )}}$, ${\textstyle u_{l}^{(\xi {-1)}}}$ and ${\textstyle f_{l}^{(\xi {-1)}}}$, respectively, and ${\textstyle {\boldsymbol {\omega }}=(\omega _{1},\ldots ,\omega _{d})}$ is the ${\textstyle d}$-dimensional counterpart in the frequency domain associated to the discrete spatial variable ${\textstyle \mathbf {n} }$. The operator ${\textstyle Q({\boldsymbol {\omega }})}$ performs the spatial derivatives in the frequency domain and allows for their calculation by means of the product of spectra (i.e., the translation of the spatial convolution into the frequency domain); as deduced in [40], its analytical expression is the following:

$Q({\boldsymbol {\omega }})={\Bigl (}2\sum _{m=1}^{d}(1-\cos \omega _{m}){\Bigr )}^{\lambda }\,.$

(14)

It should be noted that, mathematically, any value ${\textstyle \lambda \in [1,2]}$ makes sense in the frequency domain (but not in the spatial domain). This allows for the design of hybrid diffusion-curvature regularizers with adaptable properties, please refer to [25] for further details.

As explained in previous paragraphs, it is taken into account that the datasets are discrete and then the spatial variable ${\textstyle \mathbf {x} }$ gives rise to the discrete spatial index ${\textstyle \mathbf {n} }$. Similarly, instead of handling continuous spectra, the frequency domain is also discretized and only the ${\textstyle N_{m}}$ uniformly sampled frequencies ${\textstyle \omega _{m}={\bigl (}0,{\frac {2\pi }{N_{m}}},\ldots ,{\frac {2\pi }{N_{m}}}(N_{m}-1){\bigr )}}$ are evaluated in each dimension. This way the iteration (13) can be implemented efficiently using the fast algorithms for the computation of the DFT which are provided by many programming languages (e.g., MATLAB's ${\textstyle fftn}$ built-in function which is based on the FFTW library by [16]).

Finally, the iteration of the proposed registration algorithm is the following:

$u_{l}^{(\xi )}[\mathbf {n} ]=\mathrm {IFFT} \left\{H[\mathbf {k} ]\,\,\mathrm {FFT} \{{}u_{l}^{(\xi {-1)}}[\mathbf {n} ]-\tau \,f_{l}^{(\xi {-1)}}[\mathbf {n} ]\}{}\right\}\,,$

(15)

where ${\textstyle H[\mathbf {k} ]=(1+\tau \,\alpha \,Q[\mathbf {k} ])^{-1}}$, ${\textstyle Q[\mathbf {k} ]={\bigl (}2\sum _{m=1}^{d}(1-\cos({\frac {2\pi }{N_{m}}}k_{m})){\bigr )}^{\lambda }}$, ${\textstyle \mathbf {k} =(k_{1},\ldots ,k_{d})}$, and ${\textstyle k_{m}=0,\ldots ,N_{m}-1}$. Due to the fact that ${\textstyle Q[\mathbf {k} ]}$ results in a circulant block matrix, all the spectra products and pseudo-inversions become Hadamard (i.e., pointwise) products and divisions, respectively [10].

3. Results

In order to assess the performance of the proposed methodology, it is tested on 15 medical experiments involving triple-phase 3D computed tomography (CT) volumes of the liver under contrast agent injection. Although the acquisition of the different phases is continuous in most cases, there is no exact correspondence between them, so they must be registered in order to show the results in a common 3D framework. First, a study without contrast agent is acquired. Once the contrast agent is injected, it reaches the arteries (arterial phase), then the portal veins and next the hepatic veins. Hepatic and portal veins are then visible in the portal venous phase. Image registration allows to locate exactly the vessels in 3D at each phase of contrast-enhanced CT data in order to measure distances and volumes and provide objective parameters of the pathology which facilitate comparisons between patients, the tracking of tumors [9], to make calculations on the volume of the liver to be preserved prior to a liver resection [12], or to generate vessel models for planning surgical procedures [22]. The experiments carried out involve data from 5 patients. The acquisition device is a GE LightSpeed VTC (General Electric Medical Systems). The size of the volumes vary from ${\textstyle 512\times {512}\times {34}}$ to ${\textstyle 512\times {512}\times {51}}$ voxels, with a resolution of ${\textstyle 0.9102\times {0.9102}\times {5}}$ millimeters.

For the assessment of the proposed method, we carry out a comparison with the purely intensity-based variational method recently presented by the authors of this work in [26]. This CR-based approach was reported to outperform publicly available state-of-the art methods such as Elastix and ANTs in the medical setting. As can be seen in Figure 1, the proposed framework shows excellent results for the three considered registration scenarios (arterial-portal, arterial-non-contrast and portal-non-contrast), reaching average values of 1.47, 1.44 and 1.52 bits in terms of mutual information, corresponding to the arterial-portal, arterial-non-contrast and portal-non-contrast cases, respectively; this represents a mean improvement of 28.9%, 48.45% and 51.16% in relative terms of mutual information, thus outperforming the CR-based registration algorithm, which achieves a mean improvement of 26.48%, 44.22% and 43.25%, respectively. Additionally, due to the analogous behavior (i.e., comparable final values of mutual information) of the proposed method in the three scenarios, all available experiments can be grouped into one ensemble in order to assess a more comprehensive validation of the actual registration error. A ground truth was established by an expert in the form of identifiable anatomical locations (landmarks) for all experiments. The registration errors were then obtained by computing the spatial distance between the corresponding landmarks in the reference and registered template datasets. Figures 2(a) and 2(b) show through box plots the registration error (in millimeters) achieved by the methods under comparison, gathering the results from the three considered registration scenarios. These box plots collect the final spatial distances between corresponding landmarks, along with the median distance error and its statistical significance (notch showing the 95% confidence interval of the true median). According to Figure 2(b), the proposed method significantly improves on the registration error of the CR-based approach, since it reduces the initial median error from 9.50 mm to a residual median distance between landmarks of 1.41 mm, decreasing at the same time the outliers occurrence.

Figure 1. Mean similarity between images in terms of mutual information for the three considered scenarios (arterial-portal, arterial-non-contrast and portal-non-contrast) before and after the registration

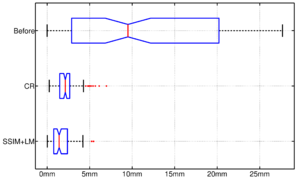
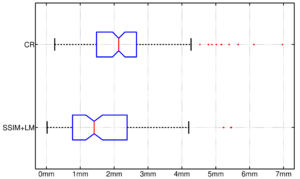
(a) Box plot of the registration error	(b) Close-up view of (a)
Figure 2. Spatial distances (in millimeters) between corresponding landmarks before and after the registration process

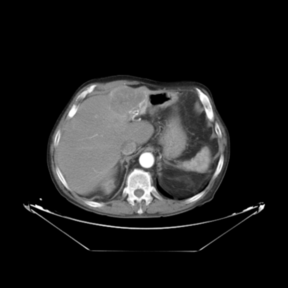
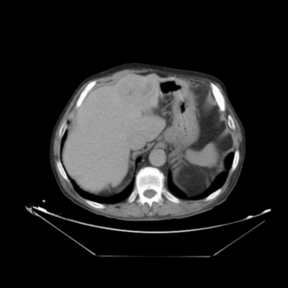
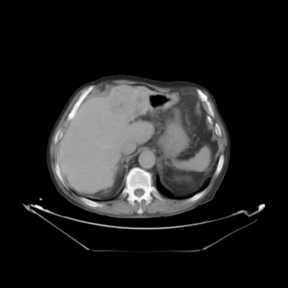
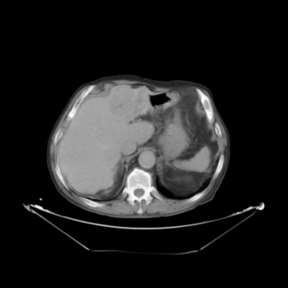
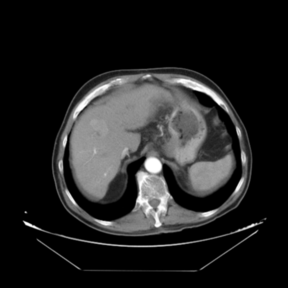
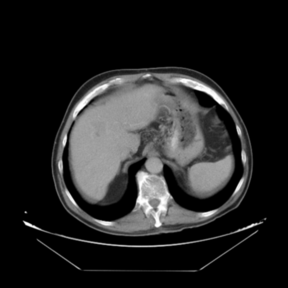
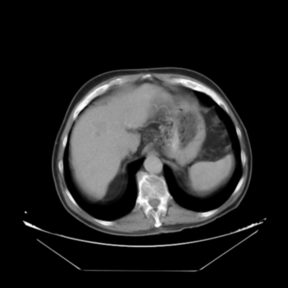
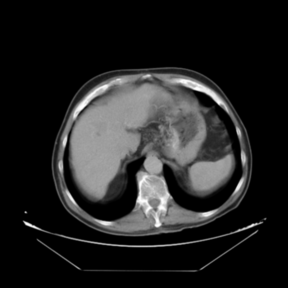
In addition to the previous measurements, the visual outcomes of two of the experiments are shown in Figures 3 and 4, whose purpose is to highlight the most illustrative differences (from a medical point of view) between the results provided by the compared methods. In Figure 3, we observe a normal size of the liver, with discretely irregular contours and homogeneous signal intensity. In hepatic segment II, there is a lesion of 40 mm of maximum axis, encapsulated and with well-defined contours and heterogeneous enhancement in arterial phase (after administration of intravenous contrast), suggestive of hepatocellular carcinoma (HCC). In this slice of the CT scan, we can also observe the aorta that shines in the arterial phase, the lower area of the stomach and the upper area of the spleen. In Figure 4, the liver has a normal size with discretely irregular contours in relation to changes due to chronic liver disease. In hepatic segment IV, a 36 mm diameter focal lesion is identified, which has arterial phase enhancement with a small area of necrosis of 13 mm; it corresponds to a HCC previously chemoembolized with partial necrosis. In this slice of CT, we can also observe the aorta, the gastric chamber and the spleen. When comparing the two methods under study, it can be seen how in Figure 3 the resulting registered datasets are very similar. However, looking closely, it can be noticed that in the right part of the image (left side of the patient) the shape and width of the structures corresponding to the stomach and the spleen in Figure 3(d) match better those in the reference dataset. Likewise, the part of the rib at the upper right of the image is more similar to the same region in the reference dataset by using the proposed method. Regarding the experiment shown in Figure 4, it can be easily appreciated how the geometrical matching (with respect to the reference dataset, Figure 4(a)) of the structures in the right side of the image (specially the gastric chamber) is visually more satisfactory in Figure 4(d). Moreover, the area of tumor necrosis which results from the proposed method is also slightly better aligned.

(a) Arterial phase (reference dataset, ${\textstyle R}$)	(b) Non-contrast phase (template dataset, ${\textstyle T}$)
(c) Registered template, ${\textstyle T_{\mathbf {u} }}$ (CR-based method)	(d) Registered template, ${\textstyle T_{\mathbf {u} }}$ (proposed method)
Figure 3. Visual outcomes of experiment 1 (slice 9): registration of arterial and non-contrast phases of patient 1

(a) Arterial phase (reference dataset, ${\textstyle R}$)	(b) Portal venous phase (template dataset, ${\textstyle T}$)
(c) Registered template, ${\textstyle T_{\mathbf {u} }}$ (CR-based method)	(d) Registered template, ${\textstyle T_{\mathbf {u} }}$ (proposed method)
Figure 4. Visual outcomes of experiment 5 (slice 12): registration of arterial and portal venous phases of patient 2

Throughout this work, the SSIM-based term uses the following parameters setting: ${\textstyle C_{1}=0.01}$ and ${\textstyle C_{2}=0.03}$. These are the empirically obtained values suggested in the reference paper [43]. Regardless, we find that in the current scenario, the performance of the proposed registration algorithm is fairly insensitive to variations of these values. Regarding the remaining parameters, which are exclusively related to our variational approach, the values of ${\textstyle \lambda =2}$ (i.e., curvature smoother, since the deformations to be corrected are notable in some cases), ${\textstyle \alpha =200}$, ${\textstyle \beta =5}$ (only applicable to the combined SSIM- and landmark-based method) and ${\textstyle \tau =1}$ were used for all experiments —we recommend a common set which achieves a good balance between generalization and performance—. This parameter setting was obtained following the guidelines first introduced in [23]. As for the number of iterations, a value of ${\textstyle \xi _{\max }=80}$ grants convergence in all cases; the cost function stabilizes after 50–70 iterations for both the CR-based and the proposed algorithm. From the results gathered in Table 1, it can be concluded that the computational overhead introduced by the novel approach does not increase significantly the execution time of the CR-based algorithm. Moreover, both variational approaches outperform well-established registration methods such as Elastix in terms of efficiency. Elastix was the fastest method which provided better results among the open source methods of image registration which entered in the second phase of Empire10 Challenge [30]. The overall complexity of each iteration of the compared algorithms is ${\textstyle {\mathcal {O}}(N)}$ —where ${\textstyle N}$ is the number of voxels of the datasets—, since doubling ${\textstyle N}$ means doubling the computational time.

Table 1. Mean execution time per iteration (in seconds) of the considered variational methods and Elastix, involving datasets of different sizes. These times were obtained on a PC with Intel Core i5-2500K, 3.3 GHz, 16 GB RAM, running Windows 8.1 (64 bits). All methods have been implemented in C++

Size	CR	SSIM+LM	Elastix
${\textstyle 512\times {512}\times {16}}$	2.40	2.52	5.69
$512\times {512}\times {32}$	5.03	5.27	11.20
$512\times {512}\times {64}$	10.42	10.93	22.01

4. Conclusions and discussion

In this work, a theoretical framework has been presented for approaching the image registration problem. In particular, we have formalized the variational formulation of image registration, making it valid even for a general ${\textstyle d}$-dimensional case. The resulting semi-implicit iteration, which is solved in the frequency domain, allows for an efficient implementation if fast algorithms for the computation of the DFT are taken into account. The main novelty of this paper lies in the inclusion within such a framework of a disparity energy which combines the information provided by both the structural similarity index (SSIM) and the location of geometrical identifiable points (landmarks). With this purpose, the corresponding external forces fields of the resulting Euler-Lagrange equation have been deduced, and their analytical expressions are explicitly provided.

The suitability of the proposed methodology in the medical setting has been validated by means of illustrative experiments involving liver CT data under different contrast agent injection. When compared with an intensity-based method which was recently reported to outperform other popular state-of-the-art methods, it has been shown that the novel approach achieves higher values for both the similarity measure considered (mutual information) and the actual registration error (distance in space between corresponding landmarks). Moreover, the results provided by the method proposed in this paper are subjectively considered more satisfying after being visually inspected by an expert. However, the main advantage of the proposed registration method is its efficiency. As expected, the FFT-based, C++ implementation of our approach outperforms fast methods such as Elastix in terms of computational cost, while keeping the execution times in the range of its main contestant (the previously proposed CR-based algorithm). In a clinical environment, where computational times should be kept as low as possible, this feature can be of paramount importance. Regardless, it should be noted that comparing the performance of different image registration algorithms is not a trivial task, since each approach has its own set of user-defined parameters, which may heavily influence the final outcome. For instance, if they are tested on datasets with different characteristics (e.g., modality or anatomical region), new optimal parameters need to be determined. In this sense, open challenges are an interesting way to categorize image registration software packages in a common context.

It should be noted that the proposed method considers the input directional field as a periodic signal. Unless this is taken into account, the vectors located near the boundaries will be erroneous. As stated by other authors —see e.g. [13]—, this is hardly a problem if the data is contained within a uniform background (e.g., when dealing with medical images or volumes, as in the current scenario), or else it can be overcome by using a folded algorithm which extends the dataset symmetrically, thus resulting in additional reflections of the original input, see e.g. [3].

The most notable limitation of the present method is that the SSIM-based term would not be an appropriate choice for the combined disparity energy unless matching voxels of the datasets have similar intensities (i.e., in pure monomodal or pseudo-monomodal scenarios). In fact, this is an inherent drawback of the structural similarity index, not a problem which arises with our methodology. However, even if the aim was to register multimodal datasets, one could still use the proposed variational approach, but considering an alternative distance term instead (e.g., a combined CR- and landmark-based disparity energy).

In ongoing research, we would like to address the application of our methodology to other scenarios, such as the fusion of datasets from different modalities: for example, anatomical (CT and MRI), metabolic (spectroscopic MRI and PET) and functional (f-MRI) volumes in the medical setting. Alternative definitions of the joint functional, including additional energy terms —e.g., a measure of the differences between forward and reverse transformations, so that the resulting displacement field is consistent—, are currently being explored within the presented theoretical framework.

Appendix A. Variational formulation of SSIM

In this work, we propose the opposite of the structural similarity index as the intensity-based part of the disparity term of the joint energy functional (first addend in equation (2)). Thus, a maximization problem is transformed into the minimization of the following cost function:

${\mathcal {D}}^{\mbox{SSIM}}[R,T;\mathbf {u} ]:=-\mathrm {=} R,T_{\mathbf {u} }={\frac {-(2\,\mu _{R}\,\mu _{T}+C_{1})(2\,\sigma _{RT}+C_{2})}{(\mu _{R}^{2}+\mu _{T}^{2}+C_{1})(\sigma _{RR}+\sigma _{TT}+C_{2})}}\,.$

(A.1)

The mathematical expectations, variances and covariance ${\textstyle \mu _{R}}$, ${\textstyle \mu _{T}}$, ${\textstyle \sigma _{RR}}$, ${\textstyle \sigma _{TT}}$ and ${\textstyle \sigma _{RT}}$ are defined as follows:

$\mu _{R}=\mathrm {E} \{{}R\}{}=\int _{\mathcal {I}}i_{r}\,p_{R}(i_{r})di_{r}\,,$

(A.2)

$\mu _{T}=\mathrm {E} \{{}T_{\mathbf {u} }\}{}=\int _{\mathcal {I}}i_{t}\,p_{T_{\mathbf {u} }}(i_{t})di_{t}\,,$

(A.3)

$\sigma _{RR}=\mathrm {Var} \{{}R\}{}=\int _{\mathcal {I}}i_{r}^{2}\,p_{R}(i_{r})di_{r}-\mathrm {E} ^{2}\{{}R\}{}\,,$

(A.4)

$\sigma _{TT}=\mathrm {Var} \{{}T_{\mathbf {u} }\}{}=\int _{\mathcal {I}}i_{t}^{2}\,p_{T_{\mathbf {u} }}(i_{t})di_{t}-\mathrm {E} ^{2}\{{}T_{\mathbf {u} }\}{}\,,$

(A.5)

$\sigma _{RT}=\mathrm {Cov} \{{}R,T_{\mathbf {u} }\}{}=\int _{{\mathcal {I}}^{2}}i_{r}\,i_{t}\,p_{R,T_{\mathbf {u} }}(i_{r},i_{t})di_{r}\,di_{t}-\mathrm {E} \{{}R\}{}\,\mathrm {E} \{{}T_{\mathbf {u} }\}{}\,,$

(A.6)

where ${\textstyle p_{R}}$ and ${\textstyle p_{T_{\mathbf {u} }}}$ denote the marginal intensity distributions estimated from ${\textstyle R}$ and ${\textstyle T_{\mathbf {u} }}$, respectively, and ${\textstyle p_{R,T_{\mathbf {u} }}}$ stands for an estimate of the joint intensity distribution. The intensities of the datasets, ${\textstyle i_{r}\,,i_{t}\in {\mathcal {I}}\subset \mathbb {R} }$, are considered as random variables whose probability densities are respectively given by ${\textstyle p_{R}}$ and ${\textstyle p_{T_{\mathbf {u} }}}$.

In order to obtain the external forces field related to the SSIM-based energy term (i.e., the first addend in the Euler-Lagrange equation (5)), the computation of the corresponding Gateaux derivative ${\textstyle \mathrm {d} {\mathcal {D}}^{\mbox{SSIM}}}$ is required. Therefore, we carry out an explicit computation from the definition of the Gateaux derivative (see Eq.(4)):

$\mathrm {d} {\mathcal {D}}^{\mbox{SSIM}}[R,T;\mathbf {u} ;\mathbf {z} ]={\frac {\partial }{\partial \epsilon }}\left.{\mathcal {D}}^{\mbox{SSIM}}[R,T;\mathbf {u} +\epsilon \mathbf {z} ]\right|_{\epsilon =0}$ $=-{\frac {(\mu _{R}^{2}+\mu _{T}^{2}+C_{1})(\sigma _{RR}+\sigma _{TT}+C_{2})(2\,\mu _{R}\,\mu _{T}'(2\,\sigma _{RT}+C_{2})+2\,\sigma _{RT}'(2\,\mu _{R}\,\mu _{T}+C_{1}))}{(\mu _{R}^{2}+\mu _{T}^{2}+C_{1})^{2}(\sigma _{RR}+\sigma _{TT}+C_{2})^{2}}}$ $+\left.{\frac {(2\,\mu _{R}\,\mu _{T}+C_{1})(2\,\sigma _{RT}+C_{2})(2\,\mu _{T}\,\mu _{T}'(\sigma _{RR}+\sigma _{TT}+C_{2})+\sigma _{TT}'(\mu _{R}^{2}+\mu _{T}^{2}+C_{1}))}{(\mu _{R}^{2}+\mu _{T}^{2}+C_{1})^{2}(\sigma _{RR}+\sigma _{TT}+C_{2})^{2}}}\right|_{\epsilon =0}$ $=\int _{{\mathcal {I}}^{2}}\left.L_{\mathbf {u} +\epsilon \mathbf {z} }^{\mbox{SSIM}}(i_{r},i_{t}){\frac {\partial }{\partial \epsilon }}p_{R,T_{\mathbf {u} +\epsilon \mathbf {z} }}(i_{r},i_{t})di_{r}\,di_{t}\right|_{\epsilon =0}\,,$

(A.7)

with ${\textstyle L_{\mathbf {u} +\epsilon \mathbf {z} }^{\mbox{SSIM}}}$ being an intensity operator —whose definition, not necessary at this point, is not explicitly provided for the sake of simplicity—, and where the notation ${\textstyle (\cdot )'={\frac {\partial }{\partial \epsilon }}(\cdot )}$ is used.

Assuming a displacement ${\textstyle \mathbf {u} +\epsilon \mathbf {z} }$, the joint intensity distribution estimated from ${\textstyle R}$ and ${\textstyle T_{\mathbf {u} +\epsilon \mathbf {z} }}$ is provided by a non-parametric Parzen-Rozenblatt density model [11]:

$p_{R,T_{\mathbf {u} +\epsilon \mathbf {z} }}(i_{r},i_{t})={\frac {1}{{\mathcal {V}}_{\mathbf {\Psi } }}}\int _{\mathbf {\Psi } }{\hat {G}}_{\rho }\left(R(\mathbf {x} )-i_{r},T(\mathbf {x} +\mathbf {u} (\mathbf {x} )+\epsilon \mathbf {z} (\mathbf {x} )-i_{t})\right)d\mathbf {x} \,,$

(A.8)

where ${\textstyle {\mathcal {V}}_{\mathbf {\Psi } }}$ denotes the hypervolume of ${\textstyle \mathbf {\Psi } }$ and ${\textstyle {\hat {G}}_{\rho }:{\mathcal {I}}^{2}\rightarrow \mathbb {R} }$ is a Gaussian kernel (strictly positive and differentiable):

${\hat {G}}_{\rho }(i_{r},i_{t})={\frac {1}{2\pi \rho ^{2}}}\,e^{-{\frac {i_{r}^{2}+i_{t}^{2}}{2\rho ^{2}}}}\,.$

(A.9)

At this point, derivatives of ${\textstyle p_{R,T_{\mathbf {u} +\epsilon \mathbf {z} }}}$ can be easily computed. In particular,

${\frac {\partial }{\partial \epsilon }}p_{R,T_{\mathbf {u} +\epsilon \mathbf {z} }}(i_{r},i_{t})={\frac {1}{{\mathcal {V}}_{\mathbf {\Psi } }}}\int _{\mathbf {\Psi } }{\frac {\partial }{\partial i_{t}}}{\hat {G}}_{\rho }\left(R(\mathbf {x} )-i_{r},T\left(\mathbf {x} +\mathbf {u} (\mathbf {x} )+\epsilon \mathbf {z} (\mathbf {x} )\right)-i_{t}\right)\nabla T\left(\mathbf {x} +\mathbf {u} (\mathbf {x} )+\epsilon \mathbf {z} (\mathbf {x} )\right)\mathbf {z} (\mathbf {x} )d\mathbf {x} \,.$

(A.10)

We now replace (A.10) in (A.7), and then let ${\textstyle \epsilon =0}$:

$\mathrm {d} {\mathcal {D}}^{\mbox{SSIM}}[R,T;\mathbf {u} ;\mathbf {z} ]={\frac {1}{{\mathcal {V}}_{\mathbf {\Psi } }}}\int _{\mathbf {\Psi } }\int _{{\mathcal {I}}^{2}}L_{\mathbf {u} }^{\mbox{SSIM}}(i_{r},i_{t}){\frac {\partial }{\partial i_{t}}}{\hat {G}}_{\rho }\left(R(\mathbf {x} )-i_{r},T\left(\mathbf {x} +\mathbf {u} (\mathbf {x} )\right)-i_{t}\right)\nabla T\left(\mathbf {x} +\mathbf {u} (\mathbf {x} )\right)\mathbf {z} (\mathbf {x} )di_{r}\,di_{t}\,d\mathbf {x}$ $=\int _{\mathbf {\Psi } }{\Bigl \langle }{\frac {1}{{\mathcal {V}}_{\mathbf {\Psi } }}}\left({\hat {G}}_{\rho }\ast {\frac {\partial L_{\mathbf {u} }^{\mbox{ SSIM}}}{\partial i_{t}}}{\Bigl (}R(\mathbf {x} ),T\left(\mathbf {x} +\mathbf {u} (\mathbf {x} )\right){\Bigr )}\right)\nabla T\left(\mathbf {x} +\mathbf {u} (\mathbf {x} )\right),\mathbf {z} (\mathbf {x} ){\Bigr \rangle }_{\mathbb {R} ^{d}}d\mathbf {x}$ $=\int _{\mathbf {\Psi } }{\bigl \langle }\mathbf {f} ^{\mbox{ SSIM}}(\mathbf {x} ;\mathbf {u} ),\mathbf {z} (\mathbf {x} ){\bigr \rangle }_{\mathbb {R} ^{d}}d\mathbf {x} \,.$

(A.11)

In the previous equation, a bidimensional convolution with respect to the intensity variable ${\textstyle \mathbf {i} =(i_{r},i_{t})}$ appears naturally. This convolution conmutes with the derivative ${\textstyle {\frac {\partial }{\partial i_{t}}}}$ (since both are linear operators). Moreover, by identifying the resulting expression with an inner product in ${\textstyle \mathbb {R} ^{d}}$, the external forces field of the Euler-Lagrange equation (5) which corresponds to the SSIM-based energy term can be finally obtained:

$\mathbf {f} ^{\mbox{SSIM}}={\frac {1}{{\mathcal {V}}_{\mathbf {\Psi } }}}\left({\hat {G}}_{\rho }\ast {\frac {\partial L_{\mathbf {u} }^{\mbox{SSIM}}}{\partial i_{t}}}\right)\nabla T_{\mathbf {u} }\,,$

(A.12)

with

${\frac {\partial L_{\mathbf {u} }^{\mbox{SSIM}}}{\partial i_{t}}}={\frac {\gamma _{0}+C_{1}\,\gamma _{1}+C_{2}\,\gamma _{2}+C_{1}C_{2}\,\gamma _{3}}{(\mu _{R}^{2}+\mu _{T}^{2}+C_{1})^{2}(\sigma _{RR}+\sigma _{TT}+C_{2})^{2}}}\,,$

(A.13)

and where the definitions of ${\textstyle \gamma _{0}}$, ${\textstyle \gamma _{1}}$, ${\textstyle \gamma _{2}}$ and ${\textstyle \gamma _{3}}$ can be found in Eqs.(7)-(10).

References

[1] Amintoosi M., Fathy M., Mozayani N. Precise image registration with structural similarity error measurement applied to superresolution. EURASIP Journal on Advances in Signal Processing, 2009:1–7, 2009.

[2] Amit Y. A nonlinear variational problem for image matching. SIAM Journal of Scientific Computing, 15:207–224, 1994.

[3] Bai J., Feng X.C. Fractional-order anisotropic diffusion for image denoising. IEEE Transactions on Image Processing, 16:2492–2502, 2007.

[4] Ben Sassi O., Delleji T., Taleb-Ahmed A., Feki I., Ben Hamida A. Mr image monomodal registration using structure similarity index. Image Processing Theory, Tools and Applications, 2008:1–5, 2008.

[5] Bookstein F.L. Principal warps: thin-plate splines and the decomposition of deformations. IEEE Transactions on Pattern Analysis and Machine Intelligence, 11:567–585, 1989.

[6] Brown L.G. A survey of image registration techniques. ACM Computing Surveys, 24:325–376, 1992.

[7] Brunet D., Vrscay E., Wang Z. On the mathematical properties of the structural similarity index. IEEE Transactions on Image Processing, 21:1488–1499, 2012.

[8] Cachier P., Bardinet E., Dormont D., Pennec X., Ayache N. Iconic feature based nonrigid registration: the PASHA algorithm. Computer Vision and Image Understanding, 89:272–298, 2003.

[9] Charnoz A., Agnus V., Malandain G., Forest C., Tajine M., Soler L. Liver registration for the follow-up of hepatic tumors. Lecture Notes in Computer Science, 3750:155–162, 2005.

[10] Davis P.J. Circulant matrices. Wiley-Interscience, NY, 1979.

[11] Duda R., Hart P. Pattern classification and scene analysis. Wiley, 1973.

[12] Elhawary H., Oguro S., Tuncali K., Morrison P., Shyn P., Tatli S., Silverman S., Hata N. Intra-operative multimodal non-rigid registration of the liver for navigated tumor ablation. Lecture Notes in Computer Science, 5761:837–844, 2009.

[13] Fischer B., Modersitzki J. Fast inversion of matrices arising in image processing. Numerical Algorithms, 22:1–11, 1999.

[14] Fischer B., Modersitzki J. Fast diffusion registration. Contemporary Mathematics, Inverse Problems, Image Analysis, and Medical Imaging, 313:117–129, 2002.

[15] Fischer B., Modersitzki J. A unified approach to fast image registration and a new curvature based registration technique. Linear Algebra and its Applications, 308:107–124, 2004.

[16] Frigo M., Johnson S.G. The design and implementation of FFTW3. Proceedings IEEE, 93:216–231, 2005.

[17] Huang Y.H., Ou T.S., Su P.Y., Chen H. Perceptual rate-distortion optimization using structural similarity index as quality metric. IEEE Transactions on Circuits and Systems for Video Technology, 20:1614–1624, 2010.

[18] Johnson H.J., Christensen G.E. Consistent landmark and intensity-based image registration. IEEE Transactions on Medical Imaging, 21:450–461, 2002.

[19] Kalinic H., Loncaric S., Bijnens B. A novel image similarity measure for image registration. Image and Signal Processing and Analysis, 2011:195–199, 2011.

[20] Klein S., Staring M., Murphy K., Viergever M.A., Pluim J.P.W. Elastix: a toolbox for intensity-based medical image registration. IEEE Transactions on Medical Imaging, 29:196–205, 2010.

[21] Kolesov I., Lee J., Sharp G., Vela P., Tannenbaum A. A stochastic approach to diffeomorphic point set registration with landmark constraints. IEEE Transactions on Pattern Analysis and Machine Intelligence, 38:238–251, 2016.

[22] Lange T., Wenckebach T.H., Lamecker H., Seebass M., Hünerbein M., Eulenstein S., Gebauer B., Schlag P.M. Registration of different phases of contrast-enhanced CT/MRI data for computer-assisted liver surgery planning: evaluation of state-of-the-art methods. The International Journal of Medical Robotics and Computer Assisted Surgery, 1:6–20, 2005.

[23] Larrey-Ruiz J., Morales-Sánchez J. Optimal parameters selection for non-parametric image registration methods. Lecture Notes in Computer Science, 4179:564–575, 2006.

[24] Larrey-Ruiz J., Morales-Sánchez J., Verdú-Monedero R. Generalized regularization term for non-parametric multimodal image registration. Signal Processing, 87:2837–2842, 2007.

[25] Larrey-Ruiz J., Verdú-Monedero R., Morales-Sánchez J. A Fourier domain framework for variational image registration. Journal of Mathematical Imaging and Vision, 32:57–72, 2008.

[26] Legaz-Aparicio A.G., Verdú-Monedero R., Larrey-Ruiz J., Morales-Sánchez J., López-Mir F., Naranjo V., Bernabéu A. Efficient variational approach to multimodal registration of anatomical and functional intra-patient tumorous brain data. International Journal of Neural Systems, 27:1–11, 2017.

[27] Loizou C.P., Theofanous C., Pantziaris M., Kasparis T. Despeckle filtering software toolbox for ultrasound imaging of the common carotid artery. Computer Methods and Programs in Biomedicine, 114:109 – 124, 2014.

[28] Maintz J., Viergever M. A survey of medical image registration. Medical Image Analysis, 2:1–36, 1998.

[29] Modersitzki J. Numerical Methods for Image Registration. Oxford University Press, NY, 2004.

[30] Murphy K., van Ginneken B., Reinhardt J., Kabus S., Ding K., Deng X., Cao K., Du K., Christensen G., Garcia V., Vercauteren T., Ayache N., Commowick O., Malandain G., Glocker B., Paragios N., Navab N., Gorbunova V., Sporring J., de Bruijne M., Han X., Heinrich M., Schnabel J., Jenkinson M., Lorenz C., Modat M., McClelland J., Ourselin S., Muenzing S., Viergever M., De Nigris D., Collins D., Arbel T., Peroni M., Li R., Sharp G., Schmidt-Richberg A., Ehrhardt J., Werner R., Smeets D., Loeckx D., Song G., Tustison N., Avants B., Gee J., Staring M., Klein S., Stoel B., Urschler M., Werlberger M., Vandemeulebroucke J., Rit S., Sarrut D., Pluim J. Evaluation of registration methods on thoracic CT: the Empire10 challenge. IEEE Transactions on Medical Imaging, 30:1901–1920, 2011.

[31] Myronenko A., Song X. Intensity-based image registration by minimizing residual complexity. IEEE Transactions on Medical Imaging, 29:1882–1891, 2010.

[32] Naranjo V., Morales S., Legaz-Aparicio A.G., Larrey-Ruiz J., Bernabéu A., Fuentes-Hurtado F. A software for surgical and radiotherapy planning through multimodal brain image registration and fusion. International Journal of Computer Assisted Radiology and Surgery, 10:15–17, 2015.

[33] Ou Y., Akbari H., Bilello M., Da X., Davatzikos C. Comparative evaluation of registration algorithms in different brain databases with varying difficulty: results and insights. IEEE Transactions on Medical Imaging, 33:2039–2065, 2014.

[34] Rehman A., Wang Z., Brunet D., Vrscay E. SSIM-inspired image denoising using sparse representations. Acoustics, Speech and Signal Processing, 2011:1121–1124, 2011.

[35] Rohr K. Landmark-based image analysis: using geometric and intensity models. Computational Imaging and Vision Series, Kluwer Academic Publishers, Dordrecht, 2001.

[36] Sotiras A., Davatzikos C., Paragios N. Deformable medical image registration: a survey. IEEE Transactions on Medical Imaging, 32:1153–1190, 2013.

[37] Sotiras A., Ou Y., Paragios N., Davatzikos C. Graph-based deformable image registration, in: Paragios, N., Duncan, J., Ayache, N. (Eds.), Handbook of Biomedical Imaging: Methodologies and Clinical Research, Springer, 2015.

[38] Tosun D., Rettmann M.E., Prince J.L. Mapping techniques for aligning sulci across multiple brains. Medical Image Analysis, 8:295–309, 2004.

[39] Urschler M., Zach C., Ditt H., Bischof H. Automatic point landmark matching for regularizing nonlinear intensity registration: application to thoracic CT images. Lecture Notes in Computer Science, 4191:710–717, 2006.

[40] Verdú-Monedero R., Larrey-Ruiz, J., Morales-Sánchez, J. Frequency implementation of the Euler-Lagrange equations for variational image registration. IEEE Signal Processing Letters, 15:321–324, 2008.

[41] Vishnukumar S., Wilscy M. A comparative study on adaptive local image registration methods. International Conference on Signal Processing Systems, 2009:140–145, 2009.

[42] Wang J., Zhang J.Q. An iterative refinement dsa image registration algorithm using structural image quality measure. Intelligent Information Hiding and Multimedia Signal Processing, 2009:973–976, 2009.

[43] Wang Z., Bovik A.C., Sheikh H.R., Simoncelli E.P. Image quality assessment: from error visibility to structural similarity. IEEE Transactions on Image Processing, 13:600–612, 2004.

[44] Wen C., Wang D., Shi L., Chu W.C.W., Cheng J.C.Y., Lui L.M. Landmark constrained registration of high-genus surfaces applied to vestibular system morphometry. Computerized Medical Imaging and Graphics, 44:1–12, 2015.

[45] Wirth M., Bobier B. Registration of the Prokudin-Gorskii colour photographs using a multiresolution SSIM algorithm. Lecture Notes in Computer Science, 5627:917–926, 2009.

[46] Zhang Z., Jiang Y., Tsui H. Consistent multi-modal non-rigid registration based on a variational approach. Pattern Recognition Letters, 27:715–725, 2006.

[47] Zitová B., Flusser J. Image registration methods: a survey. Image and Vision Computing, 21:997–1000, 2003.