Computational Homogenization of Inelastic Materials using Model Order Reduction

Acknowledgments

The research leading to these results has received funding from, on the one hand, the European Research Council under the European Union's Seventh Framework Programme (FP/2007-2013) / ERC Grant Agreement n. 320815, Advanced Grant Project COMP-DES-MAT, and, on the other hand, the Spanish Ministry of Science and Innovation under grant BIA2011-24258.

Abstract

The present work is concerned with the application of projection-based, model reduction techniques to the efficient solution of the cell equilibrium equation appearing in (otherwise prohibitively costly) two-scale, computational homogenization problems. The main original elements of the proposed Reduced-Order Model (ROM) are fundamentally three. Firstly, the reduced set of empirical, globally-supported shape functions are constructed from pre-computed Finite Element (FE) snapshots by applying, rather than the standard Proper Orthogonal Decomposition (POD), a partitioned version of the POD that accounts for the elastic/inelastic character of the solution. Secondly, we show that, for purposes of fast evaluation of the nonaffine term (in this case, the stresses), the widely adopted approach of replacing such a term by a low-dimensional interpolant constructed from POD modes, obtained, in turn, from FE snapshots, leads invariably to ill-posed formulations. To safely avoid this ill-posedness, we propose a method that consists in expanding the approximation space for the interpolant so that it embraces also the gradient of the global shape functions. A direct consequence of such an expansion is that the spectral properties of the Jacobian matrix of the governing equation becomes affected by the number and particular placement of sampling points used in the interpolation. The third innovative ingredient of the present work is a points selection algorithm that does acknowledge this peculiarity and chooses the sampling points guided, not only by accuracy requirements, but also by stability considerations. The efficiency of the proposed approach is critically assessed in the solution of the cell problem corresponding to a highly complex porous metal material under plane strain conditions. Results obtained convincingly show that the computational complexity of the proposed ROM is virtually independent of the size and geometrical complexity of the considered representative volume, and this affords gains in performance with respect to finite element analyses of above three orders of magnitude without significantly sacrificing accuracy –-hence the appellation High-Performance ROM.

1 Introduction

1.1 Motivation

1.1.1 Moore's and Parkinson's laws in computational modeling

A basic precept in constructing a successful computational model –-one that strikes the right balance between accuracy and simplicity–- is, quoting M.Ashby [1], ``to unashamedly distort the inessentials in order to capture the features that really matter. Yet with the general availability of fast computers with large memories, and the exponential growth presaged by Moore's law of such capacities, it is becoming increasingly difficult to resist the temptation to violate this basic precept and, in the quest for higher accuracy, indiscriminately include features that do not contribute significantly to the overall response of the modeled system. As pointed out by Venkataraman et al.[2], this had led to the paradox that certain engineering problems that were computationally tackled for the first time 40 years ago appear to remain comparatively costly, even though the capacity of computers have increased one trillion-fold during this period. This apparent paradox is of course not exclusive of computational physical modeling, but rather just another manifestation of the general adage “software applications will invariably grow to fill up increased computer memory, processing capabilities and storage space”, known as the computerized Parkinson's law [3].

1.1.2 The two-scale homogenization problem

An engineering research area that seems to be falling into this paradigmatic trend is, as we intend to argue in the ensuing discussion, the two-scale modeling, via homogenization, of materials such as composites and polycrystalline metals, characterized by exhibiting a clear heterogeneous composition at some lower length scale –-the micro-, or meso-, scale–-, but that can be regarded as homogeneous at the length scale at which engineering predictions are needed –-the macro-scale. The actual challenge in the macro-scale continuum description of the mechanical behavior of such materials lies in the determination of a constitutive connection between macro-stresses and macro-strains that accurately reflects the material properties and geometrical arrangement of the distinct phases at the micro-/meso-scale. Under the hypotheses of either periodicity or statistical homogeneity, on the one hand; and scale separation, on the other hand, it is well-known [4] that this constitutive link can be systematically established by solving, for each point at the coarse scale, a boundary value problem (BVP) on a certain representative microscopic subdomain (the cell equilibrium problem). In a strain-driven formulation of this BVP, the macro-strain at a given point acts as “loading parameter”, in the form of appropriate essential boundary conditions, whereas the associated macro-stress is obtained through volume averaging –-i.e., homogenization–- of the corresponding micro-stress field.

1.1.3 Evolution of homogenization approaches

When the discipline of continuum micromechanics began to flourish in the 60's and 70's of the last century, research focus was fundamentally directed, absent powerful computational tools (if any), towards the development of approximated, closed-form solutions of this BVP for certain types of geometrically and constitutively simple micro-structures. To arrive at these solutions, pioneers such as R. Hill [5], Z. Hashin [6], and K. Tanaka [7] struggled to identify and retain, guided sometimes by an uncanny physical intuition, only those features of the microstructural response that has a significant impact on the accuracy of coarse-scale predictions –-filtering out, thus, the “inessentials”. The advent of increasingly fast computers, and the concomitant advancement of numerical methods to solve differential equations, progressively fostered a shift towards the development of homogenization techniques that rely less on analytical results and more on numerical solutions, widening thereby their scope; for comprehensive surveys of these semi-analytical homogenization methods, the reader is referred to Refs. [8,9,10]. The approach termed by some authors [11,12] computational homogenization (or direct computational homogenization ) can be regarded as the culmination of this shift towards purely numerical methods: in this approach, the microscopic boundary value problem at each coarse-scale point is attacked using no other approximation than the spatial discretization of the pertinent solution strategy (finite element method, for instance), thus, circumventing the need for simplifying assumptions regarding the topological arrangement of the micro-phases and/or their collective constitutive behavior.

1.1.4 Infeasibility of direct computational homogenization methods

Although no doubt the most versatile and accurate homogenization technique, with no other limitation in scope than the imposed by the aforementioned hypotheses of statistical homogeneity and scale separation, the direct computational homogenization approach violates squarely the modeling precept outlined at the outset –-it does not discriminate between essential and irrelevant features in solving the fine-scale BPVs–-, making the accuracy/parsimony balance to tilt unduly towards the accuracy side and far from the parsimony one. The consequence is its enormous computational cost (in comparison with analytical and semi-analytical homogenization techniques). For instance, when the Finite Element (FE) method is the strategy of choice for both scales –-the commonly known as multilevel finite element method, abbreviated FE${\textstyle ^{2}}$ method [13]–-, one has to solve, at every increment and every Newton-Raphson iteration of the global, coarse-scale FE analysis, and for each Gauss point of the coarse-scale mesh, a local, non-linear finite element problem which, in turn, may involve several thousand of degrees of freedom. To put it metaphorically, in the FE${\textstyle ^{2}}$ method, the complexity of the overall analysis is submitted to the “tyranny of scales” [14,15,16]–- it depends on the resolution of both coarse- and fine- scale grids. This explains why, presently, almost five decades after R.Hill [17] laid the foundations of non-linear continuum micro-mechanics, and despite the dizzying speed of today's computers, the routine application of this general and versatile homogenization method to model the inelastic behavior of large structural systems featuring complex micro-/meso-structures is still considered intolerably costly, especially when the system has to be analyzed for various configurations, as in design optimization or inverse analysis.

1.1.5 Shortcomings of semi-analytical approaches

The foregoing review and critical appraisal of how things have evolved in the field of continuum micromechanics clearly teaches us that, to defeat the tyranny of scales, and develop a successful homogenization method, one should strive to adhere to Ashby's modeling principle and introduce –-as actually done in analytical and semi-analytical approaches–- appropriate simplifications in dealing with the fine-scale BVPs. Negating the need for such simplifications in the hope that the upcoming generations of peta-, exa- (and so forth) flops computers will eventually come to the rescue and cope with the resulting complexity, is, in the authors' opinion, a mistaken view, at odds with the true spirit of physical modeling, and the culprit for the paradoxical trend alluded to earlier.

Yet finding, for a given, arbitrarily complex microstructure, a suitable set of simplifying assumptions, let alone incorporating in a consistent manner such assumptions in the formulation of the local BVPs, is in general a formidably challenging endeavor. The admittedly brilliant idea underlying many advanced semi-analytical homogenization methods, such as the Transformation Field Analysis (TFA) [18] and variants thereof [19,20,21,22], of pre-computing certain characteristic operators (strain localization and influence tensors) by solving a carefully chosen battery of fine-scale BPVs has only partially relieved modelers from this burden: these methods are still predicated, to a lesser or greater extent, on ad-hoc assumptions connected with the constitutive description of the involved phases. Consideration of new materials with unstudied compositions will thereby require additional research efforts by specialists in the field and eventual modifications of the corresponding mathematical and numerical formulations –-in contrast to direct computational homogenization approaches, such as the FE${\textstyle ^{2}}$ method, in which the formulation is “material-independent”, and hence more versatile.

1.2 Goal

The current state of affairs in the field of two-scale homogenization seems to call, thus, for a unified homogenization approach that combines somewhat the advantages of direct computational homogenization and semi-analytical techniques. It would be desirable to have a homogenization method with a computational cost virtually independent of the geometric complexity of the considered representative volume, as in semi-analytical techniques –-i.e., one that defies the tyranny of scales. At the same time, it would be also interesting to arrive at a method whose mathematical formulation dispenses with ad-hoc, simplifying assumptions related with the composition of the heterogeneous material; i.e, one enjoying the versatility, unrestricted applicability and “user-friendliness” –-insofar as it would totally relieve the modeler from the often exceedingly difficult task of visualizing such assumptions –- of direct computational homogenization methods. The goal of the present work is to show that these desirable, apparently conflicting attributes can be conceivably achieved, for arbitrarily complex heterogeneous materials well into the inelastic range, by using the so-called [23] Reduced-Basis (RB) approximation in the solution of the cell BVPs.

1.3 Reduced-basis approach

1.3.1 Essence of the approach

Generally speaking, the reduced-basis approximation is simply a class of Galerkin approximation procedure that employs, as opposed to the FE method, but similarly to classical Rayleigh-Ritz solution techniques [24], globally supported basis functions. The main difference with respect to classical Rayleigh-Ritz schemes is that these basis functions or modes are not constructed from globally supported polynomials or transcendental functions (sines, cosines ...), but rather are determined from a larger set of previously computed, using the finite element (FE) method or other classical solution techniques, solutions of the BVP at appropriately selected values of the input of interest. These functions are commonly termed empirical basis functions [25], the qualifier empirical meaning “derived from computational experiments”.

As noted earlier, the input of interest or “loading” parameter in the fine-scale cell problem is the macro-scale strain tensor. Accordingly, the starting point for constructing the basis functions in the case under study would consist in solving a battery of cell BVPs for various, judiciously chosen macro-strain values. In the linear elastic regime, for instance, the displacement solution depends linearly on the prescribed macro-strain tensor, and hence it would suffice to perform 6 linear FE analysis (stretch in three directions and three shears); the corresponding modes would simply arise from orthonormalizing the displacement solutions of these problems. By constraining the cell to deform only into these 6 pre-defined, shape functions, one automatically obtains a genuine reduced-order model (ROM) of the cell. Note that the dimension of this ROM is totally independent of the spatial discretization (and, therefore, of the geometric complexity of the cell) used in the preliminary or offline FE analyses.

1.3.2 Dimensionality reduction

Things get a little bit more complicated in the inelastic range. The solution of the problem not only ceases to bear a linear relation to the prescribed macro-strain tensor: it also depends in general on the entire history of this coarse-scale kinematic variable. As a consequence, instead of single linear FE analyses, it becomes necessary to perform nonlinear FE studies on the cell subjected to various, representative macro-strain histories. The outcome of these FE calculations is a data set comprising an ensemble of hundred or even thousand (depending on the number of time steps into which the strain histories are discretized) displacement field solutions (also called snapshots). Were all these snapshots barely correlated with each other, the dimension of the manifold spanned by them would prove overly high, rendering the entire approach impractical –-it would no longer qualify as a truly reduced basis method. Fortunately, as we show in the present work, in general, most of these snapshots do display strong linear correlations between each other –-i.e., they have redundant information–-, and, in addition, contain deformation modes that are irrelevant to the quality of coarse-scale predictions –-in the sense that their associated stress fields have vanishing or negligible average volumes. Accordingly, all that is required to obtain a much lower dimensional representation of the solution data set, and therewith the desired reduced basis, is an automatic means to identify and remove this redundant and irrelevant information, while preserving, as much as possible, its essential features. This problem of removing unnecessary complexity from huge data sets so as to uncover dominant patterns is the central concern of disciplines such as digital image and video compression [26], and patter recognition [27], to name but a few, and thereby many efficient dimensionality reduction (or data compression, in more common parlance) algorithms already exist to deal with it. In the present work, we employ the arguably simplest and most popular of such algorithms: the Proper Orthogonal Decomposition (POD).

It becomes clear from the above discussion that, in the reduced basis approach, the inescapable task of discriminating what is essential and what is not is automatically carried out by these dimensionality reduction methods. In other words, the “burden” of simplification of the cell BVP in the RB approach is entirely borne by the computer, and not by the modeler, as it occurs in analytical and, to a lesser extent, in semi-analytical homogenization methods. It is precisely this feature that confers the advantages of versatility and “user-friendliness” alluded to earlier.

1.3.3 Numerical integration

Once the global shape functions have been computed, the next step in the construction of the reduced-order model of the cell is to introduce an efficient method for numerically evaluating the integrals appearing in the weak form of the cell BVP. Of course one can simply use the same Gauss quadrature formulae and the same sampling points (a total number of ${\textstyle n_{g}={\mathcal {O}}(n)}$, ${\textstyle n}$ being the number of mesh nodes) as the underlying finite element model. But this would be akin to integrating, say, a third-order polynomial function using thousand of sampling points–-a profligate waste of computational resources. Since displacement solutions for the cell BVP are constrained to lie in a reduced-order space of dimension ${\textstyle n_{u}<<n}$, it is reasonable to expect that the corresponding stresses, internal forces and Jacobians will also reside in reduced-order spaces of dimensions of order ${\textstyle {\mathcal {O}}(n_{u})}$, and consequently, only ${\textstyle p={\mathcal {O}}(n_{u})<<n_{g}}$ sampling points would suffice in principle to accurately evaluate the corresponding integrals. The challenging questions that have to be confronted are where to locate these ${\textstyle p}$ sampling points and, loosely speaking, how to determine their associated weighting functions so that maximum accuracy in the integration is attained.

Approaches found in the model reduction literature that, directly or indirectly, deal with these fundamental questions can be broadly classified either as interpolatory approaches [28,29,30,31,32] or Gauss-type quadrature approaches [33,34], the former having a wider scope, for they also serve to reduce models derived from finite difference approximations [32,31]. The starting point for both is to collect, during the alluded to earlier finite element calculations, snapshots of the integrand or part of the integrand. In interpolatory approaches, the resulting ensemble of snapshots is submitted to a dimensionality reduction process, in the manner described previously for the solution basis functions, in order to compute a reduced set of dominant, orthogonal modes. Such orthogonal modes are employed to construct an interpolant of the integrand, using as interpolation points (the desired sampling points) those minimizing the interpolation error over the finite element snapshots. In the spirit of classical, interpolatory quadrature schemes such as Newton-Cotes [35], the resulting quadrature formula, and therefore, the weighting functions, emerges from approximating the integrand by this reduced-order interpolant. In Gauss-type quadrature procedures [33,34], by contrast, the selection of sampling points and the calculation of the accompanying weighting factors are simultaneously carried out, guided by a criterion of minimum integration error over the snapshots–-in a vein, in turn, similar to that used in classical Gauss-Legendre quadrature rules [35]. A more comprehensive review on both type of integration methods can be found in Ref. [36].

In the BVP under consideration, the output of interest is the volume average of the stresses over the cell domain and, therefore, accuracy is required not only in the integration of the equilibrium equation, but also on the approximation of the stresses themselves. This is the reason why, notwithstanding the presumably higher efficiency of Gauss-type quadrature (less integration error for the same number of sample points), attention is focused in the present work on interpolatory integration strategies, the variable subject to spatial interpolation being precisely the stresses.

1.4 Originality of this work

The idea of exploiting the synergistic combination of multiscale modeling and reduced basis approximation is admittedly not new. In the specific context of two-scale homogenization, it has been recently explored by Boyaval [37], Yvonnet et al. [38], and Monteiro et al. [39]. Traces of this idea can also be found in articles dealing with more general hierarchical multiscale techniques –-that do not presuppose either scale separation or periodicity/statistical homogeneity, or both–-, namely, in the multiscale finite element method [40,41,42] and in the heterogeneous multiscale method [43,44]. However, it should be noted that none of the above cited papers confronts the previously described, crucial question of how to efficiently integrate the resulting reduced-order equations, simply because, in most of them [37,40,41,42,43,44], integration is not an issue –- the fine-scale BVPs addressed in these works bear an affine relation with the corresponding coarse-scale, input parameter, as in linear elasticity, and, consequently, all integrals can be pre-computed, i.e., evaluated offline, with no impact in the online computational cost. Thus, the development of cell reduced-order models endowed with efficient, mesh-size independent integration schemes –-able to handle any material composition–- is a research area that, to the best of the authors' knowledge, still remains uncharted.

1.4.1 Main original contribution

The theory underlying ROMs that incorporate efficient interpolatory integration schemes, henceforth termed High-Performance ROMs (HP-ROMs), is still at its embryonic stage of development –-the first general proposal for parametrized BVPs dates back to 2004 [28]–- and many fundamental issues remain to be addressed. Foremost among these is the crucial question of well-posedness of the resulting system of algebraic equations: does the replacement of the integrand, or nonaffine term in the integrand, by a reduced-order interpolant always lead to a well-posed, discrete problem ? Examination of the reduced basis literature indicates that apparently no researcher has so far been confronted with ill-posed reduced-order equations, a fact that might certainly promote the view that uniqueness of solution can be taken for granted whenever the full-order model is well-posed. Unfortunately, this is not always so: we demonstrate in this work that the choice of the reduced-order space in which the interpolant of the integrand resides has a profound impact on the well-posedness of the discrete problem. In particular, we show that, in the case of the cell boundary-value problem, the widely adopted [29] approach of determining the basis functions for this space from (converged) FE snapshots leads invariably to ill-posed, discrete formulations. The main original contribution of the present work to the field of reduced-order modeling is the development of an interpolatory integration method that safely overcomes this type of ill-posedness. The gist of the method is to expand the interpolation space so that it embraces, aside from the span of the POD stress basis functions, the space generated –-and herein lies the novelty–- by the gradient of the (reduced-order) shape functions.

1.4.2 Other original contributions

An inevitable consequence of adopting the aforementioned expanded space approach is that, in contrast to the situation encountered when using standard interpolatory schemes in other parametrized BVPs [29], in the proposed method, the number and particular placement of sampling points within the integration domain influence notably the spectral properties (positive definiteness) of the Jacobian matrix of the governing equation, and therefore, the convergence characteristics of the accompanying Newton-Raphson solution algorithm. Another innovative ingredient of the present work is a points selection algorithm that does acknowledge this peculiarity and chooses the desired sampling points guided, not only by accuracy requirements (minimization of the interpolation error over the FE stress snapshot), but also by stability considerations.

Lastly, a further original contribution of the present work is the strategy for computing the global shape functions and stress basis functions. Instead of directly applying the POD over the snapshots to obtain the dominant modes, we first decompose these snapshots into (mutually orthogonal) elastic and inelastic components, and then apply separately the standard POD to the resulting elastic and inelastic snapshots. In so doing, the resulting reduced-order model is guaranteed to deliver linear elastic solutions with the same accuracy as the underlying (full-order) finite element model.

1.5 Organization of the document

The remaining of this document is organized as follows. Chapter 2is devoted to the formulation and finite element implementation of the cell equilibrium problem. Chapter 3, on the other hand, is concerned with the issue of the offline computation of the POD reduced basis. In Section 3.2, the Galerkin projection of the cell equilibrium equation onto the space spanned by the POD basis is presented. Chapter 4 outlines the procedure for efficiently integrating the reduced-order equilibrium equation. In Section 4.3, we discuss the crucial issue of where the low-dimensional approximation of the stress field should lie in order to obtain an accurate and at the same time well-posed reduced-order problem; in Section 4.3.3, the original proposal of expanding the stress basis with the gradient of the (reduced-order) shape functions is put forward. Section 4.4 delineates the derivation of the modal coefficients in the approximation of the stress field in terms of the stress values computed at the set of pre-specified sampling points. The determination of the optimal location of these sampling points is addressed in Section 4.5. For the reader's convenience and easy reference, in Section 4.6, both the offline and online steps leading to the proposed reduced-order model are conveniently summarized. Chapter 5 is dedicated to numerically assess the efficiency of the proposed model reduction strategy. Finally, in Chapter 6, some concluding remarks are presented.

In order to preserve the continuity of the presentation, details concerning the algorithmic implementation of the computation of the reduced basis and the selection of sampling points are relegated to the appendices.

2 First-order homogenization

2.1 Basic assumptions

The fundamental assumptions upon which the homogenization approach followed in this work rests are presented below. For a more in-depth description of the underlying axiomatic framework, the reader is referred to Refs. [45,46,47,48].

2.1.1 Existence of a representative subvolume

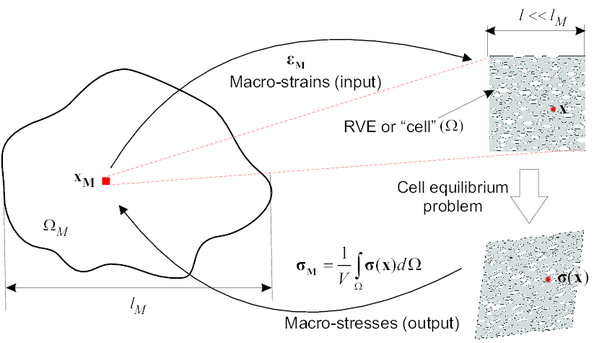
The homogenization approach employed in this work –-commonly known as first-order homogenization–- is only valid for materials that either display statistical homogeneity or spatial periodicity [45]. In both type of materials, it is possible to identify a subvolume ${\textstyle \Omega \subset \mathbb {R} ^{d}\,(d=2,3)}$, of characteristic length ${\textstyle l}$, that is representative, in a sense that will be properly defined later, of the heterogeneous material as a whole. Furthermore, this subvolume ${\textstyle \Omega }$ has to be small enough that it can approximately be regarded as a point at the coarse-scale level [4] (i.e, ${\textstyle l<<l_{M}}$, ${\textstyle l_{M}}$ being the characteristic length of the macro-continuum ${\textstyle \Omega _{M}}$, see Figure 1). This is the so-called scale separation hypothesis. In micro-structures that exhibit statistical homogeneity, this domain receives the name of Representative Volume Element (RVE), whereas in micro-structures that display periodicity, it is commonly known as repeating unit cell (RUC), or simply unit cell [45]. In the sequel, both the acronym RVE and the more generic term “cell” will be used interchangeably to refer to ${\textstyle \Omega }$.

Figure 1: First-order homogenization.

2.1.2 Decomposition into macroscopic and microscopic contributions

The displacement ${\textstyle {\boldsymbol {u}}_{\mu }}$ at any point ${\textstyle \mathbf {x} \in \Omega }$ is assumed to be decomposed into macroscopic and microscopic parts; under the hypothesis of infinitesimal deformations, this decomposition can be written as:

${\boldsymbol {u}}_{\mu }(\mathbf {x} )={\boldsymbol {\epsilon _{M}}}\,\mathbf {x} +{\boldsymbol {u}}(\mathbf {x} ),$

(2.1)

where ${\textstyle {\boldsymbol {\epsilon _{M}}}}$ stands¹ for the macroscopic strain tensor (the input parameter in the BVP we wish to efficiently solve) and ${\textstyle {\boldsymbol {u}}(\mathbf {x} )}$ denotes the so-called displacement fluctuation field (in turn, the basic unknown of this BVP). The macroscopic term ${\textstyle {\boldsymbol {\epsilon _{M}}}\,\mathbf {x} }$ represents the displacements that would have been observed had the material been homogeneous, whereas the fluctuating contribution ${\textstyle {\boldsymbol {u}}}$ accounts for the deviations from this homogeneous state due to the presence of heterogeneities [49].

The decomposition of the microscopic strain tensor ${\textstyle {\boldsymbol {\epsilon }}}$ follows from simply differentiating Eq.(2.1):

${\boldsymbol {\epsilon }}(\mathbf {x} )={\boldsymbol {\epsilon _{M}}}+\nabla ^{s}{{\boldsymbol {u}}(\mathbf {x} )}.$

(2.2)

Notice that, in writing Eq.(2.2), one is tacitly assuming that the macroscopic strain tensor ${\boldsymbol {\epsilon _{M}}}$ is uniform over the spatial length associated to the cell size . This proviso renders the employed homogenization approach –-commonly termed first-order homogenization [12,48]–- not suitable for appropriately handling localization problems. For this reason, in the present work, we shall presuppose that localization of strains does not take place within the deforming cell.

Implicit in the scale separation assumption is the fact that fine-scale deformations only influence coarse-scale behavior through its volume average over the RVE; this implies that

${\boldsymbol {\epsilon _{M}}}={\dfrac {1}{V}}\displaystyle \int _{\Omega }{\boldsymbol {\epsilon }}\,d\Omega ,$

(2.3)

where ${\textstyle V}$ stands for the volume of the RVE:

$V=\displaystyle \int _{\Omega }\,d\Omega {.}$

(2.4)

By virtue of Eq.(2.2), this condition is equivalent to impose the volume average of the fluctuation contribution ${\textstyle \nabla ^{s}{{\boldsymbol {u}}(\mathbf {x} )}}$ to vanish:

$\displaystyle \int _{\Omega }\nabla ^{s}{{\boldsymbol {u}}(\mathbf {x} )}\,d\Omega ={\boldsymbol {0}}.$

(2.5)

(¹) Some remarks concerning notation are in order here. Firstly, macroscopic variables will be identified by appending a subscript “M”, while variables associated to the fine scale will be designated by bare symbols. For instance, we shall write ${\boldsymbol {\epsilon _{M}}}$ and ${\boldsymbol {\epsilon }}(\mathbf {x} )$ to denote the macroscopic strain tensor and the fine-scale strain field, respectively. Secondly, readers accustomed to classical continuum mechanics notation are reminded that, in this work, the symbol ${\boldsymbol {u}}$ does not represent the displacement field, but rather the fluctuating part –-due to the presence of heterogeneities in the concerned RVE–- of such a field.

2.1.3 Hill-Mandel principle of macro-homogeneity

The scale bridging is completed by the Hill-Mandel principle of macro-homogeneity, that states that the stress power at any point ${\textstyle \mathbf {x} _{M}}$ of the macro-continuum must equal the volume average (over the RVE) of the corresponding fine-scale, stress power field (making, thus, both coarse- and fine-scale, continuum description energetically equivalent [8]). The variational statement of this principle is as follows [47]: let ${\textstyle {\boldsymbol {\sigma }}}$ be a statically admissible, fine-scale stress field, and ${\textstyle {\boldsymbol {\sigma _{M}}}}$ the associated macroscopic stress tensor, then, the identity

${\boldsymbol {\sigma _{M}}}:{\boldsymbol {{\dot {\epsilon }}_{M}}}={\dfrac {1}{V}}\displaystyle \int _{\Omega }{\boldsymbol {\sigma }}(\mathbf {x} ):{\dot {\boldsymbol {\epsilon }}}(\mathbf {x} )\,d\Omega$

(2.6)

must hold for any kinematically admissible strain rate ${\textstyle {\dot {\boldsymbol {\epsilon }}}}$. Inserting the rate form of Eq.(2.2) into the above equation, and by virtue of Eq.(2.3), it follows that, for identity (2.6) to hold, the macroscopic stress tensor ${\textstyle {\boldsymbol {\sigma _{M}}}}$ must be the volume average of the microscopic stress field ${\textstyle {\boldsymbol {\sigma }}={\boldsymbol {\sigma }}(\mathbf {x} ),\;\mathbf {x} \in \Omega }$:

${\boldsymbol {\sigma _{M}}}={\dfrac {1}{V}}\displaystyle \int _{\Omega }{\boldsymbol {\sigma }}\,d\Omega {.}$

(2.7)

Another necessary condition for Eq.(2.6) to hold is that:

$\displaystyle \int _{\Omega }{\boldsymbol {\sigma }}:\nabla ^{s}{\boldsymbol {\dot {u}}}\,d\Omega =0$

(2.8)

for any kinematically admissible displacement fluctuation field ${\textstyle {\boldsymbol {\dot {u}}}}$. It is shown in Ref. [47] that this condition amounts to requiring that the external surface traction and body force field in the RVE be purely reactive –-i.e., a reaction to the kinematic constraints imposed upon the RVE. This is why the upcoming cell equilibrium equation does not contain neither external boundary traction nor body force terms.

2.2 RVE equilibrium problem

2.2.1 Boundary conditions

To address the issue of boundary conditions (BCs), it proves first convenient to, using Gauss' theorem, recast equation (2.5) in terms of boundary displacement fluctuations:

$\displaystyle \int _{\Omega }\nabla ^{s}{{\boldsymbol {u}}(\mathbf {x} )}\,d\Omega =\displaystyle \int _{\partial \Omega }{\boldsymbol {u}}(\mathbf {x} )\otimes ^{s}{\boldsymbol {n}}(\mathbf {x} )\,d\Omega =0,$

(2.9)

where ${\textstyle \partial \Omega }$ represents the boundary of ${\textstyle \Omega }$, ${\textstyle {\boldsymbol {n}}}$ is the outer unit normal vector to ${\textstyle \partial \Omega }$ and the symbol ${\textstyle \otimes ^{s}}$ denotes the symmetrized tensor product. Any type of boundary conditions prescribed on the cell must obey this condition.

The natural choice for a repeating unit cell (RUC) –-defined as the smallest volume that allows one to generate, by periodic repetition, the entire microstructure of a periodic media [49]–- is to employ periodic boundary conditions for the displacement fluctuations. By definition, the boundary of an RUC comprises ${\textstyle K}$ pairs of identical –-appropriately shifted in space–- surfaces ${\textstyle \partial \Omega _{k}^{+}}$ and ${\textstyle \partial \Omega _{k}^{-}}$ (${\textstyle k=1,2\ldots K}$), with the property that for every ${\textstyle \mathbf {x} _{k}^{+}\in \partial \Omega _{k}^{+}}$, ${\textstyle {\boldsymbol {n}}(\mathbf {x} _{k}^{+})=-{\boldsymbol {n}}(\mathbf {x} _{k}^{-})}$, ${\textstyle \mathbf {x} _{k}^{-}}$ being, loosely speaking, the “counterpart” of ${\textstyle \mathbf {x} _{k}^{+}}$ in ${\textstyle \partial \Omega _{k}^{-}}$. Periodicity of displacement fluctuations implies that for every ${\textstyle \mathbf {x} _{k}^{+}\in \partial \Omega _{k}^{+}}$, ${\textstyle {\boldsymbol {u}}(\mathbf {x} _{k}^{+})={\boldsymbol {u}}(\mathbf {x} _{k}^{-})}$. (See Refs. [8,49] for more details on this type of BCs).

In statistically homogeneous micro-structures, by contrast, the situation is not so clear-cut. The concept of RVE admits various, alternative interpretations and, as a consequence, there is a certain latitude in the choice of boundary conditions (vanishing fluctuations, uniform tractions, quasi-periodic conditions …); the reader interested in this topic is urged to consult Refs. [45,50,51]. Arguably, the most practical choice –-from an implementational point of view–- in a strain-driven finite element context (and the one adopted here) is to use vanishing boundary conditions for the displacement fluctuations (${\textstyle {\boldsymbol {u}}(\mathbf {x} )=0,\forall \mathbf {x} \in \partial \Omega }$), and correspondingly determine the RVE as the smallest subvolume of the statistically homogeneous microstructure whose mechanical response is, under this type of boundary conditions, indistinguishable from that of the material-at-large.

2.2.2 Trial and test function spaces

It is not hard to see that both periodic and vanishing BCs are just particular instances of the more general case of homogeneous boundary conditions [52], i.e, conditions of the form:

${\boldsymbol {A}}_{0}{\boldsymbol {u}}={\boldsymbol {0}},\;\;on\;\;\;\partial \Omega ,$

(2.10)

${\textstyle {\boldsymbol {A}}_{0}}$ being the corresponding linear operator. An immediate corollary of this observation is that the set of all kinematically admissible displacement fluctuation fields, henceforth denoted by ${\textstyle {\mathcal {V}}_{u}}$, will form for both type of boundary conditions a vector space; this space is defined formally as:

${\mathcal {V}}_{u}=\left\lbrace {\boldsymbol {u}}\in H^{1}(\Omega )^{d}\;|\;{\boldsymbol {A}}_{0}{\boldsymbol {u}}={\boldsymbol {0}},\;\;on\;\;\;\partial \Omega \right\rbrace .$

(2.11)

Here, ${\textstyle H^{1}(\Omega )^{d}}$ stands for the Sobolev space of functions possessing square integrable derivatives over ${\textstyle \Omega }$. Since the test functions ${\textstyle {\boldsymbol {\eta }}}$ are kinematically admissible variations, we can write

${\boldsymbol {\eta }}={u}-{v},\;\;\;{u},{v}\in {\mathcal {V}}_{u},$

(2.12)

from which it follows that ${\textstyle {\boldsymbol {\eta }}\in {\mathcal {V}}_{u}}$, i.e., the spaces of trial and test functions coincide.

Observation 1: As will be further explained later, ${\textstyle {\mathcal {V}}_{u}}$ having structure of linear space confers a unique advantage –-not enjoyed by ROMs of BVPs with general inhomogeneous boundary conditions [25]–- for model reduction purposes: reduced-order responses will invariably and automatically conform to the imposed boundary conditions, regardless of the level of approximation.

2.2.3 Variational statement

Consider a time discretization of the interval of interest ${\textstyle [t_{0},t_{f}]=\bigcup _{n=1}^{n_{stp}}[t_{n},t_{n+1}]}$. The current value of the microscopic stress tensor ${\textstyle {\boldsymbol {\sigma }}_{n+1}}$ at each ${\textstyle \mathbf {x} \in \Omega }$ is presumed to be entirely determined by, on the one hand, the current value of the microscopic strain tensor ${\textstyle {\boldsymbol {\epsilon }}_{n+1}(\mathbf {x} )={\boldsymbol {\epsilon _{M}}}_{n+1}+\nabla ^{s}{{\boldsymbol {u}}_{n+1}(\mathbf {x} )}}$, and, on the other hand, a set of microscopic internal variables ${\textstyle {\boldsymbol {\xi }}_{n+1}}$ –-that encapsulate the history of microscopic deformations. The relationship between these variables is established by (phenomenological) rate constitutive equations; these equations may vary from point to point within the cell (multiphase materials). Likewise, the considered RVE may contain also voids distributed all over the domain. The (incremental) RVE equilibrium problem at time ${\textstyle t_{n+1}}$ can be stated as follows (see Ref. [47]): given the initial data ${\textstyle \{{\boldsymbol {u}}_{n}(\mathbf {x} ),{\boldsymbol {\epsilon _{M}}}_{n},{\boldsymbol {\xi }}_{n}\!(\mathbf {x} )\}}$ and the prescribed macroscopic strain tensor ${\textstyle {\boldsymbol {\epsilon _{M}}}_{n+1}}$, find ${\textstyle {\boldsymbol {u}}_{n+1}\in {\mathcal {V}}_{u}}$ such that

$\displaystyle \int _{\Omega }\nabla ^{s}{\boldsymbol {\eta }}:{\boldsymbol {\sigma }}_{n+1}({\boldsymbol {\epsilon _{M}}}_{n+1}+\nabla ^{s}{{\boldsymbol {u}}_{n+1}},{\boldsymbol {\xi }}_{n+1})\,d\Omega =0,$

(2.13)

for all ${\textstyle {\boldsymbol {\eta }}\in {\mathcal {V}}_{u}}$. The actual output of interest in this fine-scale BVP is not the displacement fluctuation field per se, but rather the macroscopic stress tensor ${\textstyle \left.{\boldsymbol {\sigma _{M}}}\right|_{n+1}}$:

$\left.{\boldsymbol {\sigma _{M}}}\right|_{n+1}={\dfrac {1}{V}}\displaystyle \int _{\Omega }{\boldsymbol {\sigma }}_{n+1}\,d\Omega {.}$

(2.14)

In order to keep the notation uncluttered, the superindex “n+1” will be hereafter dropped out and all quantities will be assumed to be evaluated at time ${\textstyle t_{n+1}}$; only when confusion is apt to show up, the pertinent distinction will be introduced.

2.3 Finite element formulation

Let ${\textstyle \Omega =\bigcup _{n=1}^{n_{e}}\Omega ^{e}}$ be a finite element discretization of the cell. It will be assumed that this discretization is fine enough to consider the exact and FE approximated solutions indistinguishable at the accuracy level of interest. Let ${\textstyle \left\lbrace N_{1}(\mathbf {x} ),N_{2}(\mathbf {x} )\ldots N_{N}(\mathbf {x} )\right\rbrace }$ (${\textstyle n}$ denotes the number of nodes of the discretization) be a set of shape functions associated to this discretization such that

${\mathcal {V}}_{u}^{h}={\textrm {span}}\!\left\lbrace N_{I}\right\rbrace _{I=1}^{n}\subset {\mathcal {V}}_{u}.$

(2.15)

In the case of vanishing displacement fluctuations, this can be achieved by simply ensuring that:

$N_{I}(\mathbf {x} )=0,\;\;\;\forall \mathbf {x} _{I}\in \partial \Omega .\;\;$

(2.16)

As for periodic boundary conditions, let us suppose, for simplicity, that the spatial grid is such that every node ${\textstyle \mathbf {x} ^{+}\in \partial \Omega _{k}^{+}}$ (${\textstyle k=1,2\ldots K}$) has a “counterpart” node ${\textstyle \mathbf {x} ^{-}\in \partial \Omega _{k}^{-}}$ (and vice versa), and that, in addition, no nodes are placed at the intersection of adjoining surfaces. Such being the case, it can be readily shown that the conditions that the shape functions of a given node ${\textstyle \mathbf {x} _{I}\in \partial \Omega _{k}^{+}}$ and its counterpart ${\textstyle \mathbf {x} _{L}\in \partial \Omega _{k}^{-}}$ have to satisfy for proviso (2.15) to hold are:

$N_{I}(\mathbf {x} _{J})=\delta _{IJ}+\delta _{LJ}\;\;\;\;(J=1,2\ldots n)$

(2.17)

$N_{L}(\mathbf {x} _{J})=0\;\;\;(J=1,2\ldots n).$

(2.18)

The reader is referred to Refs. [49,53] for guidelines on how to enforce periodicity conditions in a more general scenario.

Now we approximate ${\textstyle {\boldsymbol {u}}\in {\mathcal {V}}_{u}}$ and ${\textstyle {\boldsymbol {\eta }}\in {\mathcal {V}}_{u}}$ as:

${\boldsymbol {u}}(\mathbf {x} ;{\boldsymbol {\epsilon _{M}}})\approx {\boldsymbol {u}}^{(h)}(\mathbf {x} ;{\boldsymbol {\epsilon _{M}}})=\displaystyle \sum _{I=1}^{n}\!N_{I}(\mathbf {x} ){\boldsymbol {U}}_{I}({\boldsymbol {\epsilon _{M}}}),$

(2.19)

${\boldsymbol {\eta }}(\mathbf {x} )\approx {\boldsymbol {\eta ^{(h)}}}(\mathbf {x} )=\displaystyle \sum _{I=1}^{n}\!N_{I}(\mathbf {x} ){\boldsymbol {\eta }}_{I},$

(2.20)

where ${\textstyle {\boldsymbol {U}}_{I}\in \mathbb {R} ^{d}}$ and ${\textstyle {\boldsymbol {\eta }}_{I}\in \mathbb {R} ^{d}}$ (${\textstyle I=1,2\ldots n}$) denote the nodal values of the displacement fluctuations and test functions, respectively. Inserting these approximations in Eq.(2.13), and exploiting the arbitrariness of coefficients ${\textstyle {\boldsymbol {\eta }}_{I}}$ (${\textstyle I=1,2\ldots n}$), one arrives at the following set of discrete equilibrium equations (repeated indices implies summation):

$\displaystyle \int _{\Omega }{\dfrac {\partial N_{I}}{\partial x_{j}}}{\boldsymbol {\sigma }}_{ij}({\boldsymbol {\epsilon _{M}}}+\nabla ^{s}{{\boldsymbol {u}}^{(h)}},{\boldsymbol {\xi }})\,d\Omega ={0}\;\;(i=1\ldots d;\;I=1\ldots n).$

(2.21)

Introducing Voigt's notation¹, the above equation can be expressed in matrix format as:

$\displaystyle \int _{\Omega }{\boldsymbol {B}}^{T}{\boldsymbol {\sigma }}({\boldsymbol {\epsilon _{M}}}+{\boldsymbol {B}}{\boldsymbol {U}},{\boldsymbol {\xi }})\,d\Omega ={\boldsymbol {0}}.$

(2.22)

where ${\textstyle {\boldsymbol {\sigma }}:\Omega \rightarrow \mathbb {R} ^{s}}$ represents, with a slight abuse of notation², the column matrix form of the stress tensor ( ${\textstyle s=4}$ and ${\textstyle s=6}$ for plane and 3D problems, respectively), and ${\textstyle {\boldsymbol {B}}:\Omega \rightarrow \mathbb {R} ^{s\times n\cdot d}}$ is the classical, global ``${\textstyle {\boldsymbol {B}}}$-matrix" connecting strains at a given point with the vector ${\textstyle {\boldsymbol {U}}\in \mathbb {R} ^{n\cdot d}}$ containing all nodal displacements:

${\boldsymbol {U}}{\mathrel {\mathop {:}}}={\begin{bmatrix}{\boldsymbol {U}}_{1}\\{\boldsymbol {U}}_{2}\\\vdots \\{\boldsymbol {U}}_{n}\end{bmatrix}}.$

(2.23)

As usual, numerical evaluation of the integral in Eq.(2.22) is carried out by Gaussian quadrature:

$\displaystyle \int _{\Omega }{\boldsymbol {B}}^{T}{\boldsymbol {\sigma }}\,d\Omega \approx \displaystyle \sum _{g=1}^{n_{g}}w_{g}{{\boldsymbol {B}}^{T}}\!\!(\mathbf {x} _{g}){\boldsymbol {\sigma }}(\mathbf {x} _{g},;)={\boldsymbol {0}}.$

(2.24)

Here, ${\textstyle n_{g}={\mathcal {O}}(n)}$ stands for the total number of Gauss points of the mesh; ${\textstyle w_{g}}$ denotes the weight associated to the ${\textstyle g-th}$ Gauss point ${\textstyle \mathbf {x} _{g}}$ (this weight includes both the quadrature weight itself and the corresponding Jacobian determinant.); and ${\textstyle {\boldsymbol {B}}(\mathbf {x} _{g})}$ and ${\textstyle {\boldsymbol {\sigma }}(\mathbf {x} _{g},;)}$ stand for the B-matrix and the stress vector at Gauss point ${\textstyle \mathbf {x} _{g}}$, respectively.

(¹) Here, it is convenient to use the so-called modified Voigt's notation rather than the standard one. In the modified Voigt's notation, both stress ${\boldsymbol {\sigma }}$ and strain ${\boldsymbol {\epsilon }}$ tensors are represented as column vectors ($\left\lbrace {\boldsymbol {\sigma }}\right\rbrace$ and $\left\lbrace {\boldsymbol {\epsilon }}\right\rbrace$, respectively ) in which the shear components are multiplied by ${\sqrt {2}}$. The advantage of this notation over the conventional, engineering Voigt's notation is the equivalence between norms; viz., $\Vert {\boldsymbol {\sigma }}\Vert ={\sqrt {{\boldsymbol {\sigma }}:{\boldsymbol {\sigma }}}}=\Vert \left\lbrace {\boldsymbol {\sigma }}\right\rbrace \Vert ={\sqrt {\left\lbrace {\boldsymbol {\sigma }}\right\rbrace ^{T}\left\lbrace {\boldsymbol {\sigma }}\right\rbrace }}$. The reader is urged to consult [54] for further details on this notation.

(²) The same symbol is used to denote the stress tensor and its counterpart in Voigt's notation.

3 Reduced-order model of the RVE

3.1 Computation of reduced basis

A basic, intuitive picture of the strategy for computing the reduced basis onto which to project the cell equilibrium equation (2.13) was already given in the introductory Chapter. In the following, we put the idea behind this strategy on a more rigorous footing. We begin by noting that, from a functional analysis standpoint, the term model reduction is conceptually akin to the more common term model discretization, since both connote transitions from higher-dimensional to lower-dimensional solution spaces. Indeed, whereas model discretization is used to refer to the (classical) passage from the infinite dimensional space ${\textstyle {\mathcal {V}}_{u}}$ to the finite element subspace ${\textstyle {\mathcal {V}}_{u}^{h}\subset {\mathcal {V}}_{u}}$, model reduction denotes a transition from this finite dimensional space ${\textstyle {\mathcal {V}}_{u}^{h}}$ to a significantly smaller manifold ${\textstyle {\mathcal {V}}_{u}^{*}\subset {\mathcal {V}}_{u}^{h}}$ –-the reduced-order space. This latter transition is not carried out directly, but in two sequential steps, namely, sampling of the parameter space and dimensionality reduction. The precise meaning of these terms is explained below.

3.1.1 Sampling of the input parameter space

In constructing the finite element space of kinematically admissible functions ${\textstyle {\mathcal {V}}_{u}^{h}}$, the only restrictions placed on the motion of the mesh nodes are those imposed at the boundaries through conditions (2.16) (for RVEs) and (2.17), (2.18) (for RUCs). The finite element solution space, thus, does not presuppose any constraint on the motion of the interior nodes of the mesh.

However, in actuality, interior nodes cannot fluctuate freely, independently from each other, but they rather move according to deformational patterns dictated by the constitutive laws that govern the mechanical behavior of the distinct phases in the cell –-as noted by Lubliner [55], constitutive laws can be regarded as internal restrictions on the kinds of deformation a body can suffer. This means that the solution of the finite element equilibrium equation (2.13) for given values of the macro-strain tensor ${\textstyle {\boldsymbol {\epsilon _{M}}}}$ actually lives in a smaller subspace ${\textstyle {\mathcal {V}}_{u}^{\epsilon }\subset {\mathcal {V}}_{u}^{h}}$ (in the parlance of model reduction [23,56], ${\textstyle {\mathcal {V}}_{u}^{\epsilon }}$ is the manifold induced by the parametric dependence of the BVP on the input variables).

Yet, in general, this manifold cannot be precisely determined –-such a task would require finite element analyses of the cell under all conceivable strain paths. Rather, one has to be content to construct an approximation of it as the span of the displacement fluctuation solutions obtained for a judiciously chosen set of ${\textstyle n_{hst}}$ input strain histories ${\textstyle \{{^{\,t}}{\boldsymbol {\epsilon _{M}}}{_{}}^{1},{^{\,t}}{\boldsymbol {\epsilon _{M}}}{_{}}^{2},\ldots {^{\,t}}{\boldsymbol {\epsilon _{M}}}{_{}}^{n_{hst}}\}}$. Suppose, for simplicity, that each of these strain histories is discretized into equal number of steps ${\textstyle n_{stp}}$, and let

${\boldsymbol {u}}^{k}(\mathbf {x} )={\boldsymbol {u}}(\mathbf {x} ;{^{\,t}}{\boldsymbol {\epsilon _{M}}}{_{j}}^{i}),\;\;k=(i-1)n_{hst}+j$

(3.1)

denote the displacement fluctuation solution at the ${\textstyle j-th}$ time step of the ${\textstyle i-th}$ strain history (${\textstyle i=1,2\ldots n_{hst}}$, ${\textstyle j=1,2\ldots n_{stp}}$). The approximating space for ${\textstyle {\mathcal {V}}_{u}^{\epsilon }}$, henceforth called the snapshots space, is then defined as:

${\mathcal {V}}_{u}^{snp}={\textrm {span}}\left\lbrace {\boldsymbol {u}}^{1}(\mathbf {x} ),{\boldsymbol {u}}^{2}(\mathbf {x} ),\ldots {\boldsymbol {u}}^{n_{snp}}(\mathbf {x} )\right\rbrace \subseteq {{\mathcal {V}}_{u}^{\epsilon }},$

(3.2)

${\textstyle n_{snp}=n_{stp}n_{hst}}$ being the total number of snapshots. Likewise, the matrix containing, in columns, the nodal values of these displacement fluctuations solutions:

${\boldsymbol {X}}_{u}={\begin{bmatrix}{\boldsymbol {U}}^{1}&{\boldsymbol {U}}^{2}&\cdots &{\boldsymbol {U}}^{n_{snp}}\end{bmatrix}}={\begin{bmatrix}{\boldsymbol {U}}_{1}^{1}&{\boldsymbol {U}}_{1}^{2}&\cdots &{\boldsymbol {U}}_{1}^{n_{snp}}\\{\boldsymbol {U}}_{2}^{1}&{\boldsymbol {U}}_{2}^{2}&\cdots &{\boldsymbol {U}}_{2}^{n_{snp}}\\\vdots &\vdots &\vdots &\vdots \\{\boldsymbol {U}}_{n}^{1}&{\boldsymbol {U}}_{n}^{2}&\cdots &{\boldsymbol {U}}_{n}^{n_{snp}}\\\end{bmatrix}}\in \mathbb {R} ^{n\cdot d\times n_{snp}}$

(3.3)

will correspondingly be termed the (displacement fluctuations) snapshot matrix.

Remark 1: The first error incurred in solving the cell equilibrium equations using the reduced basis approach arises in approximating ${\textstyle {\mathcal {V}}_{u}^{\epsilon }}$ by this space of snapshots ${\textstyle {\mathcal {V}}_{u}^{snp}}$. In order to keep this error to a minimum, one should strive to select the set of strain histories in such a way that the span of the corresponding displacement fluctuation solutions cover as much as possible the space ${\textstyle {\mathcal {V}}_{u}^{\epsilon }}$ (or at least, the region or regions of particular interest), while, at the same time, trying to keep the total number of snapshots in check –-the computational cost of the subsequent dimensionality reduction process grows considerably with the size of the snapshot matrix. In this respect, it may be interesting to note that this task of sampling the input parameter space (also known as “training”¹) is somehow akin to the experimental process whereby material parameters of standard phenomenological models are calibrated in a laboratory. In this analogy, the RVE plays the role of the corresponding experimental specimen, whereas the macro-strain training trajectories represent the loading paths of the pertinent calibration tests. As opposed to the situation encountered in standard laboratory experiments, however, in the training process, one has “privileged” information regarding the phenomenological behavior of the constituents. Hindsight and elementary physical considerations can therefore aid in restricting the number of strain histories (and hence of snapshots) necessary to characterize the response. For instance, if the behavior of the materials that compose the cell is governed by rate-independent constitutive models, we know beforehand that it is not necessary to study the response under varying rates of deformation. Strategies for efficiently sampling the input parameter space in general model reduction contexts can be found in Refs. [58,59,60,61].

(¹) The term “training”, which, incidentally, is borrowed from the neural network literature [57], is used throughout the text to refer to the offline generation of snapshots.

3.1.2 Dimensionality reduction

The next and definitive step in the transition from the high-dimensional finite element space ${\textstyle {\mathcal {V}}_{u}^{h}}$ to the desired reduced-order space ${\textstyle {\mathcal {V}}_{u}^{*}}$ –-in which the cell BVP is to be finally posed–- is the dimensionality reduction process, in which, as pointed out in the introductory Chapter, the dominant deformational patterns of the cell response are identified and unveiled by washing out the “inessentials”.

3.1.2.1 Proper Orthogonal Decomposition

To accomplish this central task, we employ here the Proper Orthogonal Decomposition (POD). The formal statement of the POD problem goes as follows: given the ensemble of snapshots ${\textstyle \{{\boldsymbol {u}}^{1},{\boldsymbol {u}}^{2},\ldots {\boldsymbol {u}}^{n_{snp}}\}}$, find a set of ${\textstyle n_{u}<n_{snp}}$ orthogonal basis functions ${\textstyle \{{\boldsymbol {\mathit {\Phi }}}_{1},{\boldsymbol {\mathit {\Phi }}}_{2},\ldots {\boldsymbol {\mathit {\Phi }}}_{n_{u}}\}}$ (${\textstyle {\boldsymbol {\mathit {\Phi }}}_{i}\in {\mathcal {V}}_{u}^{snp}}$) such that the error defined as

${e}_{u}(n_{u}){\mathrel {\mathop {:}}}={\sqrt {\displaystyle \sum _{k=1}^{n_{snp}}\Vert {\boldsymbol {u}}^{k}-\mathbf {P} ^{*}{\boldsymbol {u}}^{k}\Vert _{L_{2}(\Omega )}^{2}}}$

(3.4)

is minimized. Here, ${\textstyle \mathbf {P} ^{*}{\boldsymbol {u}}^{k}}$ represents the projection of ${\textstyle {\boldsymbol {u}}^{k}}$ onto the subspace spanned by the basis functions ${\textstyle \{{\boldsymbol {\mathit {\Phi }}}_{i}\}_{i=1}^{n_{u}}}$, and ${\textstyle \Vert \cdot \Vert _{L_{2}(\Omega )}}$ symbolizes the ${\textstyle L_{2}}$ norm. It is shown in Ref. [62] that the solution of this optimization problem can be obtained by first solving the following eigenvalue problem:

${\boldsymbol {L}}{v}=\lambda {v},\;\;\;\Vert {v}\Vert =1,$

(3.5)

where ${\textstyle {\boldsymbol {L}}\in \mathbb {R} ^{n_{snp}\times n_{snp}}}$ is a symmetric matrix defined as:

${\boldsymbol {L}}_{ij}{\mathrel {\mathop {:}}}=\left\langle {{\boldsymbol {u}}^{i}},{{\boldsymbol {u}}^{j}}\right\rangle _{L_{2}(\Omega )}=\displaystyle \int _{\Omega }{\boldsymbol {u}}^{i}{\boldsymbol {u}}^{j}\,d\Omega ,$

(3.6)

i.e., ${\textstyle {\boldsymbol {L}}_{ij}}$ is the ${\textstyle L_{2}}$ inner product between snapshots ${\textstyle {\boldsymbol {u}}^{i}}$ and ${\textstyle {\boldsymbol {u}}^{j}}$. In statistical terms, ${\textstyle {\boldsymbol {L}}}$ can be interpreted as a covariance matrix: the off-diagonal entries captures the degree of linear correlation or redundancy between pair of snapshots (the covariance), whereas the diagonal terms are the variances [63]. The goal in diagonalizing ${\textstyle {\boldsymbol {L}}_{ij}}$ by solving the eigenvalue problem (3.5) is to re-express the snapshots data in axes that filter out the redundancies and reveals the actual dominant displacement fluctuation patterns.

Since ${\textstyle {\boldsymbol {u}}^{i}(\mathbf {x} )=\sum _{I=1}^{n}N_{I}(\mathbf {x} ){\boldsymbol {U}}_{I}^{i}}$, expression (3.6) for the covariance matrix can be rewritten in terms of the snapshot matrix as follows:

${\boldsymbol {L}}_{ij}=\displaystyle \sum _{I=1}^{n}\sum _{J=1}^{n}{\boldsymbol {U}}_{I}^{i}{\boldsymbol {U}}_{J}^{j}\int _{\Omega }N_{I}(\mathbf {x} )N_{J}(\mathbf {x} )\,d\Omega ,$

(3.7)

or in matrix form:

${\boldsymbol {L}}={\boldsymbol {X}}_{u}^{T}\mathbf {M} {\boldsymbol {X}}_{u},$

(3.8)

where

$\mathbf {M} _{IJ}{\mathrel {\mathop {:}}}=\displaystyle \int _{\Omega }N_{I}(\mathbf {x} )N_{J}(\mathbf {x} )\,d\Omega \;\;\;\;\;\;\;I,J=1,2\ldots n.$

(3.9)

Note that, except for the density factor, this matrix ${\textstyle \mathbf {M} }$ is similar to the “mass matrix” appearing in finite element implementations of dynamical problems.

Once the eigenvalues problem (3.5) has been solved, the desired reduced basis ${\textstyle \{{\boldsymbol {\mathit {\Phi }}}_{1},{\boldsymbol {\mathit {\Phi }}}_{2},\ldots {\boldsymbol {\mathit {\Phi }}}_{n_{u}}\}}$ is calculated from the ${\textstyle n_{u}}$ largest eigenvalues ${\textstyle \lambda _{1}\geq \lambda _{2}\geq \ldots \lambda _{n_{u}-1}\geq \lambda _{n_{u}}>0}$ and associated eigenvectors through the following expression:

${\boldsymbol {\mathit {\Phi }}}_{i}(\mathbf {x} )=\displaystyle \sum _{k=1}^{n_{snp}}{\boldsymbol {u}}^{k}(\mathbf {x} ){\dfrac {{v}_{i}}{\sqrt {\lambda _{i}}}},\;\;\;i=1,2\ldots n_{u},$

(3.10)

(modes are judged to be essential or dominant, and hence worthy of being included in the reduced basis set, if their associated eigenvalues have relatively large magnitudes). Substitution of ${\textstyle {\boldsymbol {u}}^{k}(\mathbf {x} )=\sum _{I=1}^{n}N_{I}(\mathbf {x} ){\boldsymbol {U}}_{I}^{k}}$ into the above equation yields:

${\boldsymbol {\mathit {\Phi }}}_{i}(\mathbf {x} )=\displaystyle \sum _{I=1}^{n}N_{I}(\mathbf {x} )\sum _{k=1}^{n_{snp}}{\boldsymbol {U}}_{I}^{k}{\dfrac {{v}_{i}}{\sqrt {\lambda _{i}}}}=\sum _{I=1}^{n}N_{I}(\mathbf {x} ){\boldsymbol {\Phi }}_{Ii},\;\;\;i=1,2\ldots n_{u},$

(3.11)

where¹ ${\textstyle {\boldsymbol {\Phi }}_{Ii}\in \mathbb {R} ^{d}}$ is given by

${\boldsymbol {\Phi }}_{Ii}=\sum _{k=1}^{n_{snp}}{\boldsymbol {U}}_{I}^{k}{\dfrac {{v}_{i}}{\sqrt {\lambda _{i}}}}\;\;\;I=1,2\ldots n,\;i=1,2\ldots n_{u},$

(3.12)

and stands for the value of the basis function ${\textstyle {\boldsymbol {\mathit {\Phi }}}_{i}(\mathbf {x} )}$ at the ${\textstyle I-th}$ node of the finite element grid. The matrix ${\textstyle {\boldsymbol {\Phi }}\in \mathbb {R} ^{n\cdot d\times n_{u}}}$ defined by the above equation will be hereafter called the reduced basis matrix. Each column ${\textstyle {\boldsymbol {\Phi }}_{i}\in \mathbb {R} ^{n\cdot d}}$ (${\textstyle i=1,2\ldots n_{u}}$) of this matrix can be compactly expressed in terms of the snapshot matrix as follows:

${\boldsymbol {\Phi }}_{i}={\boldsymbol {X}}_{u}{\dfrac {{v}_{i}}{\sqrt {\lambda _{i}}}},\;\;\;\;i=1,2\ldots n_{u}.$

(3.13)

3.1.2.2 Singular value decomposition

Instead of solving the eigenvalue problem (3.5), and then obtaining the reduced basis matrix ${\textstyle {\boldsymbol {\Phi }}}$ from expression (3.12), one can alternatively compute this basis matrix using the Singular Value Decomposition. Indeed, let ${\textstyle \mathbf {M} ={\bar {\mathbf {M} }}^{T}{\bar {\mathbf {M} }}}$ be the Cholesky decomposition of ${\textstyle \mathbf {M} }$, and let ${\textstyle {\boldsymbol {\bar {X}}}_{u}}$ denote the matrix defined as:

${\boldsymbol {\bar {X}}}_{u}{\mathrel {\mathop {:}}}={\bar {\mathbf {M} }}{\boldsymbol {X}}_{u}.$

(3.14)

It can be shown (see Appendix A) that the ${\textstyle i-th}$ column of the reduced basis matrix ${\textstyle {\boldsymbol {\Phi }}}$ is related to the ${\textstyle i-th}$ left singular vector of ${\textstyle {\boldsymbol {\bar {X}}}_{u}}$, denoted by ${\textstyle {\boldsymbol {\bar {U}}}_{i}}$, through expression

${\boldsymbol {\Phi }}_{i}={\bar {\mathbf {M} }}^{-1}{\boldsymbol {\bar {U}}}_{i},\;\;\;\;i=1,2\ldots n_{u}.$

(3.15)

3.1.2.3 Elastic/Inelastic reduced basis functions

The POD can be viewed as a multidimensional data fitting procedure intended to obtain a sequence of orthogonal basis functions whose span best approximate the space of snapshots. As such, the POD is a purely data-driven process, “agnostic” to the physical origin of the data [64,63]. For instance, for POD basis construction purposes, it is completely immaterial whether a given snapshot corresponds to a purely linear elastic solution or to a solution well into the inelastic regime. The task of discriminating which features of the cell response are essential and which are not is exclusively guided by statistical considerations: if the elastic response happens to be poorly represented within the snapshot ensemble, the POD may regard as unimportant the contribution of these snapshots, and, as a consequence, the basis functions with largest associated eigenvalues –-i.e., the essential modes–- would hardly contain any information of this range. To accurately replicate the apparently trivial linear elastic behavior, thus, one may be forced to take a relatively large number of basis functions, and this may translate into a significant increase in the overall online computational cost. This fact certainly places the POD-based reduced basis approach at a competitive disadvantage compared with semi-analytical homogenization approaches such as the Nonlinear Transformation Field Analysis [20], which do capture exactly (and effortlessly) the linear elastic response of the cell.

To eliminate this shortcoming, we propose here a slightly different strategy for constructing the reduced basis. The essence of the proposal is to partition the space of snapshots ${\textstyle {\mathcal {V}}_{u}^{snp}}$ into elastic (${\textstyle {\mathcal {V}}_{u,el}^{snp}}$) and inelastic (${\textstyle {\mathcal {V}}_{u,inel}^{snp}}$) subspaces:

${\mathcal {V}}_{u}^{snp}={\mathcal {V}}_{u,el}^{snp}\oplus {\mathcal {V}}_{u,inel}^{snp},$

(3.16)

(${\textstyle \oplus }$ symbolizes direct sum of subspaces [65]) and then obtain the reduced basis as the union of the bases for both subspaces. Below, we describe this strategy more in detail.

The first step is to determine an orthogonal basis for ${\textstyle {\mathcal {V}}_{u,el}^{snp}}$. One can do this by simply performing ${\textstyle m_{e}}$ independent, linear elastic finite element analysis of the cell (${\textstyle m_{e}=6}$ for 3D problems, and ${\textstyle m_{e}=3}$ for plane strain), and then orthonormalizing the resulting displacement fluctuation fields. These ${\textstyle m_{e}}$ elastic modes will be considered as the first ${\textstyle m_{e}}$ basis functions of the reduced basis:

${\textrm {span}}\!\left\lbrace {\boldsymbol {\mathit {\Phi }}}_{1},{\boldsymbol {\mathit {\Phi }}}_{2},\ldots ,{\boldsymbol {\mathit {\Phi }}}_{m_{e}}\right\rbrace ={\mathcal {V}}_{u,el}^{snp}.$

(3.17)

Once we have at our disposal this set of elastic basis functions, we compute the (orthogonal) projection of each snapshot ${\textstyle {\boldsymbol {u}}^{k}}$ onto the orthogonal complement of ${\textstyle {\mathcal {V}}_{u,el}^{snp}}$ (which is precisely the aforementioned inelastic space ${\textstyle {\mathcal {V}}_{u,inel}^{snp}}$):

${\boldsymbol {u}}_{inel}^{k}{\mathrel {\mathop {:}}}={\boldsymbol {u}}^{k}-\displaystyle \sum _{i=1}^{m_{e}}\left\langle {{\boldsymbol {\mathit {\Phi }}}_{i}},{{\boldsymbol {u}}^{k}}\right\rangle _{L_{2}(\Omega )}{\boldsymbol {\mathit {\Phi }}}_{i},\;\;\;\;k=1,2\ldots n_{snp}.$

(3.18)

It is now on this ensemble of inelastic snapshots ${\textstyle \{{\boldsymbol {u}}_{inel}^{k}\}_{k=1}^{n_{snp}}}$ that the previously described POD is applied to obtain the remaining ${\textstyle n_{u}-m_{e}}$ basis functions. Thus, we finally have:

${\mathcal {V}}_{u}^{*}={\mathcal {V}}_{u,el}^{snp}\oplus {\mathcal {V}}_{u,inel}^{snp}={\textrm {span}}\{\overbrace {{\boldsymbol {\mathit {\Phi }}}_{1},{\boldsymbol {\mathit {\Phi }}}_{2},\ldots ,{\boldsymbol {\mathit {\Phi }}}_{6}} ^{\textrm {Elasticmodes}},\overbrace {{\boldsymbol {\mathit {\Phi }}}_{7},\ldots ,{\boldsymbol {\mathit {\Phi }}}_{n_{u}}} ^{\textrm {'Essential'Inelasticmodes}}\}.$

(3.19)

for 3D problems, and

${\mathcal {V}}_{u}^{*}={\textrm {span}}\{\overbrace {{\boldsymbol {\mathit {\Phi }}}_{1},{\boldsymbol {\mathit {\Phi }}}_{2},{\boldsymbol {\mathit {\Phi }}}_{3}} ^{\textrm {Elasticmodes}},\overbrace {{\boldsymbol {\mathit {\Phi }}}_{4},\ldots ,{\boldsymbol {\mathit {\Phi }}}_{n_{u}}} ^{\textrm {'Essential'inelasticmodes}}\}.$

(3.20)

for plane strain.

Observation 2: In placing the ${\textstyle m_{e}}$ elastic modes within the first ${\textstyle m_{e}}$ positions, the reduced-order model is guaranteed to deliver linear elastic solutions with the same accuracy as the underlying (full-order) finite element model (obviously, provided that ${\textstyle n_{u}\geq m_{e}}$).

Further details concerning the numerical implementation of this apparently novel –-to the best of the authors' knowledge–- basis construction strategy can be found in Appendix B.

(¹) It is necessary at this point to further clarify the notation employed for referring to the basis functions. A bold italic “phi” symbol with one subscript is employed to denote the basis function itself, i.e., ${\boldsymbol {\mathit {\Phi }}}_{i}:\Omega \rightarrow \mathbb {R} ^{d}$ ($i=1,2\ldots n_{u}$). Bold normal “phi” symbols, on the other hand, are employed to represent values of such basis functions at the nodes of the underlying finite element mesh. For instance, the value of the $i-th$ basis functions at the $I-th$ node is symbolized as ${\boldsymbol {\Phi }}_{Ii}={\boldsymbol {\mathit {\Phi }}}_{i}(\mathbf {x} _{I})\in \mathbb {R} ^{d}$. When accompanied by only one (lowercase) subscript, the bold normal “phi” symbol denotes a column vector containing the nodal values of the pertinent basis functions at all gauss points: ${\boldsymbol {\Phi }}_{i}={{\begin{bmatrix}{\boldsymbol {\Phi }}_{1i}^{T}&{\boldsymbol {\Phi }}_{2i}^{T}&\ldots &{\boldsymbol {\Phi }}_{ni}\end{bmatrix}}^{T}}\in \mathbb {R} ^{n\cdot d}$ ($i=1,2\ldots n_{u}$). Lastly, when no subscript is attached, ${\boldsymbol {\Phi }}$ represents the reduced basis matrix: ${\boldsymbol {\Phi }}={\begin{bmatrix}{\boldsymbol {\Phi }}_{1}&{\boldsymbol {\Phi }}_{2}&\cdots &{\boldsymbol {\Phi }}_{n_{u}}\end{bmatrix}}\in \mathbb {R} ^{n\cdot d\times n_{u}}$.

3.2 Galerkin projection onto the reduced subspace

We now seek to pose the boundary-value problem represented by Eq.(2.13) in the reduced-order space ${\textstyle {\mathcal {V}}_{u}^{*}\subseteq {\mathcal {V}}_{u}^{h}}$ spanned by the basis functions ${\textstyle \{{\boldsymbol {\mathit {\Phi }}}_{1},{\boldsymbol {\mathit {\Phi }}}_{2},\ldots ,{\boldsymbol {\mathit {\Phi }}}_{n_{u}}\}}$. To this end, we approximate both test ${\textstyle {\boldsymbol {\eta }}\in {\mathcal {V}}_{u}}$ and trial ${\textstyle {\boldsymbol {u}}\in {\mathcal {V}}_{u}}$ functions by the following linear expansions:

${\boldsymbol {u}}(\mathbf {x} ;{\boldsymbol {\epsilon _{M}}})\approx {\boldsymbol {u}}^{*}(\mathbf {x} ;{\boldsymbol {\epsilon _{M}}})=\displaystyle \sum _{i=1}^{n_{u}}{\boldsymbol {\mathit {\Phi }}}_{i}(\mathbf {x} )U_{i}^{*}({\boldsymbol {\epsilon _{M}}}),$

(3.21)

${\boldsymbol {\eta }}(\mathbf {x} )\approx {\boldsymbol {\eta }}^{*}(\mathbf {x} )=\displaystyle \sum _{i=1}^{n_{u}}{\boldsymbol {\mathit {\Phi }}}_{i}(\mathbf {x} ){\eta }_{i}^{*},$

(3.22)

${\textstyle {\boldsymbol {u}}^{*}(\mathbf {x} )}$ and ${\textstyle {\boldsymbol {\eta }}^{*}(\mathbf {x} )}$ being the low-dimensional approximations of trial and test functions, respectively (hereafter, asterisked symbols will be used to denote low-dimensional approximations of the associated variables). Inserting Eqs. (3.21) and (3.22) into Eq.(2.13), and exploiting the arbitrariness of coefficients ${\textstyle {\eta }_{i}^{*}}$ (${\textstyle i=1,2\ldots n_{u}}$), we arrive at the following set of ${\textstyle n_{u}}$ equilibrium equations:

$\displaystyle \int _{\Omega }\nabla ^{s}{{\boldsymbol {\mathit {\Phi }}}_{i}(\mathbf {x} )}:{\boldsymbol {\sigma }}(\mathbf {x} ;{\boldsymbol {\epsilon _{M}}}+\nabla ^{s}{{\boldsymbol {u}}^{*}},{\boldsymbol {\xi }})\,d\Omega =0,\;\;\;i=1,2\ldots n_{u}.$

(3.23)

Expressing now the reduced basis functions in the above equation in terms of finite element shape functions (through expression ${\textstyle {\boldsymbol {\mathit {\Phi }}}_{i}(\mathbf {x} )=\sum _{I=1}^{n}N_{I}(\mathbf {x} ){\boldsymbol {\Phi }}_{Ii}}$), we get (in Voigt's notation):

$\displaystyle \int _{\Omega }{{\boldsymbol {B}}_{i}^{*}}^{T}\!\!(\mathbf {x} )\,{\boldsymbol {\sigma }}(\mathbf {x} ;{\boldsymbol {\epsilon _{M}}}+{{\boldsymbol {B}}^{*}}{\boldsymbol {U}}^{*},{\boldsymbol {\xi }})\,d\Omega ={\boldsymbol {0}},\;\;\;i=1,2\ldots n_{u},$

(3.24)

or more compactly:

$\displaystyle \int _{\Omega }{{\boldsymbol {B}}^{*}}^{T}\!\!(\mathbf {x} )\,{\boldsymbol {\sigma }}(\mathbf {x} ;{\boldsymbol {\epsilon _{M}}}+{{\boldsymbol {B}}^{*}}{\boldsymbol {U}}^{*},{\boldsymbol {\xi }})\,d\Omega ={\boldsymbol {0}}.$

(3.25)

Here, ${\textstyle {\boldsymbol {U}}^{*}\in \mathbb {R} ^{n_{u}}}$ denotes the vector containing the reduced displacement fluctuations ${\textstyle U_{i}^{*}\in \mathbb {R} ^{}}$ ${\textstyle (i=1,2\ldots n_{u})}$ –-the basic unknowns of the reduced-order problem:

${\boldsymbol {U}}^{*}{\mathrel {\mathop {:}}}={\begin{bmatrix}U_{1}^{*}\\U_{2}^{*}\\\vdots \\U_{n_{u}}^{*}\end{bmatrix}}$

(3.26)

and ${\textstyle {{\boldsymbol {B}}^{*}}:\Omega \rightarrow \mathbb {R} ^{s\times n_{u}}}$ stands for the reduced “B-matrix”, defined as:

${{\boldsymbol {B}}^{*}}(\mathbf {x} ){\mathrel {\mathop {:}}}={\boldsymbol {B}}(\mathbf {x} ){\boldsymbol {\Phi }},$

(3.27)

and that connects the gradient of the displacement fluctuation field with the vector of reduced displacement fluctuations, i.e.:

$\nabla ^{s}{{\boldsymbol {u}}^{*}}=\displaystyle \sum _{i=1}^{n_{u}}{{\boldsymbol {B}}_{i}^{*}\!}U_{i}^{*}=\overbrace {\begin{bmatrix}{{\boldsymbol {B}}_{1}^{*}\!}&{{\boldsymbol {B}}_{2}^{*}\!}&\ldots &{{\boldsymbol {B}}_{n_{u}}^{*}\!}\end{bmatrix}} ^{{\boldsymbol {B}}^{*}}\overbrace {\begin{bmatrix}U_{1}^{*}\\U_{2}^{*}\\\vdots \\U_{n_{u}}^{*}\end{bmatrix}} ^{{\boldsymbol {U}}^{*}}$ $={{\boldsymbol {B}}^{*}}{\boldsymbol {U}}^{*}={\boldsymbol {B}}{\boldsymbol {\Phi }}{\boldsymbol {U}}^{*}.$

(3.28)

For implementational purposes, it is more expedient to express Eq.(3.27) in terms of elemental ${\textstyle B-}$matrices. To this end, we write:

${\boldsymbol {B}}(\mathbf {x} )=\left\lbrace {\begin{array}{l}{\boldsymbol {B}}^{e}(\mathbf {x} ),\;\;\;\;{\textrm {if}}\,\mathbf {x} \in \Omega ^{e}\\{\boldsymbol {0}},\;\;\;\;\;\;\;{\textrm {otherwise}}\\\end{array}}\right.$

(3.29)

where ${\textstyle {\boldsymbol {B}}^{e}\in \mathbb {R} ^{s\times d\cdot {\bar {n}}_{e}}}$ denotes the local ${\textstyle B}$-matrix of element ${\textstyle \Omega ^{e}}$ (${\textstyle {\bar {n}}_{e}}$, in turn, is the number of nodes in ${\textstyle \Omega ^{e}}$). Thus,

${{\boldsymbol {B}}^{*}}(\mathbf {x} )={\boldsymbol {B}}(\mathbf {x} ){\boldsymbol {\Phi }}={\boldsymbol {B}}^{e}(\mathbf {x} ){\boldsymbol {\Phi }}^{e}.$

(3.30)

In the above equation, ${\textstyle {\boldsymbol {\Phi }}^{e}\in \mathbb {R} ^{d{\bar {n}}_{e}\times n_{u}}}$ represents the block matrix of ${\textstyle {\boldsymbol {\Phi }}}$ corresponding to the ${\textstyle {\bar {n}}_{e}}$ nodes of finite element ${\textstyle \Omega ^{e}}$ (${\textstyle e=1,2\ldots n_{e}}$).

4 Numerical integration

4.1 Classical Gauss quadrature: the standard ROM

A straightforward –-but, as already mentioned, ostensibly inefficient–- route for numerically evaluating the integral appearing in the reduced-order equilibrium equation (3.24) is to simply use the same Gauss quadrature formulae and the same set of Gauss points as the underlying finite element model (see Eq.(2.24)):

$\displaystyle \int _{\Omega }{{\boldsymbol {B}}^{*}}^{T}{\boldsymbol {\sigma }}\,d\Omega \approx \displaystyle \sum _{g=1}^{n_{g}}w_{g}{{{\boldsymbol {B}}^{*}}^{T}}\!\!(\mathbf {x} _{g}){\boldsymbol {\sigma }}(\mathbf {x} _{g};\cdot )={\boldsymbol {0}}.$

(4.1)

Low-rank approximations that employ the underlying finite element Gauss points for numerically evaluating integrals in the weak statement of the problem are commonly known as standard reduced-order models [66].

4.2 Efficient numerical integration: the High-Performance ROM (HP-ROM)

4.2.1 Overview

As outlined in the introductory Chapter, approaches found in the model reduction literature that, directly or indirectly, deal with the still underexplored question of how to efficiently –-at an online computational cost independent of the dimension ${\textstyle n}$ of the underlying finite element model–- integrate reduced-order equations can be broadly classified either as interpolatory approaches [28,29,30,31,32] or Gauss-type quadrature methods [33,34]. The integration strategy proposed in the present work falls into the former category of interpolatory approaches. Recall that the basic idea in such approaches is to replace the nonaffine term in the BVP by a low-dimensional approximation. In our case, a glance at the reduced-order equilibrium equation (3.24) reveals that such “offending”, nonaffine term is the stress field –-the reduced ${\textstyle B}$-matrix ${\textstyle {{\boldsymbol {B}}^{*}}={{\boldsymbol {B}}^{*}}(\mathbf {x} )}$ is independent of the input parameter ${\textstyle {\boldsymbol {\epsilon _{M}}}}$ and hence need not be subject to approximation. The proposed integration scheme, thus, is predicated on the assumption that, not only the displacement fluctuations, but also the stress field over the cell admits an accurate, low-dimensional approximation. Numerical experiments confirm (see Chapter 5) that, luckily, this premise generally holds whenever the displacement fluctuations field itself lives in a low-dimensional space.

Let ${\textstyle {\boldsymbol {\mathit {\Psi }}}_{i}(\mathbf {x} )\in L_{2}(\Omega )^{s}}$ (${\textstyle i=1,2\ldots n_{\sigma }}$) denote a set of ${\textstyle n_{\sigma }={\mathcal {O}}(n_{u})}$ orthogonal basis functions for such low-dimensional, stress approximation space. Then, the reduced-order approximation of the stress field may be written as:

${\boldsymbol {\sigma }}(\mathbf {x} ;{\boldsymbol {\epsilon _{M}}}+\nabla ^{s}{{\boldsymbol {u}}^{*}},{\boldsymbol {\xi }}_{})\approx {\boldsymbol {\sigma }}^{*}(\mathbf {x} ;{\boldsymbol {\epsilon _{M}}}+\nabla ^{s}{{\boldsymbol {u}}^{*}},{\boldsymbol {\xi }}_{})=\displaystyle \sum _{i=1}^{n_{\sigma }}{\boldsymbol {\mathit {\Psi }}}_{i}(\mathbf {x} )c_{i}({\boldsymbol {\epsilon _{M}}}+\nabla ^{s}{{\boldsymbol {u}}^{*}},{\boldsymbol {\xi }}_{})$

(4.2)

(notice that, in keeping with the notational convention introduced in Section 3.2, the low-dimensional approximation of the stress field is represented by attaching an asterisk to the stress symbol). In the spirit of classical polynomial quadrature (such as Newton-Cotes formulae [35]), coefficients ${\textstyle c_{i}\in \mathbb {R} ^{}}$ (${\textstyle i=1,2\ldots p}$) in Eq.(4.2) are calculated by fitting this linear expansion to the stress values computed at a set of ${\textstyle p={\mathcal {O}}(n_{u})\geq n_{\sigma }}$ pre-specified sampling points:

${\mathcal {X}}=\{\mathbf {x} _{1}^{s},\mathbf {x} _{2}^{s},\ldots \mathbf {x} _{p}^{s}\},\;\;\;\;\mathbf {x} _{i}^{s}\in \Omega .$

(4.3)

Approximation (4.2) becomes therefore expressible as:

${\boldsymbol {\sigma }}^{*}(\mathbf {x} ;{\boldsymbol {\epsilon _{M}}}+\nabla ^{s}{{\boldsymbol {u}}^{*}},{\boldsymbol {\xi }}_{})=\displaystyle \sum _{i=1}^{p}{\boldsymbol {\mathcal {R}}}_{i}(\mathbf {x} ){\boldsymbol {\sigma }}(\mathbf {x} _{i}^{s};{\boldsymbol {\epsilon _{M}}}+\nabla ^{s}{{\boldsymbol {u}}^{*}},{\boldsymbol {\xi }}_{}),$

(4.4)

where ${\textstyle {\boldsymbol {\mathcal {R}}}_{i}(\mathbf {x} )}$ (${\textstyle i=1,2\ldots p}$) stands for the interpolation or, more generally, reconstruction operator¹ at sampling point ${\textstyle \mathbf {x} _{i}^{s}}$, whereas

${\boldsymbol {\sigma }}(\mathbf {x} _{i}^{s};{\boldsymbol {\epsilon _{M}}}+\nabla ^{s}{{\boldsymbol {u}}^{*}},{\boldsymbol {\xi }}_{})={\mathcal {F}}(\mathbf {x} _{i}^{s};{\boldsymbol {\epsilon _{M}}}+{{\boldsymbol {B}}^{*}}(\mathbf {x} _{i}^{s}){\boldsymbol {U}}^{*},{\boldsymbol {\xi }}_{}(\mathbf {x} _{i}^{s}))$

(4.5)

represents the stress vector evaluated at sampling point ${\textstyle \mathbf {x} _{i}^{s}}$ through the pertinent constitutive relation ${\textstyle {\mathcal {F}}(\mathbf {x} _{i}^{s};\cdot )}$.

Substitution of the above approximation into equation Eq.(3.25) leads to:

$\displaystyle \int _{\Omega }{{\boldsymbol {B}}^{*}}^{T}\!\!(\mathbf {x} )\,{\boldsymbol {\sigma }}(\mathbf {x} ;{\boldsymbol {\epsilon _{M}}}+\nabla ^{s}{{\boldsymbol {u}}^{*}},{\boldsymbol {\xi }}_{})\,d\Omega$ $\approx \displaystyle \sum _{i=1}^{p}\overbrace {\left(\int _{\Omega }{{\boldsymbol {B}}^{*}}^{T}\!\!(\mathbf {x} ){\boldsymbol {\mathcal {R}}}_{i}(\mathbf {x} )\,d\Omega \right)} ^{{\boldsymbol {Q}}_{i}^{T}}{\boldsymbol {\sigma }}(\mathbf {x} _{i}^{s};{\boldsymbol {\epsilon _{M}}}+\nabla ^{s}{{\boldsymbol {u}}^{*}},{\boldsymbol {\xi }}_{})={\boldsymbol {0}}.$

(4.6)

The bracketed integral (denoted by ${\textstyle {\boldsymbol {Q}}_{i}^{T}\in \mathbb {R} ^{n_{u}\times p}}$) in the above equation is independent of the input parameter –-the macroscopic strain ${\textstyle {\boldsymbol {\epsilon _{M}}}}$–-, and, hence, it can be entirely pre-computed offline, using, for instance, the full set of finite element Gauss points:

${\boldsymbol {Q}}_{i}^{T}{\mathrel {\mathop {:}}}=\int _{\Omega }{{\boldsymbol {B}}^{*}}^{T}\!\!(\mathbf {x} ){\boldsymbol {\mathcal {R}}}_{i}(\mathbf {x} )\,d\Omega \approx \displaystyle \sum _{g=1}^{n_{g}}w_{g}{{\boldsymbol {B}}^{*}}^{T}\!\!(\mathbf {x} _{g}){\boldsymbol {\mathcal {R}}}_{i}(\mathbf {x} _{g}),\;\;\;\;i=1,2\ldots p.$

(4.7)

Introducing the above definition into Eq.(4.6) finally yields the quadrature formula for the reduced equilibrium equation:

$\displaystyle \int _{\Omega }{{\boldsymbol {B}}^{*}}^{T}\!\!(\mathbf {x} )\,{\boldsymbol {\sigma }}(\mathbf {x} ;{\boldsymbol {\epsilon _{M}}}+\nabla ^{s}{{\boldsymbol {u}}^{*}},{\boldsymbol {\xi }}_{})\,d\Omega \approx \sum _{i=1}^{p}{\boldsymbol {Q}}_{i}^{T}\,{\boldsymbol {\sigma }}(\mathbf {x} _{i}^{s};{\boldsymbol {\epsilon _{M}}}+\nabla ^{s}{{\boldsymbol {u}}^{*}},{\boldsymbol {\xi }}_{})={\boldsymbol {0}}.$

(4.8)

It is noteworthy that this quadrature formula requires evaluation of stresses at only ${\textstyle p={\mathcal {O}}(n_{u})}$ sampling points within the cell domain (in contrast to the standard ROM (4.1), that needs ${\textstyle n_{g}={\mathcal {O}}(n)>>n_{u}}$ Gauss points). Furthermore, inserting Eq.(4.4) into Eq.(2.14), we get:

${\boldsymbol {\sigma _{M}}}={\dfrac {1}{V}}\displaystyle \int _{\Omega }\!\!{\boldsymbol {\sigma }}(\mathbf {x} ;{\boldsymbol {\epsilon _{M}}}+\nabla ^{s}{{\boldsymbol {u}}^{*}},{\boldsymbol {\xi }}_{})\,d\Omega$ $\approx \displaystyle \sum _{i=1}^{p}\overbrace {\left({\dfrac {1}{V}}\int _{\Omega }{\boldsymbol {\mathcal {R}}}_{i}(\mathbf {x} )\,d\Omega \right)} ^{{\boldsymbol {T}}_{i}}{\boldsymbol {\sigma }}(\mathbf {x} _{i}^{s};{\boldsymbol {\epsilon _{M}}}+\nabla ^{s}{{\boldsymbol {u}}^{*}},{\boldsymbol {\xi }}_{})$ $=\sum _{i=1}^{p}{\boldsymbol {T}}_{i}\,{\boldsymbol {\sigma }}(\mathbf {x} _{i}^{s};{\boldsymbol {\epsilon _{M}}}+\nabla ^{s}{{\boldsymbol {u}}^{*}},{\boldsymbol {\xi }}_{}),$

(4.9)

where

${\boldsymbol {T}}_{i}{\mathrel {\mathop {:}}}={\dfrac {1}{V}}\int _{\Omega }{\boldsymbol {\mathcal {R}}}_{i}(\mathbf {x} )\,d\Omega \approx {\dfrac {\displaystyle \sum _{g=1}^{n_{g}}w_{g}{\boldsymbol {\mathcal {R}}}_{i}(\mathbf {x} _{g})}{\displaystyle \sum _{g=1}^{n_{g}}w_{g}}},\;\;\;\;i=1,2\ldots p.$

(4.10)

Note that ${\textstyle {\boldsymbol {T}}_{i}}$ (${\textstyle i=1,2\ldots p}$) can also be pre-computed offline.

In summary, in projecting the cell equilibrium equation onto the displacement fluctuations, reduced space, and in additionally adopting the above described integration scheme, one automatically arrives at a reduced-order model in which the operation count –-the complexity–- in both solving the cell equilibrium equation and calculating the macroscopic stress tensor depends exclusively on the dimension $n_{u}$ of the reduced basis. We shall refer to this model as the High-Performance, Reduced-Order Model (HP-ROM), to highlight the tremendous gains in performance that affords this model over the previously described standard ROM, let alone over the full-order, finite model, discussed in Section 2.3–-in the numerical example shown in Chapter 5, we report speedup factors of above three order of magnitudes.

(¹) The term interpolation usually connotes that the fit is exact at the sampling points, and this only occurs when $p=n_{\sigma }$.

4.3 Stress approximation space

Two crucial aspects of the integration scheme sketched in the foregoing remains to be addressed, namely, the determination of the vector space (hereafter denoted by ${\textstyle {\mathcal {V}}_{\sigma }^{apr}}$) in which the low-dimensional approximation of the stress field should lie in order to obtain an accurate and at the same time well-posed HP-ROM; and the calculation of the optimal location of the sampling or integration points at which the stress tensor is to be evaluated. Attention here and in the next Section is confined to the aspect related to the stress approximation space, while the discussion of the issue related to the selection of sampling points is deferred to Section 4.5.

4.3.1 The reduced-order subspace of statically admissible stresses (V_σ^*)

Similarly to the problem addressed in Chapter 3 concerning the reduced basis for the displacement fluctuations, the problem of constructing a ${\textstyle {\mathcal {O}}(n_{u})}$-dimensional representation of the stress field reduces, in principle, to finding a set of orthogonal basis functions ${\textstyle \{{\boldsymbol {\mathit {\Psi }}}_{1}(\mathbf {x} ),{\boldsymbol {\mathit {\Psi }}}_{2}(\mathbf {x} )\ldots {\boldsymbol {\mathit {\Psi }}}_{n_{\sigma }}(\mathbf {x} )\}}$ (${\textstyle n_{\sigma }={\mathcal {O}}(n_{u})}$) such that its span accurately approximates the set of all possible stress solutions –-that is, the set of all statically admissible stresses. Accordingly, the procedure to compute the reduced basis for the stress field would be, mutatis mutandis, formally identical to that explained earlier for the displacement fluctuations. Firstly, finite element, stress distributions over the cell are computed for representative, input macro-strain histories (the most practical and somehow consistent choice regarding these strain trajectories is to use the same as in the computation of the displacement fluctuations snapshots). Then, the elastic/inelastic dimensionality reduction process set forth in Section 3.1.2 is applied to the resulting ensemble of stress solutions ${\textstyle \{{\boldsymbol {\sigma }}^{1}(\mathbf {x} ),{\boldsymbol {\sigma }}^{2}(\mathbf {x} )\ldots {\boldsymbol {\sigma }}^{n_{snp}}(\mathbf {x} )\}}$, in order to identify both the elastic and the essential inelastic stress modes. The space spanned by these modes will be denoted hereafter by ${\textstyle {\mathcal {V}}_{\sigma }^{*}}$ and termed the reduced-order subspace of statically admissible stresses:

${\mathcal {V}}_{\sigma }^{*}={\textrm {span}}\{\overbrace {{\boldsymbol {\mathit {\Psi }}}_{1}(\mathbf {x} ),{\boldsymbol {\mathit {\Psi }}}_{2}(\mathbf {x} ),\ldots ,{\boldsymbol {\mathit {\Psi }}}_{m_{e}}(\mathbf {x} )} ^{\hbox{Elastic stress modes}},\overbrace {{\boldsymbol {\mathit {\Psi }}}_{m_{e}+1}(\mathbf {x} ),{\boldsymbol {\mathit {\Psi }}}_{m_{e}+2}(\mathbf {x} ),\ldots ,{\boldsymbol {\mathit {\Psi }}}_{n_{\sigma }}(\mathbf {x} )} ^{\hbox{'Essential', inelastic stress modes}}\}.$

(4.11)

4.3.2 Ill-posedness of the HP-ROM

At first sight, it appears reasonable to simply construct the low-dimensional approximation ${\textstyle {\boldsymbol {\sigma }}^{*}}$ required in the proposed integration method as a linear combination of the above described stress reduced basis–- hence making ${\textstyle {\mathcal {V}}_{\sigma }^{apr}={\mathcal {V}}_{\sigma }^{*}}$–-; i.e.,

${\boldsymbol {\sigma }}(\mathbf {x} ;{\boldsymbol {\epsilon _{M}}},{\boldsymbol {U}}^{*})\approx {\boldsymbol {\sigma }}^{*}(\mathbf {x} ;{\boldsymbol {\epsilon _{M}}},{\boldsymbol {U}}^{*})=\displaystyle \sum _{i=1}^{n_{\sigma }}{\boldsymbol {\mathit {\Psi }}}_{i}(\mathbf {x} )c_{i}({\boldsymbol {\epsilon _{M}}},{\boldsymbol {U}}^{*}),$

(4.12)

where ${\textstyle c_{i}\in \mathbb {R} ^{}}$ (${\textstyle i=1,2\ldots n_{\sigma }}$). This strategy of approximating the offending, nonaffine term in the BVP by a linear combination of pre-computed basis functions –-obtained, in turn, from samples of the nonaffine term evaluated at the solution–- has been successfully applied by several authors, with no apparent –-or at least not reported–- computational pitfalls, to a wide gamut of problems: nonlinear monotonic elliptic and nonlinear parabolic BPVs [67,29], nonlinear miscible viscous fingering in porous media [68,31], uncertainty quantification in inverse problems [69], and nonlinear heat conduction problems [32,66], to cite but a few.

However, a closer examination of the the cell equilibrium problem reveals that, in this case, this “standard” strategy proves completely fruitless, for it leads to patently ill-posed reduced-order equations. To show this, let us first substitute approximation (4.12) into Eq.(3.24):

$\displaystyle \int _{\Omega }{{\boldsymbol {B}}^{*}}^{T}(\mathbf {x} )\,{\boldsymbol {\sigma }}(\mathbf {x} ;{\boldsymbol {\epsilon _{M}}},{\boldsymbol {U}}^{*})\,d\Omega \approx \displaystyle \int _{\Omega }{{\boldsymbol {B}}^{*}}^{T}(\mathbf {x} )\,{\boldsymbol {\sigma }}^{*}(\mathbf {x} ;{\boldsymbol {\epsilon _{M}}},{\boldsymbol {U}}^{*})=$ $\displaystyle \sum _{i=1}^{n_{\sigma }}\left(\int _{\Omega }{{\boldsymbol {B}}^{*}}^{T}(\mathbf {x} ){\boldsymbol {\mathit {\Psi }}}_{i}(\mathbf {x} )\,d\Omega \right)c_{i}({\boldsymbol {\epsilon _{M}}},{\boldsymbol {U}}^{*})={\boldsymbol {0}}.$

(4.13)

By virtue of Eq.(3.27), the bracketed integral in the preceding equation can be rephrased as:

$\displaystyle \int _{\Omega }{{\boldsymbol {B}}^{*}}^{T}(\mathbf {x} ){\boldsymbol {\mathit {\Psi }}}_{i}(\mathbf {x} )\,d\Omega ={\boldsymbol {\Phi }}^{T}\!\!\left(\int _{\Omega }{\boldsymbol {B}}^{T}(\mathbf {x} ){\boldsymbol {\mathit {\Psi }}}_{i}(\mathbf {x} )\,d\Omega \right),\;\;\;i=1,2\ldots n_{\sigma }.$

(4.14)

Each basis function ${\textstyle {\boldsymbol {\mathit {\Psi }}}_{i}(\mathbf {x} )}$ (${\textstyle i=1,2\ldots n_{\sigma }}$) is, by construction (see Chapter 3), a linear combination of the stress snapshots collected during the offline, finite element analysis; thus, we can write:

${\boldsymbol {\mathit {\Psi }}}_{i}=\displaystyle \sum _{j=1}^{n_{snp}}\beta _{ij}{\boldsymbol {\sigma }}^{j}\;\;\;i=1,2\ldots n_{\sigma },$

(4.15)

${\textstyle \beta _{ij}\in \mathbb {R} ^{}}$ being the corresponding coefficients in the linear combination. Inserting the above equation into Eq.(4.14) and considering that ${\textstyle {\boldsymbol {\sigma }}^{j}}$ (${\textstyle j=1,2\ldots n_{snp}}$) are finite element stress solutions –-and therefore fulfill the finite element equilibrium equation (2.22)–-, we finally arrive at:

${\boldsymbol {\Phi }}^{T}\!\!\left(\int _{\Omega }{\boldsymbol {B}}^{T}(\mathbf {x} ){\boldsymbol {\mathit {\Psi }}}_{i}(\mathbf {x} )\,d\Omega \right)={\boldsymbol {\Phi }}^{T}\!\!\sum _{j=1}^{n_{snp}}\beta _{ij}\overbrace {\left(\int _{\Omega }{\boldsymbol {B}}^{T}{\boldsymbol {\sigma }}^{j}\,d\Omega \right)} ^{=0}={\boldsymbol {0}},\;\;\;i=1,2\ldots n_{\sigma },$

(4.16)

that is, the integral (4.14) appearing in the equilibrium equation (4.13), and hence, the left-hand side of the equation itself, vanishes identically regardless of the value of the modal coefficients ${\textstyle c_{i}\in \mathbb {R} ^{}}$ (${\textstyle i=1,2\ldots n_{\sigma }}$), and therefore, regardless of the value of the reduced displacement fluctuations ${\textstyle {\boldsymbol {U}}^{*}}$–-hence the ill-posedness.

4.3.3 Proposed remedy: the expanded space approach

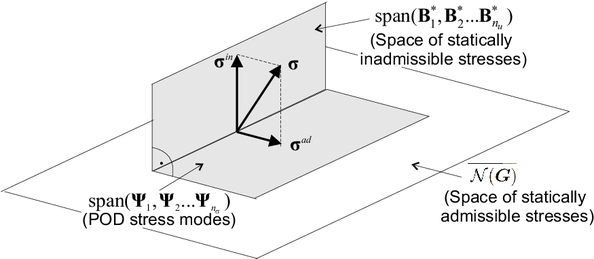
It is clear from the foregoing discussion that the root cause of the ill-posedness lies in the fact that the set of all admissible stress fields (${\textstyle {\mathcal {V}}_{\sigma }}$) forms a vector space, and, consequently, the POD stress modes ${\textstyle {\boldsymbol {\mathit {\Psi }}}_{i}\in {\mathcal {V}}_{\sigma }}$ (${\textstyle i=1,2\ldots n_{\sigma }}$) –-and any linear combination of them–- turn out to be self-equilibrated fields. Thus, for the reduced-order problem to be well-posed, the approximation space ${\textstyle {\mathcal {V}}_{\sigma }^{apr}}$ cannot be only formed by statically admissible stresses, but it must also include statically inadmissible fields –-i.e. stress functions that do not satisfy the reduced-order equilibrium equation (3.24).

One plausible route for determining a low-dimensional approximation space that embraces both statically admissible and statically inadmissible stresses might be to collect, during the offline finite element calculations, not only converged stresses, but also the unconverged ones –-i.e., those generated during the corresponding iterative algorithm–-, and then perform the POD-based dimensionality reduction over the whole ensemble of snapshots¹. In the present work, however, we pursue an approach that precludes the necessity of undertaking this computationally laborious and in some aspects objectionable –-there is no guarantee that the span of selected, unconverged stress snapshots covers the entire space of statically inadmissible stresses–-process. The idea behind the employed approach was originally conceived, but not fully developed, by the authors in a recent report [36]. Here, the theory underlying such an idea is further elaborated and cast into the formalisms of functional analysis.

(¹) Incidentally, this way of proceeding has the flavor of the nonlinear model reduction strategy advocated by Carlberg and co-workers [78,80], in which the reduction is carried over the linearized form of the pertinent governing equation

4.3.3.1 Continuum formulation

To originate our considerations from a general standpoint, it proves convenient first to rephrase the left-hand side of the reduced-order equilibrium equation Eq.(3.24) as the action of a certain linear operator ${\textstyle {\boldsymbol {G}}:L_{2}(\Omega )^{s}\rightarrow \mathbb {R} ^{n_{u}}}$ on the stress field over the cell:

$\displaystyle \int _{\Omega }{{\boldsymbol {B}}_{i}^{*}}^{T}\!\,{\boldsymbol {\sigma }}\,d\Omega =\left\langle {{\boldsymbol {B}}_{i}^{*}\!},{\boldsymbol {\sigma }}\right\rangle _{L_{2}(\Omega )}=({\boldsymbol {G}})_{i}\;\;\;i=1,2\ldots n_{u}.$

(4.17)

Invoking now the orthogonal decomposition of ${\textstyle L_{2}(\Omega )^{s}}$ induced by this operator, one obtains:

$L_{2}(\Omega )^{s}={\mathcal {N}}({\boldsymbol {G}})\oplus {\textrm {span}}\!\left\lbrace {{\boldsymbol {B}}_{i}^{*}\!}\right\rbrace _{i=1}^{n_{u}},$

(4.18)

where ${\textstyle {\mathcal {N}}({\boldsymbol {G}})}$ stands for the nullspace of ${\textstyle {\boldsymbol {G}}}$. Since the cell equilibrium equation has a vanishing right-hand side term, it follows that ${\textstyle {\mathcal {N}}({\boldsymbol {G}})}$ is actually the space of statically admissible stress fields. Its orthogonal complement, ${\textstyle {\textrm {span}}\!\left\lbrace {{\boldsymbol {B}}_{i}^{*}\!}\right\rbrace _{i=1}^{n_{u}}}$, can be therefore construed as the aforementioned space of statically inadmissible stresses. The key fact here is that such a space is inherently $n_{u}$-dimensional and, thus, there is no need to perform any dimensionality reduction whatsoever over unconverged snapshots to arrive at the desired basis: the strain-displacement functions ${\textstyle \{{{\boldsymbol {B}}_{1}^{*}\!},{{\boldsymbol {B}}_{2}^{*}\!}\ldots {{\boldsymbol {B}}_{n_{u}}^{*}\!}\}}$ themselves are linearly independent (albeit not orthogonal) and can thereby serve this very purpose.

According to the preceding decomposition, any ${\textstyle {\boldsymbol {\sigma }}\in L_{2}(\Omega )^{s}}$ can be resolved as (see Figure 2):

${\boldsymbol {\sigma }}={\boldsymbol {\sigma }}^{ad}+{\boldsymbol {\sigma }}^{in},\;\;\;{\textrm {with}}\left\langle {{\boldsymbol {\sigma }}^{ad}},{{\boldsymbol {\sigma }}^{in}}\right\rangle _{L_{2}(\Omega )}=0,$

(4.19)

where ${\textstyle {\boldsymbol {\sigma }}^{ad}\in {\mathcal {N}}({\boldsymbol {G}})}$ and ${\textstyle {\boldsymbol {\sigma }}^{in}\in {\textrm {span}}\!\left\lbrace {{\boldsymbol {B}}_{i}^{*}\!}\right\rbrace _{i=1}^{n_{u}}}$ stand for the statically admissible and statically inadmissible components of ${\textstyle {\boldsymbol {\sigma }}}$, respectively. Following the standard approach, the statically admissible component ${\textstyle {\boldsymbol {\sigma }}^{ad}}$ –-i.e., the stress solution we wish to calculate for a given input ${\textstyle {\boldsymbol {\epsilon _{M}}}}$–- is forced to lie in the span of the POD modes ${\textstyle {\boldsymbol {\mathit {\Psi }}}_{i}}$ (${\textstyle i=1,2\ldots n_{\sigma }}$) obtained from converged snapshots:

${\boldsymbol {\sigma }}^{ad}\approx {\boldsymbol {\sigma }}^{*}=\sum _{i=1}^{n_{\sigma }}{\boldsymbol {\mathit {\Psi }}}_{i}c_{i}^{ad},$

(4.20)

${\textstyle c_{i}^{ad}\in \mathbb {R} ^{}}$ (${\textstyle i=1,2\ldots n_{\sigma }}$) being the corresponding modal coefficients. The non-equilibrated component ${\textstyle {\boldsymbol {\sigma }}^{in}}$, on the other hand, resides naturally in the span of the reduced strain-displacement functions, so we can directly write–-i.e., without introducing further approximations–-:

${\boldsymbol {\sigma }}^{in}=\sum _{i=1}^{n_{u}}{{\boldsymbol {B}}_{i}^{*}\!}c_{i}^{in},$

(4.21)

with ${\textstyle c_{i}^{in}\in \mathbb {R} ^{}}$ (${\textstyle i=1,2\ldots n_{u}}$). The low-dimensional approximation required in the proposed integration method, denoted in what follows by ${\textstyle {\boldsymbol {\sigma }}^{ex*}}$ (the appended superscript “ex” means ``stress approximated in the expanded space), is finally obtained as the sum of Eq.(4.20) and Eq.(4.21) :

${\boldsymbol {\sigma }}^{ex*}=\displaystyle \sum _{i=1}^{n_{\sigma }}{\boldsymbol {\mathit {\Psi }}}_{i}c_{i}^{ad}+\sum _{j=1}^{n_{u}}{{\boldsymbol {B}}_{j}^{*}\!}c_{j}^{in}.$

(4.22)

Figure 2: Expanded space approach. The stress approximation space is expanded so that it embraces, not only the span of the stress POD modes, but also the span of the reduced strain-displacement functions $\{{{\boldsymbol {B}}_{1}^{*}\!},{{\boldsymbol {B}}_{2}^{*}\!}\ldots {{\boldsymbol {B}}_{n_{u}}^{*}\!}\}$. The reduced-order cell equilibrium problem boils down to find the reduced displacement fluctuations vector ${\boldsymbol {U}}^{*}$ that makes the non-equilibrated component ${\boldsymbol {\sigma }}^{in}$ to vanish (${\boldsymbol {\sigma }}^{in}({\boldsymbol {U}}^{*},{\boldsymbol {\epsilon _{M}}})={\boldsymbol {0}}$ ).

Substituting the above approximation into the equilibrium equation, one gets:

$\displaystyle \int _{\Omega }{{\boldsymbol {B}}_{i}^{*}}^{T}\!(\mathbf {x} )\,{\boldsymbol {\sigma }}^{ex*}(\mathbf {x} ;{\boldsymbol {\epsilon _{M}}},{\boldsymbol {U}}^{*})$ $=\displaystyle \sum _{j=1}^{n_{\sigma }}\overbrace {\left(\int _{\Omega }{{\boldsymbol {B}}_{i}^{*}}^{T}\!(\mathbf {x} ){\boldsymbol {\mathit {\Psi }}}_{j}(\mathbf {x} )\,d\Omega \right)} ^{=0}c_{j}^{ad}({\boldsymbol {\epsilon _{M}}},{\boldsymbol {U}}^{*})+\sum _{j=1}^{n_{u}}\left(\int _{\Omega }{{\boldsymbol {B}}_{i}^{*}}^{T}\!(\mathbf {x} ){{\boldsymbol {B}}_{j}^{*}\!}(\mathbf {x} )\,d\Omega \right)c_{j}^{in}({\boldsymbol {\epsilon _{M}}},{\boldsymbol {U}}^{*})$ $=\sum _{j=1}^{n_{u}}\left(\int _{\Omega }{{\boldsymbol {B}}_{i}^{*}}^{T}\!(\mathbf {x} ){{\boldsymbol {B}}_{j}^{*}\!}(\mathbf {x} )\,d\Omega \right)c_{j}^{in}({\boldsymbol {\epsilon _{M}}},{\boldsymbol {U}}^{*})={\boldsymbol {0}},\;\;\;\;i=1,2\ldots n_{u}.$

(4.23)

Since ${\textstyle \{{{\boldsymbol {B}}_{1}^{*}\!},{{\boldsymbol {B}}_{2}^{*}\!}\ldots {{\boldsymbol {B}}_{n_{u}}^{*}\!}\}}$ are linearly independent functions, it becomes immediately clear that the above equations holds only if:

$c_{j}^{in}({\boldsymbol {\epsilon _{M}}},{\boldsymbol {U}}^{*})=0,\;\;j=1,2\ldots n_{u},$

(4.24)

i.e., if the ${\textstyle n_{u}}$ coefficients multiplying ${\textstyle {{\boldsymbol {B}}_{i}^{*}\!}\in L_{2}(\Omega )^{s}}$ (${\textstyle i=1,2\ldots n_{u}}$) are identically zero. In adopting the proposed integration approach, thus, the reduced-order cell equilibrium problem (3.24) is transformed into the problem of finding, for a given input macroscopic strain tensor ${\textstyle {\boldsymbol {\epsilon _{M}}}}$, the reduced displacement fluctuations vector ${\textstyle {\boldsymbol {U}}^{*}\in \mathbb {R} ^{n_{u}}}$ that makes the non-equilibrated component ${\textstyle {\boldsymbol {\sigma }}^{in}}$ (defined in Eq.(4.21)) to vanish.

In a nutshell, the ill-posedness exhibited by the discrete problem when adopting the standard approach of using only POD modes is eliminated by expanding the stress approximation space so that it embraces also the span of the reduced strain-displacement functions (or strain modes²) ${\textstyle {{\boldsymbol {B}}_{i}^{*}\!}\in L_{2}(\Omega )^{s}}$ (${\textstyle i=1,2\ldots n_{u}}$):

${\mathcal {V}}_{\sigma }^{apr}={\mathcal {V}}_{\sigma }^{*}\,\oplus \,{\textrm {span}}\!\left\lbrace {{\boldsymbol {B}}_{i}^{*}\!}\right\rbrace _{i=1}^{n_{u}}={\textrm {span}}\{\overbrace {{\boldsymbol {\mathit {\Psi }}}_{1},{\boldsymbol {\mathit {\Psi }}}_{2}\ldots {\boldsymbol {\mathit {\Psi }}}_{n_{\sigma }}} ^{n_{\sigma }\;{\hbox{stress modes}}},\overbrace {{{\boldsymbol {B}}_{1}^{*}\!},{{\boldsymbol {B}}_{2}^{*}\!}\ldots {{\boldsymbol {B}}_{n_{u}}^{*}\!}} ^{n_{u}\;{\hbox{strain modes}}}\}.$

(4.25)

4.3.3.2 Discrete formulation

In typical finite element implementations, both stresses and gradients of shape functions are only calculated and stored at the Gauss points of the underlying spatial discretization. For practical reasons, thus, it proves imperative to reformulate the above explained expanded space strategy and treat both magnitudes as spatially discrete variables, defined only at such Gauss points.

The discrete counterparts of the continuously defined fields ${\textstyle {\boldsymbol {\sigma }}\in L_{2}(\Omega )^{s}}$ and ${\textstyle {{\boldsymbol {B}}_{i}^{*}\!}\in L_{2}(\Omega )^{s}}$ (${\textstyle i=1,2\ldots n_{u}}$) will be denoted by ${\textstyle {\boldsymbol {\mathcal {S}}}\in \mathbb {R} ^{n_{g}\cdot s}}$ and ${\textstyle {\boldsymbol {{\mathcal {B}}^{*}}}={\begin{bmatrix}{\boldsymbol {{\mathcal {B}}_{1}^{*}}}&{\boldsymbol {{\mathcal {B}}_{2}^{*}}}&\cdots &{\boldsymbol {{\mathcal {B}}_{n_{u}}^{*}}}\end{bmatrix}}\in \mathbb {R} ^{n_{g}\cdot s\times n_{u}}}$, and termed the global stress vector, and the global matrix of strain modes, respectively. The global stress vector ${\textstyle {\boldsymbol {\mathcal {S}}}}$ is constructed by stacking the stress vectors ${\textstyle {\boldsymbol {\sigma }}(\mathbf {x} _{g};\cdot )\in \mathbb {R} ^{s}}$ (${\textstyle g=1,2\ldots n_{g}}$) at the Gauss points of the finite element grid into a single column vector:

${\boldsymbol {\mathcal {S}}}{\mathrel {\mathop {:}}}={\begin{bmatrix}{\boldsymbol {\sigma }}(\mathbf {x} _{1};\cdot )\\{\boldsymbol {\sigma }}(\mathbf {x} _{2};\cdot )\\\vdots \\{\boldsymbol {\sigma }}(\mathbf {x} _{n_{g}};\cdot )\end{bmatrix}}.$

(4.26)

Similarly, the global matrix of strain modes ${\textstyle {\boldsymbol {{\mathcal {B}}^{*}}}}$ is constructed as:

${\boldsymbol {{\mathcal {B}}^{*}}}{\mathrel {\mathop {:}}}={\begin{bmatrix}{{\boldsymbol {B}}^{*}}(\mathbf {x} _{1})\\{{\boldsymbol {B}}^{*}}(\mathbf {x} _{2})\\\vdots \\{{\boldsymbol {B}}^{*}}(\mathbf {x} _{n_{g}})\end{bmatrix}}={\begin{bmatrix}{{\boldsymbol {B}}_{1}^{*}\!}(\mathbf {x} _{1})&{{\boldsymbol {B}}_{2}^{*}\!}(\mathbf {x} _{1})&\cdots &{{\boldsymbol {B}}_{n_{u}}^{*}\!}(\mathbf {x} _{1})\\{{\boldsymbol {B}}_{1}^{*}\!}(\mathbf {x} _{2})&{{\boldsymbol {B}}_{2}^{*}\!}(\mathbf {x} _{2})&\cdots &{{\boldsymbol {B}}_{n_{u}}^{*}\!}(\mathbf {x} _{2})\\\vdots &\vdots &\vdots &\vdots \\{{\boldsymbol {B}}_{1}^{*}\!}(\mathbf {x} _{n_{g}})&{{\boldsymbol {B}}_{2}^{*}\!}(\mathbf {x} _{n_{g}})&\cdots &{{\boldsymbol {B}}_{n_{u}}^{*}\!}(\mathbf {x} _{n_{g}})\end{bmatrix}}.$

(4.27)

With definitions (4.26) and (4.27) at hand, the standard ROM equilibrium equation (4.1) can be readily rephrased in the following compact, matrix form:

$\left\langle {{\boldsymbol {B}}_{i}^{*}\!},{\boldsymbol {\sigma }}\right\rangle _{L_{2}(\Omega )}=\displaystyle \int _{\Omega }{{\boldsymbol {B}}_{i}^{*}}^{T}\!(\mathbf {x} ){\boldsymbol {\sigma }}(\mathbf {x} ;\cdot )\,d\Omega \approx \displaystyle \sum _{g=1}^{n_{g}}w_{g}{{{\boldsymbol {B}}_{i}^{*}}^{T}\!}\!(\mathbf {x} _{g}){\boldsymbol {\sigma }}(\mathbf {x} _{g};\cdot )=0$ $\Rightarrow {\boldsymbol {{\mathcal {B}}_{i}^{*}}}^{T}{\boldsymbol {W}}{\boldsymbol {\mathcal {S}}}=0,\;\;\;\;\;\;i=1,2\ldots n_{u},$

(4.28)

where ${\textstyle {\boldsymbol {W}}}$ is a diagonal matrix containing the weights at each Gauss point:

${\boldsymbol {W}}{\mathrel {\mathop {:}}}={\begin{bmatrix}w_{1}{\boldsymbol {I}}&{\boldsymbol {0}}&{\boldsymbol {0}}&\cdots &{\boldsymbol {0}}\\{\boldsymbol {0}}&w_{2}{\boldsymbol {I}}&{\boldsymbol {0}}&\cdots &{\boldsymbol {0}}\\\vdots &\vdots &\vdots &\vdots &\vdots \\{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&w_{n_{g}}{\boldsymbol {I}}\\\end{bmatrix}}^{}.$

(4.29)

(here, ${\textstyle {\boldsymbol {I}}}$ denotes the ${\textstyle s\,{\textrm {x}}\,s}$ identity matrix). Assuming that ${\textstyle w_{g}>0}$ (${\textstyle g=1,2\ldots n_{g}}$) –-Gauss quadrature rules with negative weights are excluded from our considerations–-, one can reexpress Eq.(4.28) as:

$\left\langle {{\boldsymbol {B}}_{i}^{*}\!},{\boldsymbol {\sigma }}\right\rangle _{L_{2}(\Omega )}\approx \left\langle {\boldsymbol {{\mathcal {B}}_{i}^{*}}},{\boldsymbol {\mathcal {S}}}\right\rangle _{\boldsymbol {W}}=0,\;\;\;\;\;\;i=1,2\ldots n_{u},$

(4.30)

where ${\textstyle \left\langle {\cdot },{\cdot }\right\rangle _{\boldsymbol {W}}}$ symbolizes the following ${\textstyle \mathbb {R} ^{n_{g}\cdot s}}$ inner product:

$\left\langle {a},{b}\right\rangle _{\boldsymbol {W}}={a}^{T}{\boldsymbol {W}}{b},\;\;\;\;{a},{b}\in \mathbb {R} ^{n_{g}\cdot s}.$

(4.31)

Equation (4.30) reveals that any statically admissible global stress vector ${\textstyle {\boldsymbol {\mathcal {S}}}}$ is orthogonal to the global strain modes vectors ${\textstyle {\boldsymbol {{\mathcal {B}}_{i}^{*}}}}$ (${\textstyle i=1,2\ldots n_{u}}$) in the sense of the inner product induced by ${\textstyle {\boldsymbol {W}}}$. In other words, in approximating the integral of the internal forces by Gauss quadrature, the ${\textstyle L_{2}}$ orthogonality condition translates into orthogonality in the sense of Eq.(4.31). From the point of view of numerical implementation, however, it is preferable to cast the equilibrium condition and the subsequent developments in terms of the standard euclidean scalar product in ${\textstyle \mathbb {R} ^{n_{g}\cdot s}}$ –-working with the inner product defined by Eq.(4.31) is somehow a nuisance and complicates unnecessarily the involved algebra. This can be achieved by inserting the Cholesky decomposition of the weights matrix

${\boldsymbol {W}}={\boldsymbol {W}}^{1/2}{\boldsymbol {W}}^{1/2},\;\;\;\;({\boldsymbol {W}}_{ii}^{1/2}{\mathrel {\mathop {:}}}={\sqrt {w_{i}}})$

(4.32)

into Eq.(4.26):

${\boldsymbol {{\mathcal {B}}^{*}}}^{T}{\boldsymbol {W}}{\boldsymbol {\mathcal {S}}}={({\boldsymbol {{\mathcal {B}}^{*}}}^{T}{\boldsymbol {W}}^{1/2})}({\boldsymbol {W}}^{1/2}{\boldsymbol {\mathcal {S}}})={\boldsymbol {0}}.$

(4.33)

Defining now the weighted global stress vector and weighted matrix of strain modes as

${\boldsymbol {\Sigma }}{\mathrel {\mathop {:}}}={\boldsymbol {W}}^{1/2}{\boldsymbol {\mathcal {S}}}={\begin{bmatrix}{\sqrt {w_{1}}}{\boldsymbol {\sigma }}(\mathbf {x} _{1};\cdot )\\{\sqrt {w_{2}}}{\boldsymbol {\sigma }}(\mathbf {x} _{2};\cdot )\\\vdots \\{\sqrt {w_{n_{g}}}}{\boldsymbol {\sigma }}(\mathbf {x} _{n_{g}};\cdot )\end{bmatrix}},$

(4.34)

and

${\mathbb {B} ^{*}}{\mathrel {\mathop {:}}}={\boldsymbol {W}}^{1/2}{\boldsymbol {{\mathcal {B}}^{*}}}={\begin{bmatrix}{\sqrt {w_{1}}}{{\boldsymbol {B}}^{*}}(\mathbf {x} _{1})\\{\sqrt {w_{2}}}{{\boldsymbol {B}}^{*}}(\mathbf {x} _{2})\\\vdots \\{\sqrt {w_{n_{g}}}}{{\boldsymbol {B}}^{*}}(\mathbf {x} _{n_{g}})\end{bmatrix}}$

(4.35)

respectively, and inserting these definitions into Eq.(4.26), one finally arrives at:

${\mathbb {B} ^{*}}^{T}{\boldsymbol {\Sigma }}={\boldsymbol {0}},$

(4.36)

or equivalently:

${\mathbb {B} _{i}^{*}}^{T}{\boldsymbol {\Sigma }}=0,\;\;\;\;\;\;\;i=1,2\ldots n_{u},$

(4.37)

which shows that any statically admissible weighted stress vector is orthogonal, in the sense of the standard euclidean inner product, to the weighted strain modes ${\textstyle {\mathbb {B} _{i}^{*}}^{T}}$ (${\textstyle i=1,2\ldots n_{u}}$).

Comparing Eq.(4.36) with Eq.(4.17), it becomes clear that ${\textstyle {\mathbb {B} ^{*}}^{T}}$ plays the same role as operator ${\textstyle {\boldsymbol {G}}}$ in Eq.(4.17). In analogy with Eq.(4.18), thus, we can write

$\mathbb {R} ^{n_{g}\cdot s}={\mathcal {N}}({\mathbb {B} ^{*}}^{T})\oplus {\textrm {Range}}({\mathbb {B} ^{*}})$

(4.38)

where ${\textstyle {\mathcal {N}}({\mathbb {B} ^{*}}^{T})}$ and ${\textstyle {\textrm {Range}}({\mathbb {B} ^{*}})}$ denote the null space and the range (or column space) of ${\textstyle {\mathbb {B} ^{*}}^{T}}$ and ${\textstyle {\mathbb {B} ^{*}}}$, respectively, and consequently decompose any ${\textstyle {\boldsymbol {\Sigma }}\in \mathbb {R} ^{n_{g}\cdot s}}$ as

${\boldsymbol {\Sigma }}={\boldsymbol {\Sigma ^{ad}}}+{\boldsymbol {\Sigma ^{in}}}$

(4.39)

with ${\textstyle {\boldsymbol {\Sigma ^{ad}}}\in {\mathcal {N}}({\mathbb {B} ^{*}}^{T})}$ and ${\textstyle {\boldsymbol {\Sigma ^{in}}}\in {\textrm {Range}}({\mathbb {B} ^{*}})}$. As in the continuous case (see Eq.(4.20)), the statically admissible component ${\textstyle {\boldsymbol {\Sigma ^{ad}}}}$ is now approximated by a linear combination of POD basis vectors obtained from converged stress snapshots (the methodology for obtaining these modes using the SVD is thoroughly explained in Appendix B.2):

${\boldsymbol {\Sigma ^{ad}}}\approx {\boldsymbol {\Sigma }}^{*}=\sum _{i=1}^{n_{\sigma }}c_{i}^{ad}{\boldsymbol {\Psi }}_{i}={\boldsymbol {\Psi }}{\boldsymbol {c}}^{ad},$

(4.40)

where

${\boldsymbol {\Psi }}={\begin{bmatrix}{\boldsymbol {\Psi }}_{1}&{\boldsymbol {\Psi }}_{2}&\cdots &{\boldsymbol {\Psi }}_{n_{\sigma }}\end{bmatrix}}$

(4.41)

denotes the (weighted) stress basis matrix and ${\textstyle {\boldsymbol {c}}^{ad}\in \mathbb {R} ^{n_{\sigma }}}$ stands for the vector of modal coefficients associated to such a basis matrix. Likewise, since the non-equilibrated component ${\textstyle {\boldsymbol {\Sigma ^{in}}}}$ pertains to the column space of ${\textstyle {\mathbb {B} ^{*}}}$, we can directly write

${\boldsymbol {\Sigma ^{in}}}={\mathbb {B} ^{*}}{\boldsymbol {c}}^{in},$

(4.42)

where ${\textstyle {\boldsymbol {c}}^{in}\in \mathbb {R} ^{n_{u}}}$. The low-dimensional (weighted) stress vector ${\textstyle {\boldsymbol {\Sigma }}^{ex*}}$ required in the proposed integration method is finally obtained as the sum of Eq.(4.42) and Eq.(4.40).

${\boldsymbol {\Sigma }}\approx {\boldsymbol {\Sigma }}^{ex*}={\boldsymbol {\Psi }}{\boldsymbol {c}}^{ad}+{\mathbb {B} ^{*}}{\boldsymbol {c}}^{in},$

(4.43)

or in a more compact format:

${\boldsymbol {\Sigma }}^{ex*}={\boldsymbol {\Psi }}^{ex}{\boldsymbol {c}}.$

(4.44)

where

${\boldsymbol {\Psi }}^{ex}{\mathrel {\mathop {:}}}={\begin{bmatrix}{\boldsymbol {\Psi }}&{\mathbb {B} ^{*}}\end{bmatrix}},$

(4.45)

and

${\boldsymbol {c}}={\begin{bmatrix}{\boldsymbol {c}}^{ad}\\{\boldsymbol {c}}^{in}\end{bmatrix}}.$

(4.46)

The matrix ${\textstyle {\boldsymbol {\Psi }}^{ex}\in \mathbb {R} ^{n_{g}\cdot s\times (n_{u}+n_{\sigma })}}$ defined by Eq.(4.45) will be hereafter called the expanded basis matrix for the (weighted) stresses, whereas ${\textstyle {\boldsymbol {c}}\in \mathbb {R} ^{n_{\sigma }+n_{u}}}$ will be correspondingly termed the expanded vector of modal coefficients. Inserting approximation (4.43) into Eq.(4.36), and considering that ${\textstyle {\mathbb {B} ^{*}}^{T}{\boldsymbol {\Psi }}={\boldsymbol {0}}}$ and that ${\textstyle {\mathbb {B} ^{*}}^{T}}$ is a full rank matrix, one finally arrives at the same equilibrium condition derived in the continuum case (see Eq. 4.24):

${\boldsymbol {c}}^{in}({\boldsymbol {U}}^{*},{\boldsymbol {\epsilon _{M}}})={\boldsymbol {0}}.$

(4.47)

Once the above equation is solved for ${\textstyle {\boldsymbol {U}}^{*}}$, the desired equilibrated stress vector ${\textstyle {\boldsymbol {\Sigma }}^{*}}$ is obtained by evaluating Eq.(4.40):

${\boldsymbol {\Sigma }}^{*}={\boldsymbol {\Psi }}{\boldsymbol {c}}^{ad}({\boldsymbol {U}}^{*},{\boldsymbol {\epsilon _{M}}}).$

(4.48)

(²) Indeed, functions ${{\boldsymbol {B}}_{i}^{*}\!}\in L_{2}(\Omega )^{s}$ ($i=1,2\ldots n_{u}$) can be viewed as fluctuating strain modes, since they are the symmetric gradient of the displacement fluctuation modes, see Eq. 3.27.

4.4 Determination of modal coefficients

The next step in the development of the proposed integration scheme is to deduce closed-form expressions for the vectors of modal coefficients ${\textstyle {\boldsymbol {c}}^{ad}\in \mathbb {R} ^{n_{\sigma }}}$ and ${\textstyle {\boldsymbol {c}}^{in}\in \mathbb {R} ^{n_{u}}}$ in terms of the stress values computed at a set of ${\textstyle p={\mathcal {O}}(n_{u})}$ pre-specified sampling points (to be chosen among the set of Gauss points of the underlying finite element mesh). To this end, we need first to introduce some notation and terminology.

4.4.1 Gappy vectors

Let ${\textstyle {\mathcal {I}}=\{{\mathcal {I}}_{1},{\mathcal {I}}_{2}\ldots {\mathcal {I}}_{p}\}\subset \{1,2\cdots n_{g}\}}$ denote the set of indices of sampling points. Notationally, we write ${\textstyle {\hat {\boldsymbol {\Sigma }}}_{({\mathcal {I}})}\in \mathbb {R} ^{p\cdot s}}$ to designate the subvector of ${\textstyle {\boldsymbol {\Sigma }}}$ containing the rows associated to these sampling points; viz.:

${\hat {\boldsymbol {\Sigma }}}_{({\mathcal {I}})}{\mathrel {\mathop {:}}}={\begin{bmatrix}{\sqrt {w_{{\mathcal {I}}_{1}}}}{\boldsymbol {\sigma }}(\mathbf {x} _{{\mathcal {I}}_{1}},\cdot )\\{\sqrt {w_{{\mathcal {I}}_{2}}}}{\boldsymbol {\sigma }}(\mathbf {x} _{{\mathcal {I}}_{2}},\cdot )\\\vdots \\{\sqrt {w_{{\mathcal {I}}_{p}}}}{\boldsymbol {\sigma }}(\mathbf {x} _{{\mathcal {I}}_{p}},\cdot )\end{bmatrix}}.$

(4.49)

(When confusion is not apt to arise, the parenthetical subscript indicating the set of sampling indices will be dropped, and we shall simply write ${\textstyle {\hat {\boldsymbol {\Sigma }}}}$). It proves conceptually advantageous to regard this restricted or “gappy” –-a terminology that goes back to the work of Everson et al. [70]–- stress vector ${\textstyle {\hat {\boldsymbol {\Sigma }}}_{({\mathcal {I}})}}$ as the result of the application of a certain boolean operator ${\textstyle {\boldsymbol {\mathcal {P}}}_{({\mathcal {I}})}:\mathbb {R} ^{n_{g}\cdot s}\rightarrow \mathbb {R} ^{p\cdot s}}$ over the full vector ${\textstyle {\boldsymbol {\Sigma }}}$:

${\hat {\boldsymbol {\Sigma }}}={\boldsymbol {\mathcal {P}}}_{({\mathcal {I}})}{\boldsymbol {\Sigma }}.$

(4.50)

We call ${\textstyle {\boldsymbol {\mathcal {P}}}_{({\mathcal {I}})}}$ the selection operator associated to sampling indices ${\textstyle {\mathcal {I}}}$. This operator can be of course applied to any ${\textstyle {Y}\in \mathbb {R} ^{n_{g}\cdot s\times z}}$ (${\textstyle z\geq 1,z\in \mathbb {N} ^{}}$). For instance, the restricted matrix of weighted strain modes would be defined as:

${\mathbb {\hat {B}} ^{*}}{\mathrel {\mathop {:}}}={\boldsymbol {\mathcal {P}}}_{({\mathcal {I}})}{\mathbb {B} ^{*}}={\begin{bmatrix}{\sqrt {w_{{\mathcal {I}}_{1}}}}{{\boldsymbol {B}}^{*}}(\mathbf {x} _{{\mathcal {I}}_{1}})\\{\sqrt {w_{{\mathcal {I}}_{2}}}}{{\boldsymbol {B}}^{*}}(\mathbf {x} _{{\mathcal {I}}_{2}})\\\vdots \\{\sqrt {w_{{\mathcal {I}}_{p}}}}{{\boldsymbol {B}}^{*}}(\mathbf {x} _{{\mathcal {I}}_{p})})\end{bmatrix}}$

(4.51)

Furhtermore, it is straighforward to show that

${\boldsymbol {\mathcal {P}}}_{({\mathcal {I}})}{\boldsymbol {\mathcal {P}}}_{({\mathcal {I}})}^{T}={\boldsymbol {I}},$

(4.52)

(here ${\textstyle {\boldsymbol {I}}}$ is the ${\textstyle (n_{g}\cdot s)}$x${\textstyle (n_{g}\cdot s)}$ identity matrix) and that

${\boldsymbol {\mathcal {P}}}_{({\mathcal {I}})}({A}{Y})=({\boldsymbol {\mathcal {P}}}_{({\mathcal {I}})}{A}{\boldsymbol {\mathcal {P}}}_{({\mathcal {I}})}^{T})({\boldsymbol {\mathcal {P}}}_{({\mathcal {I}})}{Y})$

(4.53)

for any ${\textstyle {A}\in \mathbb {R} ^{n_{g}\cdot s\times n_{g}\cdot s}}$ and ${\textstyle {Y}\in \mathbb {R} ^{n_{g}\cdot s\times z}}$.

4.4.2 Least-squares fit

In the spirit of classical polynomial quadrature, such as Newton-Cotes formulae [35], the modal coefficients ${\textstyle {\boldsymbol {c}}^{ad}\in \mathbb {R} ^{n_{\sigma }}}$ and ${\textstyle {\boldsymbol {c}}^{in}\in \mathbb {R} ^{n_{u}}}$ are determined by fitting the low-dimensional approximation (4.43) to the weighted stresses calculated at the pre-specified sampling points. It should be noticed that, the variable subject to approximation –-the stress–- being a vector-valued function, the total number of discrete points to be fitted does not coincide with the number of spatial sampling points (${\textstyle p}$), but rather is equal to the product of such a number times the number of stress components (${\textstyle s}$). The well-posedness of the fitting problem, thus, demands that:

$p\cdot s\geq n_{\sigma }+n_{u}$

(4.54)

i.e., the number of discrete points must be equal or greater than the number of parameters to be adjusted. For the equality to hold, both ${\textstyle n_{\sigma }+n_{u}}$ and ${\textstyle p}$ have to be multiple of ${\textstyle s}$; thus, an exact fit is in general not possible for arbitrary values of ${\textstyle n_{\sigma }}$ and ${\textstyle n_{u}}$, and recourse to an approximate fit is to be made. In this respect, we follow here the standard approach of using a least-squares, best-fit criterion, i.e., minimization of the squares of the deviations between “observed” (${\textstyle {\hat {\boldsymbol {\Sigma }}}}$) and fitted (${\textstyle {\boldsymbol {\hat {\Sigma }}}^{ex*}={\boldsymbol {\hat {\Psi }}}{\boldsymbol {a}}+{\mathbb {\hat {B}} ^{*}}{\boldsymbol {b}}}$) values (in our context, “observed” signifies “calculated through the pertinent constitutive equation”). This minimization problem can be stated as:

${\boldsymbol {c}}={\begin{bmatrix}{\boldsymbol {c}}^{ad}\\{\boldsymbol {c}}^{in}\end{bmatrix}}={\textrm {arg}}\;{\underset {{\boldsymbol {a}}\in \mathbb {R} ^{n_{\sigma }},{\boldsymbol {b}}\in \mathbb {R} ^{n_{u}}}{\textrm {min}}}\,{\Vert {\hat {\boldsymbol {\Sigma }}}-\left({\boldsymbol {\hat {\Psi }}}{\boldsymbol {a}}+{\mathbb {\hat {B}} ^{*}}{\boldsymbol {b}}\right)\Vert }$

(4.55)

where ${\textstyle \Vert \cdot \Vert }$ stands for the standard euclidean norm. Let ${\textstyle {\boldsymbol {{\hat {\Psi }}^{ex}}}={\boldsymbol {\mathcal {P}}}_{({\mathcal {I}})}{\boldsymbol {\Psi }}^{ex}=[{\boldsymbol {\hat {\Psi }}}\;\,{\mathbb {\hat {B}} ^{*}}]}$ be the gappy expanded basis matrix, and suppose that the sampling indices ${\textstyle {\mathcal {I}}}$ have been chosen so that ${\textstyle {\boldsymbol {{\hat {\Psi }}^{ex}}}}$ has full rank, i.e.:

${\textrm {rank}}({\boldsymbol {{\hat {\Psi }}^{ex}}})={\textrm {rank}}([{\boldsymbol {\hat {\Psi }}}\;\,{\mathbb {\hat {B}} ^{*}}])=n_{\sigma }+n_{u}.$

(4.56)

Then, it can be shown (see, for instance, Ref. [71]) that the solution of this standard, least-squares problem is provided by the following vector of coefficients:

${\boldsymbol {c}}={\begin{bmatrix}{\boldsymbol {c}}^{ad}\\{\boldsymbol {c}}^{in}\end{bmatrix}}={\boldsymbol {\hat {\Psi }}}^{ex^{\dagger }}{\hat {\boldsymbol {\Sigma }}},$

(4.57)

where

${\boldsymbol {\hat {\Psi }}}^{ex^{\dagger }}{\mathrel {\mathop {:}}}=\overbrace {({\boldsymbol {{\hat {\Psi }}^{ex}}}^{T}{\boldsymbol {{\hat {\Psi }}^{ex}}})^{-1}} ^{{\boldsymbol {\hat {M}}}^{-1}}{\boldsymbol {{\hat {\Psi }}^{ex}}}^{T}$

(4.58)

is the so-called pseudo-inverse of matrix ${\textstyle {\boldsymbol {{\hat {\Psi }}^{ex}}}}$.

Recall that our ultimate aim is to derive closed-form expressions for ${\textstyle {\boldsymbol {c}}^{in}}$ and ${\textstyle {\boldsymbol {c}}^{ad}}$ as functions of ${\textstyle {\hat {\boldsymbol {\Sigma }}}}$. Thus, it remains to extricate these two sub-vectors from expression (4.57). This can be done by first partitioning both ${\textstyle {\boldsymbol {\hat {M}}}={\boldsymbol {{\hat {\Psi }}^{ex}}}^{T}{\boldsymbol {{\hat {\Psi }}^{ex}}}}$ and ${\textstyle {\boldsymbol {{\hat {\Psi }}^{ex}}}^{T}}$ in terms of the gappy stress basis matrix ${\textstyle {\boldsymbol {\hat {\Psi }}}}$ and the gappy matrix of strain modes ${\textstyle {\mathbb {\hat {B}} ^{*}}}$:

${\boldsymbol {c}}={\begin{bmatrix}{\boldsymbol {c}}^{ad}\\{\boldsymbol {c}}^{in}\end{bmatrix}}={\begin{bmatrix}{\boldsymbol {\hat {\Psi }}}^{T}{\boldsymbol {\hat {\Psi }}}&{\boldsymbol {\hat {\Psi }}}^{T}{\mathbb {\hat {B}} ^{*}}\\{\mathbb {\hat {B}} ^{*^{T}}}{\boldsymbol {\hat {\Psi }}}&{\mathbb {\hat {B}} ^{*^{T}}}{\mathbb {\hat {B}} ^{*}}\end{bmatrix}}^{-1}{\begin{bmatrix}{\boldsymbol {\hat {\Psi }}}^{T}\\{\mathbb {\hat {B}} ^{*^{T}}}\end{bmatrix}}{\hat {\boldsymbol {\Sigma }}}.$

(4.59)

Invoking the blockwise inverse formula for ${\textstyle 2}$x${\textstyle 2}$ block symmetric matrices [72], and upon tedious algebra –-that has been relegated to Appendix C–-, one finally arrives at the following expressions for ${\textstyle {\boldsymbol {c}}^{ad}}$ and ${\textstyle {\boldsymbol {c}}^{in}}$

${\boldsymbol {c}}^{ad}={\boldsymbol {\hat {\Psi }}}^{\dagger }({\hat {\boldsymbol {\Sigma }}}-{\mathbb {\hat {B}} ^{*}}{\boldsymbol {c}}^{in}),$

(4.60)

${\boldsymbol {c}}^{in}={S}^{-1}{\mathbb {\hat {B}} ^{*^{T}}}\left({\boldsymbol {I}}-{\boldsymbol {\hat {\Psi }}}{\boldsymbol {\hat {\Psi }}}^{\dagger }\right){\hat {\boldsymbol {\Sigma }}},$

(4.61)

where ${\textstyle {\boldsymbol {\hat {\Psi }}}^{\dagger }}$ denotes the pseudoinverse of the gappy stress basis matrix ${\textstyle {\boldsymbol {\hat {\Psi }}}}$:

${\boldsymbol {\hat {\Psi }}}^{\dagger }=({\boldsymbol {\hat {\Psi }}}^{T}{\boldsymbol {\hat {\Psi }}})^{-1}{\boldsymbol {\hat {\Psi }}}^{T}$

(4.62)

and ${\textstyle {S}}$ is the so-called Schur complement [72] of ${\textstyle {\boldsymbol {\hat {\Psi }}}^{T}{\boldsymbol {\hat {\Psi }}}}$ in ${\textstyle {\boldsymbol {\hat {M}}}}$:

${S}{\mathrel {\mathop {:}}}={\mathbb {\hat {B}} ^{*^{T}}}({\boldsymbol {I}}-{\boldsymbol {\hat {\Psi }}}{\boldsymbol {\hat {\Psi }}}^{\dagger }){\mathbb {\hat {B}} ^{*}}$

(4.63)

(note that this matrix is invertible by virtue of the hypothesis represented by Eq.(4.56)).

Reconstruction matrix

Let us first examine expression (4.60) for the modal coefficients ${\textstyle {\boldsymbol {c}}^{ad}}$ –-those that multiply the statically admissible component of the global stress vector. Since, at the solution, ${\textstyle {\boldsymbol {c}}^{in}={\boldsymbol {0}}}$, we have that:

${\boldsymbol {c}}^{ad}={\boldsymbol {\hat {\Psi }}}^{\dagger }({\hat {\boldsymbol {\Sigma }}}-{\mathbb {\hat {B}} ^{*}}\overbrace {{\boldsymbol {c}}^{in}} ^{={\boldsymbol {0}}})={\boldsymbol {\hat {\Psi }}}^{\dagger }{\hat {\boldsymbol {\Sigma }}}.$

(4.64)

(Notice that this result can also be obtained by directly solving minimization problem (4.55) with ${\textstyle {\boldsymbol {b}}={\boldsymbol {0}}}$). Substitution of this equation into Eq.(4.48) yields:

${\boldsymbol {\Sigma }}^{*}={\boldsymbol {\Psi }}{\boldsymbol {c}}^{ad}=\overbrace {{\boldsymbol {\Psi }}{\boldsymbol {\hat {\Psi }}}^{\dagger }} ^{\boldsymbol {R}}{\hat {\boldsymbol {\Sigma }}}={\boldsymbol {R}}\,{\hat {\boldsymbol {\Sigma }}},$

(4.65)

where

${\boldsymbol {R}}{\mathrel {\mathop {:}}}={\boldsymbol {\Psi }}{\boldsymbol {\hat {\Psi }}}^{\dagger }={\boldsymbol {\Psi }}({\boldsymbol {\hat {\Psi }}}^{T}{\boldsymbol {\hat {\Psi }}})^{-1}{\boldsymbol {\hat {\Psi }}}^{T}.$

(4.66)

Inspection of Eq.(4.65) reveals that the matrix ${\textstyle {\boldsymbol {R}}\in \mathbb {R} ^{n_{g}\cdot s\times p\cdot s}}$ defined above is the operator that allows one to reconstruct the (weighted) statically admissible stress vector ${\textstyle {\boldsymbol {\Sigma }}^{*}\in \mathbb {R} ^{n_{g}\cdot s}}$ using only the (weighted) stress values (${\textstyle {\hat {\boldsymbol {\Sigma }}}\in \mathbb {R} ^{p\cdot s}}$) calculated at the pre-selected sampling points ${\textstyle {\mathcal {I}}}$. For this reason, we shall use the term weighted reconstruction matrix (or simply reconstruction matrix) to refer to this operator. It must be emphasized here that this matrix only depends on the POD stress basis matrix ${\textstyle {\boldsymbol {\Psi }}}$ and on the selected sampling indices ${\textstyle {\mathcal {I}}}$ –-i.e., it is independent of the input parameter, the macro-strain ${\textstyle {\boldsymbol {\epsilon _{M}}}}$–-and, therefore, it can be pre-computed offline.

4.4.3 “Hyperreduced” cell equilibrium equation

As for the expression for the set of “statically inadmissible” coefficients ${\textstyle {\boldsymbol {c}}^{in}\in \mathbb {R} ^{n_{u}}}$, we know that, at the solution, these coefficients must vanish; thus, from Eq.(4.61), we have

${\boldsymbol {c}}^{in}({\boldsymbol {U}}^{*},{\boldsymbol {\epsilon _{M}}})={S}^{-1}{\mathbb {\hat {B}} ^{*^{T}}}\left({\boldsymbol {I}}-{\boldsymbol {\hat {\Psi }}}{\boldsymbol {\hat {\Psi }}}^{\dagger }\right){\hat {\boldsymbol {\Sigma }}}({\boldsymbol {U}}^{*},{\boldsymbol {\epsilon _{M}}})={\boldsymbol {0}}.$

(4.67)

Since ${\textstyle {S}}$ is a nonsingular matrix, the above condition is equivalent to

${\mathbb {\hat {B}} ^{*^{T}}}\left({\boldsymbol {I}}-{\boldsymbol {\hat {\Psi }}}{\boldsymbol {\hat {\Psi }}}^{\dagger }\right){\hat {\boldsymbol {\Sigma }}}({\boldsymbol {U}}^{*},{\boldsymbol {\epsilon _{M}}})={\boldsymbol {0}}.$

(4.68)

Furthermore, examination of Eq.(4.66) and Eq.(4.68) readily shows that the bracketed term ${\textstyle {\boldsymbol {\hat {\Psi }}}{\boldsymbol {\hat {\Psi }}}^{\dagger }}$ in Eq.(4.68) is nothing but the submatrix of the reconstruction matrix ${\textstyle {\boldsymbol {R}}}$ formed by the rows associated to sampling points ${\textstyle {\mathcal {I}}}$, i.e.:

${\boldsymbol {\hat {\Psi }}}{\boldsymbol {\hat {\Psi }}}^{\dagger }={\boldsymbol {\mathcal {P}}}_{({\mathcal {I}})}({\boldsymbol {\Psi }}{\boldsymbol {\hat {\Psi }}}^{\dagger })={\boldsymbol {\mathcal {P}}}_{({\mathcal {I}})}{\boldsymbol {R}}={\boldsymbol {\hat {R}}}.$

(4.69)

Substitution of expression (4.69) into Eq.(4.68) finally leads to:

${\mathbb {\hat {B}} ^{*^{T}}}({\boldsymbol {I}}-{\boldsymbol {\hat {R}}}){\hat {\boldsymbol {\Sigma }}}({\boldsymbol {U}}^{*},{\boldsymbol {\epsilon _{M}}})={\boldsymbol {0}}.$

(4.70)

As previously noted (see Figure 2), the purpose of enforcing condition ${\textstyle {\boldsymbol {c}}^{in}({\boldsymbol {U}}^{*},{\boldsymbol {\epsilon _{M}}})={\boldsymbol {0}}}$ is to ensure that the stress solution lies entirely in the space of equilibrated stresses. Equation (4.70) can be viewed, thus, as the “hyperreduced” form of the original cell equilibrium equation.

Observation 3: The “hyperreduced” qualifier –-coined by D. Ryckelynck [73,74]–- is used here to indicate that Eq.(4.70) is the result of two subsequent steps of complexity reduction: firstly, in the number of degrees of freedom (when passing from the finite element model to the standard ROM), and, secondly, in the number of integration points (when passing from this standard ROM to what we have baptized “High-Performance” ROM ). This double complexity reduction can be better appreciated by rephrasing both Eq.(4.70) and the FE cell equation (2.24) in a format similar to that of Eq.(4.36), viz.:

$\overbrace {{\mathbb {\hat {B}} ^{*^{T}}}({\boldsymbol {I}}-{\boldsymbol {\hat {R}}})} ^{\mathbb {\hat {B}} ^{**^{T}}}{\hat {\boldsymbol {\Sigma }}}={\mathbb {\hat {B}} ^{**^{T}}}{\hat {\boldsymbol {\Sigma }}}={\boldsymbol {0}},$

(4.71)

and

$\displaystyle \sum _{g=1}^{n_{g}}w_{g}{{\boldsymbol {B}}^{T}}\!\!(\mathbf {x} _{g}){\boldsymbol {\sigma }}(\mathbf {x} _{g},;)={\mathbb {B} }^{T}{\boldsymbol {\Sigma }}={\boldsymbol {0}},$

(4.72)

respectively (here, ${\textstyle {\mathbb {B} }\in \mathbb {R} ^{n_{g}\cdot s\times n\cdot d}}$ is the finite element counterpart of ${\textstyle {\mathbb {B} ^{*}}}$, defined in Eq.(4.27)). With Eq.(4.72), Eq.(4.36) and Eq.(4.71) at our disposal, the aforementioned process of complexity reduction can be symbolically represented as

${\boldsymbol {\hat {R}}}{\hat {\boldsymbol {\Sigma }}}={\boldsymbol {\mathcal {P}}}_{({\mathcal {I}})}({\boldsymbol {R}}{\boldsymbol {\hat {\Sigma }}}^{*})={\boldsymbol {\mathcal {P}}}_{({\mathcal {I}})}{\boldsymbol {\Sigma }}^{*}={\boldsymbol {\hat {\Sigma }}}^{*}.$

(4.73)

the relation between ${\textstyle {\mathbb {B} }\in \mathbb {R} ^{n_{g}\cdot s\times n\cdot d}}$, ${\textstyle {\mathbb {B} ^{*}}\in \mathbb {R} ^{n_{g}\cdot s\times n_{u}}}$ and ${\textstyle {\mathbb {\hat {B}} ^{**}}\in \mathbb {R} ^{p\cdot s\times n_{u}}}$ being¹

${\mathbb {B} ^{*}}={\mathbb {B} }{\boldsymbol {\Phi }}$

(4.74)

and

${\mathbb {\hat {B}} ^{**}}{\mathrel {\mathop {:}}}=({\boldsymbol {I}}-{\boldsymbol {\hat {R}}}){\mathbb {\hat {B}} ^{*}}=({\boldsymbol {I}}-{\boldsymbol {\hat {R}}}){\boldsymbol {\mathcal {P}}}_{({\mathcal {I}})}{\mathbb {B} ^{*}},$

(4.75)

with ${\textstyle p={\mathcal {O}}(n_{u})<<n_{g}={\mathcal {O}}(n)}$. It is interesting to see how the reduction in complexity of the cell equilibrium equation is reflected in the gradual reduction of the dimensions of the “B” operators that act on the weighted vector of stresses.

Physical interpretation

Aside from a “compressed” version of the original, full-order cell condition, the hyperreduced cell equation (4.70) can be alternatively interpreted as a balance between “observed” and “fitted” internal forces at the selected sampling points. Such an interpretation becomes readily identifiable by realizing that the product ${\textstyle {\boldsymbol {\hat {R}}}{\hat {\boldsymbol {\Sigma }}}}$ appearing in Eq.(4.70) is but the (weighted) vector of fitted stresses at the selected sampling points. Indeed, by virtue of Eq.(4.65) and, considering the properties of the selection operator ${\textstyle {\boldsymbol {\mathcal {P}}}_{({\mathcal {I}})}}$, we have that

${\boldsymbol {\hat {R}}}{\hat {\boldsymbol {\Sigma }}}={\boldsymbol {\mathcal {P}}}_{({\mathcal {I}})}({\boldsymbol {R}}{\boldsymbol {\hat {\Sigma }}}^{*})={\boldsymbol {\mathcal {P}}}_{({\mathcal {I}})}{\boldsymbol {\Sigma }}^{*}={\boldsymbol {\hat {\Sigma }}}^{*}.$

(4.76)

Using the above equality, Eq.(4.70) is expressible as

${\mathbb {\hat {B}} ^{*^{T}}}{\hat {\boldsymbol {\Sigma }}}={\mathbb {\hat {B}} ^{*^{T}}}{\boldsymbol {\hat {\Sigma }}}^{*},$

(4.77)

or, reverting to the original, summation notation:

${\mathbb {\hat {B}} ^{*^{T}}}{\hat {\boldsymbol {\Sigma }}}={\begin{bmatrix}{\sqrt {w_{{\mathcal {I}}_{1}}}}{{\boldsymbol {B}}^{*}}^{T}\!\!(\mathbf {x} _{{\mathcal {I}}_{1}})&{\sqrt {w_{{\mathcal {I}}_{2}}}}{{\boldsymbol {B}}^{*}}^{T}\!\!(\mathbf {x} _{{\mathcal {I}}_{2}})&\cdots &{\sqrt {w_{{\mathcal {I}}_{p}}}}{{\boldsymbol {B}}^{*}}^{T}\!\!(\mathbf {x} _{{\mathcal {I}}_{p}})\end{bmatrix}}{\begin{bmatrix}{\sqrt {w_{{\mathcal {I}}_{1}}}}{\boldsymbol {\sigma }}(\mathbf {x} _{{\mathcal {I}}_{1}};\cdot )\\{\sqrt {w_{{\mathcal {I}}_{2}}}}{\boldsymbol {\sigma }}(\mathbf {x} _{{\mathcal {I}}_{2}};\cdot )\\\vdots \\{\sqrt {w_{{\mathcal {I}}_{p}}}}{\boldsymbol {\sigma }}(\mathbf {x} _{{\mathcal {I}}_{p}};\cdot )\end{bmatrix}}$ $=\displaystyle \sum _{j\in {\mathcal {I}}}^{}{w_{j}}{{\boldsymbol {B}}^{*}}^{T}\!\!(\mathbf {x} _{j}){\boldsymbol {\sigma }}(\mathbf {x} _{j};\cdot ),$

(4.78)

as

$\displaystyle \sum _{j\in {\mathcal {I}}}{w_{j}}{{\boldsymbol {B}}^{*}}^{T}\!\!(\mathbf {x} _{j}){\boldsymbol {\sigma }}(\mathbf {x} _{j};\cdot )=\sum _{j\in {\mathcal {I}}}{w_{j}}{{\boldsymbol {B}}^{*}}^{T}\!\!(\mathbf {x} _{j}){\boldsymbol {\sigma }}^{*}(\mathbf {x} _{j};\cdot {).}$

(4.79)

Note that both sides of the above equation represent the same physical quantity, namely, the sum of internal forces, in reduced coordinates, at the sampling Gauss points ${\textstyle \{\mathbf {x} _{{\mathcal {I}}_{1}},\mathbf {x} _{{\mathcal {I}}_{2}}\cdots \mathbf {x} _{{\mathcal {I}}_{p}}\}}$. The difference lies in the stresses employed for computing these internal forces. In the left-hand side, they are calculated using “observed” stresses ${\textstyle {\boldsymbol {\sigma }}}$ –-stresses that arise directly from evaluating the corresponding constitutive equation–-, whereas, in the right-hand side, “fitted” stresses ${\textstyle {\boldsymbol {\sigma }}^{*}}$ are used –-that is, stresses obtained from fitting the approximation constructed using the POD stress basis functions ${\textstyle {\boldsymbol {\Psi }}_{1},{\boldsymbol {\Psi }}_{2}\ldots {\boldsymbol {\Psi }}_{n_{\sigma }}}$ to the observed data. Thus, the HP-ROM equilibrium condition (4.79) is telling us that, at the solution, the sum of internal forces –-at the pre-selected sampling points–- computed using either observed or fitted stresses² must coincide.

(¹) ${\mathbb {\hat {B}} ^{**}}$ is nothing but the compact form of the weighting factors ${\boldsymbol {Q}}_{i}$ $(i=1,2\ldots p)$ introduced in Section 4.2.1 (see Eq.(4.7)).

(²) It should be mentioned in this respect that, in general, ${\boldsymbol {\sigma }}^{*}(\mathbf {x} _{j};\cdot )\neq {\boldsymbol {\sigma }}(\mathbf {x} _{j};\cdot )$ since, as expression (4.54) indicates, the number of data items to be fitted ($p\cdot s$) is always greater than the number of stress modes ($n_{\sigma }$). Observed and fitted stresses coincide only when the stress vector ${\boldsymbol {\Sigma }}$ one wishes to approximate pertains to the column space of the stress basis matrix ${\boldsymbol {\Psi }}$ (consult Appendix D.1 (Observation 8) for a demonstration of this property. )

4.4.4 Jacobian matrix

Needless to say, the dependence of the stresses on the reduced vector of reduced displacement fluctuations ${\textstyle {\boldsymbol {U}}^{*}}$ is in general non-linear, and, thereby, an iterative method is required for solving Eq.(4.70). Here we employ the standard Newton-Raphson procedure. The iterative scheme corresponding to this procedure is given by the following expression (the parenthetical superscript indicates iteration number):

${{\boldsymbol {U}}^{*}}^{(k+1)}={{\boldsymbol {U}}^{*}}^{(k)}-{{\boldsymbol {K}}^{*(k)}}^{-1}{{\boldsymbol {F}}^{*}}^{(k)},$

(4.80)

where

${{\boldsymbol {F}}^{*}}^{(k)}={\mathbb {\hat {B}} ^{*^{T}}}\!\!({\boldsymbol {I}}-{\boldsymbol {\hat {R}}})\,{\hat {\boldsymbol {\Sigma }}}({\boldsymbol {\epsilon _{M}}},{{\boldsymbol {U}}^{*}}^{(k)})$

(4.81)

and

${{\boldsymbol {K}}^{*}}^{(k)}={\mathbb {\hat {B}} ^{*^{T}}}\!\!({\boldsymbol {I}}-{\boldsymbol {\hat {R}}})\,{\boldsymbol {\mathbb {\hat {C}} }}({\boldsymbol {\epsilon _{M}}},{{\boldsymbol {U}}^{*}}^{(k)})\,{\mathbb {\hat {B}} ^{*}}.$

(4.82)

In the above equation, ${\textstyle {\boldsymbol {\mathbb {\hat {C}} }}\in \mathbb {R} ^{p\cdot s\times p\cdot s}}$ denotes a block diagonal matrix containing the algorithmic, constitutive tangent matrices at each sampling point:

${\boldsymbol {\mathbb {\hat {C}} }}{\mathrel {\mathop {:}}}={\begin{bmatrix}{\boldsymbol {C}}(\mathbf {x} _{{\mathcal {I}}_{1}};\cdot )&{\boldsymbol {0}}&{\boldsymbol {0}}&\cdots &{\boldsymbol {0}}\\{\boldsymbol {0}}&{\boldsymbol {C}}(\mathbf {x} _{{\mathcal {I}}_{2}};\cdot )&{\boldsymbol {0}}&\cdots &{\boldsymbol {0}}\\\vdots &\vdots &\vdots &\vdots &\vdots \\{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {0}}&{\boldsymbol {C}}(\mathbf {x} _{{\mathcal {I}}_{p}};\cdot )\\\end{bmatrix}}^{}.$

(4.83)

Positive definiteness

Because of its relevance in the overall robustness of the proposed method, it is worthwhile at this point to digress and discuss thoroughly the spectral properties of the Jacobian matrix represented by Eq.(4.82). In particular, it would be interesting to ascertain whether positive definiteness of the algorithmic tangent matrices ${\textstyle {\boldsymbol {C}}(\mathbf {x} _{{\mathcal {I}}_{1}};\cdot ),\,{\boldsymbol {C}}(\mathbf {x} _{{\mathcal {I}}_{2}};\cdot ),\cdots {\boldsymbol {C}}(\mathbf {x} _{{\mathcal {I}}_{p}})}$ at the selected sampling points, and thus of matrix ${\textstyle {\boldsymbol {\mathbb {\hat {C}} }}}$, ensures positive definiteness of the Jacobian matrix ${\textstyle {\boldsymbol {K}}^{*}}$ –-as it occurs when using classical Gauss quadrature rules with positive weights–-, and, if not, which remedies can be applied to obtain such a desirable property.

Positive definiteness of the Jacobian matrix (4.82) requires that the function defined as

$F({U})={U}^{T}{\boldsymbol {K}}^{*}{U}=({\mathbb {\hat {B}} ^{*}}{U})^{T}({\boldsymbol {I}}-{\boldsymbol {\hat {R}}})\,{\boldsymbol {\mathbb {\hat {C}} }}({\mathbb {\hat {B}} ^{*}}{U})$

(4.84)

be positive for all non-zero ${\textstyle {U}\in \mathbb {R} ^{n_{u}}}$. Since ${\textstyle {\mathbb {\hat {B}} ^{*}}}$ is a full rank matrix –-by virtue of Eq.(4.56)–-, condition ${\textstyle F({U})>0}$ is equivalent to:

$G({V})={V}^{T}({\boldsymbol {I}}-{\boldsymbol {\hat {R}}})\,{\boldsymbol {\mathbb {\hat {C}} }}\,{V}>0$

(4.85)

for all non-zero ${\textstyle {V}\in {\textrm {Range}}({\mathbb {\hat {B}} ^{*}})}$.

To go further, we need to demonstrate that ${\textstyle {\boldsymbol {\hat {R}}}\in \mathbb {R} ^{n_{g}\cdot s\times n_{g}\cdot s}}$ –-recall that ${\textstyle {\boldsymbol {\hat {R}}}}$ is the matrix that maps the vector of “observed” stresses ${\textstyle {\hat {\boldsymbol {\Sigma }}}}$ to the vector of fitted stresses ${\textstyle {\boldsymbol {\hat {\Sigma }}}^{*}}$–- actually represents an orthogonal projection¹ onto the the column space of the gappy stress basis matrix ${\textstyle {\boldsymbol {\hat {\Psi }}}}$. This can be shown by simply noting that ${\textstyle {\boldsymbol {\hat {R}}}}$ is, on the one hand, symmetric:

${\boldsymbol {\hat {R}}}^{T}=({\boldsymbol {\hat {\Psi }}}({\boldsymbol {\hat {\Psi }}}^{T}{\boldsymbol {\hat {\Psi }}})^{-1}{\boldsymbol {\hat {\Psi }}}^{T})^{T}={\boldsymbol {\hat {\Psi }}}({\boldsymbol {\hat {\Psi }}}^{T}{\boldsymbol {\hat {\Psi }}})^{-T}{\boldsymbol {\hat {\Psi }}}^{T}={\boldsymbol {\hat {R}}}$

(4.86)

and, on the other hand, idempotent:

${\boldsymbol {\hat {R}}}^{2}=({\boldsymbol {\hat {\Psi }}}{\boldsymbol {\hat {\Psi }}}^{\dagger })^{2}={\boldsymbol {\hat {\Psi }}}\overbrace {({\boldsymbol {\hat {\Psi }}}^{T}{\boldsymbol {\hat {\Psi }}})^{-1}{\boldsymbol {\hat {\Psi }}}^{T}{\boldsymbol {\hat {\Psi }}}} ^{={\boldsymbol {I}}}({\boldsymbol {\hat {\Psi }}}^{T}{\boldsymbol {\hat {\Psi }}})^{-1}{\boldsymbol {\hat {\Psi }}}^{T}={\boldsymbol {\hat {\Psi }}}({\boldsymbol {\hat {\Psi }}}^{T}{\boldsymbol {\hat {\Psi }}})^{-1}{\boldsymbol {\hat {\Psi }}}^{T}={\boldsymbol {\hat {R}}}.$

(4.87)

With this property at hand, we can decompose any ${\textstyle {V}\in {\textrm {Range}}({\mathbb {\hat {B}} ^{*}})}$ as

${V}={V}^{||}+{V}^{\bot }$

(4.88)

where ${\textstyle {V}^{||}={\boldsymbol {\hat {R}}}{V}\in {\textrm {Range}}({\boldsymbol {\hat {\Psi }}})}$ –-the component of ${\textstyle {V}}$ along the column space of ${\textstyle {\boldsymbol {\hat {\Psi }}}}$–- and ${\textstyle {V}^{\bot }=({\boldsymbol {I}}-{\boldsymbol {\hat {R}}}){V}}$ –-the component of ${\textstyle {V}}$ along the orthogonal complement of ${\textstyle {\textrm {Range}}({\boldsymbol {\hat {\Psi }}})}$. Introducing the above decomposition into Eq.(4.85), we arrive at

$G={{V}^{\bot }}^{T}{\boldsymbol {\mathbb {\hat {C}} }}{V}^{\bot }+{{V}^{\bot }}^{T}\,{\boldsymbol {\mathbb {\hat {C}} }}{V}^{||}.$

(4.89)

While the first term ${\textstyle {{V}^{\bot }}^{T}{\boldsymbol {\mathbb {\hat {C}} }}{V}^{\bot }}$ in the preceding equation is, in virtue of the positive definiteness of ${\textstyle {\boldsymbol {\mathbb {\hat {C}} }}}$, eminently positive for all nonzero ${\textstyle {V}^{\bot }\in \mathbb {R} ^{p\cdot s}}$, nothing can be said in principle about the second term ${\textstyle {{V}^{\bot }}^{T}\,{\boldsymbol {\mathbb {\hat {C}} }}{V}^{||}}$: numerical experience shows that the sign and relative magnitude of this term depends further on the chosen set of sampling indices ${\textstyle {\mathcal {I}}}$.

Remark 2: From the above observation, it follows that the positive definiteness of the Jacobian matrix ${\textstyle {\boldsymbol {K}}^{*}}$ is determined, not only by the spectral properties of ${\textstyle {\boldsymbol {\mathbb {\hat {C}} }}}$, but –-not surprisingly–- also by the number and the location within the RVE of the sampling points employed in the integration.

The foregoing remark naturally leads to wonder whether it is possible to select the sampling indices ${\textstyle {\mathcal {I}}}$ so as to ensure the positive definiteness of ${\textstyle {\boldsymbol {K}}^{*}}$ (assuming, obviously, that ${\textstyle {\boldsymbol {\mathbb {\hat {C}} }}}$ enjoys this property). To shed light on this question, let us first divide Eq.(4.89) by ${\textstyle {{V}^{\bot }}^{T}{\boldsymbol {\mathbb {\hat {C}} }}{V}^{\bot }}$ (notice that hypothesis (4.56) precludes the possibility of ${\textstyle {V}^{\bot }}$ being zero)

${\bar {G}}={\dfrac {G}{{{V}^{\bot }}^{T}{\boldsymbol {\mathbb {\hat {C}} }}{V}^{\bot }}}=1+{\dfrac {{{V}^{\bot }}^{T}\,{\boldsymbol {\mathbb {\hat {C}} }}{V}^{||}}{{{V}^{\bot }}^{T}{\boldsymbol {\mathbb {\hat {C}} }}{V}^{\bot }}}.$

(4.90)

Suppose now, for the sake of argument, that ${\textstyle {\boldsymbol {\mathbb {\hat {C}} }}}$ is also symmetric. Such being the case, the above equation can be legitimately rewritten as:

${\bar {G}}=1+{\textrm {cos}}({V}^{\bot },{V}^{||})_{\boldsymbol {\mathbb {\hat {C}} }}{\dfrac {\Vert {V}^{||}\Vert _{\boldsymbol {\mathbb {\hat {C}} }}}{\Vert {V}^{\bot }\Vert _{\boldsymbol {\mathbb {\hat {C}} }}}},$

(4.91)

where

${\textrm {cos}}({V}^{\bot },{V}^{||})_{\boldsymbol {\mathbb {\hat {C}} }}={\dfrac {\left\langle {{V}^{\bot }},{{V}^{||}}\right\rangle _{\boldsymbol {\mathbb {\hat {C}} }}}{\Vert {V}^{\bot }\Vert _{\boldsymbol {\mathbb {\hat {C}} }}\Vert {V}^{||}\Vert _{\boldsymbol {\mathbb {\hat {C}} }}}}.$

(4.92)

In the above equation, ${\textstyle \left\langle {\cdot },{\cdot }\right\rangle _{\boldsymbol {\mathbb {\hat {C}} }}}$ symbolizes the inner product defined by ${\textstyle {\boldsymbol {\mathbb {\hat {C}} }}}$ (i.e., ${\textstyle \left\langle {x},{y}\right\rangle _{\boldsymbol {\mathbb {\hat {C}} }}={x}^{T}{\boldsymbol {\mathbb {\hat {C}} }}{y}}$), whereas ${\textstyle \Vert \cdot \Vert _{\boldsymbol {\mathbb {\hat {C}} }}}$ denotes the norm associated to such an inner product (${\textstyle \Vert {x}\Vert _{\boldsymbol {\mathbb {\hat {C}} }}^{\!}=\left\langle {x},{x}\right\rangle _{\boldsymbol {\mathbb {\hat {C}} }}}$). From Eq.(4.90), it can be deduced that a sufficient (yet not necessary) condition for ${\textstyle {\bar {G}}>0}$, and thus for ${\textstyle {\boldsymbol {K}}^{*}}$ to be positive definite, is that

${\dfrac {\Vert {V}^{||}\Vert _{\boldsymbol {\mathbb {\hat {C}} }}}{\Vert {V}^{\bot }\Vert _{\boldsymbol {\mathbb {\hat {C}} }}}}<1$

(4.93)

for all nonzero ${\textstyle {V}\in {\textrm {Range}}({\mathbb {\hat {B}} ^{*}})}$, or equivalently (setting ${\textstyle {V}={\mathbb {\hat {B}} ^{*}}{U}}$):

${\dfrac {\Vert {\boldsymbol {\hat {R}}}{\mathbb {\hat {B}} ^{*}}{U}\Vert _{\boldsymbol {\mathbb {\hat {C}} }}}{\Vert ({\boldsymbol {I}}-{\boldsymbol {\hat {R}}}){\mathbb {\hat {B}} ^{*}}{U}\Vert _{\boldsymbol {\mathbb {\hat {C}} }}}}<1$

(4.94)

for all nonzero ${\textstyle {U}\in \mathbb {R} ^{n_{u}}}$.

Useful guidelines on how to choose ${\textstyle {\mathcal {I}}}$ so as to make positive definite the Jacobian matrix ${\textstyle {\boldsymbol {K}}^{*}}$ can be inferred from inequality (4.94). Firstly, given a fixed number of sampling points ${\textstyle p}$, expression (4.94) indicates that such points should be selected so that the columns of the gappy strain basis matrix ${\textstyle {\mathbb {\hat {B}} ^{*}}={\boldsymbol {\mathcal {P}}}_{({\mathcal {I}})}{\mathbb {B} ^{*}}=[{\mathbb {\hat {B}} ^{*}}_{1}\,{\mathbb {\hat {B}} ^{*}}_{2}\ldots {\mathbb {\hat {B}} ^{*}}_{n_{u}}]}$ are, loosely speaking, “as orthogonal as possible” to ${\textstyle {\textrm {Range}}({\boldsymbol {\hat {R}}})={\textrm {Range}}({\boldsymbol {\hat {\Psi }}})}$ –-the column space of the gappy stress basis matrix ${\textstyle {\boldsymbol {\hat {\Psi }}}={\boldsymbol {\mathcal {P}}}_{({\mathcal {I}})}{\boldsymbol {\Psi }}}$. In so doing, the factor defined as

$f_{\boldsymbol {\mathbb {\hat {C}} }}{\mathrel {\mathop {:}}}={\dfrac {\sqrt {\displaystyle \sum _{i=1}^{n_{u}}\Vert {\boldsymbol {\hat {R}}}{\mathbb {\hat {B}} ^{*}}_{i}\Vert _{\boldsymbol {\mathbb {\hat {C}} }}^{2}}}{\sqrt {\displaystyle \sum _{i=1}^{n_{u}}\Vert ({\boldsymbol {I}}-{\boldsymbol {\hat {R}}}){\mathbb {\hat {B}} ^{*}}_{i}\Vert _{\boldsymbol {\mathbb {\hat {C}} }}^{2}}}},$

(4.95)

would diminish, and so would, consequently, the left-hand side of inequality Eq.(4.94). In practice, however, factor ${\textstyle f_{\boldsymbol {\mathbb {\hat {C}} }}}$ cannot be used as a criterion for guiding the selection of sampling points, simply because it is defined in terms of the norm induced by ${\textstyle {\boldsymbol {\mathbb {\hat {C}} }}}$, and this matrix virtually changes at every time step and iteration. One has to be content to estimate this factor using other norm; for instance, employing the standard euclidean norm ${\textstyle \Vert \cdot \Vert }$, one gets

$f_{\boldsymbol {\mathbb {\hat {C}} }}\sim f_{F}{\mathrel {\mathop {:}}}={\dfrac {\sqrt {\displaystyle \sum _{i=1}^{n_{u}}\Vert {\boldsymbol {\hat {R}}}{\mathbb {\hat {B}} ^{*}}_{i}\Vert ^{2}}}{\sqrt {\displaystyle \sum _{i=1}^{n_{u}}\Vert ({\boldsymbol {I}}-{\boldsymbol {\hat {R}}}){\mathbb {\hat {B}} ^{*}}_{i}\Vert ^{2}}}}={\dfrac {\Vert {\boldsymbol {\hat {R}}}{\mathbb {\hat {B}} ^{*}}\Vert _{F}}{\Vert ({\boldsymbol {I}}-{\boldsymbol {\hat {R}}}){\mathbb {\hat {B}} ^{*}}\Vert _{F}}},$

(4.96)

where ${\textstyle \Vert \cdot \Vert _{F}}$ stands for the Frobenius norm.

Aside from seeking orthogonality between ${\textstyle {\mathbb {\hat {B}} ^{*}}}$ and ${\textstyle {\boldsymbol {\hat {R}}}}$, expression (4.95) suggests that another way of lowering factor ${\textstyle f_{F}}$ may be to reduce the ratio defined as

$\beta _{F}{\mathrel {\mathop {:}}}={\dfrac {\Vert {\boldsymbol {\hat {R}}}\Vert _{F}}{\Vert {\boldsymbol {I}}-{\boldsymbol {\hat {R}}}\Vert _{F}}}.$

(4.97)

Since ${\textstyle {\boldsymbol {\hat {R}}}}$ and, consequently, ${\textstyle {\boldsymbol {I}}-{\boldsymbol {\hat {R}}}}$ are matrices representing orthogonal projections, we have that

$\Vert {\boldsymbol {\hat {R}}}\Vert _{F}={\sqrt {{\textrm {rank}}({\boldsymbol {\hat {R}}})}}={\sqrt {n_{\sigma }}}$

(4.98)

and

$\Vert {\boldsymbol {I}}-{\boldsymbol {\hat {R}}}\Vert _{F}={\sqrt {{\textrm {rank}}({\boldsymbol {I}}-{\boldsymbol {\hat {R}}})}}={\sqrt {p\cdot s-n_{\sigma }}}.$

(4.99)

Therefore,

$\beta _{F}={\sqrt {\dfrac {n_{\sigma }}{p\cdot s-n_{\sigma }}}}.$

(4.100)

Observation 4: From the above expression, thus, one can conclude that increasing the number of sampling points ${\textstyle \,p}$ while keeping the number of stress modes ${\textstyle n_{\sigma }}$ constant also contributes to reduce factor ${\textstyle f_{F}}$ in Eq.(4.94), and, hence, in improving the spectral properties (positive defineteness) of the Jacobian matrix ${\textstyle {\boldsymbol {K}}^{*}}$. Notice that this property is totally consistent with the fact that, in the limiting case of taking all Gauss points (${\textstyle p=n_{g}}$), the reduced matrices ${\textstyle {\boldsymbol {\hat {R}}}}$ and ${\textstyle {\mathbb {\hat {B}} ^{*}}}$ degenerate into their full order counterparts ${\textstyle {\boldsymbol {R}}}$ and ${\textstyle {\mathbb {\hat {B}} ^{*}}}$, for which the condition ${\textstyle {\boldsymbol {R}}{\mathbb {\hat {B}} ^{*}}={\boldsymbol {0}}}$ holds –-they span subspaces that are mutually orthogonal–-, hence making ${\textstyle f_{F}=f_{\boldsymbol {\mathbb {\hat {C}} }}=0}$.

(¹) ${\boldsymbol {\hat {R}}}$ is the so-called “hat” matrix of linear regression models [75].

4.5 Selection of sampling points

The last theoretical issue to be discussed in the present work is the selection –-among the full set of Gauss points of the underlying finite element mesh–- of appropriate sampling or interpolation points. At the very least, the set of sampling indices ${\textstyle {\mathcal {I}}=\{i_{1},i_{2}\ldots i_{p}\}}$ must be chosen so that the gappy expanded basis matrix has full rank (see section 4.4.2):

${\textrm {rank}}({\hat {\boldsymbol {\Psi }}}_{({\mathcal {I}})}^{ex})={\textrm {rank}}([{\boldsymbol {\hat {\boldsymbol {\Psi }}}}_{({\mathcal {I}})}\;\,{\mathbb {\hat {B}} _{({\mathcal {I}})}^{*}}])=n_{\sigma }+n_{u}.$

(4.101)

Any set of sampling indices fulfilling this necessary condition is said to be admissible.

4.5.1 Optimality criteria

Accuracy

As in any other model reduction problem, the overriding concern when choosing the sampling points is obviously the accuracy of the approximation: we would like to position such points so that maximum similarity between the “high-fidelity”, finite element solution and the reduced-order response is obtained. In particular, since the ultimate aim of solving the cell BVP is to, given an input macroscopic strain trajectory, calculate the associated macroscopic stress response, it seems reasonable to use as optimality indicator the following error estimate:

${E}_{M,\sigma }({\boldsymbol {\Psi }},{\mathcal {I}}){\mathrel {\mathop {:}}}={\sqrt {\sum _{i=1}^{n_{snp}}\Vert {\boldsymbol {\sigma _{M}}}^{i}-{{\boldsymbol {\sigma _{M}}}^{*\,i}}({\boldsymbol {\Psi }},{\mathcal {I}})\Vert ^{2}}},$

(4.102)

where

${\boldsymbol {\sigma _{M}}}^{i}={\boldsymbol {\sigma _{M}}}({^{\,t}}{\boldsymbol {\epsilon _{M}}}{_{k}}^{j})\;\;\;(i=(j-1)n_{hst}+k).$

(4.103)

In the above equations, ${\textstyle {\boldsymbol {\sigma _{M}}}^{i}}$ denotes the finite element, macroscopic stress response corresponding to the the ${\textstyle k-th}$ (${\textstyle k=1,2\ldots n_{stp}}$) time step of the “training” strain trajectory ${\textstyle {^{\,t}}{\boldsymbol {\epsilon _{M}}}{_{}}^{j}}$ (${\textstyle j=1,2\ldots n_{hst}}$) –-i.e., the ${\textstyle j-th}$ strain path employed in the construction of both the displacement and stress basis, see Chapter 3. The variable ${\textstyle {{\boldsymbol {\sigma _{M}}}^{*\,i}}({\boldsymbol {\Psi }},{\mathcal {I}})}$, on the other hand, stands for the low-dimensional approximation of ${\textstyle {\boldsymbol {\sigma _{M}}}^{i}}$, calculated through formula (4.65) using the stress basis matrix ${\textstyle {\boldsymbol {\Psi }}}$ and the finite element solution at sampling points ${\textstyle \{\mathbf {x} _{{\mathcal {I}}_{\sigma }(1)},\mathbf {x} _{{\mathcal {I}}_{\sigma }(2)}\ldots \mathbf {x} _{{\mathcal {I}}_{\sigma }(p)}\}}$.

It is shown in Proposition D.1.1 of Appendix D.1 that an upper bound for ${\textstyle {E}_{M,\sigma }}$ is given by

${{e}_{\sigma }}({\boldsymbol {\Psi }},{\mathcal {I}}){\mathrel {\mathop {:}}}={\sqrt {{{{e}_{\sigma }^{trun}}^{2}}({\boldsymbol {\Psi }})+{{{e}_{\sigma }^{rec}}^{2}}({\boldsymbol {\Psi }},{\mathcal {I}})}}$

(4.104)

where

${e}_{\sigma }^{trun}{\mathrel {\mathop {:}}}={\dfrac {1}{V}}{\sqrt {\displaystyle \sum _{i=1}^{r_{\sigma }-n_{\sigma }}{{S}_{ii}^{\Gamma }}^{2}}}$

(4.105)

(${\textstyle r_{\sigma }}$ is the rank of the stress snapshot matrix) and

${e}_{\sigma }^{rec}{\mathrel {\mathop {:}}}={\dfrac {1}{V}}{\sqrt {\displaystyle \sum _{i=1}^{r_{\sigma }-n_{\sigma }}{{S}_{ii}^{\Gamma }}^{2}\Vert ({\boldsymbol {\hat {\boldsymbol {\Psi }}}}_{({\mathcal {I}})}^{T}{\boldsymbol {\hat {\boldsymbol {\Psi }}}}_{({\mathcal {I}})})^{-1}{\boldsymbol {\hat {\boldsymbol {\Psi }}}}_{({\mathcal {I}})}^{T}{{\boldsymbol {\hat {\Gamma }}}_{i}}_{({\mathcal {I}})}\Vert ^{2}}}$

(4.106)

In the above equations, ${\textstyle {\boldsymbol {\Gamma }}={\begin{bmatrix}{\boldsymbol {\Gamma }}_{1}&{\boldsymbol {\Gamma }}_{2}&\cdots &{\boldsymbol {\Gamma }}_{r_{\sigma }-n_{\sigma }}\end{bmatrix}}}$ designates the matrix of trailing (or inessential) inelastic stress modes, while ${\textstyle {S}_{ii}^{\Gamma }\in \mathbb {R} ^{}}$ ${\textstyle (i=1,2\ldots r_{\sigma }-n_{\sigma })}$ stand for the singular values associated to ${\textstyle {\boldsymbol {\Gamma }}}$. Note that ${\textstyle {e}_{\sigma }^{trun}}$ in Eq.(4.105) only depends on the number of stress modes employed in the approximation (but not on the employed sampling indices); thus, it provides an estimate of the stress truncation error. The term that actually measures the quality, in terms of accuracy, of a given set of admissible sampling points is the other one, ${\textstyle {e}_{\sigma }^{rec}}$–-it provides an (a priori) estimate of the stress reconstruction error. For this reason, and also because the cost of evaluating expression (4.106) is independent on the total number of snapshots and Gauss points –-and hence significantly lower than in the case of the original error estimate ${\textstyle {E}_{M,\sigma }}$–-, we shall use in what follows ${\textstyle {e}_{\sigma }^{rec}}$ as error estimator for guiding the selection of sampling points.

Spectral properties

Yet the optimality of a given set of sampling points cannot be measured only in terms of accuracy of the approximation. As demonstrated in the preceding section, the number and particular placement of such points influence also the spectral properties (positive definiteness) of the Jacobian matrix of the equilibrium equation, and therefore, the convergence characteristics of the accompanying Newton-Raphson algorithm. We saw that, to preserve the positive definiteness of the full-order Jacobian matrix, one should strive to choose the sampling indices ${\textstyle {\mathcal {I}}}$ so as to make the factor –-defined previously in Eq.(4.96)–-:

$f_{F}({\boldsymbol {\Psi }},{\mathbb {B} ^{*}},{\mathcal {I}})={\dfrac {\Vert {\boldsymbol {\hat {R}}}_{({\mathcal {I}})}{\mathbb {\hat {B}} ^{*}}_{({\mathcal {I}})}\Vert _{F}}{\Vert ({\boldsymbol {I}}-{\boldsymbol {\hat {R}}}_{({\mathcal {I}})}){\mathbb {\hat {B}} ^{*}}_{({\mathcal {I}})}\Vert _{F}}}$

(4.107)

as small as possible.

4.5.2 Optimization approach: basic and stabilizing sampling points

Unfortunately, the minimization of the approximation error represented by expression Eq.(4.106) and the minimization of Eq.(4.107) are in general conflicting goals. For instance, numerical experiments show that when the selection is driven exclusively by accuracy considerations, the resulting Jacobian matrix becomes indefinite at certain states of deformation –-especially when inelastic deformations are severe–-, leading occasionally to convergence failures. These goals must be therefore balanced in order to arrive at an accurate and at the same time robust solution scheme.

To accomodate these conflicting requirements, we propose here a heuristic strategy that basically consists in treating the minimization of Eq.(4.106) and Eq.(4.107) as two separated, sequential problems –-in the spirit of the so-called “greedy” optimization algorithms [76]. The set of sampling points is assumed to be divided into two disjoint subsets ${\textstyle {\mathcal {I}}_{\sigma }}$ and ${\textstyle {\mathcal {I}}_{B}}$:

${\mathcal {I}}={\mathcal {I}}_{\sigma }\cup {\mathcal {I}}_{B}.$

(4.108)

The first subset ${\textstyle {\mathcal {I}}_{\sigma }=\{i_{1},i_{2},\cdots i_{p_{\sigma }}\}}$ is obtained as the minimizer of the error estimation given in Eq.(4.106), viz.:

${\mathcal {I}}_{\sigma }={\textrm {arg}}\;{\underset {{\mathcal {K}}\subseteq \{1,2\ldots n_{g}\}}{\textrm {min}}}\,{e}_{\sigma }^{rec}({\boldsymbol {\Psi }},{\mathcal {K}}).$

(4.109)

Once the set ${\textstyle {\mathcal {I}}_{\sigma }}$ is determined, the remaining sampling indices ${\textstyle {\mathcal {I}}_{B}=\{j_{1},j_{2}\cdots j_{p_{B}}\}}$ (${\textstyle p_{\sigma }+p_{B}=p}$) are calculated as

${\mathcal {I}}_{B}={\textrm {arg}}\;{\underset {{\mathcal {K}}\subseteq \{1,2\ldots n_{g}\}}{\textrm {min}}}\,f_{F}({\boldsymbol {\Psi }},{\mathbb {B} ^{*}},{\mathcal {I}}_{\sigma }\cup {\mathcal {K}}).$

(4.110)

Remark 3: It must be noted here that the minimization problem represented by Eq.(4.109) is in essence the same problem addressed in (standard) interpolatory-based, model reduction approaches for determining, given a set of empirical basis functions, the optimal location of associated interpolations points. For this reason, we shall refer to the set of points arising from solving this minimization problem as the standard or basic sampling points –-these are the Best Interpolation Points of Nguyen et al. [30], or the “magic points” of Maday et al. [67]. By contrast, the necessity of introducing points that attempt to solve problem (4.110) is a consequence of expanding the stress approximation space in the first place –-the main innovative feature of our approach–-, and it is therefore not present in other model reduction strategies. We shall call ${\textstyle \{\mathbf {x} _{{\mathcal {I}}_{B}(1)},\mathbf {x} _{{\mathcal {I}}_{B}(2)}\ldots \mathbf {x} _{{\mathcal {I}}_{B}(p_{B})}\}}$ the set of stabilizing sampling points.

The number of basic sampling points must satisfy the necessary condition ${\textstyle p_{\sigma }\geq n_{\sigma }/s}$. In general, taking ${\textstyle p_{\sigma }=n_{\sigma }}$ suffices to ensure highly satisfactory approximations. How many, on the other hand, stabilizing sampling points have to be added to safely render positive definite the Jacobian matrix –-for at least a representative range of macroscopic state deformations–- is a question that can only be answered empirically. In the examples presented in the ensuing Chapter, it has been found that a conservative answer is to use as many stabilizing sampling points as displacement basis modes (${\textstyle p_{B}=n_{u}}$).

In order not to disrupt the continuity of the presentation, the discussion concerning the algorithms employed here for addressing optimization problems (4.109) and (4.110) is postponed to Appendix D.

4.6 Summary

Lastly, for the reader's convenience and easy reference, the online HP-ROM cell problem, along with the offline steps that leads to the the hyperreduced operators appearing in the online problem, are summarized in Boxes 4.6.1 and 4.6.2 .

1. Compute FE displacement fluctuations and stress snaphots for representative, input macro-strain histories. Apply –-see Appendix B–- the elastic/inelastic POD to the resulting snapshot matrices to obtain the displacement fluctuation and stress basis matrices (${\textstyle {\boldsymbol {\Phi }}\in \mathbb {R} ^{n\cdot d\times n_{u}}}$ and ${\textstyle {\boldsymbol {\Psi }}\in \mathbb {R} ^{n_{g}\cdot s\times n_{\sigma }}}$, respectively).
2. Calculate the weighted matrix of fluctuating strain modes ${\textstyle {\mathbb {B} ^{*}}\in \mathbb {R} ^{n_{g}\cdot s\times n_{\sigma }}}$ using Eqs. (3.30) and (4.35).
3. Select a set ${\textstyle {\mathcal {I}}}$ of sampling indices optimal for the basis matrices ${\textstyle {\boldsymbol {\Psi }}}$ and ${\textstyle {\mathbb {B} ^{*}}}$ following the procedure sketched in Section 4.5 –-and described more in detail in Appendix D.
4. Finally, using ${\textstyle {\boldsymbol {\Psi }}}$, ${\textstyle {\mathbb {B} ^{*}}}$ and ${\textstyle {\mathcal {I}}}$, construct the hyperreduced-order matrices ${\textstyle {\mathbb {\hat {B}} ^{**}}\in \mathbb {R} ^{p\cdot s\times n_{u}}}$ and ${\textstyle \mathbb {T} \in \mathbb {R} ^{s\times p\cdot s}}$; the expressions for these matrices read:

   ${\mathbb {\hat {B}} ^{**}}=({\boldsymbol {I}}-{\boldsymbol {\hat {R}}}){\mathbb {\hat {B}} ^{*}}=({\boldsymbol {I}}-{\boldsymbol {\mathcal {P}}}_{({\mathcal {I}})}{\boldsymbol {R}})({\boldsymbol {\mathcal {P}}}_{({\mathcal {I}})}{\mathbb {B} ^{*}})$

   (4.111)

and

$\mathbb {T} {\mathrel {\mathop {:}}}={\dfrac {1}{V}}{\begin{bmatrix}{\sqrt {w_{1}}}{\boldsymbol {I}}&{\sqrt {w_{2}}}{\boldsymbol {I}}&\cdots &{\sqrt {w_{n_{g}}}}{\boldsymbol {I}}\end{bmatrix}}{\boldsymbol {R}}$

(4.112)

where ${\textstyle {\boldsymbol {R}}={\boldsymbol {\Psi }}({\boldsymbol {\hat {\Psi }}}^{T}{\boldsymbol {\hat {\Psi }}})^{-1}{\boldsymbol {\hat {\Psi }}}^{T}}$ and ${\textstyle {\boldsymbol {\hat {\Psi }}}={\boldsymbol {\mathcal {P}}}_{({\mathcal {I}})}{\boldsymbol {\Psi }}}$ (Note: ${\textstyle \mathbb {T} }$ is the global matrix form of the weighting matrices presented previously in Eq.(4.10)).

Box 4.6.1 Offline stage. Pre-computation of reduced basis and hyperreduced operators (Note: ).

1. Initial data: ${\textstyle {\boldsymbol {U}}_{n}^{*}\in \mathbb {R} ^{n_{u}}}$ (reduced vector of displacement fluctuations at ${\textstyle t_{n}}$), ${\textstyle {\boldsymbol {\epsilon _{M}}}_{n}}$ (macroscopic strain vector at ${\textstyle t_{n}}$), and ${\textstyle \{{\boldsymbol {\xi }}_{n}\!(\mathbf {x} _{{\mathcal {I}}_{1}}),{\boldsymbol {\xi }}_{n}\!(\mathbf {x} _{{\mathcal {I}}_{2}}),\ldots {\boldsymbol {\xi }}_{n}\!(\mathbf {x} _{{\mathcal {I}}_{p}})\}}$ (internal variables at ${\textstyle t_{n}}$ at the selected sampling points).
2. Input data: ${\textstyle {\boldsymbol {\epsilon _{M}}}_{n+1}}$ (macroscopic strain vector at ${\textstyle t_{n+1}}$)
3. Given the above initial and input data, find ${\textstyle {\boldsymbol {U}}_{n+1}^{*}\in \mathbb {R} ^{n_{u}}}$ such that

   ${\mathbb {\hat {B}} ^{**^{T}}}{\hat {\boldsymbol {\Sigma }}}({\boldsymbol {\epsilon _{M}}}_{n+1},{\boldsymbol {U}}_{n+1}^{*})={\boldsymbol {0}},$

   (4.113)

where

${\hat {\boldsymbol {\Sigma }}}={\begin{bmatrix}{\sqrt {w_{{\mathcal {I}}_{1}}}}{\boldsymbol {\sigma }}^{T}(\mathbf {x} _{{\mathcal {I}}_{1}},\cdot )&{\sqrt {w_{{\mathcal {I}}_{2}}}}{\boldsymbol {\sigma }}^{T}(\mathbf {x} _{{\mathcal {I}}_{2}},\cdot )&\cdots &w_{{\mathcal {I}}_{p}}{\boldsymbol {\sigma }}^{T}(\mathbf {x} _{{\mathcal {I}}_{p}},\cdot )\end{bmatrix}}^{T}$

(4.114)

(here, ${\textstyle {\boldsymbol {\sigma }}(\mathbf {x} _{{\mathcal {I}}_{i}},\cdot )}$ denotes the stress vector evaluated at the ${\textstyle i-th}$ sampling point through the corresponding constitutive equation).

4. Output data: Once Eq.(4.117) has been solved for ${\textstyle {\boldsymbol {U}}_{n+1}^{*}}$, update the macroscopic stress vector as

   $\left.{\boldsymbol {\sigma _{M}}}\right|_{n+1}=\mathbb {T} \,{\hat {\boldsymbol {\Sigma }}}({\boldsymbol {\epsilon _{M}}}_{n+1},{\boldsymbol {U}}_{n+1}^{*}).$

   (4.115)

Box 4.6.2 Online stage (solution of the hyperreduced-order RVE equilibrium problem for given macroscopic strains).

5 Numerical results

This section is intended to illustrate the performance and assess the efficiency of the proposed model reduction strategy in solving the fine scale BVP corresponding to a porous metal material under plane strain conditions.

5.1 Microstructure description

The voids are elliptical in shape (with eccentricity equal to 0.3), randomly distributed (with porosity equal to 0.3), and have aligned major axes ranging in length –-according to the cumulative probability distribution displayed in figure 3.b–- from 0.2 to 1.5 mm.

Figure 3: a) Finite element mesh of the RVE corresponding to the porous metal material. b) Cumulative probability distribution followed by the length of the pore major axes.

The mechanical behavior of the metal matrix is modeled by a rate-independent, Von Mises elastoplastic model endowed with the following non-linear, isotropic hardening saturation law (consult Ref. [77] for details on the implementation of this elastoplastic model):

$\sigma _{u}(\alpha )=\sigma _{0}+{\bar {H}}\alpha +(\sigma _{\infty }-\sigma _{0})(1-exp(-\alpha \delta {)).}$

(5.1)

Here, ${\textstyle \sigma _{u}}$ stands for the yield stress, ${\textstyle \alpha \geq 0}$ denotes the equivalent plastic strain; and ${\textstyle \sigma _{0}=75.0\;MPa}$, ${\textstyle \sigma _{\infty }=100.0\;MPa}$, ${\textstyle \delta =2500.0}$ and ${\textstyle {\bar {H}}=5000}$ ${\textstyle MPa}$ are material constants. The Young's modulus and Poisson's coefficient, on the other hand, are equal to ${\textstyle E_{m}=75\,GPa}$ and ${\textstyle \nu _{m}=0.3}$, respectively (these material constants corresponds approximately to Aluminum).

5.2 RVE and finite element discretization

The size of the RVE was determined by conducting finite element analyses on square domains of increasing size subject to vanishing displacement fluctuations boundary conditions. It was found that the macroscopic stress responses calculated under representative macroscopic strain paths (stretching along the longitudinal and transversal directions, and shearing) of all samples above ${\textstyle 20}$x${\textstyle 20}$ ${\textstyle mm^{2}}$ were practically indistinguishable. According to the definition of RVE provided in Section 2.1.1, this fact indicates that any subvolume of ${\textstyle 20}$x${\textstyle 20}$ ${\textstyle mm^{2}}$ can be considered as a Representative Volume Element (RVE) of the porous material under study.

The finite element discretization corresponding to the particular ${\textstyle 20}$x${\textstyle 20}$ ${\textstyle mm^{2}}$ RVE employed in the ensuing simulations is shown in figure 3.a. The number of (four-node bilinear) elements is ${\textstyle n_{e}=9746}$, and the number of nodes ${\textstyle n=11825}$. The employed quadrature formula, on the other hand, is the standard ${\textstyle 2}$x${\textstyle 2}$ Gauss rule, the total number of Gauss points amounting thus to ${\textstyle n_{g}=4\,n_{e}=38984}$. To overcome incompressibility issues while maintaining the displacement-based formulation presented in the preceding sections, the commonly known as “B-bar” approach is adopted. (This means that, in this case, the reduced “B-matrix” ${\textstyle {{\boldsymbol {B}}^{*}}(\mathbf {x} )}$ appearing in the formulation of the HP-ROM is not constructed using the gradients of the shape functions, as indicated by Eq.(3.27), but rather using the modified “B-matrix” emanating from the three-field Hu-Washizu variational principle [77]). The constitutive differential equations are integrated in time using the classical (fully implicit) backward-Euler scheme.

5.3 Sampling of parameter space

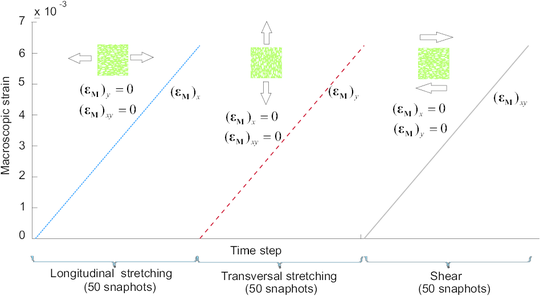
Figure 4: Macro-strain trajectories used for generating the displacement and stress snapshots.

The first step in the process of constructing the reduced basis is the sampling of the input parameter space; we saw in Section 3.1.1 that, in the cell equilibrium BVP, this process amounts to select representative macroscopic strain histories. The three macroscopic strain histories (${\textstyle n_{hst}=3}$) used in the case under study are depicted in figure 4. In each of these strain trajectories, one of the (independent) strain components follows a linear ascending path while the magnitude of the other two components is set to zero. The time domain for each strain history is discretized into ${\textstyle n_{stp}=50}$ equally spaced steps, resulting in a total number of ${\textstyle n_{snp}=n_{hst}\cdot n_{stp}=150}$ snapshots.

5.4 Dimensionality reduction: a priori error analysis

The finite element displacement fluctuation and stress fields computed at each time step of the input strain trajectories shown above are multiplied by their corresponding weighting matrices (${\textstyle {\bar {\mathbf {M} }}}$ and ${\textstyle {\boldsymbol {W}}^{1/2}}$) and stored, in the snapshot matrices ${\textstyle {\boldsymbol {\bar {X}}}_{u}\in \mathbb {R} ^{n\cdot d\times n_{snp}}}$ (${\textstyle n\cdot d=11825\cdot 2=23650}$) and ${\textstyle {\boldsymbol {X}}\in \mathbb {R} ^{n_{g}\cdot s\times n_{snp}}}$ (${\textstyle n_{g}\cdot s=38984\cdot 4=155936}$), respectively. Then, these matrices are subjected to the SVD-based, elastic/inelastic dimensionality reduction process sketched in Section 3.1.2 –-and described more in detail in Appendix B–- in order to generate an optimal set of basis vectors for both the displacements fluctuation and stress solution spaces.

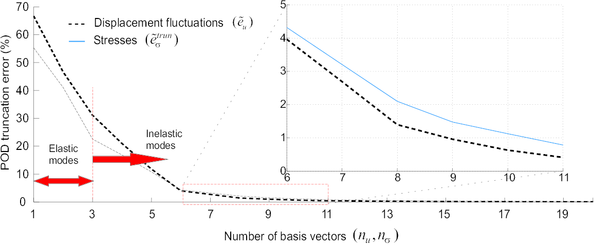
Figure 5: POD truncation error estimates ${\tilde {e}}_{u}$ (for the displacement fluctuations, see Eq.(5.2)) and ${\tilde {e}}_{\sigma }^{trun}$ (for the stresses, see Eq.(5.3)) versus number of basis vectors employed in the approximation ($n_{u}$ and $n_{\sigma }$, respectively). The portion between 6 and 11 modes is shown in magnified form.

To elucidate which of these basis vectors constitute the “essential” modes of the response, we plot in Figure 5 the dimensionless POD truncation error estimates defined, for the displacement fluctuations, as:

${\tilde {e}}_{u}(n_{u}){\mathrel {\mathop {:}}}={\dfrac {\Vert {\boldsymbol {\bar {X}}}_{u}-{\boldsymbol {\bar {X}}}_{u}^{*}(n_{u})\Vert _{F}}{\Vert {\boldsymbol {\bar {X}}}_{u}\Vert _{F}}},$

(5.2)

and for the stresses:

${{\tilde {e}}_{\sigma }^{trun}}(n_{\sigma }){\mathrel {\mathop {:}}}={\dfrac {\Vert {\boldsymbol {X}}-{\boldsymbol {X}}^{*\bot }(n_{\sigma })\Vert _{F}}{\Vert {\boldsymbol {X}}\Vert _{F}}},$

(5.3)

${\textstyle {\boldsymbol {\bar {X}}}_{u}^{*}(n_{u})}$ and ${\textstyle {\boldsymbol {X}}^{*\bot }(n_{\sigma })}$ being the orthogonal projection of ${\textstyle {\boldsymbol {\bar {X}}}_{u}}$ and ${\textstyle {\boldsymbol {X}}}$ onto the span of the first ${\textstyle n_{u}}$ and ${\textstyle n_{\sigma }}$ basis vectors, respectively (Remark: these error measures can be expressed in terms of singular values arising from the SVD of the snapshot matrices ${\textstyle {\boldsymbol {\bar {X}}}_{u}}$ and ${\textstyle {\boldsymbol {X}}}$; see Propositions B.1.1 and D.1).

Figure 6: Contour plots of the euclidean norm of the first 6 displacement fluctuations modes ($\Vert {\boldsymbol {\mathit {\Phi }}}_{i}\Vert$, $i=1,2\ldots 5$). Deformed shapes are scaled up by a factor of 15.

It can be observed in Figure 5 that both error measures decrease monotonically with increasing order of truncation –-this is a mere consequence of the optimality properties of the SVD–-, and at approximately the same rate; the decay is more pronounced from 1 to 6 modes, and becomes more gradual thereafter, tending asymptotically to zero as the number of modes increases. The truncation error for both stresses and displacement fluctuations at ${\textstyle n_{\sigma }=n_{u}=6}$ is around ${\textstyle 5\%}$. In terms of dimensionality reduction, this means that the data contained in the snapshot matrices can be “compressed” to a factor of ${\textstyle (n_{u}/n_{snp})\cdot 100=(6/150)\cdot 100=4\%}$ and still retain 95% of the information –-the essential information. The first 6 basis functions (3 elastic and 3 inelastic) for both stresses and displacement fluctuations, therefore, are to be regarded as essential modes in the characterization of the mechanical response of the concerned RVE. By way of illustration, we plot in Figure 6 the contour plots of the euclidean norm of such 6 essential displacement fluctuations modes (${\textstyle \Vert {\boldsymbol {\mathit {\Phi }}}_{i}\Vert }$, ${\textstyle i=1,2\ldots 6}$).

Observation 5: A noteworthy feature in Figure 5 is that the truncation errors ${\textstyle {\tilde {e}}_{u}}$ and ${\textstyle {\tilde {e}}_{\sigma }^{trun}}$ are of the same order of magnitude for all level of truncations. This fact suggests that the optimum relation between order of truncations may be not too far from ${\textstyle n_{\sigma }/n_{u}=1}$. For this reason, and for the sake of simplicity in the ensuing parametric studies, we shall assume hereafter that ${\textstyle n_{\sigma }=n_{u}}$ (equal levels of truncation for both stresses and displacement fluctuations). Physically, this seems to be a fairly reasonable choice: the quality of the stress solution depends largely, through the pertinent constitutive relationships, on the quality of the displacement solution, and vice versa. Therefore, it seems pointless to increase the quality of the approximation in stresses without accompanying such an increase with a concomitant enlargement of the displacement solution space.

5.5 Sampling points

5.5.1 Basic sampling points

Once the stress and displacement fluctuation basis vectors have been determined, the next offline step consists in the selection –-among the full set of finite element Gauss points–-of an optimal set of sampling points. Following the strategy described in Section 4.5.2, we carry out such a selection by first computing the location of what we have called basic sampling points 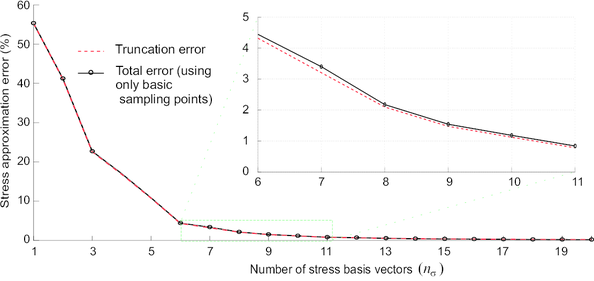${\textstyle \{\mathbf {x} _{{\mathcal {I}}_{\sigma }(1)},\mathbf {x} _{{\mathcal {I}}_{\sigma }(2)}\ldots \mathbf {x} _{{\mathcal {I}}_{\sigma }(p_{\sigma })}\}}$.

Figure 7: Estimates for the POD truncation (${\tilde {e}}_{\sigma }^{trun}$, see Eq.(5.3)) and total (${\tilde {e}}_{\sigma }$, see Eq.(5.4)) stress error versus number of basis vectors employed in the approximation ($n_{\sigma }$). The total error estimate is computed using only the set of basic sampling points (${\tilde {e}}_{\sigma }={\tilde {e}}_{\sigma }(n_{\sigma },{\mathcal {I}}_{\sigma })$, with $p_{\sigma }=n_{\sigma }$). The portion between 6 and 11 modes is shown in magnified form.

To assess the efficiency of the employed Hierarchical Interpolation Points Method, abbreviated HIPM, (set out in Appendix D.2.1), we plot in Figure 7 the estimates for both the POD truncation (shown previously in Figure 5) and total stress error versus the number of stress modes ${\textstyle n_{\sigma }}$ (in using this algorithm, it is assumed that ${\textstyle p_{\sigma }=n_{\sigma }}$). The total stress error estimate is defined as

${\tilde {e}}_{\sigma }(n_{\sigma },{\mathcal {I}}_{\sigma }){\mathrel {\mathop {:}}}={\dfrac {\Vert {\boldsymbol {X}}-{\boldsymbol {X}}^{*}(n_{\sigma },{\mathcal {I}}_{\sigma })\Vert _{F}}{\Vert {\boldsymbol {X}}\Vert _{F}}}$

(5.4)

where ${\textstyle {\boldsymbol {X}}^{*}(n_{\sigma },{\mathcal {I}}_{\sigma })}$ denotes the oblique projection (calculated using sampling points ${\textstyle {\mathcal {I}}_{\sigma }}$) of ${\textstyle {\boldsymbol {X}}}$ onto the span of the first ${\textstyle n_{\sigma }}$ basis vectors (${\textstyle {\boldsymbol {\Psi }}_{1},{\boldsymbol {\Psi }}_{2}\ldots {\boldsymbol {\Psi }}_{n_{\sigma }}}$). The number of effective trailing modes employed in the calculations is ${\textstyle n_{\Gamma }=20}$. (The connection between this error estimate and the singular values of the trailing stress modes is disclosed in Appendix 10.1). It can be appreciated in Figure 7 that both the total error and the truncation error curves are practically coincident, a fact that indicates that the contribution of the reconstruction error:

${\tilde {e}}_{\sigma }^{rec}={\sqrt {{{\tilde {e}}_{\sigma }}^{2}-{{\tilde {e}}_{\sigma }^{trun\,2}}}}={\dfrac {\Vert {\boldsymbol {X}}^{*\bot }(n_{\sigma })-{\boldsymbol {X}}^{*}(n_{\sigma },{\mathcal {I}}_{\sigma })\Vert _{F}}{\Vert {\boldsymbol {X}}\Vert _{F}}}$

(5.5)

( the error introduced as a result of using only ${\textstyle p_{\sigma }}$ sampling points instead of the entire set of finite element Gauss points, see Section 4.5.1) is negligible in comparison to the discrepancies due to truncation of the POD basis. For ${\textstyle n_{\sigma }=p_{\sigma }=6}$, for instance, the reconstruction error is less than ${\textstyle 3\%}$ of the total stress error. In view of these results, it becomes clear that further refinements in the algorithm for selecting the basic sampling points are in principle not necessary: the employed HIPM optimization algorithm, however heuristic, satisfactorily fulfills this purpose. If one wishes to lower the stress approximation error, it is far more effective to simply increase the level of truncation.

5.5.2 Stabilizing sampling points

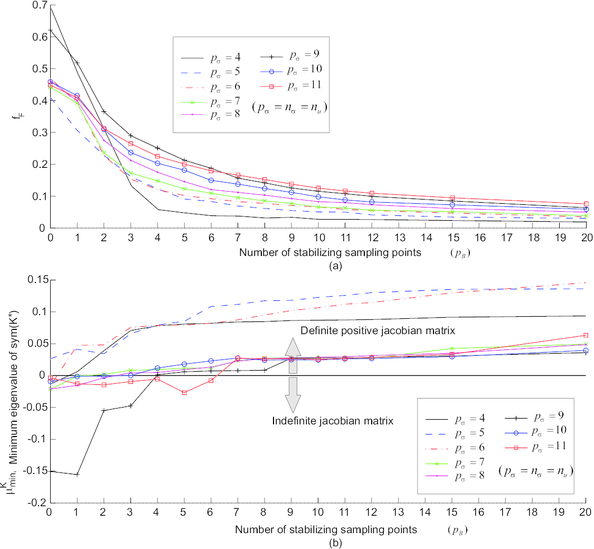
Figure 8: a) Factor $f_{F}$ (defined in Eq.(4.98)) versus number of stabilizing sampling points $p_{B}$ for varying numbers of basic sampling points $p_{\sigma }$ (with $p_{\sigma }=n_{\sigma }=n_{u}$). b) Minimum eigenvalue $\mu _{min}^{K}$ (over all time steps and iterations for each $p_{\sigma }$) of the symmetric part of the reduced-order Jacobian matrix ${\boldsymbol {K}}^{*}$ versus number of stabilizing sampling points $p_{B}$.

Concerning what we have termed “stabilizing sampling points”, Figure 8.a contains the graphs, for varying levels of truncation, of factor ${\textstyle f_{F}}$ defined in Eq.(4.96) as a function of the number of stabilizing sampling points ${\textstyle p_{B}}$. To study the influence of including such points on the spectral properties –-positive defineteness–- of the stiffness matrix, these graphs are accompanied, see figure 8.b, by the plots of the minimum eigenvalue ${\textstyle \mu _{min}^{K}}$ (over all time steps and iterations for each case) of the symmetric part of the reduced-order Jacobian matrix ${\textstyle {\boldsymbol {K}}^{*}}$ versus ${\textstyle p_{B}}$. It can be seen that ${\textstyle f_{F}}$ decreases monotonically as the number of stabilizing sampling points increases, and such a decrease is reflected, as theoretically anticipated in Section 4.4.4, in the improvement of the spectral properties of the reduced-order Jacobian matrix (higher ${\textstyle \mu _{min}^{K}}$ as ${\textstyle p_{B}}$ raises). For clarity, the minimum number of stabilizing sampling points required, for each level of truncation, to render positive definite ${\textstyle {\boldsymbol {K}}^{*}}$ is plotted in Figure 9.

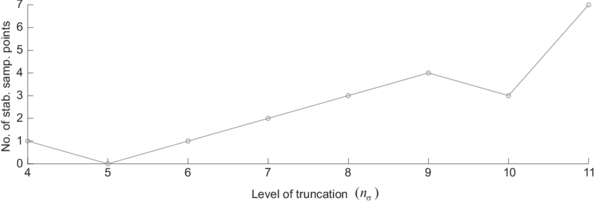
Figure 9: Minimum number of stabilizing sampling points required to make the Jacobian matrix ${\boldsymbol {K}}^{*}$ definite positive for each level of truncation $n_{\sigma }=n_{u}=p_{\sigma }$ (deduced from Figure 8).

From this plot, it can be gleaned that, roughly, the higher the level of truncation (and thus the number of basic sampling points), the more stabilizing sampling points appear to be needed to ensure the positive definiteness of ${\textstyle {\boldsymbol {K}}^{*}}$. For ${\textstyle n_{\sigma }=p_{\sigma }=6}$, adding just one stabilizing sampling points suffices, while for ${\textstyle n_{\sigma }=p_{\sigma }=11}$, 7 points are required.

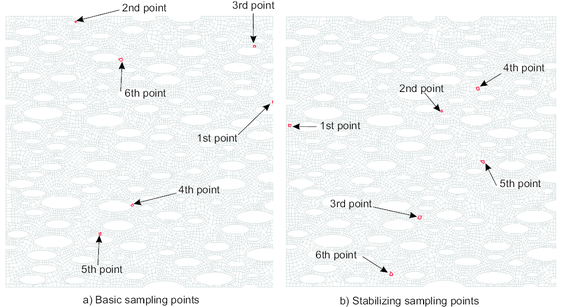
Figure 10: Location within the RVE of the finite elements (marked in red) that contains the first $p_{\sigma }=p_{B}=6$ basic and stabilizing sampling points.

Observation 6: The values shown in Figure 9 correspond to the minimum ${\textstyle p_{B}}$ that leads to positive definite ${\textstyle {\boldsymbol {K}}^{*}}$ when the prescribed strain path coincides with any of the “training” strain trajectory (displayed in Figure 4 ). Unfortunately, there is no guarantee that the Jacobian matrix will also exhibit this desirable property for prescribed strain histories different from the training ones. Thus, in view of such uncertainty, and in the interest of robustness, it is preferable to stay on the side of “caution” in this regard and use more stabilizing sampling points that the minimum number indicated by the analysis based on the training strain trajectories. It is the authors' experience that a “safe” estimate for ${\textstyle p_{B}}$ is to simply take ${\textstyle p_{B}=p_{\sigma }}$ –-that is, equal number of basic and stabilizing sampling points. In adopting such a rule, the authors have not observed any convergence failures whatsoever, neither in the example under consideration nor in other cases not shown here. The location of the first ${\textstyle p_{\sigma }=6}$ basic sampling points and the corresponding ${\textstyle p_{B}=6}$ stabilizing sampling points is depicted in Figure 10.

5.6 A posteriori errors: consistency analysis

The error measures displayed previously in Figures 5 and 7 only depend on the outcome of the SVD of the snapshot matrices; they can be calculated, thus, before actually constructing the reduced-order model. Error analyses based on such measures serve the useful purpose of providing a first hint of how many stress and displacement fluctuations modes are needed to satisfactorily replicate the full-order, finite element solution, and thereby, of prospectively evaluating the viability of the reduced basis approach itself.

However, these a priori error estimates do not tell the whole story. Expression (5.4) for the stress approximation error presumes that the stress solution at the chosen sampling points is the one provided by the finite element model, thus ignoring the fact that, actually, in the reduced-order model, and for the general case of nonlinear, dissipative materials –-for linear elasticity, the approximation is exact, see Remarks 1 and D.1.2–- the stress information at such points at a given time step is already polluted by truncation (in displacement fluctuations and stresses) and reconstruction (in stresses) errors originated in previous time steps. To quantify the extent to which this amalgam of accumulated errors affects the predictions furnished by the HP-ROM, it is necessary to perform a consistency analysis.

Generally speaking, a reduced basis approximation is said to be consistent if, in the limit of no truncation, it introduces no additional error in the solution of the same problem for which the data used in constructing the basis functions were acquired [78]. In the BVP under consideration, thus, consistency implies that, when using as input macro-strain paths the same trajectories employed in the “training” process, results obtained with the HP-ROM should converge, as ${\textstyle n_{\sigma }}$ and ${\textstyle n_{u}}$ increases, to the solution furnished by the full-order, finite element model. This condition can be checked by studying the evolution of the error measures defined as

${\tilde {e}}_{u}^{ROM}(n_{u},n_{\sigma },{\mathcal {I}}){\mathrel {\mathop {:}}}={\dfrac {\Vert {\boldsymbol {\bar {X}}}_{u}-{\boldsymbol {\bar {X}}}_{u}^{*ROM}(n_{u},n_{\sigma },{\mathcal {I}})\Vert _{F}}{\Vert {\boldsymbol {\bar {X}}}_{u}\Vert _{F}}},$

(5.6)

for the displacement fluctuations, and

${\tilde {e}}_{\sigma }^{ROM}(n_{u},n_{\sigma },{\mathcal {I}}_{\sigma }){\mathrel {\mathop {:}}}={\dfrac {\Vert {\boldsymbol {X}}-{\boldsymbol {X}}^{*ROM}(n_{u},n_{\sigma },{\mathcal {I}}_{\sigma })\Vert _{F}}{\Vert {\boldsymbol {X}}\Vert _{F}}},$

(5.7)

for the stresses. ( The superscript “ROM” is appended to highlight that, unlike ${\textstyle {\boldsymbol {\bar {X}}}_{u}^{*}}$ and ${\textstyle {\boldsymbol {X}}^{*}}$ in Eqs. (5.2) and (5.4), ${\textstyle {\boldsymbol {\bar {X}}}_{u}^{*ROM}}$ and ${\textstyle {\boldsymbol {X}}^{*ROM}}$ are matrices of displacement fluctuation and stress snapshots computed using the HP-ROM). Figures 11.a and 11.b contain the graphs of these a posteriori error measures, along with their respective a priori counterparts ${\textstyle {\tilde {e}}_{u}}$ (Eq. 5.2) and ${\textstyle {\tilde {e}}_{\sigma }}$ (Eq. 5.4), versus the level of truncation. It becomes clear from these graphs that consistency, in the sense given above, is observed in terms of both displacement fluctuations and stresses: the a posteriori error measures ${\textstyle {\tilde {e}}_{u}^{ROM}}$ and ${\textstyle {\tilde {e}}_{\sigma }^{ROM}}$ mimic essentially the decreasing tendency of their a priori counterparts ${\textstyle {\tilde {e}}_{u}}$ and ${\textstyle {\tilde {e}}_{\sigma }}$, respectively. It can be seen also that the a priori error estimations ${\textstyle {\tilde {e}}_{u}}$ and ${\textstyle {\tilde {e}}_{\sigma }}$ constitute (rather tight) lower bounds for their a posteriori counterparts ${\textstyle {\tilde {e}}_{u}^{ROM}}$ and ${\textstyle {\tilde {e}}_{\sigma }^{ROM}}$, respectively. This can be better appreciated, for the stresses, in Figure 12, where the ratio ${\textstyle {\tilde {e}}_{\sigma }^{ROM}/{\tilde {e}}_{\sigma }}$ versus the level of truncation is plotted.

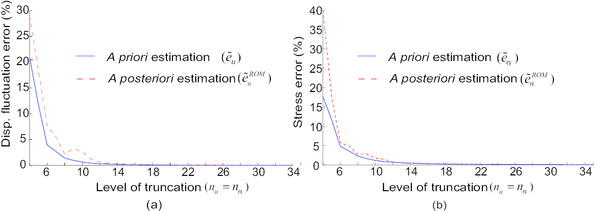
Figure 11: Comparison of the evolution of a priori and a posteriori error measures versus the level of truncation (using $n_{u}=n_{\sigma }=p_{\sigma }=p_{B}$). a) Displacement fluctuations (see Eqs. 5.2 and 5.6). b) Stresses (see Eqs. 5.4 and 5.7)

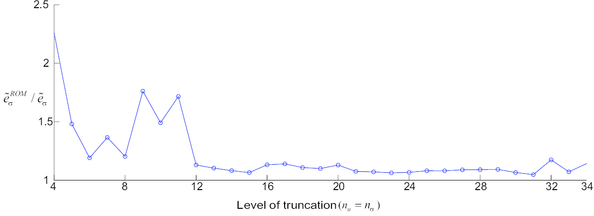
Figure 12: Ratio ${\tilde {e}}_{\sigma }^{ROM}/{\tilde {e}}_{\sigma }$ between the a posteriori and a priori measures for the stress approximation error against the level of truncation (using $n_{u}=n_{\sigma }=p_{\sigma }=p_{B}$).

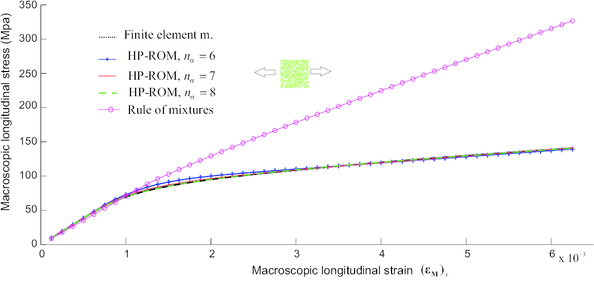
Figure 13: Longitudinal macroscopic stress versus longitudinal macroscopic strain computed using the FEM, the HP-ROM with $n_{\sigma }=n_{u}=6,7,8$, and the elementary rule of mixtures.

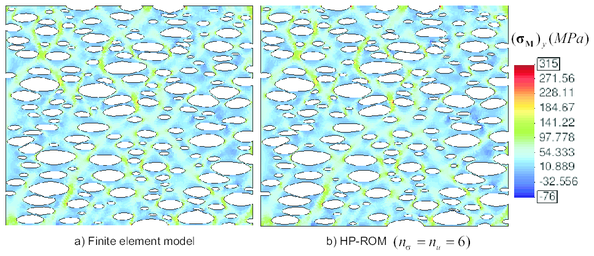
Figure 14: Contour plot of transversal stresses computed at the end of the first “training” strain history using a) FEM (b) HP-ROM with $n_{\sigma }=n_{u}=6$. Deformed shapes are exaggerated (by a factor of 20).

The degree of approximation that can be achieved using the proposed HP-ROM is quantified in a more “engineering” fashion in Figure 13, where we plot, for the case of the first training strain history (stretching in the longitudinal direction), the longitudinal, macroscopic stress-strain curves computed using the FE model, on the one hand, and the HP-ROM with ${\textstyle n_{u}=n_{\sigma }=6,7,8}$ modes, on the other hand. In order to highlight the non-trivial character of such a stress-strain response, we include also in Figure 13 the solution provided by the classical rule of mixtures (zero fluctuations at all points in the RVE [47]). Observe that the maximum deviation from the FE response when using 6 modes (3 elastic and 3 inelastic) takes place at the onset of plastic yielding and is below 8%; remarkably, as deformation continues, this deviation gradually diminishes, being practically negligible at the end of the process –-in stark contrast to the case of the simplistic rule of mixtures, that overpredicts in more than 300% the final stress. Furthermore, by just increasing the order of truncation to ${\textstyle n_{\sigma }=n_{u}=8}$, differences between the HP-ROM and the FEM responses become virtually imperceptible at all levels of deformation. Resemblance between HP-ROM and FEM results can also be appreciated in terms of stress distribution in the contour plots shown in Figure 14. Visually, there are no discernible differences between the two contour plots.

5.7 “Training” errors

The studies presented in the preceding subsections were aimed at examining the errors incurred in approximating the snapshot solution space ${\textstyle {\mathcal {V}}_{u}^{snp}}$ by the reduced-order subspace ${\textstyle {\mathcal {V}}_{u}^{*}\in {\mathcal {V}}_{u}^{snp}}$ spanned by the POD basis vectors –-in the terminology of Section 3.1.1–-, and to check that when ${\textstyle {\mathcal {V}}_{u}^{*}\rightarrow {\mathcal {V}}_{u}^{snp}}$, the solution provided by the HP-ROM converges to that obtained with the FEM. But recall that the snapshot space ${\textstyle {\mathcal {V}}_{u}^{snp}}$ is but a (presumably representative) subspace of ${\textstyle {\mathcal {V}}_{u}^{\epsilon }}$, the manifold of ${\textstyle {\mathcal {V}}_{u}^{h}}$ induced by the parametric dependence of the cell BVP on the prescribed macroscopic strain history. Consequently, in general –-for an arbitrary input strain trajectory–- the HP-ROM solution will not converge to the solution provided by the FEM. To complete the error assessment analysis, thus, it is necessary to estimate also the errors inherent to the sampling of the parameter space –-we call them training errors–- and judge whether the selected training strain trajectories generate a snapshot subspace that is indeed representative of such a solution space¹ ${\textstyle {\mathcal {V}}_{u}^{\epsilon }}$.

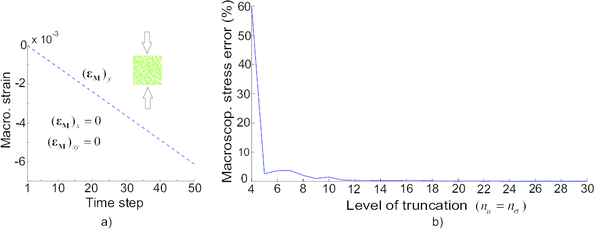
Figure 15: a) First strain trajectory employed for assessing training errors. b) Plot of the macroscopic error estimator ${\tilde {E}}_{\sigma ,M}^{ROM}$ (see Eq.(5.8)) corresponding to this testing trajectory versus level of truncation ($n_{\sigma }=n_{u}$)

Ideally, one should carry out this error assessment by picking up, guided by some sound, statistically-based procedure, a sufficiently large set of strain paths and by comparing the solutions computed by the FEM and HP-ROM under such input strain paths for varying levels of truncation. Such a degree of rigor, however, is beyond the scope of the present work. Here, we limit ourselves here to analyze the quality of the HP-ROM approximation obtained for two different input strain histories, namely, a uniaxial compression test, and a biaxial loading/unloading test.

(¹) To put it in less mathematical terms –-by appealing to the the analogy, introduced in Remark 1, between the training of the cell reduced-order model and the calibration of standard phenomenological models–- we have “calibrated” our HP-ROM using the training tests displayed previously in Figure 4, and we have shown that the model is able to exactly replicate the behavior of the cell in these tests when $n_{u}=n_{\sigma }$ is sufficiently large. Similarly to the situation encountered when dealing with standard phenomenological models, it remains now to assess the capability of the proposed HP-ROM to predict the behavior of the cell under conditions different from those used in the “calibration” (training) process.

5.7.1 Uniaxial compression

The first strain path employed for the assessment is displayed in Figure 15.a; it represents a monotonic compression in the transversal direction (the model, see Figure 4, was trained using only stretching and shear, but not compression, tests). For purposes of evaluating the quality of the HP-ROM approximation, it is convenient to introduce the following macroscopic¹ stress error estimate:

${\tilde {E}}_{\sigma ,M}^{ROM}{\mathrel {\mathop {:}}}={\sqrt {\dfrac {\sum _{i=1}^{n_{stp}^{t}}\Vert {\boldsymbol {\sigma _{M}}}^{i}-{{\boldsymbol {\sigma }}_{M}^{*\,i,ROM}}(n_{\sigma },n_{u},{\mathcal {I}})\Vert ^{2}}{\sum _{i=1}^{n_{stp}^{t}}\Vert {\boldsymbol {\sigma _{M}}}^{i}\Vert ^{2}}}},$

(5.8)

where ${\textstyle {\boldsymbol {\sigma _{M}}}^{i}}$ and ${\textstyle {{\boldsymbol {\sigma }}_{M}^{*\,i,ROM}}}$ denote the macroscopic stress at the ${\textstyle i-th}$ time step computed by the FEM and the HP-ROM, respectively. This error estimate is plotted in Figure 15.b versus the level of truncation ${\textstyle n_{u}=n_{\sigma }}$. Observe that the error goes to zero as the number of employed modes increase. In this particular case, thus, there is no additional error due to sampling of the parameter space.

Remark 4: This simple example fittingly illustrates one of the acclaimed advantages of POD/Galerkin reduced-order approaches over “black box” methods such as artificial neural networks –-that are also based on the partitioned offline-online computational paradigm–-: POD/Galerkin reduced-order approaches preserve the “physics” of the problem one wishes to model and, as a consequence, are able to make physically-based extrapolations. For instance, in this case, the reduced-order model is able to exactly replicate (for sufficiently large ${\textstyle n_{u}=n_{\sigma })}$ the macroscopic compressive behavior of the RVE, even though no information regarding this deformational state has been supplied to the model in the calibration (training) phase; the HP-ROM is “aware”, figuratively speaking, that the matrix material in the RVE exhibits similar behavior in tension and compression (J2 plasticity).

(¹) Recall that the output of interest in solving the cell BVP is the macroscopic stress tensor; thus, the error estimate defined in Eq.(5.8) (${\tilde {E}}_{\sigma ,M}^{ROM}$) provides a more meaningful indication of the quality of the approximation than the stress error measure defined previously in Eq.(5.7) (${\tilde {e}}_{\sigma }^{ROM}$). The latter is more suited for examining convergence properties of the HP-ROM approximation, since the minimization problem that underlies the SVD is posed in terms of the Frobenis norm. Nevertheless, it is straightforward to show that, actually, ${\tilde {e}}_{\sigma }^{ROM}$ is an upper bound for ${\tilde {E}}_{\sigma ,M}^{ROM}$ (see Proposition D.1).

5.7.2 Biaxil loading/unloading test

A more severe test for assessing errors associated to the training process is provided by the strain trajectory shown in Figure 16. Indeed, while the training strain histories of Figure 4 only included monotonic, uniaxial stretching, the strain history displayed in Figure 16 consists of a cycle of biaxial, loading/unloading stretching (time steps 1 to 100) and biaxial loading/unloading compression (time steps 101 to 200). The graph of the macroscopic error estimator (5.8) corresponding to this input strain path as a function of the level of truncation is represented in Figure 17.a. It can be readily perceived that, in this case, and in contrast to the situation encountered in the previously discussed input strain trajectory, the macroscopic stress does not go to zero as the number of POD modes included in the basis increases. Rather, the graph drops sharply from 24% to approximately 5% at ${\textstyle n_{\sigma }=n_{u}=5}$ (second inelastic mode), and then fluctuates erratically, with no apparent trend, between ${\textstyle 3\%}$ and ${\textstyle 10\%}$ –-a level of accuracy that, nevertheless, may be deemed more than acceptable in most practical applications. A more clear picture of the accuracy of the approximation for the particular case of ${\textstyle n_{\sigma }=n_{u}=6}$ can be obtained from the stress-strain diagrams shown in figure 18.

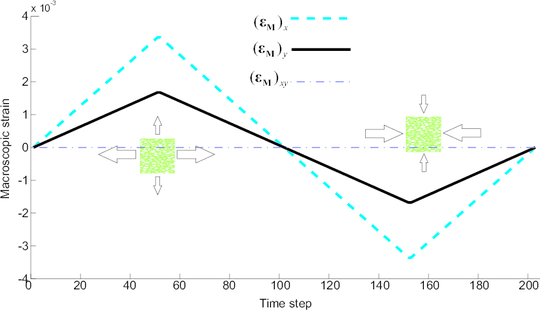
Figure 16: Second strain trajectory employed for assessing training errors.

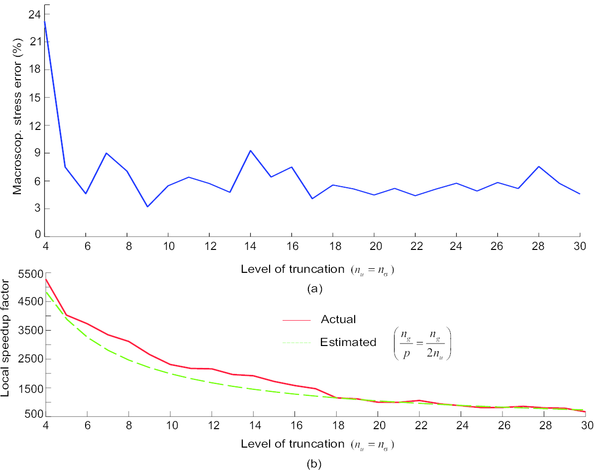
Figure 17: a) Macroscopic error estimator ${\tilde {E}}_{\sigma ,M}^{ROM}$ (see Eq.(5.8)) versus level of truncation ($n_{\sigma }=n_{u}$) for the case of testing trajectory shown in Figure 16,. b) Local speedup factor $S_{loc}$ (defined in Eq.(5.9)) reported for this case versus level of truncation. This plot is accompanied by the graph of the ratio $n_{g}/p$, where $n_{g}=38984$ is the total number of Gauss points of the finite element mesh, and $p=2n_{\sigma }$ the number of sampling points employed for numerically integrating the HP-ROM.

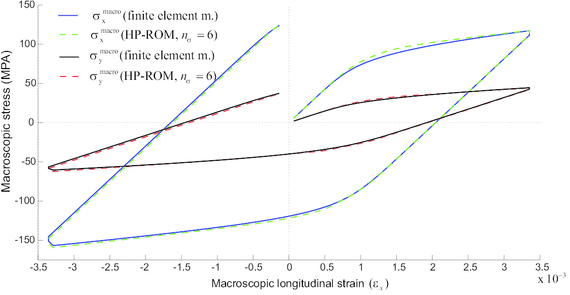
Figure 18: Longitudinal and transversal macroscopic stress versus longitudinal macroscopic strain computed using the FEM and the HP-ROM with $n_{\sigma }=n_{u}=6$ (for the case of the testing trajectory shown in Figure 16)

5.8 Speedup analysis

Lastly, we turn our attention to one of the main concerns of the present work: the issue of computational efficiency. For a given error level, how many times can the proposed HP-ROM speed up the calculation of the cell response with respect to the reference finite element model? Let us define the local speedup factor as the ratio

$S_{loc}{\mathrel {\mathop {:}}}={\dfrac {t_{FE}(n,n_{g})}{t_{ROM}(n_{\sigma },n_{u},p)}},$

(5.9)

where ${\textstyle t_{FE}}$ and ${\textstyle t_{ROM}}$ denote the CPU times required to compute the FE and HP-ROM macro-stress responses, respectively, induced by a given input strain history¹ In Figure 17.b, we show the graph of the speedup factor reported in the the case of the input strain path of Figure 16 as a function of the number of POD modes included in the analysis (recall in this respect that ${\textstyle n_{u}=n_{\sigma }=p/2}$). We plot also in Figure 17.b the ratio ${\textstyle {n_{g}}/{p}}$, i.e., the relation between the total number of integration points in the finite element model ( ${\textstyle n_{g}=38984}$) and in the reduced order model (${\textstyle p}$). It can be gleaned from Figure 17.b that the reported speedup factors are of the same order of magnitude as the ratio ${\textstyle n_{g}/p}$; i.e.:

$S_{loc}\sim {\dfrac {n_{g}}{p}}={\dfrac {n_{g}}{2n_{\sigma }}},$

(5.10)

(this indicates that the evaluation of the stresses at the integration points dominates the total computational cost). Although these results are no doubt influenced and biased by the particular programming language and coding style employed –-we use an in-house, non-vectorized Matlab program operating in a Linux platform–-, and, consequently, this trend may not be exactly observed when using other programming languages and/or platforms, they serve to provide an idea of the tremendous gains in performance that can be achieved using the proposed ROM; for ${\textstyle n_{\sigma }=p=6}$ modes, for instance, the computational cost is reduced by a factor above ${\textstyle 3600}$, while still capturing 95% of the full-order, high-fidelity information –-the essential information.

Remark 5: The foregoing analysis considers only the relation between speedup factors and error for varying sampling points in the reduced-order model (${\textstyle p}$) and fixed number of Gauss points (${\textstyle n_{g}}$) in the finite element model. It may be wondered about the reverse behavior, i.e., what would happen if ${\textstyle n_{g}}$ increases while ${\textstyle p}$ is kept constant. In Reference [36], the authors investigate this issue, and prove that the approximation error is, interestingly, relatively insensitive to mesh refinement; that is, if the mesh is refined by a certain factor, one need not commensurately increase the number of sampling points in the reduced-order model to preserve the same level of accuracy. The striking implication of this property is that the speedup factors provided by the HP-ROM will invariably grow –-at a rate roughly proportional to the factor of refinement–- as the spatial discretization of the RVE becomes finer. Thus, if the mesh shown previously in Figure 3 is refined by a factor of, say, 3, speedup factors above 10000 can be conceivably obtained at ${\textstyle n_{u}=p/2=6}$ for approximately the same level of approximation (${\textstyle 5\%}$).

(¹) The computational cost associated to the offline stage –-generation of snapshots plus the comparatively negligible expenses of applying the POD and selecting the sampling points–-has been deliberately ruled out from this speedup analysis because, in two-scale homogenization contexts, the cell equilibrium problem is to be solved a sheer number of times and, consequently, this overhead cost is quickly amortized.

6 Concluding remarks

It is an unarguable fact that, in constructing a computational model of a given physical system, one's perception of what is essential and what is not is strongly influenced by the capabilities of the computer that will carry out the pertinent simulation: the more powerful the computer, the more details are regarded, at times unconsciously, but very often deliberately –-to skip the ever difficult task of concocting appropriate simplifications–-, as essential by the modeler, and thus eventually included in the simulation. To reverse this seemingly natural, but regrettable tendency –-it is inexorably conducive to misuse of available computational resources–-, in the present work, and for the particular problem of multiscale homogenization, we have proposed an approach in which the task of reducing the inherent complexity of the governing equations (in this case, the cell equilibrium equation ) is entirely delegated to the computer itself, and hence not affected by the vagaries of the modeler's appreciation.

The proposed approach revolves around the realization that, in two-scale homogenization problems, the fine-scale fields over the RVE induced by the parametric dependence on the input macroscopic strains can be accurately approximated by functions whose dimensionality is relatively low and, furthermore, totally independent of the geometric complexity of the RVE. Central to the approach is therefore the determination of optimal reduced-order spaces for these approximated functions. The optimality of these spaces depends, on the one hand, on the representativeness of the snapshots obtained in the a priori FE analysis, and, on the other hand, on the suitability of the dimensionality reduction tool employed to unveil the dominant modes from these snapshots. In the present work, attention has been focused on the latter aspect: we have developed a novel, partitioned POD that allows capturing the elastic behavior of the RVE with the same accuracy as the underlying FE model. By contrast, the former aspect (choice of the macro-strain values at which to obtain the snapshots) has been addressed only on intuitive basis, and thus, should receive more careful consideration in future developments. In particular, it would be desirable to systematize this crucial task, as well as to provide some statistical means to certify, so to speak, the representativeness of the chosen snapshots.

One of the the most striking features of the proposed theory is perhaps the conceptual simplicity of the cell equilibrium equation in its hyperreduced-order form: the sum of (reduced) internal forces at the pre-selected sampling points must give identical result either calculated using observed stresses or fitted stresses. Although this condition appears, in hindsight, rather reasonable, even obvious –-it ensures maximum resemblance between reduced-order and full-order responses at the sampling points–- it would require uncommon physical intuition to arrive at it without the benefit of the integration procedure –-based on the notion of expanded approximation space –- advocated in the present work.

The hyperreduced form of the cell equilibrium equation excels not only in its conceptual simplicity; the corresponding solution scheme is also very simple to implement. Taking as departure point an existing FE code, one has only to replace the typical loop over elements in the FE code by a loop over the pre-selected sampling points ${\textstyle \{\mathbf {x} _{{\mathcal {I}}_{1}},\mathbf {x} _{{\mathcal {I}}_{2}},\ldots \mathbf {x} _{{\mathcal {I}}_{p}}\}}$. The stress vectors and corresponding constitutive tangent matrices obtained at each stage of the loop are stored in the gappy weighted vector ${\textstyle {\hat {\boldsymbol {\Sigma }}}}$ and the matrix ${\textstyle {\boldsymbol {\mathbb {\hat {C}} }}}$, respectively, and, then the residual vector and the Jacobian matrix are computed as ${\textstyle {\mathbb {\hat {B}} ^{**^{T}}}{\hat {\boldsymbol {\Sigma }}}}$ and ${\textstyle {\mathbb {\hat {B}} ^{**^{T}}}\!{\boldsymbol {\mathbb {\hat {C}} }}\,{\mathbb {\hat {B}} ^{*}}}$, respectively. Notice that no assembly process is needed, nor has one to worry about imposing boundary conditions. Once convergence is achieved, the macroscopic stress value is simply calculated as ${\textstyle {\boldsymbol {\sigma _{M}}}=\mathbb {T} {\hat {\boldsymbol {\Sigma }}}}$. It should be emphasized again that the operation count in both solving this hyperreduced cell equation and updating the macroscopic stress vector depends exclusively on the reduced dimensions ${\textstyle n_{u}}$ and ${\textstyle p}$ (number of fluctuation modes and number of sampling points, respectively). Likewise, storage of history data (internal variables) is only required at the pre-selected sampling points. Computational savings accrue, thus, not only in terms of number of operations, but also in terms of memory requirements.

As already mentioned, the hyperreduced matrices ${\textstyle {\mathbb {\hat {B}} ^{**}}=({\boldsymbol {I}}-{\boldsymbol {\hat {R}}}){\mathbb {\hat {B}} ^{*}}}$ and ${\textstyle \mathbb {T} }$ appearing in the online solution of the HP-ROM are calculated in the offline stage, prior to the overall multiscale analysis. These operators –-whose dimensions are independent of the size of the underlying finite element mesh–- encode the essential information regarding the geometrical arrangement and interaction of the distinct phases and/or pores at the fine scale; they are, thus, somehow intrinsic to the micro-/meso-structure one wishes to macroscopically model. In the light of this observation, one may venture to think of creating an extensive digital material library in which to include, once their approximating quality has been properly certified, these operators together with the properties (Young's modulus, type of hardening law, etc.) exhibited by the heteregoneous material at the sampling points. Given the inherent modular character of hierarchical multiscale models, any user having a two-scale HP-ROM homogenization code could easily incorporate and leverage the information contained in this library.

A topic we have purposefully refrained to touch in this work is the application of model reduction when strain localization (formation of discontinuities) takes place in the RVE. The reason is that homogenization in the presence of such events is a controversial, diffuse subject in its own right –-even the existence of an RVE in such cases is questionable–-, and, consequently, a rigorous treatment of it would have taken us too far afield. The most challenging and intriguing questions that will surely pose the application of model reduction techniques in these problems are connected with the aforementioned offline task of determining the dominant deformational and stress modes of the RVE. Can the deformational behavior of a cell affected by multiple propagating cracks be represented also in a parsimonious manner, as in the case of strain hardening? Or will the number of modes necessary to accurately replicate its response combinatorially increase with the number of potential crack propagation paths (i.e., with the geometrical complexity of the RVE). Research in this front is currently in progress and will be reported in forthcoming publications.

Appendix A. Connection between POD and SVD

We saw in Section 3.1.2 that the POD problem for the displacement fluctuations boils down to the solution of the following eigenvalue problem:

$({\boldsymbol {X}}_{u}^{T}\mathbf {M} {\boldsymbol {X}}_{u}){v}=\lambda {v},\;\;\;\Vert {v}\Vert =1,$

(A.1)

where ${\textstyle \mathbf {M} }$ is the typical finite element “mass matrix” (with density equal one):

$\mathbf {M} _{IJ}=\displaystyle \int _{\Omega }N_{I}(\mathbf {x} )N_{J}(\mathbf {x} )\,d\Omega \;\;\;\;(I,J=1,2\ldots n).$

(A.2)

The desired reduced basis matrix ${\textstyle {\boldsymbol {\Phi }}\in \mathbb {R} ^{n\cdot d\times n_{u}}}$ is then calculated from the ${\textstyle n_{u}}$ largest eigenvalues ${\textstyle \lambda _{1}\geq \lambda _{2}\ldots \lambda _{n_{u}-1}\geq \lambda _{n_{u}}>0}$ and associated eigenvectors ${\textstyle {v}_{1},{v}_{2}\,\ldots \,{v}_{n_{u}}}$ of such a problem by the following expression (see Eq. (3.13)):

${\boldsymbol {\Phi }}_{i}={\boldsymbol {X}}_{u}{\dfrac {{v}_{i}}{\sqrt {\lambda _{i}}}},\;\;\;\;i=1,2\ldots n_{u}.$

(A.3)

Proposition 1: Let ${\textstyle \mathbf {M} ={\bar {\mathbf {M} }}^{T}{\bar {\mathbf {M} }}}$ be the Cholesky decomposition of ${\textstyle \mathbf {M} }$, and ${\textstyle {\boldsymbol {\bar {X}}}_{u}}$ the matrix defined as:

${\boldsymbol {\bar {X}}}_{u}={\bar {\mathbf {M} }}{\boldsymbol {X}}_{u}.$

(A.4)

Consider now the the (reduced) Singular Value Decomposition (SVD) [79] of ${\textstyle {\boldsymbol {\bar {X}}}_{u}}$, that is, the factorization:

${\boldsymbol {\bar {X}}}_{u}={\boldsymbol {\bar {U}}}{\boldsymbol {\bar {S}}}{\boldsymbol {\bar {V}}}^{T},$

(A.5)

wherein ${\textstyle {\boldsymbol {\bar {V}}}\in \mathbb {R} ^{n_{snp}\times r}}$ (${\textstyle r}$ is the rank of ${\textstyle {\boldsymbol {\bar {X}}}_{u}}$) and ${\textstyle {\boldsymbol {\bar {U}}}\in \mathbb {R} ^{n\cdot d\times r}}$ stand for the matrices of right and left singular vectors, respectively; and ${\textstyle {\boldsymbol {\bar {S}}}\in \mathbb {R} ^{r\times r}}$ is a diagonal matrix containing the singular values of ${\textstyle {\boldsymbol {X}}_{u}}$. Then, the ${\textstyle i-th}$ column of the basis matrix defined by Eq.(A.3) can be alternatively calculated as:

${\boldsymbol {\Phi }}_{i}={\bar {\mathbf {M} }}^{-1}{\boldsymbol {\bar {U}}}_{i},\;\;\;\;i=1,2\ldots n_{u},$

(A.6)

${\textstyle {\boldsymbol {\bar {U}}}_{i}}$ being the ${\textstyle i-th}$ left singular vector of ${\textstyle {\boldsymbol {\bar {X}}}_{u}}$.

Proof. Post-multiplying both sides of Eq.(A.5) by ${\textstyle {\boldsymbol {\bar {V}}}_{i}{{\boldsymbol {\bar {S}}}_{ii}}^{-1}}$, one gets:

${\boldsymbol {\bar {X}}}_{u}{\boldsymbol {\bar {V}}}_{i}{{\boldsymbol {\bar {S}}}_{ii}}^{-1}=({\boldsymbol {\bar {U}}}{\boldsymbol {\bar {S}}}{\boldsymbol {\bar {V}}}^{T}){\boldsymbol {\bar {V}}}_{i}{{\boldsymbol {\bar {S}}}_{ii}}^{-1}=\left(\sum _{j=1}^{r}{\boldsymbol {\bar {U}}}_{j}{\boldsymbol {\bar {S}}}_{jj}{\boldsymbol {\bar {V}}}_{j}^{T}\right){\boldsymbol {\bar {V}}}_{i}{{\boldsymbol {\bar {S}}}_{ii}}^{-1}={\boldsymbol {\bar {U}}}_{i}.$

(A.7)

Pre-multiplying now ${\textstyle {\boldsymbol {\bar {U}}}_{i}={\boldsymbol {\bar {X}}}_{u}{\boldsymbol {\bar {V}}}_{i}{{\boldsymbol {\bar {S}}}_{ii}}^{-1}}$ by ${\textstyle {\bar {\mathbf {M} }}^{-1}}$, and considering Eq.(A.4), one arrives at:

${\boldsymbol {\bar {U}}}_{i}={\boldsymbol {\bar {X}}}_{u}{\boldsymbol {\bar {V}}}_{i}{{\boldsymbol {\bar {S}}}_{ii}}^{-1}={\bar {\mathbf {M} }}{\boldsymbol {X}}_{u}{\boldsymbol {\bar {V}}}_{i}{{\boldsymbol {\bar {S}}}_{ii}}^{-1}$ $\Rightarrow {\bar {\mathbf {M} }}^{-1}{\boldsymbol {\bar {U}}}_{i}={\boldsymbol {X}}_{u}{\boldsymbol {\bar {V}}}_{i}{{\boldsymbol {\bar {S}}}_{ii}}^{-1}.$

(A.8)

The proof reduces, thus, to showing that the eigenvectors and eigenvalues of problem (A.1) are indeed the right singular vectors and the square root of the singular values, respectively, of the Singular Value Decomposition (SVD) of ${\textstyle {\boldsymbol {\bar {X}}}_{u}}$. This follows easily by, first, substituting the Cholesky decomposition ${\textstyle \mathbf {M} ={\bar {\mathbf {M} }}^{T}{\bar {\mathbf {M} }}}$ into Eq.(A.1):

$({\boldsymbol {X}}_{u}^{T}{\bar {\mathbf {M} }}^{T})({\bar {\mathbf {M} }}{\boldsymbol {X}}_{u})=({\boldsymbol {\bar {X}}}_{u}^{T}{\boldsymbol {\bar {X}}}_{u}){v}=\lambda {v},$

(A.9)

and then inserting Eq.(A.5) into the above equation:

$({\boldsymbol {\bar {U}}}{\boldsymbol {\bar {S}}}{\boldsymbol {\bar {V}}}^{T})^{T}({\boldsymbol {\bar {U}}}{\boldsymbol {\bar {S}}}{\boldsymbol {\bar {V}}}^{T}){v}=({\boldsymbol {\bar {V}}}{\boldsymbol {\bar {S}}}^{2}{\boldsymbol {\bar {V}}}^{T}){v}=\left(\displaystyle \sum _{i=1}^{r}{\boldsymbol {\bar {S}}}_{ii}^{2}{\boldsymbol {\bar {V}}}_{i}{\boldsymbol {\bar {V}}}_{i}^{T}\right){v}=\lambda {v}.$

(A.10)

Finally, setting ${\textstyle {v}={\boldsymbol {\bar {V}}}_{j}}$ in the above:

$\left(\displaystyle \sum _{i=1}^{r}{\boldsymbol {\bar {S}}}_{ii}^{2}{\boldsymbol {\bar {V}}}_{i}{\boldsymbol {\bar {V}}}_{i}^{T}\right){\boldsymbol {\bar {V}}}_{j}={\boldsymbol {\bar {S}}}_{jj}^{2}{\boldsymbol {\bar {V}}}_{j}=\lambda {\boldsymbol {\bar {V}}}_{j},$

(A.11)

which proves, as asserted, that ${\textstyle {v}_{j}={\boldsymbol {\bar {V}}}_{j}}$ and ${\textstyle {\boldsymbol {\bar {S}}}_{jj}^{2}=\lambda _{jj}}$ (${\textstyle j=1,2\ldots n_{u}}$).

Appendix B. Elastic/Inelastic reduced basis matrix

This appendix is devoted to provide further details concerning the actual numerical implementation of the elastic/inelastic partitioned strategy, presented in Section 3.1.2, for the computation of the reduced basis matrices ${\textstyle {\boldsymbol {\Phi }}}$ (displacement fluctuations) and ${\textstyle {\boldsymbol {\Psi }}}$ (stresses).

B.1 Displacement fluctuations

As pointed out in Section 3.1.2, the essence of this strategy lies in the orthogonal decomposition –-in the sense of the ${\textstyle L_{2}}$ inner product–- of the space of snapshots ${\textstyle {\mathcal {V}}_{u}^{snp}\subset H^{1}(\Omega )^{d}}$ into elastic (${\textstyle {\mathcal {V}}_{u,el}^{snp}}$) and inelastic (${\textstyle {\mathcal {V}}_{u,inel}^{snp}}$) subspaces. This decomposition naturally translates into an orthogonal decomposition of the range of the snapshot matrix ${\textstyle {\boldsymbol {X}}_{u}}$, denoted by ${\textstyle {\textrm {Range}}({\boldsymbol {X}}_{u})\subset \mathbb {R} ^{n\cdot d}}$, into pertinent elastic and inelastic manifolds. According to Eq.(3.8), orthogonality in the case of the displacement fluctuations is in the sense of the ${\textstyle \mathbb {R} ^{n\cdot d}}$ inner product induced by the “mass matrix” ${\textstyle \mathbf {M} }$ (see Eq. (3.9)):

$\left\langle {u},{w}\right\rangle _{\mathbf {M} }={u}^{T}\mathbf {M} {w},\;\;\;\;{u},{w}\in \mathbb {R} ^{n\cdot d}.$

(B.1)

The steps to arrive at the desired matrix basis ${\textstyle {\boldsymbol {\Phi }}}$ are summarized in the following.

1. Compute finite element stress solutions for representative, input macro-strain histories.
2. Store the displacement fluctuation solutions computed at each time step of these macro-strain trajectories in the displacement fluctuations snapshot matrix ${\textstyle {\boldsymbol {X}}_{u}\in \mathbb {R} ^{n\cdot d\times n_{snp}}}$:

   ${\boldsymbol {X}}_{u}={\begin{bmatrix}{\boldsymbol {U}}^{1}&{\boldsymbol {U}}^{2}&\cdots &{\boldsymbol {U}}^{n_{snp}}\end{bmatrix}}={\begin{bmatrix}{\boldsymbol {U}}_{1}^{1}&{\boldsymbol {U}}_{1}^{2}&\cdots &{\boldsymbol {U}}_{1}^{n_{snp}}\\{\boldsymbol {U}}_{2}^{1}&{\boldsymbol {U}}_{2}^{2}&\cdots &{\boldsymbol {U}}_{2}^{n_{snp}}\\\vdots &\vdots &\vdots &\vdots \\{\boldsymbol {U}}_{n}^{1}&{\boldsymbol {U}}_{n}^{2}&\cdots &{\boldsymbol {U}}_{n}^{n_{snp}}\\\end{bmatrix}}.$

   (B.2)

3. Pick up from ${\textstyle {\boldsymbol {X}}_{u}}$ a minimum of ${\textstyle m_{e}}$ (${\textstyle m_{e}=6}$ for 3D problems, and ${\textstyle m_{e}=3}$ for plane strain) linearly independent columns corresponding to purely elastic solutions. Store these columns in a matrix ${\textstyle {\boldsymbol {Z}}_{u}^{el}}$.
4. Perform the reduced singular value decomposition (SVD) of the matrix defined as

   ${\bar {\boldsymbol {Z}}}_{u}^{el}{\mathrel {\mathop {:}}}={\bar {\mathbf {M} }}{\boldsymbol {Z}}_{u}^{el}$

   (B.3)

where ${\textstyle {\bar {\mathbf {M} }}}$ is the matrix of the Cholesky factorization of ${\textstyle \mathbf {M} }$ ( ${\textstyle \mathbf {M} ={\bar {\mathbf {M} }}^{T}{\bar {\mathbf {M} }}}$). A basis matrix for ${\textstyle {\textrm {Range}}({\boldsymbol {Z}}_{u}^{el})}$ is finally obtained as

${\boldsymbol {D}}^{el}{\mathrel {\mathop {:}}}={\bar {\mathbf {M} }}^{-1}{\boldsymbol {\bar {D}}}^{el}$

(B.4)

${\textstyle {\boldsymbol {\bar {D}}}^{el}\in \mathbb {R} ^{n\cdot d\times m_{e}}}$ being the matrix of left singular vectors arising from the SVD of ${\textstyle {\bar {\boldsymbol {Z}}}_{u}^{el}}$. Notice that ${\textstyle {\boldsymbol {D}}^{el}}$ is columnwise orthogonal in the sense of the inner product defined by Eq.(B.1):

${{\boldsymbol {D}}^{el}}^{T}\mathbf {M} {\boldsymbol {D}}^{el}=({{\boldsymbol {\bar {D}}}^{el}}^{T}{\bar {\mathbf {M} }}^{-T})({\bar {\mathbf {M} }}^{T}{\bar {\mathbf {M} }})({\bar {\mathbf {M} }}^{-1}{{\boldsymbol {\bar {D}}}^{el}})$ $={{\boldsymbol {\bar {D}}}^{el}}^{T}{\boldsymbol {\bar {D}}}^{el}={\boldsymbol {I}}.$

(B.5)

As such, it may be used in principle as the desired elastic basis matrix ${\textstyle {\boldsymbol {\Phi }}^{el}}$. However, ${\textstyle {\boldsymbol {D}}^{el}}$ does not enjoy any optimality property with respect to ${\textstyle {\boldsymbol {X}}_{u}}$–-it is only optimal with respect to the matrix ${\textstyle {\boldsymbol {Z}}_{u}^{el}}$ of chosen elastic snapshots.

5. For consistency in the approximation, thus, it is preferable to derive ${\textstyle {\boldsymbol {\Phi }}^{el}}$ from the the “elastic component” of ${\textstyle {\boldsymbol {X}}_{u}}$ –-the orthogonal projection of ${\textstyle {\boldsymbol {X}}_{u}}$ onto ${\textstyle {\textrm {Range}}({\boldsymbol {D}}^{el})}$–-; the expression for this projection reads:

   ${\boldsymbol {X}}_{u}^{el}={\boldsymbol {D}}^{el}({{\boldsymbol {D}}^{el}}^{T}\mathbf {M} {\boldsymbol {X}}_{u})$

   (B.6)

According to Eq.(A.5) of Proposition A.0.1, the elastic basis matrix can be finally calculated from ${\textstyle {\boldsymbol {X}}_{u}^{el}}$ as:

${\boldsymbol {\Phi }}^{el}{\mathrel {\mathop {:}}}={\bar {\mathbf {M} }}^{-1}{\boldsymbol {\bar {\Phi }}}^{el}.$

(B.7)

where ${\textstyle {\boldsymbol {\bar {\Phi }}}^{el}}$ is the matrix of left singular vectors emerging from the reduced SVD of ${\textstyle {\boldsymbol {\bar {X}}}_{u}^{el}{\mathrel {\mathop {:}}}={\bar {\mathbf {M} }}{\boldsymbol {X}}_{u}^{el}}$; i.e:

${\boldsymbol {\bar {X}}}_{u}^{el}={\boldsymbol {\bar {\Phi }}}^{el}{\boldsymbol {\bar {S}}}_{u}^{el}{{\boldsymbol {\bar {V}}}_{u}^{el}}^{T}.$

(B.8)

6. Calculate the “inelastic component” ${\textstyle {\boldsymbol {X}}_{u}^{in}}$ of the snapshot matrix ${\textstyle {\boldsymbol {X}}_{u}}$ as:

   ${\boldsymbol {X}}_{u}^{in}={\boldsymbol {X}}_{u}-{\boldsymbol {X}}_{u}^{el};$

   (B.9)

that is, ${\textstyle {\boldsymbol {X}}_{u}^{in}}$ is the orthogonal projection –-in the sense, again, of Eq.(B.1)–- of ${\textstyle {\boldsymbol {X}}_{u}}$ onto the orthogonal complement, in ${\textstyle {\textrm {Range}}({\boldsymbol {X}}_{u})}$, of ${\textstyle {\textrm {Range}}({\boldsymbol {\Phi }}^{el})}$.

7. It is now on this inelastic snapshot matrix ${\textstyle {\boldsymbol {X}}_{u}^{in}}$ that we apply the POD in order to identify and unveil the essential or most “energetic” inelastic fluctuation modes. According to Proposition A.0.1 in Appendix A, this is done by first carrying out the reduced SVD of ${\textstyle {\boldsymbol {\bar {X}}}_{u}^{in}={\bar {\mathbf {M} }}{\boldsymbol {X}}_{u}^{in}}$:

   ${\boldsymbol {\bar {X}}}_{u}^{in}={\boldsymbol {\bar {D}}}^{in}{\boldsymbol {\bar {S}}}_{u}^{in}{{\boldsymbol {\bar {V}}}_{u}^{in}}^{T}.$

   (B.10)

The ${\textstyle i-th}$ POD basis vector of ${\textstyle {\boldsymbol {X}}_{u}^{in}}$ is then given by:

${\boldsymbol {\Phi }}_{i}^{in}={\bar {\mathbf {M} }}^{-1}{\boldsymbol {\bar {D}}}_{i}^{in},\;\;\;\;i=1,2\ldots n_{u}-m_{e}.$

(B.11)

8. The desired basis matrix ${\textstyle {\boldsymbol {\Phi }}\in \mathbb {R} ^{n\cdot d\times n_{u}}}$ adopts finally the form:

   ${\boldsymbol {\Phi }}=[{\boldsymbol {\Phi }}^{el}\;{\boldsymbol {\Phi }}^{in}]=[\overbrace {{\boldsymbol {\Phi }}_{1}^{el}\;{\boldsymbol {\Phi }}_{2}^{el}\,\cdots \,{\boldsymbol {\Phi }}_{m_{e}}^{el}} ^{\textrm {Elasticmodes}}\;\overbrace {{\boldsymbol {\Phi }}_{1}^{in}\;{\boldsymbol {\Phi }}_{2}^{in}\,\cdots \,{\boldsymbol {\Phi }}_{n_{u}-m_{e}}^{in}} ^{\textrm {Essentialinelasticmodes}}]$

   (B.12)

B.1.1 Displacement truncation error

Proposition B.1.1: The fluctuation displacement truncation error defined in Eq.(3.4):

${e}_{u}(n_{u})={\sqrt {\displaystyle \sum _{k=1}^{n_{snp}}\Vert {\boldsymbol {u}}^{k}-{{\boldsymbol {u}}^{*}}^{k}(n_{u})\Vert _{L_{2}(\Omega )}^{2}}}$

(B.13)

can be calculated as

${e}_{u}(n_{u})={\sqrt {\displaystyle \sum _{i=n_{u}^{in}+1}^{r_{u}-n_{u}^{in}}\!{{\boldsymbol {\bar {S}}}_{u,ii}^{in}}^{\!}}}$

(B.14)

where ${\textstyle n_{u}^{in}=n_{u}-m_{e}}$, and ${\textstyle {{\boldsymbol {\bar {S}}}_{u,ii}^{in}}}$ stands for the ${\textstyle i-th}$ singular value of the inelastic snapshot matrix ${\textstyle {\boldsymbol {\bar {X}}}_{u}^{in}={\bar {\mathbf {M} }}{\boldsymbol {X}}_{u}^{in}}$ (see Eq.(B.10) ).

Proof. We begin the proof by showing that ${\textstyle {{e}_{u}}^{2}}$ is equal to the Frobenius norm of the difference between the “weighted” snapshot matrix ${\textstyle {\boldsymbol {\bar {X}}}_{u}}$ and its low-dimensional approximation ${\textstyle {\boldsymbol {\bar {X}}}_{u}^{*}}$. Indeed, following the same logic that led to Eq.(3.8), we get:

${{e}_{u}}^{2}=\displaystyle \sum _{k=1}^{n_{snp}}\Vert \overbrace {{\boldsymbol {u}}^{k}-{{\boldsymbol {u}}^{*}}^{k}(n_{u})} ^{{\Delta {\boldsymbol {u}}^{*}}^{k}}\Vert _{L_{2}(\Omega )}^{2}$ $=\displaystyle \sum _{k=1}^{n_{snp}}\left\langle {{\Delta {\boldsymbol {u}}^{*}}^{k}},{{\Delta {\boldsymbol {u}}^{*}}^{k}}\right\rangle _{L_{2}(\Omega )}$ $=\displaystyle \sum _{k=1}^{n_{snp}}\left(\sum _{I=1}^{n}\sum _{J=1}^{n}{\Delta {\boldsymbol {u}}^{*}}_{I}^{k}{\Delta {\boldsymbol {u}}^{*}}_{J}^{k}\left\langle {N_{I}},{N_{J}}\right\rangle _{L_{2}(\Omega )}\right)$ $={\textrm {tr}}(({\boldsymbol {X}}_{u}-{\boldsymbol {X}}_{u}^{*})^{T}\mathbf {M} ({\boldsymbol {X}}_{u}-{\boldsymbol {X}}_{u}^{*}))$

(B.15)

where

${\boldsymbol {X}}_{u}^{*}={\boldsymbol {\Phi }}({\boldsymbol {\Phi }}^{T}\mathbf {M} {\boldsymbol {X}}_{u}).$

(B.16)

Inserting now the Cholesky decomposition of ${\textstyle \mathbf {M} }$ in the above equation, we arrive finally at

${{e}_{u}}^{2}={\textrm {tr}}(({\boldsymbol {X}}_{u}-{\boldsymbol {X}}_{u}^{*})^{T}\mathbf {M} ({\boldsymbol {X}}_{u}-{\boldsymbol {X}}_{u}^{*}))={\textrm {tr}}(({\boldsymbol {\bar {X}}}_{u}-{\boldsymbol {\bar {X}}}_{u}^{*})^{T}({\boldsymbol {\bar {X}}}_{u}-{\boldsymbol {\bar {X}}}_{u}^{*}))$ $=\Vert {\boldsymbol {\bar {X}}}_{u}-{\boldsymbol {\bar {X}}}_{u}^{*}\Vert _{F}^{2},$

(B.17)

where ${\textstyle {\boldsymbol {\bar {X}}}_{u}^{*}={\bar {\mathbf {M} }}{\boldsymbol {X}}_{u}^{*}}$.

On the other hand, ${\textstyle {\boldsymbol {\bar {X}}}_{u}}$ can be written from Eq.(B.8) and Eq.(B.10) as:

${\boldsymbol {\bar {X}}}_{u}={\boldsymbol {\bar {X}}}_{u}^{el}+{\boldsymbol {\bar {X}}}_{u}^{in}=$ $={\boldsymbol {\bar {\Phi }}}^{el}{\boldsymbol {\bar {S}}}_{u}^{el}{{\boldsymbol {\bar {V}}}_{u}^{el}}^{T}+{\boldsymbol {\bar {D}}}^{in}{\boldsymbol {\bar {S}}}_{u}^{in}{{\boldsymbol {\bar {V}}}_{u}^{in}}^{T}$ $={\boldsymbol {\bar {\Phi }}}^{el}{\boldsymbol {\bar {S}}}_{u}^{el}{{\boldsymbol {\bar {V}}}_{u}^{el}}^{T}+\displaystyle \sum _{i=1}^{n_{u}^{in}}\!{\boldsymbol {\bar {D}}}_{i}^{in}{{\boldsymbol {\bar {S}}}_{u,ii}^{in}}{{\boldsymbol {\bar {V}}}_{u,i}^{in}}^{T}+\displaystyle \sum _{i=n_{u}^{in}+1}^{r_{u}-n_{u}^{in}}\!{\boldsymbol {\bar {D}}}_{i}^{in}{{\boldsymbol {\bar {S}}}_{u,ii}^{in}}{{\boldsymbol {\bar {V}}}_{u,i}^{in}}^{T}$

(B.18)

where ${\textstyle n_{u}^{in}=n_{u}-m_{e}}$. Substitution of this decomposition in the expression for ${\textstyle {\boldsymbol {\bar {X}}}_{u}^{*}}$ yields:

${\boldsymbol {\bar {X}}}_{u}^{*}={\bar {\mathbf {M} }}{\boldsymbol {X}}_{u}^{*}={\bar {\mathbf {M} }}{\boldsymbol {\Phi }}({\boldsymbol {\Phi }}^{T}\mathbf {M} {\boldsymbol {X}}_{u})$ $=\overbrace {{\bar {\mathbf {M} }}{\boldsymbol {\Phi }}} ^{\boldsymbol {\bar {\Phi }}}({\bar {\mathbf {M} }}{\boldsymbol {\Phi }})^{T}{\boldsymbol {\bar {X}}}_{u}={\boldsymbol {\bar {\Phi }}}{\boldsymbol {\bar {\Phi }}}^{T}{\boldsymbol {\bar {X}}}_{u}$ $={\boldsymbol {\bar {\Phi }}}^{el}{\boldsymbol {\bar {S}}}_{u}^{el}{{\boldsymbol {\bar {V}}}_{u}^{el}}^{T}+\displaystyle \sum _{i=1}^{n_{u}^{in}}\!{\boldsymbol {\bar {D}}}_{i}^{in}{{\boldsymbol {\bar {S}}}_{u,ii}^{in}}{{\boldsymbol {\bar {V}}}_{u,i}^{in}}^{T}$

(B.19)

Using Eq.(B.18) and Eq.(B.19) in Eq.(B.17), and exploiting the orthonormality of the left and right singular vectors, one finally obtains:

${{e}_{u}}^{2}=\Vert {\boldsymbol {\bar {X}}}_{u}-{\boldsymbol {\bar {X}}}_{u}^{*}\Vert _{F}^{2}=\Vert \displaystyle \sum _{i=n_{u}^{in}+1}^{r_{u}-n_{u}^{in}}\!{\boldsymbol {\bar {D}}}_{i}^{in}{{\boldsymbol {\bar {S}}}_{u,ii}^{in}}{{\boldsymbol {\bar {V}}}_{u,i}^{in}}^{T}\Vert _{F}^{2}$ $=\displaystyle \sum _{i=n_{u}^{in}+1}^{r_{u}-n_{u}^{in}}\!{{\boldsymbol {\bar {S}}}_{u,ii}^{in}}^{\!}$

(B.20)

as asserted.

B.2 Stresses

The methodology for constructing the reduced basis matrix ${\textstyle {\boldsymbol {\Psi }}}$ for the stresses parallels, in essence, that explained in the preceding discussion. Nevertheless, for completeness, we summarize below the steps to be followed in this case.

1. Compute finite element stress solutions for representative, input macro-strain histories. The most practical and somehow consistent choice regarding these strain trajectories is to use the same as in the computation of the displacement fluctuations snapshots.
2. Store the weighted global stress vectors ${\textstyle {\boldsymbol {\Sigma }}^{i}\in \mathbb {R} ^{n_{g}\cdot s}}$ (${\textstyle i=1,2\ldots n_{snp}}$) (see Eq.(4.26)) computed at each time step in the snapshot matrix ${\textstyle {\boldsymbol {X}}\in \mathbb {R} ^{n_{g}\cdot s\times n_{snp}}}$:

${\boldsymbol {X}}={\begin{bmatrix}{\boldsymbol {\Sigma }}^{1}&{\boldsymbol {\Sigma }}^{2}&\cdots &{\boldsymbol {\Sigma }}^{n_{snp}}\end{bmatrix}}$

(B.21)

3. Select from ${\textstyle {\boldsymbol {X}}}$ a minimum of ${\textstyle m_{e}}$ linearly independent columns corresponding to purely elastic solutions. Store these columns in a matrix ${\textstyle {\boldsymbol {Z}}_{\sigma }^{el}}$.
4. Determine an orthogonal basis matrix for ${\textstyle {\textrm {Range}}({\boldsymbol {Z}}_{\sigma }^{el})}$ as the matrix of left singular vectors, denoted by ${\textstyle {\boldsymbol {D}}_{\sigma }^{el}}$, arising from the reduced SVD of ${\textstyle {\boldsymbol {Z}}_{\sigma }^{el}}$.
5. Compute the “elastic component” of ${\textstyle {\boldsymbol {X}}}$, i.e., the orthogonal projection of ${\textstyle {\boldsymbol {X}}}$ onto ${\textstyle {\textrm {Range}}({\boldsymbol {D}}_{\sigma }^{el})}$:

   ${\boldsymbol {X}}_{\sigma }^{el}={{\boldsymbol {D}}_{\sigma }^{el}}\left({{\boldsymbol {D}}_{\sigma }^{el}}^{T}{\boldsymbol {X}}\right).$

   (B.22)

6. Perform the reduced SVD of ${\textstyle {\boldsymbol {X}}_{\sigma }^{el}}$ to finally arrive at the desired elastic basis matrix ${\textstyle {\boldsymbol {\Psi ^{el}}}}$:

   ${\boldsymbol {X}}_{\sigma }^{el}={\boldsymbol {\Psi ^{el}}}{\boldsymbol {S}}^{el}{{\boldsymbol {V}}^{el}}^{T}.$

   (B.23)

7. Compute the “inelastic” snapshot matrix ${\textstyle {\boldsymbol {X}}^{in}}$ as

   ${\boldsymbol {X}}^{in}={\boldsymbol {X}}-{\boldsymbol {X}}_{\sigma }^{el}.$

   (B.24)

8. Perform the SVD of ${\textstyle {\boldsymbol {X}}^{in}}$:

   ${\boldsymbol {X}}^{in}={\boldsymbol {D}}^{in}{\boldsymbol {S}}^{in}{{\boldsymbol {V}}_{\Sigma }^{in}}^{T}.$

   (B.25)

The remaining ${\textstyle n_{\sigma }-m_{e}}$ basis vectors –-the essential or dominant inelastic modes–- are the first ${\textstyle n_{\sigma }-m_{e}}$ columns of the matrix of left singular values ${\textstyle {\boldsymbol {D}}^{in}}$.

${\boldsymbol {\Psi ^{in}}}={\begin{bmatrix}{\boldsymbol {D}}_{1}^{in}&{\boldsymbol {D}}_{2}^{in}&\cdots &{\boldsymbol {D}}_{n_{\sigma }-m_{e}}^{in}\end{bmatrix}}.$

(B.26)

9. The desired basis matrix ${\textstyle {\boldsymbol {\Psi }}\in \mathbb {R} ^{n_{g}\cdot s\times n_{\sigma }}}$ adopts finally the form:

   ${\boldsymbol {\Psi }}=[{\boldsymbol {\Psi ^{el}}}\;{\boldsymbol {\Psi ^{in}}}]=[\overbrace {{\boldsymbol {\Psi _{1}^{el}}}\;{\boldsymbol {\Psi _{2}^{el}}}\,\cdots \,{\boldsymbol {\Psi _{m_{e}}^{el}}}} ^{\textrm {Elasticmodes}}\;\overbrace {{\boldsymbol {\Psi _{1}^{in}}}\;{\boldsymbol {\Psi _{2}^{in}}}\,\cdots \,{\boldsymbol {\Psi _{n_{\sigma }-m_{e}}^{in}}}} ^{\textrm {Essentialinelasticmodes}}]$

   (B.27)

B.2.1 Generalized elastic/inelastic SVD

For formulation purposes (see Appendix D.2.2), it is convenient to decompose matrix ${\textstyle {\boldsymbol {X}}^{in}}$ in equation Eq.(B.25) as

${\boldsymbol {X}}^{in}={\boldsymbol {D}}^{in}{\boldsymbol {S}}^{in}{{\boldsymbol {V}}_{\Sigma }^{in}}^{T}={\begin{bmatrix}{\boldsymbol {\Psi ^{in}}}&{\boldsymbol {\Gamma }}\end{bmatrix}}{\begin{bmatrix}{\boldsymbol {S}}^{in,\Psi }&{\boldsymbol {0}}\\{\boldsymbol {0}}&{\boldsymbol {S}}^{\Gamma }\end{bmatrix}}{\begin{bmatrix}{{\boldsymbol {V}}^{in,\Psi }}^{T}\\{{\boldsymbol {V}}^{\Gamma }}^{T}\end{bmatrix}}$ $={\boldsymbol {\Psi ^{in}}}{\boldsymbol {S}}^{in,\Psi }{{\boldsymbol {V}}^{in,\Psi }}^{T}+{\boldsymbol {\Gamma }}{\boldsymbol {S}}^{\Gamma }{{\boldsymbol {V}}^{\Gamma }}^{T}$

(B.28)

Here, ${\textstyle {\boldsymbol {\Gamma }}}$ denotes the matrix of the inessential inelastic modes, and ${\textstyle {\boldsymbol {S}}^{\Gamma }}$ and ${\textstyle {\boldsymbol {V}}^{\Gamma }}$ their associated matrix of singular values and right singular vectors, respectively. Having decompositions (B.23) and (B.28) at hand, we can finally write the snapshot matrix as:

${\boldsymbol {X}}={\boldsymbol {\Psi ^{el}}}{\boldsymbol {S}}^{el}{{\boldsymbol {V}}^{el}}^{T}+{\boldsymbol {\Psi ^{in}}}{\boldsymbol {S}}^{in,\Psi }{{\boldsymbol {V}}^{in,\Psi }}^{T}+{\boldsymbol {\Gamma }}{\boldsymbol {S}}^{\Gamma }{{\boldsymbol {V}}^{\Gamma }}^{T}$ $=\overbrace {\begin{bmatrix}{\boldsymbol {\Psi ^{el}}}&{\boldsymbol {\Psi ^{in}}}\end{bmatrix}} ^{\boldsymbol {\Psi }}\overbrace {\begin{bmatrix}{\boldsymbol {S}}^{el}&{\boldsymbol {0}}\\{\boldsymbol {0}}&{\boldsymbol {S}}^{in,\Psi }\end{bmatrix}} ^{{\boldsymbol {S}}^{\Psi }}\overbrace {\begin{bmatrix}{{\boldsymbol {V}}^{el}}^{T}\\{{\boldsymbol {V}}^{in,\Psi }}^{T}\end{bmatrix}} ^{{\boldsymbol {V}}^{\Psi }}+{\boldsymbol {\Gamma }}{\boldsymbol {S}}^{\Gamma }{{\boldsymbol {V}}^{\Gamma }}^{T}$ $={\boldsymbol {\Psi }}{\boldsymbol {S}}^{\Psi }{{\boldsymbol {V}}^{\Psi }}^{T}+{\boldsymbol {\Gamma }}{\boldsymbol {S}}^{\Gamma }{{\boldsymbol {V}}^{\Gamma }}^{T}$ $={\begin{bmatrix}{\boldsymbol {\Psi }}&{\boldsymbol {\Gamma }}\end{bmatrix}}{\begin{bmatrix}{\boldsymbol {S}}^{\Psi }&{\boldsymbol {0}}\\{\boldsymbol {0}}&{\boldsymbol {S}}^{\Gamma }\end{bmatrix}}{\begin{bmatrix}{{\boldsymbol {V}}^{\Psi }}^{T}\\{{\boldsymbol {V}}^{\Gamma }}^{T}\end{bmatrix}}$

(B.29)

Appendix C. Block matrix pseudoinverse of the expanded basis matrix

The inverse of a ${\textstyle 2}$x${\textstyle 2}$ symmetric block matrix is given by the following expression (see, for instance, Ref. [72]):

${M}^{-1}={\begin{bmatrix}{A}&{B}\\{B}^{T}&{C}\end{bmatrix}}^{-1}={\begin{bmatrix}{A}^{-1}+{A}^{-1}{B}{S}^{-1}{B}^{T}{A}^{-1}&-{A}^{-1}{B}{S}^{-1}\\-{S}^{-1}{B}^{T}{A}^{-1}&{S}^{-1}\end{bmatrix}}$

(C.1)

where

${S}={C}-{B}^{T}{A}^{-1}{B}$

(C.2)

is the so-called Schur complement of ${\textstyle {A}}$ in ${\textstyle {M}}$. This formula can be used to derive closed-form expressions for the modal coefficients ${\textstyle {\boldsymbol {c}}^{ad}}$ and ${\textstyle {\boldsymbol {c}}^{in}}$ (see Section 4.4.2). The departure point is equation Eq.(4.59):

${\begin{bmatrix}{\boldsymbol {c}}^{ad}\\{\boldsymbol {c}}^{in}\end{bmatrix}}=([{\boldsymbol {\hat {\Psi }}}\;{\mathbb {\hat {B}} ^{*}}])^{\dagger }{\hat {\boldsymbol {\Sigma }}}={\begin{bmatrix}{\boldsymbol {\hat {\Psi }}}^{T}{\boldsymbol {\hat {\Psi }}}&{\boldsymbol {\hat {\Psi }}}^{T}{\mathbb {\hat {B}} ^{*}}\\{\mathbb {\hat {B}} ^{*^{T}}}{\boldsymbol {\hat {\Psi }}}&{\mathbb {\hat {B}} ^{*^{T}}}{\mathbb {\hat {B}} ^{*}}\end{bmatrix}}^{-1}{\begin{bmatrix}{\boldsymbol {\hat {\Psi }}}^{T}\\{\mathbb {\hat {B}} ^{*^{T}}}\end{bmatrix}}{\hat {\boldsymbol {\Sigma }}},$

(C.3)

where ${\textstyle ([{\boldsymbol {\hat {\Psi }}}\;{\mathbb {\hat {B}} ^{*}}])^{\dagger }}$ designates the pseudo-inverse of the gappy expanded basis matrix. By setting:

${A}={\boldsymbol {\hat {\Psi }}}^{T}{\boldsymbol {\hat {\Psi }}},\;\;\;\;{B}={\boldsymbol {\hat {\Psi }}}^{T}{\mathbb {\hat {B}} ^{*}},\;\;\;\;\;\;{C}={\mathbb {\hat {B}} ^{*^{T}}}{\mathbb {\hat {B}} ^{*}},\;\;\;\;\;$

(C.4)

and by inserting Eq.(C.1) into Eq.(C.3), one obtains upon expansion:

${\boldsymbol {c}}^{in}={S}^{-1}\left(-{B}^{T}{A}^{-1}{\boldsymbol {\hat {\Psi }}}^{T}+{\mathbb {\hat {B}} ^{*^{T}}}\right){\hat {\boldsymbol {\Sigma }}}$

(C.5)

and

${\boldsymbol {c}}^{ad}=\left(\left({A}^{-1}+{A}^{-1}{B}{S}^{-1}{B}^{T}{A}^{-1}\right){\boldsymbol {\hat {\Psi }}}^{T}-{A}^{-1}{B}{S}^{-1}{\mathbb {\hat {B}} ^{*^{T}}}\right){\hat {\boldsymbol {\Sigma }}}$ $={A}^{-1}{\boldsymbol {\hat {\Psi }}}^{T}{\hat {\boldsymbol {\Sigma }}}+{A}^{-1}{B}\overbrace {{S}^{-1}\left(-{B}^{T}{A}^{-1}{\boldsymbol {\hat {\Psi }}}^{T}+{\mathbb {\hat {B}} ^{*^{T}}}\right){\hat {\boldsymbol {\Sigma }}}} ^{{\boldsymbol {c}}^{in}}$ $={A}^{-1}{\boldsymbol {\hat {\Psi }}}^{T}{\hat {\boldsymbol {\Sigma }}}+{A}^{-1}{B}{{\boldsymbol {c}}^{in}}.$

(C.6)

By substituting back Eq.(C.4) into the above equation, and taking into account that:

${\boldsymbol {\hat {\Psi }}}^{\dagger }=({\boldsymbol {\hat {\Psi }}}^{T}{\boldsymbol {\hat {\Psi }}})^{-1}{\boldsymbol {\hat {\Psi }}}^{T}$

(C.7)

one finally gets:

${\boldsymbol {c}}^{ad}={\boldsymbol {\hat {\Psi }}}^{\dagger }({\hat {\boldsymbol {\Sigma }}}-{\mathbb {\hat {B}} ^{*}}{\boldsymbol {c}}^{in}),$

(C.8)

${\boldsymbol {c}}^{in}={S}^{-1}{\mathbb {\hat {B}} ^{*^{T}}}\left({\boldsymbol {I}}-{\boldsymbol {\hat {\Psi }}}{\boldsymbol {\hat {\Psi }}}^{\dagger }\right){\hat {\boldsymbol {\Sigma }}},$

(C.9)

where

${S}={\mathbb {\hat {B}} ^{*^{T}}}({\boldsymbol {I}}-{\boldsymbol {\hat {\Psi }}}{\boldsymbol {\hat {\Psi }}}^{\dagger }){\mathbb {\hat {B}} ^{*}}.$

(C.10)

Appendix D. Sampling points selection algorithms

D.1 Upper bound for the macroscopic stress error

Proposition D.1.1: Let ${\textstyle {E}_{M,\sigma }}$ be the error estimate defined as (see Section 4.5.1):

${E}_{M,\sigma }({\boldsymbol {\Psi }},{\mathcal {I}}){\mathrel {\mathop {:}}}={\sqrt {\sum _{i=1}^{n_{snp}}\Vert {\boldsymbol {\sigma _{M}}}^{i}-{{\boldsymbol {\sigma _{M}}}^{*\,i}}({\boldsymbol {\Psi }},{\mathcal {I}})\Vert ^{2}}}.$

(D.1)

Here, ${\textstyle {\boldsymbol {\sigma _{M}}}^{i}}$ denotes the finite element, macroscopic stress solution corresponding to the ${\textstyle i-th}$ “training snapshot”, whereas ${\textstyle {{\boldsymbol {\sigma _{M}}}^{*\,i}}({\boldsymbol {\Psi }},{\mathcal {I}})}$ stands for the low-dimensional approximation of ${\textstyle {\boldsymbol {\sigma _{M}}}^{i}}$, calculated through formula (4.65) using the stress basis matrix ${\textstyle {\boldsymbol {\Psi }}}$ and the sampling indices ${\textstyle {\mathcal {I}}}$. On the other hand, consider the following decomposition of the weighted snapshot matrix ${\textstyle {\boldsymbol {X}}}$ –-this decomposition is derived in Appendix B.2.1:

${\boldsymbol {X}}=\overbrace {{\boldsymbol {\Psi }}({\boldsymbol {\Psi }}^{T}{\boldsymbol {X}})} ^{{\boldsymbol {X}}^{\Psi }}+\overbrace {{\boldsymbol {\Gamma }}{\boldsymbol {S}}^{\Gamma }{{\boldsymbol {V}}^{\Gamma }}^{T}} ^{{\boldsymbol {X}}^{\Gamma }}$ $={\boldsymbol {X}}^{\Psi }+{\boldsymbol {X}}^{\Gamma },$

(D.2)

where ${\textstyle {\boldsymbol {\Psi }}={\begin{bmatrix}{\boldsymbol {\Psi ^{el}}}&{\boldsymbol {\Psi ^{in}}}\end{bmatrix}}}$ denotes the basis matrix of elastic and dominant (or essential) inelastic modes; ${\textstyle {\boldsymbol {\Gamma }}}$ designates the basis matrix of trailing (or inessential) inelastic modes (recall that ${\textstyle {\boldsymbol {\Psi }}^{T}{\boldsymbol {\Gamma }}={\boldsymbol {0}}}$); and, finally, ${\textstyle {\boldsymbol {S}}^{\Gamma }}$ and ${\textstyle {\boldsymbol {V}}^{\Gamma }}$ stand for the singular values and right singular vectors, respectively, associated to ${\textstyle {\boldsymbol {\Gamma }}}$. Then, it can be shown that:

${E}_{M,\sigma }({\boldsymbol {\Psi }},{\mathcal {I}})\leq {{e}_{\sigma }}={\sqrt {{{e}_{\sigma }^{trun}}^{2}({\boldsymbol {\Psi }})+{{e}_{\sigma }^{rec}}^{2}({\boldsymbol {\Psi }},{\mathcal {I}})}}$

(D.3)

where

${e}_{\sigma }^{trun}{\mathrel {\mathop {:}}}={\dfrac {1}{V}}\Vert {\boldsymbol {S}}^{\Gamma }\Vert _{F}={\dfrac {1}{V}}{\sqrt {\displaystyle \sum _{i=1}^{r_{\sigma }-n_{\sigma }}{{S}_{ii}^{\Gamma }}^{2}}}$

(D.4)

(${\textstyle r_{\sigma }}$ is the rank of ${\textstyle {\boldsymbol {X}}}$), and

${e}_{\sigma }^{rec}{\mathrel {\mathop {:}}}={\dfrac {1}{V}}\Vert ({\boldsymbol {\hat {\boldsymbol {\Psi }}}}_{({\mathcal {I}})}^{T}{\boldsymbol {\hat {\boldsymbol {\Psi }}}}_{({\mathcal {I}})})^{-1}{\boldsymbol {\hat {\boldsymbol {\Psi }}}}_{({\mathcal {I}})}^{T}{\boldsymbol {\hat {\Gamma }}}_{({\mathcal {I}})}{\boldsymbol {S}}^{\Gamma }\Vert _{F}$ $={\dfrac {1}{V}}{\sqrt {\displaystyle \sum _{i=1}^{r_{\sigma }-n_{\sigma }}{{S}_{ii}^{\Gamma }}^{2}\Vert ({\boldsymbol {\hat {\boldsymbol {\Psi }}}}_{({\mathcal {I}})}^{T}{\boldsymbol {\hat {\boldsymbol {\Psi }}}}_{({\mathcal {I}})})^{-1}{\boldsymbol {\hat {\boldsymbol {\Psi }}}}_{({\mathcal {I}})}^{T}{{\boldsymbol {\hat {\Gamma }}}_{i}}_{({\mathcal {I}})}\Vert ^{2}}}$

(D.5)

with ${\textstyle {\boldsymbol {\hat {\boldsymbol {\Psi }}}}_{({\mathcal {I}})}={\boldsymbol {\mathcal {P}}}_{({\mathcal {I}})}{\boldsymbol {\Psi }}}$ and ${\textstyle {\boldsymbol {\hat {\Gamma }}}_{({\mathcal {I}})}={\boldsymbol {\mathcal {P}}}_{({\mathcal {I}})}{\boldsymbol {\Gamma }}={\boldsymbol {\mathcal {P}}}_{({\mathcal {I}})}{\begin{bmatrix}{\boldsymbol {\Gamma }}_{1}&{\boldsymbol {\Gamma }}_{2}&\cdots &{\boldsymbol {\Gamma }}_{r_{\sigma }-n_{\sigma }}\end{bmatrix}}}$. The variable ${\textstyle {e}_{\sigma }^{trun}}$ in Eq.(D.4) represents an upper bound for the stress truncation error, while ${\textstyle {e}_{\sigma }^{rec}}$ is an upper bound for the stress reconstruction error.

Proof. We begin the proof by applying to Eq.(D.1) the Cauchy-Schwarz inequality:

${{E}_{M,\sigma }}^{2}={\sum _{i=1}^{n_{snp}}\Vert {\boldsymbol {\sigma _{M}}}^{i}-{{\boldsymbol {\sigma _{M}}}^{*\,i}}({\boldsymbol {\Psi }},{\mathcal {I}})\Vert ^{2}}$ $={\dfrac {1}{V}}\sum _{i=1}^{n_{snp}}\Vert \displaystyle \int _{\Omega }{\boldsymbol {\sigma }}^{i}(\mathbf {x} )-{{\boldsymbol {\sigma }}^{*}}^{i}(\mathbf {x} ,{\boldsymbol {\Psi }},{\mathcal {I}})\,d\Omega \Vert ^{2}$ $\leq {\dfrac {1}{V}}\sum _{i=1}^{n_{snp}}\int _{\Omega }\Vert \displaystyle {\boldsymbol {\sigma }}^{i}(\mathbf {x} )-{{\boldsymbol {\sigma }}^{*}}^{i}(\mathbf {x} ;{\boldsymbol {\Psi }},{\mathcal {I}})\Vert ^{2}\,d\Omega {.}$

(D.6)

Approximating now the integral in the above equation by Gauss quadrature, and using the weighted global stress vectors introduced in Section 4.3.3, one gets

${{E}_{M,\sigma }}^{2}\leq {\dfrac {1}{V}}\sum _{i=1}^{n_{snp}}\sum _{g=1}^{n_{g}}w_{g}\Vert \displaystyle {\boldsymbol {\sigma }}^{i}(\mathbf {x} _{g})-{{\boldsymbol {\sigma }}^{*}}^{i}(\mathbf {x} _{g};{\boldsymbol {\Psi }},{\mathcal {I}})\Vert ^{2}$ $={\dfrac {1}{V}}\sum _{i=1}^{n_{snp}}\sum _{g=1}^{n_{g}}\Vert \displaystyle {\sqrt {w_{g}}}{\boldsymbol {\sigma }}^{i}(\mathbf {x} _{g})-{\sqrt {w_{g}}}{{\boldsymbol {\sigma }}^{*}}^{i}(\mathbf {x} _{g};{\boldsymbol {\Psi }},{\mathcal {I}})\Vert ^{2}$ $={\dfrac {1}{V}}\sum _{i=1}^{n_{snp}}\Vert {\boldsymbol {\Sigma }}^{i}-{\boldsymbol {\Sigma }}^{*\,i}({\boldsymbol {\Psi }},{\mathcal {I}})\Vert ^{2}$ $={\dfrac {1}{V}}\Vert {\boldsymbol {X}}-{\boldsymbol {X}}^{*}({\boldsymbol {\Psi }},{\mathcal {I}})\Vert _{F},$

(D.7)

where

${\boldsymbol {X}}={\begin{bmatrix}{\boldsymbol {\Sigma }}^{1}&{\boldsymbol {\Sigma }}^{2}&\cdots &{\boldsymbol {\Sigma }}^{n_{snp}}\end{bmatrix}}$

(D.8)

and

${\boldsymbol {X}}^{*}={\begin{bmatrix}{{\boldsymbol {\Sigma }}^{*}}^{1}&{{\boldsymbol {\Sigma }}^{*}}^{2}&\cdots &{{\boldsymbol {\Sigma }}^{*}}^{n_{snp}}\end{bmatrix}}.$

(D.9)

The error estimate for the macroscopic stresses defined in Eq.(4.102) is, thus, bounded above by the Frobenius norm of the difference between the (weighted) stress snapshot matrix ${\textstyle {\boldsymbol {X}}}$ and its low-dimensional approximation ${\textstyle {\boldsymbol {X}}^{*}}$. This bound will be hereafter designated by ${\textstyle {{e}_{\sigma }}}$

${{e}_{\sigma }}({\boldsymbol {\Psi }},{\mathcal {I}}){\mathrel {\mathop {:}}}={\dfrac {1}{V}}\Vert {\boldsymbol {X}}-{\boldsymbol {X}}^{*}({\boldsymbol {\Psi }},{\mathcal {I}})\Vert _{F}.$

(D.10)

The link between ${\textstyle {\boldsymbol {X}}}$ and ${\textstyle {\boldsymbol {X}}^{*}}$, on the other hand, is established through the reconstruction matrix ${\textstyle {\boldsymbol {R}}_{({\mathcal {I}})}}$ defined in Section 4.4.2:

${\boldsymbol {X}}^{*}({\boldsymbol {\Psi }},{\mathcal {I}})={\boldsymbol {R}}_{({\mathcal {I}})}({\boldsymbol {\mathcal {P}}}_{({\mathcal {I}})}{\boldsymbol {X}})=$ $={\boldsymbol {\Psi }}({\boldsymbol {\hat {\boldsymbol {\Psi }}}}_{({\mathcal {I}})}^{T}{\boldsymbol {\hat {\boldsymbol {\Psi }}}}_{({\mathcal {I}})})^{-1}{\boldsymbol {\hat {\boldsymbol {\Psi }}}}_{({\mathcal {I}})}^{T}{\boldsymbol {\hat {X}}}_{({\mathcal {I}})},$

(D.11)

where ${\textstyle {\boldsymbol {\hat {\boldsymbol {\Psi }}}}_{({\mathcal {I}})}={\boldsymbol {\mathcal {P}}}_{({\mathcal {I}})}{\boldsymbol {\Psi }}}$. Inserting decomposition Eq.(D.2) into Eq.(D.11), and exploiting the fact that ${\textstyle {\boldsymbol {R}}_{({\mathcal {I}})}{\boldsymbol {\mathcal {P}}}_{({\mathcal {I}})}(\cdot )}$ represents an oblique projection onto ${\textstyle {\textrm {Range}}({\boldsymbol {\Psi }})}$ –-and therefore ${\textstyle {\boldsymbol {R}}_{({\mathcal {I}})}{\boldsymbol {\hat {X}}}_{({\mathcal {I}})}^{\Psi }={\boldsymbol {X}}^{\Psi }}$–-, one obtains

${\boldsymbol {X}}^{*}={\boldsymbol {R}}_{({\mathcal {I}})}({\boldsymbol {\mathcal {P}}}_{({\mathcal {I}})}{\boldsymbol {X}}^{\Psi }+{\boldsymbol {\mathcal {P}}}_{({\mathcal {I}})}{\boldsymbol {X}}^{\Gamma })$ $=\overbrace {{\boldsymbol {R}}_{({\mathcal {I}})}{\boldsymbol {\hat {X}}}_{({\mathcal {I}})}^{\Psi }} ^{{\boldsymbol {X}}^{\Psi }}+{\boldsymbol {R}}_{({\mathcal {I}})}{\boldsymbol {\hat {X}}}_{({\mathcal {I}})}^{\Gamma }$ $={\boldsymbol {X}}^{\Psi }+{\boldsymbol {R}}_{({\mathcal {I}})}{\boldsymbol {\hat {X}}}_{({\mathcal {I}})}^{\Gamma },$

(D.12)

Substitution of Eqs. (D.12) and (D.2) into expression (D.10) yields:

${{e}_{\sigma }}={\dfrac {1}{V}}\Vert {\boldsymbol {X}}^{\Gamma }+{\boldsymbol {R}}_{({\mathcal {I}})}{\boldsymbol {\hat {X}}}_{({\mathcal {I}})}^{\Gamma }\Vert _{F}.$

(D.13)

Since the column space of ${\textstyle {\boldsymbol {R}}_{({\mathcal {I}})}}$ and ${\textstyle {\boldsymbol {X}}^{\Gamma }}$ are, by construction, mutually orthogonal, it follows that:

${{e}_{\sigma }}^{2}={\dfrac {1}{V}}\Vert {\boldsymbol {X}}^{\Gamma }\Vert _{F}^{2}+{\dfrac {1}{V}}\Vert {\boldsymbol {R}}_{({\mathcal {I}})}{\boldsymbol {\hat {X}}}_{({\mathcal {I}})}^{\Gamma }\Vert _{F}^{2}.$

(D.14)

Replacing now ${\textstyle {\boldsymbol {X}}^{\Gamma }}$ in the preceding equation by its singular value decomposition, one finally arrives at

${{e}_{\sigma }}^{2}={\dfrac {1}{V}}\Vert {\boldsymbol {\Gamma }}{\boldsymbol {S}}^{\Gamma }{{\boldsymbol {V}}^{\Gamma }}^{T}\Vert _{F}^{2}+{\dfrac {1}{V}}\Vert {\boldsymbol {R}}_{({\mathcal {I}})}{\boldsymbol {\hat {\Gamma }}}_{({\mathcal {I}})}{\boldsymbol {S}}^{\Gamma }{{\boldsymbol {V}}^{\Gamma }}^{T}\Vert _{F}^{2}$ $={\dfrac {1}{V}}\Vert {\boldsymbol {\Gamma }}{\boldsymbol {S}}^{\Gamma }{{\boldsymbol {V}}^{\Gamma }}^{T}\Vert _{F}^{2}+{\dfrac {1}{V}}\Vert {\boldsymbol {\Psi }}({\boldsymbol {\hat {\boldsymbol {\Psi }}}}_{({\mathcal {I}})}^{T}{\boldsymbol {\hat {\boldsymbol {\Psi }}}}_{({\mathcal {I}})})^{-1}{\boldsymbol {\hat {\boldsymbol {\Psi }}}}_{({\mathcal {I}})}^{T}{\boldsymbol {\hat {\Gamma }}}_{({\mathcal {I}})}{\boldsymbol {S}}^{\Gamma }{\boldsymbol {V}}^{\Gamma }\Vert _{F}^{2}.$

(D.15)

The proof is completed by noting that ${\textstyle {\boldsymbol {\Psi }}}$, ${\textstyle {\boldsymbol {\Gamma }}}$ and ${\textstyle {\boldsymbol {V}}^{\Gamma }}$ are columnwise orthonormal matrices, and, therefore:

${{e}_{\sigma }}^{2}={\dfrac {1}{V}}\Vert {\boldsymbol {\Gamma }}{\boldsymbol {S}}^{\Gamma }{{\boldsymbol {V}}^{\Gamma }}^{T}\Vert _{F}^{2}+{\dfrac {1}{V}}\Vert {\boldsymbol {\Psi }}({\boldsymbol {\hat {\boldsymbol {\Psi }}}}_{({\mathcal {I}})}^{T}{\boldsymbol {\hat {\boldsymbol {\Psi }}}}_{({\mathcal {I}})})^{-1}{\boldsymbol {\hat {\boldsymbol {\Psi }}}}_{({\mathcal {I}})}^{T}{\boldsymbol {\hat {\Gamma }}}_{({\mathcal {I}})}{\boldsymbol {S}}^{\Gamma }{\boldsymbol {V}}^{\Gamma }\Vert _{F}^{2}$ $=\overbrace {{\dfrac {1}{V}}\Vert {\boldsymbol {S}}^{\Gamma }\Vert _{F}^{2}} ^{{{e}_{\sigma }^{trun}}^{2}}+\overbrace {{\dfrac {1}{V}}\Vert ({\boldsymbol {\hat {\boldsymbol {\Psi }}}}_{({\mathcal {I}})}^{T}{\boldsymbol {\hat {\boldsymbol {\Psi }}}}_{({\mathcal {I}})})^{-1}{\boldsymbol {\hat {\boldsymbol {\Psi }}}}_{({\mathcal {I}})}^{T}{\boldsymbol {\hat {\Gamma }}}_{({\mathcal {I}})}{\boldsymbol {S}}^{\Gamma }\Vert _{F}^{2}} ^{{{e}_{\sigma }^{rec}}^{2}}$ $={{e}_{\sigma }^{trun}}^{2}+{{e}_{\sigma }^{rec}}^{2}$

(D.16)

as asserted.

Observation 7: From Eq.(D.3) and Eq.(D.4), we have that:

${e}_{\sigma }^{rec}={\dfrac {1}{V}}\Vert ({\boldsymbol {\hat {\boldsymbol {\Psi }}}}_{({\mathcal {I}})}^{T}{\boldsymbol {\hat {\boldsymbol {\Psi }}}}_{({\mathcal {I}})})^{-1}{\boldsymbol {\hat {\boldsymbol {\Psi }}}}_{({\mathcal {I}})}^{T}{\boldsymbol {\hat {\Gamma }}}_{({\mathcal {I}})}{\boldsymbol {S}}^{\Gamma }\Vert _{F}$ $\leq {\dfrac {1}{V}}\Vert ({\boldsymbol {\hat {\boldsymbol {\Psi }}}}_{({\mathcal {I}})}^{T}{\boldsymbol {\hat {\boldsymbol {\Psi }}}}_{({\mathcal {I}})})^{-1}{\boldsymbol {\hat {\boldsymbol {\Psi }}}}_{({\mathcal {I}})}^{T}{\boldsymbol {\hat {\Gamma }}}_{({\mathcal {I}})}\Vert _{F}\Vert {\boldsymbol {S}}^{\Gamma }\Vert _{F}$ $=\Vert ({\boldsymbol {\hat {\boldsymbol {\Psi }}}}_{({\mathcal {I}})}^{T}{\boldsymbol {\hat {\boldsymbol {\Psi }}}}_{({\mathcal {I}})})^{-1}{\boldsymbol {\hat {\boldsymbol {\Psi }}}}_{({\mathcal {I}})}^{T}{\boldsymbol {\hat {\Gamma }}}_{({\mathcal {I}})}\Vert _{F}\,\,{e}_{\sigma }^{trun}.$

(D.17)

i.e., the bound for the reconstruction error ${\textstyle {e}_{\sigma }^{rec}}$ diminishes as the truncation error is reduced. Furthermore, since ${\textstyle \Vert {\boldsymbol {\Psi }}\Vert _{F}={\sqrt {n_{\sigma }}}}$ and ${\textstyle \Vert {\boldsymbol {\Gamma }}\Vert _{F}={\sqrt {r_{\sigma }-n_{\sigma }}}}$, it follows that ${\textstyle \Vert {\boldsymbol {\hat {\boldsymbol {\Psi }}}}_{({\mathcal {I}})}\Vert _{F}\leq {\sqrt {n_{\sigma }}}}$ and ${\textstyle \Vert {\boldsymbol {\hat {\Gamma }}}_{({\mathcal {I}})}\Vert _{F}\leq {\sqrt {r_{\sigma }-n_{\sigma }}}}$, and consequently

${e}_{\sigma }^{rec}\leq \Vert ({\boldsymbol {\hat {\boldsymbol {\Psi }}}}_{({\mathcal {I}})}^{T}{\boldsymbol {\hat {\boldsymbol {\Psi }}}}_{({\mathcal {I}})})^{-1}{\boldsymbol {\hat {\boldsymbol {\Psi }}}}_{({\mathcal {I}})}^{T}{\boldsymbol {\hat {\Gamma }}}_{({\mathcal {I}})}\Vert _{F}\,\,{e}_{\sigma }^{trun}$ $\leq {\sqrt {n_{\sigma }(r_{\sigma }-n_{\sigma })}}\Vert ({\boldsymbol {\hat {\boldsymbol {\Psi }}}}_{({\mathcal {I}})}^{T}{\boldsymbol {\hat {\boldsymbol {\Psi }}}}_{({\mathcal {I}})})^{-1}\Vert _{F}\,\,{e}_{\sigma }^{trun}.$

(D.18)

It may be inferred from the above that the only contribution to the reconstruction error that can grow unboundedly depending on the chosen sampling points is ${\textstyle \Vert ({\boldsymbol {\hat {\boldsymbol {\Psi }}}}_{({\mathcal {I}})}^{T}{\boldsymbol {\hat {\boldsymbol {\Psi }}}}_{({\mathcal {I}})})^{-1}\Vert _{F}}$. A poorly conditioned matrix ${\textstyle {\boldsymbol {\hat {\boldsymbol {\Psi }}}}_{({\mathcal {I}})}^{T}{\boldsymbol {\hat {\boldsymbol {\Psi }}}}_{({\mathcal {I}})}}$ is likely to give rise to large reconstruction errors. Therefore, one must seek to choose such points so that the columns –-and hence the rows–- of ${\textstyle {\boldsymbol {\hat {\boldsymbol {\Psi }}}}_{({\mathcal {I}})}}$ are “as linearly independent as possible”. To put it alternatively, the stress information associated to the chosen sampling points should be as “uncorrelated” as possible. This observation concurs with one's intuitive expectations, for it seems to make little sense to choose, say, spatially close points at which stress responses are expected to be very similar.

Observation 8: Any stress snapshot ${\textstyle {\boldsymbol {\Sigma }}}$ pertaining to the column space of the stress basis matrix ${\textstyle {\boldsymbol {\Psi }}}$ is exactly approximated regardless of the chosen set of admissible sampling points; that is, if ${\textstyle {\boldsymbol {\Sigma }}\in {\textrm {Range}}({\boldsymbol {\Psi }})}$ then

${\boldsymbol {\Sigma }}={\boldsymbol {\Sigma }}^{*}({\boldsymbol {\Psi }},{\mathcal {I}})={\boldsymbol {R}}_{({\mathcal {I}})}({\boldsymbol {\mathcal {P}}}_{({\mathcal {I}})}{\boldsymbol {\Sigma }}),$

(D.19)

for all admissible ${\textstyle {\mathcal {I}}}$. The proof follows easily from the observation, made earlier when deriving Eq.(D.12), that ${\textstyle {\boldsymbol {R}}_{({\mathcal {I}})}{\boldsymbol {\mathcal {P}}}_{({\mathcal {I}})}(\cdot )}$ represents actually an oblique projection onto ${\textstyle {\textrm {Range}}({\boldsymbol {\Psi }})}$. A far-reaching implication of this property is that, the elastic stress modes being contained in ${\textstyle {\boldsymbol {\Psi }}}$, the reduced-order model will furnish linear elastic solutions with the same accuracy as the underlying finite element model regardless of the set of admissible sampling points used for reconstructing the stress field.

D.2 Basic sampling points

D.2.1 Hierarchical Interpolation Points Method

The algorithm employed in the present work to deal with the discrete minimization problem (4.109) is inspired in the Hierarchical Interpolation Points (HPI) method proposed by Nguyen et al.[30]. In fact, the only difference with respect to the proposal by Nguyen et al. is the format of the equation for the objective function . In Ref. [30], the reconstruction error is directly calculated as the norm of the difference between the coefficients of the orthogonal projection and the oblique projection (using sampling points ${\textstyle {\mathcal {I}}}$) of ${\textstyle {\boldsymbol {X}}}$ onto the column space of the basis matrix ${\textstyle {\boldsymbol {\Psi }}}$ ( i.e, ${\textstyle \Vert {\boldsymbol {\Psi }}^{T}{\boldsymbol {X}}-{\boldsymbol {\hat {\boldsymbol {\Psi }}}}_{({\mathcal {I}})}^{\dagger }{\boldsymbol {\hat {X}}}_{({\mathcal {I}})}\Vert _{F}}$). However, we have just shown in Proposition D.1.1 that the expression for this estimate can be notably simplified by introducing the singular value decomposition of ${\textstyle {\boldsymbol {X}}^{\Gamma }={\boldsymbol {X}}-{\boldsymbol {\Psi }}({\boldsymbol {\Psi }}^{T}{\boldsymbol {X}})}$; the final result reads (see Eq.(D.5)):

${e}_{\sigma }^{rec}={\dfrac {1}{V}}{\sqrt {\displaystyle \sum _{i=1}^{r_{\sigma }-n_{\sigma }}{{S}_{ii}^{\Gamma }}^{2}\Vert \overbrace {({\boldsymbol {\hat {\boldsymbol {\Psi }}}}_{({\mathcal {I}})}^{T}{\boldsymbol {\hat {\boldsymbol {\Psi }}}}_{({\mathcal {I}})})^{-1}{\boldsymbol {\hat {\boldsymbol {\Psi }}}}_{({\mathcal {I}})}^{T}} ^{{\boldsymbol {\hat {\boldsymbol {\Psi }}}}_{({\mathcal {I}})}^{\dagger }}{{\boldsymbol {\hat {\Gamma }}}_{i}}_{({\mathcal {I}})}\Vert ^{2}}}$ $={\dfrac {1}{V}}{\sqrt {\displaystyle \sum _{i=1}^{r_{\sigma }-n_{\sigma }}{{S}_{ii}^{\Gamma }}^{2}\Vert {\boldsymbol {\hat {\boldsymbol {\Psi }}}}_{({\mathcal {I}})}^{\dagger }{{\boldsymbol {\hat {\Gamma }}}_{i}}_{({\mathcal {I}})}\Vert ^{2}}}.$

(D.20)

In principle, the summation in the preceding equation should extend over all inessential or trailing modes ${\textstyle {\boldsymbol {\Gamma }}_{i}}$ (${\textstyle i=1,2\ldots r_{\sigma }-n_{\sigma }}$). In practice, however, there is no need to include all such trailing modes in the evaluation of ${\textstyle {e}_{\sigma }^{rec}}$ objective function: the contribution of each such modes is weighted by their corresponding singular values ${\textstyle {S}_{ii}^{\Gamma }}$ (${\textstyle i=1,2\ldots r_{\sigma }-n_{\sigma }}$), whose magnitude is already comparatively small –-this is the very reason why they are deemed inessential–-and, furthermore, decays exponentially as ${\textstyle i}$ increases. For practical purposes, including ${\textstyle n_{\Gamma }={\mathcal {O}}(n_{\sigma })}$ trailing modes suffices to satisfactorily approximate ${\textstyle {e}_{\sigma }^{rec}}$:

${e}_{\sigma }^{rec}\approx {\dfrac {1}{V}}{\sqrt {\displaystyle \sum _{i=1}^{n_{\Gamma }}{{S}_{ii}^{\Gamma }}^{2}\Vert {\boldsymbol {\hat {\boldsymbol {\Psi }}}}_{({\mathcal {I}})}^{\dagger }{{\boldsymbol {\hat {\Gamma }}}_{i}}_{({\mathcal {I}})}\Vert ^{2}}}.$

(D.21)

We call these first ${\textstyle n_{\Gamma }}$ inessential basis vectors the effective trailing modes. The advantage that accrues from using Eq.(D.21) instead of the objective function employed in [30] is evident: the operation count in evaluating the objective function becomes independent of the total number of snapshots ${\textstyle n_{snp}}$ (that may be arbitrarily large), thus reducing significantly the overall cost of the algorithm.

D.2.2 Proposed algorithm

The essence of the proposed algorithm is to construct, in a greedy fashion¹, the set of indices by solving a sequence of one-dimensional minimization problems. Let us define for this purpose a matrix containing the ${\textstyle n_{\sigma }}$ dominant stress modes and the first ${\textstyle n_{\Gamma }}$ trailing stress modes:

${\boldsymbol {H}}{\mathrel {\mathop {:}}}={\begin{bmatrix}{\boldsymbol {\Psi }}_{1}&{\boldsymbol {\Psi }}_{2}&\cdots &{\boldsymbol {\Psi }}_{n_{\sigma }}&{\boldsymbol {\Gamma }}_{1}&{\boldsymbol {\Gamma }}_{2}&\cdots &{\boldsymbol {\Gamma }}_{n_{\Gamma }}\end{bmatrix}}$

(D.22)

Likewise, the matrix of singular values associated to these modes is defined as:

${\boldsymbol {\Theta }}{\mathrel {\mathop {:}}}={\begin{bmatrix}{\boldsymbol {S}}^{\Psi }&{\boldsymbol {0}}\\{\boldsymbol {0}}&{\boldsymbol {S}}^{\Gamma }\end{bmatrix}}.$

(D.23)

Here, ${\textstyle {\boldsymbol {S}}^{\Psi }\in \mathbb {R} ^{n_{\sigma }\times n_{\sigma }}}$ and ${\textstyle {\boldsymbol {S}}^{\Gamma }\in \mathbb {R} ^{n_{\Gamma }\times n_{\Gamma }}}$ are the matrices of singular values corresponding to the dominant and first ${\textstyle n_{\Gamma }}$ inelastic trailing inelastic modes, respectively.

The index ${\textstyle {\mathcal {I}}_{\sigma }(1)}$ corresponding to the first basic sampling points is obtained as that minimizing the reconstruction error obtained when only the first dominant mode is used:

${\mathcal {I}}_{\sigma }(1)={\textrm {arg}}\;{\underset {j\in \{1,2\ldots n_{g}\}}{\textrm {min}}}\,{e}_{\sigma }^{rec}({\boldsymbol {\Psi }}_{1},j)$ $={\textrm {arg}}\;{\underset {j\in \{1,2\ldots n_{g}\}}{\textrm {min}}}\,\displaystyle \sum _{i=2}^{n_{\sigma }+n_{\Gamma }}\!\!{\Theta }_{ii}^{2}\Vert {\boldsymbol {\hat {\boldsymbol {\Psi }}}}_{{\boldsymbol {1}}(j)}^{\dagger }{{\boldsymbol {\hat {\Gamma }}}_{i}}_{(j)}\Vert ^{2}$ $={\textrm {arg}}\;{\underset {j\in \{1,2\ldots n_{g}\}}{\textrm {min}}}\,\displaystyle \sum _{i=2}^{n_{\sigma }+n_{\Gamma }}\!\!\left({\Theta }_{ii}{\dfrac {{\Gamma }_{ji}}{\Psi _{j1}}}\right)^{2}$

(D.24)

Proceeding inductively, the ${\textstyle k-th}$ index would be determined as that minimizing the reconstruction error obtained when only the first ${\textstyle k}$ (${\textstyle k\leq n_{\sigma }}$) dominant modes are included in the basis matrix (note that, in using this algorithm, we are tacitly assuming that ${\textstyle p_{\sigma }=n_{\sigma }}$):

${\mathcal {I}}_{\sigma }(k)={\textrm {arg}}\;{\underset {j\in \{1,2\ldots n_{g}\}}{\textrm {min}}}\,{e}_{\sigma }^{rec}({\boldsymbol {Z^{k}}},{\mathcal {J}})$ (D.25.a) $={\textrm {arg}}\;{\underset {j\in \{1,2\ldots n_{g}\}}{\textrm {min}}}\,{\sqrt {\displaystyle \sum _{i=k}^{n_{\sigma }+n_{\Gamma }}{{\Theta }_{ii}^{2}}\Vert {\boldsymbol {{\hat {Z}}^{k}}}_{\!\!\!\!\!({\mathcal {J}})}^{\dagger }{{\boldsymbol {{\hat {H}}_{i}}}_{\!({\mathcal {J}})}}\Vert ^{2}}}$ (D.25.b) ${\mathcal {J}}=\{{\mathcal {I}}_{\sigma }(1),{\mathcal {I}}_{\sigma }(2),\cdots {\mathcal {I}}_{\sigma }(k-1),j\}$ (D.25.c)

where

${\boldsymbol {Z^{k}}}={\begin{bmatrix}{\boldsymbol {\Psi }}_{1}&{\boldsymbol {\Psi }}_{2}&\cdots &{\boldsymbol {\Psi }}_{k}\end{bmatrix}}.$

(D.26)

(¹) A greedy method is any algorithm that solves the problem by making the locally optimal choice at each step with the hope of finding the global optimum.

D.3 Complementary sampling points

The heuristic employed for addressing the minimization problem (4.110) is also based on the greedy paradigm. The ${\textstyle k-th}$ (${\textstyle k=1,2\ldots p_{B}}$) index is selected by solving the following, one-dimensional minimization problem:

${\mathcal {I}}_{B}(k)={\textrm {arg}}\;{\underset {j\in \{1,2\ldots n_{g}\}}{\textrm {min}}}\,f_{F}({\boldsymbol {\Psi }},{\mathbb {B} ^{*}},{\mathcal {K}})$ (D.27.a) ${\mathcal {K}}={\mathcal {I}}_{\sigma }\cup \{{\mathcal {I}}_{B}(1),{\mathcal {I}}_{B}(2)\cdots {\mathcal {I}}_{B}(k-1),j\}.$ (D.27.b)

i.e.:

${\mathcal {I}}_{B}(k)={\textrm {arg}}\;{\underset {j\in \{1,2\ldots n_{g}\}}{\textrm {min}}}\,{\dfrac {\Vert {\boldsymbol {\hat {R}}}_{({\mathcal {K}})}{\mathbb {\hat {B}} ^{*}}_{({\mathcal {K}})}\Vert _{F}}{\Vert ({\boldsymbol {I}}-{\boldsymbol {\hat {R}}}_{({\mathcal {K}})}){\mathbb {\hat {B}} ^{*}}_{({\mathcal {K}})}\Vert _{F}}}$ (D.28.a) ${\mathcal {K}}={\mathcal {I}}_{\sigma }\cup \{{\mathcal {I}}_{B}(1),{\mathcal {I}}_{B}(2)\cdots {\mathcal {I}}_{B}(k-1),j\}.$ (D.28.b)

BIBLIOGRAPHY

[1] Ashby, M.F. (1992) "Physical modelling of materials problems", Volume 8. Maney Publishing. Materials Science and Technology 2 102–111

[2] Venkataraman, S. and Haftka, RT. (2004) "Structural optimization complexity: what has Moore’s law done for us?", Volume 28. Springer. Structural and Multidisciplinary Optimization 6 375–387

[3] Thimbleby, H. (1993) "Computerised Parkinson's law", Volume 4. IET. Computing & Control Engineering Journal 5 197–198

[4] Gross, D. and Seelig, T. (2011) "Fracture mechanics: with an introduction to micromechanics". Springer

[5] Hill, R. (1963) "Elastic properties of reinforced solids: some theoretical principles", Volume 11. Elsevier. Journal of the Mechanics and Physics of Solids 5 357–372

[6] Hashin, Z. and Shtrikman, S. (1963) "A variational approach to the theory of the elastic behaviour of multiphase materials", Volume 11. Elsevier. Journal of the Mechanics and Physics of Solids 2 127–140

[7] Mori, T. and Tanaka, K. (1973) "Average stress in matrix and average elastic energy of materials with misfitting inclusions", Volume 21. Elsevier. Acta metallurgica 5 571–574

[8] Bohm, H.J. (1998) "A short introduction to basic aspects of continuum micromechanics", Volume 3. Citeseer. CDL-FMD Report

[9] Zaoui, A. (2002) "Continuum micromechanics: survey", Volume 128. American Society of Civil Engineers. Journal of Engineering Mechanics 8 808–816

[10] Pindera, M.J. and Khatam, H. and Drago, A.S. and Bansal, Y. (2009) "Micromechanics of spatially uniform heterogeneous media: A critical review and emerging approaches", Volume 40. Elsevier. Composites Part B: Engineering 5 349–378

[11] Yuan, Z. and Fish, J. (2008) "Towards Realization of Computational Homogenization in Practice1", Volume 73. Wiley Online Library. Int. J. Numer. Meth. Engng 361–380

[12] Geers, M.G.D. and Kouznetsova, VG and Brekelmans, WAM. (2010) "Multi-scale computational homogenization: Trends and challenges", Volume 234. Elsevier. Journal of computational and applied mathematics 7 2175–2182

[13] Feyel, F. and Chaboche, J.L. (2000) "FE-2 multiscale approach for modelling the elastoviscoplastic behaviour of long fibre SiC/Ti composite materials", Volume 183. Elsevier. Computer methods in applied mechanics and engineering 3 309–330

[14] Oden, J.T. and Belytschko, T. and Fish, J. and Hughes, TJ and Johnson, C. and Keyes, D. and Laub, A. and Petzold, L. and Srolovitz, D. and Yip, S. (2006) "Revolutionizing engineering science through simulation". National Science Foundation (NSF), Blue Ribbon Panel on Simulation-Based Engineering Science [3, 7, 101, 123]

[15] Oskay, C. and Fish, J. (2007) "Eigendeformation-based reduced order homogenization for failure analysis of heterogeneous materials", Volume 196. Elsevier. Computer Methods in Applied Mechanics and Engineering 7 1216–1243

[16] Robert W. Batterman. (2011) "The Tyranny of Scales"

[17] Hill, R. (1965) "Continuum micro-mechanics of elastoplastic polycrystals", Volume 13. Elsevier. Journal of the Mechanics and Physics of Solids 2 89–101

[18] Dvorak, GJ and Wafa, AM and Bahei-El-Din, YA. (1994) "Implementation of the transformation field analysis for inelastic composite materials", Volume 14. Springer. Computational Mechanics 3 201–228

[19] Michel, J.C. and Suquet, P. (2003) "Nonuniform transformation field analysis", Volume 40. Elsevier. International journal of solids and structures 25 6937–6955

[20] Michel, J.C. and Suquet, P. (2004) "Computational analysis of nonlinear composite structures using the nonuniform transformation field analysis", Volume 193. Elsevier. Computer methods in applied mechanics and engineering 48-51 5477–5502

[21] Roussette, S. and Michel, J.C. and Suquet, P. (2009) "Nonuniform transformation field analysis of elastic-viscoplastic composites", Volume 69. Elsevier. Composites Science and Technology 1 22–27

[22] Fish, J. and Shek, K. and Pandheeradi, M. and Shephard, M.S. (1997) "Computational plasticity for composite structures based on mathematical homogenization: Theory and practice", Volume 148. Elsevier. Computer Methods in Applied Mechanics and Engineering 1-2 53–73

[23] Maday, Y. and Patera, AT and Turinici, G. (2002) "Reliable real-time solution of parametrized partial differential equations: Reduced-basis output bound methods"

[24] R.D. Cook. (1995) "Finite element modeling for stress analysis". John Wiley and Sons.

[25] Krysl, P. and Lall, S. and Marsden, JE. (2001) "Dimensional model reduction in non-linear finite element dynamics of solids and structures", Volume 51. Wiley Online Library. International Journal for Numerical Methods in Engineering 4 479–504

[26] Salomon, D. (2004) "Data compression: the complete reference". Springer-Verlag New York Incorporated

[27] Bishop, C.M. and SpringerLink (Service en ligne). (2006) "Pattern recognition and machine learning", Volume 4. springer New York

[28] Barrault, M. and Maday, Y. and Nguyen, N.C. and Patera, A.T. (2004) "An empirical interpolation'method: application to efficient reduced-basis discretization of partial differential equations", Volume 339. Elsevier. Comptes Rendus Mathematique 9 667–672

[29] Grepl, M.A. and Maday, Y. and Nguyen, N.C. and Patera, A.T. (2007) "Efficient reduced-basis treatment of nonaffine and nonlinear partial differential equations", Volume 41. edpsciences. org. Mathematical Modelling and Numerical Analysis 3 575–605

[30] Nguyen, NC and Patera, AT and Peraire, J. (2008) "A best points interpolation method for efficient approximation of parametrized functions", Volume 73. Wiley Online Library. Int. J. Numer. Meth. Engng 521–543

[31] Chaturantabut, S. and Sorensen, D.C. (2010) "Discrete empirical interpolation for nonlinear model reduction". IEEE. Decision and Control, 2009 held jointly with the 2009 28th Chinese Control Conference. CDC/CCC 2009. Proceedings of the 48th IEEE Conference on 4316–4321

[32] Astrid, P. (2004) "Reduction of process simulation models: a proper orthogonal decomposition approach". Technische Universiteit Eindhoven

[33] An, S.S. and Kim, T. and James, D.L. (2009) "Optimizing cubature for efficient integration of subspace deformations", Volume 27. NIH Public Access. ACM transactions on graphics 5 165

[34] Kim, T. and James, D.L. (2009) "Skipping steps in deformable simulation with online model reduction". ACM. ACM SIGGRAPH Asia 2009 papers 1–9

[35] J. D. Hoffman. (2001) "Numerical Methods for Engineers and Scientists". Marcel Dekker

[36] J. A. Hernández and J. Oliver and A.E. Huespe and M. Caicedo. (2012) "High-performance model reduction procedures in multiscale simulations". CIMNE

[37] Boyaval, S. (2007) "Reduced-basis approach for homogenization beyond the periodic setting". Arxiv preprint math/0702674

[38] Yvonnet, J. and He, Q.C. (2007) "The reduced model multiscale method (R3M) for the non-linear homogenization of hyperelastic media at finite strains", Volume 223. Elsevier. Journal of Computational Physics 1 341–368

[39] Monteiro, E. and Yvonnet, J. and He, QC. (2008) "Computational homogenization for nonlinear conduction in heterogeneous materials using model reduction", Volume 42. Elsevier. Computational Materials Science 4 704–712

[40] Nguyen, NC. (2008) "A multiscale reduced-basis method for parametrized elliptic partial differential equations with multiple scales", Volume 227. Elsevier. Journal of Computational Physics 23 9807–9822

[41] Efendiev, Yalchin and Galvis, Juan and Gildin, Eduardo. (2012) "Local–global multiscale model reduction for flows in high-contrast heterogeneous media", Volume 231. Elsevier. Journal of Computational Physics 24 8100–8113

[42] Efendiev, Yalchin and Galvis, Juan and Thomines, Florian. (2012) "A systematic coarse-scale model reduction technique for parameter-dependent flows in highly heterogeneous media and its applications", Volume 10. SIAM. Multiscale Modeling & Simulation 4 1317–1343

[43] Abdulle, Assyr and Bai, Yun. (2012) "Reduced basis finite element heterogeneous multiscale method for high-order discretizations of elliptic homogenization problems", Volume 231. Elsevier. Journal of Computational Physics 21 7014–7036

[44] Abdulle, Assyr and Bai, Yun. (2013) "Adaptive reduced basis finite element heterogeneous multiscale method", Volume 257. Elsevier. Computer Methods in Applied Mechanics and Engineering 203–220

[45] Drago, A. and Pindera, M.J. (2007) "Micro-macromechanical analysis of heterogeneous materials: Macroscopically homogeneous vs periodic microstructures", Volume 67. Elsevier. Composites science and technology 6 1243–1263

[46] Miehe, C. and Schotte, J. and Schroder, J. (1999) "Computational micro-macro transitions and overall moduli in the analysis of polycrystals at large strains", Volume 16. Elsevier. Computational Materials Science 1-4 372–382

[47] de Souza Neto, EA and Feijóo, RA. (2006) "Variational foundations of multi-scale constitutive models of solid: small and large strain kinematical formulation", Volume 16. LNCC Research & Development Report

[48] Kouznetsova, V.G. (2002) "Computational homogenization for the multi-scale analysis of multi-phase materials". Technische Universiteit Eindhoven

[49] Michel, JC and Moulinec, H. and Suquet, P. (1999) "Effective properties of composite materials with periodic microstructure: a computational approach", Volume 172. Elsevier. Computer methods in applied mechanics and engineering 1-4 109–143

[50] Kanit, T. and Forest, S. and Galliet, I. and Mounoury, V. and Jeulin, D. (2003) "Determination of the size of the representative volume element for random composites: statistical and numerical approach", Volume 40. Elsevier. International Journal of Solids and Structures 13 3647–3679

[51] Nguyen, V.P. and Lloberas-Valls, O. and Stroeven, M. and Sluys, L.J. (2010) "On the existence of representative volumes for softening quasi-brittle materials-a failure zone averaging scheme". Elsevier. Computer Methods in Applied Mechanics and Engineering

[52] B. D. Reddy. (1998) "Introductory Functional Analysis". Springer-Vedag

[53] Giusti, SM and Blanco, PJ and de Souza Netoo, EA and Feijóo, RA. (2009) "An assessment of the Gurson yield criterion by a computational multi-scale approach", Volume 26. Emerald Group Publishing Limited. Engineering Computations 3 281–301

[54] Couégnat, Guillaume. (2008) "Approche multiéchelle du comportement mécanique de matériaux composites a renfort tissé". Université Sciences et Technologies-Bordeaux I

[55] J. Lubliner. (1990) "Plasticity Theory". McMillan

[56] Rozza, G. (2009) "Reduced basis methods for Stokes equations in domains with non-affine parameter dependence", Volume 12. Springer. Computing and Visualization in Science 1 23–35

[57] Hu, Y.H. and Hwang, J.N. and Perry, S.W. (2002) "Handbook of neural network signal processing", Volume 111. The Journal of the Acoustical Society of America 2525

[58] Bui-Thanh, T. (2007) "Model-constrained optimization methods for reduction of parameterized large-scale systems". Citeseer

[59] Bui-Thanh, T. and Willcox, K. and Ghattas, O. (2008) "Model reduction for large-scale systems with high-dimensional parametric input space", Volume 30. Citeseer. SIAM Journal on Scientific Computing 6 3270–3288

[60] Carlberg, K. and Farhat, C. (2008) "A Compact Proper Orthogonal Decomposition Basis for Optimization-Oriented Reduced-Order Models", Volume 5964. AIAA Paper 10–12

[61] Kunisch, K. and Volkwein, S. (2010) "Optimal snapshot location for computing POD basis functions", Volume 44. ESAIM: Mathematical Modelling and Numerical Analysis 3 509

[62] Rowley, C.W. and Colonius, T. and Murray, R.M. (2004) "Model reduction for compressible flows using POD and Galerkin projection", Volume 189. Elsevier. Physica D: Nonlinear Phenomena 1-2 115–129

[63] Smith, L.I. (2002) "A tutorial on principal components analysis", Volume 51. Cornell University, USA 52

[64] Carlberg, K. and Farhat, C. (2011) "A low-cost, goal-oriented ‘compact proper orthogonal decomposition’basis for model reduction of static systems", Volume 86. Wiley Online Library. International Journal for Numerical Methods in Engineering 3 381–402

[65] A. Quarteroni and R. Sacco and F. Saleri. (2000) "Numerical Mathematics". Springer

[66] Astrid, P. and Weiland, S. and Willcox, K. and Backx, T. (2008) "Missing point estimation in models described by proper orthogonal decomposition", Volume 53. IEEE. Automatic Control, IEEE Transactions on 10 2237–2251

[67] Maday, Y. and Nguyen, N.C. and Patera, A.T. and Pau, G.S.H. (2007) "A general, multipurpose interpolation procedure: the magic points"

[68] Chaturantabut, Saifon and Sorensen, Danny C. (2011) "Application of POD and DEIM on dimension reduction of non-linear miscible viscous fingering in porous media", Volume 17. Taylor & Francis. Mathematical and Computer Modelling of Dynamical Systems 4 337–353

[69] Galbally, D. and Fidkowski, K. and Willcox, K. and Ghattas, O. (2010) "Non-linear model reduction for uncertainty quantification in large-scale inverse problems", Volume 81. John Wiley & Sons. International Journal for Numerical Methods in Engineering 12 1581–1608

[70] Everson, R. and Sirovich, L. (1995) "Karhunen–Loeve procedure for gappy data", Volume 12. OSA. Journal of the Optical Society of America A 8 1657–1664

[71] DeVore, R.A. and Iserles, A. and Suli, E. (2001) "Foundations of computational mathematics". Cambridge Univ Pr

[72] Boyd, S.P. and Vandenberghe, L. (2004) "Convex optimization". Cambridge Univ Pr

[73] Ryckelynck, D. (2005) "A priori hyperreduction method: an adaptive approach", Volume 202. Elsevier. Journal of computational physics 1 346–366

[74] Ryckelynck, D. (2009) "Hyper-reduction of mechanical models involving internal variables", Volume 77. John Wiley & Sons. International Journal for Numerical Methods in Engineering 1 75–89

[75] Montgomery, D.C. and Runger, G.C. (2010) "Applied statistics and probability for engineers". Wiley

[76] Lovasz, L. and Pelikan, J. and Vesztergombi, K. (2003) "Discrete Mathematics: Elementary and Beyond". Springer

[77] J. C. Simo and T. J. R. Hughes. (1998) "Computational inelasticity". Springer

[78] Carlberg, K. and Bou-Mosleh, C. and Farhat, C. (2011) "Efficient non-linear model reduction via a least-squares Petrov–Galerkin projection and compressive tensor approximations", Volume 86. Wiley Online Library. International Journal for Numerical Methods in Engineering 2 155–181

[79] Hogben, L. (2006) "Handbook of linear algebra". Chapman & Hall/CRC

[80] Carlberg, K., Cortial, J., Amsallem, D., Zahr, M. and Farhat, C. (2011) "The gnat nonlinear model reduction method and its application to fluid dynamics problems", In 6th AIAA Theoretical Fluid Mechanics Conference, Honolulu, Hawaii, June, volume 2730, pages 2011–3112