Graphical solutions of the two-dimensional Saint-Venant equations by means of channels reticles

Resumen

Los conocimientos de los pueblos ancestrales son retomados como un saber importante en su relación con la naturaleza y para enfrentar el cambio climático; cultura que debe ser confirmada por la ciencia. La retícula de canales era usada por dichos pueblos para irrigar los cultivos; aplicando las ecuaciones de aguas someras se puede simular el comportamiento hidrodinámico y disipación de la energía al pasar un caudal en una retícula de canales. Para modelar la retícula se dibujó la geometría de las redes de flujo utilizadas en geotecnia, las redes son una solución ingenieril a la ecuación de Laplace. Al hacer pasar el agua por la retícula se observó, en una simulación en 2D con el software Iber v2.5, que el calado permanece constante. También se observó que la retícula es una forma eficiente de disipar la energía. De esta manera se descubrió que la retícula de canales es una solución a las ecuaciones de un fluido en aguas someras. Mediante los resultados obtenidos se intuye un campo de investigación al modelar retículas de canales para el aprovechamiento y la gestión del agua.

Palabras clave: Aguas someras, calado constante, disipacion de la energía, flujo lámina libre, hidrodinámica en canales

Abstract

The knowledge of ancestral peoples is retaken as an important knowledge in their relationship with nature and to face climate change; culture that must be confirmed by science. To give the reason for the mentioned knowledge, when using channel lattices for their plots, it is necessary to model them using flow equations. Applying the equations of shallow water can simulate the hydrodynamic behavior and dissipation of energy by passing a flow in a lattice of channels. To model the grid the geometry of the flow networks used in geotechnics was drawn, the networks are an engineering solution to the Laplace equation. When passing the water through the reticle it was observed, in a 2D simulation with the Iber v2.5 software, that the draft remains constant. It was also noted that the reticle is an efficient way to dissipate energy. In this way it was discovered that the channel lattice is a solution to the equations of a shallow water joint. Through the results obtained, a field of research is intuited when modeling reticles of channels for the use and management of water.

Keywords: Shallow water, constant depth, energy dissipation, open channel flow, channel hydrodynamic

(¹) Correspondence: Justino Alavez Ramírez (jalavezrg@gmail.com). This is an article distributed under the terms of the Creative Commons BY-NC-SA license

1. Introducción

Hoy en día muchas de las investigaciones sobre ecuaciones diferenciales se centran en obtener solución a problemas de evolución temporal [1], los escurrimientos hidrológicos están dentro de esta categoría. La mayoría de este tipo de problemas es resuelto en forma aproximada por métodos de discretización [2]. Los flujos hidráulicos se basan en el modelado de ecuaciones diferenciales hiperbólicas, estas ecuaciones tienen una difícil solución por métodos exclusivamente analíticos cuando las condiciones de contorno e inicial son complicadas, y en muchos casos no es factible encontrar una solución analítica y es casi imposible de aplicar en problemas reales que tienen regiones con una geometría irregular [1].

Intuitivamente las civilizaciones antiguas gestionaban el agua en forma óptima con base en conocimientos prácticos y, con dichos conocimientos, lograban un comportamiento deseable de los escurrimientos del líquido [3]. Varias civilizaciones antiguas utilizaron, para sus parcelas, canales con una geometría específica. La distribución de estos canales no es azarosa [4], ellos por lo general utilizaban una distribución con aspecto de retícula y formando geometrías regulares. Desde las chinampas de los mexicas hasta los pólderes holandeses, en la actualidad, se repite dicha distribución en forma de red [5].

Por ello, el problema a tratar es conocer la hidrodinámica del comportamiento del agua en una retícula de canales; geometría que se ha visto repetida en humedales artificiales en diferentes civilizaciones y épocas. En las referencias bibliográficas existen pocos estudios hidrodinámicos sobre retículas de canales [6,7].

En este documento llamaremos retícula de canales a la geometría regular que presentan las parcelas cuadradas, o cuasi cuadrilátero, rodeadas de canales.

1.1 Bases para modelar retícula de canales con Iber

En su artículo, Blade menciona una serie de aplicaciones de la herramienta de Iber, entre ellas el cálculo hidráulico de redes de canales en lámina libre [8]. Al hacer circular agua, mediante la entrada de un caudal dentro de una retícula, el caudal tiende a establecer un calado constante en la red; esto pasa aun cuando en sus cruces y en los canales se presente turbulencia. Así mismo, cabe señalar que al hacer circular líquido en una retícula de canales la energía del mismo se disipa en la red [9,10].

2. Metodología

2.1 Modelo numérico

Se utiliza el modelo numérico incorporado en el módulo hidrodinámico de Iber, el cual resuelve las ecuaciones de Saint-Venant bidimensionales [5]. Para todos los casos que se tratan en este documento también está incorporado el módulo de la turbulencia de Iber, eligiéndose el modelo ${\textstyle k-\varepsilon }$ de Rastogi y Rodi [5].

Las ecuaciones de Saint-Venant son válidas al cumplirse las suposiciones de presión hidrostática y velocidad uniforme en profundidad. En las simulaciones que se reportan en la Sección 3.1, el número de entradas y salidas del agua en la retícula de canales se hacen variar, para mostrar los efectos en el calado.

Las ecuaciones de aguas someras y las del modelo ${\textstyle k-\varepsilon }$, se resuelven en Iber mediante el método de volúmenes finitos para mallas bidimensionales, se emplea el mallado estructurado y no estructurado de las retículas. En todos los casos que se pueda aplicar una malla estructurada se implementa para optimizar cálculo y resultados. La malla entonces se ajusta a la geometría, así, para retículas con parcelas cuadradas se modelará en forma estructurada, para retículas con seudo-cuadrados se modelará con malla no estructurada [5].

2.2 Analogía de las redes de flujo y la retícula de canales

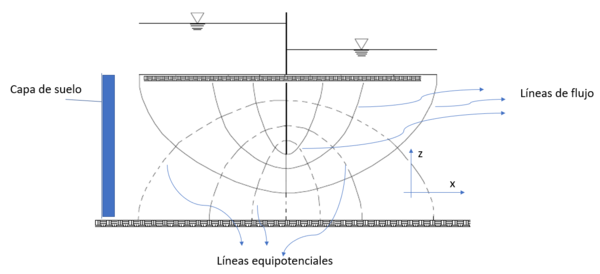
El método gráfico de las redes de flujo (Figura 1) fue ideado por Forchheimer en 1930 [11]. Este método no ha sufrido modificaciones desde su origen, y se ha reconocido por su aplicación práctica en la ingeniería de suelos y geotecnia. La red de flujo se usa para la idealización de un flujo en un medio poroso, su aplicación resuelve problemas de la cantidad de flujo que pasa en el suelo y de la pérdida de energía en dicho proceso. La base de la red de flujo es la ecuación de continuidad en dos dimensiones. El modelo numérico, para el estudio de la filtración del agua en el suelo, está basado en la aplicación de la ecuación de Laplace. Los conceptos y las soluciones gráficas a problemas están dados por Flores Berrones [11].

Figura 1. Red de flujo en un “tablaestacado”

2.3 Construcción de la red de flujo y de una retícula de canales

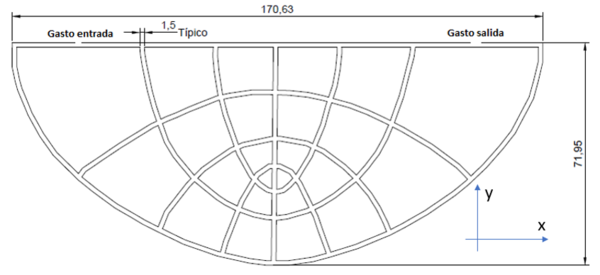
Algunos de los pasos para el trazado de la red de flujo de acuerdo con Flores Berrones [11] son: 1) Iniciar trazando con línea suave las líneas de flujo, que por lo general son las más extensas; 2) La forma de las líneas de flujo debe ser elípticas o parabólicas, con transiciones suaves; 3) Señalar las fronteras; 4) Buscar la simetría; 5) Dar forma pseudo-cuadrada a la familia de curvas, además que los cruces estén en 90${\textstyle ^{\circ }}$. La Figura 1 está representada en ejes ortogonales $x-z$, donde $z$ son alturas. Para ocupar la misma forma, pero ahora para que las líneas representen canales con cierto ancho, se coloca la Figura 1 en un plano horizontal de coordenadas $x-y$ y la profundidad del canal en el eje $z$ como se muestra en la Figura 2.

Figura 2. Construcción de la retícula de canales bajo el mismo procedimiento que la red de flujo

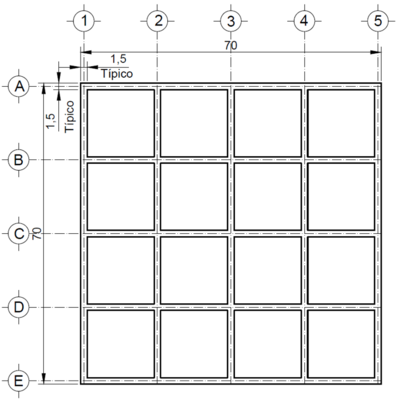
Se simula, también, el flujo en una retícula de canales con parcelas cuadradas (Figura 3) y sometida a condiciones diferentes de entradas y salidas según la Tabla 1. La relación del ancho de canal y ancho de parcela es cercano al 10%.

Figura 3. Retícula de canales de 16 parcelas

Tabla 1. Asignación de gastos y entradas en la retícula de canales para las diferentes simulaciones

Experimento	Entrada	Salida
${\textstyle 1}$	Una. Entre los ejes 2-3 y el eje A	Una. Entre los ejes 2-3 y el eje E
${\textstyle 2}$	Dos. Entre los ejes 1-2, y 3-4 eje A	Una. Entre los ejes 2-3 y el eje E
${\textstyle 3}$	Dos. Entre los ejes 1-2, y 3-4 eje A	Dos. Entre los ejes 1-2 y 3-4 eje E
${\textstyle 4}$	Dos. Entre los ejes 1-2 y 3-4 eje A	Tres. Entre los ejes 1-2, 2-3, y 3-4 eje E
${\textstyle 5}$	Tres. Entre los ejes 1-2, 2-3, y 3-4 eje A	Una. Entre los ejes 2-3 eje E
${\textstyle 6}$	Tres. Entre los ejes 1-2, 2-3 y 3-4 eje A	Dos. Entre los ejes 1-2 y 3-4 eje E
${\textstyle 7}$	Tres. Entre los ejes 1-2, 2-3, y 3-4 eje A	Tres. Entre los ejes 1-2, 2-3, 3-4 eje E
${\textstyle 8}$	Dos. Entre los ejes 1-2 eje A y A-B eje 1	Dos. Entre los ejes 3-4 y C-D eje 5

3. Resultados

3.1 Experimentos del 1 al 8. Simulación de retículas cuadradas

Se simuló la retícula Tabla 1) con un gasto de 10 m${\textstyle ^{3}}$ insertados para una entrada; repartido en 2 para dos entradas y partido en 3 para 3 entradas. Las entradas de caudal suman siempre 10 m${\textstyle ^{3}}$. Cuando el gasto de entrada igualaba al gasto de salida se detenía la simulación.

Datos: ancho de entrada y salida 2 m al centro de ejes, rugosidad concreto, calado inicial 0, malla estructurada y de tamaño ${\textstyle 0.5}$ y módulo de turbulencia (${\textstyle k-\varepsilon }$) activado.

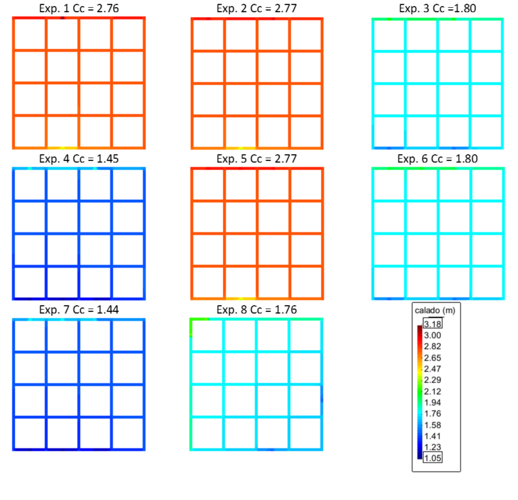
Los resultados de los diferentes calados se muestran en la Figura 4. Se observa en los experimentos 1, 2 y 5 que tienen calados muy similares. De igual manera los experimentos 3, 6 y 8. Lo que indica que no impacta en el calado el número de entradas de agua, pero si el número de salidas. Esto se comprueba con los experimentos 4 y 7, los cuales tienen mayor número de salidas.

Figura 4. Comparación de los calados de la Tabla 1 cuando el caudal está en régimen permanente. Cc significa calado al centro de la retícula

3.2 Experimento 9. Efectuando la analogía de redes de flujo y retícula de canales

Se dibujó la geometría de la red de flujo de la Figura 1 y se cambiaron las líneas en canales para formar una retícula de canales (Figura 2). Los datos son: gasto 10 m${\textstyle ^{3}}$, ancho de la entrada y salida 2 m, rugosidad concreto, calado inicial 0, malla no estructurada y de tamaño ${\textstyle 0.5}$ y módulo de turbulencia ${\textstyle k-\varepsilon }$ activado.

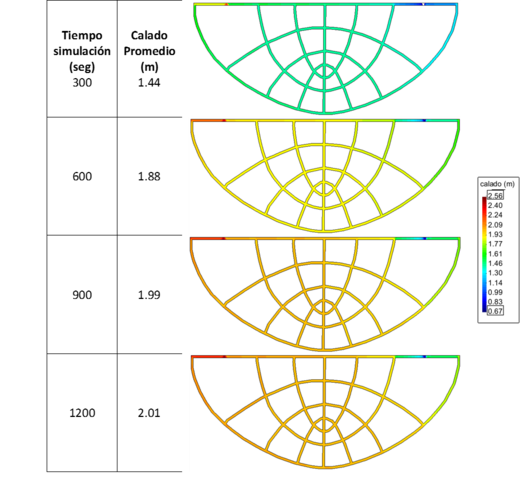
La Figura 5 muestra la evolución del calado en relación con el tiempo. Existe poca variación en él a medida que se acerca al régimen permanente, siendo considerablemente igual el calado en la mayoría de la retícula por cada intervalo de tiempo simulado. Este fenómeno se puede recrear para otras formas de redes de flujo modificadas a retícula de canales. El calado constante en el proceso para llegar a régimen permanente se presentó también en los experimentos del 1 al 8.

Figura 5. Evolución del calado en la retícula de canales con forma de red de flujo de la Figura 1

Se modelaron otras formas de redes de flujo convertidas a retícula de canales y se obtuvieron resultados similares al del experimento 9. La evolución del calado, en todos los casos, tiende a ser casi constante aún sin alcanzar el régimen permanente.

3.3 Experimento 10. Retícula de canales de forma de dodecágono

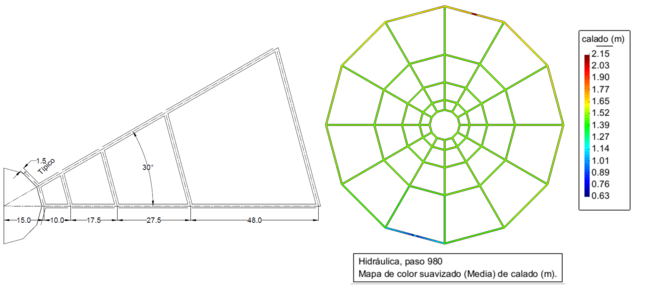
La Figura 6 muestra la dimensión de un lado del dodecágono, las parcelas trapeciales están formadas por el promedio del lado mayor y el lado menor para formar los lados no paralelos. Así, para el trapecio más grande, el resultado de la semisuma del lado mayor y el lado menor se obtiene de 48 metros, como se muestra en la Figura 6.

Variables independientes:

Gasto 10 m${\textstyle ^{3}}$, entrada y salida 5 m, rugosidad concreto, calado inicial 0, malla no estructurada y de tamaño ${\textstyle 0.5}$ y módulo de turbulencia ${\textstyle k-\varepsilon }$ activado.

Figura 6. Izquierda: Medidas de un elemento típico en el dodecágono. Derecha: la retícula de canales al final de la simulación

En realidad, en las retículas de canales la evolución del calado tiende a ser uniforme como se observa en retículas anteriores. Ciertamente hay una sutil diferencia a lo largo de la retícula entre la entrada y la salida, acentuándose al aumentar la distancia entre ellas, sin embargo, el porcentaje de diferencia es mínimo en relación al calado medio.

3.4 Resultados de la disipación de la energía

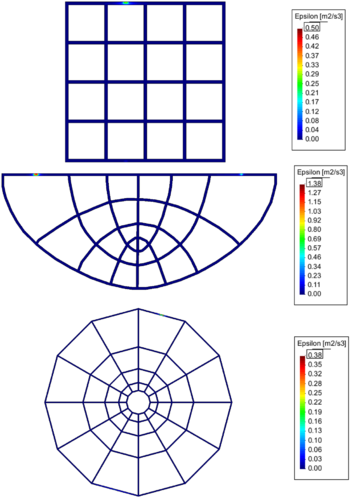
La Figura 7 muestra la disipación de la energía de los experimentos antes mencionados.

Figura 7. Ilustración de la disipación de la energía en los experimentos cuando el flujo es permanente.

4 Conclusiones

Se realizaron aún más experimentos de los mostrados en este documento, en todos los casos la retícula de canales construida por cuadrados o por las instrucciones del apartado 2.3 se comportaron con un calado constante cuando se hacía circular el fluido a través de los canales. Se observó también, que los cruces de los canales aceptan cierta tolerancia en ángulos mayores; así, una retícula que tuviera un cruce formado de 3 canales en ángulo de 120${\textstyle ^{\circ }}$ los calados seguían la evolución de lo mostrado en la Figura 5. La dispersión de la energía, bajo el metodo ${\textstyle k-\varepsilon }$, siempre fue constante y con valor de 0, como se muestra en la Figura 7. Por lo anterior, se puede afirmar que la retícula de canales es una solución gráfica de las ecuaciones de Saint-Venant cuando se desea obtener un calado constante aun sin régimen permanente y bajo o nulo valor en la disipación de la energía.

Quedan por demostrar otras cualidades de las retículas de canales, pero a medida que las aplicaciones aumenten, se podrán detectar otras cualidades; o definir relaciones óptimas entre las dimensiones de ancho parcela, ancho canal y profundidad. Queda mencionar que se abren muchas posibilidades de aplicación a la ingeniería ambiental, agrícola e hidráulica.

Referencias

[1] Bladé E., Gómez M. Modelación del flujo en lámina libre sobre cauces naturales. Análisis integrado en una y dos dimensiones. Monograph CIMNE No. 97, 2006.

[2] Garcia Conca, J.M. Estimación computacional del error de discretización. Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería, 3(1):12-22, 1987.

[3] Beach T., Luzzadder-Beach S., Krause S., Guderjan T., Valdez Jr. F., Fernandez-Diaz J.C., Eshleman S., Doyle C. Ancient Maya wetland fields revealed under tropical forest canopy from laser scanning and multiproxy evidence. Proceedings of the National Academy of Sciences, 116(43):21469-21477, 2019.

[4] Chapin M. The seduction of models. Chinampa agriculture in Mexico. Grassroots Development, 12(1):8-17, 1988.

[5] Armillas P. Gardens and Swamps. Science, 174(4010):653-661, 1971.

[6] Liu B., Wang N., Chen M., Wu X., Mo D., Liu J., Xu S., Zhuang Y. Earliest hydraulic enterprise in China, 5,100 years ago. Proceedings of the National Academy of Sciences, 114(52):13637-13642, 2017.

[7] Comptour M., Caillon S., Rodrigues L., Mckey D. Wetland raised-field agriculture and its contribution to sustainability: ethnoecology of a present-day african system and questions about pre-Columbian systems in the American tropics. Sustainability, 10(3120):1-23, 2018.

[8] Bladé E., Cea L., Corestein G., Escolano E., Puertas J., Vázquez-Cendón E., Dolz J., Coll A. Iber: herramienta de simulación numérica del flujo en ríos. Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería, 30(1):1-10, 2014.

[9] Ávalos E., Munguía E., López G., Hernández R. Análisis de rejas de canales según propuesta ancestral y actual. Pakbal, 41:31-36, 2018.

[10] Munguía E., Blanco A., Alavez J. Análisis hidrodinámico de rejas de canales mediante simulaciones numéricas bidimensionales. Ingeniería y Ciencia, 12(23):73-92, 2016.

[11] Flores, R. Flujo de agua a través de suelos. 4a. edición, Asociación Mexicana de Hidráulica - Instituto Mexicano de Tecnología del Agua, 2000.