Lateral buckling of steel beams. Compared analysis of CTE DB SE-A, EAE and EC3 codes

Resumen

El Documento Básico Seguridad Estructural, Acero del Código Técnico de la Edificación proporciona fórmulas de cálculo de la resistencia a pandeo lateral de vigas de acero laminado. En dichas expresiones interviene el coeficiente C₁ que tiene en cuenta la variación del momento flector a lo largo de la viga. Sin embargo, este documento sólo proporciona valores para diagramas de momentos flectores con variación lineal.

La instrucción para Acero Estructural que reproduce la última versión del Eurocódigo 3, no indica como calcular el momento crítico de pandeo lateral en dominio elástico. Por el contrario, sí que incluye una tabla con coeficientes de corrección para varios tipos de diagramas de flectores.

En este documento se combinan ambos procedimientos y se comparan los resultados con los obtenidos utilizando otras versiones del Eurocódigo 3. Finalmente se aportan tablas que facilitan el dimensionado de vigas de acero laminado frente al pandeo lateral.

Palabras clave: Pandeo lateral, vigas de acero, DB SE-A, EAE, eurocódigo 3

Abstract

The Basic Document, Structural Safety, Steel of the Spanish Technical Building Code provides mathematical expressions to obtain the lateral buckling resistance of hot-rolled steel beams. These expressions include a coefficient, $C_{1}$, that accounts for variation of the bending moment along the beam. However, this document only provides values for linear diagrams of bending moments.

The instruction for Structural Steel, a copy of the latest version of Eurocode 3, does not include any method to obtain the elastic critical moment. On the contrary, a table with correction factors applicable to different types of bending moments diagrams is included.

In this document both procedures have been combined and results have been compared to those obtained using other versions of the Eurocode 3. Finally, tables have been provided to ease the design of hot-rolled steel beams while preventing the lateral buckling.

Keywords: Lateral buckling, steel beams, Spanish steel code, CTE DB SE-A, Spanish code EAE, eurocode 3

1. Introducción

En el año 2006 se aprueba el Código Técnico de la Edificación [1] que establece las exigencias básicas (prestaciones) que deben cumplir los edificios en relación con los requisitos básicos de seguridad y habitabilidad establecidos en la Ley de Ordenación de la Edificación [2]. Estas exigencias básicas se desarrollan tanto en la parte 1 como en los distintos Documentos Básicos (DB) del Código Técnico de la Edificación (CTE). La aplicación de los DB garantiza el cumplimiento de dichas prestaciones.

El Documento Básico, Seguridad Estructural, Acero [3] incluye los procedimientos para verificar la seguridad estructural de los elementos metálicos de una edificación construidos con acero.

Entre las verificaciones de resistencia incluidas en el Documento Básico, Seguridad Estructural, Acero (DB SE-A) se encuentra, artículo 6.3.3.2, la correspondiente al cálculo de la resistencia frente a pandeo lateral, ${\textstyle M_{b,Rd}}$, de los elementos solicitados a flexión. Dicha resistencia depende de la esbeltez adimensional frente al pandeo lateral, ${\textstyle {\overline {\lambda }}_{Lt}}$, cuyo valor se obtiene a partir del momento crítico elástico de pandeo lateral, ${\textstyle M_{cr}}$.

El artículo 6.3.3.2 propone una ecuación para determinar dicho momento crítico en aquellos casos en los que la carga actúe a lo largo del eje de la barra y los apoyos en los extremos impidan la rotación debida a la torsión. De acuerdo con las expresiones contenidas en dicho artículo, el valor de ${\textstyle M_{cr}}$ se obtiene teniendo en cuenta, entre otros factores, el módulo de torsión uniforme de la sección transversal, ${\textstyle I_{t}}$, y el coeficiente ${\textstyle C_{1}}$. Este último coeficiente depende de las condiciones de apoyo y de la ley de momentos flectores que solicita a la barra. Los valores del coeficiente ${\textstyle C_{1}}$ incluidos en el DB SE-A se refieren sólo a tramos de barra a lo largo de los cuales el momento flector es constante o varía linealmente, pero no contempla otros tipos de variación (p. ej. parabólica) ni tampoco proporciona el valor de ${\textstyle C_{1}}$ para los casos de carga transversal directamente aplicada sobre la barra.

En el año 2011 se aprueba la Instrucción de Acero Estructural [4] cuyo objeto es establecer los requisitos relativos a seguridad estructural, seguridad en caso de incendio y protección del medio ambiente que deben cumplir las estructuras de acero, incluyendo los procedimientos que garantizan su cumplimiento.

En el título 4º Dimensionamiento y comprobación, capítulo IX Estados Límite Últimos de la Instrucción de Acero Estructural (EAE) se incluyen las condiciones para comprobar el pandeo lateral de elementos de sección constante (artículo 35.2.1).

En la EAE, la expresión para calcular la resistencia de cálculo frente al pandeo lateral es la misma que la del DB SE-A, es decir, el valor de ${\textstyle M_{b,Rd}}$ depende del momento crítico elástico, ${\textstyle M_{cr}}$, que, según se indica en la EAE, “se obtendrá considerando las características de la sección transversal bruta, teniendo en cuenta el estado de carga, la distribución real de momentos flectores y los arriostramientos laterales”, pero, a diferencia del DB SE-A, no aporta ninguna ecuación para calcular su valor. Sin embargo, sí que propone una serie de valores para el factor de corrección, ${\textstyle k_{c}}$, que permite tener en cuenta distintas distribuciones de momentos flectores entre los puntos arriostrados lateralmente, incluyendo, entre otros, algunos casos de carga transversal directamente aplicada sobre la barra (tabla 35.2.2.1.b de la EAE).

Tanto el procedimiento de cálculo de la EAE como los valores de ${\textstyle k_{c}}$ son iguales al procedimiento incluido en el artículo 6.3.2. de la norma UNE EN 1993-1-1 Eurocódigo 3. Versión oficial, en español, publicada por AENOR en abril de 2013 [5]. Esta versión del Eurocódigo 3 (EC3-2013) tampoco incluye entre su articulado fórmula o procedimiento alguno para calcular el momento crítico elástico de pandeo lateral (para su obtención establece las mismas consideraciones que la EAE).

Por otro lado, la versión para el Reino Unido del Eurocódigo 3 publicado por la European Convention for Constructional Steelwork [6], a la que nos referiremos como EC3-UK para distinguirla del EC3-2013, incluye una expresión para el cálculo del momento crítico para el caso estándar: barra biarticulada con sección doblemente simétrica y solicitada por un momento flector constante. Este momento crítico estándar, ${\textstyle {M}_{cr}^{E}}$, depende tanto del módulo de torsión ${\textstyle I_{t}}$ como del módulo de alabeo ${\textstyle I_{w}}$. Adicionalmente, para tener en cuenta distintos estados de carga, hace referencia, entre otras, a las ecuaciones propuestas por Clark & Hill [7] y Galéa [8] aplicables a barras con secciones simétricas respecto del eje débil, solicitadas a flexión simple en el eje fuerte y teniendo en cuenta distintas situaciones de enlace y estados de carga. En estas expresiones el valor del momento crítico se obtiene considerando, además de los módulos de torsión y alabeo, ${\textstyle I_{t}}$ e ${\textstyle I_{w}}$, los coeficientes ${\textstyle C_{1}}$, ${\textstyle C_{2}}$ y ${\textstyle C_{3}}$, cuyos valores dependen de las condiciones de apoyo, de la posición de la carga y la distribución de momentos flectores a lo largo de la barra.

Finalmente, el anejo F de la norma UNE ENV 1993-1-1 Eurocódigo 3. Versión oficial, en español de la Norma Europea Experimental publicada por AENOR en 1996 [9], a la que nos referiremos como EC3-1996, reproduce las expresiones propuestas por Clark & Hill y Galéa aunque con ligeras modificaciones en los valores de los coeficientes ${\textstyle C_{1}}$, ${\textstyle C_{2}}$ y ${\textstyle C_{3}}$.

En resumen, el DB SE-A del CTE proporciona fórmulas para calcular el momento crítico y la resistencia de cálculo a pandeo lateral de una viga solicitada a flexión. También facilita los valores de un coeficiente, ${\textstyle C_{1}}$, que tiene en cuenta la distribución de momentos flectores, pero sólo contempla los casos de barras sometidas a momento flector constante o a distribuciones que sólo varíen linealmente. Por otro lado, la EAE y el EC3-2013, no incluyen expresión alguna para calcular el momento crítico elástico de pandeo lateral, ${\textstyle M_{cr}}$, pero sí que proporcionan los valores de un factor corrector, ${\textstyle k_{c}}$, que permite abordar las distribuciones de momentos flectores más frecuentes, incluidas las generadas por cargas transversales directamente aplicadas sobre la barra.

Finalmente, la versión para el Reino Unido del Eurocódigo 3 (EC3-UK) incluye una fórmula para obtener el momento crítico elástico estándar, ${\textstyle {M}_{cr}^{E}}$, y también caracteriza los diferentes estados de carga y sustentación utilizando los coeficientes ${\textstyle C_{1}}$, ${\textstyle C_{2}}$ y ${\textstyle C_{3}}$, con valores similares a los propuestos por el EC3-1996.

Con objeto salvar las limitaciones detectadas en las mencionadas normas y para facilitar la comprobación a pandeo lateral en el mayor número posible de casos, se ha analizado la posible aplicación combinada de tales normas para calcular la resistencia a pandeo lateral, ${\textstyle M_{b,Rd}}$, en el caso de barras de acero construidas con perfiles laminados de la serie IPE de acero S275.

Como paso previo se han determinado los módulos de torsión, ${\textstyle I_{t}}$, y de alabeo, ${\textstyle I_{w}}$ para tales perfiles. Así mismo, se ha realizado un análisis de sensibilidad y se ha evaluado el impacto que tiene cada componente en los resultados obtenidos.

2. Análisis comparado de la normativa

Los artículos 6.3.3.2 del DB SE-A, el 35.2.1. de la EAE, y el 6.3.2.1 del EC3-2013 establecen que el valor de cálculo de la resistencia frente a pandeo lateral, ${\textstyle M_{b,Rd}}$, se podrá determinar de acuerdo con la ecuación (1)

${\textstyle {M}_{b,Rd}={\chi }_{LT}\cdot {W}_{y}\cdot {\frac {{f}_{y}}{{\gamma }_{M1}}}}$

(1)

donde ${\textstyle {W}_{y}}$ es el módulo resistente de la sección que adopta el valor del módulo plástico ${\textstyle {W}_{pl,y}}$ para secciones clase 1 y 2 y el elástico ${\textstyle {W}_{el,y}}$ para secciones clase 3; ${\textstyle {f}_{y}}$ es el límite elástico del acero, y ${\textstyle {\gamma }_{M1}}$ el coeficiente parcial de seguridad relativo a los fenómenos de inestabilidad, de valor 1.05.

El factor de reducción de pandeo lateral, ${\textstyle {\chi }_{LT}}$, se calcula a partir de la expresión de la ecuación (2)

${\textstyle {\chi }_{LT}={\frac {1}{{\phi }_{LT}+{\sqrt {{\phi }_{LT}^{2}-{\overline {\lambda }}_{LT}^{2}}}}}\leq 1}$

(2)

El valor de ${\textstyle {\phi }_{LT}}$ se obtiene de la ecuación (3)

${\textstyle {\phi }_{LT}=0.5\left[1+{\alpha }_{LT}\left({\overline {\lambda }}_{LT}-\right.\right.}$$\left.\left.0.2\right)+{\overline {\lambda }}_{LT}^{2}\right]$

(3)

En el caso de los perfiles laminados con sección en doble T, el coeficiente de imperfección, ${\textstyle {\alpha }_{LT}}$, toma los valores: ${\textstyle \,{\alpha }_{LT}=}$$0.34$ si ${\textstyle h/b>2}$ y ${\textstyle {\alpha }_{LT}=0.21\,\,si\,\,h/b\,\leq 2}$.

Finalmente, establecen que la esbeltez adimensional frente al pandeo lateral, ${\textstyle {\overline {\lambda }}_{LT}}$, se determinará según la relación de la ecuación (4), donde ${\textstyle M_{cr}}$ es el momento crítico elástico de pandeo lateral

${\textstyle {\overline {\lambda }}_{LT}={\sqrt {\displaystyle {\frac {{W}_{y}\cdot {f}_{y}}{{M}_{cr}}}}}}$

(4)

En los epígrafes siguientes se muestran los detalles del cálculo de la resistencia frente a pandeo lateral, ${\textstyle M_{b,Rd}}$, en cada una de las normas referenciadas.

2.1 DB SE acero del CTE

Según el artículo 6.3.3.3 del DB SE-A, para aquellas situaciones en las que la carga actúa sobre el eje de la barra, y los apoyos extremos tienen impedida la deformación por torsión, el momento crítico elástico de pandeo lateral (al que llamaremos ${\textstyle {M}_{cr}^{CTE})\,}$ se podrá determinar según la ecuación (5). En esta expresión ${\textstyle M_{LT,v}}$ es la componente del momento crítico que representa la resistencia de la barra a la torsión uniforme (torsión de Saint Venant), mientras que ${\textstyle M_{LT,v}}$ representa la resistencia de la barra a la torsión no uniforme (alabeo). El cálculo de ambas componentes se efectúa utilizando las ecuaciones (6) y (7)

${\textstyle {M}_{cr}^{CTE}={\sqrt {{M}_{LT,v}^{2}+{M}_{LT,w}^{2}}}}$

(5)

${\textstyle {M}_{LT,v}={C}_{1}\cdot {\frac {\pi }{{L}_{c}}}\cdot {\sqrt {G\cdot {I}_{t}\cdot E\cdot {I}_{z}}}}$

(6)

${\textstyle {M}_{LT,w}={C}_{1}\cdot {W}_{el,y}\cdot \displaystyle {\frac {{\pi }^{2}\cdot E}{{L}_{c}^{2}}}\cdot {i}_{f,z}^{2}}$

(7)

siendo ${\textstyle I_{t}}$ el módulo de torsión, ${\textstyle I_{z}}$ el momento de inercia de la sección respecto del eje débil, y ${\textstyle M_{el,v}}$, el módulo resistente elástico de la sección respecto del eje fuerte.

Por otro lado, ${\textstyle i_{f,z}}$ es el radio de giro, con respecto al eje de menor inercia, de la parte de la sección transversal que comprende el ala comprimida más un tercio de la zona comprimida del alma adyacente al ala comprimida.

${\textstyle E}$ y ${\textstyle G}$ son los módulos de elasticidad longitudinal y transversal respectivamente y ${\textstyle L_{c}}$ es la longitud de pandeo lateral (distancia entre los puntos de apoyo que impiden el pandeo lateral).

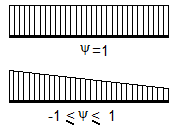
Finalmente, $C_{1}$ es un factor que depende de las condiciones de sustentación y de la ley de momentos flectores que solicita a la barra. El DB SE-A sólo propone valores de $C_{1}$ para aquellos casos de tramos de barra a lo largo de los cuales el momento flector es constante o varía linealmente. En tales casos, $C_{1}$ varía entre 1.00 (momento flector constante) y 2.75 (diagrama bi-triangular con los mismos valores en ambos extremos, pero de signo contrario).

2.2 Instrucción de acero estructural EAE y eurocódigo 3 (EC3-2013)

La EAE y el EC3-2013 también incluyen las expresiones (1), (2), (3) y (4), pero, a diferencia del DB SE-A, no proporcionan ninguna fórmula que permita calcular el momento crítico elástico de pandeo lateral, ${\textstyle M_{cr}}$, que aparece en la ecuación (4) ni se menciona cómo tener en cuenta las condiciones de apoyo y la distribución de momentos flectores de la barra a comprobar.

Sin embargo, en el artículo 35.2.2.1 “Curvas de pandeo lateral para perfiles laminados o secciones soldadas equivalentes” de la EAE, se propone utilizar, de manera alternativa para esos tipos de sección, la ecuación (1), pero con un valor modificado del coeficiente de reducción por pandeo lateral, ${\textstyle {\chi }_{LT}}$, que ambas normas denominan ${\textstyle \,{\chi }_{LT,mod}}$ y que ya incluiría las condiciones de sustentación y el efecto de la distribución de momentos flectores. Estas normas no mencionan el factor $C_{1}$, sino que proponen la utilización de otro factor de corrección, ${\textstyle k_{c}}$. Bajo este epígrafe, y antes de explicar cómo tener en cuenta el factor ${\textstyle k_{c}}$, la EAE incluye las fórmulas (8) y (9) alternativas a las ecuaciones (2) y (3).

Lógicamente, los valores de ${\textstyle {\chi }_{LT}}$, y ${\textstyle {\phi }_{LT}}$ obtenidos con las fórmulas (2) y (3) son diferentes de los obtenidos con las ecuaciones (8) y (9) ya estos que dependen del coeficiente $\beta$ y de la esbeltez adimensional inicial ${\textstyle {\overline {\lambda }}_{LT,0}}$. Los valores recomendados son: ${\textstyle {\overline {\lambda }}_{LT,0}=}$$0.4$ y $\beta =0.75$.

El coeficiente reductor por pandeo lateral modificado, ${\textstyle \,{\chi }_{LT,mod}}$, que se calcula con la expresión (10), tiene en cuenta no sólo los valores de ${\textstyle {\chi }_{LT}}$, y ${\textstyle {\phi }_{LT\,}}$, sino también el parámetro ${\textstyle f}$ que se obtiene de la ecuación (11) y que tiene en cuenta la distribución de momentos flectores a través del factor de corrección, ${\textstyle k_{c}}$, de la Tabla 1.

${\textstyle {\chi }_{LT}=\displaystyle {\frac {1}{{\phi }_{LT}+{\sqrt {{\phi }_{LT}^{2}-\beta {\overline {\lambda }}_{LT}^{2}}}}}\leq 1}$

(8)

${\textstyle {\phi }_{LT}=0.5\left[1+{\alpha }_{LT}\left({\overline {\lambda }}_{LT}-\right.\right.}$$\left.\left.{\overline {\lambda }}_{LT,0}\right)+\beta {\overline {\lambda }}_{LT}^{2}\right]$

(9)

${\textstyle {\chi }_{LT,mod}={\frac {{\chi }_{LT}}{f}}\,\,{\hbox{siendo }}\left\{{\begin{matrix}{\chi }_{LT,mod\,\leq \,1}\\{\chi }_{LT,mod\,\leq \,\,{\frac {1}{{\overline {\lambda }}_{LT}^{2}}}}\end{matrix}}\right.}$

(10)

${\textstyle f=1-0.5(1-{k}_{c})\left[1-{2\left({\overline {\lambda }}_{LT}-0.8\right)}^{2}\right]}$

(11)

Ni la EAE ni el EC3-2013 aclaran si el factor de corrección se puede aplicar al caso general calculando un coeficiente reductor por pandeo lateral modificado, ${\textstyle \,{\chi }_{LT,mod}}$, obtenido a partir de las ecuaciones (2), (3), (10) y (11). El hecho de que la introducción de ${\textstyle k_{c}}$ se encuentre dentro del artículo 35.2.2.1 parece indicar lo contrario.

Tabla 1. Factor de corrección ${\textstyle k_{c}}$ (EAE)

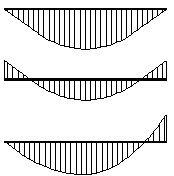
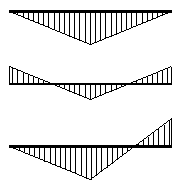
Diagrama de flectores	${\textstyle k_{c}}$
	$1$
	${\frac {1}{1.33-0.33\psi }}$
	$0.94$
	$0.90$
	$0.91$
	$0.86$
	$0.77$
	$0.82$

2.3 Eurocódigo 3. UNE-ENV 1993-1-1. EC3-1996

El anexo F del EC3-1993 incluye una expresión que permite calcular el momento crítico elástico en el caso de secciones simétricas respecto del eje de menor inercia con distintas condiciones de carga, coacciones en los extremos y posición de la carga respecto del centro de esfuerzos cortantes de la sección.

Dicha expresión, particularizada para secciones con doble simetría y cargas transversales aplicadas en el centro de esfuerzos cortantes, ${\textstyle {M}_{cr}^{EC3}}$, se concreta en la de la ecuación (12).

${\textstyle {M}_{cr}^{EC3}={C}_{1}\cdot \displaystyle {\frac {{\pi }^{2}\cdot E\cdot {I}_{z}}{(k\cdot L{)}^{2}}}\cdot {\sqrt {{\left(\displaystyle {\frac {k}{{k}_{w}}}\right)}^{2}\cdot \displaystyle {\frac {{I}_{w}}{{I}_{z}}}+\displaystyle {\frac {(k\cdot L{)}^{2}\cdot G\cdot {I}_{t}}{{\pi }^{2}\cdot E\cdot {I}_{z}}}}}}$

(12)

siendo ${\textstyle L}$ la distancia entre los puntos de apoyo que impiden el pandeo lateral, (equivalente a ${\textstyle L_{c}}$ en la expresión del DB SE-A) e ${\textstyle I_{w}}$ el módulo de alabeo. Por otro lado, ${\textstyle k}$ y ${\textstyle k_{w}}$ son los coeficientes de longitud eficaz que dependen de las condiciones de enlace de las secciones extremas.

El coeficiente ${\textstyle k}$ se refiere a la posible rotación alrededor del eje débil (z) y ${\textstyle k_{w}}$ a la posible restricción al alabeo de las secciones extremas. Sus valores varían entre 0.5 (giro/alabeo impedido en ambos extremos), 0.7 (giro/alabeo impedido en un extremo y libre en el otro) y 1.0 (giro/alabeo libre en ambos extremos). Teniendo en cuenta que en la mayor parte de las situaciones reales tan solo se consigue restringir parcialmente la rotación y el alabeo, es aconsejable adoptar, del lado de la seguridad, el valor unidad para ambos coeficientes.

Finalmente, $C_{1}$ es el coeficiente que tiene en cuenta la forma del diagrama de momentos flectores. En el caso barras con rotación libre en ambos extremos y variación lineal de momentos flectores a lo largo de toda la barra, los valores de $C_{1}$ coinciden con los del DB SE-A. Además, la Tabla 2 (que se corresponde con la tabla F.1.2 del EC3-1996) proporciona valores adicionales de $C_{1}$ para algunos casos donde las cargas transversales están directamente aplicadas sobre la barra.

Tabla 2. Valores del coeficiente $C_{1}$ (EC3-1996)

Condiciones de carga y diagrama de flectores	$k$	$C_{1}$
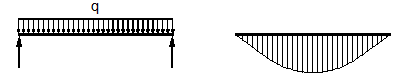
	1	1.132
	0.5	0.972
	1	1.285
	0.5	0.712
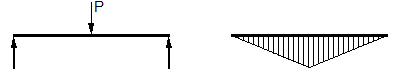
	1	1.365
	0.5	1.070
	1	1.565
	0.5	0.938
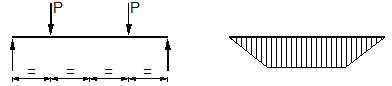
	1	1.046
	0.5	1.010

2.4 Eurocódigo 3. UNE EN 1993-1-1. EC3 -UK

La edición para Reino Unido del Eurocódigo 3 (EC3 UK) proporciona la expresión (13) para el cálculo del momento crítico elástico estándar, ${\textstyle {M}_{cr}^{E}}$, aplicable a la barra biarticulada, sección doblemente simétrica y momento flector constante.

${\textstyle {M}_{cr}^{E}=\displaystyle {\frac {\pi }{L}}\cdot {\sqrt {G\cdot {I}_{t}\cdot E\cdot {I}_{z}\left(1+\displaystyle {\frac {{\pi }^{2}\cdot E\cdot {I}_{w}}{{L}^{2}\cdot G\cdot {I}_{t}}}\right)}}}$

(13)

En dicha expresión el momento crítico elástico depende del momento de inercia de la sección respecto al eje débil ${\textstyle I_{z}}$, de los módulos de torsión ${\textstyle I_{t}}$ y alabeo ${\textstyle I_{w}}$, y de los módulos de elasticidad longitudinal y transversal del acero, ${\textstyle E}$ y ${\textstyle G}$, respectivamente. ${\textstyle L}$ es la distancia entre los puntos de la viga arriostrados lateralmente, equivalente a ${\textstyle L_{C}}$ y ${\textstyle L}$ en las ecuaciones (6), (7) y (12). Para otros estados de carga, los autores del EC3-UK recomiendan, entre otras, el uso de las fórmulas propuestas por Clark & Hill y Galéa aplicable a la mayor parte de casos prácticos.

La expresión recomendada para el cálculo del momento crítico elástico correspondiente a una viga de sección con doble simetría y cargas transversales aplicadas en el centro de esfuerzos cortantes, coincide con la expresión (12) del EC3-1996 con ligeras modificaciones en los valores del coeficiente $C_{1}$.

2.5 Módulos de torsión y alabeo

En el cálculo del $M_{cr}$ intervienen, entre otras propiedades geométricas y mecánicas, los módulos de torsión y de alabeo de la sección transversal de la barra. Los valores de dichos módulos deberían estar incluidos en las tablas de propiedades geométricas y mecánicas de los perfiles de acero. Sin embargo, la norma española UNE 36526 (Productos de acero, Perfiles en I con alas paralelas (IPE) de acero laminado en caliente de noviembre de 2018 [10], no los incluye.

No obstante, es posible encontrar valores para los módulos de torsión y alabeo en la literatura técnica – Argüelles [11] y Monfort [12] –, o en las tablas de propiedades geométricas y mecánicas proporcionadas por los productores de perfiles de acero.

Alternativamente, para obtener el valor del módulo de torsión de los perfiles doble T se puede utilizar la expresión matemáticade la ecuacion (14) y para calcular valores aproximados del módulo de alabeo, la ecuación (15), propuesta por Hughes [13].

${I}_{t}={\frac {1}{3}}(2b\cdot {t}_{f}^{3}+{h}_{w}\cdot {t}_{w}^{3})$

(14)

${I}_{w}\approx {\frac {{I}_{z}\cdot {(h{-t}_{f})}^{2}}{4}}$

(15)

siendo

$b$: el ancho del ala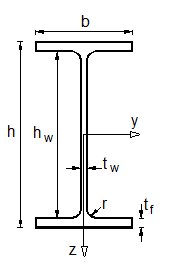
$t_{f}$: el espesor del ala
$h_{w}$: el canto del alma
$t_{w}$: el espesor del alma
$I_{z}$: el momento de inercia respecto al eje débil
$h$: el canto del perfil

En la Tabla 3, se recogen los valores de los módulos de torsión y alabeo de la serie IPE calculados a partir de las ecuaciones (14) y (15).

Tabla 3. Valores para los módulos de torsión $I_{t}$ y alabeo $I_{w}$

Perfil IPE	$I_{t}$ calculado	$I_{t}$ Argüelles [11]	$I_{t}$ Monfort [12]	$I_{t}$ ArcelorMittal [16]	$I_{w}$ calculado	$I_{w}$ Argüelles [11]	$I_{w}$ ArcelorMittal [16]
	mm4 $\times 10^{3}$	mm4 $\times 10^{3}$	mm4 $\times 10^{3}$	mm4 $\times 10^{3}$	mm6 $\times 10^{6}$	mm6 $\times 10^{6}$	mm6 $\times 10^{6}$
IPE 80	5.59	7.21	7.0	7	119	118	120
IPE 100	8.83	11.4	12.0	12	353	351	350
IPE 120	13.72	17.7	17.4	17	895	890	890
IPE 140	20.35	26.3	24.5	25	1989	1981	1980
IPE 160	28.20	36.4	36.0	36	3976	3959	3960
IPE 180	39.20	50.6	47.9	48	7470	7431	7430
IPE 200	51.65	66.7	69.8	70	13019	12990	13000
IPE 220	70.91	91.5	90.7	91	22774	22670	22700
IPE 240	92.80	120	128.8	129	37624	37390	37400
IPE 270	119.43	154	159.0	159	70871	70580	70600
IPE 300	155.74	201	201.2	201	126379	125900	126000
IPE 330	205.40	265	281.5	282	199841	199100	199000
IPE 360	289.26	373	373.2	373	314510	313600	314000
IPE 400	374.33	483	510.8	511	492215	490000	490000
IPE 450	510.71	659	668.7	669	794312	791000	791000
IPE 500	711.68	918	892.9	893	1254441	1249000	1249000
IPE 550	947.43	1220	1232.0	1230	1893452	1884000	1884000
IPE 600	1329.70	1720	1654.0	1650	2858298	2846000	2846000

También se incluyen, para poder comparar, los valores propuestos por Argüelles, que coinciden con los recogidos en la Norma Básica de Edificación de Estructuras de Acero, EA95 [14] derogada y sustituida por el DB SE-A del CTE; los proporcionados por Monfort (sólo incluye valores del módulo de torsión), tomados de la norma DIN 1025-5 [15], y los incluidos en las tablas de perfiles I de alas paralelas de la empresa siderúrgica ArcelorMittal [16], correspondientes a los valores de la norma DIN 1025-5 redondeados.

Como se puede observar en la Tabla 3, los valores del módulo de torsión, $I_{t}$, proporcionados por Argüelles, Monfort y ArcelorMittal son similares, mientras que los calculados a partir de la ecuación (14), son bastante menores.

En cuanto al módulo de alabeo, $I_{w}$, se da el caso contrario. Los valores calculados a partir de la ecuación (15), son un poco mayores, siendo los valores de las otras dos columnas, Argüelles y ArcelorMittal, prácticamente iguales.

La diferencia entre los valores calculados con las ecuaciones (14) y (15) y los propuestos por la literatura técnica se justifica, en el primer caso, en la no consideración del área encerrada por los radios de acuerdo ala-alma, y en el segundo en que se trata de una expresión aproximada, siendo necesario recurrir al método de los elementos finitos para obtener valores más precisos de ambas constantes.

2.6 Influencia del procedimiento de cálculo de los módulos de torsión y alabeo

Antes de proceder al cálculo del ${\textstyle M_{b,Rd}}$ con las ecuaciones incluidas en el epígrafe anterior conviene determinar la influencia que pudiera tener en la evaluación del momento crítico elástico las variaciones en la magnitud de los módulos de torsión y alabeo puestas en evidencia en el apartado anterior.

Con este objeto se han calculado, para los perfiles de la serie IPE y aplicando la ecuación (13), dos valores del momento crítico elástico estándar: ${\textstyle M_{cr(AM)}}$ y ${\textstyle M_{cr(CAL)}}$. En el primer caso se han utilizado los valores de $I_{t}$ e $I_{w}$ proporcionados por ArcelorMittal, y en el segundo caso los obtenidos con las expresiones (14) y (15). En ambos casos, el cálculo se ha realizado para longitudes $L_{c}$ entre 1 y 10 metros.

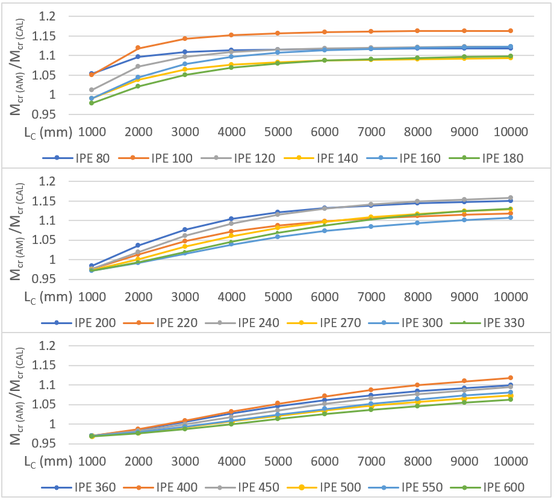
La ratio ${\textstyle M_{cr(AM)}}$/${\textstyle M_{cr(CAL)}}$ para toda la serie IPE se muestra en la gráfica de la Figura 1.

En ellas se observa que el momento crítico estándar obtenido a partir de los valores de $I_{t}$ e $I_{w}$ proporcionados por ArcelorMittal, ${\textstyle M_{cr(AM)}}$, es, en líneas generales, mayor que el calculado, ${\textstyle M_{cr(CAL)}}$, utilizando las expresiones (14) y (15). Siendo la diferencia en todos los casos inferior al 16.5%, siendo menos acusado en los perfiles mayores (IPE 360 a IPE 600) la media de los valores obtenidos se representa en con un trazo grueso de color negro.

Figura 1. Influencia del valor de $I_{t}$ e $I_{w}$ en el cálculo del ${\textstyle M_{cr}}$ estándar

Para el cálculo del momento crítico elástico en los siguientes epígrafes se van a utilizar los valores de $I_{t}$ e $I_{w}$ recogidos en las tablas de ArcelorMittal, por corresponder a la normativa europea más reciente y por considerar que, siendo fabricantes de perfiles estructurales acero como los estudiados en este artículo, presumiblemente habrán contrastado empíricamente los valores que indican en las tablas de resistencia que proporcionan.

3. Cálculo de la resistencia a pandeo lateral

Ec3-1996 vs db se-a:ec3-1996

A continuación, se ha explorado la posibilidad de combinar las siguientes expresiones y normativas, con objeto de poder calcular la resistencia a pandeo lateral, ${\textstyle M_{b,Rd}}$, utilizando las expresiones del DB SE-A, pero ampliando su uso a varios casos usuales de distribuciones de momentos flectores generados por cargas transversales directamente aplicadas sobre la barra que han sido omitidas en el DB SE-A:

- DB SE-A del Código Técnico ${\textstyle {M}_{cr}^{CTE}}$ (ecuación (5)).

- Versión de 1996 del Eurocódigo 3 ${\textstyle {M}_{cr}^{EC3}}$ (ecuación (12)).

- Versión inglesa del Eurocódigo 3 ${\textstyle {M}_{cr}^{E}}$ (ecuación (13)).

El análisis se ha realizado particularizando las expresiones anteriores para la serie de perfiles IPE de acero S275, teniendo en cuenta que las secciones son clase 1 en flexión simple, y variando la distancia entre puntos arriostrados transversalmente entre 1 y 10 metros.

3.1 Viga con momento flector constante

El caso analizado se muestra en la Figura 2. Se trata de una barra sometida a una distribución de momentos flectores constante en toda su longitud. En sus extremos no se restringe ni el giro ni el alabeo.

Figura 2. Viga con momento flector constante

Analizando los resultados obtenidos, se ha podido constatar que, a pesar de que las expresiones (12) y (13) son formalmente diferentes, los valores de la resistencia a pandeo lateral, ${\textstyle M_{b,Rd}}$, calculada con la fórmula (13) de la versión inglesa del EC3 (${\textstyle M_{b,Rd,E}}$) son iguales a los valores obtenidos con la expresión (12) de la versión de 1996 del Eurocódigo 3 (${\textstyle M_{b,Rd,EC3}}$).

En este último caso se ha considerado que los valores de los coeficientes a aplicar para tener en cuenta las condiciones de contorno son: ${\textstyle k_{w}=k=C_{1}=1}$.

También se han calculado la resistencia a pandeo lateral según el EC3-1996, ${\textstyle M_{b,Rd,EC3}}$, y esa misma resistencia, ${\textstyle M_{b,Rd,CTE}}$, utilizando los criterios del DB SE-A (${\textstyle C_{1}=1}$) y la fórmula del momento crítico elástico dada en la ecuación (5). Las ratios entre ambos valores, para cada uno de los perfiles de la serie, se representan gráficamente en la Figura 3, correspondiendo la línea de trazo grueso color negro a la media de los valores calculados. En esta gráfica se observa que las diferencias entre los valores obtenidos con uno u otro método son inferiores al 6%_0. Por lo tanto, en este caso (distribución de flectores constante) y a los efectos prácticos, resulta irrelevante la expresión que se utilice para calcular el momento crítico elástico.

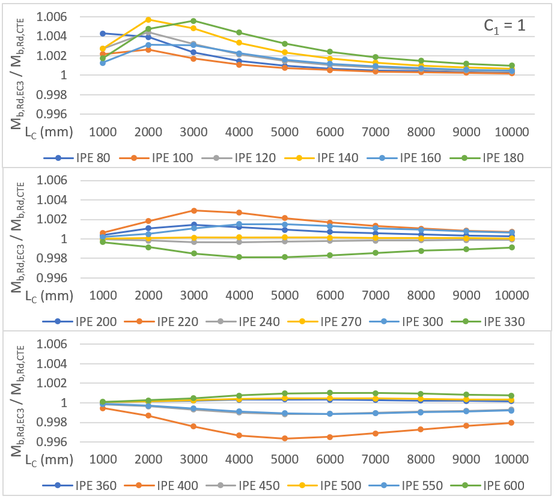
Figura 3. Comparación de la resistencia a pandeo lateral para momento flector constante, según el EC3-1996 y el DB SE-A con ${\textstyle C_{1}=1,0}$

3.2 Viga biarticulada con carga uniformemente repartida

Las expresiones que propone el DB SE-A para calcular las dos componentes del momento crítico, ${\textstyle M_{LTv}}$ y ${\textstyle M_{LTw}}$, incluyen un coeficiente ${\textstyle C_{1}}$ que permite tener en cuenta distintas distribuciones de momento flector, aunque, como ya se ha comentado, sólo proporciona valores para el caso de variaciones lineales.

Por otro lado, la versión de 1996 del EC3 proporciona valores para el coeficiente ${\textstyle C_{1}}$ que, además, incluye casos en los que las distribuciones de momentos flectores son el resultado de aplicar cargas transversales directamente sobre la barra.

Dichos valores se muestran en la Tabla 2 en función del coeficiente ${\textstyle k}$ que caracteriza las restricciones a la rotación alrededor del eje débil (z) de las secciones de los extremos de la barra. Cuando está permitida la rotación en ambos extremos el coeficiente ${\textstyle k=1.0}$.

En este epígrafe se pretende conocer si es posible ampliar el abanico de casos en los que se puede aplicar la ecuación (5) proporcionada por el DB SE-A del CTE. Con este objeto se ha calculado la resistencia a pandeo lateral, ${\textstyle M_{b,Rd,EC3}}$, de la viga de la Figura 4 utilizando la ecuación (12) proporcionada por el EC3-1996 y tomando los valores ${\textstyle k=1.0}$ y ${\textstyle C_{1}=1.132}$ (Tabla 2). Posteriormente se ha calculado la resistencia a pandeo lateral, ${\textstyle M_{b,Rd,CTE}}$, de la misma viga utilizando la ecuación (5) del DB SE-A y un coeficiente ${\textstyle C_{1}=1.132}$.

Figura 4. Viga con carga uniformemente repartida

Las ratios obtenidas en este caso se comparan en la Figura 5 y se observa que, representando la línea de trazo grueso color negro los valores medios, se alcanza, prácticamente, la misma resistencia a pandeo lateral con la ecuación (5) que con la ecuación (12). Por tanto, aunque el DB SE-A no proporcione el valor de ${\textstyle C_{1}}$ para el caso de la viga biarticulada con carga uniformemente repartida, parece factible utilizar el coeficiente ${\textstyle C_{1}=1.132}$ al comprobar la resistencia a pandeo lateral según la ecuación (5) del CTE.

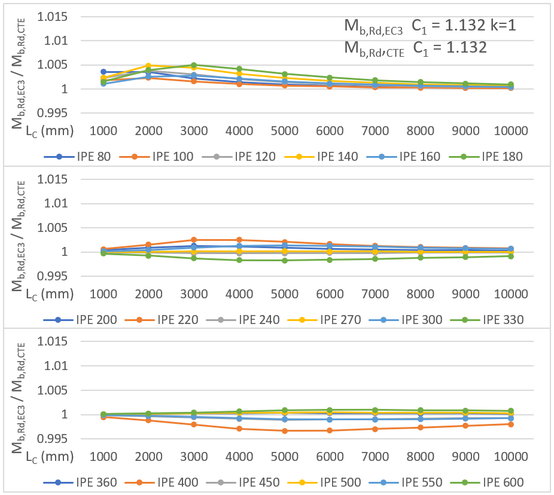
Figura 5. Comparación de la resistencia a pandeo lateral para carga uniformemente repartida, según el EC3-1996 y el DB SE-A con ${\textstyle C_{1}=1.132}$ y ${\textstyle k=1.0}$

Por otro lado, la Tabla 2 proporciona un segundo valor de ${\textstyle C_{1}}$ cuando el coeficiente ${\textstyle k=0.5}$. Con objeto de valorar si es factible utilizar este segundo valor del coeficiente ${\textstyle C_{1}}$ para el caso que nos ocupa, se repite el proceso anterior:

• Se calcula ${\textstyle M_{b,Rd,EC3}}$, utilizando la ecuación (12) propuesta por el EC3-96 y tomando los valores ${\textstyle k=0.5}$ y ${\textstyle C_{1}=0.912}$ (Tabla 2).

• Se obtiene la resistencia a pandeo lateral, ${\textstyle M_{b,Rd,CTE}}$, de la misma viga utilizando la ecuación (5) del DB SE-A con el mismo valor del coeficiente ${\textstyle C_{1}}$.

• La relación entre ambos momentos se representa en la Figura 6, en la que la línea de trazo grueso de color negro corresponde a los valores medios.

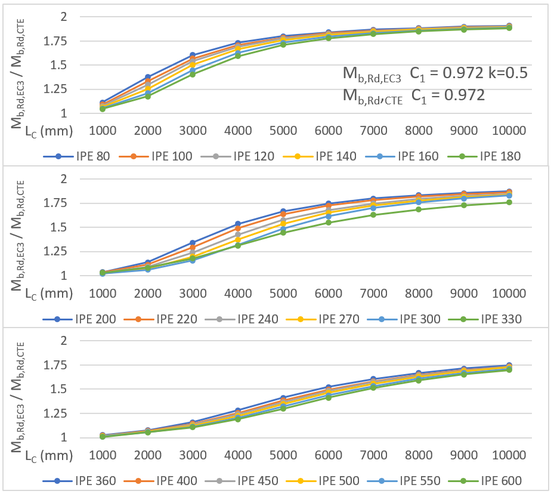
Como puede observarse en dicha figura, los resultados obtenidos con la expresión del EC3-1996 son bastante mayores que los obtenidos al calcular el momento crítico con la ecuación del DB SE-A. Dichas diferencias se deben a que las condiciones de enlace de ambas vigas no son semejantes. El coeficiente ${\textstyle k=0.5}$ de la expresión del EC3-1996 implica una coacción al giro alrededor del eje débil que repercute directamente en una mayor resistencia al pandeo lateral (casi el doble en algunos casos). Sin embargo, las expresiones del DB SE-A no contemplan esa posible coacción, dando lugar a momentos resistentes bastante inferiores.

Figura 6. Comparación de la resistencia a pandeo lateral para carga uniformemente repartida, según el EC3-1996 y el DB SE-A con ${\textstyle C_{1}=0.972}$ y ${\textstyle k=0.5}$

3.3 Vigas con otras leyes de flectores parabólicas

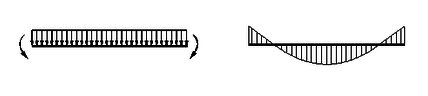
En este epígrafe se analiza la resistencia frente a pandeo lateral de barras sometidas a una distribución de flectores parabólica en la que los momentos en los extremos son no nulos (Figura 7).

Figura 7. Viga con carga uniforme y momentos no nulos en extremos

Para ello, se comparan los resultados obtenidos con la ecuación (12) propuesta por el EC3-1996 y la fórmula (5) incluida en el DB SE-A aplicando en ambas el mismo coeficiente ${\textstyle C_{1}}$.

Dado que la Tabla 2 proporciona de nuevo dos valores para el coeficiente ${\textstyle C_{1}}$ dependiendo de la sujeción lateral garantizada en los extremos de la viga, se analizan las siguientes opciones:

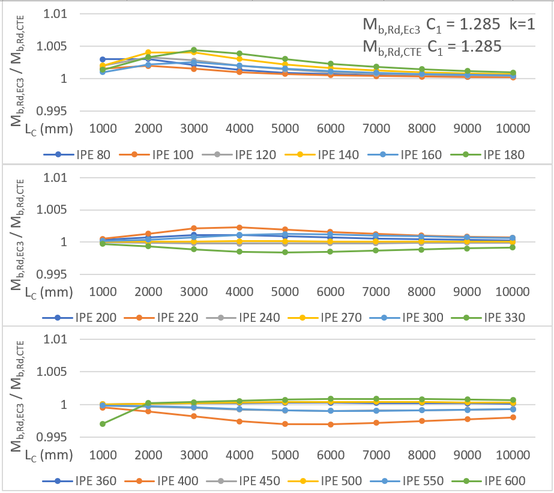
• ${\textstyle M_{b,Rd,EC3}}$, calculado con ${\textstyle C_{1}=1.285}$ y ${\textstyle k=1.0}$ y ${\textstyle M_{b,Rd,CTE}}$, obtenido con ${\textstyle C_{1}=1.285}$. Los resultados se comparan en la Figura 8, en la que el trazo grueso de color negro representa los valores medios y donde se observa que las diferencias entre ambos métodos son despreciables (inferiores al 5%₀).

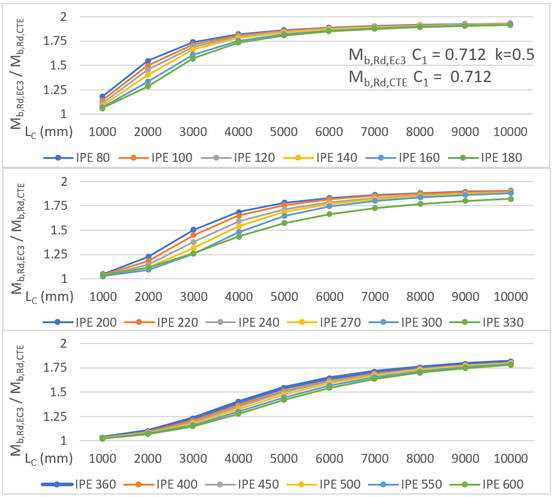
• ${\textstyle M_{b,Rd,EC3}}$, calculado con ${\textstyle C_{1}=0.712}$ y ${\textstyle k=0.5}$ y ${\textstyle M_{b,Rd,CTE}}$, obtenido con ${\textstyle C_{1}=0.712}$. Los resultados se comparan en la Figura 9, representando los valores medios con el trazo negro de color negro.

Estas últimas gráficas ponen de nuevo en evidencia que las diferencias entre ambos métodos son significativas (casi en doble en algunos casos) consecuencia del desajuste entre ambos modelos respecto al coeficiente de sujeción lateral (coeficiente ${\textstyle k}$).

Figura 8. Comparación de la resistencia a pandeo lateral para carga uniformemente repartida y momentos no nulos en los extremos, según el EC3-1996 y DB SE-A, con ${\textstyle C_{1}=1.285}$ y ${\textstyle k=1.0}$

Figura 9. Comparación de la resistencia a pandeo lateral para carga uniformemente repartida y momentos no nulos en los extremos, según el EC3-1996 y DB SE-A, con ${\textstyle C_{1}=0.712}$ y ${\textstyle k=0.5}$

4. Cálculo de la resistencia a pandeo lateral

EC3-1996 vs DB SE-A:EAE

Como alternativa a utilizar las expresiones del DB SE-A, combinadas con los valores del coeficiente ${\textstyle C_{1}}$ de la Tabla 2, para tener en cuenta distribuciones de momentos flectores generados por cargas transversales directamente aplicadas sobre la barra que han sido omitidas en el DB SE-A, en esta sección se analiza el posible uso del factor de corrección ${\textstyle k_{c}}$, incluido en la EAE.

Para ello se ha calculado el coeficiente reductor por pandeo lateral modificado, ${\textstyle \,{\chi }_{LT,mod}}$, válido para perfiles laminados y obtenido a partir de las ecuaciones (8), (9), (10) y (11).

En esta última ecuación se ha utilizado el factor de corrección ${\textstyle k_{c}}$, dado en la Tabla 1.

4.1 Viga biarticulada con carga uniformemente repartida

Es el caso de una viga sometida a una distribución de momentos flectores parabólica (Figura 4). Para esta situación, la Tabla 1 recomienda un valor del factor de corrección ${\textstyle k_{c}=0.94}$.

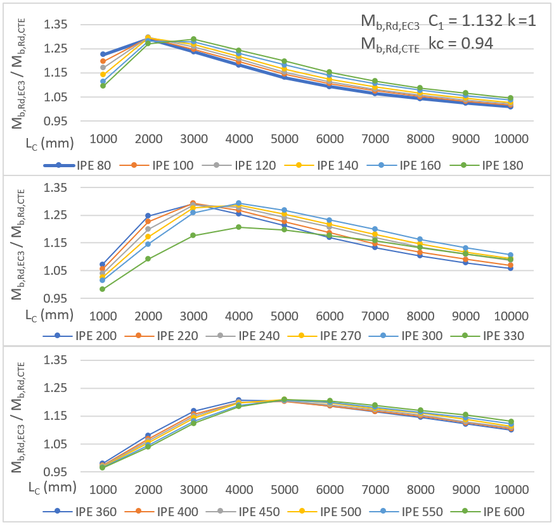
En la Figura 10 se representa la relación entre los resultados obtenidos considerando la expresión del EC3-1996 (${\textstyle M_{b,Rd,EC3}}$) con los coeficiente ${\textstyle C_{1}=1.132}$ y ${\textstyle k=1.0}$ y los obtenidos a partir de las expresiones del DB SE-A para obtener el momento crítico, teniendo en cuenta las modificaciones propuestas por la EAE para calcular el coeficiente reductor por pandeo lateral ${\textstyle \,{\chi }_{LT,mod}}$, para perfiles laminados, incluyendo el factor de corrección ${\textstyle k_{c}=0.94}$.

En la gráfica de la Figura 10, se observa que en este caso los valores proporcionados por las expresiones del EC3-1996 son, en la mayor parte de las situaciones mayores que los obtenidos con el DB SE-A. Los incrementos se sitúan en un rango que va del 10% al 30%, representando el trazo grueso de color negro los valores medios. Por tanto, el uso del coeficiente ${\textstyle k_{c}}$ en el caso que nos ocupa da lugar a valores bastante conservadores.

Figura 10. Comparación de la resistencia a pandeo lateral para carga uniformemente repartida, según el EC3-1996 y DB SE-A, con ${\textstyle C_{1}=1.132}$ y ${\textstyle k=1.0}$ y ${\textstyle k_{c}=0.94}$ (EAE)

4.2 Vigas con otras leyes de flectores parabólicas

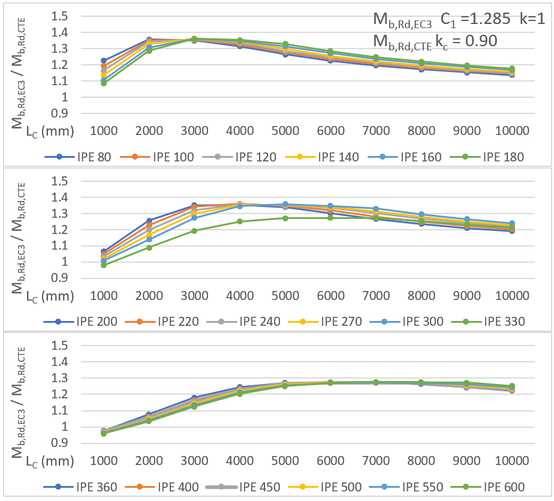
Este caso se muestra en la Figura 7 y corresponde a una distribución de momentos flectores parabólica con momentos no nulos en los extremos. Según la Tabla 1, el valor del factor de corrección es ${\textstyle k_{c}=0.90}$.

Los resultados obtenidos al comparar el ${\textstyle M_{b,Rd,EC3}}$, calculado con ${\textstyle C_{1}=1.285}$ y ${\textstyle k_{z}=1}$, con el ${\textstyle M_{b,Rd,CTE}}$ modificado con el factor de corrección ${\textstyle k_{c}=0.90}$, se han representado en la Figura 11. En esta ocasión, los resultados del ${\textstyle M_{b,Rd,EC3}}$ también son bastante mayores, aunque las diferencias son todavía más significativas ya que en algunos casos superan el 40%.

Figura 11. Comparación de la resistencia a pandeo lateral para carga uniformemente repartida y momentos no nulos en los extremos, según el EC3-1996 y DB SE-A, con ${\textstyle C_{1}=1.285}$ y ${\textstyle k=1.0}$ y ${\textstyle k_{c}=0.90}$ (EAE)

5. Discusión

Los resultados obtenidos del análisis comparado muestran que los valores de la resistencia a pandeo lateral considerando una distribución de momentos flectores constante (Figura 2) calculados con las expresiones del DB SE-A son prácticamente iguales (Figura 3) a los proporcionados por las fórmulas del EC3-UK y EC3-1996, pese a las diferencias formales de las expresiones que permiten calcular el momento crítico elástico.

En el caso de una viga biarticulada con carga uniformemente repartida (Figura 4), las gráficas que recogen los resultados del análisis, basados en las formulaciones proporcionadas por distintas normas y que caracterizan el problema mediante el coeficiente ${\textstyle C_{1}}$, muestran (Figura 5) que los valores de la resistencia de cálculo frente al pandeo lateral son similares, siempre y cuando se utilicen los valores de ${\textstyle C_{1}}$ correspondientes al coeficiente ${\textstyle k}$ igual a la unidad (rotación alrededor del eje débil permitida en ambos extremos).

Así mismo, en el caso de una carga uniformemente repartida (distribución de momentos flectores parabólica) pero con momentos negativos en los extremos (Figura 7), los resultados siguen mostrando diferencias muy pequeñas cuando, de nuevo, el valor del coeficiente ${\textstyle C_{1}}$ utilizado corresponde al caso de coeficiente ${\textstyle k=1}$ (Figura 8).

Por lo tanto, para el caso de distribución de flectores parabólica, es admisible aplicar en las expresiones del DB SE-A el coeficiente ${\textstyle C_{1}=1.132}$ (EC3-1996) cuando los momentos son nulos en los extremos, y el valor de ${\textstyle C_{1}=1.285}$ (EC3-1996) cuando hay, además, momentos negativos en los extremos. Para facilitar la aplicación práctica, se han confeccionado las Tablas 4, 5 y 6 con los valores del coeficiente reductor de la resistencia a pandeo lateral, ${\textstyle {\chi }_{LT}}$, para la serie de los perfiles IPE de acero S275, utilizando los valores de los módulos de torsión y alabeo propuestos por ArcelorMittal.

En estas tablas se puede observar que el coeficiente reductor por pandeo lateral correspondiente al caso de momento constante es inferior al obtenido para la distribución de flectores parabólica, correspondiendo los mayores valores a la distribución parabólica con momentos negativos en los extremos.

En consecuencia, sería admisible utilizar en el dimensionado los valores correspondientes a la distribución de flectores constante, independientemente del estado de carga. Esta opción quedaría del lado de la seguridad.

La aplicación de los valores de ${\textstyle C_{1}}$ correspondientes a los casos en que ${\textstyle k=0.5}$ no es recomendable, pues el DB SE-A no contempla condiciones de enlace en los extremos distintas al giro libre alrededor del eje débil (Figuras 6 y 9) en el cálculo del momento crítico elástico de pandeo lateral.

Por otro lado, los cálculos llevados a cabo según el procedimiento del DB SE-A, pero con el factor de corrección ${\textstyle k_{c}}$ propuesto por la EAE y el vigente Eurocódigo 3 (EC3-2013) para tener en cuenta distintas distribuciones de momentos flectores, muestran diferencias significativas respecto a los valores obtenidos con el EC3-1996 de tal modo que, al aplicar el coeficiente ${\textstyle k_{c}}$, los valores de la resistencia a pandeo lateral son más conservadores.

Finalmente, hay que señalar que la aplicación del factor corrector ${\textstyle k_{c}}$ de la EAE en las expresiones del DB SE-A da lugar a resultados todavía más conservadores.

Tabla 4. ${\textstyle {\chi }_{LT}}$ obtenidos con las ecuaciones del DB SE A para momento constante

${\textstyle C_{1}=1}$	${\textstyle L_{c}=1m}$	${\textstyle L_{c}=2m}$	${\textstyle L_{c}=3m}$	${\textstyle L_{c}=4m}$	${\textstyle L_{c}=5m}$	${\textstyle L_{c}=6m}$	${\textstyle L_{c}=7m}$	${\textstyle L_{c}=8m}$	${\textstyle L_{c}=9m}$	${\textstyle L_{c}=10m}$
IPE 80	0.82978	0.59285	0.43294	0.33728	0.27567	0.23300	0.20177	0.17793	0.15916	0.14398
IPE 100	0.85649	0.62599	0.45790	0.35626	0.29090	0.24572	0.21270	0.18754	0.16772	0.15172
IPE 120	0.87910	0.65559	0.47809	0.37018	0.30133	0.25405	0.21964	0.19350	0.17296	0.15639
IPE 140	0.89919	0.69055	0.50463	0.38888	0.31541	0.26529	0.22901	0.20154	0.18002	0.16269
IPE 160	0.91651	0.73096	0.54243	0.41790	0.33824	0.28402	0.24489	0.21533	0.19222	0.17365
IPE 180	0.92958	0.76338	0.57483	0.44215	0.35660	0.29859	0.25693	0.22560	0.20118	0.18160
IPE 200	0.94103	0.79710	0.61814	0.47924	0.38679	0.32366	0.27830	0.24422	0.21768	0.19643
IPE 220	0.95100	0.82510	0.65646	0.51200	0.41253	0.34428	0.29535	0.25873	0.23031	0.20761
IPE 240	0.95957	0.85110	0.70088	0.55699	0.45133	0.37717	0.32362	0.28343	0.25224	0.22733
IPE 270	0.96884	0.87537	0.74011	0.59407	0.47946	0.39793	0.33931	0.29571	0.26215	0.23555
IPE 300	0.97628	0.89527	0.77759	0.63675	0.51561	0.42641	0.36186	0.31399	0.27734	0.24847
IPE 330	0.96884	0.85961	0.73082	0.60055	0.49315	0.41277	0.35334	0.30853	0.27383	0.24625
IPE 360	0.97483	0.87326	0.75349	0.62752	0.51868	0.43486	0.37208	0.32453	0.28766	0.25840
IPE 400	0.97962	0.88392	0.77122	0.64919	0.53950	0.45277	0.38703	0.33703	0.29825	0.26750
IPE 450	0.98343	0.89206	0.78423	0.66451	0.55329	0.46351	0.39491	0.34268	0.30228	0.27036
IPE 500	0.98718	0.90025	0.79809	0.68246	0.57131	0.47915	0.40775	0.35309	0.31077	0.27738
IPE 550	0.99067	0.90798	0.81174	0.70164	0.59252	0.49926	0.42559	0.36864	0.32432	0.28927
IPE 600	0.99390	0.91504	0.82410	0.71928	0.61252	0.51854	0.44282	0.38362	0.33731	0.30061

Tabla 5. ${\textstyle {\chi }_{LT}}$, obtenidos con las ecuaciones del DB SE A para diagrama de flectores parabólico

${\textstyle C_{1}=1.132}$	${\textstyle L_{c}=1m}$	${\textstyle L_{c}=2m}$	${\textstyle L_{c}=3m}$	${\textstyle L_{c}=4m}$	${\textstyle L_{c}=5m}$	${\textstyle L_{c}=6m}$	${\textstyle L_{c}=7m}$	${\textstyle L_{c}=8m}$	${\textstyle L_{c}=9m}$	${\textstyle L_{c}=10m}$
IPE 80	0.85123	0.63885	0.47739	0.37522	0.30799	0.26095	0.22632	0.19981	0.17887	0.16191
IPE 100	0.87415	0.67041	0.50347	0.39573	0.32469	0.27501	0.23847	0.21050	0.18843	0.17056
IPE 120	0.89368	0.69799	0.52436	0.41070	0.33610	0.28419	0.24616	0.21714	0.19427	0.17578
IPE 140	0.91120	0.72985	0.55150	0.43073	0.35146	0.29658	0.25654	0.22608	0.20213	0.18281
IPE 160	0.92645	0.76582	0.58950	0.46155	0.37626	0.31715	0.27409	0.24139	0.21572	0.19503
IPE 180	0.93809	0.79413	0.62139	0.48705	0.39610	0.33310	0.28737	0.25277	0.22568	0.20390
IPE 200	0.94836	0.82321	0.66299	0.52554	0.42849	0.36044	0.31088	0.27335	0.24399	0.22039
IPE 220	0.95739	0.84721	0.69880	0.55897	0.45587	0.38279	0.32956	0.28935	0.25797	0.23282
IPE 240	0.96519	0.86952	0.73914	0.60391	0.49663	0.41821	0.36039	0.31651	0.28220	0.25468
IPE 270	0.97369	0.89045	0.77386	0.64003	0.52577	0.44037	0.37742	0.32995	0.29312	0.26377
IPE 300	0.98055	0.90776	0.80642	0.68050	0.56262	0.47052	0.40177	0.34991	0.30982	0.27804
IPE 330	0.97509	0.87504	0.75937	0.63886	0.53389	0.45179	0.38938	0.34150	0.30402	0.27401
IPE 360	0.98068	0.88737	0.77980	0.66436	0.55935	0.47464	0.40920	0.35867	0.31901	0.28725
IPE 400	0.98515	0.89702	0.79573	0.68462	0.57988	0.49301	0.42492	0.37202	0.33044	0.29715
IPE 450	0.98872	0.90441	0.80739	0.69881	0.59336	0.50395	0.43317	0.37805	0.33478	0.30026
IPE 500	0.99223	0.91187	0.81981	0.71534	0.61084	0.51981	0.44656	0.38911	0.34392	0.30787
IPE 550	0.99550	0.91893	0.83204	0.73289	0.63120	0.54001	0.46508	0.40556	0.35844	0.32074
IPE 600	0.99853	0.92539	0.84313	0.74892	0.65022	0.55922	0.48281	0.42134	0.37233	0.33298

Tabla 6. ${\textstyle {\chi }_{LT}}$, obtenidos con las ecuaciones del DB SE-A para diagrama de flectores parabólico y momentos negativos en extremos

${\textstyle C_{1}=1.285}$	${\textstyle L_{c}=1m}$	${\textstyle L_{c}=2m}$	${\textstyle L_{c}=3m}$	${\textstyle L_{c}=4m}$	${\textstyle L_{c}=5m}$	${\textstyle L_{c}=6m}$	${\textstyle L_{c}=7m}$	${\textstyle L_{c}=8m}$	${\textstyle L_{c}=9m}$	${\textstyle L_{c}=10m}$
IPE 80	0.87001	0.68340	0.52469	0.41706	0.34420	0.29253	0.25421	0.22473	0.20137	0.18242
IPE 100	0.88972	0.71247	0.55138	0.43901	0.36242	0.30802	0.26767	0.23663	0.21204	0.19209
IPE 120	0.90665	0.73737	0.57249	0.45493	0.37482	0.31812	0.27619	0.24401	0.21855	0.19793
IPE 140	0.92198	0.76559	0.59955	0.47608	0.39146	0.33171	0.28766	0.25393	0.22731	0.20577
IPE 160	0.93548	0.79688	0.63664	0.50830	0.41818	0.35420	0.30701	0.27090	0.24243	0.21941
IPE 180	0.94588	0.82121	0.66705	0.53462	0.43940	0.37157	0.32161	0.28349	0.25349	0.22928
IPE 200	0.95514	0.84606	0.70570	0.57368	0.47373	0.40116	0.34736	0.30620	0.27379	0.24762
IPE 220	0.96332	0.86657	0.73808	0.60691	0.50240	0.42518	0.36772	0.32379	0.28924	0.26141
IPE 240	0.97045	0.88572	0.77372	0.65046	0.54442	0.46288	0.40111	0.35350	0.31593	0.28561
IPE 270	0.97826	0.90383	0.80381	0.68450	0.57391	0.48621	0.41943	0.36815	0.32792	0.29564
IPE 300	0.98459	0.91896	0.83172	0.72163	0.61050	0.51760	0.44544	0.38979	0.34620	0.31136
IPE 330	0.98105	0.88928	0.78563	0.67576	0.57527	0.49292	0.42825	0.37761	0.33741	0.30493
IPE 360	0.98627	0.90042	0.80392	0.69942	0.60014	0.51616	0.44897	0.39586	0.35354	0.31929
IPE 400	0.99045	0.90918	0.81817	0.71803	0.61995	0.53467	0.46528	0.40999	0.36579	0.33000
IPE 450	0.99378	0.91591	0.82859	0.73098	0.63285	0.54562	0.47380	0.41635	0.37044	0.33336
IPE 500	0.99707	0.92271	0.83969	0.74599	0.64945	0.56137	0.48757	0.42798	0.38018	0.34156
IPE 550	1.00000	0.92916	0.85063	0.76183	0.66861	0.58128	0.50646	0.44518	0.39563	0.35540
IPE 600	1.00000	0.93508	0.86057	0.77626	0.68633	0.60001	0.52441	0.46158	0.41032	0.36851

6. Conclusiones

En este trabajo se ha analizado la pertinencia de utilizar las comprobaciones a pandeo lateral incluidas en el DB SE-A y propuestas inicialmente para barras con distribución de momentos flectores lineal, junto con los coeficientes propuestos por varias versiones del Eurocódigo 3 y de la EAE para analizar barras sometidas a otras leyes de momentos flectores más complejas y cercanas a los casos reales habituales.

Se ha comprobado en qué casos es recomendable utilizar los coeficientes $C_{1}$ y $k$ propuestos por el EC3-1996, y se han confeccionado unas tablas para facilitar la aplicación práctica. Finalmente se ha constatado que los valores obtenidos con el coeficiente $k_{c}$ propuesto por la EAE son excesivamente conservadores.

Referencias

[1] Ministerio de Vivienda. Código Técnico de la Edificación. Recuperado de https://www.codigotecnico.org/, 2006. Último acceso febrero 2020.

[2] Ley 38/1999 de 5 de noviembre, de Ordenación de la edificación. Boletín Oficial del Estado, núm. 266, de 6 de noviembre de 1999. Recuperado de https://www.boe.es/buscar/doc.php?id=BOE-A-1999-21567. Último acceso febrero 2020.

[3] Ministerio de vivienda. Documento Básico, Seguridad Estructural, Acero. Texto modificado por RD 1371/2007, de 19 de octubre (BOE 23/10/2007) y corrección de errores (BOE 25/01/2008) Recuperado de https://www.codigotecnico.org/images/stories/pdf/seguridadEstructural/DBSE-A.pdf, 2006. Último acceso mayo 2020.

[4] Ministerio de presidencia. Instrucción de Acero Estructural. Boletín Oficial del Estado, núm. 149, de 23 de junio de 2011. Recuperado de https://www.mitma.gob.es/organos-colegiados/comision-permanente-de-estructuras-de-acero/cpa/instrucciones/instruccion-eae-version-en-castellano, 2011. Último acceso febrero 2020.

[5] Comité Europeo de Normalización. UNE EN 1993-1-1 Eurocódigo 3: proyecto de estructuras de acero. Parte 1-1: Reglas generales y reglas de edificios. Versión oficial, en español, de las Normas Europeas EN 1993-1-1:2005 y EN 1993-1-1: 2005/AC: 2009. Publicada por Asociación Española de Normalización (AENOR) en abril de 2013.

[6] Simões da Silva L., Simões R., Gervásio H., Couchman, G. Design of steel structures. U.K. Edition. Publicado por ECCS – European Convention for Constructional Steelwork, 2014.

[7] Clark J.W., Hill N.H. Lateral buckling of beams. Proceedings ASCE, Journal of the Structural Division, 68(7):175-196, 1960.

[8] Galéa Y. Abaques de deversement pour profilés lamines. Construction Métallique, 4:39-51, 1981.

[9] Comité Europeo de Normalización UNE ENV 1993-1-1 Eurocódigo 3: proyecto de estructuras de acero. Parte 1-1: reglas generales y reglas para edificación. Versión oficial, en español de la Norma Europea Experimental ENV 1993-1-1 de abril 1992 + ENV 1993-1-1 AC de octubre 1992, (1992). Anulada y sustituida por UNE-EN 1993-1-1.

[10] AENOR. UNE 36526 Productos de acero. Perfiles en I con alas paralelas (IPE) de acero laminado en caliente. Asociación Española de Normalización (AENOR). Sustituye y anula la Norma UNE 36526:1994, 2018.

[11] Argüelles Alvarez R., Argüelles Bustillo R., Arriaga Martitegui F., Argüelles Bustillo J.M., Atienza Reales J.R. Estructuras de acero. Cálculo. 2ª Edición Ampliada y Actualizada, Bellisco, Ediciones Técnicas y Científicas, Madrid, 2005.

[12] Monfort Lleonart, J. Estructuras metálicas para edificación. Editorial UPV, Valencia, 2006.

[13] Hughes A.F., IIes D.C., Malik A.S. Design of steel beams in torsion. In accordance with Eurocodes and the UK National Annexes, The Steel Construction Institute, Publication number P385, 2011.

[14] Ministerio de Obras Públicas, Transportes y Medio Ambiente. Norma Básica de la Edificación NBE EA-95 Estructuras de Acero en Edificación. BOE núm. 16 de 18 de enero de 1996. Recuperado de https://www.boe.es/buscar/doc.php?id=BOE-A-1996-1223, 1996. Último acceso mayo 2020.

[15] DIN 1025-5 Hot rolled and H sections (IPE series); dimensions, mass and static parameters.

[16] ArcerolMittal. Gama de perfiles en I: IPE: Perfiles I de alas paralelas. Recuperado de https://constructalia.arcelormittal.com/files/IPE-132701863935bd4449844afaea558c1a.pdf, 2017. Último acceso mayo 2020.