Estimation of peak flow in flood-producing rivers using numerical simulation, geospatial information and evolutionary algorithms

Resumen

Las inundaciones producen enormes pérdidas humanas y materiales cada año. Evaluar su extensión y severidad, y sobre todo simular posibles escenarios futuros puede mejorar la respuesta, mitigación y la prevención de los efectos de este fenómeno. En este trabajo se presenta una metodología para reproducir la extensión de inundaciones producidas por el desbordamiento de cauces y registradas mediante imágenes de satélite, identificando el gasto máximo que la produjo mediante la solución numérica de las ecuaciones de aguas someras en 2D y Evolución Diferencial. El objetivo es minimizar la diferencia entre la extensión del área inundada registrada en las imágenes de satélite, y la que se obtiene en la simulación ajustando el valor máximo de la curva de gasto empleada a la entrada del cauce en el dominio de la solución. La propuesta se aplica a datos e imágenes correspondientes a un área localizada al sur de la ciudad de Villahermosa, en el estado mexicano de Tabasco, que es una zona susceptible de inundarse por el desbordamiento del Río de la Sierra. Nuestra propuesta muestra que es posible contar con información más precisa de extensión y altura del agua en el área inundada que la mostrada por el satélite, que se puede usar como información para planes de prevención y mitigación de los efectos adversos de la inundación.

Palabras clave: Modelado de inundaciones, gasto máximo en ríos, Iber, Evolución Diferencial

Abstract

Floods produce enormous human and material losses every year. Evaluating their extent and severity, and especially simulating possible future scenarios can improve the response, mitigation and prevention of the effects of this phenomenon. This paper presents a methodology to reproduce the extent of floods produced by channel overflows and recorded by satellite images, identifying the maximum discharge that produced it by means of the numerical solution of the 2D shallow water equations and Differential Evolution. The objective is to minimize the difference between the extent of the flooded area recorded in the satellite images, and that obtained in the simulation by adjusting the maximum value of the flow curve used at the entrance of the channel in the solution domain. The proposal is applied to data and images corresponding to an area located south of the city of Villahermosa, in the Mexican state of Tabasco, which is an area susceptible to flooding by the overflow of the Río de la Sierra. Our proposal shows that it is possible to have more accurate information on the extent and height of water in the flooded area than that shown by the satellite, which can be used as information for prevention and mitigation plans for the adverse effects of flooding.

Keywords: Flooding modelling, river peak-flow, Iber, Differential Evolution

1. Introducción

En la actualidad, la evaluación de riesgos y vulnerabilidad ante los desastres naturales tiene una gran relevancia a nivel mundial, siendo un aspecto importante en la elaboración de políticas públicas relativas a la planeación urbana y a la gestión de recursos para la prevención y atención de los impactos socioeconómicos que causan [1,2]. De entre todos los fenómenos naturales que pueden conducir a desastres, los de inundación se cuentan entre los más numerosos y frecuentes: solamente en 2022, en el mundo se reportaron 387 desastres naturales, de los cuales 176 fueron inundaciones [3]. En México, los desastres asociados a fenómenos hidrometeorológicos (entre los que se incluyen las inundaciones) fueron los causantes del 81% de los daños y pérdidas materiales del total reportado en el 2022 [4]. Aun cuando las inundaciones no son el tipo de desastre natural que cobra el mayor número de vidas humanas, son fenómenos que ocurren con frecuencia [5], de ahí la importancia de la evaluación de los riesgos ante ellas. Ahora bien, se trata de una tarea compleja debido a la gran cantidad de variables involucradas y al volumen de información que se necesita para ello. Las metodologías más utilizadas en la actualidad se basan en técnicas empíricas, y en la modelación numérica del fenómeno hidrodinámico, teniendo cada una sus ventajas y dificultades. Una revisión de las metodologías existentes a la fecha figura en [6].

Las metodologías empíricas se basan fundamentalmente en información estadística de una región en particular, tanto de la actividad socioeconómica de la misma, como de los registros históricos de las precipitaciones pluviales y las crecidas de los cuerpos de agua que se encuentran dentro de ella y sus vecindades. Las metodologías basadas en la modelación del fenómeno físico intentan reproducir mediante simulación numérica los eventos de inundaciones de la manera más realista posible. Para validar este tipo de modelos, se intenta reproducir eventos de inundación pasados y de los cuales se tienen registros documentados [6,7]. En la actualidad se cuenta con formulaciones matemáticas y métodos numéricos capaces de resolver el problema hidrodinámico con precisión, sin embargo la alta variabilidad espacial y temporal de las principales variables que intervienen dificultan la reproducción del fenómeno real de manera fiel. Por tanto, lo más adecuado es realizar no sólo una simulación sino una serie de simulaciones, donde cada una contempla un escenario probable y diferente de los demás. Entre más escenarios se contemplen el problema se vuelve computacionalmente más costoso, por lo cual es conveniente acotar el número de dichos escenarios basándose en estadísticas históricas e información geoespacial como la que se emplea en las metodologías empíricas. Se han realizado varios trabajos que combinan ambas metodologías, empleando modelos hidrológicos de lluvia-escurrimiento como los que figuran en [8] y que se usan como datos de entrada en la simulación numérica. Algunos ejemplos recientes de ello figuran en [9-13]. En la mayoría de los casos, los modelos hidrológicos necesitan ser calibrados con el fin de obtener resultados fiables.

Un enfoque diferente es emplear métodos estocásticos y/o técnicas de optimización para ajustar los parámetros de entrada que se utilizan en la simulación numérica, con el fin de cubrir la incertidumbre que se tiene en ciertos datos de entrada, o incluso la falta de ellos. Zhang et al. [14] emplearon diferentes algoritmos evolutivos para calibrar los parámetros del modelo hidrológico SWAT. Chen et al. [15] ajustaron parámetros mediante PSO para mejorar el modelo hidrológico Liuxihe. En este trabajo, se propone el uso de algoritmos evolutivos para ajustar parámetros de entrada a emplear en simulación numérica en 2D del fenómeno hidráulico (mediante la solución de las ecuaciones de aguas someras), comparando los resultados de la simulación con imágenes binarias de satélite-radar, similares a las empleadas en [16].

1.1 Antecedentes

La simulación numérica moderna del fenómeno de inundación está basada en la solución de ecuaciones diferenciales de la mecánica de fluidos, para lo cual existen formulaciones en 1, 2 y 3 dimensiones [6,7,17]. En este caso nos interesa la modelación en 2D mediante la solución de las ecuaciones de aguas someras [18], las cuales se derivan de las ecuaciones generales de Navier-Stokes y que describen el flujo hidrodinámico sobre la superficie del terreno teniendo en cuenta su configuración topográfica (altimetría). Existen diversas variantes de dichas ecuaciones dependiendo de las hipótesis que consideren, así como de métodos para resolverlas (diferencias finitas, elementos finitos, volumen finito) según el software que las implementen. Para este trabajo en particular se empleó Iber [19,20], que resuelve el problema hidrodinámico mediante volumen finito y emplea la siguiente versión de las ecuaciones de aguas someras:

${\frac {\partial h}{\partial t}}+h\left({\frac {\partial {U}_{x}}{\partial x}}+{\frac {\partial {U}_{y}}{\partial y}}\right)=$$0$

${\frac {\partial (h{U}_{x})}{\partial t}}+{\frac {\partial }{\partial x}}\left(h{U}_{x}^{2}+\right.$$\left.g{\frac {{h}^{2}}{2}}\right)+{\frac {\partial }{\partial y}}\left(h{U}_{x}{U}_{y}\right)=$$-gh{\frac {\partial {Z}_{b}}{\partial x}}-{\frac {{\tau }_{b,x}}{\rho }}+{\frac {\partial }{\partial x}}\left({\nu }_{t}h{\frac {\partial {U}_{x}}{\partial x}}\right)+$${\frac {\partial }{\partial y}}\left({\nu }_{t}h{\frac {\partial {U}_{x}}{\partial y}}\right)$

${\frac {\partial (h{U}_{y})}{\partial t}}+{\frac {\partial }{\partial y}}\left(h{U}_{y}^{2}+\right.$$\left.g{\frac {{h}^{2}}{2}}\right)+{\frac {\partial }{\partial x}}\left(h{U}_{x}{U}_{y}\right)=$$-gh{\frac {\partial {Z}_{b}}{\partial y}}-{\frac {{\tau }_{b,y}}{\rho }}+{\frac {\partial }{\partial x}}\left({\nu }_{t}h{\frac {\partial {U}_{y}}{\partial x}}\right)+$${\frac {\partial }{\partial y}}\left({\nu }_{t}h{\frac {\partial {U}_{y}}{\partial y}}\right)$

donde:

${\textstyle ({U}_{x},{U}_{y})}$ son los vectores de velocidad de flujo,

${\textstyle h}$ es la altura de la superficie horizontal del agua (calado),

${\textstyle g}$ es la aceleración de la gravedad,

${\textstyle \rho }$ es la densidad del agua,

${\textstyle {Z}_{b}}$ es la cota topográfica del fondo,

${\textstyle {\nu }_{t}}$ es la viscosidad turbulenta del agua, y

${\textstyle {\tau }_{b}}$ es la fricción debida al rozamiento del agua con el fondo, calculada mediante la fórmula de Manning por ${\textstyle {\tau }_{b,x}=}$$\rho gh{\frac {{n}^{2}{U}_{x}\left|U\right|}{{h}^{4/3}}}$ ${\textstyle {\tau }_{b,y}=}$$\rho gh{\frac {{n}^{2}{U}_{y}\left|U\right|}{{h}^{4/3}}}$.

La preparación de los modelos de cálculo para la simulación del fenómeno hidrodinámico requiere información de naturaleza diversa, y de la cual depende la calidad de los resultados. Los datos necesarios en Iber son los siguientes:

• La topografía del terreno de la zona a estudiar. Se caracteriza mediante una malla tridimensional de triángulos y/o cuadriláteros planos, la cual conforma el dominio espacial del problema.

• La rugosidad de la superficie del terreno, que caracteriza la resistencia al flujo del agua sobre ella. Se emplean coeficientes de Manning.

• Las entradas y salidas de flujo de agua en la zona en estudio, caracterizadas por los cauces superficiales que cruzan el dominio de cálculo, la precipitación pluvial y la infiltración hacia el subsuelo.

En cuanto a la topografía, es posible obtener la configuración de las alturas de terreno en un área definida mediante escáneres láser (LIDAR) montados sobre aeronaves, que proporcionan una nube de puntos que permiten caracterizar grandes extensiones de terreno con buena precisión. Los parámetros de rugosidad se suponen en función del tipo de suelo, de la vegetación predominante y del uso humano del terreno, lo cual es identifica mediante imágenes de satélite georrefereciadas. Para las entradas y salidas de flujo, se emplean valores calculados o bien medidos directamente en el sitio: gasto de los cauces que cruzan la zona, precipitaciones pluviales e infiltración según el tipo de suelo.

Para elaborar un modelo de cálculo a ejecutar en Iber, se emplea la siguiente información:

• Archivos de datos para la caracterización del relieve topográfico (llamados modelos de elevación digital DTM). Típicamente se emplean archivos tipo ráster, los cuales consisten en una cuadrícula con coordenadas planas y las alturas del terreno en el centro de los cuadros.

• Mapas vectoriales del tipo de uso de suelo en la región a estudiar. Con dicha información se genera la malla de cálculo bidimensional a emplear en la simulación, asignándose los coeficientes de rugosidad según el tipo de terreno. Posteriormente se ajustan las alturas Z de las coordenadas de la malla empleando los modelos DTM [19].

• Caracterización de la precipitación pluvial y el flujo de agua a la entrada de los cauces que crucen la zona de interés, en una ventana de tiempo que abarque el evento de inundación a reproducir. Se asignan hietogramas de la lluvia por regiones, y curvas de gasto a la entrada de los cauces en los bordes del dominio espacial del modelo.

Además de la información anterior, es necesario asignar condiciones de frontera que indiquen la manera en que el agua puede salir del domino de cálculo, pudiendo ser borde cerrado o borde libre. También se deben asignar condiciones iniciales de altura de agua en caso de que se tengan embalses permanentes en el interior del dominio. De manera opcional se puede considerar la infiltración del agua en el terreno.

Una vez que se tienen todos los datos asignados, se define el tiempo total que se desea simular (en segundos), así como el intervalo de tiempo para la impresión y visualización de los resultados. Entre más tiempo de simulación se especifica, mayor es el tiempo de cómputo requerido. Y a menor tamaño de intervalo de resultados se tendrán archivos de resultados más grandes, pero también se tienen más imágenes de resultados para visualizar y procesar, pudiendo elaborarse animaciones con ellas. Para simular distintos escenarios del fenómeno de inundación en el mismo dominio de cálculo se cambian los valores de los datos de entrada.

2. Metodología

Para reproducir un evento de inundación real que se haya registrado en una zona específica mediante simulación numérica, es necesario comparar los resultados del cálculo con la información que se haya registrado del evento, y en base a ello hacer los ajustes necesarios en los datos de entrada. Si se dispone de imágenes de satélite georreferenciadas que hayan capturado la evolución del evento entonces la comparación de los resultados puede ser más precisa en el espacio en función de una métrica de similitud. El objetivo ahora es realizar el ajuste de los parámetros de manera automática, modificando los valores mediante algún algoritmo de optimización. Para ello se requiere definir una función objetivo a optimizar, y entonces se ejecutan varias simulaciones en el mismo dominio con diferentes valores de los parámetros para calcular dicha función. Tanto los valores iniciales como el rango de los parámetros a determinar se establecen a partir de información estadística histórica (como la intensidad de lluvia o el caudal en un cauce). De esta manera pueden ajustarse los parámetros deseados.

En este trabajo, se intenta reproducir el flujo máximo que se presenta durante la crecida de un cauce que genera un fenómeno de inundación específico mediante Evolución Diferencial (DE) [21], comparando los resultados con imágenes georreferenciadas. Para este propósito, el uso de Iber como motor de solución del problema hidrodinámico tiene características útiles, las cuales mencionamos a continuación:

1. Se puede ejecutar desde un programa externo al que llamamos “programa padre”.

2. Los datos que necesita para realizar un cálculo son leídos desde archivos de texto plano fáciles de modificar desde el programa padre.

3. Los resultados son escritos en archivos de texto plano con una estructura sencilla de leer y entender, con la cual el programa padre realiza cálculos y ajustes en valores de los parámetros a determinar.

4. Tiene algoritmos que pueden correr de manera paralela en GPU con un rendimiento numérico eficiente, lo que reduce mucho el tiempo de cálculo necesario.

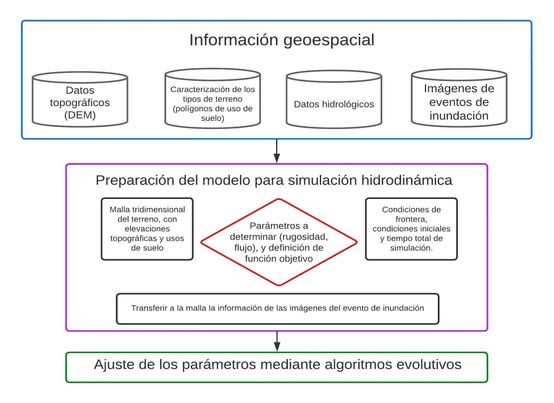
La metodología propuesta se puede resumir mediante el diagrama mostrado en la Figura 1.

Figura 1. Esquema general de la metodología propuesta

Con la información geoespacial se prepara el modelo de cálculo que servirá como plantilla inicial para ejecutar el proceso (en este caso un modelo completo de Iber). En este paso debe establecerse la totalidad de los datos a utilizar en el modelo: malla de cálculo que caracterice la topografía, parámetros de rugosidad, entradas de flujo, permeabilidad, condiciones iniciales, condiciones de frontera (entradas y salidas de flujo por los bordes), tiempo de simulación e intervalos de tiempo para imprimir los resultados. Por defecto, Iber establece algunos otros parámetros que no dependen del modelo pero que inciden fuertemente en el tiempo de cómputo y en menor medida en la precisión de los resultados, como son el algoritmo específico para la solución del problema en el tiempo. El modelo base debe ser probado para asegurarse de que funcione correctamente antes de poder emplearlo en un proceso de optimización. Una vez hecho eso, mediante un programa externo (escrito en C++) se especifican los parámetros que se van a ajustar mediante algoritmos de optimización: en este caso, los valores del flujo de entrada en los cauces que cruzan la región caracterizados mediante curvas dependientes del tiempo.

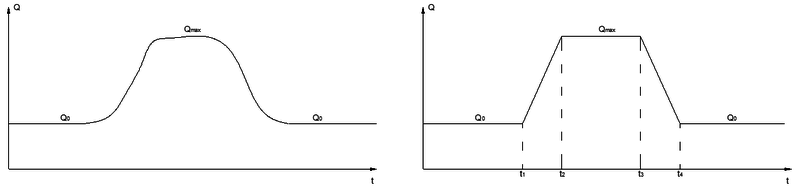
Para poder establecer el valor del flujo máximo que produce el desbordamiento de un río (y por consiguiente una inundación), se parte desde un valor inicial ${\textstyle Q_{0}}$ y se hace crecer hasta un valor máximo ${\textstyle Q_{\max }}$, el cual actúa durante un periodo de tiempo observado durante el fenómeno real. La Figura 2 muestra una curva de gasto idealizada que ilustra dicha variación.

Figura 2. A la izquierda se tiene una curva de gasto real con una crecida del caudal, del lado derecho se muestra una idealización que permite parametrizarla

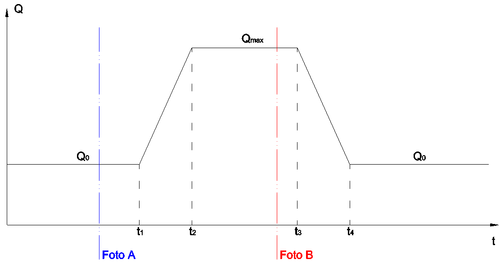
El valor de flujo ${\textstyle Q_{0}}$ puede determinarse a partir del monitoreo rutinario del cauce en cuestión, y debe ser tal que no produzca desbordamiento en ningún punto del cauce dentro de la zona a estudiar. El valor ${\textstyle Q_{\max }}$ es el que produce un desbordamiento, y las áreas inundadas en un instante de tiempo X se comparan con las registradas en imágenes de satélite, tal como se muestra en la Figura 3.

Figura 3. Instantes de tiempo en los cuales se capturan fotografías de satélite en una zona a estudiar, antes y después de la crecida en un cauce que provoca una inundación

Inicialmente, por el cauce circula un flujo dado por ${\textstyle Q_{0}}$. Se debe correr la simulación un tiempo suficiente ${\textstyle t_{1}}$ de tal modo que se logre una solución estacionaria, y de cuyo estado se dispone de una fotografía satelital en el instante A (correspondiente a una situación normal). Entonces, se simula la crecida del cauce desde el valor dado por ${\textstyle Q_{0}}$ hasta ${\textstyle Q_{\max }}$, con un valor constante entre los instantes ${\textstyle t_{2}}$ hasta ${\textstyle t_{3}}$, de tal manera que se produce una inundación durante la cual se capturó la fotografía satelital en el instante B. Es importante señalar que los periodos de tiempo comprendidos entre los instantes ${\textstyle t_{1}}$, ${\textstyle t_{2}}$, ${\textstyle t_{1}}$, y ${\textstyle t_{4}}$ no se están considerando como parámetros a determinar, sino como datos que se estiman a partir de los registros que se hayan observado durante el fenómeno de inundación real. Aunque estas suposiciones son demasiado simplistas (la curva de flujo real puede ser muy diferente a la supuesta), esto nos permite reducir el espacio de búsqueda del problema y así disminuir el número total de simulaciones a realizar, dado que una sola simulación del fenómeno requiere un gran volumen de cálculo y por tanto mucho tiempo de cómputo al tener que abarcar una ventana de varios días en escala de tiempo real.

El siguiente paso es la definición de la función objetivo que permita ajustar el valor del gasto máximo. En este trabajo se emplean imágenes binarias de eventos de inundación, de tal manera que cada pixel toma el valor de 1 si el recuadro que representa está inundado, y 0 si no lo está. La información de las imágenes se transfiere a la malla a utilizar en la simulación, de manera que en cada elemento se tiene uno de los dos estados posibles. Esto se realiza superponiendo las mallas en una proyección plana y haciendo cálculos locales con las áreas de los elementos (las imágenes siempre son mallas cuadriláteras), y una vez hecho esto es posible realizar comparaciones con los resultados de la simulación numérica. La función objetivo propuesta es la suma de las áreas de los elementos cuyo estado seco o inundado es diferente de la solución original, para cada paso de tiempo de la simulación correspondiente a la imagen satelital. La ecuación que describe la función objetivo es la siguiente, y se explica con ayuda de la Figura 4

${F}_{obj}=\sum _{t=0,1,2,\ldots k}^{}\left(\sum \left|{f}_{i}\left(t\right)-{F}_{i}(t)\right|\cdot {A}_{i}\right)$

donde:

${\textstyle t=0,1,2,\ldots k}$ son los pasos de tiempo en los cuales se realizan las comparaciones entre la solución candidata y el objetivo a reproducir,

${\textstyle {f}_{i}\left(t\right)}$ es el estado del elemento i-ésimo de la malla en el paso de tiempo t (0 para estado seco, 1 para estado inundado) en la solución candidata,

${\textstyle {F}_{i}(t)}$ es el estado del elemento i-ésimo de la malla para el mismo paso de tiempo t (0 seco, 1 inundado) en la imagen del evento que se quiere reproducir, y

${\textstyle A-i}$ es el área del triángulo del elemento iésimo.

Estado de los elementos de la malla en la solución candidata, ${\textstyle {f}_{i}\left(t\right)}$ Estado de los elementos de la malla en el evento que se quiere reproducir, ${\textstyle {F}_{i}(t)}$ ${F}_{obj}=\sum _{t=0,1,2,\ldots k}^{}\left(\sum \left|{f}_{i}\left(t\right)-{F}_{i}(t)\right|\cdot {A}_{i}\right)$

Figura 4. Función objetivo propuesta para el problema de optimización

Si la correspondencia entre los estados de los elementos de la malla es total en ambos escenarios entonces el valor de la función objetivo es cero, por lo cual buscamos el mínimo valor posible. El estado de los elementos se multiplica por el área con el fin de equilibrar la incidencia que tienen en la función objetivo según su tamaño. Definida la función objetivo, se emplea un algoritmo de optimización para resolver el problema. En este trabajo en particular se empleó Evolución Diferencial dada su probada capacidad para resolver problemas con variables continuas del tipo “caja negra”, teniendo pocos parámetros de control que deben calibrarse.

Con el fin de probar la metodología propuesta y hacer ajustes al algoritmo, se realizaron dos ejemplos totalmente artificiales, para medir la capacidad del algoritmo para reproducir los resultados esperados. Posteriormente, se presenta un ejemplo donde se emplearon datos e imágenes de satélite reales.

3. Validación mediante ejemplos sintéticos

3.1 Ejemplo 1: Camping Forcanada, Río Garona

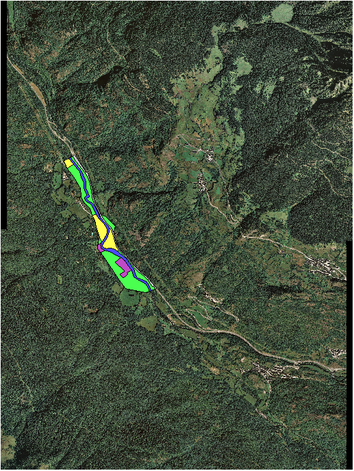
Este ejemplo fue tomado del material didáctico utilizado en los cursos de capacitación de Iber y es de acceso público [22]. Es una pequeña región al norte de España, cerca de la frontera con Francia. Se trata de un cauce poco profundo ubicado en una zona montañosa, bordeado por una carretera, un área de acampar y algunas pequeñas construcciones, cuya imagen satelital junto con el dominio considerado se muestra en la Figura 5. La fotografía abarca un área de 16.4 kilómetros cuadrados (${\textstyle 4.7\times 3.5}$ kilómetros), pero el dominio para la simulación hidrodinámica es un área mucho más pequeña, tomando únicamente las áreas cercanas al cauce (áreas coloreadas). Los polígonos sombreados delimitan el uso de suelo de cada zona considerada dentro del dominio, cuyas características de rugosidad se muestran en la Tabla 1. El área considerada abarca una franja de 1.5 kilómetros de longitud por 200 metros de ancho.

La topografía del terreno se representa mediante una malla tridimensional de elementos triangulares de 5 metros de lado, teniéndose en total 21890 elementos. Las coordenadas en ${\textstyle Z}$ se fijan sobre una malla plana de triángulos previamente generada, modificando las alturas interpolando datos de un modelo DTM. La Figura 6 muestra una vista en 3D de la malla para dar idea del relieve del terreno.

Figura 5. Fotografía satelital del área empleada en el ejemplo 1 [22]

Tabla 1. Coeficientes de rugosidad por tipo de uso de suelo empleados en el ejemplo 1

Tipo de suelo y valores de rugosidad (Manning)			Área (m2)	% del total
1	Rio	0.035	42310.45	16.48%
2	Vegetación dispersa	0.080	132695.21	51.68%
3	Camino pavimentado	0.020	22872.14	8.91%
4	Edificios bajos	0.070	41271.65	16.07%
5	Industrial	0.100	17617.13	6.86%

Figura 6. Topografía del dominio utilizado en el ejemplo 1, caracterizada por una malla de 21890 triángulos

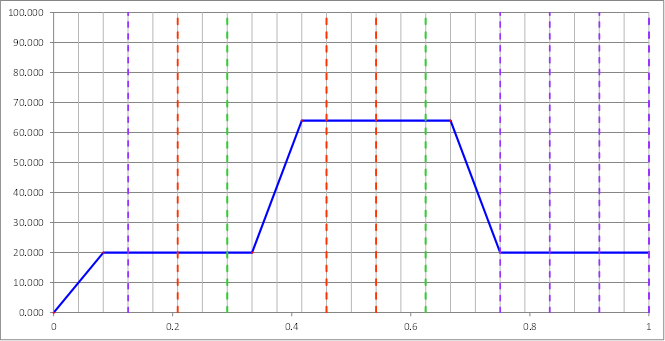
Se imponen condiciones de entrada de flujo de agua por el extremo sur del dominio, y condiciones de salida libre por el extremo norte. El flujo que se tiene a la entrada del dominio varía con el tiempo, originalmente desde 0 a un 20m³/s hasta alcanzar una solución estacionaria sin que se produzca desbordamiento. Alcanzadas las 10 horas de tiempo total en esas condiciones (36000 segundos), el flujo aumenta linealmente durante 2 horas hasta alcanzar un valor máximo de 64m³/s, el cual actúa durante 6 horas en total para entonces bajar linealmente durante otras dos horas hasta los 20m³/s originales, permaneciendo constante hasta el fin de la simulación, hasta completar un total de 86400 segundos (24 horas). La Figura 7 ilustra la curva de flujo a la entrada que se emplea como base, y de la cual se intentará reproducir el valor de ${\textstyle Q_{\max }=}$64m³/s.

Figura 7. Curva original de flujo a la entrada del cauce empleada en el ejemplo 1

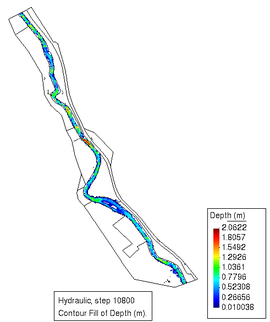
Con el fin de acotar el problema, ${\textstyle Q_{\max }}$ podrá tomar valores desde 22 hasta 88m³/s. Iber imprime resultados a intervalos regulares de tiempo en la simulación, para este ejemplo se fijó que se imprimieran a cada 3600 segundos (1 hora, líneas de división verticales en la figura), por lo que en total se tendrá un conjunto de 24 imágenes, cada una de ellas correspondería a una “fotografía” de satélite. A fin de calibrar el algoritmo, se realizaron pruebas con 10, 5 y 2 “imágenes”, correspondientes a los instantes de tiempo señalados por las líneas punteadas verticales de la figura. La Figura 8 ilustra los resultados del calado en la simulación en Iber para los instantes ${\textstyle t=10800}$s (paso 4, 3 horas) y ${\textstyle t=54000}$s (paso 16, 15 horas), y que corresponden a estados del cauce sin desbordar y de inundación máxima, respectivamente.

Figura 8. Alturas del agua (calado) obtenidas en la simulación del ejemplo 1, con la curva de flujo de la Figura 7

Para ambos instantes de tiempo, la Figura 9 muestra cómo podrían verse las imágenes satelitales binarias que se emplearían para la metodología propuesta.

Figura 9. Imágenes binarias correspondientes a las alturas del agua mostradas en los mismos instantes de la Figura 8

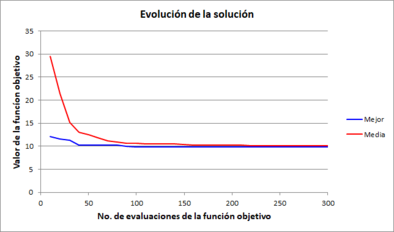
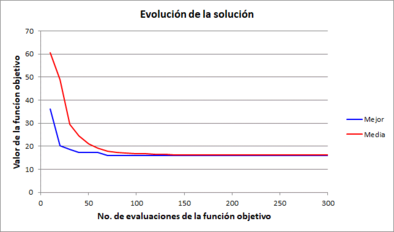
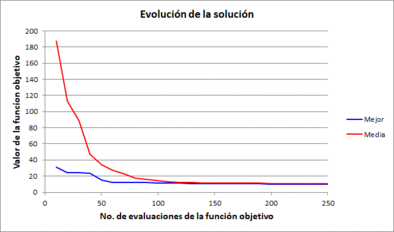
Para cada variante, se empleó una población de 10 individuos y 30 generaciones, por lo cual se realizan en total 300 evaluaciones de la función objetivo. La Tabla 2 muestra los resultados de la solución a la que se llegó en una de las tres pruebas, incluyendo además los valores calculados de la función objetivo para cada una de las soluciones, considerando 10, 5 y 2 pasos de tiempo o “fotos”. En la diagonal de dicha matriz se ha resaltado el valor de la función objetivo con la cual se resolvió el problema de optimización, los otros dos valores son de referencia. En la Figura 10 se muestran las gráficas de evolución de la función objetivo contra el número total de evaluaciones para cada una de las tres pruebas, mostrándose tanto el valor de la mejor solución como la media de la población. Dichas gráficas nos ayudan a visualizar si el algoritmo tiene o no un comportamiento convergente, lo cual es útil para determinar si el número de evaluaciones es adecuado, en función del tamaño de la población y el número de generaciones.

Tabla 2. Resumen del mejor resultado para cada una de las 3 series de pruebas planteadas con un número fijo de fotos utilizadas en el cálculo de la función objetivo

Prueba	10 fotos	5 fotos	2 fotos
Evaluaciones	300	300	300
Qmax	64.1775	64.1047	64.0827
Error	0.17747	0.10474	0.08267
Fobj 10 fotos	20.4157	20.4574	20.6432
Fobj 5 fotos	8.5599	9.0306	8.2047
Fobj 2 fotos	2.4889	2.1423	2.1062

Figura 10. Gráficas de evolución de la mejor solución obtenida en cada serie de prueba

En las gráficas observamos que en todos los casos se tiene un comportamiento convergente del valor promedio de la función objetivo de toda la población, por lo que el número de evaluaciones es adecuado. En estricto sentido, las únicas fases que producen variaciones en la solución (y que contribuyen significativamente a la función objetivo), son las salidas correspondientes a los pasos de tiempo (“fotos”) 12, 14, 16, 19, 21, 23 y 25, pues son los que se presentan durante y después de la crecida del cauce. Los pasos de tiempo anteriores no contribuyen a la función objetivo, pues en todos los casos se tiene el mismo valor de flujo ${\textstyle Q_{0}=20}$m³/s.

De los resultados de la Tabla 2, llama la atención que la prueba realizada con la función que utiliza menos “fotos” para calcular la función objetivo, es la que registró el resultado más cercano al objetivo esperado. Sin embargo, al comparar los valores calculados de las funciones objetivo para la solución a la que llegó el algoritmo en cada una de las pruebas realizadas, encontramos que no siempre el menor valor de los tres que figuran en el mismo renglón corresponde al de la función empleada para realizar la optimización. Esto nos indica la dificultad que implica resolver el problema de optimización, y de la dependencia que se tiene de los instantes de tiempo que se elijan para hacer la comparación con las imágenes de satélite.

3.2 Ejemplo 2: Huapinol – Río de la Sierra

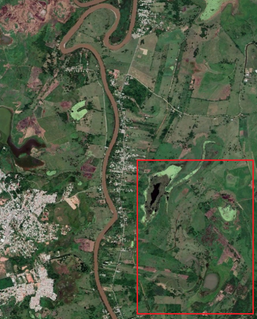
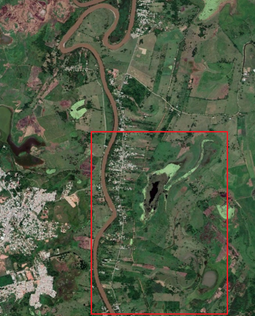
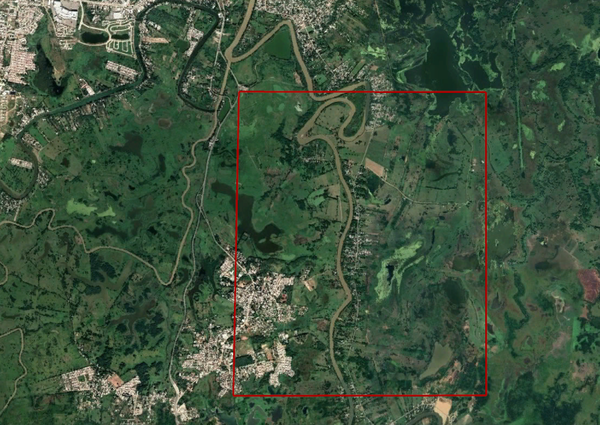
Se trata de una zona pantanosa ubicada al sur de la ciudad de Villahermosa, la capital del estado de Tabasco, en México. El lugar en estudio ha sufrido varias inundaciones al estar en una zona cercana a varios ríos caudalosos, con fuertes precipitaciones pluviales durante la temporada de lluvias. Se tienen datos DTM tomados mediante LIDAR, con resoluciones máximas entre 1.5 y 5 metros, proporcionadas por el INEGI de México [23], series e15d11a y e15d11b. A fin de simplificar el problema, se eligió una región más pequeña de manera que se tiene un solo cauce que la cruza, correspondiente a un tramo del Río de la Sierra poco antes de unirse con el Río Pichucalco y que aguas abajo se convierte en el Río Grijalva al juntarse con el río Carrizal en las inmediaciones de Villahermosa. El Río de La Sierra nace en el estado de Chiapas, y es producto de la unión de los caudales de los ríos Tacotalpa, Puyacatengo y Teapa antes de unirse con el Río Pichucalco. Su cauce no está regulado por ninguna presa, por lo cual su caudal sólo puede ser estimado a partir de métodos probabilísticos basados en mediciones directas en puntos de interés. Por encargo de la Comisión Nacional del Agua de México se han realizado diferentes estudios para estimar y/o medir el gasto promedio diario y las avenidas máximas de los 4 ramales que forman el río, con datos tomados desde 1964 hasta el 2009, presentándose valores con alta variación para la zona de interés [24,25]. En cuanto al gasto promedio diario, se midieron valores entre 140 y 285 m³/s, siendo estos datos la base del cálculo para determinar el flujo que produce una inundación en la zona [26]. Se empleó un valor de 254 m³/s como gasto inicial ${\textstyle Q_{0}}$, pues además de ser un valor promedio a los reportados en [26], al ser probado en el modelo de Iber para el dominio de interés no se produjo desbordamiento del cauce. La Figura 11 muestra una fotografía satelital amplia del área en estudio elegida, resaltando con un cuadro rojo el dominio que se empleó en este ejemplo.

Figura 11. Fotografía satelital del área empleada en el ejemplo 2 (Google Earth)

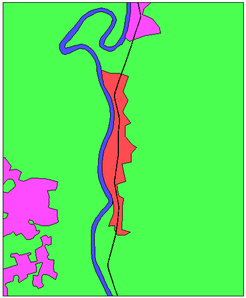
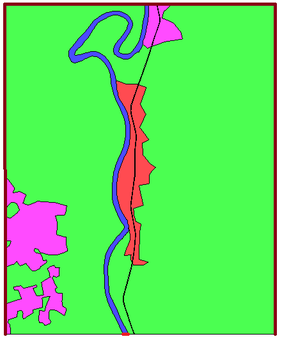
El área de estudio seleccionada está centrada en las coordenadas geográficas (17.9310°N 92.8932°O), abarcando un área de 20.5 kilómetros cuadrados (${\textstyle 5.03\times 4.07}$). El área se vectorizó directamente sobre la imagen de satélite en Google Earth con el fin de poder separar zonas con diferente uso de suelo, de manera que se puedan asignar los valores del coeficiente de rugosidad correspondiente. Con esta geometría se genera la malla de triángulos planos que es la base para caracterizar la topografía del terreno, modificando las alturas en la coordenada Z mediante los datos DTM-LIDAR disponibles para el área en estudio [23]. La Figura 12 ilustra los polígonos de uso de suelo identificados en el dominio de cálculo y los valores de rugosidad empleados en este ejemplo.

Coeficientes de rugosidad por tipo de suelo Río 0.025 Zona urbana con densidad baja 0.035 Zona urbana uso residencial 0.15 Camino pavimentado 0.02 Vegetación baja 0.08

Figura 12. Caracterización del uso de suelo del dominio empleado en este ejemplo

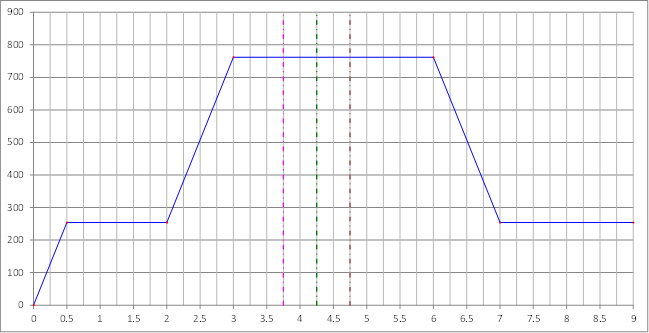
Para la simulación hidrodinámica, se consideró salida libre por 3 bordes, dejando cerrado el lado sur, y como condición de entrada se tiene únicamente un flujo variable por la parte sur del cauce. Con el fin de ejecutar el ejemplo sintético y así poder calibrar los parámetros del algoritmo de optimización, se escogió un valor de caudal pico de 762 m³/s, el cual presenta la variación sobre el tiempo que se ilustra en la siguiente figura. Entre los días 2 y 3 se tiene la crecida del caudal desde los 254 hasta los 762 m³/s, manteniéndose constante por un periodo de 3 días para entonces bajar nuevamente a 254 durante un día, permaneciendo constante de ahí en adelante (Figura 13). El valor máximo de 762 m³/s se fijó arbitrariamente, dado que produce un desbordamiento del río al emplearlo en la simulación con Iber.

Figura 13. Curva de flujo impuesta a la entrada del cauce. Las líneas verticales punteadas ilustran los instantes de tiempo utilizados para calcular la función objetivo en el problema de optimización

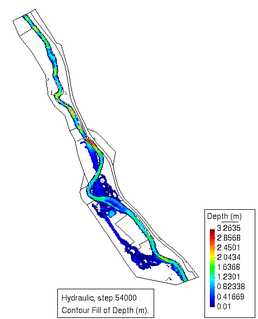
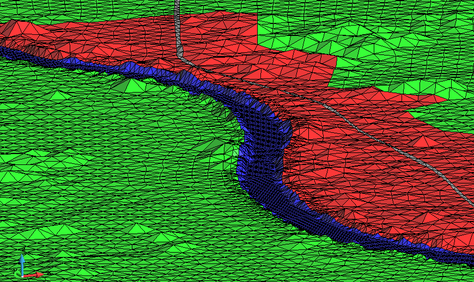
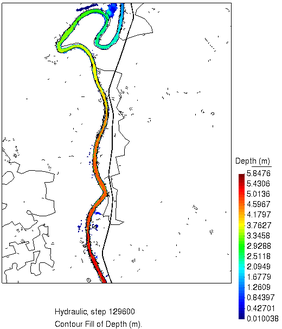
Se empleó una malla de 68867 triángulos y 34775 nodos, teniendo una resolución máxima de 10 metros en la zona del río y aledañas, y de 30 metros en el resto del dominio. Se simuló un tiempo de 604800 segundos (168 horas, o 7 días), imprimiendo resultados a cada 21600 segundos (6 horas), por lo que en total se tienen 37 pasos de tiempo impresos (cada paso de tiempo impreso corresponde a una “foto” distinta). Cada simulación de este caso en Iber consume un tiempo desde 300 hasta 850 segundos en una computadora equipada con una GPU Nvidia Titan RTX, esto constituye una dificultad importante ya que se requiere realizar muchas ejecuciones para completar cada una de las pruebas. En la Figura 14 se muestran dos imágenes de la malla de cálculo ajustada con las alturas de la topografía con los modelos DTM, así como las condiciones de frontera en el dominio descritas anteriormente. La Figura 15 muestra resultados del calado en los instantes ${\textstyle t=129600}$ y ${\textstyle t=324000}$ (pasos 6 y 15, respectivamente).

Figura 14. Arriba: malla de cálculo y condiciones de frontera impuestas en el dominio utilizado para el ejemplo 2. Abajo: detalle de la topografía del terreno caracterizada por la malla. Se aprecia claramente el cauce del río

Figura 15. Resultados del calado para los pasos t=129600 y t=324000, antes y después del desbordamiento del río

Se ejecutaron 3 series de 10 pruebas del algoritmo de optimización, cada una de las pruebas se realizó con una población de 10 individuos y 25 generaciones, teniéndose 250 evaluaciones de la función objetivo en total. La única diferencia entre cada una de las series es que se empleó un instante diferente de tiempo para calcular la función objetivo, correspondientes a los pasos 16, 18 y 20 (${\textstyle t=324000}$, ${\textstyle t=367200}$ y ${\textstyle y=410400}$), las cuales se presentan dentro de la meseta del gasto máximo de entrada por la parte sur del cauce, y que corresponden a las 3 líneas punteadas verticales que aparecen en la gráfica de la curva de gasto. Las Tablas 3, 4 y 5 muestran los resultados que se obtuvieron para cada una de las series de pruebas.

Tabla 3. Resultados de las pruebas de optimización empleando el paso 16 (t=324000) para calcular la función objetivo

Prueba	1	2	3	4	5	6	7	8	9	10
Evaluaciones	250	250	250	250	250	250	250	250	250	250
Qmax	762.491	762.295	762.177	761.828	762.428	762.114	761.827	762.114	762.412	761.970
Error	0.49053	0.29470	0.17725	0.17238	0.42789	0.11428	0.17309	0.11428	0.41222	0.03041
No. Gen. Solución	25	19	12	22	18	24	21	24	25	8
#Foto (paso)	Valor de función objetivo de la solución, utilizando diferente foto como base de cálculo
16	8.4283	8.9810	8.2282	8.2974	8.9179	8.3551	8.6378	8.3551	7.4605	8.5571
17	13.4301	13.5030	12.9287	12.4470	12.2418	14.2211	12.8875	14.2211	13.6793	11.4013
18	11.0241	11.3736	14.3726	11.7498	13.8055	12.7832	12.9785	12.7832	12.5463	10.8503
19	13.3236	11.3497	16.2130	13.7998	11.7069	11.7800	12.4427	11.7800	13.0092	11.8211
20	14.4670	12.5118	14.9764	13.3436	14.4588	12.2802	13.9383	12.2802	13.7974	12.7531
21	14.6492	14.4059	13.2867	13.7962	12.8499	11.5748	13.8435	11.5748	14.7238	12.5173
22	14.2310	14.2838	16.3861	13.7999	12.9236	14.2268	11.9941	14.2268	17.0002	8.8581
23	14.0047	11.9707	13.6995	14.0919	13.9769	14.7207	12.2045	14.7207	13.6786	13.4705
24	14.2052	12.1309	13.8275	12.6589	12.7349	10.1158	11.3414	10.1158	13.2387	10.7311

En cada una de las tablas de resultados, se resalta en fondo amarillo la columna donde se obtuvo el menor valor de la función objetivo, mientras en fondo verde se resalta la columna donde se obtuvo el valor más cercano a la solución esperada (${\textstyle Q_{\max }=762}$ m³/s). Se muestran también los valores calculados de la función objetivo para cada uno de los pasos de tiempo correspondientes entre los pasos 16 a 24, todos dentro de la meseta de la curva de gasto de entrada, resaltando en magenta el renglón correspondiente al paso de tiempo que se empleó para hacer la optimización en esa prueba.

Tabla 4. Resultados de las pruebas de optimización empleando el paso 18 (t=367200) para calcular la función objetivo

Prueba	1	2	3	4	5	6	7	8	9	10
Evaluaciones	250	250	250	250	250	250	250	250	250	250
Qmax	762.154	761.810	761.734	762.126	761.615	761.415	762.005	761.587	761.986	761.449
Error	0.15375	0.19032	0.26557	0.12573	0.38485	0.58537	0.00488	0.41335	0.01373	0.55086
No. Gen. Solución	20	18	24	25	22	24	20	22	22	24
No. Foto	Valor de función objetivo de la solución, utilizando diferente foto como base de cálculo
16	10.2026	11.1108	10.8708	10.2653	11.0255	11.6884	11.0550	10.7647	12.7853	11.7360
17	12.9252	13.1759	13.2934	13.4520	11.7546	12.6932	13.4423	13.8834	11.6246	12.1299
18	8.7364	9.9706	10.0185	9.6130	10.1219	10.0082	9.6614	9.6693	9.9816	10.1468
19	11.6919	12.9679	14.0714	11.8451	12.2805	13.0008	11.6969	12.5372	13.3116	11.5406
20	12.2828	15.6826	14.0380	11.9118	14.3364	12.8030	12.2952	13.3515	13.4360	13.6333
21	14.7137	12.2402	12.3669	13.4901	13.3255	12.6631	11.8650	12.2655	11.8504	14.6627
22	14.1357	14.7901	12.9397	14.9181	13.2085	12.8548	13.4843	10.0107	11.3651	13.7344
23	13.7265	12.6552	12.4589	13.0699	13.7266	11.7144	13.3184	9.9195	13.2987	13.9291
24	12.6844	13.6156	13.5552	12.4598	12.7687	12.3204	15.1399	12.8317	10.4143	10.9898

Tabla 5. Resultados de las pruebas de optimización empleando el paso 20 (${\textstyle t=410400}$) para calcular la función objetivo

Prueba	1	2	3	4	5	6	7	8	9	10
Evaluaciones	250	250	250	250	250	250	250	250	250	250
Qmax	761.903	761.607	761.823	761.477	761.848	761.751	762.494	761.926	761.422	761.819
Error	0.09723	0.39329	0.17718	0.52256	0.15185	0.24880	0.49443	0.07422	0.57753	0.18085
No. Gen. Solución	17	15	23	16	23	20	17	19	15	21
No. Foto	Valor de función objetivo de la solución, utilizando diferente foto como base de cálculo
16	11.9820	14.6696	10.7420	12.3436	11.0066	11.8373	10.5647	13.0730	11.1639	10.7015
17	13.0743	14.9033	11.2619	13.8467	11.7371	12.3081	11.4560	12.9999	12.6554	12.2618
18	11.9918	10.2767	12.2379	13.8788	13.9547	11.8759	12.6624	11.1198	11.2092	11.3237
19	11.4203	14.9129	11.8457	9.9273	13.0706	10.7437	13.6647	12.4960	11.0458	11.7241
20	10.5494	10.7647	11.4171	11.0811	11.1339	10.3342	10.6219	10.6912	10.6040	10.8142
21	13.8403	12.1874	13.1405	15.6681	13.6125	14.2000	13.5549	13.3257	14.4558	14.4466
22	12.2301	11.6937	14.0293	13.5066	11.6264	11.8969	14.1471	13.1064	14.2646	13.1525
23	12.7273	12.3415	12.5343	12.2953	12.3374	13.3306	16.7932	12.3525	13.6143	13.9673
24	12.0774	11.6518	9.7918	13.0276	11.9221	11.2964	11.9934	13.3834	15.6278	11.8388

En todas las tablas se observa que la prueba con el resultado más cercano al esperado no coincide con la que obtuvo menor valor de la función objetivo, lo cual indica la dificultad del problema de optimización. Sin embargo, el error respecto al valor objetivo es relativamente pequeño. La Tabla 6 resume los resultados de cada una de las pruebas. En ella se observa que la desviación estándar máxima es de 0.298 m³/s, y que corresponde a un error menor al 4% respecto al valor del gasto objetivo.

Tabla 6. Resumen de resultados y estadísticas de las pruebas realizadas para el ejemplo 2

Indicador	Foto 16	Foto 18	Foto 20
Mejor	761.970	762.005	761.926
Peor	762.491	761.415	761.477
Media	762.166	761.788	761.807
Varianza	0.052	0.066	0.080
σ	0.241	0.271	0.298

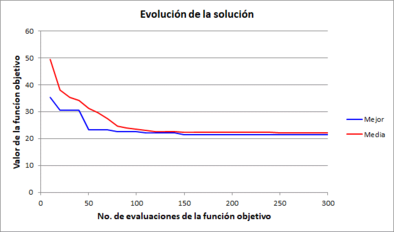
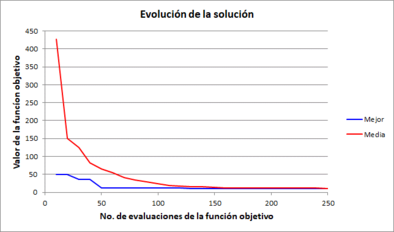
La Figura 16 muestra las gráficas de evolución de la función objetivo en los resultados correspondientes tanto a la mejor solución como a la peor solución que se obtuvieron en el conjunto completo de 30 pruebas realizadas. En todas ellas se observa un comportamiento convergente, por lo cual se tiene que tanto el tamaño de la población como el número de generaciones fueron adecuados para este ejercicio.

Figura 16. Gráficas de evolución de la mejor y peor solución obtenidas en este ejemplo

4. Aplicación a un caso real: Huapinol – Río de la Sierra (noviembre 2020)

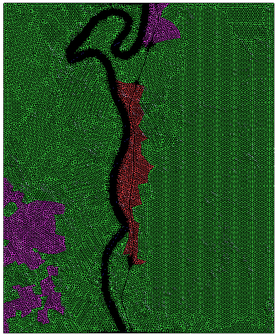
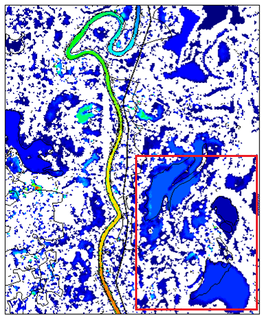
En este ejemplo se empleó el mismo dominio del caso anterior, pero ahora con una imagen real tomada de un evento de inundación catastrófico ocurrido en noviembre del 2020 en esa zona [27]. La Figura 17 muestra la imagen binaria empleada para correr el algoritmo, junto con una fotografía en color del evento del cual proviene. La imagen fue capturada por el satélite Sentinel-1 de la Agencia Espacial Europea, y se le aplicó el proceso descrito en [28] para obtener la imagen binaria.

(a) (b)

Figura 17. (a) Imagen binaria de satélite del evento de inundación ocurrido en la zona de estudio en noviembre del 2020. (b) Fotografía satelital de las mismas fechas (Google Earth)

Ya que en este caso se intenta reproducir un evento de inundación real, es muy importante el estado inicial de la zona al momento en que se considera la crecida del río. En consecuencia, fue indispensable revisar imágenes del mismo tipo, de la misma zona y tomadas unos días antes de que ocurriera el evento de inundación, lo cual se muestra en la Figura 18. En dichas imágenes se aprecian algunas lagunas que es necesario capturar en el estado inicial del dominio antes de correr el algoritmo de optimización. Como el origen preciso del agua presente en dichas lagunas es incierto, se optó por imponer condiciones iniciales de lluvia durante un tiempo fijo en la zona además del caudal normal en el río, tratando de obtener un estado inicial parecido al que se observa en las imágenes reales. En este caso particular, se utilizó una precipitación uniforme de 25mm durante un periodo de 24 horas (correspondiente a una lluvia fuerte), y que fue una situación no muy lejana a la que se presentó en esa zona en los días previos al evento de inundación [27].

(a) (b)

Figura 18. (a) Imagen binaria de satélite en la misma zona, dos semanas antes del evento de inundación. (b) Fotografía satelital un año antes del evento de inundación (Google Earth)

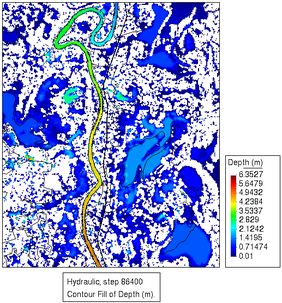
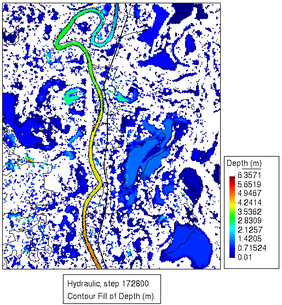
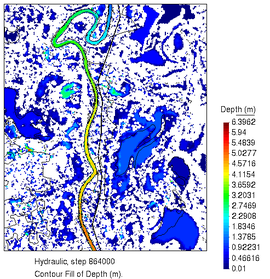
En la Figura 19 se muestran las alturas del agua resultantes al final de la lluvia inicial, y justo antes de que empiece la crecida del río, correspondientes a los pasos de tiempo t=86400 y t=172800. Comparando estas imágenes con las mostrados en la figura 18, observamos que si bien se obtienen con claridad las lagunas que salen en la imagen binaria, hay bastantes discrepancias respecto a las que se observan tanto en la imagen en color como en las resultantes de la simulación, siendo más extensas las zonas de las lagunas tanto en la imagen satelital en color como en la simulación respecto a la imagen binaria de satélite.

(a) (b)

Figura 19. Alturas del agua para los instantes ${\textstyle t=86400}$ (a) y ${\textstyle t=172800}$ (b), correspondientes a las condiciones iniciales del problema (fin de la lluvia inicial, y antes del inicio de la crecida del flujo en el cauce)

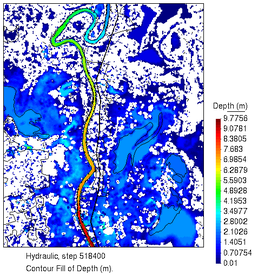
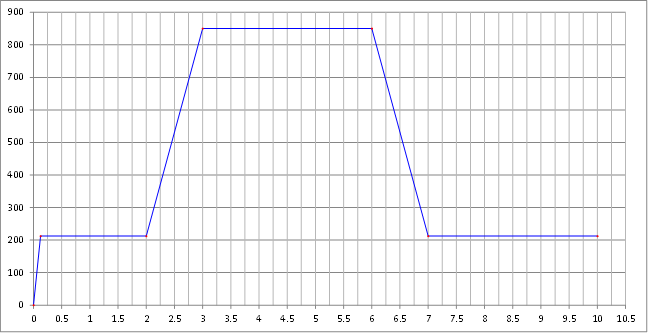
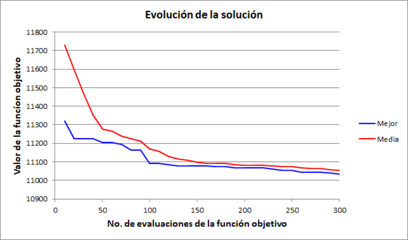
Con estas limitantes se ejecutó el algoritmo de optimización, de manera similar al ejemplo sintético mostrado en la sección anterior. Para esto se imprimieron resultados a cada 21600 segundos (6 horas), y se corrió la simulación durante un periodo de tiempo correspondiente a 6 días a fin de ahorrar tiempo de cálculo. Se eligió el instante t=518400 para hacer la comparación con la imagen satelital, que corresponde al fin de la meseta de la curva de gasto máximo mostrada en la Figura 20. Se empleó una población de 10 individuos y 30 generaciones en total. La Figura 21 muestra la gráfica de evolución de la función objetivo, tanto del mejor individuo como de la media de la población, observándose un comportamiento convergente.

Figura 20. Curva de gasto paramétrica utilizada en el ejemplo 3

Figura 21. Gráfica de evolución de la solución obtenida en el ejemplo 3

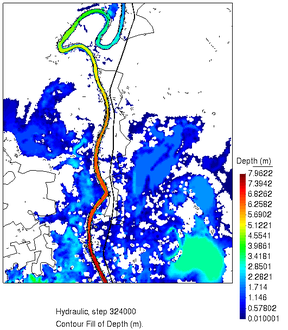
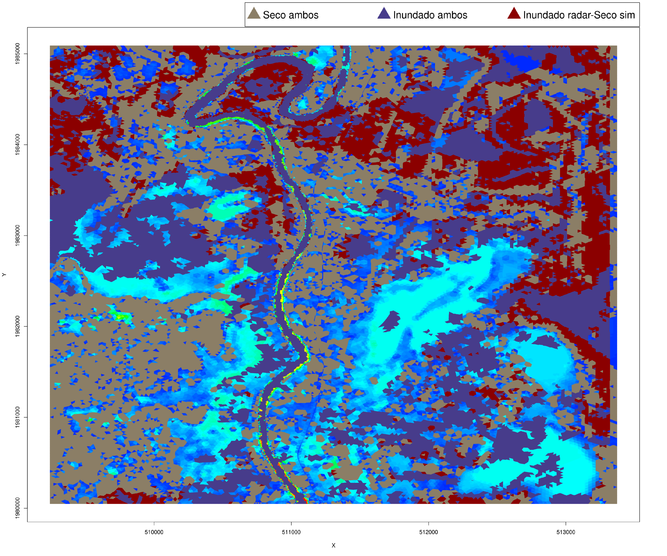
Se obtuvo un gasto máximo de 2900 m³/s, con un tiempo de cómputo total de 40 horas empleando en paralelo dos computadoras equipadas con GPU Nvidia Titan RTX, y que cada simulación tardaba en ejecutarse desde 400 hasta 850 segundos. La Figura 22 muestra los resultados del calado para el instante de comparación (${\textstyle t=518400}$), y para el instante ${\textstyle t=86400}$, tres días después del fin de la crecida del río de acuerdo con la curva de gasto de la figura 20. Comparando la imagen de la izquierda en la Figura 22 con la imagen del satélite de la Figura 17, podemos notar que no hay una correspondencia total entre las zonas inundadas que aparecen en una y en otra. Esto queda más claro en la Figura 23, en la cual aparecen ambos resultados superpuestos (de la simulación y de la imagen). Se observa en dicha figura que la inundación en la simulación tiende a presentarse más en la zona sur de la región en estudio, mientras que en la imagen del satélite se concentran más al norte. Aunque esto puede parecer desalentador en un inicio, es necesario realizar un análisis más minucioso de la zona y del evento de inundación real para explicar lo que ocurrió. La Figura 24 muestra un acercamiento de la imagen del satélite justo en la zona por la cual se produjo el desbordamiento del río, y que es donde el cauce forma un meandro en el norte del dominio en estudio.

(a) (b)

Figura 22. Alturas del agua en los instantes ${\textstyle t=518400}$ (a) y ${\textstyle t=86400}$ (b), para la mejor solución encontrada

Figura 23. Imagen de resultados superpuestos para el instante ${\textstyle t=518400}$

Figura 24. Ampliación de la fotografía satelital en la zona donde se produjo el desbordamiento real del río (Google Earth)

En dicha imagen podemos observar que el río se desborda por una zona muy diferente a la que se produce en la simulación, y a partir de ahí el flujo de agua por fuera del cauce ya es muy distinto. Esto significa que la topografía del terreno en el momento de la inundación real es diferente a la empleada en el modelo de cálculo. Si bien los modelos DTM utilizados en la zona corresponden al año en que se produjo el evento de inundación, en la descripción de los archivos se indica que las alturas del terreno no están exentas de errores debidos a diversos factores que afectan la precisión y la resolución de las alturas del terreno, como la densidad de la vegetación y la nubosidad presente al momento de la captura de los datos. Además de ello, dado que la velocidad de la corriente aumenta con el flujo, los bordes del cauce son más propensos a erosionarse y eventualmente producirse una ruptura. Esta condición es mucho más difícil de simular pues implica más variables, y al modificarse la topografía es necesario modificar la malla de cálculo en tiempo de ejecución.

En la Figura 25 se muestra una fotografía de la misma zona en estudio, pero que data del año 2003. Abajo a la derecha de dicha imagen se aprecia un cuerpo de agua con una forma muy similar a uno que aparece en los resultados de la simulación antes y después de la crecida del río (Figuras 19 y 22). Dicho cuerpo de agua tiene una forma muy distinta en las fotografías del año 2020 (Figuras 17 y 18), lo que nos lleva a pensar que la información topográfica utilizada en la simulación no se corresponde del todo con la topografía real del terreno al momento de la inundación que se intentó reproducir. En la Figura 26 se hace un énfasis en ello, mostrando juntas las imágenes mencionadas.

Figura 25. Fotografía satelital en la zona en marzo del 2003 (Google Earth

(a) Septiembre 2019 (Google Earth) (b) Noviembre 2020 (Google Earth) (c) Resultados simulación (Figura 19(b)) (d) Marzo 2003 (Google Earth)

Figura 26. Comparación entre imágenes de la misma zona en diferentes fechas con resultados de la simulación

Hay más factores que influyen en los resultados. En la imagen binaria de la Figura 18, el cauce del río aparece cortado en algunas zonas, lo cual no es posible ya que el Río de la Sierra tiene un caudal de agua permanente (Figura 27). Esto significa que el proceso de detección de las zonas inundadas por medio de la adquisición y procesamiento de imágenes de satélite y radar no está exento de fallas.

(a) (b) (c) (bd)

Figura 27. En las imágenes binarias del satélite algunos cuerpos de agua se ven más pequeños en comparación con las imágenes en color de Google Earth (ver recuadros resaltados). En la imagen antes de la inundación el cauce del río incluso parece “cortado”

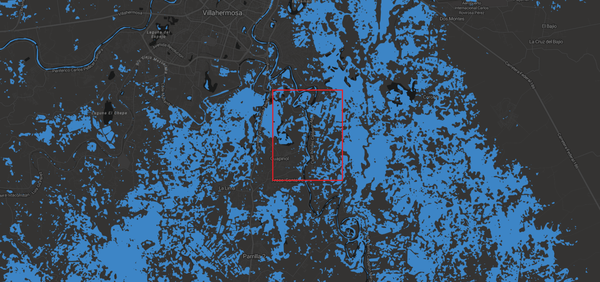
Además de todo lo anterior, la zona elegida para el estudio es complicada por su topografía tan plana y la confluencia de varios ríos caudalosos cerca de ella, por lo que se puede presentar entrada de flujo por zonas no consideradas en el modelo de cálculo. En esta liga de Internet figura una visualización de los eventos de inundación de noviembre del 2020 cercanos a la ciudad de Villahermosa [28], y que corresponden al evento de donde se extrajeron las imágenes binarias empleadas en este ejemplo. La Figura 28 muestra una panorámica centrada en la zona que se utilizó en el modelo de cálculo. Se aprecia en dicha imagen, que la inundación abarcó una zona mucho más amplia que la considerada, lo que dificulta la asignación de condiciones de entradas y salidas de flujo por las fronteras de dominio de cálculo y que influyen por completo en los resultados de la simulación.

Figura 28. Vista general del evento de inundación de noviembre del 2020 cerca del área de estudio de este segundo ejemplo [28]

5. Conclusiones

Presentamos una metodología para la estimación del área inundada, por medio de simulación y optimización numérica, que reproduce aproximadamente la capturada por el Sentinel-1. La simulación permite determinar con mayor precisión tanto el área real inundada como su profundidad. Como se muestra en los resultados, existen cuerpos de agua permanentes que son evidentes en las imágenes de color real, pero que no son capturados de manera precisa por la imagen de radar satelital, estos pueden ser identificados en la simulación. Adicionalmente, ninguna imagen de radar provee datos sobre la altura del agua, mientras que la simulación permite tener un estimador de esta altura e incluso del volumen de agua que inunda la región.

El método propuesto no permite obtener información fiable de la dinámica de la inundación; sin embargo si provee la extensión y altura necesarias para evaluar daños y riesgos, además de que es posible  generar escenarios cercanos, mayores y menores, en extensión, altura y volumen de agua, esta información cuantitativa es relevante para la previsión de escenarios futuros, que se esperan cada vez sean más frecuentes y extremos debido al cambio climático.

De la misma manera, encontrar condiciones de simulación que reproducen aproximadamente la realidad podría ser de utilidad para determinar zonas riesgosas para el desarrollo habitacional o industrial, y usarse para evaluar la idoneidad del terreno antes de que se realicen los cambios de uso de suelo.

Finalmente,  el trabajo futuro es determinar una mayor cantidad de parámetros que sirvan para aproximar la dinámica de la inundación y no sólo la extensión en un instante de tiempo. Es decir, tomar varías imágenes de referencia, y funciones de flujo más complejas y, posiblemente, parámetros de rugosidad y condiciones de frontera. Estas simulaciones dinámicas podrían ser de utilidad para determinar la extensión y altura del agua en la zona inundada en tiempo real, y pronosticar posibles escenarios inmediatos usando pronósticos del tiempo climatológico.

Agradecimientos

Los autores agradecen al CIMNE por la licencia de uso de GiD, entorno gráfico en el cual funciona Iber y que se utilizó para preparar los modelos empleados en este artículo.

El primer autor agradece al CONAHCyT de México por el apoyo económico recibido mediante una beca para estancia posdoctoral, sin la cual no hubiese sido posible el desarrollo de este trabajo. Así mismo, agradece el apoyo brindado por el CIMAT por el acceso a sus clusters de supercómputo para ejecutar los ejemplos mostrados.

Referencias

[1] CEPAL. Manual para la evaluación de desastres, 2014.

[2] Wen A. A comprehensive methodology for evaluating the economic impacts of floods: An application to Canada, Mexico, and the United States. Sustainability, 14(21), 14139, 2022.

[3] CRED. 2022 Disasters in numbers. Reliefweb, 2023.

[4] CENAPRED. Impacto socioeconómico de los principales desastres ocurridos en México. Resumen Ejecutivo 2022, 2023.

[5] IFRC. World disasters report 2022, 2023. [En línea]. Available: https://www.ifrc.org/sites/default/files/2023-01/20230130_2022_WDR_DataAnnex.pdf. [Último acceso: 22 11 2023].

[6] Mudashiru R.B. et al. Flood hazard mapping methods: A review. Journal of Hydrology, 603(Part A), 126846, 2021.

[7] Bellos V. Ways for flood hazard mapping in urbanised environments: A short literature review. Water Utility Journal, 4:25-31, 2012.

[8] Devia G.K., Ganasri B.P., Dwarakish G.S. A review on hydrological models. Aquatic Procedia, 4:1001-1007, 2015.

[9] Zang S. et al. Improving the flood prediction capability of the Xin’anjiang model by formulating a new physics-based routing framework and a key routing parameter estimation method. Journal of Hydrology, 603(Part A), 126867, 2021.

[10] Gutiérrez J.V. et al. Modelación hidráulica en Iber para prevención de inundaciones en la cuenca Tesechoacán. Revista Mexicana de Ciencias Forestales, 13(71), 2022.

[11] David A., Schmalz B. Flood hazard analysis in small catchments: Comparison of hydrological and hydrodynamic approaches by the use of direct rainfall. Journal of Flood Risk Management, Special Issue: Computational Advances and Innovations in Flood Risk Mapping, 13(4), e12639, 2020.

[12] Shrestha S., Lohpaisankrit W. Flood hazard assessment under climate change scenarios in the Yang River Basin, Thailand. International Journal of Sustainable Built Environment, 6(2):285-298, 2017.

[13] Wang Y., Yang X. A coupled hydrologic–hydraulic model (XAJ–HiPIMS) for flood simulation. Water, 12(5), 1288, 2020.

[14] Zhang X., et al. Evaluation of global optimization algorithms for parameter calibration of a computationally intensive hydrologic model. Hydrol. Process, 23(3):430-441, 2009.

[15] Chen Y., et al. Improving flood forecasting capability of physically based distributed hydrological models by parameter optimization. Hydrol. Earth Syst. Sci. Dissc., 20(1):375–392, 2016.

[16] Mason D.C., et al. Detection of flooded urban areas in high resolution Synthetic Aperture Radar images using double scattering. International Journal of Applied Earth Observation and Geoinformation, 28:150-159, 2014.

[17] Anees M.T., et al. Numerical modeling techniques for flood analysis. Journal of African Earth Sciences, 124:478-486, 2016.

[18] Kinnmark I. Equation formulation. The Shallow Water Wave Equations: Formulation, Analysis and Application, 15:12-26, 1986.

[19] Bladé E. Iber: Herramienta de simulación numérica del flujo en ríos. Rev. int. métodos numér. cálc. diseño ing., 30(1):1-10, 2014.

[20] Cea B., Bladé E. A simple and efficient unstructured finite volume scheme for solving the shallow water equations in overland flow applications. Water Resources Research, 51(7):5464-5486, 2015.

[21] Storn R., Price K. Differential evolution - A simple and efficient heuristic for global optimization over continous spaces. Journal of Global Optimizations, 11:341–359, 1997.

[22] IberAula, [En línea]. Available: https://www.iberaula.es/vnews/0/2702/egu-teaching-package. [Último acceso: 21 11 2023].

[23] INEGI. Relieve continental. [En línea]. Available: https://www.inegi.org.mx/temas/relieve/continental/#descargas. [Último acceso: 23 11 2023].

[24] CONAGUA. Plan hídrico integral de Tabasco (PHIT) - Primera Etapa 2008, Cap. 4, 2009.

[25] CONAGUA. Plan hídrico integral de Tabasco (PHIT) - Segunda Etapa 2009. Cap. 4.A, 2010.

[26] Khalidou M. Modelación hidrológica de la cuenca del río La Sierra, 2009. [En línea]. Available: https://imta.gob.mx/potamologia/images/docs/evento/KhalidouMBa.pdf.

[27] Global Disaster Preparedness Center. Inundaciones de 2020 en Tabasco, 2022. [En línea]. Available: https://preparecenter.org/resource/inundaciones-de-2020-en-tabasco-aprender-del-pasado-para-preparar-el-futuro/. [Último acceso: 21 11 2023].

[28] CentroGeo, MCA Tabasco 2020. [En línea]. Available: https://geoint.centrogeo.edu.mx/inundaciones/. [Último acceso: 23 11 2023].