Resumen
En este trabajo se presenta el análisis de la aplicación del modelo de un algoritmo de punto de cambio (Change Point Model, CPM), basado en tests no paramétricos, para la detección de estructuras turbulentas en un flujo de aire. Se busca detectar los vórtices generados en la estela de un perfil aerodinámico dotado de un dispositivo de control pasivo de flujo (mini flap de Gurney) ubicado en el borde de fuga. De la muestra de datos obtenida se analiza la aplicación de modelos CPM, con el fin de determinar los posibles cambios de la fluctuación de la velocidad sensada, comparando los resultados con análisis tradicionales.
El objetivo principal del estudio es el de detectar las frecuencias características de las estructuras turbulentas inmersas en el campo del flujo.
De los resultados obtenidos se desprende que el modelo CPM basado en el test de Cramer-von Mises (CPM-CvM) presenta una buena concordancia con las detecciones esperadas (diferencias menores al 9,5%), mostrando ser una herramienta alternativa para el análisis de estos tipos de flujo en tiempo real.
Este trabajo muestra, finalmente, una nueva aplicación para CPM en la detección de cambios en señales aleatorias dependientes del tiempo que tienen una distribución, a priori, desconocida.
Abstract
The present work shows the application of a change point model (CPM) algorithm, based on non-parametric tests, to turbulent structures detection in an airflow. It seeks to detect the vortices generated in the wake of an airfoil, equipped with a passive flow control device (Gurney mini flap) in its trailing edge. By applying CPM models to the sample data, this paper seeks to determine the possible changes to the velocity fluctuations and compare the models effectiveness to traditional methods.
The main objective of this study is to detect the characteristic frequencies of the turbulent structures immersed in the airflow.
The results show that the CPM methodology, based on the Cramer- von Mises (CPM-CvM) test, produces results that coincide with values predicted by traditional methods (less than 9.5% of mismatch), validating its use as a real time alternative tool for the analysis of these types of flows.
Finally, this work shows a new application of CPM for detecting changes in a time-dependent random signal, which has an a priori unknown distribution.
Palabras clave
Turbulencia;Escala temporal;Frecuencia característica;Algoritmo de detección;Punto de cambio
Keywords
Turbulence;Temporal scale;Characteristic frequency;Detection algorithm;Change point
1. Introducción
Se denomina flujo turbulento en un fluido a aquel en el que las variables: velocidad, densidad, presión, temperatura, etc. se comportan en forma aleatoria en cada punto del fluido y en cada instante de tiempo [1].
El estudio de los flujos turbulentos es de gran importancia en muchas aplicaciones tecnológicas: Ingenierías Aeronáutica, Naval, Mecánica y Estructural, fenómenos de flujo interno, transferencia, combustión, etc.
Existen características particulares de la estructura turbulenta de un flujo que cambian la forma en que se mueve el fluido en el entorno de los objetos generando fuerzas de carácter fluidodinámico sobre ellos. Dichos cambios pueden ser pérdidas de cantidad de movimiento en el flujo, generadas por la aparición de remolinos y disipación viscosa, siendo estos efectos comúnmente observados en aplicaciones aeronáuticas, navales, flujos internos, etc. [1].
Si se pretende mejorar u optimizar un problema de ingeniería que involucre turbulencia será preciso entender y controlar el conjunto de eventos o estructuras turbulentas que lo gobiernan [2].
Un análisis meticuloso de un flujo turbulento global permitiría detectar la existencia de estructuras turbulentas particulares en el mismo, normalmente ocultas.
Desde mediados de 1960 el análisis de la turbulencia fue revolucionado gracias al empleo de sofisticadas metodologías de análisis de datos experimentales. Existe una vasta bibliografía sobre metodologías para el análisis de mediciones de flujos en régimen turbulento, entre las más recientes, podemos mencionar las llamadas funciones ortogonales propias (POD-Proper Orthogonal Decomposition) [3], los métodos de análisis multiresolución [4], el uso del ARMA (Auto Regressive Moving Average) [5], etc. Todas estas metodologías precisan de un importante poder computacional para su implementación, lo cual las hace importantes a la hora de realizar análisis de turbulencia en tiempo no real, no así en las condiciones del ensayo experimental.
A partir de la aplicación de dichas metodologías se comprendió que en muchos casos la turbulencia, que contenía una importante porción de la energía cinética, estaba organizada en estructuras diferentes y particulares. Dicha organización ocurre, por ejemplo, en remolinos de forma y tamaño muy diversos.
El enfoque moderno de la turbulencia se concentra en el estudio meticuloso de las diversas estructuras turbulentas, mediante el análisis de la forma en que se desenvuelve el flujo en el entorno de los objetos. La determinación de dicho comportamiento permite inferir los efectos sobre un objeto en movimiento. Es de interés la detección de las formas particulares del movimiento del fluido detectando, por ejemplo, la aparición de eventos turbulentos específicos (remolinos) que se generan al desprenderse el flujo del objeto. Dichos remolinos nos permiten inferir efectos importantes referidos a las fuerzas actuantes sobre dicho objeto, dichos remolinos, habitualmente, están inmersos en el movimiento del flujo turbulento [1].
Cuando las mediciones, en particular en experimentos en túnel de viento, son realizadas con equipos de medición puntual de la velocidad (Anemómetros de hilo caliente/Hot Wire Anemometry-HWA [6] o basados en técnicas láser doppler, Laser Doppler Anemometry-LDA [7]) resulta interesante la posibilidad de realizar un procesamiento de la señal aleatoria sensada, con el fin de lograr la detección de este tipo de eventos turbulentos y caracterizar sus frecuencias de aparición e intermitencia. A partir de ello, se trata de analizar y comprender la forma en que un objeto procesa el fluido en el que se mueve, y de esta manera permite predecir el comportamiento del objeto en movimiento.
Nuestro objetivo, entonces, es aplicar técnicas estadísticas de detección de cambios en una señal sensada en el tiempo [8], en particular para las fluctuaciones de la velocidad en un flujo turbulento. Se consideran dos objetivos principales, por un lado, el empleo de estas metodologías con el fin de analizar mediciones realizadas con anemometría de hilo caliente, incorporándolas como una herramienta más que nos permita determinar la aparición de eventos particulares en un campo fluidodinámico, con el fin de realizar su análisis y estudio. En segunda instancia, nos parece importante su posibilidad de aplicación como una herramienta en el software de adquisición de datos con el objetivo final de optimizar las mediciones que se realizan, aprovechando las posibilidades de detección de algún cambio particular en la señal en forma rápida.
2. Metodologías de punto de cambio
El problema de la detección de un cambio ha sido una vasta área de investigación desde la década de 1950 [9]; [10] ; [11]. Debido a que el problema tiene una naturaleza muy general, la literatura es muy diversa y se desarrolla en campos muy diversos. En particular, muchos de los métodos tienen su origen en la comunidad del control de calidad, donde el objetivo principal es monitorear los resultados de un proceso de manufactura industrial, buscando la detección de fallas en el mismo lo más tempranamente posible [8]. Sin embargo, existen muchas otras aplicaciones donde las técnicas de detección de cambios resultan importantes, por ejemplo, en el estudio de secuencias genéticas, estudios climatológicos, aplicaciones bioinformáticas, intrusión en redes de computadoras, evoluciones de mercados financieros, etc. De todos estos temas existe mucha bibliografía que hace referencia a la temática, pero su aplicación al análisis de señales anemométricas no es conocido. Para nuestro caso, la señal sensada corresponde a los valores fluctuantes de la velocidad del aire en un flujo turbulento.
En los últimos años [12] se ha comenzado a trabajar exhaustivamente en la temática de detección de cambios en un proceso y se han definido ciertos criterios básicos. Muchos problemas estadísticos requieren la identificación de puntos de cambio en una secuencia de datos. El control estadístico de procesos (SPC–Statistical Process Control) se refiere al monitoreo de procesos debido a un cambio en su distribución. En los métodos tradicionales se asume que la distribución del proceso es totalmente conocida previo a cualquier cambio, incluyendo todos sus parámetros, en cuyo caso se dice que el proceso está “en control”, y “fuera de control” si ocurre un cambio que causa que el proceso se corresponda a una distribución diferente. Se busca diseñar cartas de control que puedan detectar desviaciones de la distribución de base. Usualmente, en cartas de control, se emplea la función de Longitud de Corrida Promedio (ARL–Average Run Lenght), donde ARL0 indica el número promedio de observaciones entre la detección de falsos positivos asumiendo que no ha ocurrido un cambio y ARLδ que indica el retraso medio antes que un cambio de tamaño δ sea detectado. Esto es análogo a la idea clásica aplicada en el diseño de test de hipótesis de tener un error de Tipo1 acotado y un error de Tipo 2 controlado.
Históricamente las cartas de control fueron desarrolladas con el propósito de monitorear cambios en el valor medio de un proceso, pero hoy día se han desarrollado variaciones que permiten, además, monitorear los cambios en la desviación estándar, tanto en distribuciones gausianas como no gausianas, este hecho nos impulsó a investigar la aplicabilidad de dichas nuevas metodologías a la detección de cambios en una señal aleatoria turbulenta.
Las cartas de control, tradicionalmente, requieren el conocimiento total del proceso “en control”, pero ello no es un problema si existe una muestra de referencia grande de observaciones que son conocidas para generar la distribución “en control”. En el caso de tratarse de muestras de tamaño fijo se considera el llamado análisis Fase I, mientras que si se realiza un monitoreo secuencial del proceso cuando las observaciones son recibidas en el tiempo se lo denomina análisis Fase II[12].
En algunos casos la muestra de referencia puede ser pequeña o no existir. En estos casos sería imposible estimar con exactitud los parámetros “en control”. Esto tiene importantes implicaciones, se encontró que aún pequeñas desviaciones a partir de los valores reales pueden causar que las cartas muestren un ARL0 significativamente diferente respecto al valor deseado [13]. Una situación peor puede ocurrir cuando la distribución “en control” es incorrectamente especificada, como el empleo de una distribución gausiana para procesos que exhiben asimetría estadística (skewness). En estas circunstancias son necesarias cartas de control no paramétricas tal que no asuman ningún conocimiento de la distribución “en control” (cartas de “distribución libre”), manteniendo un valor deseado del ARL0 sin importar la distribución verdadera del proceso en estudio.
En trabajos previos [14] ; [15], se iniciaron los estudios para analizar la aplicación de modelos de punto de cambio (Change Point Model, CPM), utilizados para detectar desviaciones en la señal sensada. En el presente trabajo se consideran, nuevamente, tests no paramétricos para la implementación del modelo CPM, en este caso utilizamos, para la aplicación del algoritmo de detección, rutinas codificadas en lenguaje R (https://cran.r-project.org/web/packages/cpm/index.html) [16], las cuales son de dominio público, empleando los tests de Cramer-von Mises (CPM-CvM) y Kolmogorov-Smirnov (CPM-KS) [12], y por otro lado la técnica CUSUM [17] ; [18].
En el presente trabajo se realiza un estudio detallado de las tres señales estudiadas en [xx]. En primera instancia se muestra el estudio del flujo pulsante de un inyector para dos frecuencias de pulsado, se muestra un análisis detallado de los resultados mediante tablas comparativas entre los valores de tiempo real de la señal y los modelos CUSUM, CPM-CvM y CPM-KS. En segunda instancia, se muestra un análisis más detallado de los resultados obtenidos para el caso de una señal de la estela de un perfil aerodinámico con un dispositivo en el borde de fuga (mini flap de Gurney), estableciendo una tabla comparativa en la que constan las diferencias absoluta y relativa de los cambios encontrados en la señal sensada entre la metodología de wavelets (de uso habitual en este tipo de estudios) y los resultados obtenidos con CPM mediante los modelos de CUSUM, CPM-CvM y CPM-KS. Además, se presenta una sección sobre el análisis de los tiempos de procesamiento de las señales para cada modelo, mostrando en un gráfico los resultados obtenidos.
En lo que sigue realizaremos una breve descripción de las metodologías de CUSUM, CPM-CvM y CPM-KS.
2.1. Sumas Acumulativas (CUSUM)
Para el análisis estadístico de los datos se puede emplear el concepto de sumas acumulativas, utilizado para detectar pequeñas desviaciones del promedio de la muestra. Para obtener el diagrama de las sumas acumulativas, se procede de la siguiente manera. Primero se determina el valor medio de la muestra de observaciones fija,
|
|
(1) |
donde N es el número total de valores de la muestra, Xi son los valores correspondientes.
Para obtener la sucesión de valores de las sumas acumulativas, se considera el primer valor S0 = 0, luego se comienza a determinar las sumas sucesivas empleando para ello la siguiente fórmula de recurrencia,
|
|
(2) |
Luego se confecciona el gráfico de sumas acumulativas de los Si versus el período correspondiente. Lo que se busca en éste tipo de gráficos es observar si aparece una variación en la pendiente, lo que indicaría un posible cambio en la media de la muestra. El segmento del período en el cual los valores tienden a estar por encima de la media, se puede detectar en estos gráficos con un incremento de la pendiente, y por el contrario los segmentos de tiempo en los cuales los valores se encuentran por debajo de la media se visualizan en el gráfico con un decremento en la pendiente. Mediante dichos gráficos se podría advertir la posibilidad de la presencia de cambios en el valor de la media.
Una vez detectado un cambio en la pendiente del gráfico de sumas acumulativas se procede a estimar el lugar donde ocurre dicho cambio. Sea m tal que,
|
|
(3) |
Sm es el punto más alejado del cero en el gráfico de sumas acumulativas. Este punto m estima el último punto antes de que el cambio ocurra, y el punto m + 1 estima el primer punto después del cambio. Una vez detectado el primer cambio se divide la muestra en dos partes, una antes del cambio y otra después, y se repite el procedimiento antes descripto para detectar otros posibles cambios [18].
2.2. Test CPM-CvM/CPM-KS
Consideraremos el problema de detectar un punto de cambio en una secuencia de observaciones fija. Identificando las observaciones como {X1, …. Xt}, el objetivo es testear si han sido generadas por la misma distribución de probabilidad. Asumimos que no se conoce a priori esa distribución. Utilizando el lenguaje de test de hipótesis estadístico, la hipótesis nula es la que refiere a que no hay punto de cambio y todas las observaciones provienen de la misma distribución, mientras que la hipótesis alternativa es la que indica que existe un punto de cambio τ en la secuencia que la particiona en dos conjuntos, con X1, …. Xτ que provienen de la distribución F0 previa al cambio, y Xτ+1, …. Xt que provienen de una distribución F1 diferente luego del cambio [11],
|
|
(4) |
Se puede testear si existe un punto de cambio inmediatamente después de cualquier observación Xk particionando las observaciones en dos muestras S1 = {X1, …. Xk} y S2 = {Xk+1…. Xt} de tamaños n1 = k y n2 = t–k, respectivamente, y entonces se aplica un test de hipótesis a las dos muestras. Nosotros para estos test emplearemos el CvM. Este test se basa en la comparación de la función de distribución empírica de las dos muestras, definidas como,
|
|
(5) |
donde I(Xi< x) es la función indicador
|
|
(6) |
El test CvM se basa en el cuadrado de la distancia promedio entre las dos distribuciones empíricas,
|
|
(7) |
donde dFt es la distribución empírica de la muestra total recopilada, y puede ser aplicado directamente, como la siguiente suma [11] ; [13],
|
|
(8) |
Nuevamente rechazamos la hipótesis nula H0 si Wk,t > hk,t para algún umbral hk,t.
Como no se conoce dónde va a estar ubicado el punto de cambio, no sabemos qué valor de k utilizar para el particionado de la muestra, es por ello que se especifica una hipótesis nula H0 más general, no hay ningún cambio en la secuencia de valores. La hipótesis alternativa H1 es que existe un punto de cambio para algún valor de k no específico. Entonces podemos hacer este test mediante el cálculo del estadístico Wk,t en cada valor 1 < k < t y tomar el valor máximo. Como la varianza del estadístico Wk,t depende del valor de k, se debe estandarizar el estadístico de forma que tenga igual media y varianza para todos los valores de k. Para nuestro caso la estandarización es simple obteniéndose las siguientes media y varianza para el estadístico [12] ; [19],
|
|
(9) |
Esto lleva a la maximización del test estadístico
|
|
(10) |
Si el estadístico Wt > ht, donde ht es algún posible umbral elegido, entonces la hipótesis nula H0 es desechada y concluimos que ha ocurrido un cambio en algún punto de la secuencia de datos. En este caso, el mejor estimador τ de la ubicación del punto de cambio es en el valor k que maximiza Wt. Si Wt ≤ ht, entonces no se rechaza la hipótesis nula H0, y por ello se concluye que no ha ocurrido ningún cambio.
Habiendo considerado el problema de detectar puntos de cambio de una muestra de tamaño fijo, ahora veremos como se implementa en el caso de tener observaciones que se van sucediendo en el tiempo. Sea Xt la t-ésima observación, siendo t incrementada con el tiempo. A medida que una nueva observación Xt es recibida, se puede tratar a {X1, …. Xt} como si fuera una muestra de tamaño fijo y utilizar la metodología descripta previamente para testear si algún cambio ha ocurrido. De esta forma el problema del monitoreo secuencial se reduce a desarrollar una secuencia de test de tamaño fijo. Es por ello que, en esta primera instancia de análisis previo a su utilización en mediciones en tiempo real, solo planteamos realizar un análisis de Fase I de la señal.
Una de las cuestiones más importantes en la aplicación de este modelo CPM es el número de observaciones previas al cambio, este tiene un gran impacto en el desempeño del modelo. Como la distribución previa al cambio es desconocida, será fácil de detectar cambios cuando el número de observaciones previo sea grande, permitiendo obtener una mejor estimación de la distribución, y una función de distribución empírica más exacta.
En cuanto al test KS el estadístico se define como la máxima diferencia entre las distribuciones empíricas vistas precedentemente ecuaciones (5) y (6) siendo,
|
|
(11) |
Igualmente que en el caso anterior, el procedimiento para el test de hipótesis es similar. Sin embargo, resulta más compleja la estandarización del estadístico KS. En vez de considerar el estadístico Dk,t se emplea la probabilidad de observar un valor más extremo que Dk,t que se define como pk,t.
Siendo qk,t = 1–pk,t, se define,
|
|
(12) |
En este caso tendremos que si qt > ht, donde ht es algún posible umbral elegido, entonces la hipótesis nula H0 es desechada y concluimos que ha ocurrido un cambio en algún punto de la secuencia de datos, de igual forma que para el caso del CvM.
3. Aplicación de modelos CPM a un flujo pulsante
En primera instancia mostraremos los resultados obtenidos de la aplicación de los modelos CUSUM, CPM-CvM y CPM-KS, sobre las mediciones realizadas con anemometría de hilo caliente, que tenían el objeto de caracterizar el flujo de aire pulsante saliendo de un inyector, diseñado para realizar experimentos de control de flujo en el interior de una cavidad de relación de aspecto 1. Nuestro interés, ya que esta señal no es devenida de un flujo turbulento libre sino de una distribución particular de flujo generada por la boquilla del inyector, era ver el comportamiento de los estimadores en estudio con el fin de establecer su capacidad en la detección de cambios en la señal sensada, siendo la misma totalmente conocida.
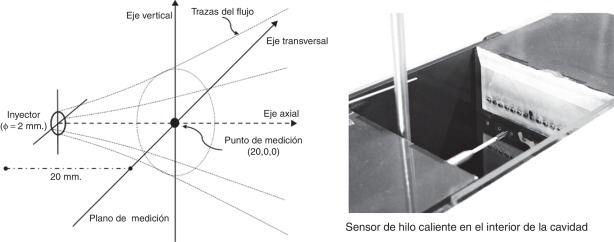
En la salida de la boquilla del inyector se realizó un relevamiento vertical y transversal del campo de velocidades para determinar la distribución de velocidades de inyección. Además, dicho flujo de aire se regulaba con electroválvulas (frecuencias de accionamiento en un rango admisible de 0 a 250 Hz.) en un sistema neumático (ver fig. 1). En este caso mostramos dos señales específicas de la pulsación del aire por el inyector para frecuencias de accionamiento de 10 Hz y 100 Hz.
|
|
|
Figura 1. Esquema de medición centrado en el eje del inyector. Imagen de la medición en la cavidad.
|
Aplicamos un análisis Fase I a los datos de la componente longitudinal de la velocidad del aire medida en el eje axial de salida del inyector, a una distancia de 20 mm. del mismo. Lasvelocidades fueron medidas con un anemómetro de hilo caliente de temperatura constante marca Dantec modelo Streamline. Se empleó una punta de prueba X-wire Dantec 55R51 con una frecuencia de adquisición de datos de 2000 Hz por canal, midiendo dos componentes de la velocidad (longitudinal u y vertical v).
En la tabla 1 y la tabla 2 se observan el total de los puntos de cambio del pulso de la señal comparados con la detección realizada mediante el estimador CUSUM, el CPM-CvM y el CPM-KS, siendo analizado un tiempo de 0,8 segundos para el caso de la frecuencia de pulsado de la señal a 10 Hz. y 0,035 segundos para el caso de la frecuencia de pulsado de 100 Hz. Se muestran las diferencias relativas y absolutas de los distintos estimadores respecto a los pulsos en la señal. De un análisis de ambas Tablas se observa que CUSUM detecta los casos significativos de la señal y otros que no son significativos (marcados como N/S en las Tablas), con diferencias inferiores al 3,1%. En cuanto al modelo CPM-KS, para el caso de 10 Hz., es el que comete mayor error detectando falsos cambios y no detectando otros que sí lo son. En cuanto al modelo CvM, posee diferencias menores al 1,1%, aunque en general superiores al modelo CUSUM. Para el caso de 100 Hz. (ver tabla 2) el modelo CUSUM es el que mejor detecta los cambios, siendo que los modelos CvM y KS detectan exactamente los mismos cambios, exceptuando algunos cambios no detectados, con diferencias superiores a CUSUM en todos los casos. Existe un cambio detectado por todos los modelos, pero que posee un error de detección alto (del 16 al 22%), pudiendo considerarse este caso como un valor atípico.
| Pulso | CUSUM | CPM-CvM | CPM-KS | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Cambio [s] | Cambio [s] | Diferencia | Cambio [s] | Diferencia | Cambio [s] | Diferencia | |||
| absoluta [s] | relativa [%] | absoluta [s] | relativa [%] | absoluta [s] | relativa [%] | ||||
| N/S | 0,019 | −--- | −--- | −--- | −--- | −--- | 0,017 | −--- | −--- |
| 0,0455 | 0,0455 | 0 | 0,00 | 0,045 | −0,0005 | 1,10 | −--- | −--- | −--- |
| 0,0965 | 0,0935 | −0,003 | 3,11 | 0,096 | −0,0005 | 0,52 | 0,092 | −0,0045 | 4,66 |
| N/S | 0,129 | −--- | −--- | −--- | −--- | −--- | 0,126 | −--- | −--- |
| 0,1445 | 0,1445 | 0 | 0,00 | 0,1455 | 0,001 | 0,69 | −--- | −--- | −--- |
| 0,196 | 0,196 | 0 | 0,00 | 0,1955 | −0,0005 | 0,26 | 0,1895 | −0,0065 | 3,32 |
| N/S | 0,2375 | −--- | −--- | −--- | −--- | −--- | 0,237 | −--- | −--- |
| 0,2435 | 0,244 | 0,0005 | 0,21 | 0,2435 | 0 | 0,00 | −--- | −--- | −--- |
| 0,2955 | 0,2955 | 0 | 0,00 | 0,2945 | −0,001 | 0,34 | 0,289 | −0,0065 | 2,20 |
| N/S | 0,3235 | −--- | −--- | −--- | −--- | −--- | 0,325 | −--- | −--- |
| N/S | 0,3345 | −--- | −--- | −--- | −--- | −--- | −--- | −--- | −--- |
| 0,343 | 0,344 | 0,001 | 0,29 | 0,3435 | 0,0005 | 0,15 | −--- | −--- | −--- |
| 0,3945 | 0,3945 | 0 | 0,00 | 0,394 | −0,0005 | 0,13 | 0,388 | −0,0065 | 1,65 |
| 0,4425 | 0,4425 | 0 | 0,00 | 0,443 | 0,0005 | 0,11 | 0,4375 | −0,005 | 1,13 |
| 0,4945 | 0,494 | −0,0005 | 0,10 | 0,4935 | −0,001 | 0,20 | 0,4855 | −0,009 | 1,82 |
| 0,543 | 0,542 | −0,001 | 0,18 | 0,5425 | −0,0005 | 0,09 | 0,5335 | −0,0095 | 1,75 |
| 0,594 | 0,5935 | −0,0005 | 0,08 | 0,593 | −0,001 | 0,17 | 0,5865 | −0,0075 | 1,26 |
| 0,6415 | 0,6415 | 0 | 0,00 | 0,642 | 0,0005 | 0,08 | 0,637 | −0,0045 | 0,70 |
| 0,6935 | 0,693 | −0,0005 | 0,07 | 0,6925 | −0,001 | 0,14 | 0,6865 | −0,007 | 1,01 |
| 0,741 | 0,746 | 0,005 | 0,67 | 0,7415 | 0,0005 | 0,07 | −--- | −--- | −--- |
| 0,793 | 0,793 | 0 | 0,00 | −--- | −--- | −--- | −--- | −--- | −--- |
| Pulso | CUSUM | CPM-CvM | CPM-KS | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Cambio [s] | Cambio [s] | Diferencia | Cambio [s] | Diferencia | Cambio [s] | Diferencia | |||
| absoluta [s] | relativa [%] | absoluta [s] | relativa [%] | absoluta [s] | relativa [%] | ||||
| 0,0015 | 0,0015 | 0 | 0,00 | −--- | −--- | −--- | −--- | −--- | −--- |
| 0,007 | 0,007 | 0 | 0,00 | 0,0065 | −0,0005 | 7,14 | 0,0065 | −0,0005 | 7,14 |
| 0,009 | 0,0105 | 0,0015 | 16,67 | 0,011 | 0,002 | 22,22 | 0,011 | 0,002 | 22,22 |
| 0,0115 | 0,012 | 0,0005 | 4,35 | −--- | −--- | −--- | −--- | −--- | −--- |
| 0,017 | 0,017 | 0 | 0,00 | 0,016 | −0,001 | 5,88 | 0,016 | −0,001 | 5,88 |
| 0,02 | −--- | −--- | −--- | −--- | −--- | −--- | −--- | −--- | −--- |
| 0,0215 | 0,0215 | 0 | 0,00 | 0,0215 | 0 | 0,00 | 0,0215 | 0 | 0,00 |
| 0,027 | 0,027 | 0 | 0,00 | 0,0265 | −0,0005 | 1,85 | 0,0265 | −0,0005 | 1,85 |
| 0,03 | 0,0305 | 0,0005 | 1,67 | −--- | −--- | −--- | −--- | −--- | −--- |
| 0,031 | 0,032 | 0,001 | 3,23 | 0,0315 | 0,0005 | 1,61 | 0,0315 | 0,0005 | 1,61 |
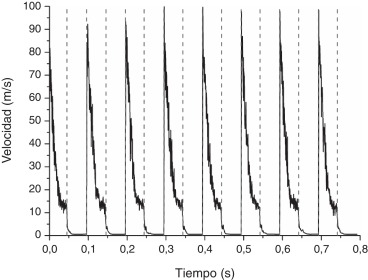
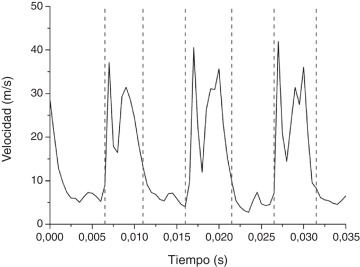
A pesar de que los errores cometidos en la detección por parte del modelo CPM-CvM, son en general mayores que con el modelo CUSUM (no superan el 7,14%), CvM detecta, para ambas señales, casi todos los casos significativos. Por lo antes expuesto, como caso de prueba, el modelo CvM resulta ser el más adecuado para la detección de cambios aplicable a la detección con monitoreo Fase II. En las Figura 2 ; Figura 3 se pueden observar las señales analizadas para las frecuencias 10 Hz. y 100 Hz, respectivamente. Mostrándose las frecuencias de cambio previstas en cada señal de 0,1 segundos y 0,01 segundos respectivamente, e indicándose la posición de los puntos de cambio encontrados por el estimador CPM-CvM (líneas a trazos verticales). Se observa la buena concordancia con la iniciación del pulso y luego con otro cambio en el corte del pulso.
|
|
|
Figura 2. Valores de la componente u de la velocidad en el eje del inyector en el punto de medición (20,0,0) (fig. 1) para una frecuencia de pulsación de 10 Hz y puntos de cambio encontrados (rectas a trazos) mediante el estimador CPM-CvM.
|
|
|
|
Figura 3. Valores de la componente u de la velocidad en el eje del inyector en el punto de medición (20,0,0) (fig. 1) para una frecuencia de pulsación de 100 Hz y puntos de cambio encontrados (rectas a trazos) mediante el estimador CPM-CvM.
|
4. Aplicación de modelos CPM a la estela de un perfil aerodinámico
En análisis de flujos turbulentos es común emplear herramientas muy conocidas como son el espectro de densidad de potencia, las autocorrelaciones, la transformada de wavelet, aplicadas directamente a los valores de la fluctuación de la velocidad obtenida de los ensayos realizados, con el objeto de encontrar las características particulares de las estructuras turbulentas que aparecen en el flujo. De esta manera se puede determinar la aparición de eventos específicos presentes en el campo del fluido, las Escalas temporales y espaciales características de dichos eventos, etc. [1]; [2]; [20] ; [21].
Presentamos los resultados obtenidos de un experimento realizado, en el cual se aplican los estimadores de punto de cambio CPM-CvM y CPM-KS (utilizando el monitoreo Fase I) y el estimador de sumas acumulativas (CUSUM), comparándolos con el mapa de wavelet de la señal. Buscamos determinar si los modelos CPM-CvM y CPM-KS son buenos estimadores para su aplicación en mediciones en tiempo real.
Respecto al tipo de cambio que se busca, en este caso nos referimos a cambios en la media puesto que en todos los casos que se presentan los eventos que se quieren detectar producen cambios en dicho parámetro en la señal sensada del anemómetro.
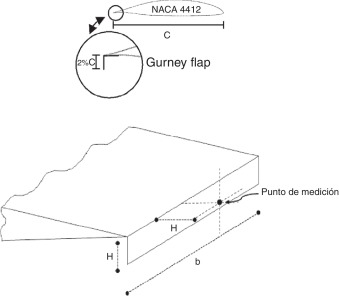
Para el siguiente caso ya se ha aplicado, previamente, la metodología CUSUM con el objeto de analizar el empleo del estimador de punto de cambio en el análisis de la señal sensada [14]. Resumidamente la señal se corresponde con una medición realizada en uno de los túneles de viento de capa límite existentes en la Unidad de Investigación, Desarrollo, Extensión y Transferencia - Laboratorio de Capa Límite y Fluidodinámica Ambiental (UIDET - LaCLyFA) del Departamento de Aeronáutica de la Facultad de Ingeniería de la Universidad Nacional de La Plata (Argentina). El modelo empleado para la medición fue una pequeña ala de 45 cm. de cuerda (C) y 80 cm. de envergadura (b) construida con un perfil aerodinámico NACA 4412 con el agregado de un dispositivo pasivo de control de flujo (mini flap de Gurney) de longitud H = 2%C (9 mm.) ubicado en el borde de fuga del perfil a 90° respecto a la cuerda (ver fig. 4). Se realizó un análisis de la señal sensada corriente abajo en la estela del perfil aerodinámico.
|
|
|
Figura 4. Esquema del modelo y la medición realizada.
|
Con la incorporación de un mini flap de Gurney un perfil aerodinámico a 0° de ángulo de ataque puede incrementar la fuerza de sustentación en un 60%, y el máximo valor de resistencia puede incrementarse un 20% [22]. Estos efectos están asociados con el desprendimiento de vórtices en la estela del mini flap.
Las velocidades fueron medidas con el mismo equipamiento comentado previamente, y en las mismas condiciones. La medición que se presenta corresponde a un punto de la estela generada por el perfil aerodinámico a una distancia igual a la altura del mini flap (H) corriente abajo del borde de fuga.
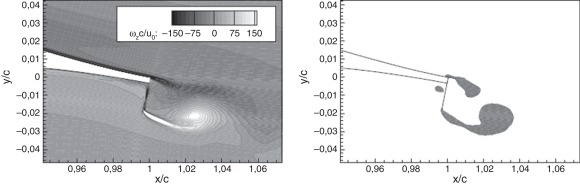
Al conocerse el campo del flujo producido por la presencia de este dispositivo y sabiendo que genera estructuras vorticosas periódicas que se desprenden del perfil, como vórtices contrarrotantes periódicos (ver fig. 5), se consideró la posibilidad de implementar esta metodología de punto de cambio con el fin de detectar los eventos esperados en la estela, los cuales fueron cuantificados mediante la aplicación de la transformada wavelet a la señal sensada. La característica de localización de frecuencia en el tiempo de la transformada wavelet[21] da una gran posibilidad de descubrir las posiciones de singularidades y discontinuidades en una señal, algo que es imposible de alcanzar en el análisis ordinario de Fourier [23]. Se compararon dichos resultados con los arrojados por las metodologías de los estimadores de punto de cambio.
|
|
|
Figura 5. Esquema de las estructuras vorticosas contrarrotativas que se desprenden corriente abajo del mini flap de Gurney - Simulaciones numéricas de la vorticidad [19].
|
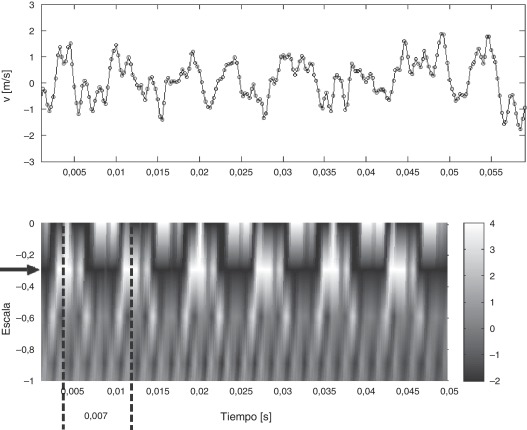
Para el análisis se presentan los resultados encontrados en los cálculos para la componente vertical de la velocidad de la señal sensada. En la figura 6 se presenta el mapa de wavelets de la aplicación de la transformada wavelet a la señal utilizando una onda del tipo Mexican Hat (wavelet de Ricker)[24] ; [25], mediante la cual se pueden rastrear máximos en una señal [21]. Allí se observa la aparición de un evento turbulento periódico asociado a uno de los vórtices contrarrotativos que se desprenden corriente abajo del dispositivo.
|
|
|
Figura 6. Mapa de wavelets y fluctuación de la velocidad vertical sensada en los primeros 0,05 segundos (Se indica el nivel de Escala en el cual aparece el vórtice–Escala = -0,3).
|
En dicha figura 6 el valor de ordenadas correspondiente a Escala se define con la siguiente expresión [23]:
|
|
(7) |
donde Δt corresponde a la longitud en segundos de la wavelet correspondiente (la del sombrero mexicano en el presente caso) para dicha Escala.
Las estructuras marcadas en el mapa de wavelets (Escala = -0,3) concuerdan con la frecuencia del pico de energía (141,6 Hz) encontrado mediante el análisis realizado por el cálculo del espectro de densidad de potencia de la misma señal [7]. Esta frecuencia se corresponde con la periodicidad encontrada en los máximos secundarios correspondientes a un intervalo de tiempo de 0,007 segundos.
De la aplicación del algoritmo del estimador de punto de cambio, aplicando el método de las sumas acumulativas (CUSUM) [14]; [15] ; [18], se obtuvieron los resultados que se muestran en la tabla 3. En la misma, también, se presentan los cambios encontrados mediante la aplicación de la metodología CPM-CvM y CPM-KS, y los valores determinados del mapa de wavelet. En dicha tabla 3 se indica el instante de tiempo en segundos en el que se produce el cambio para cada caso y las diferencias absolutas y relativas de los modelos CUSUM, CPM-CvM y CPM-KS respecto a wavelet. De los resultados obtenidos se observa que el intervalo de tiempo promedio entre cambios es 0,0032 segundos. Aquí se observa que los puntos de cambio encontrados mediante CUSUM, CPM-CvM y CPM-KS concuerdan con los máximos encontrados en el mapa de wavelets para el valor de Escala de -0,3, y la frecuencia del pico de energía, siendo la periodicidad de aparición de las estructuras vorticosas contrarrotantes de 0,007 segundos. Cabe destacar que el algoritmo de punto de cambio detecta independientemente los valores máximos y mínimos que se observan en el mapa de wavelets, por ello es que se observa una periodicidad, aproximadamente, la mitad del valor obtenido mediante CUSUM, CPM-CvM y CPM-KS.
| Wavelet | CUSUM | CPM-CvM | CPM-KS | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Cambio [s] | Cambio [s] | Diferencia absoluta [s] | Diferencia relativa [%] | Cambio [s] | Diferencia absoluta [s] | Diferencia relativa [%] | Cambio [s] | Diferencia absoluta [s] | Diferencia relativa [%] |
| 0,00225 | 0,0025 | 0,00025 | 11,11 | 0,00225 | 0,00 | 0,00 | 0,00225 | 0 | 0,00 |
| 0,00425 | 0,00475 | 0,0005 | 11,76 | 0,0045 | 0,00025 | 5,88 | 0,0045 | 0,00025 | 5,88 |
| 0,00825 | 0,009 | 0,00075 | 9,09 | 0,00875 | 0,0005 | 6,06 | 0,00875 | 0,0005 | 6,06 |
| 0,01225 | 0,01225 | 0,00 | 0,00 | 0,01175 | -0,0005 | 4,08 | 0,01175 | -0,0005 | 4,08 |
| 0,01575 | 0,01575 | 0,00 | 0,00 | 0,0155 | -0,00025 | 1,59 | 0,0155 | -0,00025 | 1,59 |
| 0,02025 | 0,020 | -0,00025 | 1,23 | 0,02 | -0,00025 | 1,23 | 0,02 | -0,0005 | 2,47 |
| 0,02375 | 0,022 | -0,00175 | 7,37 | 0,0215 | -0,00225 | 9,47 | 0,0215 | -0,002 | 8,42 |
| 0,0255 | 0,02475 | -0,00075 | 2,94 | 0,0245 | -0,001 | 3,92 | 0,0245 | -0,001 | 3,92 |
| 0,02825 | 0,02675 | -0,0015 | 5,31 | 0,028 | -0,00025 | 0,88 | 0,028 | -0,00025 | 0,88 |
| 0,0335 | 0,02925 | -0,00425 | 12,69 | 0,0335 | 0,00 | 0,00 | 0,0335 | 0 | 0,00 |
| 0,03625 | 0,03375 | -0,0025 | 6,90 | 0,03775 | 0,0015 | 4,14 | 0,03775 | 0,0015 | 4,14 |
| 0,04025 | 0,03775 | -0,0025 | 6,21 | 0,0405 | 0,00025 | 0,62 | 0,0405 | 0,00025 | 0,62 |
| 0,04425 | 0,04075 | -0,0035 | 7,91 | 0,043 | -0,00125 | 2,82 | 0,043 | -0,00125 | 2,82 |
| 0,04825 | 0,044 | -0,00425 | 8,81 | 0,048 | -0,00025 | 0,52 | ----- | ---- | ---- |
Respecto a las diferencias relativas mostradas en la tabla 3, se observa que el modelo CPM-CvM y CPM-KS presentan diferencias relativas menores (por debajo del 9,5%), en general, que con la aplicación del modelo CUSUM (por debajo del 12,7%).
Los modelos CPM-CvM y CPM-KS muestran respuestas similares, excepto para un valor que no es detectado por el modelo CPM-KS.
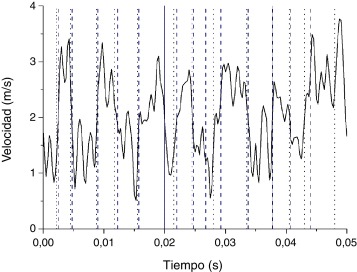
Por lo antes expuesto, en la figura 7 mostramos los valores totales de la velocidad en la fracción de la señal analizada, incorporando los puntos de cambio obtenidos por las metodologías CUSUM y CPM-CvM, indicando los mismos con rectas verticales (CUSUM-punteado y CPM-CvM-trazos). De esta manera mostramos visualmente la concordancia de los resultados obtenidos. En general los tres modelos presentan una buena aproximación en la detección de cambios de la señal, concordando con los efectos en la estela para este flujo particular.
|
|
|
Figura 7. Componente vertical de la velocidad de la señal para el caso de la estela con el mini flap de Gurney. (Puntos de cambio: CUSUM-punteado y CPM-CvM-trazos).
|
Cabe acotar que, respecto a los nuevos modelos de punto de cambio (CPM-CvM y CPM-KS) la detección de cambios en la señal es sensiblemente influenciada por el número de datos tomados inicialmente para estimar la distribución de referencia. En este caso se inicia la detección luego de muy pocos valores de comenzado el muestreo, siendo que así la detección de cambios es más precisa para este tipo de señales. Si por el contrario se comienza la detección avanzado el muestreo la detección no es tan precisa.
Por otro lado, se observa en la figura 7 que la mejor concordancia entre el estimador CUSUM y CPM-CvM se da, en general, cuando el cambio de la señal tiene una tasa de variación más pronunciada. Esto nos indica que ambos estimadores muestran diferencias en los casos en que la fluctuación de la señal no es tan alta, es decir en pequeñas fluctuaciones. Pero se debe tener en cuenta que las fluctuaciones mayores son las responsables de marcar con mayor énfasis la aparición de los eventos turbulentos comentados.
5. Tiempos de procesamiento
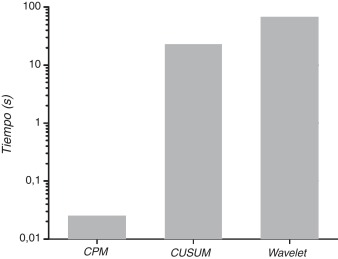
Aunque las tres técnicas (CUSUM, CPM-CvM y CPM-KS) describen correctamente los cambios, en el caso de mediciones en tiempo real, solo CPM-CvM o CPM-KS serían aplicables puesto que se puede implementar para mediciones en tiempo real, no es el caso de CUSUM que, por la metodología que posee, no permite realizar la medición en tiempo real puesto que no se puede aplicar el monitoreo de Fase II, es decir que para su empleo se debe contar con la muestra completa. Para ejemplificar este hecho presentamos una gráfica en la figura 8, en la que se muestran los tiempos de procesamiento para dichas técnicas (CPM-CvM y CPM-KS poseen similares tiempos promedio de procesamiento) y en comparación con los tiempos de cálculo mediante wavelets. En dicha figura 8 se pueden observar las grandes diferencias para cada metodología, lo cual demuestra la aplicabilidad de las metodologías CPM-CvM y CPM-KS para la detección en tiempo real.
|
|
|
Figura 8. Tiempos de computo medio, en segundos, para las distintas técnicas.
|
Los cálculos presentados, se basan en la implementación de la detección por monitoreo Fase I, puesto que se buscó estudiar la capacidad de los algoritmos para detectar los cambios esperados en la señal, en particular el análisis de Fase II se basa en un análisis Fase I con cada aparición secuencial de una nueva observación [26].
6. Discusión y conclusiones
En primera instancia, podemos mencionar que la metodología de punto de cambio muestra la factibilidad de ser aplicada a este tipo de experimentos, con dos fines principales. Por un lado, tanto CUSUM como CPM-CvM y CPM-KS demuestran que responden de manera bastante correcta para la detección de cambios en la señal sensada, los cuales provienen del fenómeno en estudio (ver tabla 3). Comparativamente, con los resultados de la transformada wavelet, tanto CUSUM como CPM-CvM y CPM-KS permiten detectar los cambios en la señal producidos por la aparición de los vórtices principales en el flujo, que resultan de fundamental importancia cuando se desea realizar un análisis rápido de la señal en busca de eventos turbulentos de interés en el flujo en estudio. Se encontró que se detectan los cambios de mayor relevancia en la señal, se perciben los vórtices de mayor intensidad (para el caso del mini flap), lo cual para una medición en tiempo real es importante, ya que se podría cambiar la frecuencia de muestreo en función de la periodicidad encontrada en los mismos permitiendo una mejor resolución en la medición.
Esta técnica resulta aplicable en cualquier flujo, en túnel de viento, en el cual aparezcan vórtices devenidos de desprendimientos ocasionados en las superficies del objeto en estudio, luego para lograr una correcta detección y análisis del flujo, se recomienda realizar visualizaciones del flujo para determinar la mejor ubicación del sensor de hilo caliente con el objetivo de efectuar una medición precisa del evento, y de esta manera lograr una mejor caracterización del mismo.
La implementación futura de los algoritmos, en la adquisición de datos, se podría realizar mediante el cálculo en un software adecuado para el control de la medición, aplicando el monitoreo Fase II, con el que se podrá realizar un análisis de los datos en forma secuencial. Buscamos, de esta manera, la detección en tiempo real de un posible punto de cambio, pudiendo así optimizar las mediciones utilizando esta metodología como un disparador para el inicio del muestreo. Ante la posible aparición de un evento turbulento coherente, que se quiera estudiar con detalle, se iniciaría automáticamente la adquisición de datos, con el fin de analizar las características finas de turbulencia en el flujo específico.
De entre los test estadísticos mencionados en este trabajo, también se evaluó la aplicabilidad del test estadístico de Anderson-Darling [27]; [28] ; [29]. Su aplicabilidad se ve supeditada a la necesidad de que sea incluido en la programación del paquete de software libre utilizado para estos estudios. Se sabe que el test ha sido programado en Matlab, según fuera utilizado por Engmann y otros [30]. Sin embargo, dicho estadístico requiere el ordenamiento de la muestra de menor a mayor para el test, lo cual implicaría un incremento de los tiempos de procesamiento que, para una muestra de datos importante, podría resultar excesivo con el fin de su aplicación en tiempo real. Por otra parte, los resultados hallados en este trabajo confirman que los tests estadísticos CPM-CvM o CPM-KS resultan correctos para los estudios realizados, sin embargo, el test estadístico CPM-CvM muestra una ligera superioridad sobre el test estadístico CPM-KS para el análisis de las señales sensadas. Respecto a los tiempos de procesamiento requerido por los distintos métodos, los modelos CPM-CvM o CPM-KS poseen tiempos muy inferiores a los requeridos por la metodología CUSUM, además esta precisa de la totalidad de la muestra para realizar la detección de cambios, por lo cual no es aplicable para el monitoreo Fase II, como fue previamente comentado.
Se prevé seguir analizando la aplicación del estimador, generando un software que lo incluya y permita el control del equipo. Además, se seguirá con el análisis para la aplicación de otras metodologías de detección y la comparación de los test estadísticos evaluados con otros de posible aplicación.
Agradecimientos
Los autores agradecen al Ing. Aer. Mariano Oscar Garcia Saínz por su aporte con la información y los datos experimentales del sistema de inyección neumático indicado, el cual forma parte de su trabajo experimental relativo a su tesis doctoral.
Bibliografía
- [1] S.B. Pope; Turbulent flows; (2 ed)Cambridge University Press (2003)
- [2] P.A. Davidson; Turbulence An Introduction for Scientists and Engineers; (1 ed)Oxford University Press (2004)
- [3] J. Borée; Extended proper orthogonal decomposition: a tool to analyse correlated events in turbulent flows; Experiments in Fluids, 35 (2) (2003), pp. 188–192
- [4] J. Pulido, D. Livescu, J. Woodring, J. Ahrens, B. Hamann; Survey and analysis of multiresolution methods for turbulence data; Comp. and Fluids, 125 (2016), pp. 39–58
- [5] D. Faranda, F.M.E. Pons, B. Dubrulle, F. Daviaud, B. Saint-Michel, E. Herbert, P.P. Cortet; Modelling and analysis of turbulent datasets using auto regressive moving average processes; Phys. Fluids, 26 (105101) (2014), pp. 1–22
- [6] F. Durst, A. Melling, J.H. Whitelaw; Principles and Practice of Laser Doppler Anemometry; (Second Edition)Academic Press, London (1981)
- [7] H. Bruun; Hot wire anemometry. Principles and signal analysis; Oxford University Press Inc, New York (1995)
- [8] T.L. Lai; Sequential Changepoint Detection in Quality Control and Dynamical Systems; Journal of the Royal Statistical Society. Series B - Methodological, 57 (4) (1995), pp. 613–658
- [9] E.S. Page; Continuous Inspection Schemes; Biometrika, 41 (1/2) (1954), pp. 100–115
- [10] S.W. Roberts; Control Chart Tests Based on Geometric Moving Averages; Technometrics, 42 (1) (1959), pp. 97–101
- [11] A.N. Pettitt; A Non-Parametric Approach to the Change-Point Problem; Journal of the Royal Statistical Society Series C - Applied Statistics, 28 (2) (1979), pp. 126–135
- [12] G.J. Ross, N.M. Adams; Two nonparametric control charts for detecting arbitrary distribution changes; Journal of Quality Technology, 44 (2) (2012), pp. 102–116
- [13] W.A. Jensen, L.A. Jones-Farmer, C.W. Champ, W.H. Woodall; Effects of Parameter Estimation on Control Chart Properties: A Literature Review; Journal of Quality Technology, 38 (2006), pp. 349–364
- [14] J. Marañón Di Leo, M.V. Calandra, J.S. Delnero; Determinación de estructuras turbulentas mediante algoritmos numéricos; Mecánica Computacional, 30 (2011), pp. 425–434
- [15] J. Marañón Di Leo, M.V. Calandra, J.S. Delnero; Detección de eventos turbulentos mediante la aplicación de algoritmos de punto de cambio; Mecánica Computacional, XXXII (2013), pp. 1297–1308
- [16] G.J. Ross, Parametric; Nonparametric Sequential Change Detection in R: The cpm Package; Journal of Statistical Software, 66 (3) (2015), pp. 1–20
- [17] I. Miller, J.E. Freund, R.A. Johnson; Probabilidad y Estadística para Ingenieros; (8 va. Ed.)Pearson, México (2012)
- [18] D.V. Hinkley; Inference about the change-point from cumulative sum tests; Biometrika, 58 (3) (1971), pp. 509–523
- [19] T.W. Anderson; On the Distribution of the Two-Sample Cramer–Von Mises Criterion; Annals of Mathematical Statistics, 33 (1962), pp. 1148–1159
- [20] J.O. Hinze; Turbulence; (2 th Ed.)Mc Graw-Hill, New York (1975)
- [21] M. Farge; Wavelet transforms and their applications to turbulence; Annu. Rev. Fluid Mech., 24 (1992), pp. 395–457
- [22] J.S. Delnero, J. Marañón Di Leo, U., Boldes, J., Colman, F.A., Bacchi, M.A.M., Martinez, E., Wassen, B., Guenther, F., Thiele, Numerical and Experimental Investigation of Mini–Flap Positions on an Airfoil, 45th AIAA Aerospace Sciences Meeting and Exhibit, Reno Nevada, 8 - 11 January 2007.
- [23] P.E.L. Giacopinelli, A.E., Scarabino, J.S., Delnero, F.A. Bacchi, Detección y análisis con wavelets de estructuras organizadas en la estela de un perfil aerodinámico, 2 do. Congreso Argentino de Ingeniería Aeronáutica (CAIA2), Córdoba, Argentina, 24 al 29 de noviembre de 2010.
- [24] N. Ricker; Wavelet functions and their polynomials; Geophysics, 9 (3) (1994), pp. 314–323
- [25] T.J. Ulrych, D.R. Velis, M.D. Sacchi; Wavelet estimation revisited; The Leading Edge, 14 (11) (1995), pp. 1139–1143
- [26] J. Marañón Di Leo, M.V. Calandra, J.S. Delnero; Análisis de detección múltiple mediante la metodología de punto de cambio en flujo turburlento; Mecánica Computacional, 33 (2014), pp. 235–243
- [27] T.W. Anderson, D.A. Darling; Asymptotic Theory of Certain Goodness of Fit Criteria Based on Stochastic Processes; The Annals of Mathematical Statistics, 23 (2) (1952), pp. 193–212
- [28] G. Marsaglia, J. Marsaglia; Evaluating the Anderson-Darling distribution; Journal of Statistical Software, 9 (1) (2004), pp. 1–5
- [29] E.D. Feigelson, G.J. Babu; Modern Statistical Methods for Astronomy with R Applications; (1 ed)Cambridge University Press (2012)
- [30] S. Engmann, D. Cousineau; Comparing distributions: The two-Sample Anderson-Darlinga Test as an Altenativa to the Komogorv-Smirnoff Test; Journal of Applied Quantitative Methods, 6 (3) (2011), pp. 1–17
Document information
Published on 20/12/17
Accepted on 24/05/17
Submitted on 24/05/17
Volume 33, Issue 4, 2017
DOI: 10.1016/j.rimni.2016.04.009
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?