Recipiente a Presión Toroidal para Almacenamiento de Hidrogeno

1 Introducción

Uno de los desafíos que se plantean en el campo energético, es la transformación del hidrogeno en energía, que conlleva a la reducción de contaminación del medio ambiente, este es un factor que influye de forma importante para su uso como combustible en automoción[1], para lo que se requieren recipientes resistentes para su almacenamiento. Una de las principales barreras en el diseño de los recipientes es la adaptabilidad y la capacidad de almacenar suficiente hidrogeno para generar la misma o mayor cantidad de energía que genera el diésel o la gasolina[2].

Generalmente se usan cilindros metálicos para el almacenamiento de gases e hidrogeno, que pesan entre 110.23lb(50Kg) y 427.7lb(194Kg), y pueden almacenar entre 80L y 200L de gas, soportando una presión aproximada de 2.9001ksi(200bar)[3], pero hay estudios que reflejan que los recipientes toroidales son muy adecuados para el almacenamiento de gas[4], por lo que se han usado en la industria aeronáutica, naval y automotriz en diferentes tipos de vehículos; inicialmente se fabricaban de material isótropo como el acero, pero a medida que se han desarrollado nuevas tecnologías de materiales compuestos se han rediseñado con este material con buenos resultados[5].

El uso de materiales compuestos en los recipientes toroidales ofrece muchas ventajas sobre los materiales convencionales y destacan por tener un peso más ligero y una gran capacidad para adaptarse a los requisitos de diseño; la rigidez, resistencia y peso, son algunas propiedades destacadas de los composites, que no se encuentran en un solo material, porque se derivan de la combinación de las propiedades de los materiales que lo conforman[6].

La fibra de carbono[7] tiene una estructura microscópica cristalina compuesta de átomos de carbono, para su fabricación[8] se toman miles de filamentos de carbono que se unen para formar un hilo, que por general tiene un diámetro entre 5 o 10 micras. La fibra junto con la matriz de resina, forma un material compuesto que destaca entre los demás por sus buenas propiedades. La matriz tiene como función mantener la forma de la estructura compuesta, mantener alineadas las fibras y actuar como medio de transferencia de tensiones y al mismo tiempo como elemento de protección de las fibras. El material compuesto carbono-epoxy, tiene un costo aceptable, por lo que su uso permite obtener materiales de bajo peso, alta resistencia y gran rigidez, y son muy usados en la industria aeronáutica como en el modelo B787 de Boeing[9] o en el A350-XWB de Airbus[10] y en la industria del automotriz[11].

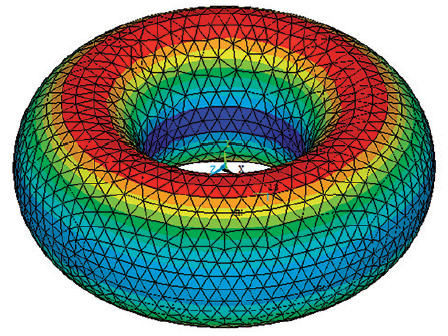
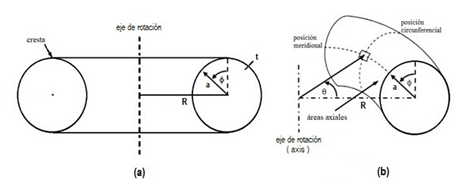
Obtener soluciones, de desplazamiento y de esfuerzos del laminado de material compuesto sobre un toroide, son más difíciles de obtener que en otras cascaras axisimétricas de revolución, debido a las peculiaridades de las ecuaciones en diferentes lugares del toroide y principalmente en su cresta (Fig.1b); varias soluciones elásticas, para toroides ortótropos sometidos a presión interna están disponibles en la literatura, [12],[13] y se han considerado optimizaciones del diseño para toroides fabricados mediante técnicas de laminación con fibra[14],[15],[16].

Mediante una técnica de optimización se soluciona el problema relacionado con la minimización del volumen de material que se requiere para construir un toroide. Hay técnicas clásicas que encuentran la solución óptima y demuestran que son la mejor manera para garantizar mínimos locales, por lo que en ocasiones tienen un bajo rendimiento. Por otra parte, están las técnicas aproximadas que evitan, en lo posible, el problema de los mínimos locales, pero la solución óptima es solo aproximada. Entre las técnicas aproximadas, destacan las metaheurísticas de optimización[17] que son consideradas como estrategias genéricas de alto nivel. Particle Swarm Optimization (PSO) es un algoritmo metaheurístico que realiza exploraciones en espacios de búsqueda de gran tamaño, brinda flexibilidad y adaptabilidad (descrita por James Kennedy y Russell C. Eberhart), inicialmente fue creado para la elaboración de modelos de conductas sociales que se reflejan en la naturaleza [18], que a la hora de hacer una búsqueda profunda la hace en el espacio en el que existe la mayor probabilidad de encontrar lo que busca[19]; esta idea fue trasladada al campo de la computación como un algoritmo para la resolución problemas en los que se plantean funciones con muchas variables, y cuyo objetivo es buscar la solución óptima o una muy cercana a la óptima[20].

En el presente trabajo se tendrá como objetivo la optimización de un recipiente toroidal M5, proveniente del análisis comparativo de recipientes a presión de forma toroidal con material compuesto registrado en[21], la geometría está en función de los radios R=14in(355.6mm) , a=6in(152.4mm) y el espesor del laminado t_c=0.75in(19.05mm) se mantiene fijo en todo el recipiente. Es de mencionar que en otro estudio [22] previo se alcanzó a reducir el volumen del material en un 17.7% llegando a soportar almacenamiento de GNC a 34.47Mpa de presión. Hay referencias que indican que el mercado energético está buscando el almacenamiento de hidrogeno como elemento de combustión y generación de energía para el mercado del automóvil, por lo que hay estudios que indican que se requiere de un recipiente que pueda almacenar hidrogeno a unos 70Mpa.

Se emplea el método de elementos finitos MEF para realizar el estudio y se realizaran simulaciones virtuales por medio del software ANSYS. El recipiente se diseña aplicando el modelo de recipientes de espesor variable y se emplea uno de los métodos de optimización disponibles en ANSYS combinado con un algoritmo externo PSO, para obtener un recipiente cuyo laminado sea liviano y que permita alcanzar la resistencia esperada.

Figura 1. Recipiente Toroidal.

2 Geometría Toroidal

El toroide de la (Figura. 1) se ha formado girando una sección transversal (Figura. 2a) o sección recta circular de radio a alrededor de un eje de rotación(axis) cuyo radio R es el radio mayor del toroide ver la (Figura. 2b), el espesor t usualmente se asume constante pero puede ser variable según [22] con lo que se alcanzaría un ahorro significativo y una reducción de espesor en su laminado.

Figura 2. Geometría del Toride.

La geometría del toroide y las tenciones que se generan dentro él se encuentra documentadas en [22].

El volumen del toroide sin incluir la pared esta dado por

${\textstyle V_{t}=2.{\pi }^{2}.R.a^{2}}$

(1)

En donde al reemplazar a por a+t se incluiría la pared

${\textstyle V_{tpi}=2.{\pi }^{2}.R.{\left(a+t\right)}^{2}}$

(2)

Puesto que ${\textstyle V_{tpi}{\mbox{ }}>{\mbox{ }}V_{t}}$ , el volumen de la pared del toroide ${\textstyle V_{pt}}$ lo determina la diferencia entre Ec (10) y Ec (9)

${\textstyle V_{pt}=V_{tpi}-V_{t}=2.{\pi }^{2}.R.\left(2.a.t+t^{2}\right)}$

(3)

El margen de diferencia entre el cálculo analítico Ec (11) y el valor que ofrece el MEF seria

${\textstyle margen=100\cdot (V_{pt}-V_{MEF})/V_{pt}}$

(4)

2.1 Laminado y material

Figura 3. Elemento Shell281.

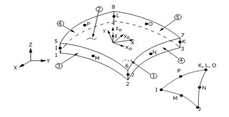
El elemento apropiado para el análisis elástico lineal de estructuras de pared delgada, es el shell281 (Figura. 3), las grandes rotaciones que se pueden dar y/o grandes deformaciones en aplicaciones no lineales su forma cuadrilátera tiene 8 nodos con 6 grados de libertad, en cada nodo: se pueden dar traslaciones en los tres ejes (x, y, z) y rotaciones alrededor de los tres ejes, puede ser usado considerando la teoría de membrana y de flexión, por lo que puede usarse para la modelación de aplicaciones de cascaras compuestas, la precisión en la modelación con shell de material compuesto está gobernada por la teoría de placas de Reissner-Mindlin [24].

Figura 4. Laminado.

Las propiedades mecánicas de las láminas, están dadas por la dirección de las fibras, por lo que la micromecánica de ellas nos permite obtener parámetros que marcan su comportamiento mecánico[25].

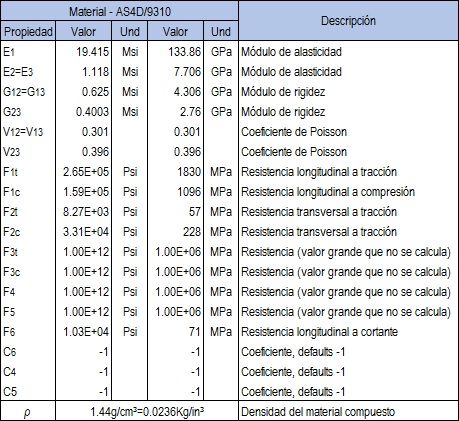
Estos composites están caracterizados por las constantes elásticas asociadas a tres direcciones mutuamente perpendiculares y tienen un comportamiento elástico representado por nueve constantes independientes formadas por tres módulos de elasticidad longitudinal, tres módulos de rigidez y tres coeficientes de Poisson según la Tabla. 1.

Las láminas unidireccionales de material compuesto formadas por fibra carbono(AS) y matriz de resina epoxi(9301) que se consideran para el proceso de optimización han dado buenas prestaciones según [21], y en pruebas realizadas en la literatura [26] donde se refleja que el material AS4D/9301 ofrece buenas prestaciones en recipientes toroidales sometidos presión.

Tabla 1: Propiedades del material AS/3501[27].

3 Método

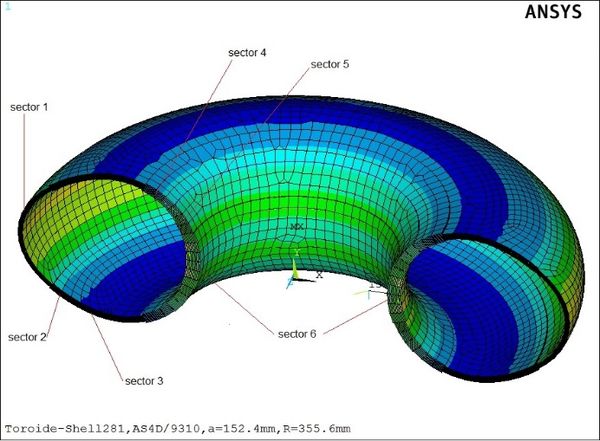
Se establece un modelo por medio de elementos finitos sobre un APDL , donde elabora el diseño inicial con un toroide de espesor fijo, para luego ser contrastado con uno de espesor variable, el toroide de espesor variable tendrá una serie de adecuaciones que se relacionan con su geometría y que tiene que ver con la sectorización de las áreas meridionales, se plantearon 6 sectores por lo que se usarán 6 espesores tk1…tk6 uno para cada sector los mismos que estarán condicionados por:

${\begin{array}{c}0\leq tk_{1}<b_{1}\\b_{1}\leq tk_{2}<b_{2}\\b_{2}\leq tk_{3}<b_{3}\\b_{3}\leq tk_{4}<b_{4}\\b_{4}\leq tk_{5}<b_{5}\\b_{5}\leq tk_{6}\leq b_{6}\end{array}}$

(5)

Con límites que cumplen con $b_{1}<b_{2}<b_{3}<b_{4}<b_{5}<b_{6}$ según la (Figura. 5)

Figura 5. Sectores del Toroide.

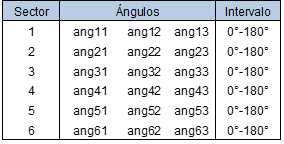
Los ángulos que se han tomado para cada sector tienen intervalos libres según se refleja en la (Tabla 3).

Tabla 2. Ángulos de las Capas del Laminado por Sectores

Para determinar el valor de los espesores en función de los ángulos de orientación de las capas del laminado, se toma como referencia información proveniente del estudio previo [16], en donde se estudió una técnica de bobinado que se la ha adaptado como técnica de laminación a emplearse en este modelo toroidal y que se refleja en la (Ec. 6)

${\textstyle {\mbox{t}}_{\mbox{α}}{\mbox{=(}}{\frac {{\mbox{(R+a)sin}}{\mbox{α}}_{\mbox{0}}}{{\mbox{(R+a}}\cdot {\mbox{cosφ)sinα}}}}{\mbox{)}}\cdot {\mbox{t}}_{\mbox{0}}}$

(6)

En la (Ec.6) se refleja que el espesor del bobinado ${\textstyle t_{\alpha }}$ está en función del ángulo ${\textstyle \alpha }$ que determina la dirección de la capa, así como el ángulo ${\textstyle \varphi }$ que representan la coordenada meridional en la curvatura geodésica del toroide, el ángulo ${\textstyle {\alpha }_{\circ }}$ es el ángulo inicial del laminado.

Tabla 3. Sectores del Toroide.

En la tabla 3. se reflejan los valores iniciales para la construcción del diseño toroidal para la optimización.

3.1 Criterio de Fallo

En el proceso de simulación hay que tener un control de las capas del laminado, la orientación angular de ellas influye en resistencia o el fallo de cada capa del laminado que se definen según (Ec. 7,8,9)

${\textstyle I_{F}={\frac {esfuerzo}{resistencia}}}$

(7)

Se predice el fallo cuando $I_{F}\geq 1$

La razón de resistencia es el inverso del índice de fallo

$R=~{\frac {1}{I_{F}}}={\frac {resistencia}{esfuerzo}}$

(8)

El fallo se predice cuando ${\textstyle R\leq 1}$

El criterio de fallo usado para contralar la resistencia del laminado en este modelo es el de Tsai-Wu según (Ec. 9) y que se encuentra descrito de forma ampliada en la literatura [25].

${\textstyle I_{F}={\frac {1}{R}}={\left[-{\frac {B}{2A}}+{\sqrt {{\left({\frac {B}{2A}}\right)}^{2}+~{\frac {1}{A}}}}\right]}^{-1}}$

(9)

La descripción de las resistencias y coeficientes de Tsai-Wu relacionados con el material se registran en la Tabla 1.

3.2 Simulación Numérica por MEF

La simulación numérica realizada por medio del método de Elementos Finitos (MEF) toma criterios de la literatura: [22],[25],[28] que se usaran en el script del ADPL(ANSYS Parametric Desing Language), para realizar un análisis elástico lineal, la técnica de mallado a usarse será local y se controlara globalmente en términos de la longitud del borde del elemento utilizado en los límites de la superficie del mismo; se usará un mallado libre con 10392 elementos de forma cuadrilátera, el tamaño global del elemento será de 0.8in(20.32mm) con 20784 nodos. Las condiciones de contorno establecen restricciones en los ejes Y,Z para los nodos 8(R+a,0,0) y 9(-R-a,0,0) y restricciones en los ejes X,Y para los nodos 3(0,0,R+a) y 14(0,0,-R-a) para mantener apoyado el toroide.

3.3 Validación Experimental del Modelo Toroidal

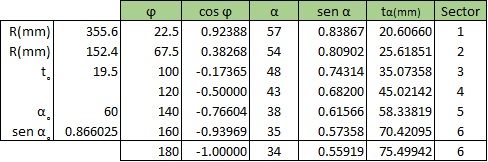
El modelo toroidal es validado con datos tomados de un toroide que fue ensayado experimentalmente en[16]; está formado por un "liner" de titanio con espesor t_o = 0.07874in(2mm) y un laminado de fibra de aramida y matriz epoxy, con un espesor por lamina de 0.01417in(0.36mm); este laminado está formado por 12 láminas. La orientación angular está en función del ángulo ϕ cuyo valor esta entre 0< ϕ <π, además emplea un ángulo α que sirve para orientar el bobinado de las fibras y para determinar el espesor tα de acuerdo a la orientación de la fibra.

Después de haberse realizado las pruebas utilizando el modelo de MEF desarrollado por nosotros, se procedió a contrastar los resultados con los resultados experimentales obtenidos por Haixiao Hu[16], obteniéndose una presión límite para comportamiento lineal en los ensayos, de 4351.13Psi(30MPa) y una presión limite en el caso de nuestro modelo numérico de 4303.27Psi(29.67MPa). Dado que el error entre el modelo numérico y experimental es de 1.1%, se acepta como válida la metodología del modelo de MEF para nuestros modelos sucesivos de recipientes toroidales.

4 Optimización

El esquema de optimización se ha realizado por medio de los métodos que se encuentran disponibles en ANSYS y con un método metaheurístico llamado PSO(Particle Swarm Optimization). Con el método RAND de Ansys se generan los diseños iniciales y que se asocian con las partículas de la población inicial para el algoritmo PSO mediante el cual se encuentra el óptimo que puede ser local o global; luego en una última pasada se usa el método aproximación de subproblema

SUB de Ansys para encontrar el óptimo global de darse el caso; se interactúa con los APDL que se ejecutan en modo Batch .

En el diseño del problema se plantea la minimización de la función objetivo Tvolumen, se definen las variables de diseño (DV) tomadas de la (Ec. 13) para los espesores y los ángulos (Tabla. 2), se establecen además 12 variables de estado (SV) cada una relacionada con el Tsai máximo de cada capa del laminado, para poder obtener el FcMax; además se cuentan con un tsai máximo por cada sector del toroide para efectos de control. Mediante las variables de estado realizamos un control de la resistencia del laminado ante la presión a la que es sometido.

5 Resultados

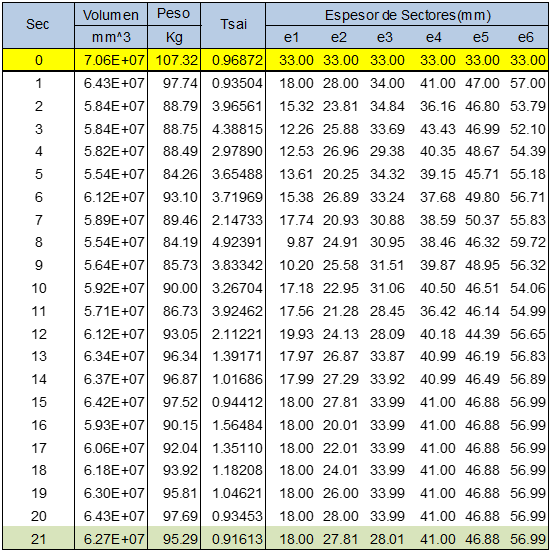
En la (Tabla 4) se reflejan los resultados de la optimización con los cuales se representan las tendencias en la (Figura 6).

Figura 6. Tendencias de Resultados

El comportamiento del volumen y del peso del material reflejados en la (Figura. 6) tienen una tendencia decreciente; los espesores tienen un comportamiento definido dentro del rango establecido en la (Ec. 5) según el condicionamiento creciente. El coeficiente de fallo es quien condiciona el proceso y este termina cuando el índice se acerca a 1.

Tabla 4. Resultados.

Con los datos tomados de la tabla 4, sec 0 (secuencia inicial) se elabora el modelo Tec modelo de espesor constante y con sec 21 modelo de espesor variable.

Figura 7. Índice de Fallo en Tec y Tev.

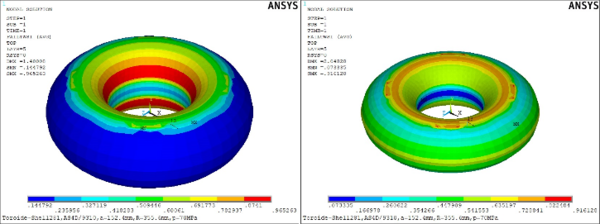
La (Figura. 7) refleja que índice de fallo de Tev es de 0.916128 se ha reducido el 5.1% con respecto al índice de Tec que es 0.965263, en ambos casos MX señala que el fallo se producirá el área axial de los toroides, pero además en Tev se aprecia que hay un mejor aprovechamiento del material en sus áreas axiales.

Figura 8. Desplazamientos de Tec y Tev.

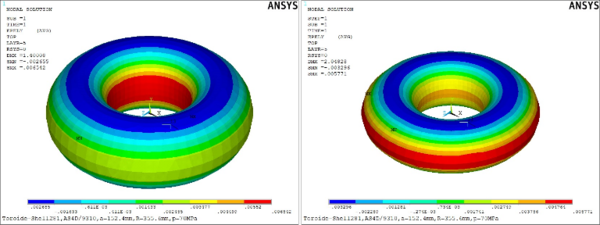
La (Figura. 8) refleja que el desplazamiento en el modelo Tev es de 0.763675mm y se ha reducido el 47.97% con respecto a Tec que tiene 1.33904mm, en ambos casos MX señala que en la cresta del toroide es donde se refleja el desplazamiento.

Figura 9. Deformación de Tec y Tev.

La (Figura. 9) refleja el índice de deformación en los modelos Tec(0.006542) y Tev(0.005771) tiene una variación de 11.79%, la deformación se ha reducido en el modelo Tev.

6 Conclusiones

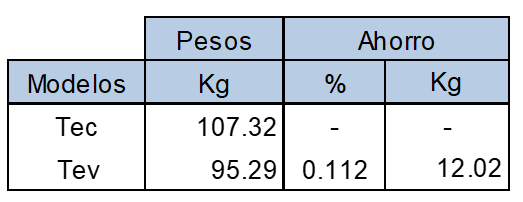
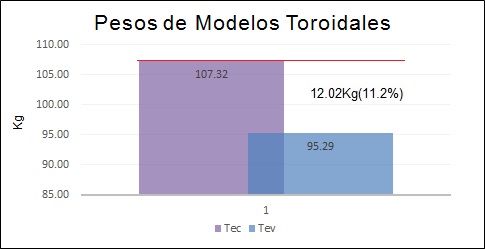
En la tabla 5, se refleja la reducción de los pesos entre el modelo toroidal de espesor constante Tec y modelo de espesor variable Tev.

Tabla 5. Ahorro de Material

La optimización ha reducido el volumen y el peso del material en un 11.2%, lo que significa que se alcanzó a reducir 12.02Kg de peso de material entre el Tec (107.32Kg) y el Tev(95.29Kg) según se aprecia en la (Figura. 10).

Figura 10. Reducción de Pesos

Los espesores se han reducido sin que se pierda la resistencia del laminado tal como lo refleja la variación del índice de deformación y el desplazamiento.

En el análisis se he determinado, que la variación angular para la ubicación de las capas del laminado en el apilamiento laminar, producen un aumento o disminución en la resistencia del laminado, cuando este es sometido a presión.

Referencias

[1] Gutiérrez Jodra, L.: El Hidrógeno, Combustible Del Futuro. Real Acad. Ciencias Exactas, Físicas y Nat. 99, 49–67 (2005). https://doi.org/10.1016/S0360-3199(98)00115-3

[2] Sirosh, N., Niedzwiecki, A.: Development of storage tanks: High-pressure vessels, http://www.scopus.com/inward/record.url?eid=2-s2.0-73749087443&partnerID=tZOtx3y1, (2008)

[3] COMPRESION, K.: Cilindros GNC Vehicular, http://www.kioshicompresion.com/vehicular.html

[4] Cook, J., Richards, B.J.: Aparato de Contención de Gas, (2002)

[5] Fowler, C.P., Orifici, A.C., Wang, C.H.: A review of toroidal composite pressure vessel optimisation and damage tolerant design for high pressure gaseous fuel storage. Int. J. Hydrogen Energy. 41, 22067–22089 (2016). https://doi.org/10.1016/j.ijhydene.2016.10.039

[6] Miravete, A.: Materiales Compuestos. Volumen I i II. Mater. compuestos. (2000). https://doi.org/10.3989/mc.2010.46908

[7] Park, S.J., Kim, B.J.: Carbon fibers and their composites. Springer Ser. Mater. Sci. (2015). https://doi.org/10.1007/978-94-017-9478-7_8

[8] Huang, X.: Fabrication and properties of carbon fibers, (2009). https://doi.org/10.3390/ma2042369

[9] Boeing: Recuperado de:www.boeing.com, www.boeing.com

[10] Airbus: Recuperado de:www.airbus.com, www.airbus.com

[11] Ferrari: Recuperado de www.ferrari.com, www.ferrari.com

[12] Maksimyuk, V.A., Chernyshenko, I.S.: Nonlinear elastic state of thin-walled toroidal shells made of orthotropic composites. Int. Appl. Mech. (1999). https://doi.org/10.1007/BF02682397

[13] Park, J.S., Hong, C.S., Kim, C.G., Kim, C.U.: Analysis of filament wound composite structures considering the change of winding angles through the thickness direction. Compos. Struct. (2002). https://doi.org/10.1016/S0263-8223(01)00137-4

[14] Zu, L., Koussios, S., Beukers, A.: Pattern design and optimization for filament - wound toroidal pressure vessels. In: 23rd Technical Conference of the American Society for Composites, Memphis, TN, USA (2008)

[15] Zu, L.: Stability of fiber trajectories for winding toroidal pressure vessels. Compos. Struct. (2012). https://doi.org/10.1016/j.compstruct.2011.11.027

[16] Hu, H., Li, S., Wang, J., Zu, L.: Structural design and experimental investigation on filament wound toroidal pressure vessels. Compos. Struct. (2015). https://doi.org/10.1016/j.compstruct.2014.11.023

[17] Yang, F., Wang, P., Zhang, Y., Zheng, L., Lu, J.: Survey of swarm intelligence optimization algorithms. In: Proceedings of 2017 IEEE International Conference on Unmanned Systems, ICUS 2017 (2018). https://doi.org/10.1109/ICUS.2017.8278405

[18] Kennedy, J., Eberhart, R.: Particle swarm optimization. Proc. ICNN’95 - Int. Conf. Neural Networks. (1995). https://doi.org/10.1109/ICNN.1995.488968

[19] Tao, W., Liu, Z., Zhu, P., Zhu, C., Chen, W.: Multi-scale design of three dimensional woven composite automobile fender using modified particle swarm optimization algorithm. Compos. Struct. (2017). https://doi.org/10.1016/j.compstruct.2017.08.065

[20] Poli, R., Kennedy, J., Blackwell, T.: Particle swarm optimization. Swarm Intell. (2007). https://doi.org/10.1007/s11721-007-0002-0

[21] Patiño, D., Corz, A.: Análisis Comparativo de Recipientes a Presión Toroidal de Material Compuesto por Elementos Finitos [ Comparative Analysis of Toroidal Pressure Vessels of Composite by Finite Elements ]. Int. J. Innov. Appl. Stud. 25, 162–175 (2018)

[22] Vick, M.J., Gramoll, K.: Finite Element Study on the Optimization of an Orthotropic Composite Toroidal Shell. J. Press. Vessel Technol. 134, 051201 (2012). https://doi.org/10.1115/1.4005873

[23] Li, S., Cook, J.: An Analysis of Filament Overwound Toroidal Pressure Vessels and Optimum Design of Such Structures. J. Press. Vessel Technol. 124, 215 (2002). https://doi.org/10.1115/1.1430671

[24] Reddy, J.N.: Mechanics of Laminated Composite Plates and Shells: Theory and Analysis, Second Edition -. Book. (2003). https://doi.org/10.1038/sj.leu.2403242

[25] Barbero, E.J.: Introduction to Composite Materials Design, Second Edition. (2010)

[26] PATIÑO PEREZ, D., CORZ RODRIGUEZ, A.: DISEÑO ÓPTIMO DE UN RECIPIENTE TOROIDAL A PRESIÓN DE MATERIAL COMPUESTO PARA VEHÍCULOS A GAS. DYNA Ing. E Ind. DYNA-ACELERADO, 0–0 (2019). https://doi.org/10.6036/9096

[27] Springer, G.S., Kollar, L.P.: Displacements, Strains, and Stresses. In: Mechanics of composite structures (2003). https://doi.org/10.1016/0263-8223(94)90053-1

[28] Barbero, E.J., Shahbazi, M.: Determination of material properties for ANSYS progressive damage analysis of laminated composites. Compos. Struct. (2017). https://doi.org/10.1016/j.compstruct.2017.05.074