1. Introducción
En este trabajo se presenta el informe correspondiente al estudio del comportamiento bajo la acción del fuego de un panel de lana de roca fabricado por la empresa de prefabricados Pretersa-Prenavisa. La referencia de la pieza a estudiar es PANEL DE 20 CON LANA DE ROCA con una longitud de 10m.
El objetivo final es analizar la estabilidad global del panel sometido a la acción del fuego. Dicha estabilidad global puede verse comprometida si las deformaciones térmicas son suficientemente grandes como para que el panel salga fuera del pilar de borde que le confiere estabilidad lateral. Asimismo debe controlarse que el desplazamiento transversal máximo del panel sea razonablemente bajo como para no comprometer la función de separación de la pieza en cuanto a los criterios de integridad y aislamiento frente a la acción del fuego. El criterio de integridad establece ciertos valores límites para asegurar que la estructura no permita la penetración de llamas o de gases calientes a través de brechas o fisuras. El criterio de aislamiento establece valores límites para el aumento de temperatura en el lado no expuesto de una estructura sometida a un fuego nominal: 140°C en promedio y 180 °C en picos locales.
El estudio se dividirá en tres partes. En primer lugar se realizará una calibración de los parámetros de los materiales que se necesitan para realizar el análisis termo-mecánico de la estructura en cuestión. Para ello se realizará una investigación documental a partir de las diferentes fuentes de información que se disponen sobre el tema: bibliografía, normativa europea, internet, etc. Asimismo se utilizarán los resultados de los ensayos experimentales realizados en los laboratorios de LGAI para calibrar los parámetros térmicos de los materiales.
En segundo lugar se realizará una puesta a punto de los códigos de elementos finitos desarrollados en CIMNE para adaptarse a los requerimientos de este estudio. Se ha utilizado el programa HTM_Concrete, el cual es una extensión de los programas Comet y Ramseries desarrollados en CIMNE para el análisis termo-higro-mecánico de estructuras de hormigón sometidas a la acción del fuego.
En tercer lugar, una vez obtenidos los parámetros termo mecánicos necesarios para realizar las simulaciones numéricas, se procederá al estudio del comportamiento frente al fuego del panel de 10m de longitud. Para ello se realizarán varias simulaciones considerando diferentes condiciones de contorno.
Finalmente a partir del análisis de los resultados de las diferentes simulaciones numéricas se elaborarán las conclusiones de este trabajo.
2. Parámetros termo-mecánicos
El tipo de hormigón utilizado en los paneles es HA/30/F/22/I. Esto lo identifica como un hormigón normal.
El análisis de una estructura de hormigón normal expuesta al fuego involucra diferentes problemas interdependientes. La clasificación más natural de dichos problema es la siguiente (Figura 1):
- Problema térmico
- Problema mecánico.
El problema térmico reside en la determinación de la distribución de temperaturas en la estructura y su evolución en el tiempo debida a las fuentes externas de calor. La variable de estado correspondiente es la temperatura T.
El problema mecánico consiste en la evaluación del campo de tensiones y deformaciones que verifican las condiciones del equilibrio y de compatibilidad a lo largo del proceso en estudio.
La interacción 1 (problema térmico → problema mecánico) se genera debido a que la variación de temperatura provoca deformaciones térmicas que a su vez dan lugar a tensiones. Asimismo la variación de temperatura provoca una evolución de las propiedades mecánicas del material.
La interacción 2 (problema mecánico → problema térmico) tiene lugar cuando la energía consumida en la disipación mecánica se incluye en la ecuación de balance térmico. Este efecto es despreciable ya que la energía de disipación mecánica es muy inferior a la energía térmica que proviene de la acción del fuego.
De esta manera el acoplamiento termo-mecánico de una estructura de hormigón normal puede considerarse débil, en el sentido de que el problema térmico modifica al mecánico pero el mecánico no modifica al térmico.
En el caso de utilizarse hormigones de alta resistencia con valores de porosidad y permeabilidad muy bajos debe analizarse simultáneamente el problema de transporte de humedad introduciendo nuevas interacciones y complicando radicalmente el planteo.
2.1 Parámetros del hormigón y acero
Todos los parámetros termo-mecánicos fueron tomados del Eurocódigo 2 [1].
Los valores utilizados en el análisis para el módulo de Young, el modulo de Poisson, la resistencia a compresión, la resistencia a tracción y la densidad a temperatura ambiente se presentan en la Tabla 1.
La evolución del modulo de Young, la resistencia a compresión y la resistencia a tracción con la temperatura se presentan en la Tabla 2.
| Modulo de Young | 30 GPa |
| Modulo de Poisson | 0.15 |
| Resistencia a compresión | 30 MN/m2 |
| Resistencia a tracción | 3 MN/m2 |
| Densidad | 2300 kg/m3 |
| Modulo de Young
E(T)/E(20ºC) |
Resistencia a
compresión fc(T)/fc(20ºC) |
Resistencia a tracción
ft(T)/ft(20ºC) | |
| 20 | 1 | 1 | 1.0 |
| 100 | 0.93 | 1 | 0.8 |
| 200 | 0.79 | 0.97 | 0.6 |
| 300 | 0.65 | 0.91 | 0.4 |
| 400 | 0.52 | 0.85 | 0.2 |
| 500 | 0.38 | 0.74 | 0.0 |
| 600 | 0.24 | 0.6 | 0.0 |
| 700 | 0.10 | 0.43 | 0.0 |
| 800 | 0.099 | 0.27 | 0.0 |
| 900 | 0.098 | 0.15 | 0.0 |
| 1000 | 0.097 | 0.06 | 0.0 |
| 1100 | 0.096 | 0.02 | 0.0 |
| 1200 | 0.095 | 0.0 | 0.0 |
En la Tabla 3 se muestra la evolución de la evolución de la deformación térmica con la temperatura.
| Deformación térmica | |
| 20 | 0.0 |
| 100 | 0.00049 |
| 200 | 0.00119 |
| 300 | 0.00206 |
| 400 | 0.00318 |
| 500 | 0.00463 |
| 600 | 0.00650 |
| 700 | 0.00888 |
| 800 | 0.01184 |
| 900 | 0.01200 |
| 1000 | 0.01200 |
| 1100 | 0.01200 |
| 1200 | 0.01200 |
La evolución de la conductividad térmica y el calor específico con la temperatura se muestran en la Tabla 4.
| Conductividad
térmica W/(ºC·m) |
Calor específico
MJ/(ºC·m3) | |
| 20 | 1.57 | 2.19 |
| 100 | 1.47 | 2.31 |
| 200 | 1.36 | 2.45 |
| 300 | 1.25 | 2.58 |
| 400 | 1.16 | 2.69 |
| 500 | 1.07 | 2.79 |
| 600 | 1.00 | 2.88 |
| 700 | 0.94 | 2.95 |
| 800 | 0.89 | 3.00 |
| 900 | 0.85 | 3.06 |
| 1000 | 0.82 | 3.09 |
| 1100 | 0.81 | 3.11 |
| 1200 | 0.80 | 3.12 |
La armadura utilizada en los paneles es un alambre de pretensar Y-1770-C de 3mm de espesor.
| Modulo de Young | 210 GPa |
| Limite elástico | 1560 MPa |
| Resistencia a tracción | 1770 MPa |
| Pretensión inicial | 1330 MPa |
La relación tensión-deformación para el acero de pretensando se toma del Eurocódigo 2 [1].
Donde los parámetros ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() y
y ![]() se identifican en la Figura 2.
se identifican en la Figura 2.
En la Tabla 6 se presenta la evolución de los parámetros ![]() ,
, ![]() ,
, ![]() ,
, ![]() y
y ![]() con la temperatura
con la temperatura
En la Tabla 7 se muestra la evolución de la evolución de la deformación térmica del acero de pretensado con la temperatura.
| Deformación térmica | |
| 20 | 0 |
| 100 | 0,000998 |
| 200 | 0,002318 |
| 300 | 0,003718 |
| 400 | 0,005198 |
| 500 | 0,006758 |
| 600 | 0,008398 |
| 700 | 0,010118 |
| 800 | 0,011 |
| 900 | 0,0118 |
| 1000 | 0,0138 |
| 1100 | 0,0158 |
| 1200 | 0,0178 |
2.2 Parámetros de lana de roca
En las referencias [2] y [3] se encuentran valores para el módulo de Young para la lana de roca comprendidos entre 70 kPa y 1600 kPa. En este trabajo se considerará un valor medio de 500 kPa. Asimismo se considerará que el modulo de Young de la lana de roca tiene la misma evolución con la temperatura que en el hormigón.
En la referencia [4] se reporta un valor de 0.0 para el modulo de Poisson.
La densidad del material indicada por el fabricante es de 55 kg/m3.
En la referencia [5] se documenta la evolución de la conductividad térmica de la lana de roca para temperaturas comprendidas entre los 20 ºC y 400 ºC. Para temperaturas superiores se considerará un aumento lineal.
| Conductividad
térmica W/(ºC·m) | |
| 20 | 0.035 |
| 100 | 0.044 |
| 150 | 0.051 |
| 200 | 0.060 |
| 250 | 0.070 |
| 300 | 0.081 |
| 350 | 0.093 |
| 400 | 0.0106 |
Asimismo en la referencia [5] se documenta que el calor específico de la lana de roca varia de 25000 J/(ºK·m3) para 20 ºC y 53000 J/(ºK·m3) para 1000 ºC. Para temperaturas superiores se considerará un aumento lineal.
2.3 Ensayos experimentales de LGAI
En los laboratorios de LGAI se ha estudiado el comportamiento térmico de un panel de 2.95mx2.95m (compuesto a su vez por un Panel 1 de 2.4mx2.95m y otro Panel 2 de 0.55mx2.95m) en el horno de ensayo al fuego.
En las Figuras 3 y 4 se muestra las características del Panel 1 y del Panel 2 respectivamente.
En las Figuras 5 y 6 se muestran el esquema del ensayo y la distribución de los temo-pares.
2.4 Simulación numérica del panel ensayado en LGAI
Para verificar la precisión de los valores de los parámetros de la lana de roca asumidos en el apartado 2.3, se ha realizado una simulación numérica del problema térmico del panel ensayado en LGAI.
Tenido en cuenta que el flujo de calor es fundamentalmente horizontal debido al pequeño espesor comparado con las otras dos dimensiones, se ha analizado solo una rebanada horizontal del panel. La geometría adoptada para la simulación se muestra en la Figura 7
La malla adoptada para la simulación es de 6216 nodos y 11800 elementos triangulares de tres nodos, la cual se muestra en la Figura 8.
Los parámetros térmicos utilizados en la simulación son los adoptados en los apartados 2.1 y 2.2.
Se adopta una temperatura inicial de 20°C. Las condiciones de contorno adoptadas en la simulación son de convección térmica y radiación.
Según las recomendaciones del Eurocodigo se adopta para la cara expuesta al calor un coeficiente de convección de 25 W/(m2·°K) y para la cara no expuesta uno de 9 W/(m2·°K). La temperatura del ambiente en la cara expuesta seguirá la evolución de la curva de fuego estándar (UNE EN 1364-1:2000). La temperatura del ambiente en la cara no expuesta adopta un valor de 20°C.
Para las condiciones de contorno de radiación también se siguen las recomendaciones del Eurocodigo adoptando una emisividad de la superficie de 0.9, un coeficiente de absorbción de 0.9 y un factor de visión de 1.0.
El campo de temperaturas obtenido en la simulación numérica se muestra en las siguientes figuras.
En la Figura 16 se compara la evolución en el tiempo de la temperatura en el punto P1 del panel (Figura 15) con evolución en el tiempo de la temperatura media obtenida del ensayo
Analizando la Figura 6 se observa una gran diferencia de los resultados numéricos con los experimentales tanto en valores como en la tendencia de las curvas.
La principal causa de esta diferencia es atribuible a los bajos valores de la conductividad térmica de la lana de roca reportados por Rockwool [5] en cuanto a su evolución con la temperatura. Por otro lado, la tendencia que muestra la curva de evolución de la temperatura en el tiempo obtenida de los ensayos experimentales no se explica con una variación suave de la conductividad térmica con la temperatura. Si por ejemplo se utilizará una variación de la conductividad térmica con la temperatura como la indicada en la Figura 17 se observaría una mejor correspondencia entre los resultados numéricos y experimentales tal como se muestra en la Figura 18.
Una justificación física razonable a esta evolución brusca de la conductividad térmica con la temperatura puede ser el hecho de que al aumentar muy rápidamente la temperatura, la placa de lana de roca se fisura notablemente generando una conductividad térmica aparente mucho mayor que la que se obtendría con el material sin fisurar. No obstante se necesitaría realizar mayor número de ensayos para ratificar esta hipótesis.
A pesar de que los valores de las temperaturas obtenidos numéricamente con una variación suave de la conductividad térmica son menores que los obtenidos experimentalmente, a efectos de la deformación global del panel están del lado de la seguridad. Esto se debe a que una menor temperatura en la cara no expuesta significa una mayor curvatura de la sección transversal del panel. Debido a que no se dispone de mayor cantidad de datos experimentales acerca de la evolución de la conductividad térmica con la temperatura se adoptará como válida la Tabla 8 propuesta por la empresa Rockwool.
3. Puesta a punto del código
Para poder realizar las simulaciones requerida en este trabajo fue preciso desarrollar dos nuevas facilidades en el código HTM_Concrete.
Por un lado se implemento un recurso de armadura de pretensado cuyos parámetros mecánicos evolucionen con la temperatura (Figura 19)
Por otro lado se implemento un recurso de apoyos elásticos no-lineales. Con este recurso se permite que los apoyos elásticos permanezcan inactivos hasta que en los nudos vinculados el desplazamiento llega a determinado valor (Figura 20).
4. Simulaciones termo-mecánicas
4.1 Introducción
Los paneles de lana de roca de 20 cm de espesor y 10m de longitud estudiados en este trabajo tienen un montaje constructivo tal como se indica en la Figura 21. Los paneles se colocan dentro de pilares de borde en forma de doble T que les sirve de guía y les confieren estabilidad lateral (Figura 22). La separación entre los paneles y los pilares de borde es de 1.5cm aproximadamente. La altura del panel es de 2.4m. Los paneles pueden apilarse verticalmente tal como se indica en la Figura 21, estableciendo alturas totales múltiplos de 2.4m.
En caso de producirse un incendio se generará un aumento paulatino de la temperatura del panel desde la cara expuesta al fuego. Esto producirá un aumento de longitud de panel y una flexión transversal debido a la distribución de deformaciones térmicas en el espesor del panel. De esta manera el panel se irá deformando casi libremente hasta llegar a unos 30 minutos de exposición al fuego momento en el que la dilatación longitudinal del panel es de 1.5cm. A partir de ese momento el pilar de borde restringirá el movimiento del panel reduciendo la flexión transversal.
Dependiendo de la ubicación del panel, la restricción al movimiento generada por el pilar de borde será fuerte o débil. Por ejemplo los paneles ubicados en tramos interiores tendrán una restricción fuerte. Por otro lado, los paneles ubicados en los extremos tendrán una restricción débil la cual irá disminuyendo en altura debido a la deformación del pilar de borde.
La rigidez de dicho pilar de borde estará también afectada por la disminución del modulo de Young y la resistencia a compresión por efecto de la temperatura. Una manera simplificada de estimar la rigidez efectiva del pilar borde es utilizar el método de la isoterma 500 ºC comentando en la referencia [6]. En dicho método se considera una sección transversal reducida en la que se eliminan totalmente aquellas partes cuya temperatura superen los 500 ºC. Por otro lado aquellas partes de la sección transversal con temperaturas inferiores a 500 ºC conservan sus propiedades originales.
Para determinar el campo de temperaturas en la sección transversal del pilar de borde se realiza una simulación numérica del problema térmico. En la Figura 23 se muestra la malla y las condiciones de borde para dicha simulación térmica. Las propiedades térmicas del hormigón, los valores de las condiciones de contorno de convección y radiación y las condiciones iniciales son las mismas que las utilizadas en el apartado 2.4.
En la Figura 24 se muestra el campo de temperaturas en el pilar de borde para un tiempo de exposición al fuego de 240 minutos. Asimismo en la Figura 25 se muestra el campo de temperaturas con valores inferiores a 500 ºC.
Analizando la Figura 25 puede observarse que la sección transversal eficaz según el criterio de la isoterma 500 ºC es la que se muestra en la siguiente figura.
Para determinar la rigidez del pilar con la sección transversal eficaz del pilar mostrada en la Figura 26 se realiza una simulación numérica del problema mecánico. La geometría y la malla utilizada para la simulación se muestran en la siguiente figura. Se ha utilizado una malla de 58194 nodos con 306821 elementos tetraédricos de 4 nodos.
Como condiciones de contorno de se consideran el borde inferior empotrado y un paramento vertical con una carga de 50 kN/m2 tal como se indica en la Figura 28.
En la Figura 29 se muestra el resultado del campo de desplazamientos en la dirección x.
En la siguiente tabla se determina la rigidez del pilar a partir de los resultados obtenidos.
| Altura [m] | Desp. x [m] | Carga [kN/m2] | Rigidez [kN/m] |
| 1.20 | 0.0025 | 50 | 4000 |
| 3.60 | 0.0155 | 50 | 645 |
Se realizan tres tipos de simulaciones termo-mecánicas considerando tres posibles casos de restricciones:
1-) Simulación 1: Panel libre de restricciones
2-) Simulación 2: Panel con restricción total
3-) Simulación 3: Panel con restricción parcial
Teniendo en cuenta que la simetría del problema se analiza solo la mitad del panel en forma bidimensional (Figura 30).
La malla utilizada para las simulaciones consta de 8421 nodos y 16800 elementos triangulares de 3 nodos tal como se muestra en la Figura 31.
Las propiedades de los materiales utilizadas para las simulaciones son las discutidas en el apartado 2.
Los valores de las condiciones de contorno de convección y radiación y las condiciones iniciales son las mismas que las utilizadas en el apartado 2.4 (Figura 32).
Para respetar las condiciones de simetría se vinculan todos los puntos contenidos sobre el eje de simetría en la dirección x. Asimismo se vincula el punto inferior izquierdo en la dirección y (Figura 33).
4.2 Simulación 1: Panel libre de restricciones
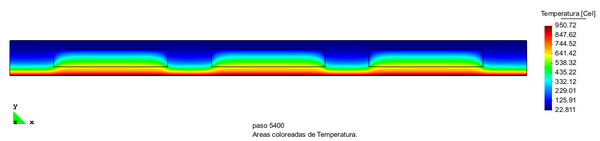
A continuación se muestra el campo de temperaturas obtenido de la simulación para distintos tiempos de exposición al fuego.
A continuación se muestra el campo de desplazamientos obtenido de la simulación para distintos tiempos de exposición al fuego.
A continuación se muestra el daño a tracción obtenido de la simulación para distintos tiempos de exposición al fuego.
A continuación se muestra la deformada obtenida de la simulación para un tiempo de exposición al fuego de 240 minutos.
A continuación se muestra el campo de desplazamientos en la dirección x obtenido de la simulación para distintos tiempo de exposición al fuego de 240 minutos.
Todos los resultados mostrados en las figuras anteriores provienen de una simulación en la que se ha considerado el proceso de fisuración del hormigón. No obstante la inclusión de este fenómeno para el problema que nos incumbe no resulta determinante para la estimación de la deformación del panel. Asimismo teniendo en cuenta este efecto se introduce una no-linealidad adicional al problema que dificulta enormemente su resolución.
Se ha realizado otra simulación con las mismas condiciones de contorno pero sin considerar la fisuración del hormigón. En la Figura 59 se muestra la evolución en el tiempo del desplazamiento lateral máximo obtenido de las simulaciones considerando y sin considerar la fisuración. Se puede observar que la diferencia entre ambos desplazamientos es menor del 7%.
4.3 Simulación 2: Panel con restricción total
Para tener en cuenta la restricción total del desplazamiento horizontal en los extremos del panel a partir de los 1.5cm, se han asignado apoyos elásticos no-lineales como se indica en la siguiente figura.
En la Figura 61 se muestra la curva fuerza-desplazamiento adoptada para simular la restricción total del desplazamiento horizontal a partir de los 1.5cm.
A continuación se muestra el campo de desplazamientos obtenido de la simulación para distintos tiempos de exposición al fuego.
A continuación se muestra la deformada obtenida de la simulación para un tiempo de exposición al fuego de 240 minutos.
En la Figura 71 se muestra el campo de desplazamientos en la dirección x obtenido de la simulación para distintos tiempo de exposición al fuego de 240 minutos.
En la Figura 72 se muestra la curva de evolución en el tiempo del desplazamiento máximo lateral del panel considerando fisuración y sin considerarla. Puede observarse que ambos curvas son casi coincidentes hasta que la curva con fisuración pierde convergencia.
En la Figura 73 se muestra las reacciones horizontales que se generan por efecto de la restricción. La suma total de reacciones horizontales es de 1.07MN.
4.4 Simulación 3: Panel con restricción parcial
Para tener en cuenta la restricción parcial del desplazamiento horizontal en los extremos del panel a partir de los 1.5cm, se han asignado apoyos elásticos no-lineales como se indica en la siguiente figura.
En la Figura 61 se muestra la curva fuerza-desplazamiento adoptada para simular la restricción total del desplazamiento horizontal a partir de los 1.5cm. Estos valores se corresponden con una rigidez horizontal de 4000 kN/m indicada en la Tabla 9.
A continuación se muestra el campo de desplazamientos obtenido de la simulación para distintos tiempos de exposición al fuego.
A continuación se muestra la deformada obtenida de la simulación para un tiempo de exposición al fuego de 240 minutos.
En la Figura 71 se muestra el campo de desplazamientos en la dirección x obtenido de la simulación para distintos tiempo de exposición al fuego de 240 minutos.
En la Figura 72 se muestra la curva de evolución en el tiempo del desplazamiento máximo lateral del panel.
5. Conclusiones
El panel de lana de roca de 20 cm y 10 m de longitud presenta una gran deformabilidad al exponerse a la acción del fuego. El desplazamiento máximo lateral varía en función del grado de restricción de los extremos del panel. Para el caso en que no exista restricción el desplazamiento máximo lateral es de 92 cm. Para el caso en que la restricción sea total dicho desplazamiento es de 22 cm.
Sin embargo para que la restricción total sea efectiva es necesario que el pilar de borde sea capaz de absorber una carga de 1.07MN por metro de altura del pilar sin mostrar prácticamente desplazamientos. El pilar de borde utilizado típicamente (Figura 22) no tiene la rigidez suficiente como para absorber dicha carga sin deformarse apreciablemente. Esto se evidencia en los resultados obtenidos de la simulación 3, donde se observa que el desplazamiento máximo lateral es de 83 cm.
El canto del panel en contacto con el pilar de borde se desplaza como una línea recta (Figura 85). El pilar de borde acompañara el desplazamiento del panel debido a su gran rigidez. De esta manera, el panel quedará siempre dentro de la guía del pilar de borde sin verse afectada su estabilidad lateral.
Deberá analizarse para cada aplicación en particular si el desplazamiento máximo lateral de 83 cm cumple con los requerimientos exigidos.
En la Figura 87 se muestra a título informativo la evolución en el tiempo del desplazamiento máximo lateral para paneles de 6 y 8m.
6. Referencias
[1] Eurocódigo 2 - Proyectos de estructuras de hormigón, Asociación Española de Normalización y Certificación (AENOR), Madrid, Año 1998.
[2] Vladislovas Kersulis, Ivan Gnip, Saulius Vaitkus, Sigitas Vejelis The Analysis of Interlaboratory Testing Results of Rock Wool Products. Material Science, Vol. 15 (4), Año 2009.
[3] N. Dauchez, M. Etchessahar, S. Sahraoui, On measurement of mechanical properties of sound absorbing materials, "2nd Biot Conference on Poromechanics”, Grenoble Francia, Año 2002.
[4] N. Atalla Andr. Panneton, F. C. Sgard and X. Olny, Acoustic absorption of macro-perforatedporous materials, Journal of Sound and vibration, 243 (4), 659-678. Año 2001.
[5] Pagina web de la companía Rockwool: www.rockwool.com
[6] Eurocode 2, Design of concrete structures, Part 1-2: General rules - structural fire design, ENV 1992-1-2, 1995.
Document information
Published on 01/01/2011
Licence: CC BY-NC-SA license
Share this document
claim authorship
Are you one of the authors of this document?