| aUniversidad de Guayaquil, Facultad de Ciencias Matematicas y Fisicas,Guayaquil,Ecuador
b Calpe Institute of Technology. Algeciras, 11205,España, c Universidad del Pais Vasco | |
|
|
| Historia del artículo:
Recibido En la versión revisada Aceptado Accesible online |
Uno de los principales objetivos en el diseño de los recipientes HSS (Hydrogen Storage Systems) para trenes, es poder almacenar el hidrógeno como gas comprimido a 70MPa de presión y considerar las tensiones y los ciclos de fatiga por la carga y descarga (depósitos tipo IV); además se incluirá en el estudio el analisis de fallo por medio de elementos finitos para la generación de modelos toroidales. En vista que otro de los aspectos del diseño es poder racionalizar el precio de los tanques de HSS, mediante la optimización de la geometría y espesores de CFRP (Carbon Fiber Reinforced Polymer) que por lo general representa el 50% del precio total, y que se lo puede hacer mediante uno de los métodos de optimización propios del Ansys que proporciona un resultado fiable a un alto costo computacional por cada nuevo patrón de recipiente que se modele; mediante el uso de técnicas de inteligencia artificial se creará un modelo que tenga la capacidad para aprender de las características de cada nuevo modelo de recipiente, pero a un bajo costo computacional y con un alto nivel de fiabilidad; la metodología de predicción estará basada en un modelo de regresión y clasificación a través de técnicas de aprendizaje supervisado y aprendizaje profundo mediante el uso de redes neuronales artificiales implementadas sobre Keras se obtendrán resultados confiables que agilizaran los ensayos virtuales en el diseño de un recipiente resistente, liviano y con una alta capacidad de almacenamiento.
|
| Palabras clave:
Hidrogeno Recipientes a Presión MEF Toroide Inteligencia Artificial | |
| Design of Toroidal Pressure Vessels for Hydrogen Trains
Using FEM and Artificial Intelligence Techniques | |
|
|
| Keywords:
Hydrogen Pressure Vessels FEM Toroid Artificial intelligence |
One of the main objectives in the design of HSS (Hydrogen Storage Systems) containers for trains is to be able to store hydrogen as a compressed gas at a pressure of 70MPa and to consider the stresses and fatigue cycles due to loading and unloading (type IV tanks). ); In addition, failure analysis by means of finite elements for the generation of toroidal models will be included in the study. Given that another aspect of the design is to be able to rationalize the price of HSS tanks, by optimizing the geometry and thickness of CFRP (Carbon Fiber Reinforced Polymer), which generally represents 50% of the total price, and which It can be done through one of Ansys' own optimization methods that provides a reliable result at a high computational cost for each new container pattern that is modelled; Through the use of artificial intelligence techniques, a model will be created that has the capacity to learn from the characteristics of each new container model, but at a low computational cost and with a high level of reliability; the prediction methodology will be based on a regression and classification model through supervised learning and deep learning techniques through the use of artificial neural networks implemented on Keras, reliable results will be obtained that will speed up virtual tests in the design of a resistant container, light and with a high storage capacity. |
1 Introducción
Uno de los desafíos planteados en el campo energético, es la transformación del hidrógeno en energía para su uso en todo tipo de transporte, que este ocasionando daño al medio ambiente por el uso de combustibles fósiles. Actualmente el sector ferroviario en Europa está aprovechando el uso del hidrógeno como elemento energético para la movilización de trenes de pasajeros o de carga, por lo que se requiere de recipientes resistentes que puedan almacenar hidrógeno comprimido a 70MPa ( 700bars) de presión.
Una de las principales barreras en el diseño de los recipientes es la adaptabilidad y la capacidad de almacenar suficiente hidrógeno para generar la misma o mayor cantidad de energía que genera el diésel o la gasolina[1]. En estudios sobre recipientes toroidales, se ha observado que existen limitaciones que ocasionan el uso de técnicas manuales para la elaboración de modelos sometidos a presión[2] , para el análisis y diseño de aquellos modelos cuya estructura eran shell de fibra carbono, se usaron herramientas computacionales con las que se podían evaluar el rendimiento del material, aplicando el método de elementos finitos y criterios de optimización como lo exponen[3]) en su trabajo; en otros estudios se analizaron el comportamiento de diversos composites en las estructuras toroidales[4] así como la predicción del daño[5]. En los últimos estudios se aplicaron criterios de optimización condicionados por el criterio de fallo de Tsai-Wu[6] experimentado en un recipiente toroidal de fibra de carbono para el almacenamiento de Hidrógeno para vehículos[7] en los que el criterio de fallo en primera lamina condiciona la finalización del proceso de optimización que se utilice; por lo que este tipo de criterio se empleara para poder elaborar el recipiente toroidal para trenes.
Además con la alta disponibilidad de recursos tecnológicos que usan técnicas de inteligencia artificial[9], así como las precisiones de predicción que ofrecen los algoritmos de aprendizaje automático o machine learning[10], para el presente estudio se ha tomado una de las técnicas del subcampo de la inteligencia artificial como lo es el deep learning[11] para la implementación de un modelo de red neuronal artificial[12] que mediante aprendizaje supervisado[13], se ha entrenado para aprender a predecir el fallo en el toroide así como el volumen de material entre otras características; se generó un dataset con las características más relevantes de varios modelos toroidales que fueron elaborados vía APDL.
2 Geometría del Recipiente
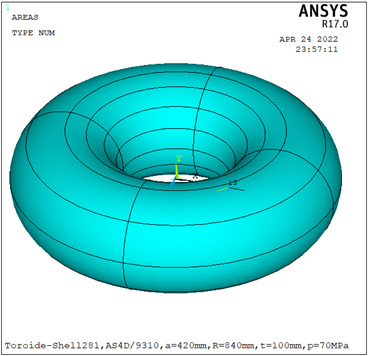
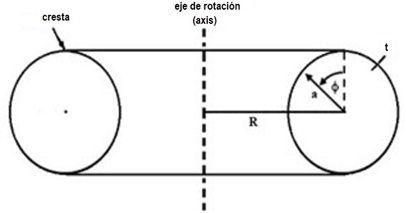
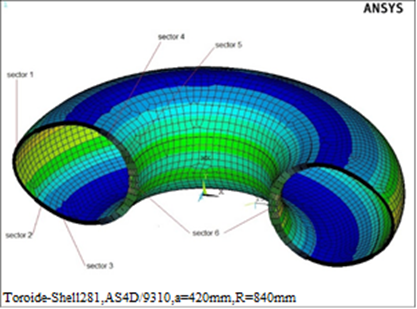
El toroide de la (Fig. 1) se ha formado girando una sección transversal (Fig. 3) o sección recta circular de radio a alrededor de un eje de rotación(axis) cuyo radio R es el radio mayor del toroide, el espesor t usualmente se asume constante para materiales metálicos pero puede ser variable para materiales ortótropos[3];
La dirección meridional para un toroide circular es tangente a la sección recta, y la dirección circunferencial sigue el círculo de revolución para el toroide (Fig. 1). La parte superior de la mitad del toroide se define a partir de , con la cresta que ocurre en .
2.1 LAMINADO Y MATERIAL
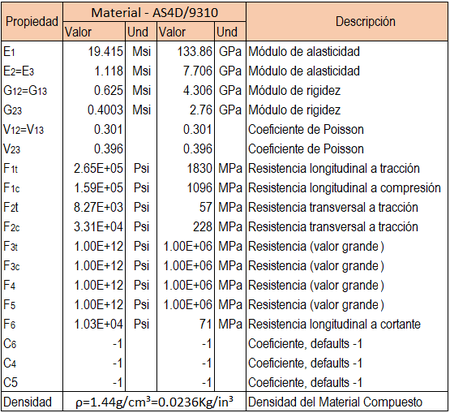
Las láminas unidireccionales de material compuesto AS4D/9310 están formadas por fibra carbono (AS4D) y matriz de resina epoxi(9310) y se consideran para el proceso de optimización, en pruebas realizadas en literatura análoga el material ofrece buenas prestaciones en recipientes toroidales sometidos a presión.
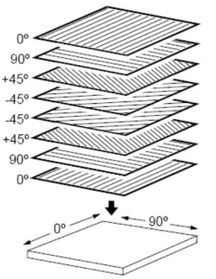
La técnica de laminación considerada en este estudio, se denomina Automated Fiber Placement (AFP) [9], consiste en la aplicación automática de bandas de fibras de carbono pre-impregnadas de epoxi sobre el molde del toroide, la ventaja de esta tecnología, es la longitud de corte mínimo de las capas de la superficie de la pieza, el espesor de las bandas normalmente serán menores a 0.315in(8mm), esta técnica permite que se puede trabajar sobre piezas con contornos muy complejos[10].
3 METODO
3.1 APLICACIÓN DEL MEF
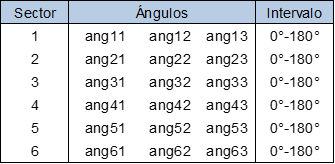
Se establece un modelo por medio de elementos finitos sobre un APDL , en donde se elabora el diseño inicial de un toroide de espesor VARIABLE, con espesores según el intervalo tk1..tk6 los que se distribuyen en la (Fig. 5) de forma sectorizada con las correspondientes áreas meridionales según la (Ec.1).
|
|
(1) |
En donde según la (Fig. 5)
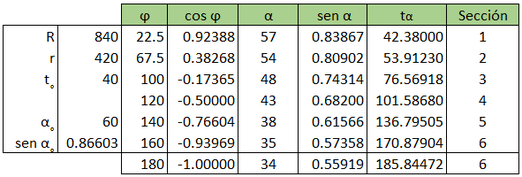
En la Tabla 2. se reflejan los valores iniciales para la construcción del diseño toroidal para la optimización, por lo que primeramente se procederá a la simulación numérica por MEF para generar el modelo toroidal. Los ángulos que se han tomado para cada sector tienen intervalos libres según se refleja en la (Tabla 3).
Para determinar el valor de los espesores en función de los ángulos de orientación de las capas del laminado, se toma como referencia información proveniente de un estudio previo realizado por Haixiao Hu [11] de donde se tomaron los criterios para establecer ángulos y los espesores por sector para luego replicar el modelo y contrastar todos sus resultados.
1.1 Aplicación de Inteligencia Artificial
Se ha empleado, un método de aprendizaje automático (machine learning) [12] de dos fases, la primera fase comprende la creación del dataset con 1000 registros, donde los toroide son obtenidos mediante el método de elementos finitos (MEF) con apartados de optimización sobre Ansys y codificado en APDL; se generaron dos especies de toroides, los que tienen fallo y los que no tienen fallo. La segunda fase, comprende la aplicación del modelo de Keras sobre Python[13], donde se crea el modelo de red neuronal artificial con más de una capa oculta que la ubica dentro de la conceptualización de aprendizaje profundo (deep learning), este modelo está compuesto por la siguiente secuencia de trabajoo: procesamiento del dataset, creación del modelo de red neuronal artificial, compilación del modelo, entrenamiento del modelo, evaluación del modelo y realización de predicciones.
Creación del Dataset
En la predicción de la cantidad del material requerido, para el diseño del recipiente mediante redes neuronales artificiales[14], se creó un dataset[15] con datos provenientes de las simulaciones numéricas que se realizaron por medio del método de elementos finitos FEM, usando un script en APDL (ANSYS Parametric Design Language); se tomó uno de los métodos disponibles en Ansys para simular las características principales de toroides optimizados con un índice de fallo aceptable, según el criterio de Tsai-Wu. El método usado fue el SUBP, que está basado en el método de subproblema y que es uno de los métodos muy dependiente de la capacidad de cómputo del ordenador[16] en términos de GPU o CPU. El proceso general, para la construcción geométrica del toroide según ciertos requisitos necesarios, para determinar la deformación así como su índice de fallo, se codificó con el lenguaje paramétrico y se ejecutó en modo batch desde ANSYS[17], por medio de un script en APDL(toroF.txt).
Previo a la carga de datos se definen una serie de bibliotecas de Python según (Fig. 6) vía importación de estas, por lo que para el procesamiento de datos se usa Pandas, para el manejo de matrices y procesamiento numérico se usa Numpy y las de Keras para la creación del modelo de Red Neuronal Artificial.
El dataset según la (Tabla 4.) contiene datos con los que se puede realizar la predicción del volumen del material TVOL por regresión lineal o la predicción del fallo por clasificación. Todas las variables de entrada que describen a cada toroide son numéricas. Esto hace que las mismas puedan procesarse de forma directa en el modelo de red neuronal artificial profunda; por lo que vía Pandas de Python se pasa del dataset al dataframe para el procesamiento interno de los datos según las siguientes líneas de código.
Procesamiento del Dataset
El dataframe (df) según (Fig. 7) contiene las características o variables de entrada al modelo de red neuronal, que son 26 columnas en el caso que la variable de salida sea el Fallo en donde 1 representa si hay fallo y 0 que no hay fallo, o 25 entradas en caso de que la salida sea el volumen del material TVOL que representa los mm^3 de material requerido para construir el toroide; y puesto que las filas son datos de un toroide especifico, todas las variables de entrada al modelo se guardarán en una matriz X y la variable de salida se almacena en un vector y, por lo que del df se tomará un % de datos para entrenamiento(training) y otro % datos para pruebas(testing).
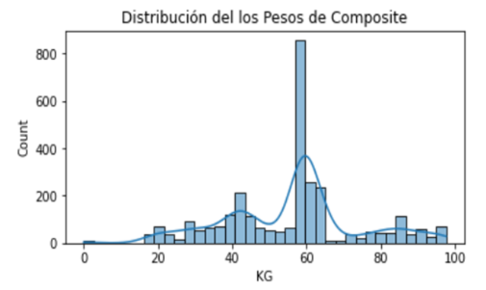
En la definición del modelo de red neuronal según (Fig.6), debemos tener en cuenta que del conjunto de datos se tomaran las 27 columnas, las primeras 26 columnas son las características de entrada mientras la 27ava columna es el valor esperado o salida dentro del marco de datos a obtenerse que dependiendo de lo que se vaya a predecir se hace una depuración del dataframe según (Fig. 8) en donde se visualiza la distribución de TVOL pero expresado en peso del material.
Creación del Modelo de RNA
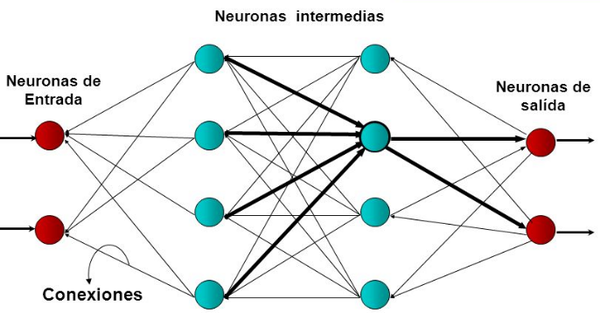
Las redes neuronales se definen en Keras como una secuencia de capas[18] y usando un conjunto de instrucciones en Python según (Fig. 9) se define al contenedor de estas capas por medio de la clase Sequential; como primer paso se creó una instancia de la clase Sequential , luego se agregó 1 capa de entrada, 3 capas ocultas y 1 capa de salida según la (Fig. 10). La primera capa de la red debe definir el número de entradas que se espera y del conjunto de datos se toma un 30% de registros para testing y un 70% para training.
Para un modelo de perceptrón multicapa[19], esto se especifica mediante el atributo "input_dim" según (Fig. 9), el modelo de red tiene 26 entradas y que están relacionada con cada una de las características del recipiente toroidal en la capa visible,256,128,16 neuronas en las 3 capas ocultas y 1 neurona en la capa de salida, cada capa con su correspondiente función de activación.
4 Resultados y Conclusiones
La (Tabla 5) contiene los espesores y ángulos de cada uno de los sectores, así como el número de láminas de un toroide de espesor variable con radio mayor R=840mm y radio menor a=420mm; estos valores son ingresados al modelo de RNA que previamente fue entrenado y el cual predice que no tiene fallo dejando por aceptado las características geométricas del toroide para el almacenamiento de Hidrógeno.
File:Draft CORZ 317697134-image25.png
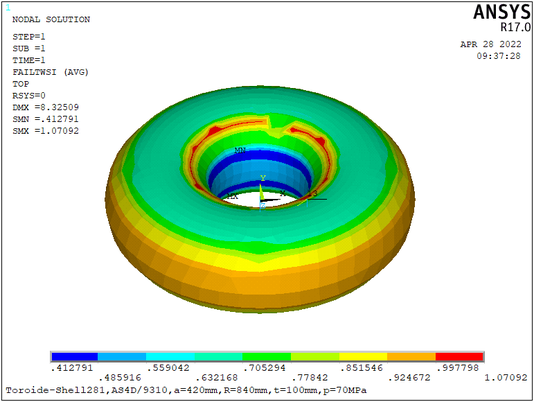
Con las dimensiones expuestas que han sido comprobadas de forma rápida con la RNA se ingresan a Ansys para crear un toroide con capacidad para almacenar hidrógeno a una presión de 70Mpa (700bars), el cual se visualiza en la (Fig. 11)
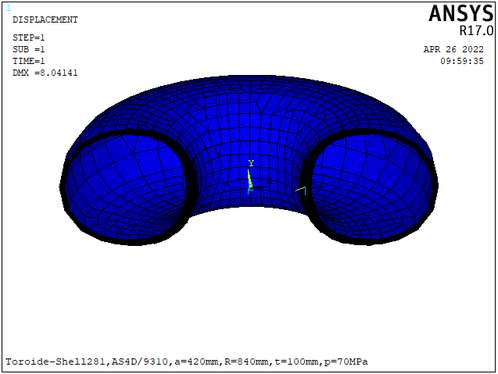
La (Fig. 11) muestra que el volumen de la pared del recipiente se minimiza al mismo tiempo que el espesor del laminado se reduce, esta reducción de volumen, peso y espesor en el toroide a una presión de 70Mpa afectan al desplazamiento de este y que está condicionado por el índice de fallo. En la (Fig. 12) se refleja el desplazamiento del modelo toroidal aceptado por la RNA.
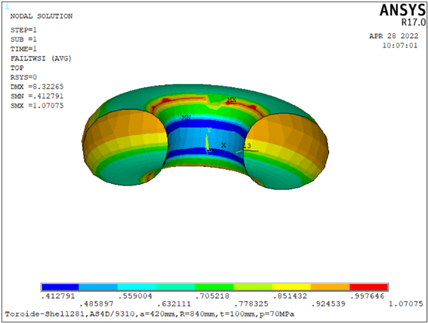
Por otra parte, en la (Fig. 13) se muestra un corte transversal del recipiente toroidal en donde se aprecia el aprovechamiento de la fibra de carbono usada en la elaboración del recipiente toroidal para el almacenamiento de hidrógeno para trenes.
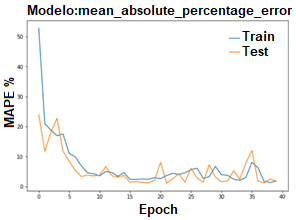
En la (Fig.14) se visualizan dos características importantes sobre el modelo, la primera es que a medida que aumenta el número de iteraciones, el error porcentual disminuye y esto indica que el modelo de RNA está aprendiendo correctamente.
La segunda característica es que a partir de (Epoch 10) la iteración 10 según (Fig 14) inicia la disminución del error porcentual; esto significa que a medida que aumenta el número de iteraciones se produce la mejora en el desempeño de aprendizaje del modelo de RNA.
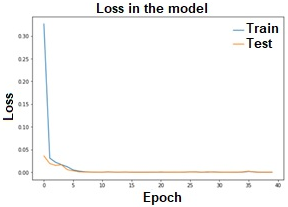
En la (Fig. 15) de igual manera se pone de manifiesto el ajuste del modelo de acuerdo con los datos. A partir de la iteración época 5 las mejoras fueron relativamente grandes.
5 Conclusiones
La (Fig. 8) expone un toroide verificado por el modelo de RNA la cual determina que no hay fallo en el mismo y en el menor tiempo posible vs la creación del toroide sobre Ansys.
En el análisis se he determinado, que la variación angular para la ubicación de las capas del laminado en el apilamiento laminar, producen un aumento o disminución en la resistencia del laminado, cuando este es sometido a presión.
Se concluye además que el recipiente toroidal optimizado ofrece muy buenas prestaciones para el almacenamiento de Hidrógeno, la fabricación de este tipo de recipiente con fibra de carbono proporcionaría un avance significativo en este campo por los beneficios económicos y energéticos que proporciona el Hidrógeno usado como medio energético en los Trenes.
El modelo de RNA ha aprendido a realizar de forma adecuada y rápida la predicción en el menor tiempo posible, usando un reducido número de épocas o epochs, considerando que un epoch es un ciclo de ejecución y que consume tiempo de computación durante una fase de entrenamiento.
Referencias
[1] N. Sirosh and A. Niedzwiecki, “Development of storage tanks: High-pressure vessels,” Hydrogen Technology: Mobile and Portable Applications (Green Energy and Technology). pp. 291–310, 2008.
[2] T. DeLay and K. Roberts, “Toroidal Tank Development for Upper-stages,” 01-Nov-2003. [Online]. Available: http://ntrs.nasa.gov/search.jsp?R=20040084002. [Accessed: 08-Feb-2016].
[3] M. J. Vick and K. Gramoll, “Finite Element Study on the Optimization of an Orthotropic Composite Toroidal Shell,” J. Press. Vessel Technol., vol. 134, no. 5, pp. 1–7, 2012.
[4] D. Patiño and A. Corz, “Comparative Analysis of Toroidal Pressure Vessels of Composite by Finite Elements,” Int. J. Innov. Appl. Stud., vol. 25, no. 1, pp. 162–175, 2018.
[5] E. J. Barbero and F. A. Cosso, “Determination of material parameters for discrete damage mechanics analysis of carbon-epoxy laminates,” Compos. Part B Eng., vol. 56, 2014.
[6] D. Patiño-Pérez and A. Corz-Rodríguez, “Optimum design of a toroidal pressure vessel of composite material for gas (CNG) powered vehicles,” Dyna, vol. 94, no. 5, pp. 546–553, 2019.
[7] D. Patiño Pérez, A. Corz Rodriguez, and C. M. Mora, “Diseño Optimo de un Recipiente a Presión Toroidal de Espesor Variable para Almacenar Hidrogeno en Automóviles Optimal Design of a Toroidal Pressure Vessel of Variable Thickness for Storing Hydrogen in Cars,” ECUADORIAN Sci. J., vol. 4, no. 2, pp. 94–100, Sep. 2020.
[8] G. S. Springer and L. P. Kollar, “Displacements, Strains, and Stresses,” in Mechanics of composite structures, 2003.
[9] D. Jesus and J. Gonzalez, “Pressure based approach for Automated Fiber Placement (AFP) with sensor based feedback loop and flexible component in the effector,” in IFAC, 2017, vol. 50, no. 1, pp. 794–799.
[10] A. J. Contreras, “Tecnología de laminado automatizado en materiales compuestos,” 2014. [Online]. Available: https://materialsbreakthroughs.wordpress.com/2014/11/03/tecnologia-de-laminado/. [Accessed: 19-May-2019].
[11] H. Hu, S. Li, J. Wang, and L. Zu, “Structural design and experimental investigation on filament wound toroidal pressure vessels,” Compos. Struct., vol. 121, pp. 114–120, 2015.
[12] D. Patiño Pérez, M. Botto-Tobar, and C. Munive Mora, “Predicción del Composite Requerido en el Diseño de un Recipiente Toroidal Mediante una Red Neuronal Artificial,” Investig. Tecnol. e Innovación, vol. 13, no. 13, 2021.
[13] J. Brownlee, “How to Use the Keras Functional API for Deep Learning,” Machinelearningmastery., no. 1, 2017.
[14] O. Agasi, J. Anderson, A. Cole, M. Berthold, M. Cox, and D. Dimov, “What is an Artificial Neural Network (ANN)? - Definition from Techopedia,” Techopedia. 2018.
[15] A. Chapman et al., “Dataset search: a survey,” in VLDB Journal, 2020, vol. 29, no. 1.
[16] D. Zou, Y. Cao, D. Zhou, and Q. Gu, “Gradient descent optimizes over-parameterized deep ReLU networks,” Mach. Learn., vol. 109, no. 3, 2020.
[17] H. Lin, A. Xu, A. Misra, and R. Zhao, “An ANSYS APDL code for topology optimization of structures with multi-constraints using the BESO method with dynamic evolution rate (DER-BESO),” Struct. Multidiscip. Optim., 2020.
[18] M. J. J. Douglass, “Book Review: Hands-on Machine Learning with Scikit-Learn, Keras, and Tensorflow, 2nd edition by Aurélien Géron,” Phys. Eng. Sci. Med., vol. 43, no. 3, 2020.
[19] “Deep Autoencoder-Based Image Compression using Multi-Layer Perceptrons,” Int. J. Soft Comput. Eng., vol. 9, no. 6, 2020.
Document information
Published on 10/01/23
Accepted on 10/01/23
Submitted on 06/07/22
Volume 07 - COMUNICACIONES MATCOMP21 (2022), Issue Núm. 3 - Materiales y Estructuras - Modelos Numéricos, 2023
DOI: 10.23967/r.matcomp.2023.01.06
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?