Setting of the parameters to capacity spectra of steel buildings

Resumen

En este artículo se presenta, en primer lugar, un marco teórico sobre el tema de los espectros de capacidad y su utilización en el estudio de la vulnerabilidad sísmica de los edificios. A continuación, se referencian los trabajos de algunos investigadores que han avanzado en la dirección de parametrizar tales curvas y se destacan sus más importantes conclusiones. Posteriormente, se introducen los modelos que se han usado en esta investigación y que se consideran representativos de las principales subclases de edificios de acero y se presentan sus espectros de capacidad. Finalmente, se procede a aplicar técnicas de parametrización de dichas curvas y se presentan los resultados obtenidos y las principales conclusiones.

Palabras clave: Espectros de capacidad, edificios de acero, vulnerabilidad sísmica, parametrización

Abstract

The first part of this paper provides a theoretical framework on the subject of capacity spectra and its usefulness in studying the seismic vulnerability of buildings. Then, the works of some researchers, which have moved forward in the direction of setting the parameters of those curves, are reported and theirs most important conclusions are highlighted. After that, the models that have been used in this research together with theirs capacity spectra are introduced. Finally, techniques for setting parameters are applied on those curves and the most important results and conclusions are presented.

Keywords: Capacity spectra, steel buildings, seismic vulnerability, setting parameters

1. Introducción

Los espectros de capacidad constituyen importantes herramientas en la caracterización del comportamiento de las estructuras ante fuerzas horizontales. Avanzar en el conocimiento de sus características es avanzar en la posibilidad de predecir la respuesta sísmica de los edificios a los que corresponden y, consecuentemente, de mejorar la capacidad de evaluación de las pérdidas que son de esperar en una zona con una determinada peligrosidad sísmica. Parametrizar estas curvas conlleva conocer sus características geométricas y definir las propiedades que determinan su forma. Con esta información se puede hacer la distinción entre los espectros de capacidad de las diferentes familias de estructuras. En particular, en este trabajo se estudiarán las dos principales subclases de estructuras de acero: edificios resistentes a momentos y edificios arriostrados.

2. Marco teórico

Las normativas para proyectar y construir edificios aceptan cuatro grandes maneras de abordar la tarea del análisis estructural (se indican entre paréntesis sus siglas en Inglés): Análisis Estático Lineal (LSP), Análisis Estático No Lineal (NSP), Análisis Dinámico Lineal (LDP) y Análisis Dinámico No lineal (NDP), y establecen las condiciones de aplicabilidad para cada una [1]. Los espectros de capacidad son empleados en el denominado Método del Espectro de Capacidad enmarcado dentro del Análisis Estático No Lineal y muy bien explicado en Seismic Evaluation and Retrofit of Concrete Buildings, ATC-40 [2]. A continuación se presenta una breve explicación sobre la manera de obtener el espectro de capacidad de una estructura y sus características más importantes.

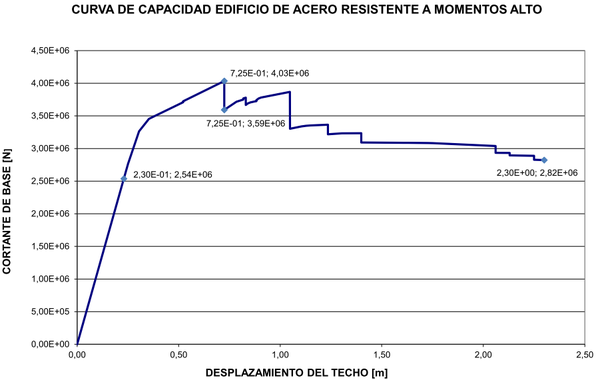
El primer paso para obtener un espectro de capacidad es obtener información sobre la manera como se deforma el edificio cuando es sometido a fuerzas horizontales. Para tal efecto, se aplican fuerzas horizontales al modelo matemático que representan las fuerzas inerciales que se originarán en la estructura cuando sea sometida a aceleraciones horizontales producidas por un movimiento sísmico. La magnitud de estas fuerzas está en función de la masa del edificio y de la peligrosidad sísmica que se ha determinado para el sitio de emplazamiento del mismo. Sin embargo, en este procedimiento no es necesario establecer de antemano dicha magnitud sino que se aplican cargas horizontales de manera incremental y se registra la respuesta de la estructura expresada como el desplazamiento del techo. Como es lógico, al ir aumentando las cargas horizontales se llegará al punto en que se alcanzará la máxima resistencia en uno de los miembros estructurales del edificio. Entonces, después de registrar los datos de desplazamiento de techo y de la fuerza cortante basal, es decir, la suma de las fuerzas horizontales aplicadas, se procede a cambiar el modelo matemático de la estructura introduciendo en él una rótula plástica en el punto donde se ha alcanzado la máxima resistencia. El procedimiento se repite hasta alcanzar el colapso de la estructura. La relación del cortante basal contra la deformación del techo constituye la denominada curva de capacidad del edificio, como la que se muestra en la Figura 1, a partir de la cual se obtiene el espectro de capacidad como se explicará más adelante, pero antes se expondrá una importante característica de las curvas de capacidad.

Figura 1. Curva de capacidad de un edificio de acero

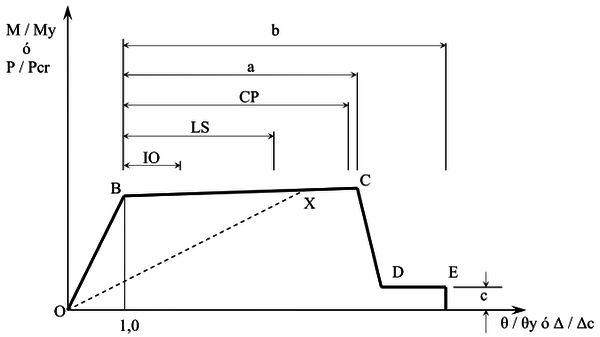
Como se observa en la figura anterior, la curva de capacidad es lineal en su primera parte hasta que ocurre una primera plastificación, en este caso en la abscisa 0.23 m, a partir de la cual se empieza a inclinar, y su inclinación va aumentando a medida que ocurren otras plastificaciones. En la figura también se destacan dos puntos en la abscisa 0.725 m en los que se manifiesta una pérdida drástica de resistencia de la estructura. Esta obedece al hecho de que las rótulas presentan un comportamiento elasto plástico limitado; cuando alcanzan una determinada deformación experimentan una fuerte pérdida de resistencia, como se muestra en la Figura 2. En esta última figura se aprecia que entre los puntos C y D la resistencia decrece drásticamente hasta un valor remanente c, y que en el punto E la resistencia de la rótula plástica se hace igual a cero. Las distancias a las que se hallan esos puntos característicos y el valor de la resistencia remanente se definen para los diferentes tipos de miembros estructuras en Seismic Evaluation and Retrofit of Existing Buildings ASCE/SEI 41-13 [1]. Para los miembros estructurales del edificio al que corresponde la curva de la Figura 1 dichas distancias aparecen en la Tabla 1.

Figura 2. Comportamiento elasto plástico con degradación de resistencia de una rótula

Tabla 1. Comportamiento elasto plástico pórtico resistente a momentos alto

Perfil	Solicitación principal	a	b	c	IO	LS	CP
W 12x336	Flexión	1,65	2,55	0,20	0,25	2,10	2,55
W 12x305	Flexión	1,65	2,55	0,20	0,25	2,10	2,55
W 12x230	Flexión	1,65	2,55	0,20	0,25	2,10	2,55
W 12x152	Flexión	1,65	2,55	0,20	0,25	2,10	2,55
W 18x143	Flexión	9,00	11,0	0,60	1,00	9,00	11,00
W 18x130	Flexión	9,00	11,0	0,60	1,00	9,00	11,00
W 18x97	Flexión	9,00	11,0	0,60	1,00	9,00	11,00
W 18x50	Flexión	9,00	11,0	0,60	1,00	9,00	11,00

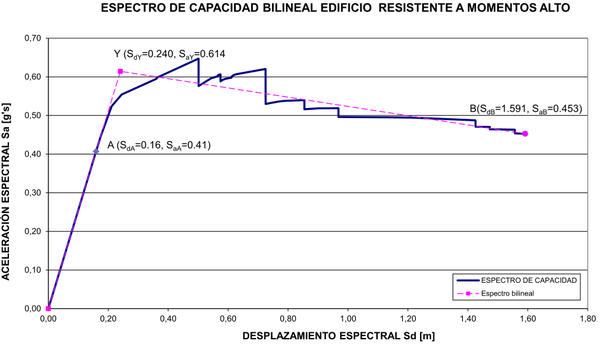
El espectro de capacidad (Figura 3) se obtiene a partir de la curva de capacidad. La fuerza cortante basal (V) se convierte en aceleración espectral ${\textstyle {\boldsymbol {(S}}_{\boldsymbol {a}}{\mathit {\boldsymbol {)}}}}$ y el desplazamiento de techo ${\textstyle \left({\delta }_{\boldsymbol {R}}\right)}$ en desplazamiento espectral ${\textstyle {\boldsymbol {(S}}_{\boldsymbol {d}}{\mathit {\boldsymbol {)\,}}}}$usando para ello dos propiedades dinámicas del edificio: el coeficiente de masa efectiva para el primer modo natural de vibración (α₁) y el factor de participación modal para el modo fundamental a nivel de techo (PF_R1). Las operaciones envueltas se muestran en las ecuaciones (1) y (2). Nótese que la fuerza cortante basal se normaliza dividiéndola por el peso del edificio (W). Puesto que esta nueva figura se obtiene a partir de la anterior mediante operaciones básicas, aparecen en ella los mismos saltos abruptos que corresponden a las pérdidas de resistencia ya mencionadas

${S}_{a}={\frac {\frac {V}{W}}{{\alpha }_{1}}}$

(1)

${S}_{d}={\frac {{\delta }_{R}}{{PF}_{RI}}}$

(2)

Figura 3. Espectro de capacidad de un edificio

En la Figura 3 también se visualiza el espectro de capacidad bilineal. En comparación con el espectro de capacidad tiene tres similitudes: (1) en el primer tramo tienen la misma pendiente (ambos pasan por el punto A), (2) terminan en el mismo punto (punto B) y (3) su área bajo la curva (A) es igual. Estas condiciones llevan a que las coordenadas del punto de plastificación (punto Y) se calculen con las ecuaciones (3) y (4):

${S}_{dY}={\frac {{S}_{dB}-{\frac {2A}{{S}_{aB}}}}{1-{\frac {{S}_{dB}}{{S}_{aB}}}{\frac {{S}_{aA}}{{S}_{dA}}}}}$

(3)

${S}_{aY}={S}_{dY}{\frac {{S}_{aA}}{{S}_{dA}}}$

(4)

Mientras la estructura se halla en el campo lineal su período fundamental de vibración es constante pero cuando empieza a plastificarse su período aumenta. Este hecho se manifiesta en el espectro de capacidad. La raíz cuadrada de la pendiente de la línea recta que une el centro del sistema cartesiano con un punto cualquiera i del espectro de capacidad es inversamente proporcional al período de la estructura en ese estado de plastificaciones, como se indica en la ecuación (5). Por lo tanto, la ecuación (3) puede reescribirse en función de los períodos en los puntos A y B (ecuación (6))

${T}_{i}={\frac {2\pi }{\sqrt {\frac {{S}_{ai}}{{S}_{di}}}}}$

(5)

${S}_{dY}={\frac {{S}_{dB}-{\frac {2A}{{S}_{aB}}}}{1-{\left[{\frac {{T}_{B}}{{T}_{A}}}\right]}^{2}}}$

(6)

3. Parametrización de los espectros de capacidad

El tema de parametrizar curvas y espectros de capacidad se ha abordado en el artículo Parametric model for capacity curves [3], del cual se hace a continuación una pequeña reseña. Sus autores proponen considerar que la curva de capacidad está compuesta por una parte lineal y otra no lineal. La primera derivada de la parte no lineal normalizada se modela mediante una función acumulativa lognormal o una función acumulativa Beta. Con esta concepción también se definen funciones de degradación de rigidez y de pérdidas totales de energía en el punto de capacidad última, un nuevo índice de daño y un modelo de fragilidad. La descomposición de la curva de capacidad se realiza mediante la ecuación (7):

${V}_{NL}={V}_{L}-V=m{\delta }_{R}-V$

(7)

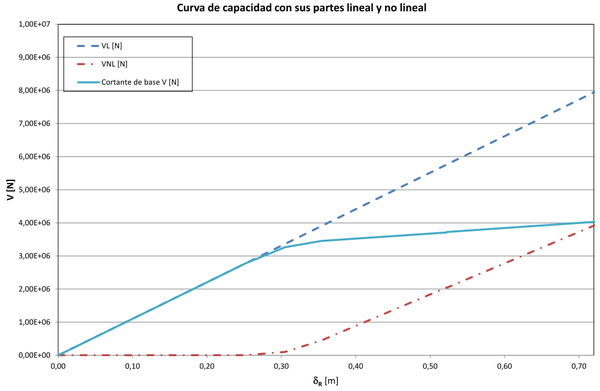
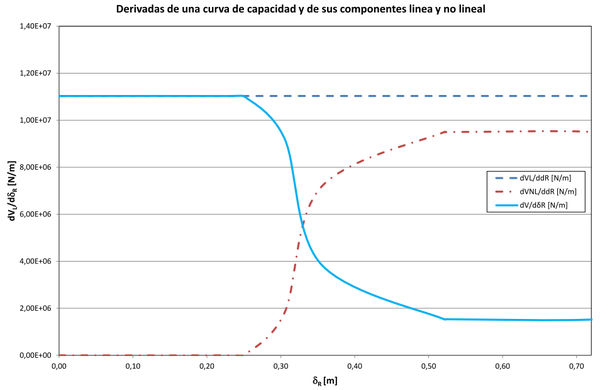
donde ${\textstyle {\boldsymbol {V}}_{\boldsymbol {NL}}}$ es la fuerza cortante no lineal, ${\textstyle {\boldsymbol {V}}_{\boldsymbol {L}}}$ es la fuerza cortante lineal, m es la pendiente del segmento lineal de la curva de capacidad, ${\textstyle {\delta }_{\boldsymbol {R}}}$ es el desplazamiento del techo y ${\textstyle {\boldsymbol {V}}}$ es la fuerza cortante basal. En la Figura 4 se muestra la curva de capacidad del mismo edificio de la Figura 1 antes de sufrir pérdidas de resistencia (curva V) y sus componentes lineal (curva VL) y no lineal (curva VNL), obtenidos con la consideración descrita. La primera derivada de cada una de estas curvas está en la Figura 5. Puede observarse que la primera derivada de la componente no lineal ${\textstyle {\boldsymbol {V}}_{\boldsymbol {NL}}}$ es ajustable a una curva de la función acumulativa lognormal definida por dos parámetros: la media, ${\textstyle \mu }$, y la desviación estándar ${\textstyle \beta }$. En esta curva está representada la degradación del edificio desde su condición de comportamiento lineal hasta la de máxima plastificación y colapso. Pujades et al. [3] recomiendan dar los siguientes pasos para efectos de lograr este ajuste matemático:

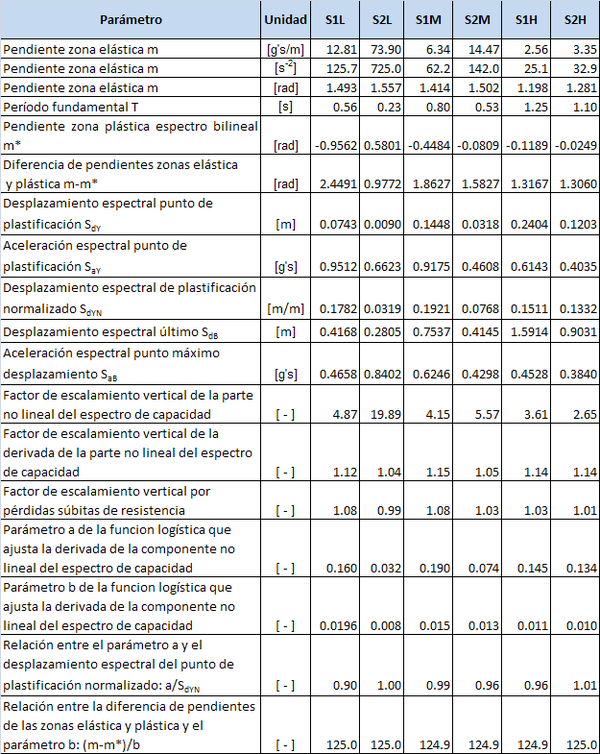
1) Obtener la derivada de la curva de capacidad, lo que incluye obtener la pendiente m de la recta que representa el comportamiento lineal del edificio. Para la estructura de la Figura 4, ${\textstyle m=1.103E7}$ N/m. Correspondientemente, la pendiente del segmento lineal del espectro de capacidad es ${\textstyle m_{cs}=2.555}$ [g's/m], o, lo que es lo mismo, ${\textstyle m_{cs}=25.07}$ [s^-2].

2) Calcular la parte no lineal de la curva de capacidad con la ecuación (7).

3) Normalizar esta última curva dividiendo las abscisas y las ordenadas por sus valores máximos.

4) Opcionalmente, normalizar también la derivada de la parte no lineal de la curva de capacidad.

5) Aplicar el método de mínimos cuadrados para obtener los parámetros ${\textstyle \mu }$ y ${\textstyle \beta }$ de la curva de la función acumulativa lognormal que mejor se ajusta la curva normalizada en el paso iii).

6) Dar los mismos pasos, pero en sentido contrario, a partir de la curva ajustada con el fin de comprobar la bondad del procedimiento por medio de comparar la curva original con la obtenida a partir de los parámetros encontrados.

Figura 4. Curva de capacidad de un edificio con sus componentes lineal y no lineal

Figura 5. Derivadas de una curva de capacidad y de sus componentes lineal y no lineal

Es de mencionar que el procedimiento descrito es aplicable tanto a la curva de capacidad como al espectro de capacidad. Los autores mencionados también aplican el modelo propuesto para obtener un nuevo índice de daño y un nuevo modelo de fragilidad. Sobre este último hacen referencia al proyecto Risk-UE, “An advanced approach to earthquake risk scenarios with applications to different European towns”, en cuyo documento “WP4: Vulnerability of current buildings” se han desarrollado modelos de vulnerabilidad y fragilidad para los tipos más representativos de los edificios europeos [4]. Lagomarsino y Giovinazzi [5], en desarrollo de los métodos allí expuestos, proponen una técnica sencilla que permite obtener las cuatro curvas de fragilidad a partir del espectro de capacidad bilineal mediante tres asunciones: (1) para cada estado de daño, k, la curva de fragilidad correspondiente tiene la forma de la distribución acumulativa lognormal, definida por los parámetros ${\textstyle \mu _{k}}$ y ${\textstyle \beta _{k}}$; (2) la distribución del daño corresponde a la distribución binomial [6] y (3) los umbrales ${\textstyle \mu _{k}}$ pueden definirse en función de los puntos característicos del espectro bilineal. Pujades et al. [3] definen estos umbrales en función de los puntos del espectro de capacidad bilineal normalizado. Para obtener el punto de plastificación de este espectro normalizado deducen la fórmula de la ecuación (8):

${\boldsymbol {S}}_{\boldsymbol {dYN}}{\boldsymbol {=1-2}}{\boldsymbol {S}}_{\boldsymbol {CN\_NL}}$

(8)

donde ${\textstyle {\boldsymbol {S}}_{\boldsymbol {dYN}}}$ es la abscisa normalizada del punto de plastificación y ${\textstyle {\boldsymbol {S}}_{\boldsymbol {CN\_NL}}}$ es el área bajo la curva de la parte no lineal normalizada. El resultado de calcular de esta manera dicho punto de plastificación se corresponde perfectamente con el obtenido con la ecuación (3). Finalmente, los autores dan un enfoque probabilístico al modelo como también lo hacen Díaz et al. [7]. A continuación, se aplicará esta técnica a edificios representativos de las principales subclases de edificios de acero, pero antes se describirán los edificios que se usaron en esta investigación.

4. Edificios de acero empleados en esta investigación

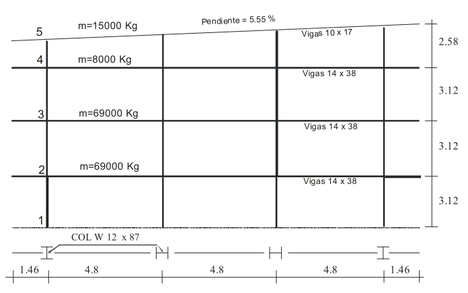
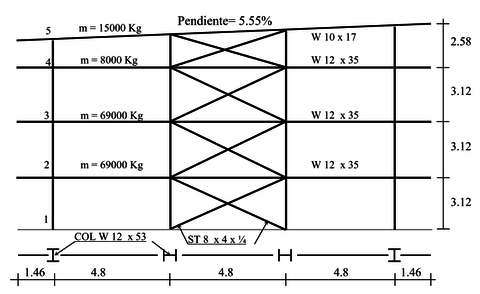
Los edificios de acero usados en este trabajo corresponden a los que se describieron y usaron en la tesis doctoral Vulnerabilidad sísmica de edificios de acero [8]. Se trata de seis edificios, que cubren las principales subclases de la clasificación establecida en la metodología HAZUS 99 [9], a saber, los edificios de acero resistentes a momento de baja, media y gran altura, en su orden subclases S1L, S1M, S1H, y los concéntricamente arriostrados de las mismas alturas, subclases S2L, S2M, S2H. Las alturas empleadas fueron: 12 m (tres plantas estructurales), 23 m (siete plantas) y 41 m (trece plantas) por lo cual son representativos de las 6 subclases mencionadas. Son regulares en planta y en altura. El área aferente en cada nivel es de 140 m². Las Figuras 6-11 presentan los miembros estructurales que las componen y su disposición. Estos fueron proyectados para las siguientes cargas: carga viva de ocupación 2 kN/m², carga muerta sobrepuesta al peso propio de la estructura, 4.2 kN/m², cargas sísmicas correspondientes a zona de peligrosidad sísmica alta, en la ciudad de Manizales, Colombia, calculadas con las Normas Colombianas de Diseño y Construcción Sismo Resistente NSR-98 [10], vigentes al momento de su construcción.

Figura 6. Pórtico resistente a momentos de baja altura

Figura 7. Pórtico arriostrado de baja altura

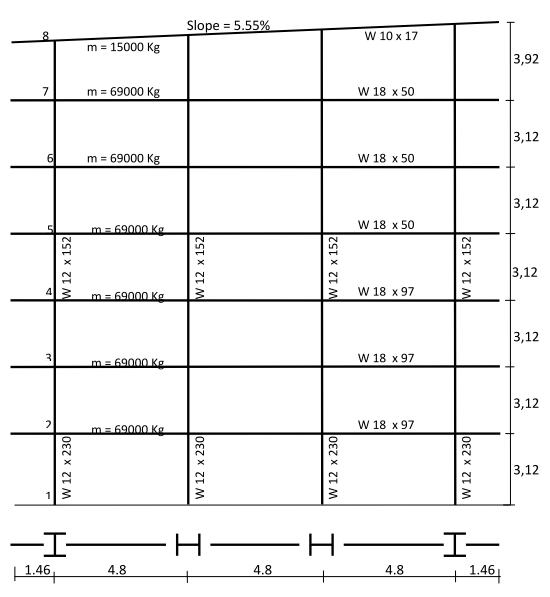
Figura 8. Pórtico resistente a momentos de altura media

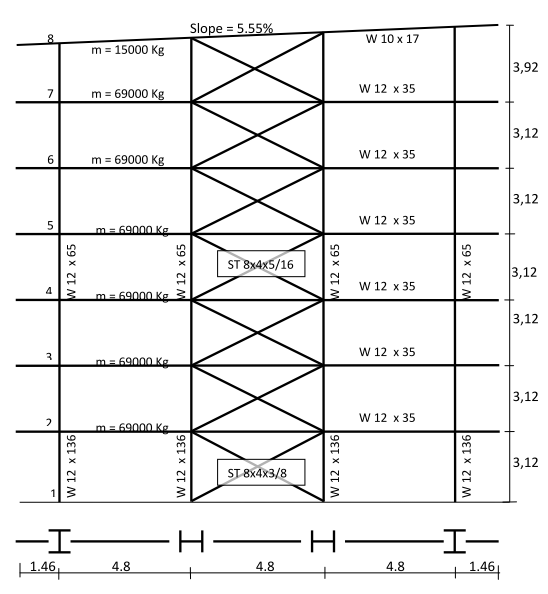
Figura 9. Pórtico resistente a momentos de altura media

Figura 10. Pórtico resistente a momentos de gran altura

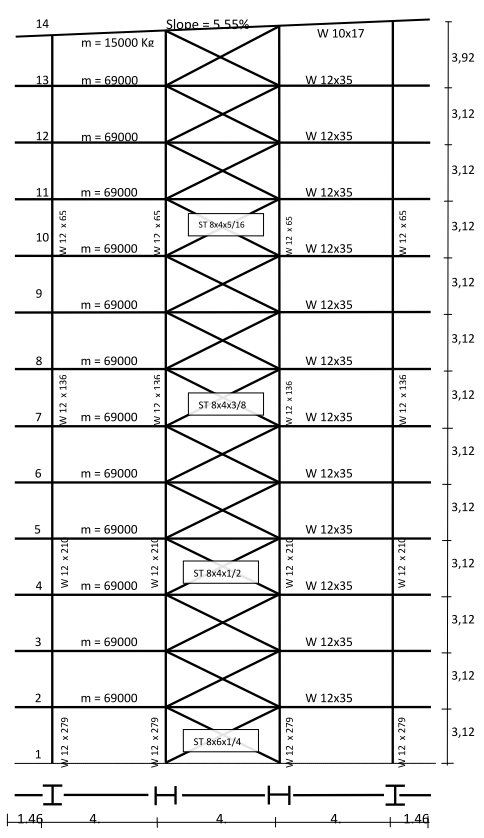
Figura 11. Pórtico arriostrado de gran altura

Un aspecto muy importante de estos edificios es que al proyectarlos se tuvo en cuenta el criterio de que la carga máxima en las columnas no debe superar el 50% de su resistencia a la compresión con el fin de que se puedan considerar miembros controlados por deformación, de alta ductilidad, en lugar de ser considerados miembros controlados por fuerza, de ductilidad nula [1]. Igualmente, se tuvo cuidado para garantizar el principio de columna fuerte, viga débil, con el fin de evitar plastificaciones tempranas en las columnas que pudieran llevar al colapso de la estructura. Para ello se aplicaron los criterios de Seismic Provisions for Structural Steel Buildings [11].

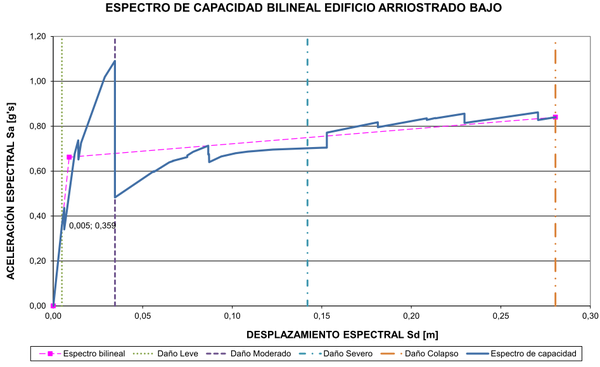
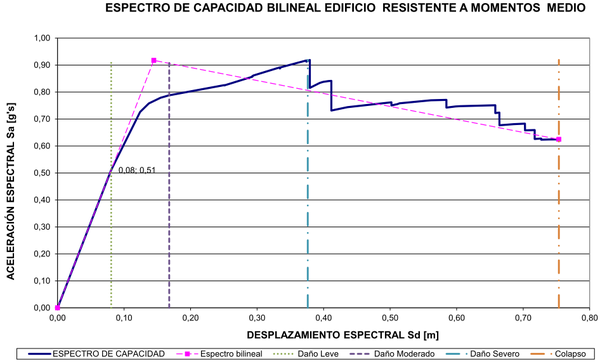
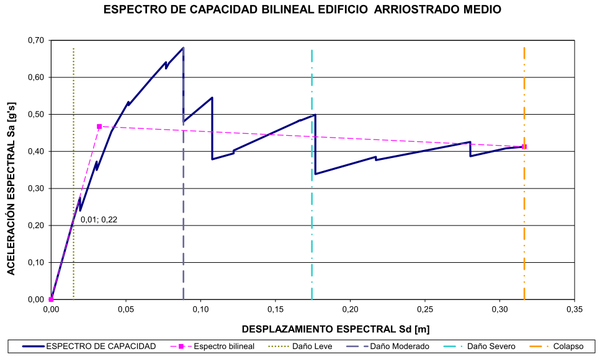
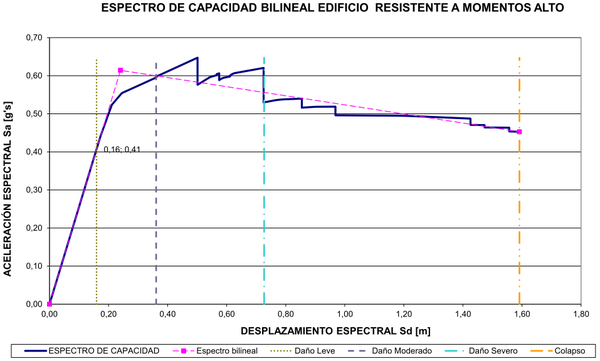
En las Figuras 8-11 se puede observar que la sección de las columnas se reduce a medida que se gana altura, como es práctica usual al proyectar edificios. Se nota así mismo que dichas reducciones no se hacen en todos los niveles sino que se mantiene la misma sección en longitudes que no superen los doce metros, máxima longitud comercial de tales perfiles. Igualmente, las secciones de las riostras se han mantenido constantes en los mismos tramos en los que se mantiene el mismo perfil de columna. Con respecto a las vigas, puede notarse que en los edificios arriostrados se mantiene la misma sección mientras que en los resistentes a momentos las secciones de las vigas cambian con la altura con el fin de contribuir a brindar la rigidez necesaria en cada piso. Como se ve, el dimensionamiento de los miembros estructurales se ha hecho atendiendo criterios de economía y practicidad por lo cual puede afirmarse que son representativos de las subclases estructurales a las que pertenecen. En las Figuras 12-17 aparecen los espectros de capacidad de estos edificios junto con los umbrales de los diferentes estados de daño.

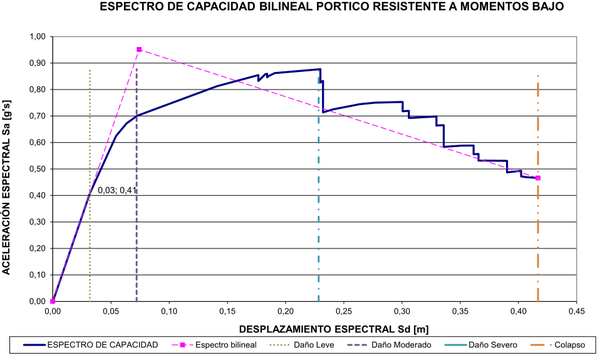
Figura 12. Espectro de capacidad edificio resistente a momentos de baja altura

Figura 13. Espectro de capacidad edificio arriostrado de baja altura

Figura 14. Espectro de capacidad edificio resistente a momentos de altura media

Figura 15. Espectro de capacidad edificio resistente a momentos de altura media

Figura 16. Espectro de capacidad edificio resistente a momentos de gran altura

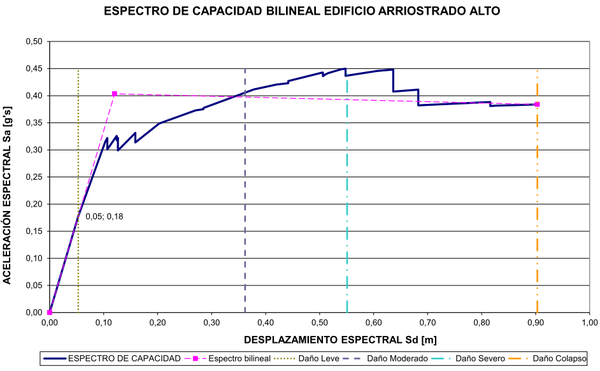
Figura 17. Espectro de capacidad edificio arriostrado de gran altura

5. Parametrización de los espectros de capacidad de edificios de acero

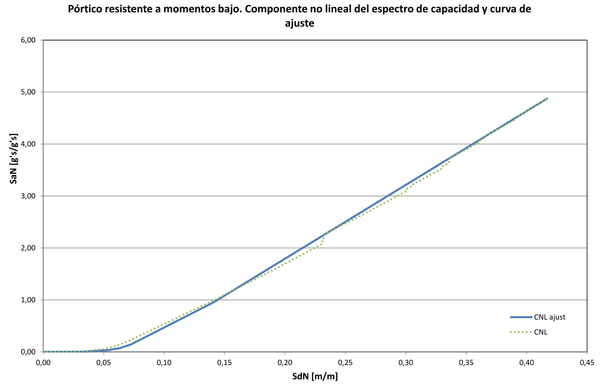
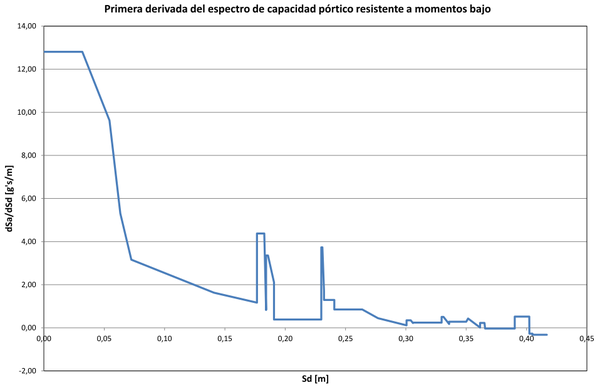
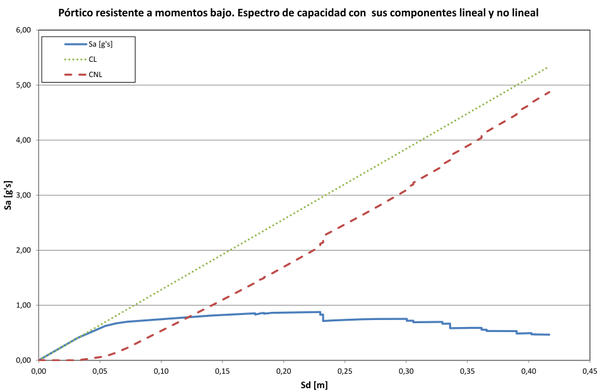
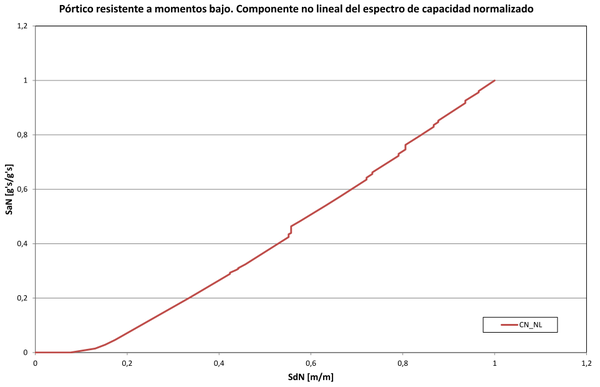
En esta sección se aplicará, con algunas modificaciones, el procedimiento propuesto por Pujades et al. [3] y que se describió en la sección 3, a los espectros de capacidad de los edificios de acero que se han presentado. En primer lugar, en la Figura 18 se presenta la primera derivada del espectro de capacidad del edificio resistente a momentos bajo, cuyo espectro de capacidad aparece en la Figura 12. En esta derivada se nota que el tramo inicial tiene una pendiente de 12.81 g’s/m, o lo que es igual, 125.7 s$^{-2}$. De acuerdo con la ecuación (5) su período es $T=0.56$ s. Con la pendiente obtenida y la ecuación (7) se calcula la parte no lineal del espectro de capacidad que puede apreciarse en la Figura 19, identificada como curva CNL. También aparece el espectro de capacidad (Curva Sa) y la parte lineal del mismo (curva CL). El siguiente paso es la normalización de la parte no lineal del espectro de capacidad. Esto se logra dividendo abscisas y ordenadas por su mayor valor. El resultado se muestra en la Figura 20. A continuación se obtiene la primera derivada del la parte no lineal del espectro de capacidad y se normaliza como se muestra en la Figura 21. Hasta este punto se ha seguido en todo el procedimiento recomendado por Pujades et al. [3].

Figura 18. Primera derivada de espectro de capacidad pórtico resistente a momentos bajo

Figura 19. Descomposición del espectro de capacidad en sus partes lineal y no lineal

Figura 20. Componente no lineal del espectro de capacidad normalizado

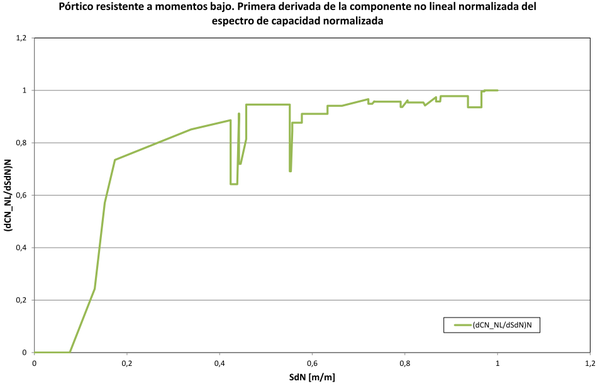
Figura 21. Primera derivada de la componente no lineal normalizada del espectro de capacidad normalizada

El siguiente paso a dar es ajustar la curva normalizada de la derivada de la componente no lineal normalizada del espectro de capacidad mediante una función matemática. En este trabajo se encontró que en lugar de usar la función lognormal es más conveniente usar la función logística, cuyas funciones de densidad de probabilidad y de distribución acumulativa están definidas por las ecuaciones (9) y (10) respectivamente. La conveniencia estriba en que la integral de la función de densidad está definida por una expresión analítica y por lo tanto no hay que recurrir a la integración numérica, como sucede en el caso de la función lognormal. Dicha integración numérica se ve afectada por el hecho de que justo en la zona donde la curva tiene un punto de inflexión, y que por ende corresponde a la media de la función de densidad, cuyos valores de probabilidad relativa son muy altos, las abscisas en las que está definida la curva no están los suficientemente cerca entre sí para que el error de la integración numérica sea bajo. El resultado final es que la integral sobre todo el espacio puede sobrepasar la unidad. Con la función logística se evita ese inconveniente. Queda definida por los parámetros a y b. Sus dos primeros momentos estadísticos son: la media ${\textstyle {\boldsymbol {\mu =a}}}$ y la varianza ${\textstyle {\sigma }^{\boldsymbol {2}}=}$${\frac {{\pi }^{\boldsymbol {2}}{\boldsymbol {b}}^{\boldsymbol {2}}}{\boldsymbol {3}}}$. En el ajuste se tuvo en cuenta no solo minimizar el error mediante el método de los mínimos cuadrados sino también el asegurarse de que la curva ajustada tuviera la misma forma de la curva original, sobretodo en su tramo inicial donde sus ordenadas son cero, con el fin de que en la reconstrucción del espectro de capacidad a partir de la curva ajustada se tuviera la verdadera pendiente que corresponde al comportamiento elástico. Para el edificio en estudio se encontró que la curva que mejor ajusta corresponde a los parámetros $a=0.16$ y $b=0.0196$ (Figura 22)

${\boldsymbol {p}}\left({\boldsymbol {x}}\right)=$${\frac {{\boldsymbol {e}}^{\left({\boldsymbol {-}}{\frac {\boldsymbol {x-a}}{\boldsymbol {b}}}\right)}}{{\boldsymbol {b}}{\left[{\boldsymbol {1+}}{\boldsymbol {e}}^{\left({\boldsymbol {-}}{\frac {\boldsymbol {x-a}}{\boldsymbol {b}}}\right)}\right]}^{\boldsymbol {2}}}}$

(9)

${\boldsymbol {F}}\left({\boldsymbol {x}}\right)=$${\frac {\boldsymbol {1}}{{\boldsymbol {1+}}{\boldsymbol {e}}^{\left({\boldsymbol {-}}{\frac {\boldsymbol {x-a}}{\boldsymbol {b}}}\right)}}}$

(10)

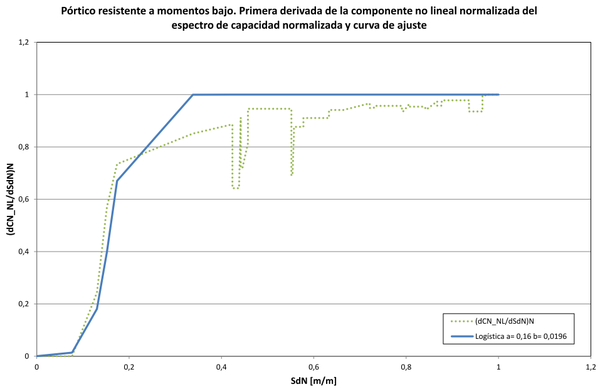
Figura 22. Primera derivada de la componente no lineal normalizada del espectro de capacidad normalizada con su curva ajustada con la función logística

Con la curva ajustada se ha procedido a dar los mismos pasos mostrados hasta ahora pero en sentido inverso. La Figura 23 contiene la integral de la curva ajustada (CN_NL ajust), la cual además ha sido mayorada por el inverso del factor de normalización de la derivada de la componente no lineal del espectro de capacidad. A pesar de dicha mayoración cuando se le compara con la obtenida previamente (curva CN_NL) se observa que no alcanza su mismo nivel. Esto sucede porque, como se ha señalado desde el principio de este artículo, el espectro de capacidad tiene pérdidas súbitas de resistencia por el agotamiento del comportamiento elasto plástico en las articulaciones plásticas. Esto obliga a que en este punto se haga una corrección a la curva ajustada por medio de multiplicarla por el inverso de la ordenada alcanzada, 0.924 en este caso, como está registrado en la figura. El resultado de este ajuste aparece en la Figura 24.

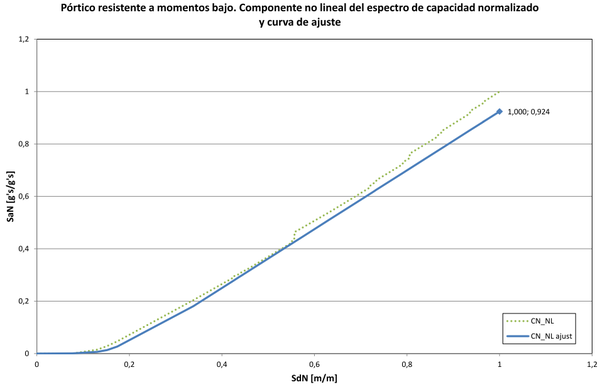
Figura 23. Integral de la curva ajustada a la parte no lineal del espectro junto al componente no lineal del espectro de capacidad normalizado original

Figura 24. Integral de la curva ajustada a la parte no lineal del espectro corregida por pérdidas de resistencia súbitas (CNL ajust) junto al componente no lineal del espectro de capacidad normalizado original (CNL)

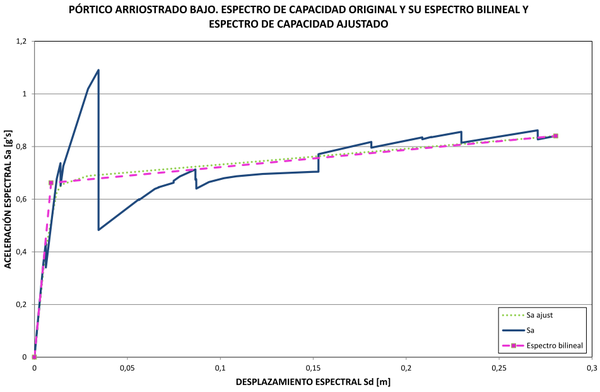
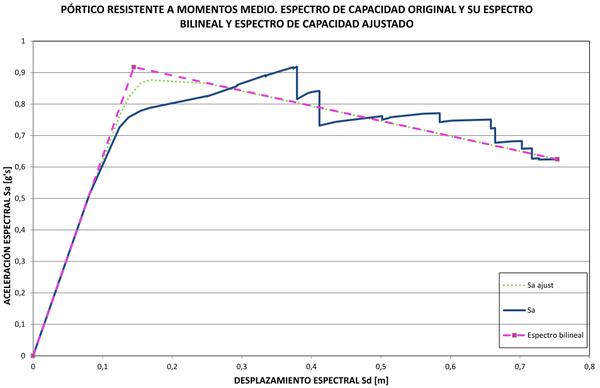
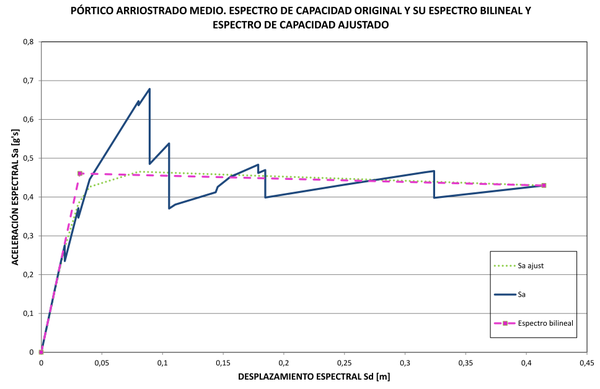
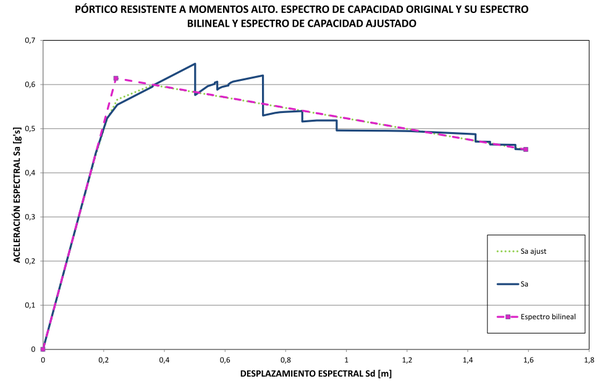
Finalmente, con la curva ajustada y corregida de la Figura 24 se puede reconstruir el espectro de capacidad del edificio aplicando inversamente la ecuación (4). El nuevo espectro aparece en la Figura 25 junto al original y su espectro bilineal. Es notable la coincidencia del espectro de capacidad ajustado con el espectro bilineal, especialmente en el tramo inicial, de comportamiento elástico, y en el tramo descendiente de degradación de resistencia hasta la rotura. El mismo procedimiento se ha llevado a cabo con los otros pórticos estudiados y el resultado final se muestra en las Figuras 26-30. De todas ellas, la de la Figura 26 es la única en la que la zona de comportamiento plástico del espectro bilineal tiene pendiente positiva. En general se nota un gran ajuste entre el espectro de capacidad obtenido con el procedimiento inverso y el espectro de capacidad bilineal original. La Tabla 2 contiene los parámetros envueltos, como son, las pendientes de los espectros bilineales, la abscisa normalizada del punto de plastificación, los factores de normalización y de corrección por pérdidas súbitas de resistencia y los parámetros a y b de la curva de ajuste de la derivada normalizada de la componente no lineal del espectro de capacidad normalizada. Además, se ha registrado en dicha tabla la relación directa que se ha encontrado entre los parámetros a y b y la geometría del espectro de capacidad bilineal. En la sección 6 se analizarán estos resultados.

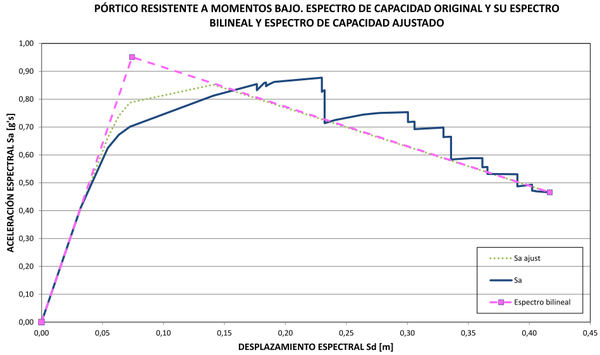
Figura 25. Espectro de capacidad original con su espectro bilineal y espectro ajustado. Edificio resistente a momentos bajo

Figura 26. Espectro de capacidad original con su espectro bilineal y espectro ajustado. Edificio arriostrado bajo

Figura 27. Espectro de capacidad original con su espectro bilineal y espectro ajustado. Edificio resistente a momentos medio

Figura 28. Espectro de capacidad original con su espectro bilineal y espectro ajustado. Edificio arriostrado medio

Figura 29. Espectro de capacidad original con su espectro bilineal y espectro ajustado. Edificio resistente a momentos alto

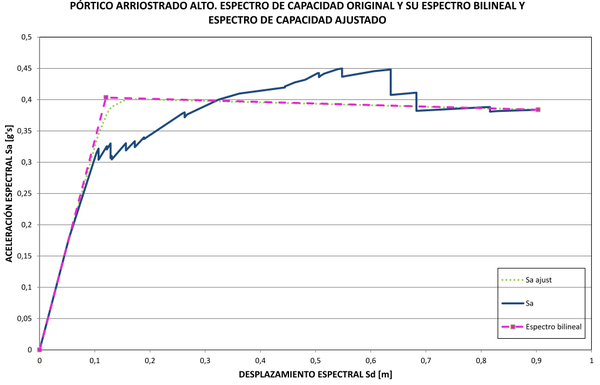
Figura 30. Espectro de capacidad original con su espectro bilineal y espectro ajustado. Edificio arriostrado alto

Tabla 2. Valores destacados del proceso de parametrización de los espectros de capacidad

6. Análisis de resultados y conclusiones

Como se indicó en la sección anterior, los dos últimos renglones de la Tabla 2 contienen interesantes relaciones entre los parámetros a y b de la función logística que ajusta la derivada de la componente no lineal del espectro de capacidad doblemente normalizada y los parámetros relacionados con la geometría del espectro de capacidad bilineal. En efecto, el parámetro a, que corresponde a la media de la función de densidad, está estrechamente relacionado con la posición del punto de plastificación en el espectro de capacidad normalizado, como se señaló en Pujades et al. [3]. Los valores indican que muchas veces la coincidencia es total y que como máximo la diferencia es del 10%.

Con respecto al parámetro b, se encontró que está directamente relacionado con la diferencia de pendientes entre la zona de comportamiento plástico y la de comportamiento elástico del espectro de capacidad bilineal. La relación entre la diferencia de dichas pendientes, medidas en radianes, y el parámetro b es una constante: 125.0. Este hecho y el indicado en el párrafo anterior permiten definir la función logística que ajusta la derivada de la componente no lineal del espectro de capacidad a partir de la geometría del espectro bilineal.

Otra importante conclusión de esta investigación es que la metodología propuesta en Parametric model for capacity curves [3] es aplicable también a los espectros de capacidad de los edificios de acero que incluyen pérdidas súbitas de resistencia por efecto del agotamiento del comportamiento elasto plástico de las rótulas plásticas, siempre y cuando se haga el ajuste correspondiente por dichas pérdidas, que para la amplia variedad de edificios cubierta en este trabajo implica el uso de un factor de corrección menor o igual a 1.08.

Como se anotó en su momento, se recomienda el uso de la función de distribución acumulativa logística, definida por la ecuación (10), para ajustar la derivada de la componente no lineal del espectro de capacidad doblemente normalizada, para evitar los inconvenientes que conlleva la integración numérica en abscisas muy distanciadas entre sí cercanas a la media de la función de densidad.

Referencias

[1] ASCE/SEI. Seismic evaluation and retrofit of existing buildings ASCE/SEI 41-13. American Society of Civil Engineers/ Structural Engineering Institute. Reston, Virginia, USA, 2013.

[2] ATC. Seismic evaluation and retrofit of concrete buildings (ATC-40). Applied Technology Council (ATC), Redwood City, California, USA, 1996.

[3] Pujades L.G., Vargas-Alzate Y.F., Barbat A.H., Gonzalez-Drigo J.R. Parametric model for capacity curves. Bull Earthquake Eng., 13:1347-1376, 2015.

[4] Milutinovic Z.V., Trendafiloski G.S. WP4 Vulnerability of Current Buildings. Risk-UE Project: An advanced approach to earthquake risk scenarios with applications to different European towns, 2003.

[5] Lagomarsino S., Giovinazzi S. Macroseismic and mechanical models for the vulnerability and damage assessment of current buildings. Bull Earthquake Eng., 4(4):415-443, 2206.

[6] Grünthal G. (ed.). European macroseismic scale 1998 EMS–98. Cahiers du Centre Européen de Géodynamique et de Séismologie, Luxembourg, 1998.

[7] Diaz S.A., Pujades L.G., Barbat A.H., Gonzalez-Drigo J.R., Hidalgo-Leiva D.A. Capacity parametric model and damage index for steel buildings. A probabilistic approach. Proceedings of the 16thWorld Conference on Earthquake Engineering, 16WCCE 2017, Santiago de Chile, 2017.

[8] Bermúdez C.A. Vulnerabilidad sísmica de edificios de acero. Tesis Doctoral, Universitat Politècnica de Catalunya, Barcelona, España, 2010.

[9] FEMA, NIBS. Earthquake loss estimation methodology (HAZUS 99). Federal Emergency Management Agency y National Institute of Building Sciences, Washington D.C., USA, 1999.

[10] AIS. Normas colombianas de diseño y construcción sismo resistente NSR-98. Asociación Colombiana de Ingeniería Sísmica, Bogotá D.C., Colombia, 1998.

[11] AISC. Seismic provisions for structural steel buildings. American Institute of Steel Construction, Chicago IL., USA, 1992.