Failure prediction in the neighbourhood of the hole in riveted joints with composite materials

1 Introducción

En uniones remachadas con presencia de laminados de materiales compuestos, requiere necesariamente la realización de taladros en las piezas a unir. Estos taladros generan un estado tensional complejo y activan mecanismos de fallo en los laminados que deben ser evaluados para una correcta predicción del fallo.

Aunque este problema se ha estudiado mediante diferentes enfoques, y sigue bajo estudio [1,2] disponer de los valores de las componentes de tensión responsables de estos mecanismos de fallo es siempre necesario.

Entre estos mecanismos de fallo que afectan a los materiales a unir, se encuentran: el fallo por tracción, el fallo por cortadura y el fallo por aplastamiento. Típicamente, el fallo por tracción está asociado a la tensión normal circunferencial σ_θθ en el contorno del taladro, el fallo por cortadura está asociado a la tensión tangencial τ_xy a lo largo de la línea de acción de carga en el espacio entre el taladro y el borde frontal del laminado, y por último, el fallo por aplastamiento está asociado a la tensión radial de compresión σ_rr motivado por el contacto del remache con la pared del taladro. Estas componentes del estado tensional (σ_θθ, τ_xy, σ_rr), responsables principales de cada uno de los mecanismos de fallo descritos (tracción, cortadura, aplastamiento) deben compararse con ciertos valore admisibles, o críticos (σ_{θθ_crit}, τ_{xy_crit}, σ_{rr_crit}) que determinan el instante en el que se cumple el criterio de fallo.

La determinación de ambos valores, el estado tensional por un lado, y las resistencias por otro, son problemas complejos. La complejidad asociada a la determinación del estado tensional alrededor del taladro (la parte izquierda de la ecuación) viene condicionada por el carácter no lineal del problema de contacto entre el remache y la pared del taladro, además de la naturaleza no isótropa de los materiales a unir. Y la dificultad asociada a la determinación de los valores de resistencia, está condicionada fuertemente por la ubicación en la que debe determinarse dicha resistencia a lo largo del contorno del taladro. Al ir variando la orientación relativa de la fibra respecto al borde del taladro, los valores de resistencia cambian fuertemente, no disponiendo típicamente de estos valores (suministrados por el fabricante) para cualquier orientación de fibras fuera de las direcciones de ortotropía del material.

Para resolver el primero de los problemas, se ha preparado un modelo de elementos finitos con el que se analizará el estado tensional alrededor del taladro para los casos de carga transferida y carga circulante (tanto de tracción como de compresión) y al 5 tipos diferentes de laminados (cuasi-isótropo, unidireccional a 0º de fibra de carbono, unidireccional a 90º de fibra de carbono, unidireccional a 0º de fibra de vidrio, y unidireccional a 90º de fibra de vidrio).

Para la determinación de las resistencias en cualquier ubicación a lo largo del contorno del taladro se va a realizar una estimación de las mismas, a partir de las resistencias conocidas en los ejes de ortotropía y aplicando la ley de transformación similar a la que se emplea con los valores de rigidez.

En el presente trabajo, e la sección 2 se detalla el modelo de elementos finitos aplicado, en la sección 3 se presentan los resultados de los modelos numéricos para los distintos casos analizados, en la sección 4 se presenta la estimación de la resistencia en cualquier punto del contorno del taladro y por último, en la sección 5 se muestra un ejemplo de como empleando los resultados del presente trabajo, es posible verificar los tres criterios de fallo (tracción, cortadura y aplastamiento) que afectan al material compuesto taladrado.

2 Modelo de Elementos Finitos

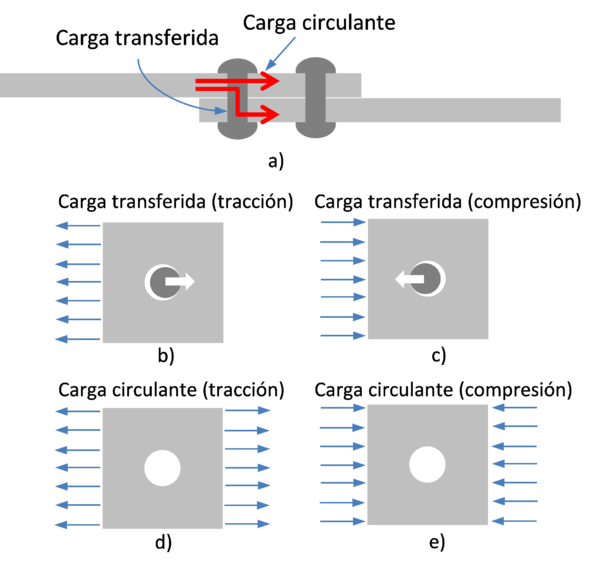
Para la evaluación de las tensiones en el entorno del taladro, se ha estudiado, por un lado, el problema de “carga transferida”, la parte de carga, en cada fila, que pasa por el remache, y por otro lado el problema de “carga circulante”, la parte de carga que circula alrededor del taladro para pasar por una fila de remaches posterior. Los problemas de carga transferida y circulante se han estudiado en tracción y compresión, que dada la no linealidad del problema de contacto, son problemas diferentes. Los cuatro casos analizados se muestran esquemáticamente en la Figura 1. Asumiendo un comportamiento lineal, cualquier estado tensional en una fila de remaches, se podrá analizar como la superposición de estos 4 estados analizados.

Figura 1. Casos analizados.

El modelo numérico se ha analizado con ANSYS imponiendo condiciones de simetría en las caras laterales (superior e inferior), aplicando tracción (o compresión) uniforme en la/las cara/s lateral/es (izquierda y/o derecha) y asumiendo para el círculo que simula el remache un comportamiento de sólido rígido.

Las propiedades mecánicas de los laminados son:

CFRP (E₁₁=141.3 GPa, E₂₂=9.58 GPa, G₁₂=5 GPa, ν₁₂=0.3), GFRP (E₁₁=39.5 GPa, E₂₂=8.22 GPa, G₁₂=4.1 GPa, ν₁₂=0.26), Isótropo (E₁₁=E₂₂=70 GPa, G₁₂=26.9 GPa, ν₁₂=0.3).

Los laminados de carbono (CFRP) y vidrio (GFRP) se han analizado con la orientación de la fibra en la dirección e la carga (0º) y perpendicular a la misma (90º).

Como elemento para la placa taladrada de material compuesto se ha usado el elemento PLANE182 (lineal, con 4 nodos y dos grados de libertad en cada nodo, u_x y u_y), para el contacto entre el remache y la pared del taladro se ha empleado el elemento CONTA172 conjuntamente con el elemento TARGE169 para un contacto superficie a superficie.

Dado que se modela una celda unidad, y se está asumiendo una separación entre remaches de 4 veces el diámetro del mismo, las dimensiones de los problemas analizados son: ratio entre las dimensiones del cuadrado (ancho = alto) y el diámetro del taladro igual a 4. El tamaño de los elementos en el contorno del taladro es de 0.035 (en relación a 1 que es el radio del taladro) lo que supone un elemento cada 2 grados.

3 Resultados del estado tensional

Para cada uno de los casos analizados, se han evaluado las tensiones circunferencial, tangencial y radial (σ_θθ, τ_xy, σ_rr), responsables de los tres mecanismos de fallo. Los resultados para las tensiones (σ_θθ, σ_rr) se evalúan a lo largo del contorno del taladro y se presentan adimensionalizadas respecto a la tensión de aplastamiento (σ_b=F/(d·t)) que es la fuerza que pasa por el remache (F), dividido por el producto del espesor del laminado (t) por el diámetro del taladro (d).

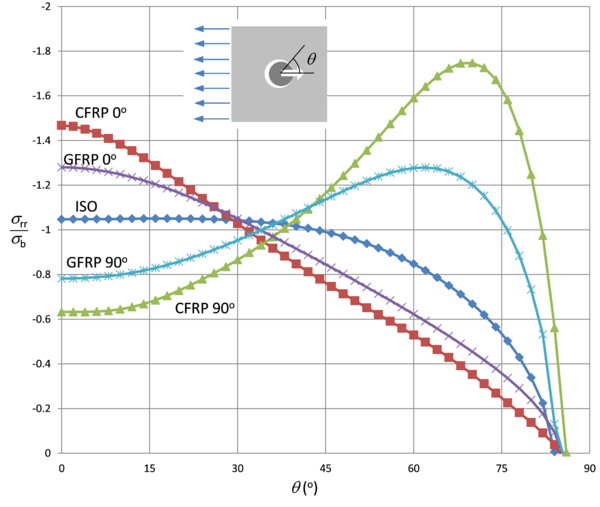
En la Figura 2 se muestra la tensión radial de compresión (σ_rr), resultante del contacto entre el remache y la pared del taladro, para 5 laminados distintos alrededor del contorno del taladro. Todos los casos presentan simetría respecto del eje horizontal y pérdida de contacto en el entorno de θ =90º, por lo que en la Figura 2, sólo se muestra el rango 0º<θ <90º.

Figura 2. Tensión σ_rrpara el caso de carga transferida de tracción.

Es interesante observar que cuando la orientación de la fibra no coincide con la dirección de aplicación de la carga, las orientaciones donde se producen los mayores valores de (σ_rr) no coinciden con la dirección de la carga, sino que están fuertemente condicionados por la orientación del material que presenta mayor rigidez (p.e. en el caso de 90º, tanto para carbono, como para vidrio, las máximas tensiones radiales se presentan en el entornode 60º< θ <70º , cerca de donde se pierde el contacto entre el remache y el taladro (θ=90º).

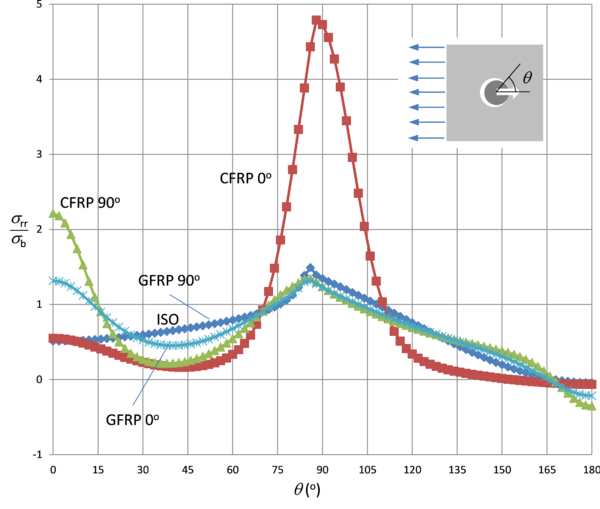
En la Figura 3 se muestra la tensión normal circunferencial (σ_θθ) a lo largo del contorno del taladro adimensionalizada con σ_b, para los mismo 5 laminados en el caso de carga transferida de tracción. Ahora el rango que se presenta es 0º<θ<180º dado que la pérdida del contacto entre el remache y el taladro no implica el valor nulo de la σ_θθ. En la Figura 3, la curva correspondiente al laminado isótropo se confunde con la curva correspondiente al laminado de vidrio de 90º.

Figura 3. Tensión σ_θθpara el caso de carga transferida de tracción.

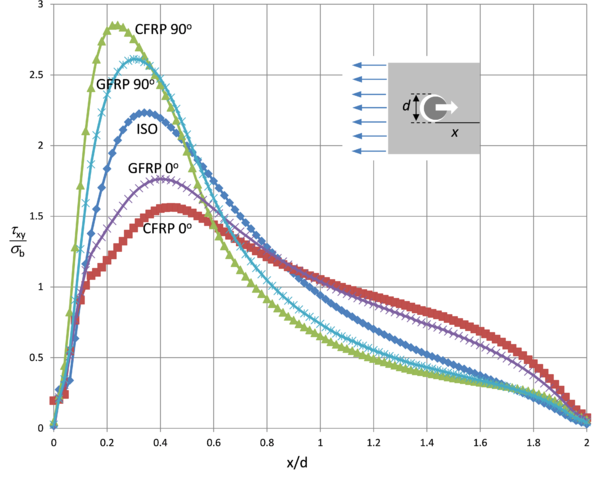
En la Figura 4 se muestra la tensión tangencial τ_xy, (adimensionalizada con σ_b) a lo largo de las líneas paralelas a la dirección de la carga y tangentes al taladro desde el mismo borde del taladro hasta el fin de la placa. El eje horizontal se presenta también adimensionalizado con el diámetro del taladro. En ambos extremos x/d=0, 2 la tensión tangencial es nula, por condiciones de contorno, tomando los mayores valores, para cualquier tipo de laminado a una distancia entre 0.2 y 0.4 veces el diámetro del taladro.

Figura 4. Tensión τ_xy,para el caso de carga transferida de tracción.

Por brevedad en la presentación de los resultados, sólo se han incluido en este apartado los resultados para el caso de carga transferida por tracción. Se han analizado y se dispone igualmente de los resultados de los casos de carga transferida por compresión, y los casos de carga circulantes (tracción y compresión) para los mismo 5 laminados.

4 Estimación de las resistencias

Una vez que disponemos de los valores del estado tensional de las componentes de tensión responsables de cada uno de los mecanismos de fallo (tracción, cortadura y aplastamiento) es necesario ahora tener una estimación de los valores de resistencia en las mismas ubicaciones donde se han evaluado las tensiones. Sin embargo, a diferencia de lo que se puede analizar numéricamente, los valores de resistencia necesitan ensayos para su determinación, y los fabricante (y laboratorios de ensayo) típicamente sólo facilitan los valores de resistencia de los laminados en direcciones de ortotropía. A efectos de evaluar los posibles criterios de fallo, estos valores sólo nos permitirían evaluar el fallo en dichas orientaciones (0º y 90º)

Una estimación de las resistencias del laminado, en cualquier orientación, se puede obtener empleando la misma ley de transformación para las resistencia que la que se emplea para los valores de rigidez (ver [2]). De este modo, la resistencia a aplastamiento σ_{rr_crit} se evaluaría multiplicando una resistencia a aplastamiento (compresión) fija del laminado, por la rigidez radial E_r que sí tendría la dependencia con la orientación de la fibra que muestra la Ecuación (1).

${\textstyle {\frac {1}{{E}_{r}}}={\frac {1}{{E}_{x}}}{cos}^{4}\theta +\left({\frac {1}{{G}_{xy}}}-\right.}$$\left.{\frac {2{\nu }_{xy}}{{E}_{x}}}\right){sen}^{2}\theta {cos}^{2}\theta +{\frac {1}{{E}_{y}}}{sen}^{4}\theta$

(1)

Lo mismo se haría con la resitencia asociada al fallo por tracción, con la rigidez E_θ asociada a la dirección tangente al taladro en cualquier punto de su contorno con una deformación máxima admisible a tracción, y al fallo por cortadura, empleando una rigidez a cortadura G_sn que se obtiene de girar la G_xy del laminado y una deformación a cortadura.

${\textstyle {\frac {1}{{E}_{\theta }}}={\frac {1}{{E}_{x}}}{sen}^{4}\theta +}$$\left({\frac {1}{{G}_{xy}}}-{\frac {2{\nu }_{xy}}{{E}_{x}}}\right){sen}^{2}\theta {cos}^{2}\theta +$${\frac {1}{{E}_{y}}}{cos}^{4}\theta$

(2)

${\textstyle {\frac {1}{{G}_{sn}}}={\frac {1}{{G}_{xy}}}+\left({\frac {1+{\nu }_{xy}}{{E}_{x}}}+\right.}$$\left.{\frac {1+{\nu }_{xy}}{{E}_{y}}}-{\frac {1}{{G}_{xy}}}\right){sen}^{2}\theta$

(3)

Empleando estas leyes de variación, sólo es necesario dispones de los valores de deformación máxima admisibles en las direcciones de ortotropía del laminado. En ausencia de dichos valores, se pueden tomar valores orientativos que sí están disponibles en la literatura (p.e. para laminados de fibra de vidrio se puede tomar: ε_{r_crit}=0.002, ε_{θ_crit}=0.0020.004, γ_{s_crit}=0.0010.0025) Téngase en cuenta que la dependencia de las resistencias con la orientación del laminado está en las correspondientes leyes de variación mostradas en las ecuaciones (1-3).

5 Ejemplo de aplicación

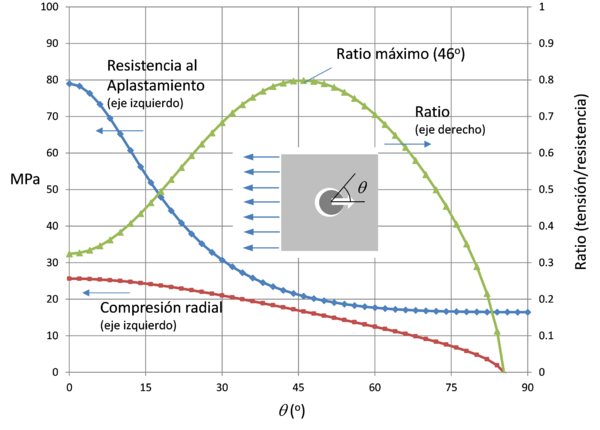
Una vez que se dispone de los valores tensionales y de resistencia, la evaluación de los criterios de fallo es sencilla. Para cada criterio de fallo se evalúa el ratio entre la tensión y la resistencia (σ_θθ, τ_xy, σ_rr) y (σ_{θθ_crit}, τ_{xy_crit}, σ_{rr_crit}) respectivamente para todas las orientaciones/ubicaciones en las que se han evaluado, obteniendo la orientación/ubicación donde se produce y el criterio de fallo más desfavorable. Como ejemplo, en la Figura 5 se muestra la evaluación del criterio de fallo por aplastamiento para un caso concreto con un remache con carga transferida por tracción y con un laminado de fibra de vidrio a 0º. La orientación más desfavorable se encuentra a 46º, donde el ratio σ_rr/σ_{rr_crít} es más alto.

Figura 5. Ejemplo de aplicación del criterio de fallo por aplastamiento.

6 Conclusiones

En el presente trabajo se ha obtenido, numéricamente, el estado tensional en el entorno de los taladros en uniones remachadas para distintos tipos de laminados (carbono y vidrio) y orientaciones (0º, 90º e isótropo).

Se han analizado los casos de carga transferida y carga circulante, que permiten, por superposición, la determinación del estado tensional completo para cualquier combinación de ambas cargas en una unión real.

La estimación de las resistencias mediante la transformación de los valores de resistencias en ejes de ortotropía a cualquier orientación en el entorno del taladro, permite comparar dichas resistencias con los valores de tensión previamente obtenidos y determinar así, a) el criterio de fallo más desfavorable en la unión, y b) la ubicación del punto donde se produce el fallo.

Referencias

[1] P.P.Camanho, G.H.Erçin, G.Catalanotti, S.Mahdi, P.Linde. A finite fracture mechanics model for the prediction of the open-hole strength of composite laminates. Composites Part A: Applied Science and Manufacturing, 43 (8), pág. 1219-1225 (2012).

[2] J.Reinoso, A.Arteiro, M.Paggi, P.P.Camanho, Strength prediction of notched thin ply laminates using finite fracture mechnics and the phase phield approach. Composites Science and Technology 150, pág. 205-216 (2017).

[3] J.L.Clarke & European Structural Polymeric Composites Group.. Structural design of polymer composites: EUROCOMP design code and handbook. London: E & FN Spon. (1996).