Mono-objective minimization of operation cost for a microgrid with renewable power generation, energy storage and electric vehicles

Resumen

Cuando se habla de Microgrid se hace alusión a un sistema de potencia a pequeña escala, compuesto de elementos activos (generación renovable y tradicional, almacenamiento de energía y cargas controlables) operando entre ellos. Diferentes estudios han evaluado y modelado el costo de operación de varios elementos que integran la Microgrid, con el fin de identificar los puntos de operación correctos. En este estudio, se evaluó un modelo de Microgrid cuyo generador principal es diésel, posee un parque de generación fotovoltaica, dos turbinas eólicas, un banco de baterías y dos agregadores que gestionan vehículos eléctricos. El objetivo de esta investigación es plantear una ecuación capaz de describir el costo de operación de una Microgrid como conjunto, teniendo en cuenta los modelamientos del costo de operación de la energía fotovoltaica, la energía eólica, el almacenamiento de energía en bancos de baterías y vehículos eléctricos. Esta ecuación ademas busca obtener la mayor rentabilidad posible o, en otras palabras, disminuir al máximo el costo de operación de la Microgrid. Para esto, se usó el método metaheurístico DEEPSO (Differential Evolutionary Particle Swarm Optimization), que es muy conocido por sus aplicaciones en sistemas de potencia. A través de este método se puede determinar las condiciones de operación de los diferentes elementos que tiene la Microgrid, con el fin de disminuir al máximo el costo de su operación. Teniendo en cuenta todos los parámetros, se encontró y visualizó el comportamiento de cada uno de los elementos de la Microgrid en un horizonte de tiempo de 24 horas para obtener el costo mínimo de operación.

Palabras Clave: Despacho económico, vehículos eléctricos, almacenamiento de energía, algoritmos metaheurísticos, microrredes, optimización mono-objetivo, energías renovables, costo de incertidumbre

Abstract

The term Microgrid refers to a power system in a small scale, made of active elements operating between them, namely renewable and traditional generation, energy storage and controllable charges. Previous studies have evaluated and modelled the operation cost of many elements that make up the Microgrid, in order to identify the correct point of operation. In this study, the researchers evaluated a model of Microgrid with diesel as traditional generator, a park of photovoltaic generation, two wind generators, one battery bank and two aggregators that manage electric vehicles. The objective of this research is to propose an equation capable of describing the operation cost of a Microgrid as a set, taking into account the modelling of the operation cost of photovoltaic energy, wind energy, and energy storage in battery banks and electric vehicles. This equation also seeks to obtain the best possible cost efficiency, i.e., decreasing the operation cost of the Microgrid. For this purpose, the Metauristic method DEEPSO (Differential Evolutionary Particle Swarm Optimization) was used, recognized for its performance for applications in power systems. Through this method, and determinate the conditions of operation of the different elements in the Microgrid. Taking into account all the parameters, the behavior of each one of the elements of the Microgrid in a 24-hour lapse was found and visualized.

Keywords: Economic dispatch, electric vehicles, energy storage, metaheuristic algorithm, microgrid, mono-objective optimization, renewable energy, uncertainty cost

1. Introducción

En la práctica, la ingeniería eléctrica no solamente busca el desarrollo de tecnologías y de soluciones para un problema en específico, sino que también debe buscar la solución más óptima. En el mundo de los negocios, esta solución se determina haciendo un balance entre el costo de la alternativa con respecto a los beneficios obtenidos por la misma. En el caso de una Microgrid (MG), siempre se busca minimizar el costo de operación mientras se mantiene con excelencia el servicio a los usuarios.

Esfuerzos recientes han utilizado diferentes algoritmos para encontrar el punto de operación óptimo en una MG. Por ejemplo en la referencia [1] se usó Hybrid differential evolution and harmony search (hybrid DE-HS) algorithm, mientrs que en la referencia [2] la función objetivo busca minimizar el costo de operar la MG teniendo en cuenta las redes AC y DC. Estos son los estudios más recientes en la evaluación de parámetros de operación de una MG, para minimizar el costo de operación sin devaluar el servicio prestado a los usuarios. Otros estudios [3,4] han considerado franjas horarias en las cuales el valor de la energía es mayor o menor dependiendo del consumo por parte de los usuarios. Por otro lado, algunas investigaciones han contemplado vehículos eléctricos en la MG, como los V2G (Vehicle2Grid) que tienen la facultad tanto de cargarse usando la energía de la red como de entregar de vuelta la energía almacenada. No obstante, esta característica tiene una serie de restricciones tanto de potencia como de energía. Las restricciones se han manejado usando la estrategia más eficaz para reducir el pico de carga y aumentar la potencia consumida en el valle que se presenta en la curva de la demanda de los usuarios. Para solucionar esto, la metodología de las referencias [5,6] fue usar diferentes precios en diferentes franjas horarias.

En una MG, no solamente se consideran los vehículos eléctricos sino también todos sus componentes, su arquitectura básica y el manejo inteligente de la energía, como se puede ver en la referencia [7]. Una parte vital para el funcionamiento de una MG es el almacenamiento de energía, por esto hay dos características importantes para definir el costo asociado al uso de este sistema. La primera es el costo de la energía utilizando los bancos de baterías y la segunda es el costo asociado a la pérdida de vida de las baterías conforme va transcurriendo el tiempo. Varios modelos utilizados fueron presentados en la referencia [8], donde un problema multiobjetivo busca optimizar en igual proporción las dos características anteriormente mencionadas.

El uso de las energías renovables para minimizar el consumo de combustible y el costo de generación con energías convencionales es una característica valiosa en las MG, como se muestra en las referencias [9]–[11]. En varias ocasiones, las energías renovables se acompañan con bancos de almacenamiento de energía [10,11]. Considerando la operación en conjunto, se han hecho estudios que buscan la optimización de varios objetivos como la optimización de los flujos de potencia [12], el manejo inteligente de la energía [13], disminución de las emisiones de CO2 [14,15] y la carga no atendida [15]. Todos estos estudios de problemas multiobjetivo usan los diagramas de Pareto para encontrar el mejor punto de operación del sistema que se evalúa en cada caso, sin embargo, todos usan algoritmos diferentes. Dela misma manera ocurre en problemas mono objetivos, como se muestra en la referencia [16], donde se busca minimizar las pérdidas totales de la red usando el algoritmo MOSEK. Como se observa, la mayoría de los artículos usan una gran variedad de algoritmos metaheurísticos y algoritmos genéticos entre muchos otros. En este trabajo, se utilizará el algoritmo DEEPSO, que fue ganador en el concurso Application of Modern Heuristic Optimization Algorithms for Solving Optimal Power Flow Problems gracias a que obtuvo los mejores resultados [17].

Uno de los problemas de la implementación de energías renovables es la incertidumbre asociada a su disponibilidad. Por esto, el modelamiento de varios elementos se tendrá en cuenta en el desarrollo de este trabajo. Estos elementos son: fuentes de energía renovables, el ciclo de vida del almacenamiento de energía a través de baterías [18] y por último, los vehículos híbridos que pueden tanto entregar como devolver energía a la red [19]. Para el análisis, se tiene en cuenta un modelo de la disponibilidad de la potencia eólica [20,21], un modelo de disponibilidad de la potencia fotovoltaica [21] y su operación con los vehículos eléctricos como un conjunto [22].

En este artículo, la operación de una MG se optimizará al máximo, minimizando el costo de operación durante un horizonte de tiempo de 24 horas, que representa un día normal de la MG. Se tendrá en cuenta el uso de Plug-in Hybrid Electric Vehicle, el uso de energías renovables como la solar y la eólica, un almacenamiento de energía y los costos asociados a los modelos de incertidumbre de la disponibilidad de potencia solar y eólica. Todo este planteamiento se resuelve usando el algoritmo DEEPSO, el cual ha tenido reconocimientos debido a que ha sido el mejor resolviendo problemas relacionados con flujos de potencia y manejo de energía en redes eléctricas.

2. Formulación del problema

En términos generales, el problema se caracteriza por los diferentes costos asociados a la operación de la MG. Estos costos, en términos generales, están descritos y expresados en la ecuación (1), donde ${\textstyle {F}_{1}\left(x\right)}$ es el costo asociado a la generación tradicional, ${\textstyle {F}_{2}\left(x\right)}$ es el costo de operar vehículos eléctricos, ${\textstyle {F}_{3}\left(x\right)}$ es el costo de operar los bancos de baterías y ${\textstyle {F}_{4}\left(x\right)}$ es el costo asociado a la incertidumbre de las energías renovables

${\textstyle {\hbox{Costo Operación }}=F_{1}\left(x\right)+{F}_{2}\left(x\right)+}$${F}_{3}\left(x\right)+{F}_{4}\left(x\right)$

(1)

1. Costo de las energías convencionales (${\textstyle {F}_{1}\left(x\right)}$):

Los costos de los generadores de energías convencionales o hidráulicas se modelan usando una función polinómica, la cual es de grado 2 la mayoría de las veces. La ecuación (2) muestra el modelo según la referencia [21]:

${\textstyle {C}_{i}\left({P}_{s,i}\right)=\,{\alpha }_{i}+{\beta }_{i}{P}_{s,i}+}$${\gamma {P}_{s,i}}^{2}$

(2)

2. Costo de operar vehículos eléctricos (${\textstyle {F}_{2}\left(x\right)}$):

Para el análisis de costos asociados a vehículos eléctricos, en este estudio se considera cierto número de Plug-in Electric Vehicles (PEVs), que se agrupan en agregadores o Parking decks. Estos agregadores se definen como un ente que agrupa un número de vehículos eléctricos para hacerse cargo de la carga de los mismos cuando sea más apropiado en términos económicos, como se muestra en la referencia [23]. A cada uno de los agregadores se asocian los valores de potencia y la cantidad de kilómetros que pueden recorrer los vehículos que se tienen a su cargo. Luego, se procede a estimar una hora de llegada del vehículo al sitio de carga, al igual que una hora de salida. El propósito es planear la carga de los vehículos en las franjas horarias de menor costo y en las de mayor costo poder entregar a la red la energía que tienen disponible, de manera que se logre minimizar el costo de operación en la gestion de los PEVs.

Toda la información referente a la función que modela el costo de la operación y carga de los vehículos, junto a sus límites y planteamiento fue tomada de la referencia [23]. Lo primero que realizan los agregadores es calcular el máximo despacho de energía para el vehículo eléctrico, para ver si es factible su operación y carga. El estado de carga de los vehículos se encuentra hora a hora durante todo el día teniendo en cuenta su estado inicial de carga ${\textstyle {SOC}_{ni}^{D,a}}$, como se muestra en la ecuación (3):

${SOC}_{ni}^{D,a}=\mathrm {min} \,({SOC}_{ni}^{D},{SOC}_{ni}^{A}+\left({\frac {{H}_{ni}\cdot \rho \cdot {P}_{max}\cdot \Delta t}{{B}_{ni}}}\right),$ $\forall ni\,\in Ni,\,\forall i\,\in$

(3)

Un PEV tiene límites tanto superiores como inferiores en el intervalo ${\textstyle [{t}_{k},{t}_{k+{H}_{i}-1}]}$, expresado analíticamente en la ecuación (4). En la ecuación (5), se tienen los límites máximos y mínimos después de su salida, y se especifica la energía mínima del PEV en el intervalo [k+j] el cual puede ser por lo menos ${\textstyle \rho \cdot {P}_{max}\cdot \Delta t}$ menor que la energía en el intervalo [k+j+1], y a su vez nunca será menor que su estado inicial de energía con la que llega. La ecuación (6) implica el estado inicial de la energía y en la ecuación (7) se asegura que el valor máximo de energía del PEV después de varios periodos de tiempo de carga no sea mayor a la energía máxima del mismo (${\textstyle {SOC}_{ni}^{D,a}{B}_{ni}}$)

${e}_{ni}^{max}\left({t}_{k+j}\right)={e}_{ni}^{min}\left({t}_{k+j}\right)={SOC}_{ni}^{D,a}{B}_{ni},\,j=$ ${H}_{ni},\,....\,,{H}_{i},\,\forall ni\,\in Ni,\,\forall i\,\in \,I$

(4)

${\textstyle {e}_{ni}^{min}\left({t}_{k+j}\right)=\mathrm {max} \,\left({e}_{ni}^{min}\left({t}_{k+j+1}\right)-\rho \cdot {P}_{max}\cdot \Delta t,\,{SOC}_{ni}^{A}\cdot {B}_{ni}\right),}$ $j=0,\ldots ,{H}_{ni}-1,\,$ $\forall ni\,\in Ni,\,\,\forall i\,\in \,I$

(5)

${\textstyle {e}_{ni}^{max}\left({t}_{k}\right)={SOC}_{ni}^{A}\cdot {B}_{ni},\,\,\forall ni\,\in Ni,\,\,\forall i\,\in \,I}$

(6)

${e}_{ni}^{max}\left({t}_{k+j}\right)=\mathrm {min} \,\left({e}_{ni}^{min}\left({t}_{k+j-1}\right)-\rho \cdot {P}_{max}\cdot \Delta t,\,{SOC}_{ni}^{D,a}\cdot {B}_{ni}\right),$ $j=0,\ldots ,{H}_{ni}-1,\,$ ${\textstyle \forall ni\,\in Ni,\,\,\forall i\,\in \,I}$

(7)

Así como se tienen límites de energía también los hay de potencia, los cuales se muestran en la ecuación (8) cuando los vehículos están conectados y en la ecuación (9) cuando los vehículos ya no están en el horizonte de tiempo en el que se cargan

${\textstyle {P}_{ni}^{\mathrm {max} \,\left({t}_{k+j}\right)}={P}_{max},}$ $j=0,\ldots ,{H}_{ni}-1,\,\qquad \forall ni\,\in \,\,Ni,\,\forall i\,\in I$

(8)

${\textstyle {P}_{ni}^{\mathrm {max} \,\left({t}_{k+j}\right)}=0,\,\,j=}$${H}_{ni},\ldots ,{H}_{i}-1,\,\left(When\,{H}_{ni}<{H}_{i}\right),\,\forall ni\,\in \,\,Ni,\,\forall i\,\in I$

(9)

De acuerdo con las ecuaciones anteriores, se plantearon los límites de energía en las ecuaciones (10) y (11) y de potencia en la ecuación (12), considerando en todas la agrupación de los vehículos

${E}_{i}^{\mathrm {min} \,\left({t}_{k+j}\right)}=\sum _{ni\,\in Ni}^{}{e}_{ni}^{\mathrm {min} \,\left({t}_{k+j}\right)},\,j=0,\ldots ,Hi,\,\forall i\,\in I$

(10)

${E}_{i}^{\mathrm {max} \,\left({t}_{k+j}\right)}=\sum _{ni\,\in Ni}^{}{e}_{ni}^{\mathrm {max} \,\left({t}_{k+j}\right)},\,j=0,\ldots ,Hi,\,\forall i\,\in I$

(11)

${\textstyle {P}_{i}^{\mathrm {max} \,\left({t}_{k+j}\right)}=\mathrm {min} \,\left(\sum _{ni\,\in \,Ni}^{}{P}_{ni}^{\mathrm {max} \,\left({t}_{k+j}\right)},\,Ai{\xi }_{i}\left({t}_{k+j}\right)\lambda \right),}$ $j=0,\ldots ,Hi-1,\qquad \forall i\,\in \,\,I$

(12)

La función ${\textstyle {F}_{2}\left(x\right)}$ se expresa como la ecuación (13), que representa el costo de operar la MG y se desea minimizar teniendo en cuenta las restricciones presentadas en las ecuaciones (14), (15), (16) y (17).

$\mathrm {min} \,j\left({t}_{k}\right)={F}_{2}\left(x\right)=\,\sum _{i\in I}^{}\sum _{j=0}^{H-1}c\left({t}_{k+j}\right)\cdot {P}_{i}^{pref}\left({t}_{k+j}\right)\cdot \Delta t+$$\mu \sum _{j=0}^{H-1}\theta \left(t\right)-\ldots$ ${\textstyle \ldots \,k\sum _{j=0}^{H-1}\left(H-j\right){P}_{i}^{pref}\left({t}_{k+j}\right)}$

(13)

${\textstyle s.t\,{P}_{i}^{pref}\left({t}_{k+j}\right)\leq {P}_{i}^{max}\left({t}_{k+j}\right),}$ $j=0,\ldots ,{H}_{i}-1\,,\qquad \forall i\in I$

(14)

${\textstyle {P}_{i}^{pref}\left({t}_{k+j}\right)=0,\,j=}$$Hi,\ldots ,\,H\,\left(Si\,aplica\right),\,\forall i\,\in I$

(15)

${E}_{i}^{min}\left({t}_{k+j}\right)\leq \sum _{\tau =0}^{J-1}\rho \cdot {P}_{i}^{pref}\left({t}_{k+\tau }\right)\cdot \Delta t+$${E}_{i}^{max}\left({t}_{k}\right)\leq {E}_{i}^{max}\left({t}_{k+j}\right),\,$ ${\textstyle J=1,\ldots ,{H}_{i},\qquad \forall i\,\in I}$

(16)

${\textstyle \sum _{i\in I}^{}{P}_{i}^{pref}\left({t}_{k+j}\right)\leq {A}_{T}\left({t}_{k+j}\right)-}$ ${L}_{b}\left({t}_{k+j}\right)+\theta \left({t}_{k+j}\right),$ $j=0,\ldots ,H-1$

(17)

La Tabla 1 muestra la notación utilizada en las ecuaciones.

Tabla 1. Notaciones costo de operación vehículos eléctricos

I	Agrupación de Parking Decks, $I=M$.
${N}_{i}$	Número de puertos de carga en cada uno de los Parking Decks.
${A}_{i}$	Capacidad del transformador de distribución local, que le sirve tanto a la comunidad como al Parking Deck i, ${\textstyle i\in I}$.
${\xi }_{i}\left({t}_{k+j}\right)$	La capacidad que está disponible en el transformador de distribución local y que puede ser usada para cargar los PEV en el intervalo (k+j).
𝜆	Factor de potencia promedio de carga.
$\rho$	Eficiencia de Carga.
${e}_{ni}^{max}\left({t}_{k+j}\right)$	Límite superior de energía de un PEV en el puerto ${\textstyle {n}_{i}}$ del Parking Deck i, en el intervalo (k+j), en KW h.
${e}_{ni}^{min}\left({t}_{k+j}\right)$	Límite inferior de energía de un PEV en el puerto ${\textstyle {n}_{i}}$ del Parking Deck i, en el intervalo (k+j), en KW h.
${p}_{ni}^{\mathrm {max} \,\left({t}_{k+j}\right)}$	Límite superior de potencia de un PEV en el puerto ${\textstyle {n}_{i}}$ del Parking Deck i, en el intervalo (k+j), en KW.
${E}_{i}^{\mathrm {max} \,\left({t}_{k+j}\right)}$	Límite superior de energía del Parking Deck i, en el intervalo (k+j), en KW h.
${E}_{i}^{min}\left({t}_{k+j}\right)$	Límite inferior de energía del Parking Deck i, en el intervalo (k+j), en KW h.
${P}_{ni}^{\mathrm {max} \,\left({t}_{k+j}\right)}$	Límite superior de potencia del Parking Deck i, en el intervalo (k+j), en KW.
${H}_{ni}$	Es el horizonte de tiempo en el que el PEV está cargándose y se prevé la planeación del PEV ubicado en el puerto de conexión ${\textstyle {n}_{i}}$ del Parking Deck i. En este número de intervalos se desea cargar cada PEV a su SOC deseado.
${H}_{i}$	Es el horizonte de tiempo del Parking Deck i, el cual es seleccionado como el número máximo de los horizontes de planeación de todos los PEVs.
${SOC}_{ni}^{D,a}$	El estado de carga máximo posible del PEV en el puerto ${\textstyle {n}_{i}}$ en el Parking Deck i.

3. Costo de operar los bancos de baterías (${\textstyle {F}_{3}\left(x\right)}$):

El costo de operar los bancos de baterías es el mismo costo de vida del equipo de generación renovable (${\textstyle {C}_{bl}}$). Esto se muestra en la ecuación (18), donde ${\textstyle {L}_{loss}}$ es la pérdida de vida de las baterías y ${\textstyle {C}_{init-bat}}$ es el costo de inversión inicial de las baterías. Se asume como convención que la potencia de las baterías cuando se están cargando son de signo negativo y cuando se están descargando de signo positivo

${\textstyle {F}_{3}\left(x\right)={C}_{bl}={L}_{loss}\cdot {C}_{init-bat}}$

(18)

La pérdida de vida de las baterías (${\textstyle {L}_{loss}}$) se define en la ecuación (19), donde ${\textstyle {A}_{c}}$ es el rendimiento acumulado en Ah efectivo en cierto periodo de tiempo y ${\textstyle {A}_{total\,}}$ es el rendimiento acumulado en Ah efectivo en el ciclo de vida. Como se menciona en la referencia [8], se estima que una batería con tamaño Q Ah puede entregar 390Q Ah efectivos a lo largo de su vida útil

${\textstyle {L}_{loss}={\frac {{A}_{c}}{{A}_{total}}}}$

(19)

${\textstyle {A}_{c}}$ se expresa en la ecuación (20) y depende del estado de carga (State of Charge, SOC) y el actual rendimiento en Ah real Ac’

${\textstyle {A}_{c}={\lambda }_{SOC}{A}_{c}^{'}}$

(20)

donde ${\textstyle {\lambda }_{SOC}}$ es el factor de ponderación efectivo. Como se muestra en la referencia [8], el ${\textstyle {SOC}_{min}}$ será de 0.5, en caso de que sea mayor se comportará aproximadamente lineal (ecuación (21))

${\textstyle {\lambda }_{SOC}=k\ast SOC+d}$

(21)

Para hallar este costo, se tienen en cuenta las restricciones del estado de carga mínimo y máximo de las baterías y la potencia de las baterías que debe ser mayor o igual a la potencia máxima de carga y menor a la potencia máxima de descarga, como se muestra en la ecuación (22)

${\textstyle {SOC}_{min}\leq SOC\leq {SOC}_{max}}$

(22)

${\textstyle {P}_{Carga-max}\leq SOC\leq {SOC}_{Descarga-max}}$

(23)

4. Costo debido a la incertidumbre (${\textstyle {F}_{4}\left(x\right)}$):

Según la referencia [21], el costo asociado a la incertidumbre se puede describir como se muestra en la ecuación (23), donde ${\textstyle {C}_{PV}}$ es el costo asociado al generador fotovoltaico y ${\textstyle {C}_{w}}$ es el costo asociado al generador eólico

${\textstyle {F}_{4}\left(x\right)={C}_{incertidumbre}={C}_{PV}+\,{C}_{w}}$

(24)

1. Generador Fotovoltaico

El costo asociado al generador fotovoltaico (${\textstyle {C}_{PV}}$) se muestra en la ecuación (24) y depende de dos funciones que se presentan en la referencia [21] y se desarrollan en la referencia [24]. La primera función ocurre porque se subestima el generador y es representada por ${\textstyle {C}_{PV,u,i}}$. La otra función es debido a que se sobrestima el generador y se representa con ${\textstyle {C}_{PV,o,i}}$. Estas dos funciones dependen de la potencia programada en el generador fotovoltaico (${\textstyle {W}_{PV,s,i}}$) y la potencia disponible en el mismo (${\textstyle {W}_{PV,i}}$)

${C}_{PV}=\sum _{i=1}^{{N}_{PV}}{C}_{PV,u,i}\left({W}_{PV,s,i},{W}_{PV,i}\right)+$$\sum _{i=1}^{{N}_{PV}}{C}_{PV,o,i}\left({W}_{PV,s,i},{W}_{PV,i}\right)$

(25)

La potencia de un panel solar se expresa dependiendo de la región de trabajo, como en Caso A o B, que se muestra continuación:

${W}_{PV}\left(G\right)=\left\{{\begin{matrix}{W}_{PV,r}\cdot {\frac {{G}^{2}}{{G}_{r}{R}_{c}}},\,\,0<G<{R}_{c},\,\,Caso\,A\\{W}_{PV,r}\cdot {\frac {{G}^{2}}{{G}_{r}}},\,\,G>{R}_{c},\,\,Caso\,B\end{matrix}}\right.$

(26)

donde: ${\textstyle {W}_{PV}\left(G\right)}$ es la potencia fotovoltaica generada como función de la irradiancia, ${\textstyle G}$ la irradiancia solar, ${\textstyle {G}_{r}}$ la irradiancia estándar en el ambiente, ${\textstyle {R}_{c}}$ un valor de irradiancia de referencia y ${\textstyle {W}_{PVr}}$ la potencia nominal de salida de la celda fotovoltaica.

1. Caso Subestimado

$E\left[{C}_{PV,u,i}\left({W}_{PV,s,i},{W}_{PV,i}\right),A\right]=\,\,$ ${\frac {\left(-1\right){C}_{PV,u,i}{W}_{PV,s,i}}{2}}\left[\mathrm {erf} \,\left({\frac {{\frac {1}{2}}\mathrm {ln} \,\left({\frac {{w}_{Rc}{G}_{r}{R}_{c}}{{W}_{PV\,r}}}\right)-\lambda }{{\sqrt {2}}\beta }}\right)-\right.$$\left.\mathrm {erf} \,\left({\frac {{\frac {1}{2}}\mathrm {ln} \,\left({\frac {{w}_{PV,s,i}{G}_{r}{R}_{c}}{{W}_{PV\,r}}}\right)-\lambda }{{\sqrt {2}}\beta }}\right)\right]+$ ${\frac {{C}_{PV,u,i}{W}_{PV\,r}{e}^{2\lambda +2{\beta }^{2}}}{{G}_{r}{R}_{c}2}}\left[\mathrm {erf} \,\left({\frac {{\frac {1}{2}}\mathrm {ln} \,\left({\frac {{w}_{Rc}{G}_{r}{R}_{c}}{{W}_{PV\,r}}}\right)-\lambda }{{\sqrt {2}}\beta }}-{\sqrt {2}}\beta \right)-\right.$$\left.\mathrm {erf} \,\left({\frac {{\frac {1}{2}}\mathrm {ln} \,\left({\frac {{w}_{PV,s,i}{G}_{r}{R}_{c}}{{W}_{PV\,r}}}\right)-\lambda }{{\sqrt {2}}\beta }}-{\sqrt {2}}\beta \right)\right]$

(27)

$E\left[{C}_{PV,u,i}\left({W}_{PV,s,i},{W}_{PV,i}\right),B\right]=\,$ ${\frac {{C}_{PV,u,i}{W}_{PV,s,i}}{2}}\left[\mathrm {erf} \,\left({\frac {\mathrm {ln} \,\left({\frac {{w}_{Rc}{G}_{r}}{{W}_{PV\,r}}}\right)-\lambda }{{\sqrt {2}}\beta }}\right)-\right.$$\left.\mathrm {erf} \,\left({\frac {\mathrm {ln} \,\left({\frac {{w}_{PV,\infty ,i}{G}_{r}}{{W}_{PV\,r}}}\right)-\lambda }{{\sqrt {2}}\beta }}\right)\right]+$ $+{\frac {{C}_{PV,u,i}{W}_{PV\,r}\cdot {e}^{\lambda +{\beta }^{2}/2}}{{2\cdot G}_{r}}}\left[\mathrm {erf} \,\left({\frac {\mathrm {ln} \,\left({\frac {{w}_{PV,\infty ,i}{G}_{r}}{{W}_{PV\,r}}}\right)-\lambda }{{\sqrt {2}}\beta }}-{\frac {\beta }{\sqrt {2}}}\right)-\right.$$\left.\mathrm {erf} \,\left({\frac {\mathrm {ln} \,\left({\frac {{w}_{Rc}{G}_{r}}{{W}_{PV\,r}}}\right)-\lambda }{{\sqrt {2}}\beta }}-{\frac {\beta }{\sqrt {2}}}\right)\right]$

(28)

2. Caso Sobreestimado

${[C}_{PV,o,i}\left({W}_{PV,s,i},{W}_{PV,i}\right),A]=\,{\frac {-{C}_{PV,o,i}{W}_{PV,s,i}}{2}}\left[\mathrm {1+erf} \,\left({\frac {\mathrm {ln} \,\left({\frac {{w}_{Rc}{G}_{r}}{{W}_{PV\,r}}}\right)-\lambda }{{\sqrt {2}}\beta }}\right)\right]+$$\ldots$ ${\frac {{C}_{PV,o,i}{W}_{PV\,r}{e}^{2\lambda +2{\beta }^{2}}}{{G}_{r}{R}_{c}2}}\left[\mathrm {erf} \,\left({\frac {{\frac {1}{2}}\mathrm {ln} \,\left({\frac {{w}_{Rc}{G}_{r}{R}_{c}}{{W}_{PV\,r}}}\right)-\lambda }{{\sqrt {2}}\beta }}-{\sqrt {2}}\beta \right)+\right.$$\left.1\right]\quad \quad \quad \quad \quad \,\,$

(29)

${[C}_{PV,o,i}\left({W}_{PV,s,i},{W}_{PV,i}\right),B]=$ ${\frac {{C}_{PV,o,i}{W}_{PV,s,i}}{2}}\left[\mathrm {erf} \,\left({\frac {\mathrm {ln} \,\left({\frac {{w}_{Rc}{G}_{r}}{{W}_{PV\,r}}}\right)-\lambda }{{\sqrt {2}}\beta }}\right)-\right.$$\left.\mathrm {erf} \,\left({\frac {\mathrm {ln} \,\left({\frac {{w}_{PV,s,i}{G}_{r}}{{W}_{PV\,r}}}\right)-\lambda }{{\sqrt {2}}\beta }}\right)\right]+$ ${\frac {{C}_{PV,o,i}{W}_{PV\,r}\cdot {e}^{\lambda +{\beta }^{2}/2}}{{2\cdot G}_{r}}}\left[\mathrm {erf} \,\left({\frac {\mathrm {ln} \,\left({\frac {{w}_{PV,s,i}{G}_{r}}{{W}_{PV\,r}}}\right)-\lambda }{{\sqrt {2}}\beta }}-{\frac {\beta }{\sqrt {2}}}\right)-\right.$$\left.\mathrm {erf} \,\left({\frac {\mathrm {ln} \,\left({\frac {{w}_{Rc}{G}_{r}}{{W}_{PV\,r}}}\right)-\lambda }{{\sqrt {2}}\beta }}-{\frac {\beta }{\sqrt {2}}}\right)\right]$

(30)

2. Generador Eólico

El costo asociado al generador fotovoltaico ( ${\textstyle {C}_{w}}$) (ecuación (27)) depende de dos funciones que aparecen en la referencia [21] y se desarrollan en la referencia [24]. La primera función es debido a que se subestima el generador, representada por ${\textstyle {C}_{PV,u,i}}$, y la otra debido a que se sobrestima el generador, representada por ${\textstyle {C}_{w,o,i}}$ . Estas dos funciones dependen de la potencia programada en el generador eólico ( ${\textstyle {W}_{w,s,i}}$) y la potencia disponible en el mismo ( ${\textstyle {W}_{w,i}}$)

${C}_{w}=\sum _{i=1}^{{N}_{w}}{C}_{w,u,i}\left({W}_{w,s,i},{W}_{w,i}\right)+\sum _{i=1}^{{N}_{w}}{C}_{w,u,i}\left({W}_{w,s,i},{W}_{w,i}\right)$

(31)

La potencia de un generador eólico se define en función de la velocidad del viento como se puede ver a continuación:

${\textstyle {W}_{w}\left(v\right)=\left\{{\begin{matrix}0,\quad \quad \,\,v<{v}_{i}\,o\,v>{v}_{o}\\\rho \cdot v+k,\quad {v}_{i}<v<{v}_{r}\\{W}_{r},\quad \quad \quad \,{v}_{r}<v<{v}_{o}\end{matrix}}\right.}$

(32)

donde ${\textstyle {W}_{w}\left(v\right)}$ es la potencia eólica generada en la función de la velocidad del viento, ${\textstyle v}$ la velocidad de viento de corte inferior del aerogenerador, ${\textstyle {v}_{i}}$ la velocidad de viento de corte inferior del aerogenerador, ${\textstyle {v}_{r}}$ la velocidad de viento nominal del aerogenerador, ${\textstyle {v}_{o}}$ la velocidad de viento de corte superior del aerogenerador y ${\textstyle {W}_{r}}$ la potencia nominal del aerogenerador

${\textstyle \rho ={\frac {{W}_{r}}{{v}_{r}-{v}_{i}}}\quad \quad y\quad \quad k=}$${\frac {-{W}_{r}{v}_{i}}{{v}_{r}-{v}_{i}}}$

(33)

1. Caso Subestimado

${C}_{w,u,i}\left({W}_{w,s,i},{W}_{w,i}\right)=$ ${\frac {{C}_{w,u,i}}{2}}\left({\sqrt {2\pi }}\rho \sigma \left(erf\left({\frac {{W}_{w,s,i}-k}{{\sqrt {2}}\rho \sigma }}\right)-\right.\right.$$\left.\left.erf\left({\frac {{W}_{r}-k}{{\sqrt {2}}\rho \sigma }}\right)\right)+\right.$$\left.2\left({W}_{w,s,i}-{W}_{r}\right){e}^{-\left({\frac {{W}_{r}-k}{{\sqrt {2}}\rho \sigma }}\right)}\right)+$ ${\frac {{C}_{w,u,i}}{2}}\left({e}^{-{\frac {{{V}_{r}}^{2}}{2{\sigma }^{2}}}}-{e}^{-{\frac {{{V}_{0}}^{2}}{2{\sigma }^{2}}}}\right)\left({W}_{r}-\right.$$\left.{W}_{w,s,i}\right)$

(34)

2. Caso Sobreestimado

${C}_{w,o,i}\left({W}_{w,s,i},{W}_{w,i}\right)={C}_{w,o,i}{W}_{w,s,i}\cdot \left(1-\right.$$\left.{e}^{-{\frac {{V}_{i}^{2}}{2{\sigma }^{2}}}}+{e}^{-{\frac {{V}_{0}^{2}}{2{\sigma }^{2}}}}+\right.$$\left.{e}^{-{\frac {{k}^{2}}{2{\rho }^{2}{\sigma }^{2}}}}\right)-$ ${\frac {{{\sqrt {2\pi }}C}_{w,u,i}\rho \sigma }{2}}\left(erf\left({\frac {{W}_{w,s,i}-k}{{\sqrt {2}}\rho \sigma }}\right)-\right.$$\left.erf\left({\frac {-k}{{\sqrt {2}}\rho \sigma }}\right)\right)$

(35)

3. Metodología de solución mediante algoritmos metaheurísticos

1. Algoritmos Heurísticos y Metaheurísticos

Cuando se tiene un problema matemático no polinomial, en la mayoría de ocasiones se necesitan grandes esfuerzos computacionales para encontrar la respuesta o simplemente no tienen solución analítica por ser no convexos. Esto significa que las soluciones de alta calidad que posee el problema no están uniformemente distribuidas en el espacio de soluciones. El método de solución heurística usa un conjunto de procedimientos simples, que la mayoría de las veces vienen de la experiencia, lo que permite resolver el sistema con menores esfuerzos computacionales. Estos métodos permiten encontrar un óptimo local que no necesariamente es el óptimo global, debido a que estos algoritmos renuncian desde el punto de vista teórico a encontrar el óptimo global. A diferencia de los metaheurísticos, estos algoritmos tienen el inconveniente de que son diseñados para encontrar soluciones buenas, más no los óptimos globales, debido a que en su algoritmo de solución no poseen mecanismos que les permitan salir de los óptimos locales en el espacio de soluciones [25].

Por el contrario, los algoritmos metaheurísticos tienen una serie de técnicas que les permiten salir de las soluciones locales. No obstante, es muy difícil lograr conseguir el valor del óptimo global, aunque se obtienen valores cercanos. Los algoritmos metaheurísticos se basan en la teoría heurística y la combinan con otros algoritmos, como por ejemplo los algoritmos genéticos, entre muchos otros. Estas combinaciones se hacen para compensar las falencias de unos algoritmos con otros, obteniendo mejores resultados en la solución del problema de optimización planteado [25].

2. Algoritmos Genéticos

Los algoritmos genéticos se consideran algoritmos metaheurísticos, útiles cuando se pretende resolver problemas buscando la solución óptima global gracias a los mecanismos que les permiten escapar de soluciones óptimas locales. Estos métodos tienen esfuerzos computacionales mayores a los heurísticos, pero siguen siendo aceptables en términos prácticos. La razón por la que se denominan algoritmos genéticos es porque están planteados de la misma forma en la que funciona la selección natural en la naturaleza, la cual conlleva la supervivencia de los más dotados y que ganan en la búsqueda de recursos. De la misma manera, el algoritmo genético parte de una población inicial que es el conjunto de soluciones iniciales, evalúa las mejores soluciones con derecho a participar en la generación de nuevos descendientes, realiza una recombinación (“Crossover”) entre estas y, finalmente, un proceso de mutación determina los elementos de la nueva generación [25].

3. Algoritmo DEEPSO

DEEPSO es el resultado de la combinación de varios métodos de optimización. Cada uno de los métodos combinados para dar lugar a DEEPSO presentan una serie de dificultades relacionadas con análisis de un problema en específico, el procesamiento y la precisión de los resultados obtenidos. Por este motivo, se combinaron varios métodos, con el fin crear un método más robusto y general.

Este algoritmo se origina del método EPSO (Evolutionary Particle Swarm Optimization) y el método PSO (Particle Swarm Optimization), el cual proporciona el poder de auto-adaptación de los Algoritmos Evolutivos (EA), para obtener como resultado lo mejor de dos mundos [26].

1. DE (Diferential Evolution)

La idea original del Diferencial Evolution (DE) es que dada una población (enjambre) de individuos (partículas, vectores), se genera una nueva solución de un individuo existente mejorándolo con una combinación de otros dos puntos. En otras palabras, en cada nueva población originada se establece una recombinación adicional que garantice una mayor diversidad y un procedimiento de selección que fabrique la siguiente generación. Esta selección es elitista y basada en uno-a-uno, esto significa que cada padre compite por la supervivencia directamente con su único hijo y solo lo mejor es retenido [26].

2. PSO (Particle Swarm Optimization)

La optimización de enjambre de partículas (PSO) se basa en una regla de movimiento que genera nuevos individuos en el espacio, a partir de un conjunto de alternativas previamente conocidas. Desde dicha regla de movimiento básica, se produce un nuevo vector individual de soluciones X para la iteración (K+1):

${\textstyle {X}^{\left\{k+1\right\}}={X}^{\left\{k\right\}}+{V}^{\left\{k\right\}}}$

(36)

donde V es la velocidad de la partícula y está definida como:

${\textstyle {V}^{\left\{k+1\right\}}=\,A{V}^{\left\{k\right\}}+B\left({b}_{i}-\right.}$$\left.{X}^{k}\right)+C\left({b}_{G}-{X}^{k}\right)$

(37)

donde ${\textstyle {b}_{G}}$ es el mejor punto hasta ahora encontrado por el enjambre y ${\textstyle {b}_{i}}$ es el mejor antepasado directo de la partícula, con ${\textstyle {b}_{i}}$, i=1, ... N partículas que es igual a ${\textstyle {P}_{b}}$ y forma el conjunto de los mejores ancestros en el comportamiento histórico de cada partícula. En este método se está considerando una población que incluye no sólo las partículas activas, sino también las que son antepasados inmediatos y el conjunto de los mejores antepasados. De esta manera, se evalúa el camino recorrido por la partícula en los cambios recientes [26].

3. EPSO (Evolutionary Particle Swarm Optimization)

Es una recombinación adaptiva evolutiva. Como se muestra en la referencia [26], el propósito del algoritmo EPSO es proporcionar la habilidad de adaptación al parámetro de recombinación. Para ello, se usan los elementos de la ecuación:

${\textstyle {V}^{\left\{k+1\right\}}=\,A{V}^{\left\{k\right\}}+B\left({b}_{i}-\right.}$$\left.{X}^{k}\right)+C\left({b}_{G}-{X}^{k}\right)$

(38)

Esta ecuación está sujeta a mutación y selección, de tal forma que se pueda obtener una mejor tasa de progreso. Si se tiene una población formada por un conjunto de partículas, la estructura general de EPSO resulta en:

• Replicación: cada partícula clonada r veces (normalmente r = 1).

• Mutación: en cada partícula r los parámetros A, B, C son mutados.

• Reproducción: cada partícula r+1 (original y clon) produce un descendiente por medio de la recombinación.

• Evaluación: se le evalúa la aptitud de cada población.

• Selección: mediante un proceso de selección como torneo estocástico, se forma una nueva generación con el mejor descendiente de cada antepasado, esto es posible ya que cada individuo perteneciente a una generación anterior tiene un descendiente.

4. Resultados de la programación de la operación de una MG de muestra

Para el desarrollo de las simulaciones fue necesario definir los parámetros asociados con las capacidades de los generadores presentes en la MG (Tabla 2). De la misma manera, el tratamiento de cada uno de los sistemas presentes tenía una serie de valores que se debían colocar para poder realizar la simulación. Estos parámetros se especifican en las Tablas 3-7.

Tabla 2. Capacidades de los generadores

Notación	Valor	Descripción y Unidades
Cbat	960	Capacidad del banco de baterías [kWh]
Cpv	100	Capacidad del sistema fotovoltaico [kW]
Cwt	210	Capacidad eólica [kW]
Cd	200	Capacidad Diésel [kW]

Tabla 3. Parámetros de la batería

Notación	Valor	Descripción y Unidades
SOCmin	0.5	Estado de carga mínimo
SOCmax	0.95	Estado de carga máximo
SOCi	0.6	Estado de carga inicial
Q	1000	Amperios hora de la batería
Atotal	390*Q	Total de Amperios acumulados durante todo el ciclo de vida
k	-1.5	Parámetro 1 para calcular el factor de ponderación efectiva
d	2.05	Parámetro 2 para calcular el factor de ponderación efectiva

Tabla 4. Costos

Notación	Valor	Descripción y Unidades
Costdiesel	0.8	Tomado de la Energy Information Administration del U.S Department of Energy (DOE)
CUbat	180	Precio de las baterías por KWh (Tomado de la referencia [27])
Ctransbat	1.5	Sobrecosto por transporte de baterías
Cinit	Cbat*CUbat*Ctransbat	Costo Inicial de las baterías, en dólares
CostSolar	0.0803	Costo de la Energía Solar (USD/kWh) (Tomado de la referencia [28])
CostWind	0.130	Costo de la energía eólica (USD/kWh)

Tabla 5. Parámetros del sistema eólico

Notación	Valor	Descripción y Unidades
Wr	29.93	Potencia Nominal del Aerogenerador [MW]
Vr	14.4774	Velocidad de viento nominal del aerogenerador [m/s]
Vin	4	Velocidad de viento de corte inferior del aerogenerador [m/s]
Vout	16.03	Velocidad del viento del corte superior del aerogenerador [m/s]

Tabla 6. Parámetros del sistema fotovoltaico

Notación	Valor	Descripción y Unidades
Wpvr	20	Potencia nominal de salida de la celda fotovoltaica [MW]
Gr	1000	Irradiación estándar en el ambiente [W/m2]
Rc	150	Valor de irradiación de referencia [W/m2]
Wpv	100	Potencia máxima [MW]

Tabla 7. Parámetros de vehículos eléctricos

Notación	Valor	Descripción y Unidades
Hllegada	20	Hora media de llegada
hpartida	7	Hora media de partida
km_media	50	Cantidad media de kilómetros recorridos
Cllegada	1	Desviación estándar de llegada
Cpartida	1	Desviación estándar de partida
Ckm	15	Desviación estándar de los kilómetros recorridos
Pcarga	3.52	Potencia de Carga

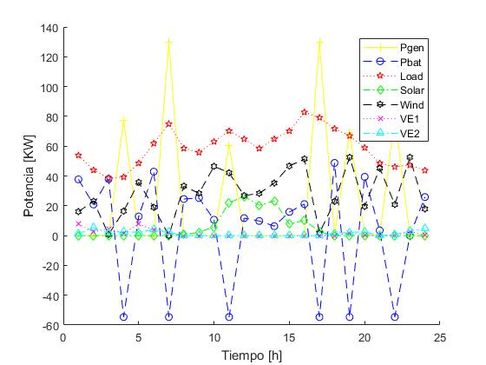
Teniendo en cuenta que el sistema hasta ahora entró en funcionamiento, después de la implementación de todas las ecuaciones y parámetros asociados al costo de la MG bajo estudio, se encontró el punto donde el costo de la operación es mínimo, el cual se muestra en la Figura 1.

Figura 1. Operación durante 24 horas de la MG cuando el sistema está nuevo

En la Figura 1, se considera que el sistema bajo análisis es nuevo. Se puede analizar que el uso de las baterías varias veces al día es la opción más atractiva para disminuir el costo de operación de la MG, sin contemplar que tendrán un periodo de vida más corto. Bajo esta premisa, se puede observar que la batería se carga 6 veces durante el día usando el generador diésel, el cual comienza a entregar potencias muy altas. Esto ocurre porque aparte de entregar la potencia que pide la carga, también suministra la potencia para cargar el banco de baterías.

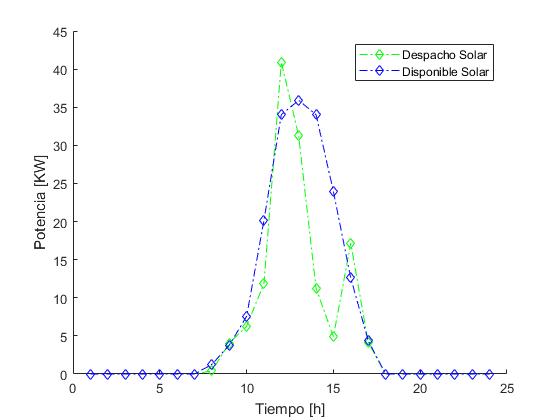
Teniendo en cuenta la participación de las energías renovables, se comienza a evaluar la utilización de la energía fotovoltaica en cada una de las horas del día. Para su análisis, la potencia disponible durante cada hora del día se graficó y se comparó con la despachada directamente a la red (Figura 2). Se puede observar que a ciertas horas del día se poseen altas cantidades de potencia proveniente de la radiación solar, donde lo mejor es despachar un poco menos de la potencia máxima para que el excedente quede almacenado en el banco de baterías del sistema. También se puede ver la característica completamente contraria, donde la potencia que se obtiene de la radiación solar es menor a la que se despacha, debido a que la potencia que hace falta se suministra usando el sistema de almacenamiento del sistema de energía solar.

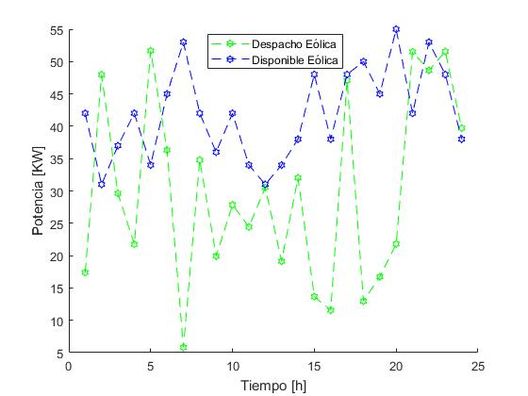
Por otra parte, la Figura 3 muestra que el comportamiento de la energía eólica es diferente al de la energía solar (Figura 2), debido a que la curva de despacho de energía eólica es mucho menor en varias horas del día con respecto a la curva de energía más probable de los generadores eólicos. Este comportamiento se puede atribuir a los costos por la sub- y sobrestimación de la disponibilidad de la energía eólica. De manera que en ciertos momentos del día, el algoritmo determina que lo menos costoso es almacenar la energía eólica en su sistema de almacenamiento y entregar a la red una cantidad de energía que permita disminuir el costo por sub- o sobrestimación. Igualmente, en diferentes tiempos se puede observar que la energía eólica entregada es mayor a la posible, ya que la energía eólica almacenada en otros instantes de tiempo se entrega en el instante adecuado para disminuir los costos asociados a horas con potencias más demandantes.

Figura 2. Energía fotovoltaica despachada (verde) vs. curva de energía más probable (azul) durante las 24h de cada día

Figura 3. Energía eólica despachada vs. energía más probable durante las 24h de cada día

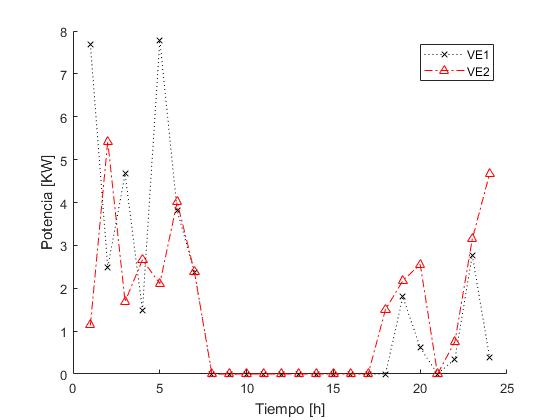
La Figura 4 muestra los horarios en donde se cargan los dos agregadores de los vehículos eléctricos. Como era de esperarse, los agregadores aprovechan el periodo de tiempo donde el costo de la energía es menor (10 pm - 6 am) y en el horario donde es más caro (2 pm a 10 pm), se cargan muy poco. Esto se debe a que este espacio de tiempo se usa solamente para obtener la carga que haría falta de la franja donde el precio es el más bajo. De esta manera, se garantizan la carga completa de los vehículos eléctricos una vez el horizonte de tiempo haya terminado y el vehículo abandone el puerto de carga.

Figura 4. Carga de los vehículos eléctricos de los dos agregadores bajo estudio

Como se mencionó en un principio, la minimización del costo de operación se hizo teniendo en cuenta que los elementos de la MG eran nuevos, entre ellos el almacenamiento en baterías de litio. En caso de que esta premisa no se cumpla y que la batería esté al final de su ciclo de vida, el comportamiento en los ciclos de carga y descarga de las baterías muy diferente. Como se puede ver en la Figura 5, pasaron de 6 cargas en un día a solamente 1 al día. El envejecimiento del sistema de almacenamiento se ve afectado directamente por los ciclos de carga y descarga a los cuales se somete en su operación. De la misma manera, el costo de operación de la MG también se ve afectado por este comportamiento, ya que al pasar el tiempo se tiene un costo más elevado debido a la operación de las baterías, lo que significa que el costo aumenta alrededor de 3 veces más que cuando el sistema esta nuevo.

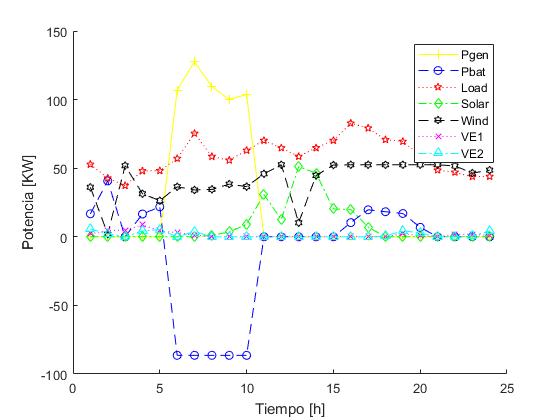
Figura 5. Operación durante 24 horas de la MG cuando el sistema de almacenamiento de baterías está llegando al final de su vida útil

5. Conclusiones

El desarrollo de la propuesta planteada en este artículo es útil para los planificadores de la operación de las MGs para mejorar su funcionamiento y planificar los despachos de potencia de una mejor manera. De esta manera, se puede optimizar la operación del sistema con el que se cuente y brindar un mejor servicio a sus usuarios.

Hoy en día, debido a la gran penetración e incentivos para aumentar el uso de las energías renovables, la inclusión de costos asociados a la sub- y sobrestimación de costos hace que este artículo tenga especial relevancia en el campo práctico, ya que soluciona o evita al máximo las pérdidas de dinero por la intermitencia de este tipo de energías.

Con el objetivo de alcanzar un correcto desempeño de la MG, trabajos futuros deberían estar encaminados a ampliar la definición del funcionamiento de este tipo de redes, en especial durante el envejecimiento del sistema. Por ejemplo, se podría incluir el costo asociado a la pérdida de vida del almacenamiento de energía al costo de operación, de forma tal que se encuentre un punto de operación adecuado para lograr un periodo de vida más largo.

Los índices de penalización asociados a la sub- y sobreestimación de la disponibilidad de la energía renovable es un factor muy importante al momento de buscar el punto de operación mínima. Por esto, en trabajos futuros sería necesario evaluar cuál es el costo en la vida real asociado a sub- o sobrestimar la disponibilidad de estas energías para incluir mejoras en el modelo que se utilizó para encontrar el costo mínimo de operación.

Acknowledgements

The authors would like to thank the Cyted Network: RED IBEROAMERICANA PARA EL DESARROLLO Y LA INTEGRACION DE PEQUENOS GENERADORES EOLICOS(MICRO-EOLO) for the continued support during thedevelopment of this work.

Referencias

[1]   Surender Reddy S., Park J.Y., Jung C.M. Optimal operation of microgrid using hybrid differential evolution and harmony search algorithm. Front. Energy, 13:134-140, 2016, doi:10.1007/s11708-016-0414-x.

[2] Bharothu J.N., Sridhar M., Rao R.S. Modified adaptive differential evolution based optimal operation and security of AC-DC microgrid systems. Int. J. Electr. Power Energy Syst., 103:185–202, 2018, doi:10.1016/J.IJEPES.2018.05.003.

[3] Kristoffersen T.K., Capion K., Meibom P. Optimal charging of electric drive vehicles in a market environment. Appl. Energy., 45:56-65, 2011, doi:10.1016/j.apenergy.2010.12.015.

[4] Li H.L., Bai X.M., Tan W. Impacts of plug-in hybrid electric vehicles charging on distribution grid and smart charging. In: 2012 IEEE Int. Conf. Power Syst. Technol. POWERCON 2012, 2012. doi:10.1109/PowerCon.2012.6401265.

[5] Ma Z., Callaway D.S., Hiskens I.A. Decentralized charging control of large populations of plug-in electric vehicles. IEEE Trans. Control Syst. Technol., 21:78-98, 2013, doi:10.1109/TCST.2011.2174059.

[6] Sheikhi A., Bahrami S., Ranjbar A.M., Oraee H. Strategic charging method for plugged in hybrid electric vehicles in smart grids. A game theoretic approach. Int. J. Electr. Power Energy Syst., 24:78-97, 2013, doi:10.1016/j.ijepes.2013.04.025.

[7] Lasseter R.H. MicroGrids. In: 2002 IEEE Power Eng. Soc. Winter Meet. Conf. Proc. (Cat. No.02CH37309), Vol. 1, pp. 305–308, 2002, doi:10.1109/PESW.2002.985003.

[8]         Zhao B., Zhang X., Chen J., Wang C., Guo L. Operation optimization of standalone microgrids considering lifetime characteristics of battery energy storage system. IEEE Trans. Sustain. Energy., 36:221-229, 2013, doi:10.1109/TSTE.2013.2248400.

[9]         Hernandez-Aramburo C.A., Green T.C., Mugniot N. Fuel consumption minimization of a microgrid. IEEE Trans. Ind. Appl., 14:67-74, 2005, doi:10.1109/TIA.2005.847277.

[10]      Ross M., Hidalgo R., Abbey C., Joós G. Energy storage system scheduling for an isolated microgrid. IET Renew. Power Gener., 67:89-98, 2011, doi:10.1049/iet-rpg.2009.0204.

[11]      Morais H., Kádár P., Faria P., Vale Z.A., Khodr H.M. Optimal scheduling of a renewable micro-grid in an isolated load area using mixed-integer linear programming. Renew. Energy., 23:98-105, 2010, doi:10.1016/j.renene.2009.02.031.

[12]      Chen S.X., Gooi H.B. Jump and shift method for multi-objective optimization. IEEE Trans. Ind. Electron., 78:98-106, 2011, doi:10.1109/TIE.2011.2116756.

[13]      Chen C., Duan S., Cai T., Liu B., Hu G. Smart energy management system for optimal microgrid economic operation. IET Renew. Power Gener., 36:34-46, 2011, doi:10.1049/iet-rpg.2010.0052.

[14]      Katsigiannis Y.A., Georgilakis P.S., Karapidakis E.S. Multiobjective genetic algorithm solution to the optimum economic and environmental performance problem of small autonomous hybrid power systems with renewables. IET Renew. Power Gener., 65:1122-1138, 2010, doi:10.1049/iet-rpg.2009.0076.

[15]      Dufo-López R., Bernal-Agustín J.L. Multi-objective design of PV-wind-diesel-hydrogen-battery systems. Renew. Energy., 89:678-690, 2008, doi:10.1016/j.renene.2008.02.027.

[16]      Li J., Liu F., Wang Z., Low S.H., Mei S., Optimal Power Flow in Stand-alone DC Microgrids. IEEE Trans. Power Syst., 33:5496–5506, 2017, doi:10.1109/TPWRS.2018.2801280.

[17]      Lezama F., Soaresa J., Vale Z., Rueda J., Rivera S., Elrich I. 2017 IEEE competition on modern heuristic optimizers for smart grid operation: Testsbeds and results 2014. Swarm and Evolutionary Computation, 14:420-427, 2017.

[18]      Sauer D.U., Wenzl H. Comparison of different approaches for lifetime prediction of electrochemical systems-Using lead-acid batteries as example. J. Power Sources., 45:78-92, 2008, doi:10.1016/j.jpowsour.2007.08.057.

[19]      Kamankesh H., Agelidis V.G., Kavousi-Fard A. Optimal scheduling of renewable micro-grids considering plug-in hybrid electric vehicle charging demand. Energy, 18:78-85, 2016, doi:10.1016/j.energy.2016.01.063.

[20]      Hetzer J., Yu D.C., Bhattarai K. An economic dispatch model incorporating wind power. IEEE Trans. Energy Convers., 46:45-59, 2008, doi:10.1109/TEC.2007.914171.

[21]      Arévalo J., Santos F., Rivera S. Application of analytical uncertainty costs of solar, wind and electric vehicles in optimal power dispatch. Ingeniería, 22:324-336, 2017, doi:10.14483/23448393.11673.

[22]      Zhao J., Wen F., Yang Dong Z., Member S., Xue Y., Po Wong K. Optimal dispatch of electric vehicles and wind power using enhanced particle swarm optimization. IEEE Trans. Ind. INFORMATICS, 8 (4):889-899, 2012, doi:10.1109/TII.2012.2205398.

[23]      Xu Z., Hu Z., Song Y., Zhao W., Zhang Y. Coordination of PEVs charging across multiple aggregators. Appl. Energy., 136:582-589, 2014, doi:10.1016/j.apenergy.2014.08.116.

[24]      Arévalo J., Santos F., Rivera S. Uncertainty cost functions for solar photovoltaic generation, wind energy generation, and plug-in electric vehicles: mathematical expected value and verification by Monte Carlo simulation. Int. J. Power Energy Convers., 10:171-207, 2018, http://www.inderscience.com/info/ingeneral/forthcoming.php?jcode=ijpec.

[25]      Ñustes w., Rivera S. Colombia: territorio de inversión en fuentes no convencionales de energía renovable para la generación eléctrica. Revista Ingeniería, Investigación y Desarrollo, 17:37-48, 2017.

[26]      Acosta J.L., Alarcon A.E., Rivera S. Reconfiguración de sistemas de distribución para minimizar pérdidas utilizando optimización heurística: Métodos BPSO y DEEPSO. Entre Ciencia e Ingeniería, 11:110–117, 2017, doi:10.31908/19098367.3556.

[27]      Chaouachi A., Kamel R.M., Andoulsi R., Nagasaka K. Multiobjective intelligent energy management for a microgrid _ Aymen Chaouachi - Academia. IEEE Trans. Ind. Electron., 60:1688–1699, 2013, doi:10.1109/TIE.2012.2188873.

[28]    Peña A., Romero D., Rivera S. Generation and demand scheduling in a micro-grid with battery-based storage systems, hybrid renewable systems and electric vehicle aggregators. WSEAS Transaction on Power Systems, 14 (2):8-23, 2019.