TDCMDA: Tripartite graph-based integrating dual-layer contrast learning into graph convolutional network for miRNA-disease association identification

Abstract

MicroRNAs (miRNAs) play essential roles in various biological regulatory processes and are closely related to the occurrence and development of complex diseases. Identifying miRNA-disease associations (MDA) is of great value for revealing the molecular mechanisms of diseases and exploring therapeutic strategies and drug development. Recently, most computer-aided MDAs identification approaches design their models tend to base on a bipartite graph (i.e., miRNA-disease network), ignoring the endogenous RNAs(ceRNAs) hypothesis in post-transcriptional control such as gene negative regulation by targeting mRNAs. Besides, the existing MDA bipartite graph could not make convincing predictions for MDA, only relying on collaborative filtering followed by the recommended system. To address the above issues, we propose a TDCMDA (Tripartite graph-based integrating Dual-layer Contrast learning into graph neural network for MDA prediction), which aims to integrate dual-layer contrast learning into graph neural network under the miRNA-disease-gene tripartite graph. Different from the existing approaches, TDCMDA introduces not only rich biologic regulatory relationships hidden in ceRNAs by a tripartite graph but also employs self-supervised dual-layer contrast learning to alleviate sparse label disadvantage. TDCMDA can learn node feature representation across three subgraph spaces such that the link representation between miRNA and disease can be obtained more biology semantically. Comprehensive experiments indicate TDCMDA is superior to several state-of-the-art approaches, and the case studies show that TDCMDA can convincingly detect novel MDA pairs and can be a promising tool for MDA identification.

Keywords: Tripartite graph, dual contrast learning, graph convolutional network, miRNA-disease association prediction

1. Introduction

MicroRNAs (miRNAs) are a family of non-coding, single-stranded RNA molecules with an average length of 22 nucleotides that are produced by endogenous genes and play a number of crucial regulatory functions in cells [1]. Their abundance, variable expression and diversity of possible regulatory targets imply that miRNA gene inactivation or abnormalities are linked to the emergence of a wide spectrum of human disorders. Numerous studies have demonstrated the link between the development of disorders, including thymic insufficiency, muscular dystrophy, viral infections, and cancer, and the components involved in their processing and functional functions [2–5]. Therefore, the study of the identification between miRNAs and diseases plays a crucial role in elucidating the pathogenesis of diseases and represents a breakthrough in the understanding of the biological functions of miRNAs [6].

In general, the correlations between miRNA and disease are validated using two different biological experimental methods: qPT-PCR [7] and Northern blot [8], but they are time-consuming and expensive. Thanks to the continuous progress of deep learning, more fast, efficient and affordable computer-aided MDA prediction techniques are being developed, leading to great changes to miRNA research. With modern deep learning technologies, MDA prediction can be conducted as an intelligent approach and to aid traditional experimental methods, which typically involve much expense and energy.

In recent years, to provide effective screening methods, more and more machine learning models have been proposed for MDA prediction. They mostly fall into three broad types, biological feature-based approaches, similarity-based approaches, and graph-based approaches. The primary biological aspect of the first type approach is to identify MDAs by using distinct biological characteristics of miRNA and disease as eigenvalues. For instance, Ma et al. developed a unique technique dubbed SFGAE with the goal of creating miRNA-self embeddings and disease-self embeddings that were independent of network interactions between two different types of nodes [9]. A machine model based on an ensemble of decision trees was introduced by Chen et al. [10]. By calculating the statistical measurements for the miRNA and disease, the theoretical graph measurements, the corresponding matrix factorization results for each MDA pair, and the feature vector was retrieved. Additionally, the theoretical feature profile for graphs and the MDA statistical feature profile were projected into a single subspace using the computational model LRSSLMDA [11]. Although these techniques helped identify MDA to some extent, their effectiveness is still constrained by the fact that they ignore the intricate connection and interplay between miRNA and disease.

The primary goal of the similarity-based methods as the second category approaches is to identify miRNAs with comparable functions that are more probable to be connected to related disorders. For example, Zhang and Zheng et al. put forward a prediction approach based on miRNA similarity; however, Zhang et al. depended on the similarity between the miRNA itself and the phenotype, whereas Zheng et al. [13], and Xuan et al. [14] applied semantic similarity to learn the MDAs based on weighted k most similar neighbors [14]. Additionally, NetGS was suggested as a way to investigate the similarities throughout the whole network, but their effectiveness is constrained by the variety of semantic expressions and the uneven quality of the available literature [15].

Graph-based approaches have also seen a lot of use recently. A graph may display the intricate details of neighbor topology between several biological items, like miRNA, disease, and genes. This approach compensates for the previous shortcomings by focusing on the topology of the nodes and various classifier algorithms. The trend of predicting the connection between miRNA and disease is toward graph-based methods [16]. Zheng et al. [17] specifically proposed a graph embedding model in detail, called MLMDA, to extract representative features through a deep self-encoder neural network and successfully predict possible associations between miRNA and diseases using a random forest classifier. MLMDA's fundamental concept was to represent the MDA issue as a link prediction in graphs. On this basis, approaches based on graph convolutional networks have been presented by Han et al. [18] and Li et al. [19]. By extracting subgraphs around MDA pairs from the network and learning the structural features of the subgraphs through labeling algorithms and neural networks, a heterogeneous network was constructed by Zhang et al. [20]. In order to predict miRNA-disease connections at the depth level utilizing graph neural networks (GNNs) and miRNA sequence features, Yan et al. created an end-to-end deep learning approach [21]. In addition, Wang et al. offer a computational framework called MKGAT that makes use of dual Laplacian regularized least squares and graph attention networks (GATs) to find possible connections between miRNAs and disease [22].

However, the majority of network-based techniques simply take into account qualities from independent tiers. For instance, some techniques solely think about the distinctive characteristics of miRNA and disease (such as neighbor topology and similarities between miRNA and disease). Besides, the existing MDA bipartite graph could not make convincing predictions for MDA, only relying on collaborative filtering followed by the recommended system. The model's stability and accuracy are still restricted by the inadequate consideration of characteristics. These approaches design their models tend to base on the bipartite graph (i.e., miRNA-disease network), ignoring the competing endogenous RNAs(ceRNAs) hypothesis in post-transcriptional control such as gene negative regulation by targeting mRNAs, which can reflect the property of miRNA to some extent [23]. MiRNA has evolved with very little change. By identifying and encouraging the formation of the gene silencing complex RISC through MREs in the 3'UTR region of the target gene, a miRNA can control the activity or stability of many target genes; many miRNAs can also work together to control the same target gene. Studies have shown that ceRNAs in malignant tumor cells can competitively bind to MREs targeting microRNAs in the 3'UTR region of proto-oncogenes, oncogenes, and mRNAs of various tumor-related signaling pathway factors, thereby promoting or inhibiting microRNA-related functions and playing an important role in tumourigenesis, progression, invasion, metastasis and even drug therapy [24]. For example, Poliseno et al. found that the pseudogene PTENP1 transcript in prostate cancer cells could increase the expression level of PTEN by competitively binding miR-19b, miR-20a, miR-214, and other microRNAs targeting PTEN. Consequently, the PI3K/Akt signaling pathway is prevented from being activated, which eventually prevents the growth of tumor cells; conversely, the inhibition of PTENP1 expression was accompanied by a downregulation of PTEN expression and an increase in tumor cell proliferation [25]. Yet, existing research approaches ignore the wealth of knowledge contained in genes associated with miRNAs and disease. In fact, this information can better reflect the properties of miRNAs and diseases.

In light of this, we think that merging the gene and miRNA-disease network is essential for developing a more precise and beneficial strategy. We supported this position by suggesting a TDCMDA (Tripartite graph-based integrating Dual-layer Contrast learning into graph neural network for MDA prediction), which aims to integrate dual-layer contrast learning into graph neural network under the miRNA-disease-gene tripartite graph. An auto-coder based on graph convolution was used to integrate miRNA-disease, miRNA-disease-gene, and disease-gene network topologies. A self-supervised learning approach was used to perform dual-layer comparative learning across networks. The model incorporates three deep learning branches. One branch consists of miRNA-disease and disease-gene heterogeneous graphs. Given the inherent heterogeneity across various things, TDCMDA utilizes cross-domain transformation to remove heterogeneity and may be able to acquire more expressive embeddings for MDA prediction. A three-layer convolutional network with a heterogeneous graph made up the second branch. In a single heterogeneous network, it aims to extract adjacent topological data and establish relationships (associations and interactions) among biological constituents. The heterogeneous network adequately took into account the many biological elements, such as miRNA, disease, and genes. The third branch was dual-layer comparative learning, which emphasizes the importance of incorporating self-supervised learning into the model to provide auxiliary information for graph representation learning. The approach exceeds other frequently used methods in the majority of performance assessment measures, according to 5-fold cross-validation results, which show that the method has an AUC value of 0.9495 and an AUPR value of 0.9509. The ability of TDCMDA to predict potential miRNA-disease associations was further confirmed by case studies of lung neoplasms, breast neoplasms, and esophageal neoplasms, and TDCMDA can be used as a useful tool for screening reliable miRNA-disease pairs.

2. Materials and methods

2.1 Overview of TDCMDA

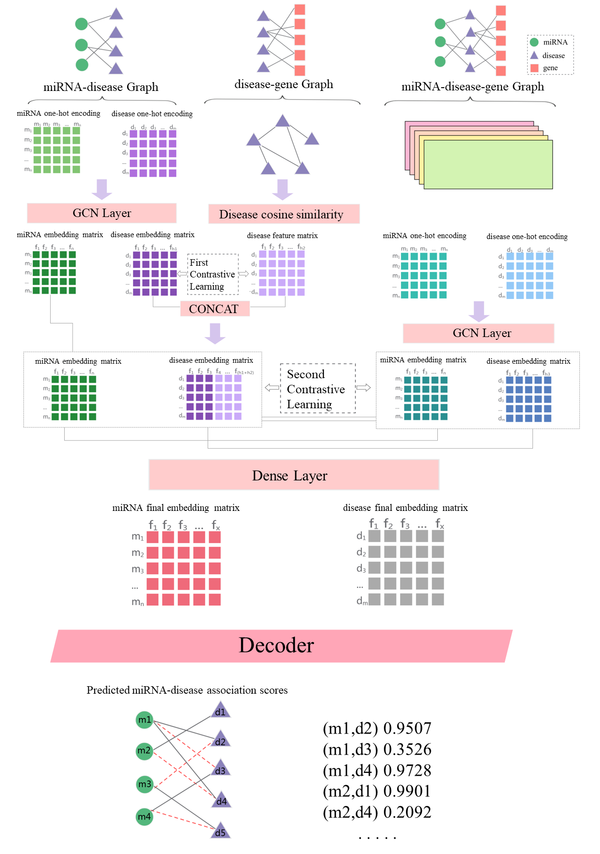
The aim of this article was to create a cutting-edge deep learning framework called TDCMDA., which integrates dual-layer contrast learning into a graph neural network under miRNA-disease-gene tripartite graph for MDA prediction. Figure 1 displays the working flow of TDCMDA, which has three primary branches. In the first branch, TDCMDA uses a cross-domain transformation to remove heterogeneity and can learn more expressive embeddedness for MDA prediction, taking into account the miRNA-disease and disease-gene heterogeneity networks and the underlying heterogeneity among different entities. The cosine similarity combined with the graph convolutional network module is applied to understand how node pairs are represented in the network. In the second branch, mRNA-disease-gene heterogeneous networks are taken into account to preserve the complete pathway information, concentrating on leveraging correlations, associations, and interactions between similarities to learn the local representation of miRNA-disease nodes. In a single heterogeneous network, it aims to extract adjacent topological data and establish relationships (associations and interactions) among biological constituents. The heterogeneous network adequately took into account the many biological entities, such as miRNA, diseases, and genes. In the third branch, cross-view contrast learning was first performed between the two views for miRNA-disease and disease-gene to learn the comprehensive node embedding at the local level.In particular, the graph neural network model used in each layer branch is the same, which is GCN, and the number of layers is set to 2. Then the lateral view contrast learning was performed between the miRNA-disease-gene tripartite map and the local view to learn the discriminative node embedding under the global view. A two-layer contrast learning was performed to underline how crucial it is to include self-supervised learning in the model to provide auxiliary information for graph representation learning.

Figure 1. Overall TDCMDA structure. Three heterogeneous networks on top are the input to TDCMDA. In these networks, various forms correspond to various entities. Based on the heterogeneous GCN module, the macroscopic attributes of all entities are learned, feature fusion and splicing are carried out, and finally comparative learning is carried out

2.2 Dataset preparation

In this study, we used the HMDD v3.0 [26] and CTD [27] databases as our primary training datasets. There are 671 miRNAs, 244 diseases, and 7243 experimentally supported miRNA-disease association entries in database HMDD v3.0, which represented the known human miRNA-disease connections. The CTD database is the Comparative Toxicogenomics Resource. It is a freely accessible resource that examines associations between chemicals, genes, phenotypes, diseases, and the environment, from which we have extracted data for 7986 disease-gene associations.

2.3 Graphical convolutional networks

GCN is a scalable semi-supervised learning method that uses effective convolutional neural networks that act directly on the graph as its foundation [28]. It is the selection of a convolutional architecture motivated by a local convolution of the spectral graph using a first-order approximation, scaling the number of graph edges increases linearly, and learning hidden layer representations that contain node characteristics and local graph structure. The established miRNA-disease collaboration view and disease-gene relationship view are encoded by the GCN approach, respectively. The trained GCN has served as a good training effect, and the GCN results are used as embedding representation nodes for subsequent prediction tasks and comparative learning.

2.4 Contrast Learning

Contrastive learning focuses on finding similarities between similar cases and identifying differences between unrelated ones. In the comparison process, distances between positive samples are shortened, while those between negative samples are lengthened.We used random sampling to randomly sample a portion of the unmatched or unlinked samples as negative samples.In contrast to generative learning, contrastive learning does not have to concentrate on the time-consuming specifics of examples but only needs to learn to set apart from between data at the feature space's abstract semantic level. As a result, the model and its optimization become more straightforward and universal.

2.5 Graph Convolutional network-based contrast learning prediction method

2.5.1 Construct experiment vector

The miRNA is described as vector ${\textstyle M}$, where ${\textstyle M=\lbrace {m}_{1},{m}_{2},\ldots {m}_{N}\rbrace }$. The disease is described as vector ${\textstyle D}$, where ${\textstyle D=\lbrace {d}_{1},{d}_{2},\ldots {d}_{M}\rbrace }$. The gene is described as vector ${\textstyle G}$, where ${\textstyle G=\lbrace {g}_{1},{g}_{2},\ldots {g}_{L}\rbrace }$. ${\textstyle M}$, ${\textstyle N}$, and ${\textstyle L}$ denote ${\textstyle M}$ diseases, ${\textstyle N}$ miRNAs, and ${\textstyle L}$ genes, respectively.

2.5.2 Construct heterogeneous graph

The miRNA-disease associations’ matrix ${\textstyle X\in {R}^{N\times M}}$ is defined where ${\textstyle {x}_{ij}=}$$1$ indicates that ${\textstyle {m}_{i}}$ associates with ${\textstyle {d}_{j}}$, miRNA ${\textstyle {m}_{i}}$ engaged with disease ${\textstyle {d}_{j}}$; otherwise ${\textstyle {x}_{ij}=0}$. Similarly, the disease-gene associations’ matrix ${\textstyle Y}$ is defined where ${\textstyle {y}_{ij}=1}$ indicates that ${\textstyle {d}_{i}}$ associates with ${\textstyle {g}_{j}}$

${X}_{ij}=\left\{{\begin{array}{llr}1,&{\hbox{if }}\,{m}_{i}&{\hbox{associates with}}\,{d}_{j}\\\\0,&&{\hbox{otherwise}}\end{array}}\right.$

(1)

${Y}_{ij}=\left\{{\begin{array}{llr}1,&{\hbox{if }}\,{d}_{i}&{\hbox{associates with}}\,{g}_{j}\\\\0,&&{\hbox{otherwise}}\end{array}}\right.$

(2)

In addition, to the miRNA-disease and disease-gene relationship matrix, we added the type of relationship between the disease and the gene as an edge to the heterogeneous graph species as well [29]. Let ${\textstyle G=\left\{(d,r,g)\vert d,g\in X,r\in R\right\}}$, where ${\textstyle d}$, ${\textstyle r}$, and ${\textstyle g}$ stand for the head, relation, and tail of a triple, respectively; they are used to refer to the sets of relations in ${\textstyle G}$.

2.5.3 Disease-disease similarity

For the ${\textstyle (d,r,g)}$ triple in ${\textstyle G}$, the graph embedding method RotatE proposed by Sun et al. was used to efficiently train the model using a new self-adversarial negative sampling technique [30]. The distance function is defined as:

${d}_{r}\left(d,g\right)=\left\|d\circ r-g\right\|$

(3)

and ${\textstyle \circ }$ is the Hadmard (or element-wise) product. Then, recursively learn the representation of diseases and genes in graph ${\textstyle G}$

${e}_{d}^{(k+1)}={\frac {1}{{M}_{i}}}\sum _{(r,g)\in {M}_{i}}^{}{e}_{r}\cdot {e}_{g}^{(k)}$

(4)

where ${\textstyle {e}_{d}^{(k)}}$ denote the representations of disease, which recorded signals associated with (k-1)-hop gene neighbours.

Then, based on the disease representation just obtained, a cosine similarity matrix of disease ${\textstyle {d}_{i}}$ and disease ${\textstyle {d}_{j}}$ is constructed, which was calculated as:

$Cos\left({d}_{i},{d}_{j}\right)={\frac {{({e}_{{d}_{i}})}^{T}\cdot {e}_{{d}_{j}}}{\left\|{e}_{{d}_{i}}\right\|\times \left\|{e}_{{d}_{j}}\right\|}}$

(5)

Thus, we obtained the cosine similarity matrix of the disease and named it ${\textstyle C}$. In order to accelerate convergence in gradient descent, we normalized the obtained matrix ${\textstyle C}$ as follows:

${\breve {C}}={(D)}^{-{\frac {1}{2}}}{\breve {C}}{(D)}^{-{\frac {1}{2}}}$

(6)

By the above method, we obtained a disease-disease similarity matrix.

To more effectively understand the disease representation and capture the disease-disease similarity, the disease representations of the different layers were summed to get the complete representation of the disease, which was calculated as follows:

${z}_{d}^{1}=\sum _{j\in N(i)}^{}{\breve {C}}{e}_{j}^{0}+\sum _{j\in N(i)}^{}{\breve {C}}{e}_{j}^{1}+\cdots +\sum _{j\in N(i)}^{}{\breve {C}}{e}_{j}^{M}$

(7)

The disease's number of neighbors is indicated by the symbol ${\textstyle N(i)}$. ${\textstyle {\breve {C}}}$ denotes the normalized sparse adjacency matrix just generated, and ${\textstyle M}$ represents the number of diseases, setting the stage for the comparative learning that follows.

2.5.4 Application of graph convolutional network models to miRNA-disease graph

For the miRNA-disease graph, an L-layer polymerization was performed using the GCN method as follows:

${H}^{(l+1)}=\sigma \left({\tilde {D}}^{-{\frac {1}{2}}}{\tilde {A}}{\tilde {D}}^{-{\frac {1}{2}}}{H}^{(l)}{W}^{(l)}\right)$

(8)

where ${\textstyle {\tilde {A}}=A+{I}_{N}}$, ${\textstyle A}$ is the adjacency matrix, ${\textstyle {I}_{N}}$ is the unit matrix, so ${\textstyle {\tilde {A}}}$ is the connection matrix for adding self-connections; ${\textstyle {\tilde {{D}_{ii}}}=}$$\sum _{j}^{}{\tilde {{A}_{ij}}}$, ${\textstyle {\tilde {D}}}$ can be understood as the diagonal is the degree matrix of node ${\textstyle i}$; ${\textstyle {W}^{(l)}}$ is the weight matrix of the l-layer of the neural network, ${\textstyle \sigma (\cdot )}$ is the activation function, ${\textstyle {H}^{(l)}}$ is the activation matrix of the l-layer. Influenced by Bojchevski and Günnemann [31], we performed one-hot encoding of miRNA and disease, respectively, and obtained an initial vector as the first layer of the graph convolution input.

The graph convolution layer assigns separate processing channels for different types of edges, and transmits messages between edges on the graph through local graph convolution, which is an embedding structure that weights features

${u}_{d}^{m}={\frac {1}{W\times H}}\sum _{m}^{M}\sum _{i=1}^{W}\sum _{j=1}^{H}{U}_{d}\left(i,j\right)$

(9)

${u}_{m}^{n}={\frac {1}{W\times H}}\sum _{n}^{N}\sum _{i=1}^{W}\sum _{j=1}^{H}{U}_{m}(i,j)$

(10)

To achieve a complete depiction of miRNA and disease in the GCN layer, we then added up all the representations as follows:

${z}_{d}^{{1}^{'}}={u}_{d}^{0}+{u}_{d}^{1}+\cdots +{u}_{d}^{m}$

(11)

${z}_{m}^{2}={u}_{m}^{0}+{u}_{m}^{1}+\cdots +{u}_{m}^{n}$

(12)

2.5.5 The first layer of contrast learning

For the disease similarity ${\textstyle {z}_{d}^{1}}$ in the learned disease-gene map and the disease representation ${\textstyle {z}_{d}^{1'}}$ in the miRNA-disease map, the first contrast learning was performed, and the disease nodes in the two views were embedded to form positive samples. We used supervised contrastive learning [32]. In both views, any further node embeddings are classified as negative samples. Supervised layer one contrast learning was initiated.

With positive and negative samples defined, the contrast loss is as follows:

${L}_{1}={\frac {-1}{2M-1}}\sum _{i=1}^{2M}\log \displaystyle {\frac {\mathrm {exp} \,({z}_{d}^{1}\cdot {z}_{d}^{1'}/\tau )}{\displaystyle \sum _{k=1}^{2M}{l}_{[k\not =i]}\cdot \mathrm {exp} \,({z}_{d}^{1}\cdot {z}_{d}^{1'}/\tau )}}$

(13)

where ${\textstyle {l}_{[k\not =i]}}$ is a signal function that takes 0 when ${\textstyle k=i}$, and 1 otherwise. ${\textstyle \tau }$ is the temperature parameter for the optimization. It can be easily seen from the formula that the supervised contrast loss expands the number of positive samples. All the sub-data identical in label information are viewed as positive samples, the similarity between all positive samples is calculated, and then the weighted average is performed. This architecture can also better characterize within-class similarity due to the increased number of positive samples.

2.5.6 Learn feature representations in miRNA-disease-disease graph.

The miRNA-disease-gene map was encoded using the graph convolution method, as shown in Equations 8 and 9, to obtain the representation ${\textstyle {e}_{m}}$ and ${\textstyle {e}_{d}}$ of miRNA and disease. Then we sum all representations up to obtain ${\textstyle {z}_{m}^{2'}}$ and ${\textstyle {z}_{d}^{2'}}$:

${z}_{m}^{2'}={e}_{m}^{0}+{e}_{m}^{1}+\cdots +{e}_{m}^{N}$

(14)

${z}_{d}^{2'}={e}_{d}^{0}+{e}_{d}^{1}+\cdots +{e}_{d}^{M}$

(15)

2.5.7 The second layer of contrast learning

The disease similarity features were fused by assigning different weights and added together to obtain the full representation ${\textstyle {z}_{d}^{2}}$ of the disease, the calculation is as follows:

${z}_{d}^{2}=\sum _{m}^{M}\alpha \cdot {\breve {C}}{e}_{d}^{m}+\beta \cdot {u}_{d}^{m}(0.1\leq \alpha ,\beta \leq 0.9)$

(16)

The second layer of contrast learning was carried out under the same positive and negative sampling strategies, and the contrast loss value was calculated as follows:

${L}_{m}^{2}={\frac {-1}{2N-1}}\sum _{i=1}^{2N}log{\frac {\mathrm {exp} \,({z}_{m}^{2}\cdot {z}_{m}^{{2}^{'}}/\tau )}{\sum _{k=1}^{2N}{l}_{[k\not =i]}\cdot \mathrm {exp} \,({z}_{m}^{2}\cdot {z}_{m}^{{2}^{'}}/\tau )}}$

(17)

${L}_{d}^{2}={\frac {-1}{2M-1}}\sum _{i=1}^{2M}log{\frac {\mathrm {exp} \,({z}_{d}^{2}\cdot {z}_{d}^{{2}^{'}}/\tau )}{\sum _{k=1}^{2M}{l}_{[k\not =i]}\cdot \mathrm {exp} \,({z}_{d}^{2}\cdot {z}_{d}^{{2}^{'}}/\tau )}}$

(18)

During training, the miRNA set has ${\textstyle N}$ samples, and two branches have ${\textstyle 2N}$ samples. The remaining ${\textstyle 2N-}$$2$ are all negative samples. The numerator is the similarity between positive samples, and the denominator is the similarity between negative samples. Loss is to make samples belonging to the same class closer and samples of different classes farther away. The same goes for the disease set. The second layer of contrast learns the total contrast loss as follows:

${L}_{2}={L}_{m}^{2}+{L}_{d}^{2}$

(19)

2.5.8 Final loss calculation

The decoder we use is inner score, which applies the sigmoid function after linear transformation of the input to obtain the final prediction score.Using the approach suggested by Rendle et al. [33], the relationship of miRNA-disease was represented as a triple, where m represents miRNA, $d$ represents disease, and $l$ represents the associated label of miRNA-disease. A miRNA ranking function for each disease association was learned through the BPR model, maximizing the marginal probabilities described above

${L}_{BPR}=-\sum _{(m,d,l)}^{}ln\sigma (f(m,d))$

(20)

By combining the first-layer and second-layer contrast losses generated previously with the BPR loss, the final loss function was obtained as follows:

${L}_{Final}={L}_{BPR}+\epsilon (\rho \cdot {L}_{1}+(1-$$\rho )\cdot {L}_{2})$

(21)

here, ${\textstyle \rho }$ is the hyperparameter set to determine the first-second contrast loss ratio, and ${\textstyle \epsilon }$ is the hyperparameter set to control the contrast loss.

3. Results and discussion

3.1 Parameter optimization

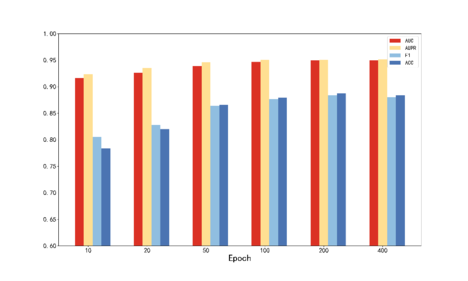
For the hyperparameters $\alpha ,\beta ,\varepsilon$ and $\rho$ involved in TDCMDA, we use grid search to optimize. Firstly, the disease similarity of different weight combinations was cross-validated, and the optimal weight ($\alpha ,\beta$) was obtained as (0.1, 0.9). The proportional hyperparameter and the loss hyperparameter in the loss function are then optimized to obtain the optimal value from ($\varepsilon ,\rho$) of (0.1, 0.1). The number of GCN layers is chosen from {2, 3, 4}, the training session epoch from {10, 20, 50, 100, 200, 500} and the learning rate from {0.01, 0.001, 0.003, 0.0001, 0.00001}. The outcomes are displayed in Figure 2. It can be seen that the optimal number of GCN layers is 2, the optimal epoch is 400, and the best learning rate is 0.003.

(a) Layer (b) Epoch (c) Learning rate

Figure 2. Parameter analysis of TDCMDA

3.2 Performance Evaluation Metrics

To avoid data imbalance throughout the training phase, the number of data for the positive samples was randomly chosen to be equal to the amount of data for the negative samples. The TDCMDA model's performance was assessed using five-fold cross-validation by evenly dividing the training set into five parts, using the data from four of them as the training set and the data from the fifth as the test set. The average test error was used as the generalization error. The benefit of this is that all of the training set samples will inevitably become training data, and all of the test set samples will inevitably turn into pages. Data from the training set may be used more effectively.

The associated data in the test set were scored using the training model, and a threshold ${\textstyle \theta }$ was set so that when the score exceeded the threshold, the forecast result was positive, and when it fell below the barrier, the outcome was negative. In order to forecast our model's performance and evaluate it against alternative approaches, we employed the following assessment criteria. After obtaining the above data, we used TP to represent the number of positive samples correctly predicted, FN to represent the number of positive group samples incorrectly predicted as negative, FP to represent the number of negative group samples incorrectly predicted as positive, and TN to represent the number of negative group samples correctly predicted. Based on these indicators, we used the following evaluation criteria to predict the performance of our model and to compare it with other methods.The TPR (true positive rate), FPR (false positive rate), Precision (precision), and Recall (recall rate) were calculated using the following equations [34]:

$TPR={\frac {TP}{TP+FN}}$

(22)

$FPR={\frac {FP}{TN+FP}}$

(23)

$precision={\frac {TP}{TP+FP}}$

(24)

$recall={\frac {TP}{TP+FN}}$

(25)

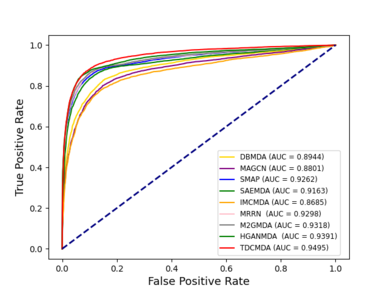
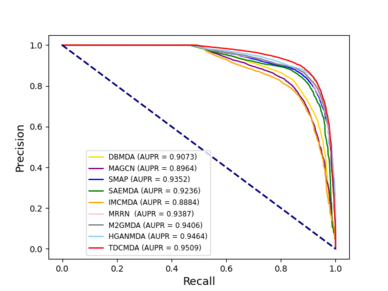
We used the method proposed by Bradley as the criteria for evaluating the model, which is area under receiver operating characteristic curves and area under precision-recall curves [35]. The results are shown in Figure 3.

(a) (b)

Figure 3. Five-fold cross receiver operating characteristic (ROC) and precision-recall (PR) curves of TDCMDA. (a) Receiver operating characteristic curves. (b) Precision-recall curves

3.3 Experimental results

3.3.1 Ablation studies

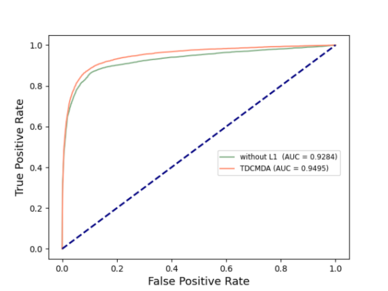
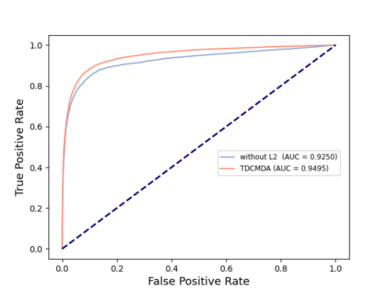
To analyze the necessity of two-layer contrast learning for our model, we adopted two variants of TDCMDA, TDCMDA-without L1 and TDCMDA-without L2, as comparison methods. Specifically, TDCMDA-without L1 means that we remove the first layer of contrast learning; that is, we do not integrate the similarities of the disease-gene heterogeneous network and only use the output of the NTH layer GCN as features. TDCMDA-without L2 removes the second layer of contrast learning and lacks the fusion loss of the tripartite graph.

The outcomes of the entire TDCMDA model were contrasted with those of the previous two models, and the experimental results are presented in Figure 4 . The ACU value of TDCMDA was improved by about 2% when compared with the model with only the first layer contrast learning and the model with only the second layer contrast learning, indicating the importance of contrast learning for our model so that the model can produce a more effective screening of features, and achieve good prediction performance.

(a) (b)

Figure 4. Comparison of ROC curves with different TDCMDA components. (a) TDCMDA without the first contrast learning. (b) TDCMDA without the second contrast learning

3.3.2 Comparing TDCMDA with baseline methods

We compared our model TDCMDA to other cutting-edge prediction techniques to show how effective it is at predicting miRNA-disease connections, including MRRN [36], SMAP [37], IMCMDA [38], MAGCN [39], HGANMDA [40], M2GMDA [41], DBMDA [13], SAEMDA [42]. As shown in Figure 5 , TDCMDA has the best prediction performance. The AUC of the ROC curve is 0.9495. TDCMDA outperforms MRRN, SMAP, IMCMDA, MAGCN, HGANMDA, M2GMDA, DBMDA, and SAEMDA by 1.97%, 2.33%, 8.10%, 6.94%,1.04%,1.77%,5.51%, and 3.22%, respectively.

(a) (b)

Figure 5. results of TDCMDA and other methods on the dataset. (a) Receiver operating characteristic curves. (b) Precision-recall curves

MRRN and IMCMDA are both matrix-based methods; MRRN has better performance due to the fact that the MRRN model combines matrix reconstruction and node reliability, while IMCMDA only designs an inductive matrix complementation model. HGANMDA and MAGCN both utilize attention mechanisms, and both achieve better results; HGANMDA is based on hierarchical graph attention networks, and MAGCN is based on multi-channel attention networks. The M2GMDA model is built on a novel multivariate pathway fusion graph embedding that predicts undiscovered miRNA-disease connections. SAEMDA model is a computational model of stacked autoencoders. The above approaches focus on similarity, matrix methods, and attention mechanisms. They neglect the potential role of the base. Extraction of disease-based disease representation of node pairs and graph convolution learning of its network representation are two benefits of TDCMDA over alternative techniques. We can also see that TDCMDA obtains better prediction of miRNA-disease association compared to other baseline methods. The outcomes demonstrate that our model performs well.

3.4 Case studies

A case study on the full dataset was carried out to show the effectiveness of TDCMDA in predicting probable miRNA-disease associations. Prediction of miRNA-disease pairs with unknown associations using TDCMDA and ranking of miRNA from highest to lowest based on prediction scores. Our research focused on case studies of lung, breast, and esophageal cancers. For each condition, we listed the top 50 miRNAs predicted by TDCMDA. For each disease, we selected the miRNA with the highest prediction score and searched for experimental evidence in the HMDD v3.2 database, a hand-collected database of miRNA-disease associations, containing a total of 1206 miRNA, 893 diseases, and 35547 miRNA-disease association data.

Lung neoplasms are the main malignant tumors of the respiratory system [43]. In Table 1 of the predicted results of TDCMDA, we can observe that the HMDD v3.2 database has verified 46 of the top 50 miRNAs anticipated to be linked to lung neoplasms. For instance, Espinosa and Slack have shown that the transcripts of the second and third-ranked hsa-let-7e, hsa-let-7d, are dramatically downregulated in human lung cancer and that low levels of hsa-let-7 are linked to poor prognosis [44]. The 11th-ranked miRNA, hsa-mir-134, has been shown by Chen et al. to regulate the growth and apoptosis of lung cancer H69 cells via ERK1/2 signaling pathway inhibition and WWOX gene targeting [45].

Table 1. Validation results of predicted associations for lung neoplasms as an unknown disease

Disease Name	Rank	miRNA	Evidence	Rank	miRNA	Evidence
Lung neoplasms	1	hsa-mir-21	HMDD v3.2	26	hsa-mir-155	HMDD v3.2
	2	hsa-let-7e	HMDD v3.2	27	hsa-mir-210	HMDD v3.2
	3	hsa-let-7d	HMDD v3.2	28	hsa-let-7f-1	unconfirmed
	4	hsa-let-7a-1	HMDD v3.2	29	hsa-mir-30d	HMDD v3.2
	5	hsa-let-7a-2	HMDD v3.2	30	hsa-let-7g	HMDD v3.2
	6	hsa-mir-18a	HMDD v3.2	31	hsa-mir-203a	unconfirmed
	7	hsa-mir-200b	HMDD v3.2	32	hsa-mir-33a	HMDD v3.2
	8	hsa-mir-200c	HMDD v3.2	33	hsa-mir-9	HMDD v3.2
	9	hsa-let-7b	HMDD v3.2	34	hsa-mir-10b	HMDD v3.2
	10	hsa-let-7a	HMDD v3.2	35	hsa-mir-34a	HMDD v3.2
	11	hsa-mir-134	HMDD v3.2	36	hsa-mir-29b	HMDD v3.2
	12	hsa-mir-183	HMDD v3.2	37	hsa-mir-143	HMDD v3.2
	13	hsa-let-7i	HMDD v3.2	38	hsa-mir-486	HMDD v3.2
	14	hsa-mir-217	HMDD v3.2	39	hsa-mir-19b	HMDD v3.2
	15	hsa-mir-193a	HMDD v3.2	40	hsa-mir-128-2	HMDD v3.2
	16	hsa-mir-29a	HMDD v3.2	41	hsa-mir-20a	unconfirmed
	17	hsa-mir-145	HMDD v3.2	42	hsa-mir-182	HMDD v3.2
	18	hsa-mir-34b	HMDD v3.2	43	hsa-mir-132	HMDD v3.2
	19	hsa-mir-30a	HMDD v3.2	44	hsa-mir-19a	HMDD v3.2
	20	hsa-mir-17	HMDD v3.2	45	hsa-mir-27a	HMDD v3.2
	21	hsa-mir-34c	unconfirmed	46	hsa-let-7a-3	HMDD v3.2
	22	hsa-mir-31	HMDD v3.2	47	hsa-mir-1-1	HMDD v3.2
	23	hsa-let-7c	HMDD v3.2	48	hsa-mir-494	HMDD v3.2
	24	hsa-mir-203	HMDD v3.2	49	hsa-let-7f-2	HMDD v3.2
	25	hsa-mir-124-1	HMDD v3.2	50	hsa-mir-125b-1	HMDD v3.2

Breast neoplasms are the most prevalent cancer among women in the world and the second most common malignancy in China. [43]. In Table 2 of the predicted results of TDCMDA, we can observe that the HMDD v3.2 database has verified 48 of the top 50 miRNAs anticipated to be linked to breast neoplasms. The 36th-ranked hsa-mir-10b, a common breast cancer oncogenic factor, was one of the first miRNAs found to affect cancer metastasis and could promote cellular value addition and migration in breast cancer through the FUT8/p-AKT axis [46]. The 47th-ranked hsa-mir-206 was the first miRNA associated with breast carcinogenesis when Lorio et al. compared the distinction between typical and abnormal miRNA expression and breast neoplasms tissues. In research by Ge et al. [47], it was discovered that Hsa-mir-206 directly inhibited the PFKFB3 molecule, having an impact on the glycolytic process as well as cellular value addition and migration in breast cancer cells.

Table 2. Validation results of predicted associations for breast neoplasms as an unknown disease

Disease Name	Rank	miRNA	Evidence	Rank	miRNA	Evidence
Breast neoplasms	1	hsa-mir-200b	HMDD v3.2	26	hsa-let-7a-1	HMDD v3.2
	2	hsa-mir-222	HMDD v3.2	27	hsa-mir-18a	HMDD v3.2
	3	hsa-let-7a	HMDD v3.2	28	hsa-mir-214	HMDD v3.2
	4	hsa-mir-452	HMDD v3.2	29	hsa-mir-19b	HMDD v3.2
	5	hsa-mir-21	HMDD v3.2	30	hsa-mir-10a	HMDD v3.2
	6	hsa-mir-342	HMDD v3.2	31	hsa-mir-145	HMDD v3.2
	7	hsa-mir-200c	HMDD v3.2	32	hsa-mir-29c	unconfirmed
	8	hsa-mir-205	unconfirmed	33	hsa-mir-96	HMDD v3.2
	9	hsa-mir-125b-1	HMDD v3.2	34	hsa-mir-574	HMDD v3.2
	10	hsa-mir-199b	HMDD v3.2	35	hsa-mir-29a	HMDD v3.2
	11	hsa-mir-93	HMDD v3.2	36	hsa-mir-10b	HMDD v3.2
	12	hsa-mir-30a	HMDD v3.2	37	hsa-let-7e	HMDD v3.2
	13	hsa-mir-27b	HMDD v3.2	38	hsa-mir-17	HMDD v3.2
	14	hsa-mir-335	HMDD v3.2	39	hsa-mir-153	HMDD v3.2
	15	hsa-mir-9	HMDD v3.2	40	hsa-mir-302b	HMDD v3.2
	16	hsa-mir-15a	HMDD v3.2	41	hsa-mir-143	HMDD v3.2
	17	hsa-mir-16	HMDD v3.2	42	hsa-mir-125b	HMDD v3.2
	18	hsa-mir-27a	HMDD v3.2	43	hsa-mir-133b	HMDD v3.2
	19	hsa-mir-141	HMDD v3.2	44	hsa-mir-31	HMDD v3.2
	20	hsa-mir-182	HMDD v3.2	45	hsa-mir-106a	HMDD v3.2
	21	hsa-mir-200a	HMDD v3.2	46	hsa-mir-423	HMDD v3.2
	22	hsa-mir-155	HMDD v3.2	47	hsa-mir-206	HMDD v3.2
	23	hsa-mir-200	HMDD v3.2	48	hsa-mir-29b-2	HMDD v3.2
	24	hsa-mir-106b	HMDD v3.2	49	hsa-let-7a-2	HMDD v3.2
	25	hsa-mir-196a	HMDD v3.2	50	hsa-mir-19a	HMDD v3.2

Esophageal neoplasms are the major malignant tumors of the digestive system [43]. In Table 3 of the predicted results of TDCMDA, we can see that HMDD v3.2 has verified all 50 of the miRNAs that were anticipated to be linked with esophageal neoplasms. The second-ranked miRNA, hsa-mir-125b, inhibits the growth of esophageal squamous cell carcinoma through the p38-MAPK signaling pathway [48]. The plasma of esophageal cancer patients had a considerable upregulation of the third-ranked miRNA, hsa-mir-21, which considerably aided recipient cells' invasion and migration [49].

Table 3. Validation results of predicted associations for esophageal neoplasms as an unknown disease

Disease Name	Rank	miRNA	Evidence	Rank	miRNA	Evidence
Esophageal neoplasms	1	hsa-mir-27a	HMDD v3.2	26	hsa-mir-155	HMDD v3.2
	2	hsa-mir-125b	HMDD v3.2	27	hsa-mir-10b	HMDD v3.2
	3	hsa-mir-21	HMDD v3.2	28	hsa-mir-20a	HMDD v3.2
	4	hsa-mir-486	HMDD v3.2	29	hsa-mir-196a-2	HMDD v3.2
	5	hsa-mir-451	HMDD v3.2	30	hsa-mir-150	HMDD v3.2
	6	hsa-mir-143	HMDD v3.2	31	hsa-mir-146a	HMDD v3.2
	7	hsa-mir-342	HMDD v3.2	32	hsa-mir-133a-1	HMDD v3.2
	8	hsa-mir-25	HMDD v3.2	33	hsa-mir-183	HMDD v3.2
	9	hsa-mir-203	HMDD v3.2	34	hsa-mir-151	HMDD v3.2
	10	hsa-mir-145	HMDD v3.2	35	hsa-mir-302f	HMDD v3.2
	11	hsa-mir-19a	HMDD v3.2	36	hsa-mir-196a-1	HMDD v3.2
	12	hsa-mir-100	HMDD v3.2	37	hsa-mir-130a	HMDD v3.2
	13	hsa-mir-92a-1	HMDD v3.2	38	hsa-mir-373	HMDD v3.2
	14	hsa-mir-31	HMDD v3.2	39	hsa-mir-194	HMDD v3.2
	15	hsa-mir-199a-1	HMDD v3.2	40	hsa-mir-26a-1	HMDD v3.2
	16	hsa-mir-15a	HMDD v3.2	41	hsa-mir-99b	HMDD v3.2
	17	hsa-let-7a-3	HMDD v3.2	42	hsa-mir-92b	HMDD v3.2
	18	hsa-mir-93	HMDD v3.2	43	hsa-mir-196b	HMDD v3.2
	19	hsa-mir-205	HMDD v3.2	44	hsa-mir-499a	HMDD v3.2
	20	hsa-mir-135b	HMDD v3.2	45	hsa-mir-193a	HMDD v3.2
	21	hsa-mir-99a	HMDD v3.2	46	hsa-mir-22	HMDD v3.2
	22	hsa-mir-210	HMDD v3.2	47	hsa-mir-130b	HMDD v3.2
	23	hsa-let-7a	HMDD v3.2	48	hsa-mir-151a	HMDD v3.2
	24	hsa-mir-126	HMDD v3.2	49	hsa-mir-720	HMDD v3.2
	25	hsa-mir-29c	HMDD v3.2	50	hsa-mir-454	HMDD v3.2

4. Conclusion

The ability to anticipate the miRNA-disease associations is crucial for the research of disease genesis and the continuous progress of new medications. In this essay, we suggest a tripartite graph-based integrating dual-layer Contrast learning into graph neural network for MDA prediction, which aims to integrate dual-layer contrast learning into graph neural network under the miRNA-disease-gene tripartite graph. GCN and contrastive learning methods were fused to join the disease-gene graph network to determine the relationship between miRNA-disease. The disease-disease similarity was first obtained using the relationship aggregation mechanism and the cosine similarity method. The spatial structural properties of the miRNA-disease heterogeneous network were then extracted using the GCN approach. Then, two layers of supervised contrast learning are added to improve the nodes' effective representation. Five-fold crossover experiments confirmed that our proposed method, TDCMDA, achieved excellent results in both AUC and AUPR and outperformed current state-of-the-art methods. The ability of TDCMDA to predict potential miRNA-disease associations was further confirmed by case studies of lung neoplasms, breast neoplasms, and esophageal neoplasms, and TDCMDA can be used as a useful tool for screening reliable miRNA-disease pairs.

However, our model also has some limitations, which need to be further explored in the following studies. For example, our model is highly dependent on the disease-gene relationship network, suffers from the problem of cold start, and cannot provide accurate predictions for new diseases. However, high-quality miRNA illness heterogeneous networks are critical for the quality of features derived by graph convolution; as a result, it's crucial to understand how to build high-quality heterogeneous networks. Future research projects need to answer these questions.

Acknowledgments

The authors thank to lab members for assistance.

Funding statement

We acknowledge financial support from the National College Students' innovation and entrepreneurship training program(no. 202210504103),National Natural Science Foundation of China (no. 31771430 to LL), Huazhong Agricultural University Scientific and Technological Self-innovation Foundation (to LL) and Hubei Hongshan Laboratory (to LL).

Conflicts of Interest 

The authors declare that they have no conflicts of interest to report regarding the present study.

References

[1] Ambros V. The functions of animal microRNAs. Nature, 431:350–355, 2004.

[2] Cron M.A., Guillochon É., Kusner L., Le Panse R. Role of miRNAs in normal and myasthenia gravis thymus. Front Immunol., 11:1074, 2020.

[3] Cacchiarelli D., Legnini I., Martone J., Cazzella V., d’Amico A., Bertini E., Bozzoni I. miRNAs as serum biomarkers for Duchenne muscular dystrophy. EMBO Mol Med., 3:258–265, 2011.

[4] Sullivan C.S., Ganem D. MicroRNAs and viral infection. Mol Cell., 20:3–7, 2005.

[5] Cimmino A., Calin G.A., Fabbri M., Iorio M.V., Ferracin M., Shimizu M., Wojcik S.E., Aqeilan R.I., Zupo S., Dono M., Rassenti L., Alder H., Volinia S., Liu C.G., Kipps T.J., Negrini M., Croce C.M. miR-15 and miR-16 induce apoptosis by targeting BCL2. Proceedings of the National Academy of Sciences, 102(39):13944–13949, 2005.

[6] Chen X., Xie D., Zhao Q., You Z.-H. MicroRNAs and complex diseases: from experimental results to computational models. Brief. Bioinform., 20:515–539, 2019.

[7] Wilkening S., Bader A. Quantitative real-time polymerase chain reaction: methodical analysis and mathematical model. J. Biomol. Tech., 15:107-111, 2004.

[8] Pall G.S., Hamilton A.J. Improved northern blot method for enhanced detection of small RNA. Nat. Protoc., 3:1077–1084, 2008.

[9] Ma M., Na S., Zhang X., Chen C., Xu J. SFGAE: A self-f eature-based g raph a uto e ncoder model for miRNA–disease associations prediction. Brief. Bioinform., 23(5), bbac340, 2022.

[10] Chen X., Zhu C.-C., Yin J. Ensemble of decision tree reveals potential miRNA-disease associations. PLoS Comput. Biol., 15, e1007209, 2019.

[11] Chen X., Huang L. LRSSLMDA: Laplacian regularized sparse subspace learning for MiRNA-disease association prediction. PLoS Comput. Biol., 13, e1005912, 2017.

[12] Chen H., Zhang Z., Similarity-based methods for potential human microRNA-disease association prediction. BMC Med. Genomics, 6:1–9, 2013.

[13] Zheng K., You Z.-H., Wang L., Zhou Y., Li L.-P., Li Z.-W. Dbmda: A unified embedding for sequence-based mirna similarity measure with applications to predict and validate mirna-disease associations. Molecular Therapy-Nucleic Acids, 19:602–611, 2020.

[14] Xuan P., Han K., Guo M., Guo Y., Li J., Ding J., Liu Y., Dai Q., Li J., Teng Z. Prediction of microRNAs associated with human diseases based on weighted k most similar neighbors. PLoS One, 8, e70204, 2013.

[15] Chen M., Lu X., Liao B., Li Z., Cai L., Gu C. Uncover miRNA-disease association by exploiting global network similarity. PLoS One, 11(12), e0166509, 2016.

[16] Wu Z., Pan S., Chen F., Long G., Zhang G., Yu P.S. A comprehensive survey on graph neural networks. Machine Learning, arXiv:1901.00596, 2019.

[17] Zheng K., You Z.-H., Wang L., Zhou Y., Li L.-P., Li Z.-W. MLMDA: A machine learning approach to predict and validate MicroRNA–disease associations by integrating of heterogenous information sources. J. Transl. Med., 17:1–14, 2019.

[18] Han H., Zhu R., Liu J.-X., Dai L.-Y. Predicting miRNA-disease associations via layer attention graph convolutional network model. BMC Med. Inform. Decis. Mak., 22, 69, 2022.

[19] Li C., Liu H., Hu Q., Que J., Yao J. A novel computational model for predicting microRNA–disease associations based on heterogeneous graph convolutional networks. Cells, 8, 977, 2019.

[20] Zhang G., Li M., Deng H., Xu X., Liu X., Zhang W. SGNNMD: Signed graph neural network for predicting deregulation types of miRNA-disease associations. Brief. Bioinform., 23, bbab464, 2022.

[21] Yan C., Duan G., Li N., Zhang L., Wu F.-X., Wang J. PDMDA: Predicting deep-level miRNA–disease associations with graph neural networks and sequence features. Bioinformatics, 38:2226–2234, 2022.

[22] Wang W., Chen H. Predicting miRNA-disease associations based on graph attention networks and dual Laplacian regularized least squares. Brief. Bioinform., 23(5), bbac292, 2022.

[23] Denzler R., Agarwal V., Stefano J., Bartel D.P., Stoffel M. Assessing the ceRNA hypothesis with quantitative measurements of miRNA and target abundance. Mol Cell., 54:766–776, 2014.

[24] Qi X., Zhang D.-H., Wu N., Xiao J.-H., Wang X., Ma W. ceRNA in cancer: Possible functions and clinical implications. J. Med. Genet., 52:710–718, 2015.

[25] Tay Y., Kats L., Salmena L., Weiss D., Tan S.M., Ala U., Karreth F., Poliseno L., Provero P., Di Cunto F. Coding-independent regulation of the tumor suppressor PTEN by competing endogenous mRNAs. Cell., 147:344–357, 2011.

[26] Huang Z., Shi J., Gao Y., Cui C., Zhang S., Li J., Zhou Y., Cui Q., HMDD v3. 0: A database for experimentally supported human microRNA–disease associations. Nucleic Acids Res., 47:D1013–D1017, 2019.

[27] Davis A.P., Wiegers T.C., Johnson R.J., Sciaky D., Wiegers J., Mattingly C.J., Comparative toxicogenomics database (CTD): Update 2023. Nucleic Acids Res., 51:D1257–D1262, 2023.

[28] Kipf T.N., Welling M. Semi-supervised classification with graph convolutional networks. ArXiv Preprint ArXiv:1609.02907, 2016.

[29] Gao B., Liu T.-Y., Wei W., Wang T., Li H. Semi-supervised ranking on very large graphs with rich metadata. In: Proceedings of the 17th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, pp. 96–104, 2011.

[30] Sun Z., Deng Z.-H., Nie J.-Y., Tang J. Rotate: Knowledge graph embedding by relational rotation in complex space. ArXiv Preprint ArXiv:1902.10197, 2019.

[31] Bojchevski A., Günnemann S. Deep Gaussian embedding of graphs: Unsupervised inductive learning via ranking. ArXiv Preprint ArXiv:1707.03815, 2017.

[32] Khosla P., Teterwak P., Wang C., Sarna A., Tian Y., Isola P., Maschinot A., Liu C., Krishnan D. Supervised contrastive learning. Adv. Neural Inf. Process Syst., 33:18661–18673, 2020.

[33] Rendle S., Freudenthaler C., Gantner Z., Schmidt-Thieme L. Bayesian personalized ranking from implicit feedback. In: Proc. of Uncertainty in Artificial Intelligence, pp. 452–461, 2014.

[34] Davis J., Goadrich M. The relationship between Precision-Recall and ROC curves. In: Proceedings of the 23rd International Conference on Machine Learning, pp. 233–240, 2006.

[35] Bradley A.P. The use of the area under the ROC curve in the evaluation of machine learning algorithms. Pattern Recognit., 30:1145–1159, 1997.

[36] Feng H., Jin D., Li J., Li Y., Zou Q., Liu T. Matrix reconstruction with reliable neighbors for predicting potential MiRNA–disease associations. Brief. Bioinform., 24(1):bbac571, 2023.

[37] Ha J. SMAP: Similarity-based matrix factorization framework for inferring miRNA-disease association. Knowledge-Based Systems, 263, 110295, 2023.

[38] Li Z., Zhang Y., Bai Y., Xie X., Zeng L. IMC-MDA: Prediction of miRNA-disease association based on induction matrix completion. Mathematical Biosciences and Engineering, 20:10659–10674, 2023.

[39] Wang W., Chen H. Predicting miRNA-disease associations based on lncRNA–miRNA interactions and graph convolution networks. Brief. Bioinform., 24(1):bbac495, 2023.

[40] Li Z., Zhong T., Huang D., You Z.-H., Nie R. Hierarchical graph attention network for miRNA-disease association prediction. Molecular Therapy, 30:1775–1786, 2022.

[41] Zhang L., Liu B., Li Z., Zhu X., Liang Z., An J. Predicting MiRNA-disease associations by multiple meta-paths fusion graph embedding model. BMC Bioinformatics. 21:1–19, 2020.

[42] Wang C.-C., Li T.-H., Huang L., Chen X. Prediction of potential miRNA–disease associations based on stacked autoencoder. Brief. Bioinform., 23(2):bbac021, 2022.

[43] Bray F., Ferlay J., Soerjomataram I., Siegel R.L., Torre L.A., Jemal A. Global cancer statistics 2018: GLOBOCAN estimates of incidence and mortality worldwide for 36 cancers in 185 countries. CA Cancer J. Clin., 68(6):394–424, 2018.

[44] Espinosa C.E.S., Slack F.J. Cancer issue: The role of microRNAs in cancer. Yale J. Biol. Med., 79(3-4): 131–140, 2006.

[45] Chen T., Gao F., Feng S., Yang T., Chen M. MicroRNA-134 regulates lung cancer cell H69 growth and apoptosis by targeting WWOX gene and suppressing the ERK1/2 signaling pathway. Biochem Biophys Res Commun., 464:748–754, 2015.

[46] Guo D., Guo J., Li X., Guan F. Enhanced motility and proliferation by miR10b/FUT8/pAKT axis in breast cancer cells. Oncol Lett., 16(2):2097–2104, 2018.

[47] Ge X., Lyu P., Cao Z., Li J., Guo G., Xia W., Gu Y. Overexpression of miR-206 suppresses glycolysis, proliferation and migration in breast cancer cells via PFKFB3 targeting. Biochem Biophys Res Commun., 463(4):1115–1121, 2015.

[48] Li T., Yu S.-S., Zhou C.-Y., Wang K., Wan Y.-C. RETRACTED ARTICLE: MicroRNA-206 inhibition and activation of the AMPK/Nampt signalling pathway enhance sevoflurane post-conditioning-induced amelioration of myocardial ischaemia/reperfusion injury. J Drug Target., 28:80–91, 2020.

[49] Liao J., Liu R.A.N., Shi Y.-J., Yin L.-H., Pu Y.-P. Exosome-shuttling microRNA-21 promotes cell migration and invasion-targeting PDCD4 in esophageal cancer. Int. J. Oncol., 48(6):2567–2579, 2016.