Hardening effects on formability limit prediction based on Gurson-type damage models and bifurcation analysis

Abstract. In this work, ductility limits of metallic materials, associated with the occurrence of strain localization, are predicted using the GTN damage model coupled with bifurcation theory. The resulting approach is implemented into the finite element code ABAQUS within the framework of large plastic strains and a fully three-dimensional formulation. A parametric study with respect to damage and hardening parameters is conducted in order to identify the most influential material parameters on strain localization. The analysis shows that the damage parameters have a significant impact on the predicted ductility limits, while the effect of hardening parameters on strain localization depends on the choice of void nucleation mechanism.

1 INTRODUCTION

It is well known that in sheet metal forming processes, different types of defects may occur, which are usually associated with operating conditions and/or material characteristics. Plastic instabilities, corresponding to the occurrence of zones of highly localized plastic strain, are examples of these undesirable phenomena. To characterize the formability of thin sheet metals, the concept of forming limit diagram has been introduced [1]. Among the most influential constitutive features on the formability limits of thin sheet metals, the damage development is of particular importance. In this context, Gurson-type damage models have been developed, among which the GTN model [2], which is adopted in this work to describe the initiation of ductile damage and its evolution during loading. This model is coupled with the bifurcation analysis [3,4] to predict the occurrence of strain localization in metallic materials. The present work investigates the respective effect of damage and hardening parameters on the prediction of ductility limits using different void nucleation mechanisms. In addition, an alternative modeling approach is explored for the analysis of hardening effects on strain localization, which consists in adopting a micromechanics-based calibration for the GTN ${\textstyle q}$ -parameters.

2 GTN DAMAGE MODEL

The ductile damage model adopted in this work is based on the Gurson model, which accounts for void nucleation and growth. This model has been subsequently modified in the literature leading to the following well-known GTN yield potential (see, e.g., [2]):

${\textstyle \Phi ={\left({\frac {{\sigma }_{eq}}{{\sigma }_{Y}}}\right)}^{2}+2q_{1}f^{\ast }cosh\left({\frac {3}{2}}q_{2}{\frac {{\sigma }_{m}}{{\sigma }_{Y}}}\right)-\left(1+q_{3}f^{\ast }{}^{2}\right)\leq 0}$ ,

(1)

where ${\textstyle q_{1}}$ , ${\textstyle q_{2}}$ and ${\textstyle q_{3}}$ are material parameters; ${\textstyle {\sigma }_{m}}$ is the hydrostatic stress defined by ${\textstyle {\sigma }_{m}=\sigma :1/3}$ , with ${\textstyle \sigma }$ being the Cauchy stress tensor and ${\textstyle 1}$ the second-order identity tensor; ${\textstyle {\sigma }_{eq}}$ is the von Mises equivalent stress defined by ${\textstyle {\sigma }_{eq}={\sqrt {3{\mbox{ }}S:S/2}}}$ , with ${\textstyle S}$ being the deviatoric part of the Cauchy stress; ${\textstyle {\sigma }_{Y}}$ is the flow stress, function of the equivalent plastic strain ${\textstyle {\overline {\epsilon }}_{m}^{pl}}$ of the fully dense matrix; ${\textstyle f^{\ast }\left(f\right)}$ is the modified void volume fraction, function of the actual void volume fraction ${\textstyle f}$ , which is defined by

${\textstyle f^{\ast }(f)=\lbrace {\begin{array}{c}f{\mbox{                             for    }}f\leq f_{cr},\\f_{cr}+{\delta }_{GTN}\left(f-f_{cr}\right){\mbox{  for    }}f_{cr}<f\leq f_{R},\end{array}}}$ with ${\textstyle {\delta }_{GTN}={\frac {f_{u}^{\ast }-f_{cr}}{f_{R}-f_{cr}}},}$

(2)

where the damage parameters ${\textstyle f_{cr}}$ and ${\textstyle f_{R}}$ are the critical void volume fraction, at which the coalescence stage starts, and the void volume fraction at final fracture, respectively. According to Eq. (2), ${\textstyle f^{\ast }(f)}$ reaches its ultimate value ${\textstyle f_{u}^{\ast }}$ when ${\textstyle f=f_{R}}$ .

The tensile flow stress ${\textstyle {\sigma }_{Y}}$ of the fully dense matrix material is assumed to be governed by an isotropic hardening law, as given by the following rate expression:

${\textstyle {\dot {\sigma }}_{Y}=h{\mbox{ }}{\dot {\overline {\epsilon }}}_{m}^{pl}}$ ,

(3)

where ${\textstyle h}$ is the plastic hardening modulus of the fully dense matrix material. The plastic flow rule follows the classical normality law, which defines the plastic strain rate ${\textstyle D^{p}}$ as

$D^{p}={\dot {\lambda }}{\frac {\partial \Phi }{\partial \sigma }}$ ,

(4)

where ${\textstyle {\dot {\lambda }}}$ is the plastic multiplier, and ${\textstyle \partial \Phi /\partial \sigma }$ is the direction of the plastic flow. The evolution of void volume fraction depends on both growth of pre-existent voids and nucleation of new ones. For the nucleation of new voids, the model proposed by Chu and Needleman [5] is adopted in this work. This model involves the contribution of both the flow stress rate of the dense matrix and the hydrostatic stress rate. The final expression of the incremental change in void volume fraction is given by

${\textstyle {\dot {f}}={\underset {growth}{\underbrace {\left(1-f\right)D^{p}:1} }}+{\underset {nucleation}{\underbrace {\left[\left(A_{N}/h\right)+B_{N}\right]{\dot {\sigma }}_{Y}+B_{N}{\dot {\sigma }}_{m}} }}}$ .

(5)

In the above equation, the constants ${\textstyle A_{N}}$ and ${\textstyle B_{N}}$ allow characterizing the void nucleation model, which is strain controlled for ${\textstyle A_{N}>0}$ and ${\textstyle B_{N}=0}$ , and stress controlled for ${\textstyle A_{N}=0}$ and ${\textstyle B_{N}>0}$ . Their expressions follow normal distribution laws as proposed in [5]

${\textstyle A_{N}={\frac {f_{N}}{s_{N}{\sqrt {2\pi }}}}exp\left[-{\frac {1}{2}}{\left({\frac {{\overline {\epsilon }}_{m}^{pl}-{\epsilon }_{N}}{s_{N}}}\right)}^{2}\right]{\mbox{ }},{\mbox{ }}{\mbox{ }}{\mbox{ }}{\mbox{ }}B_{N}={\frac {f_{N}}{s_{N}{\sigma }_{0}{\sqrt {2\pi }}}}exp\left(-{\frac {1}{2}}{\left({\frac {{\sigma }_{Y}+{\sigma }_{m}-{\sigma }_{N}}{s_{N}^{}{\sigma }_{0}}}\right)}^{2}\right)}$ ,

(6)

where ${\textstyle {\epsilon }_{N}}$ and ${\textstyle {\sigma }_{N}}$ are the mean strain and the mean stress for nucleation, respectively; ${\textstyle s_{N}}$ is the standard deviation on ${\textstyle {\epsilon }_{N}}$

${\textstyle f_{N}}$ is the volume fraction of void-nucleating particles; ${\textstyle {\sigma }_{0}}$ is the initial yield stress of the matrix surrounding the voids. In the co-rotational frame, which is associated with the Jaumann objective derivative, the Cauchy stress rate is expressed using the following hypoelastic law:

${\textstyle {\dot {\sigma }}=C^{e}:\left(D-{\dot {\lambda }}{\frac {\partial \Phi }{\partial \sigma }}\right)=C^{ep}:D}$ ,

(7)

where ${\textstyle D}$ is the strain rate tensor, ${\textstyle C^{e}}$ is the fourth-order elasticity tensor, and ${\textstyle C^{ep}}$ is the elastic–plastic tangent modulus. Using the consistency condition ${\textstyle {\dot {\Phi }}=0}$ , together with the above equations, the plastic multiplier ${\textstyle {\dot {\lambda }}}$ writes

${\textstyle {\dot {\lambda }}={\frac {1}{H_{\lambda }}}E:C^{e}:D}$ ,

(8)

where

${\textstyle E={\frac {\partial \Phi }{\partial \sigma }}+{\frac {B_{N}}{3}}{\mbox{ }}{\frac {\partial \Phi }{\partial f^{\ast }}}{\mbox{ }}{\frac {\partial f^{\ast }}{\partial f}}1}$ ,

(9)

${\textstyle H_{\lambda }=E:C^{e}:{\frac {\partial \Phi }{\partial \sigma }}-{\frac {h}{\left(1-f\right)}}{\frac {\sigma :{\frac {\partial \Phi }{\partial \sigma }}}{{\sigma }_{Y}}}\left[{\frac {\partial \Phi }{\partial {\sigma }_{Y}}}+\left({\frac {A_{N}}{h}}+B_{N}\right){\mbox{ }}{\frac {\partial \Phi }{\partial f^{\ast }}}{\mbox{ }}{\frac {\partial f^{\ast }}{\partial f}}\right]-\left(1-f\right){\frac {\partial f^{\ast }}{\partial f}}{\frac {\partial \Phi }{\partial f^{\ast }}}{\frac {\partial \Phi }{\partial \sigma }}:1{\mbox{ }}.}$

(10)

By replacing the plastic multiplier ${\textstyle {\dot {\lambda }}}$ (see Eq. (8)) into the hypoelastic law (Eq. (7)), the elasticplastic tangent modulus of the GTN model writes

${\textstyle C^{ep}=C^{e}-\left(C^{e}:{\frac {\partial \Phi }{\partial \sigma }}\right)\otimes \left(E:C^{e}\right)/H_{\lambda }}$ .

(11)

It can be observed that, in the case of strain-controlled nucleation (i.e., ${\textstyle A_{N}>0}$ and ${\textstyle B_{N}=0}$ ), the above elasticplastic tangent modulus becomes symmetric and the normality of the plastic flow rule holds. In the case of stress-controlled nucleation (i.e., ${\textstyle A_{N}=0}$ and ${\textstyle B_{N}>0}$ ), the elasticplastic tangent modulus is non-symmetric and the normality of the plastic flow rule does not hold.

3 BIFURCATION CRITERION

In this section, the constitutive equations described above are coupled with a plastic instability criterion, as proposed by Rudnicki and Rice [3] and Rice [4], in order to predict the occurrence of strain localization. This criterion is based on bifurcation theory, where the incipience of plastic flow localization in the form of an infinite band is associated with the loss of uniqueness for the solution of the rate equilibrium equations. According to this criterion, the critical condition, which also corresponds to the loss of ellipticity of the associated boundary value problem, is related to the singularity of the acoustic tensor ${\textstyle A}$ , defined as ${\textstyle A=n\cdot L\cdot n}$ , where ${\textstyle n}$ is the normal to the localization band and the tangent modulus ${\textstyle L}$ writes

${\textstyle L=C^{ep}+Z_{1}-Z_{2}-Z_{3}}$ ,

(12)

where ${\textstyle Z_{1}}$ , ${\textstyle Z_{2}}$ and ${\textstyle Z_{3}}$ are fourth-order tensors that consist of Cauchy stress components. These additional tensors originate from the large-strain framework and their complete expressions can be found in [6,7]. The critical condition is then given by

${\textstyle det\left(A\right)=det\left(n\cdot L\cdot n\right)=0}$ .

(13)

4 PREDICTION OF DUCTILITY LIMITS

In this section, the GTN model is coupled with the bifurcation analysis to predict strain localization in porous materials subjected to in-plane loading conditions. The resulting approach is implemented into the finite element code ABAQUS/Standard within the framework of large plastic strains and a fully three-dimensional formulation. The effect of hardening and damage parameters, as well as the choice of nucleation modeling, on the prediction of ductility limits is analyzed.

4.1 Strain-controlled nucleation model

In this section, nucleation of new voids is taken strain-controlled, by considering ${\textstyle A_{N}>0}$ and ${\textstyle B_{N}=0}$ in the GTN model (see Eq. (5)). It is worth noting that, in this case, the normality of the plastic flow rule holds and the elastic–plastic tangent modulus ${\textstyle C^{ep}}$ is symmetric, while the acoustic tensor ${\textstyle A}$ is non-symmetric due to the convective stress components (Eq. (12)).

The material considered here is Al5754 aluminum, with Young’s modulus and Poisson’s ratio equal to ${\textstyle 70,000}$ MPa and 0.33, respectively. The associated hardening parameters, according to the Swift isotropic hardening law, and damage parameters are summarized in Table 1 (see [8]).

Table 1: Hardening and damage parameters for Al5754

${\textstyle {\epsilon }_{0}}$	${\textstyle k}$ [MPa]	${\textstyle n}$	${\textstyle f_{0}}$	${\textstyle s_{N}}$	${\textstyle {\epsilon }_{N}}$	${\textstyle f_{N}}$	${\textstyle f_{cr}}$	${\textstyle {\delta }_{GTN}}$	${\textstyle q_{1}}$	${\textstyle q_{2}}$	${\textstyle q_{3}}$
0.00173	309.1	0.177	0.001	0.1	0.32	0.034	0.00284	7	1.5	1.0	2.15

4.1.1 Effect of damage parameters

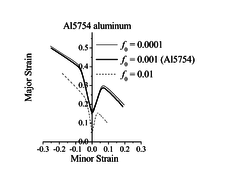
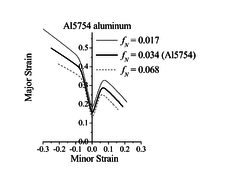
The effect of damage parameters on the ductility limit predictions for the Al5754 aluminum alloy is analyzed here. A relatively large number of damage parameters are involved in the GTN model; for conciseness, attention is focused on the initial void volume fraction ${\textstyle f_{0}}$ and the nucleation parameter ${\textstyle f_{N}}$ .

(a)	(b)

Figure 1: Effect of the initial void volume fraction ${\textstyle f_{0}}$ (a), and the nucleation parameter ${\textstyle f_{N}}$ (b) on the ductility limit predictions for Al5754 aluminum

Figure 1 shows the impact of varying one damage parameter at a time on the prediction of the ductility limits for Al5754 aluminum. Concerning the effect of the initial void volume fraction ${\textstyle f_{0}}$ (Figure 1(a)), large values for this parameter (e.g., ${\textstyle f_{0}=0.01}$) imply that the material has already entered the coalescence stage, which dramatically lowers the predicted ductility limits. However, for very small values for parameter ${\textstyle f_{0}}$, the ductility limit predictions are only slightly affected, which suggests that at such low void volume fraction levels, void growth is not the predominant mechanism for damage evolution. For the nucleation parameter ${\textstyle f_{N}}$, the predicted ductility limits are lowered as this parameter increases. This trend is consistent with the physical meaning of this parameter (volume fraction of void-nucleating particles), as larger values for the latter tend to precipitate damage, thus promoting early plastic flow localization (see Eq. (6)).

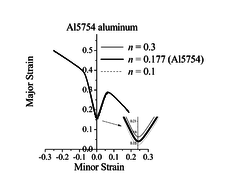
4.1.2 Effect of the hardening exponent ${\textstyle n}$4.1.2 Effect of the hardening exponent n {\textstyle n}

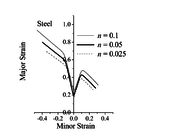
The impact of the hardening exponent ${\textstyle n}$ , associated with the Swift law, on the ductility limit predictions is analyzed here for the Al5754 aluminum material. Figure 2 shows the predicted limit strains obtained with different hardening exponents ${\textstyle n}$ for the dense matrix material. These results reveal that the effect of the hardening exponent ${\textstyle n}$ on the ductility limit predictions is much smaller than that observed for damage parameters (see the previous section). Similar results are observed when varying the ${\textstyle k}$ and ${\textstyle {\epsilon }_{0}}$ Swift hardening parameters, and are not reported here for conciseness. However, a more perceptible effect is found near the plane-strain tension (PST) loading path (see Figure 2).

Figure 2: Effect of the hardening exponent ${\textstyle n}$, associated with the Swift law, on the ductility limit predictions for Al5754 aluminum with strain-controlled nucleation

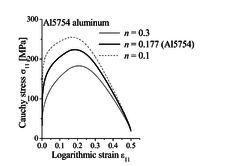
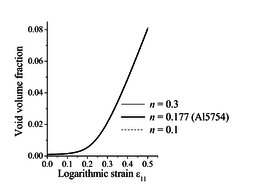
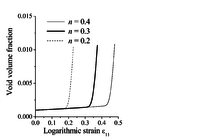
Similar trends have been observed in [9], where the GTN model was used with strain-controlled nucleation and coupled with the bifurcation theory. Indeed, in such a modeling approach, strain localization is mainly controlled by damage-induced softening, as shown in Figure 3(a) for the uniaxial tensile (UT) strain path, where it can be seen that flow localization occurs at strongly negative hardening moduli. Moreover, the evolution of void volume fraction based on strain-controlled nucleation for this particular loading path (UT) is shown to be insensitive to the strain hardening of the dense matrix material (see Figure 3(b)).

(a)	(b)

Figure 3: Effect of the hardening exponent ${\textstyle n}$ on: (a) the Cauchy stressstrain curve, and (b) void volume fraction, until localization along the uniaxial tensile strain path

4.2 Calibration of the GTN ${\textstyle q}$-parameters4.2 Calibration of the GTN q {\textstyle q} -parameters

The previous results have shown limitations of the GTN model, with strain-controlled nucleation, in accounting for the effect of strain hardening on the porosity evolution. To overcome such limitations, Faleskog et al. [10] suggested calibrating the GTN ${\textstyle q}$ -parameters in order to include the effect of strain hardening on void growth. Tables 2 and 3 summarize the calibrated ${\textstyle q}$ -parameters and the damage parameters for a steel material with yield strength ratio ${\textstyle {\sigma }_{0}/E=0.004}$ (see [10]). The isotropic hardening model used in the simulations is based on a hardening power law (see [10]).

Table 2: Calibrated ${\textstyle q}$-parameters

${\textstyle q}$-parameter	${\textstyle n=0.025}$	${\textstyle n=0.05}$	${\textstyle n=0.10}$
${\textstyle q_{1}}$	1.74	1.48	1.29
${\textstyle q_{2}}$	1.013	1.013	0.982

Table 3: Damage parameters for the GTN model

Material	${\textstyle f_{0}}$	${\textstyle s_{N}}$	${\textstyle {\epsilon }_{N}}$	${\textstyle f_{N}}$	${\textstyle f_{cr}}$	${\textstyle {\delta }_{GTN}}$
Steel	0.001	0.1	0.3	0.05	0.04	5

Figure 4: Effect of the hardening exponent ${\textstyle n}$ on the prediction of ductility limits using the calibrated ${\textstyle q}$-parameters

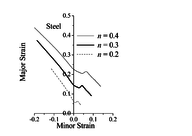
Figure 4 shows the effect of the hardening exponent ${\textstyle n}$ of the power law on the prediction of ductility limits for the studied steel material based on the calibration of the ${\textstyle q}$-parameters and strain-controlled nucleation model. The predicted ductility limits clearly show sensitivity to strain hardening for all strain paths, thanks to the use of micromechanics-based calibrated ${\textstyle q}$-parameters.

4.3 Stress-controlled nucleation model

The effect of strain hardening on the ductility limits is investigated in this section using the GTN model with stress-controlled nucleation. The associated material parameters corresponding to a steel material are summarized in Table 4. The Ludwig power law is used in the simulations for the modeling of isotropic hardening for the dense matrix material.

Table 4: Hardening and damage parameters for the studied steel material

${\textstyle {\sigma }_{0}}$ [MPa]	${\textstyle k}$ [MPa]	${\textstyle f_{0}}$	${\textstyle s_{N}}$	${\textstyle {\sigma }_{N}}$ [MPa]	${\textstyle f_{N}}$	${\textstyle f_{cr}}$	${\textstyle {\delta }_{GTN}}$	${\textstyle q_{1}}$	${\textstyle q_{2}}$	${\textstyle q_{3}}$
150	800	0.001	0.1	1000	0.05	0.04	10	1.5	1.0	2.15

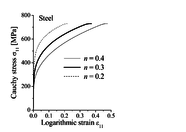
Figure 5 illustrates the effect of the hardening exponent ${\textstyle n}$ on the prediction of limit strains for the studied steel material. It is clearly shown that the consideration of non-normality in the GTN model, due to stress-controlled nucleation, allows for a significant effect of strain hardening on the limit strains. Indeed, the predicted limit strains increase as the hardening exponent ${\textstyle n}$ increases, which is consistent with the literature findings (see, e.g., [11]). The effect of the hardening exponent ${\textstyle n}$ on the evolution of the Cauchy stress and the void volume fraction until localization for the UT strain path is shown in Figure 6. It can be seen that, in contrast to the case of strain-controlled nucleation (see Figure 3(b)), the evolution of void volume fraction is significantly affected by the hardening exponent ${\textstyle n}$, which allows accounting for strain hardening effects on strain localization. Moreover, the Cauchy stress evolution reveals that the hardening modulus at localization is not strongly negative, as compared to that obtained in the case of strain-controlled nucleation. This is caused by the non-normality of the plastic flow, which plays a destabilizing role in the localization bifurcation analysis.

Figure 5: Effect of the hardening exponent ${\textstyle n}$ on the prediction of ductility limits for the studied steel material with stress-controlled nucleation

(a)	(b)

Figure 6: Effect of the hardening exponent ${\textstyle n}$ on: (a) the Cauchy stressstrain curve, and (b) void volume fraction, until localization along the UT strain path, in the case of stress-controlled nucleation

5 CONCLUSIONS

In this work, The GTN ductile damage model has been coupled with bifurcation theory to predict the occurrence of strain localization for metallic materials. The resulting approach has been implemented into the finite element software ABAQUS/standard in the framework of large plastic strains and a fully three-dimensional formulation. Ductility limits of metallic materials are then predicted using the proposed approach. A parametric study with respect to damage and hardening parameters has been conducted in order to determine the most influential parameters on strain localization. The analysis showed that the damage parameters have a significant impact on the predicted ductility limits. With regard to hardening, it is shown that the choice of void nucleation mechanism has an important influence on the sensitivity of the predicted ductility limits to strain hardening. Indeed, in the case of strain-controlled nucleation, the predicted limit strains were found almost insensitive to strain hardening for most strain paths, while a significant influence was observed in the case of stress-controlled nucleation. The latter leads to non-normality in the plastic flow rule, which plays a destabilizing role that promotes early strain localization. This work also discussed the use of a micromechanics-based calibration for the GTN ${\textstyle q}$-parameters in the case of strain-controlled nucleation, which is shown to allow accounting for hardening effects on strain localization predictions.

REFERENCES

[1] Keeler, S. and Backofen, W.A. Plastic instability and fracture in sheets stretched over rigid punches. ASM Trans. Quart. (1963) 56:25-48.

[2] Tvergaard, V. and Needleman, A. Analysis of the cup-cone fracture in a round tensile bar. Acta Metallurgica (1984) 32:157-169.

[3] Rudnicki, J.W. and Rice, J.R. Conditions for the localization of deformation in pressure sensitive dilatant materials. Journal of the Mechanics and Physics of Solids (1975) 23:371-394.

[4] Rice, J.R. The localization of plastic deformation. Theorical and Applied Mechanics. Koiter ed., 207-227, (1976).

[5] Chu, C. and Needleman, A. Void nucleation effects in biaxially stretched sheets. Journal of Engineering Materials and Technology (1980) 102:249-256.

[6] Abed-Meraim, F., Balan, T. and Altmeyer, G. Investigation and comparative analysis of plastic instability criteria: application to forming limit diagrams. International Journal of Advanced Manufacturing Technology (2014) 71:1247-1262.

[7] Ben Bettaieb, M. and Abed-Meraim, F. Investigation of localized necking in substrate-supported metal layers: Comparison of bifurcation and imperfection analyses. International Journal of Plasticity (2015) 65:168-190.

[8] Brunet, M., Mguil, S. and Morestin, F. Analytical and experimental studies of necking in sheet metal forming processes. Journal of Materials Processing Technology (1998) 80-81:40-46.

[9] Mansouri, L.Z., Chalal, H. and Abed-Meraim, F. Ductility limit prediction using a GTN damage model coupled with localization bifurcation analysis. Mechanics of Materials (2014) 76:64-92.

[10] Faleskog, J., Gao, X. and Shih, C.F. Cell model for nonlinear fracture analysis – I. Micromechanics calibration. International Journal of Fracture (1998) 89:355-373.

[11] Doghri, I. and Billardon, R. Investigation of localization due to damage in elasto-plastic materials. Mechanics of Materials (1995) 19:129-149.