Abstract: The changes in the geometry of the structures are called irregularities and are divided into two types: plant and height irregularities, the latter being widely investigated. In this sense, the objective of the present work is to study in detail the influence of the plant irregularities in the seismic resistance of a reinforced concrete structure, to quantify and locate vulnerable zones in the structure. The proposed study is developed numerically using ETABS software Nonlinear v9.7.2 and MATLAB R2009b. The results showed that plant irregularities as they are placed in the structure, this is losing its bearing capacity and therefore its ability to withstand the lateral loads.
Keywords: seismic analysis, seismic resistant structures, irregular structure
(1) Dr. Ing. Civil, Profesor Adjunto, Departamento de Estructuras, Facultad de Arquitectura y Urbanismo, Universidade de Brasília, Brasil. Email: alejandrop@unb.br
(2) Dr. Ing. Civil, Profesor Adjunto, Departamento Ingeniería Civil, Universidade de Brasília, Brasil. Email: graciela@unb.br
INTRODUCCIÓN
En los últimos años han ocurrido fuertes terremotos en diversas regiones del planeta trayendo como consecuencia catástrofes debido al colapso de muchas estructuras, como resultado de una concepción estructural equivocada o de una verificación sísmica insuficiente o precaria. Esta situación es un reflejo del desconocimiento por parte de algunos profesionales de los factores que influencian la respuesta sísmica de una estructura y del comportamiento de cada uno de sus elementos estructurales.
Un factor importante en la resistencia de una estructura es su configuración geométrica. Según las normas sismo resistentes, es recomendable diseñar y construir estructuras con geometrías simétricas, ya que este tipo de estructuras tiene caminos bien definidos de transmisión de fuerzas entre los elementos estructurales, distribuyendo de manera uniforme los esfuerzos y disminuyendo la probabilidad de daños durante un sismo.
Ya en la práctica, es común diseñar y proyectar estructuras con geometrías asimétricas o irregulares por diversos motivos. En algunos casos, esas geometrías asimétricas son causadas por inconsistencias o errores en el proceso del diseño estructural o son producto de daños acumulados a lo largo de la vida útil de la estructura. Por lo tanto, es esencial para los ingenieros estructurales adquirir una mejor comprensión de la respuesta sísmica de estructuras con geometrías asimétricas, una necesidad que también ha sido reconocida por las normas sismo resistentes actuales (NSR-10, 2010; NBR 15421, 2006).
Varios investigadores han proporcionado informaciones útiles sobre el estudio de las irregularidades estructurales. En todos estos trabajos fue utilizada una metodología de análisis similar, donde fue tomado como caso base una estructura simétrica en planta y en altura y en la cual las irregularidades fueron colocadas y estudiadas una por una mediante análisis dinámicos lineales y no lineales o análisis estático no lineal o pushover. Las respuestas sísmicas obtenidas para cada caso fueron comparadas con el caso base a fin de conocer la influencia de esas irregularidades en el comportamiento de la estructura.
Al-Ali y Krawinkler (1998) seguido por Chintanapakdee y Chopra (2004) realizaron las investigaciones más sistemáticas sobre el efecto de las irregularidades en altura en la respuesta sísmica de estructuras planas conocidas como “shear building”. Las estructuras utilizadas por Al-Ali y Krawinkler (1998) se basaron en la relación de viga fuerte-columna débil, mientras que Chintanapakdee y Chopra (2004) adoptaron una visión más realista utilizando la relación viga débil-columna fuerte. A pesar de algunas diferencias esperadas debido a los distintos enfoques utilizados, todos los estudios llegaron a conclusiones relativamente compatibles. Sin embargo, en todos los casos varias cuestiones quedaron abiertas ya que solo fueron analizadas irregularidades en altura y apenas en estructuras planas. Inan et al. (2011) hicieron un análisis paramétrico de las irregularidades estructurales definidas en la Norma Sismo Resistente de Turquía (TCE, 2007). Presentan las principales fallas en los diseños arquitectónicos relacionados con la resistencia sísmica de los edificios y son brindadas posibles soluciones que se pueden adoptar y aplicar en diseños futuros para una buena concepción sismo resistente. Le- Le-trung et al. (2010) analizaron el comportamiento sísmico de estructuras de 20 pisos con sistemas de pórticos de acero sismo resistentes y con irregularidades en altura utilizando análisis dinámicos lineales y no lineales. Todos los resultados fueron comparados con los obtenidos para el caso base o estructura simétrica y concluyeron que los resultados más críticos se presentan cuando hay una distribución no uniforme de la rigidez en todos los pisos de la estructura. Michalis et al. (2006) estudiaron la influencia de las irregularidades en altura en el desempeño sísmico de un pórtico plano (“shear building”) de 9 pisos. Cuatro tipos fueron estudiados: irregularidades en la rigidez, en la resistencia, en la masa y una combinación de las tres anteriores. Las irregularidades fueron provocadas por etapas y la respuesta sísmica fue calculada usando análisis dinámicos incrementales (IDA). Todos los resultados fueron comparados con los obtenidos para el caso base o estructura simétrica. Al igual que Le-trung et al. (2010), los resultados fueron críticos cuando se trataba de estructuras con distribución no simétrica de rigidez.
Con la idea de complementar los estudios anteriores realizados por otros autores, el objetivo de este trabajo es estudiar los efectos causados por un sismo en una estructura espacial de ocho pisos con diversas irregularidades localizadas en la planta de la edificación.
METODOLOGÍA DE ANÁLISIS
Descripción de la estructura analizada
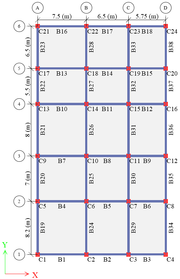
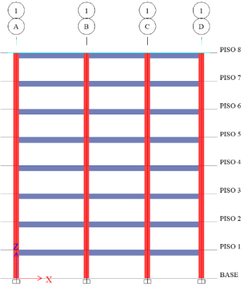
En este estudio se analiza numéricamente la influencia de las irregularidades en el comportamiento sísmico de una edificación para uso residencial con sistema estructural de pórticos de concreto armado en dos direcciones (Figura 1). La geometría en planta del edificio es rectangular, consta de 8 niveles y posee una altura total de 24 m. En el modelo estructural no se consideraron ascensores, escaleras, tanque de agua, sistemas eléctricos, aire acondicionado, entre otros.
La estructura del edificio está formada por vigas y columnas de concreto armado, las cuales tienen geometrías y configuración de refuerzos diferentes. La losa de entrepiso utilizada en este trabajo tiene 30 cm de espesor. Para identificar las vigas y columnas se utilizó la numeración detallada en la Figura 1a, donde B identifica a las vigas (Beam, elementos de color azul), C corresponde a las columnas (Column, elementos de color rojo) y X e Y son las direcciones ortogonales consideradas en este trabajo. Las Tablas 1 y 2 presentan las características de las secciones transversales de los elementos estructurales enumerados según la Figura 1a.
|
|
| (a) Planta de la edificación. | (b) Vista frontal de la edificación en la dirección X – Pórtico 1A – 1D. |
| ELEMENTOS | SECCIÓN DE LAS VIGAS |
| B1 a B18 | 0.35 x 0.45m² |
| ELEMENTOS | SECCIÓN DE COLUMNAS |
| C6, C10, C14 | 0.60 x 0.60 m² |
| Restantes | 0.50 x 0.50 m² |
En el análisis numérico se consideran los siguientes parámetros: carga muerta y carga viva de 1.80 KN/m², resistencia nominal a la compresión del concreto (f’C) de 21 MPa, módulo de elasticidad del concreto (EC) de 21,000 MPa y esfuerzo nominal de fluencia del acero de refuerzo (f’Y) de 410 MPa.
MODELOS ANALIZADOS
En la edificación de la Figura 1 el centro de masa coincide con el centro de rigidez, estando ambos localizados en el centro de la planta; por consiguiente, esa edificación se considera simétrica en planta y en altura, siendo llamada modelo de referencia en este trabajo.
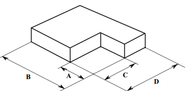
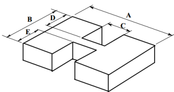
En seguida, en el modelo de referencia son introducidos, por etapas, dos tipos de irregularidades en planta definidas en las normas sismo resistente (NSR-10, 2010; NBR 15421, 2006) como “Recortes o Retrocesos en las esquinas” y “Discontinuidades en el diafragma”. Esos tipos de irregularidades están ilustrados en la Figura 2, donde las letras corresponden a las medidas de la estructura y de los recortes.
|
|
| Retrocesos en las esquinas | Discontinuidad del diafragma |
Se realizan recortes en las losas de todos los niveles en varios puntos de la edificación, con el fin de simular cada irregularidad y conocer su influencia en la respuesta sísmica de la estructura. En cada caso estudiado se hace un análisis dinámico cronológico linealmente elástico usando como carga horizontal las componentes del sismo de El Centro (1940) aplicadas en la base y posteriormente un análisis no lineal estático de plastificación progresiva o pushover.
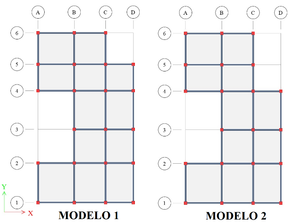
En total, se analizan 10 modelos: 4 para la irregularidad “Recortes o Retrocesos en las esquinas”, 2 para la irregularidad “Discontinuidades en el diafragma” y 4 para la combinación de ambas. Debido a la gran cantidad de datos y resultados que se obtienen, en este trabajo se presentan solo los resultados alcanzados para la combinación de ambas irregularidades correspondientes a los modelos indicados en la Figura 3.
|
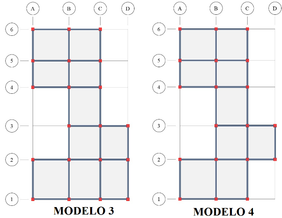
|
Como las fuerzas sísmicas son cíclicas y reversibles, los esfuerzos internos mudan, generando cambios bruscos en el equilibrio de los elementos que componen la estructura que pueden causar patologías estructurales, por lo tanto, es importante entender como varían esos esfuerzos internos en cada instante de tiempo. Siendo así, la finalidad de este trabajo es comparar las respuestas obtenidas de los modelos con irregularidades (Figura 3) con las obtenidas para el caso de referencia (Figura 1) a fin de mostrar las variaciones en la distribución de los esfuerzos internos en los elementos de la estructura provocados por las irregularidades inducidas. Fueron utilizados los softwares ETABS (Computers and Structures, 2010) para el análisis y cálculo de las respuestas sísmicas y MATLAB R2009b (MathWorks, 2009) para análisis de los resultados obtenidos.
PROGRAMAS COMPUTACIONALES UTILIZADOS
ETABS Nonlinear V9.7.2 (Computers and Structures, 2010)
ETABS Nonlinear (Computers and Structures, 2010) es un programa basado en el método de los elementos finitos para diseñar y analizar edificaciones. Para modelar las vigas y columnas se utiliza el elemento tipo “frame” disponible en la biblioteca del programa. Se incluyen zonas rígidas en los extremos de acuerdo con la geometría de los elementos que llegan a cada nudo (brazo rígido - se utiliza un factor de rigidez de 3/4).
Asimismo, para modelar la losa aligerada de entrepiso, se utiliza el elemento “frame” para representar los nervios con un peralte de 30 cm y encima de estos elementos se define una placa con espesor de 5cm como tipo “membrane” cuya función principal es distribuir las cargas a los nervios y éstos a su vez a las vigas perimetrales. La constante torsional de los nervios se asume nula. Todos los apoyos del edificio son considerados empotrados. En cada piso de la estructura se considera un diafragma rígido a fin de compatibilizar los desplazamientos laterales. Debido a la regularidad de la estructura y la simplificación del ejercicio, no se tiene en cuenta el efecto de la torsión accidental producida por la excentricidad entre el centro de masa y centro de rigidez de cada piso. En el modelo de análisis se incluyen los efectos de segundo orden utilizando la carga muerta y la carga viva instantánea con un factor de carga de 1.1.
Después de creado el modelo en el ETABS (Computers and Structures, 2010), se puede analizar la estructura por medio del análisis dinámico linealmente elástico o “time history” y del análisis no lineal estático de plastificación progresiva o pushover. Estos dos últimos análisis se utilizan en este trabajo y son explicados a seguir.
Análisis dinámico linealmente elástico
Este tipo de análisis también conocido como time history, determina la respuesta de la estructura a través de una integración numérica (integral de Duhamel) sobre pequeños incrementos de tiempo, cuando la base está sujeta a un movimiento del suelo. Consecuentemente, el análisis “time history” implica una evaluación paso a paso de la respuesta del edificio, usando registros reales o acelerogramas artificiales como movimiento de entrada. Por medio de este análisis se calculan las respuestas máximas de deflexiones, desplazamientos relativos, fuerzas en los pisos, cortante en la base y fuerzas en los elementos estructurales tales como esfuerzos axiales, fuerzas cortantes y momentos flectores.
En todos los casos estudiados, el análisis dinámico linealmente elástico se realizó en el programa ETABS (Computers and Structures, 2010), considerando como carga de sismo el registro de aceleraciones de El Centro (1940) aplicado en la base de cada modelo con intervalos de tiempo de 0.01 s.
Análisis no lineal estático de plastificación progresiva
La capacidad de una estructura depende de la resistencia y deformación máxima de sus componentes individuales. Para determinar su capacidad más allá del límite elástico, es necesario utilizar algún tipo de análisis no lineal, por ejemplo, el análisis estático no lineal (análisis pushover). Este procedimiento usa una serie de análisis elásticos secuenciales, que se superponen para aproximarse a un diagrama conocido con el nombre de curva de capacidad.
El análisis estático no lineal o pushover es una técnica simple y eficiente para estudiar la capacidad, resistencia-deformación, de una estructura bajo una distribución esperada de fuerzas inerciales. El método consiste en aplicar una distribución vertical de carga lateral a la estructura la cual debe incrementarse monótonamente hasta que la estructura alcance el máximo desplazamiento o su capacidad máxima. Para cada fuerza aplicada la estructura sufre un desplazamiento, y con esos desplazamientos se puede obtener la llamada Curva de Capacidad, que relaciona las fuerzas en la base y los desplazamientos en el nivel superior de la estructura.
MATLAB R2009b (MathWorks, 2009)
El nombre de MATLAB (MathWorks, 2009) viene de “Matrix Laboratory” y es un lenguaje de programación apropiado para el manejo de matrices. El programa contiene una biblioteca bastante amplia de funciones matemáticas, manejo de dados y amplias herramientas para generar gráficos. Con base en estas bibliotecas fue creado un programa en este lenguaje cuyo nombre es CMV y con el cual se analizan los resultados obtenidos en ETABS (Computers and Structures, 2010).
Hecho el análisis en el programa ETABS (Computers and Structures, 2010), los resultados son llevados al programa CMV, el cual confronta los resultados obtenidos del modelo de referencia (Figura 1) con los obtenidos para cada caso con irregularidad (Figura 3). El objetivo de comparar esos resultados es conocer los cambios en el comportamiento interno de los elementos de la estructura y el valor de esos cambios. En este trabajo, se presentan únicamente los resultados obtenidos al comparar las envolventes de los momentos flectores, ya que son las causantes principales de la deformación de la estructura. Ya el esfuerzo cortante es estudiado mediante el análisis pushover.
Como consecuencia de la excitación sísmica los momentos flectores internos de los elementos pueden sufrir cambios de sentido, esto quiere decir que los momentos considerados positivos pueden pasar a ser negativos o viceversa. Por otra parte, los momentos internos pueden aumentar o disminuir su valor sufriendo o no cambios de sentido. En este trabajo, esas mudanzas son llamadas de variaciones. La primera es llamada Variación I e indica si hubo cambio de sentido de los momentos flectores y la magnitud de ese cambio; la segunda es llamada Variación II, señala si hubo aumento en el valor del momento flector e informa esa magnitud, en este caso se conserva el sentido del momento flector. En esta última variación se tienen en cuenta aumentos mayores al 5%, asumiendo que el factor de seguridad cubre aumentos por debajo de ese porcentaje.
Finalmente, el CMV compara las diferentes curvas de capacidad obtenidas del análisis pushover, con el intuito de visualizar cómo evoluciona la capacidad de la estructura para resistir cargas laterales a medida que se inducen las irregularidades en el caso de referencia.
RESULTADOS Y DISCUSIONES
Primera etapa
Una medida inicial de la rigidez de los modelos se puede obtener analizando el número de ligaciones entre elementos en las direcciones ortogonales X e Y, las cuales permiten una mayor disipación de la energía generada por el sismo. Así, en las Figuras 1 y 2 se observa que en la dirección ortogonal X, el número de elementos y ligaciones es menor en comparación con la dirección Y, lo que indica que en la dirección X la rigidez lateral es menor. Luego, en este estudio se analizaron sólo los pórticos ubicados en esa dirección, ya que son los más susceptibles al colapso en caso de un evento sísmico.
A continuación, los modelos de las Figuras 1 y 2 son analizados en el ETABS (Computers and Structures, 2010). Luego, los resultados son llevados al CMV para ser confrontados. El programa facilita una tabla especificando el número total de elementos y la cantidad que presentaron los dos tipos de variaciones explicadas anteriormente. La Tabla 4 muestra los resultados obtenidos en el CMV para los modelos analizados.
Examinando los resultados mostrados en la Tabla 4, se observa que, en el caso de las vigas de todos los modelos, más del 60% presentaron alteraciones en el sentido de los momentos flectores (variación I), siendo el Modelo 4 el más crítico con el 94% de sus elementos con esa variación. Por otro lado, se observa que el número de vigas que sufrieron aumento en la magnitud del momento flector sin cambio de signo (variación II) no supera el 19%. El caso de las columnas sigue el mismo padrón, según se observa en la Tabla 4. Siendo así y considerando los resultados de la tabla anterior, se puede concluir que los elementos que presentan alteración en el sentido de sus momentos internos son más susceptibles a sufrir daños y a la formación de mecanismos plásticos.
| Modelo 1 | Modelo 2 | Modelo 3 | Modelo 4 | |
| Número Total de Vigas | 128 | 120 | 112 | 104 |
| Vigas con cambios de sentido en los momentos flectores (Variación I) | 86 | 76 | 87 | 98 |
| % Vigas con Variación I | 67.2% | 63.3% | 77.7% | 94.2% |
| Vigas con aumento de la magnitud del momento flector, pero conservando su sentido (Variación II). | 15 | 21 | 19 | 20 |
| % Vigas con Variación II | 11.7% | 17.5% | 17% | 19.2% |
| Número Total de Columnas | 176 | 168 | 160 | 152 |
| Columnas con cambios de sentido en los momentos flectores (Variación I) | 124 | 114 | 121 | 141 |
| % Columnas con Variación I | 70.5% | 67.9% | 75.6% | 92.8% |
| Columnas con aumento de la magnitud del momento flector, pero conservando su sentido (Variación II). | 7 | 14 | 18 | 18 |
| % Columnas con Variación II | 4% | 8.3% | 11.3% | 11.8% |
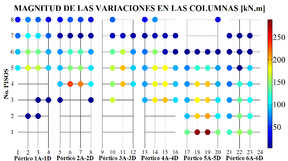
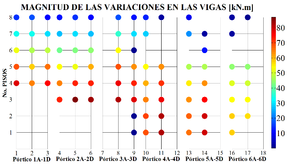
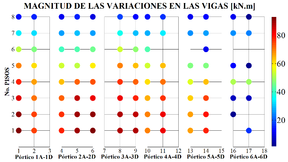
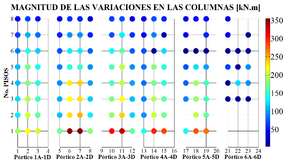
El programa CMV también permite visualizar de manera gráfica como se distribuyen espacialmente los elementos que presentan alteraciones en los momentos flectores y conocer las magnitudes de éstas. Por ejemplo, analizando la viga número 1 localizada en el Pórtico 1A-1D y en el octavo piso (ver Figura 1a): para el modelo de referencia el momento máximo fue de +7 kN.m, ya en el Modelo 1 ese valor pasó a ser -6 kN.m, aproximadamente (Pérez, 2012). Luego, la magnitud de esa mudanza dará un valor de 13 kN.m. El CMV calcula la magnitud de esa mudanza en todos los elementos restantes del Modelo 1 y al final proporciona un gráfico como el mostrado en las Figuras 4a y 4b.
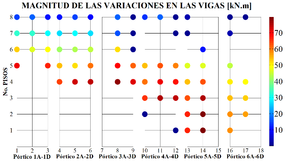
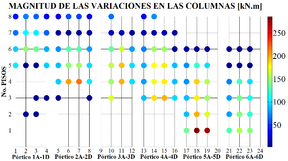
En esas figuras, el eje horizontal indica el elemento estructural enumerado según las Figuras 1a y 3. El eje vertical indica el piso donde está localizado cada elemento. Cada punto en la Figura 4 indica por medio de un color la magnitud de la variación observada. El mismo tipo de gráfico puede construirse para analizar la distribución espacial de los elementos que conservan el signo del momento flector, pero presentan cambios en la magnitud del mismo. Sin embargo, como ya se observa en la Tabla 4, esa alteración aparece en pocos elementos y por ese motivo esos diagramas no se presentan en este trabajo. Las Figuras 5, 6 y 7 presentan la distribución espacial de los elementos que presentan alteraciones en el signo del momento flector en el caso de los modelos 2, 3 y 4.

|
|
| (a) Vigas | (b) Columnas |
|
|
| (a) Vigas | (b) Columnas |
|

|
| (a) Vigas | (b) Columnas |
|
|
| (a) Vigas | (b) Columnas |
Se observa en las figuras anteriores que, a medida que el modelo se torna irregular aumenta el número de vigas y columnas que presentan cambio de sentido en los momentos flectores. En el caso de las vigas, las magnitudes elevadas provocadas por esa variación muestran cuadros críticos del primero hasta el quinto piso, entre los pórticos 2A-2D y 5A-5D, cerca de la zona donde fue localizada la irregularidad llamada “Discontinuidad en el Diafragma” (Figura 2). Del mismo modo, las columnas mostraron que las magnitudes críticas se concentran en los dos primeros pisos de la estructura, entre los pórticos 3A-3D e 4A-4D.
Es importante resaltar que en todos los casos hubo inversión de signo o cambio de sentido de los momentos flectores en las uniones viga-columna, siendo regiones importantes en la formación de mecanismos plásticos. Resumiendo, se puede decir que los elementos más críticos se encuentran localizados en la zona media de la estructura, entre el primer y el quinto piso.
SEGUNDA ETAPA
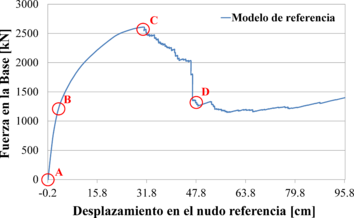
En la segunda etapa se procedió a realizar el análisis estático no linear o pushover a los modelos de la Figura 3. Para el modelo de referencia, la curva de capacidad se muestra en la Figura 8. En general, se presenta la curva de capacidad hasta el punto “C”, que representa el colapso del primer elemento estructural. En ese punto, la funcionalidad para la cual fue diseñada la estructura, acaba.
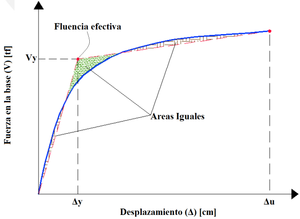
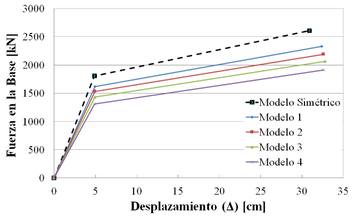
Para facilitar el cálculo de la ductilidad de cada modelo estudiado, se simplifica el diagrama que indica la capacidad portante, ajustando un diagrama bilineal utilizando el criterio de las áreas iguales como se ilustra en la Figura 9. Así, en la Figura 10 se presentan los modelos bilineales para cada caso modelado.
La inclinación en cada punto de los modelos bilineales representa la rigidez lateral de la estructura, la cual va disminuyendo a medida que la estructura se va deformando. Siendo así, en la Figura 10 se observa que a medida que se van introduciendo las irregularidades la rigidez lateral disminuye permitiendo la rápida formación de mecanismos plásticos en los elementos estructurales. La ductilidad disponible de la estructura (µ) se obtiene como la relación entre el desplazamiento último o de colapso (ΔU) y el desplazamiento de fluencia (ΔY) (ver Figura 9). Las ductilidades calculadas para cada modelo se presentan en la Tabla 5.
| Modelo simétrico | Modelo 1 | Modelo 2 | Modelo 3 | Modelo 4 | |
| Ductilidad (μ) | 6.33 | 6.56 | 6.60 | 6.64 | 6.66 |
En la Tabla 5 se observa que a medida que el modelo se torna más irregular, la ductilidad va aumentando, lo que significa que la estructura se vuelve más flexible afectando su rigidez lateral. Consecuentemente, cuanto mayor es el valor de la ductilidad, menor será la fuerza que la estructura puede soportar asumiendo que la energía sísmica es disipada a través de la plasticidad de los elementos estructurales.
CONCLUSIONES
En este trabajo fue analizada la influencia de las irregularidades estructurales en planta en el comportamiento sísmico de una estructura. El objetivo era estudiar la variación de los esfuerzos en edificios irregulares sometidos a un terremoto en particular, ocurrido en la ciudad de El Centro en 1940 en el estado de California, haciendo énfasis en la distribución de los momentos flectores en la capacidad lateral y ductilidad disponible de la estructura.
Se comprobó que las irregularidades afectan el comportamiento de la estructura para resistir cargas laterales. A medida que las irregularidades fueron introducidas en el modelo de referencia, la rigidez de la estructura disminuye tornándola más flexible y aumentando el número de elementos que presentan cambio de sentido o de signo en los momentos flectores, acrecentando el riesgo de formación de mecanismos plásticos. Esto se presenta porque la redundancia en la estructura disminuye a medida que las irregularidades son colocadas en diferentes posiciones, provocando una redistribución de esfuerzos y propagación de energía del sismo menor entre los elementos y aumentando el riesgo de colapso de éstos. Es importante mencionar que en los modelos 3 y 4 aparecieron rótulas plásticas en las columnas, con lo cual se puede decir que el principio columna fuerte – viga débil no se cumplió siendo necesario reforzar esa zona para prevenir una falla súbita.
Finalmente, se señala que a través del programa CMV fue posible cuantificar los efectos del terremoto en cada elemento estructural y encontrar los que tenían algún tipo de cambio en la distribución de los esfuerzos analizados. Además, con el CMV es posible localizar las zonas vulnerables de una estructura para luego ser reforzada, con el fin de mejorar su capacidad resistente, disminuir los efectos producidos por cargas laterales y evitar problemas futuros.
REFERENCIAS
Asociación Colombiana de Ingeniería Sísmica. Normas Colombianas de Diseño y Construcción Sismo Resistente. NSR-10. Bogotá, D.C, Colombia, 2010.
Associação Brasileira de Normas Técnicas. Projeto de estruturas resistentes a sismos – Procedimento, NBR 15421:2006. Rio de Janeiro, Brasil, 2006.
Ali, A.K. and Krawinkler, H. (1998). “Effects of Vertical Irregularities on Seismic Behavior of Building Structure”. PhD. Dissertation, Department of Civil and Environmental Engineering, Stanford University, USA.
Chintanapakdee, C. and Chopra, A.K. (2004). “Seismic Response of Vertically Irregular Frames: Response History and Modal Pushover Analyses”. International Journal of Structural Engineering ® ASCE, p.1777-1785.
Computers and Structures, INC. (2002). “Optimized Modeling and Design of Concrete Structure using ETABS”. Computers and Structures, Inc, Berkeley, California, U.S.A.
ETABS Nonlinear. Extended Three Dimensional Analysis of Building Systems, V9.7.2. Computers and Structures, Inc., California, U.S.A, 2010.
Federal Emergency Management Agency. NHERP. Guidelines for the seismic rehabilitation of buildings (FEMA 356), Washington, D.C, U.S.A, 518p, 2000.
İnan, T. and Korkmaz, K. (2011). “Evaluation of Structural Irregularities Based on Arquitectural Design Consideration in Turkey”. Paper published in Structural Survey, Emerald Group Publishing Limited, Vol.29, No. 4, 303-319.
Le-trung, K., Lee, K., Lee, J. and Lee, H. (2010). “Evaluation of Seismic Behavior of Steel Special Moment Frame Buildings with Vertical Irregularities”. Paper published online Wiley Online Library, p.215-232.
MATLAB. Matrix Laboratory - R2009b. MathWorks - MATLAB and Simulink for Technical Computing. Massachusetts, U.S.A, 2009.
Michalis, F., Dimitrios, V. and Manolis, P. (2006). “Evaluation of the Influence of Vertical Irregularities on the Seismic Performance of a Nine-Story Steel Frame”. WILEY InteScience, Earthquake Engineering and Structural Dynamics.
Pérez, L.A. (2012). Análise dos Efeitos Provocados por Abalos Sísmicos em Estruturas Irregulares. Dissertação de mestrado, Brasília, Brasil.
Seismic Evaluation and Retrofit of Concrete Buildings, Technical report, ATC-40, Applied Technology Council. Redwood City, California, U.S.A, 1996.
Document information
Published on 06/12/18
Accepted on 30/10/18
Submitted on 26/08/18
Volume 18, Issue 2, 2018
Licence: CC BY-NC-SA license