Resumen
Se realiza una variación de algunos parámetros de diseño para estimar propiedades térmicas que caracterizan una estufa solar, tomando de base un modelo térmico que reproduce experimentalmente el comportamiento de una estufa en base a un concentrador parabólico compuesto (CPC) de revolución. El modelo se presenta en términos de un sistema acoplado de tres ecuaciones diferenciales no lineales, que son resultado de considerar el balance de flujo de calor para algunos de los componentes del dispositivo, las cuales se resuelven numéricamente. Se calculan las temperaturas para el fluido, los reflectores y el contenedor de la estufa solar, en función del tiempo, a partir de eso, se infieren los valores para la potencia de cocción estándar y el rendimiento térmico.
1 Introducción
Se presenta un estudio de propiedades térmicas de una estufa solar con colector en base a un CPC de revolución. El estudio se realiza tomando de base un modelo térmico, en términos de un sistema de ecuaciones ordinarias acoplado, no lineales, que aproxima muy bien el comportamiento experimental de la temperatura del agua en el recipiente contenedor de la estufa solar [1]. En base a ello es posible estimar algunos de los parámetros térmicos, obtenidos con estándares internacionales experimentales, que caracterizan el desempeño térmico de las estufas solares.
Trabajos similares se han desarrollado, por ejemplo en [2], se muestra el rendimiento y la distribución de temperaturas obtenidas para una estufa solar de tipo caja, considerando tanto un modelo matemático de tipo transitorio, así como el trabajo experimental correspondiente. En [3] se presenta un modelo paramétrico de operación para una estufa solar para predecir su potencia de cocción basado en parámetros controlados y variables no controladas. En [4] se obtuvo un modelo matemático para una estufa solar de tipo caja que ayuda a establecer los elementos de los parámetros que determinan e influyen de manera relevante en el proceso de calentamiento de la estufa. En [5], se muestran los resultados de emplear un reflector plano en una estufa solar de tipo caja, estableciéndose los logros en el incremento de la temperatura de calentamiento y la eficiencia de la misma. Se han realizado otros modelos similares para estufas solares tipo caja y de concentración [6, 7, 8 y 9].
El modelo térmico se desarrolla mediante un análisis de física térmica de la estufa solar "Jorhejpatarnskua" [1]. El modelo simula las temperaturas promedio del agua en el recipiente absorbedor, de la superficie del concentrador y de la superficie del recipiente absorbedor. A partir de la temperatura promedio del agua en función del tiempo, se pueden estimar la potencia de cocción estándar y el rendimiento térmico de la estufa solar, en términos de algunos parámetros de diseño relevantes para el estudio de este tipo de estufas solares: el área del colector, la carga de fluido, la reflectancia del material del concentrador y el cociente absortancia-emitancia del recubrimiento del absorbedor (olla contenedora de alimentos).
2 DESCRIPCIÓN DEL MODELO TÉRMICO
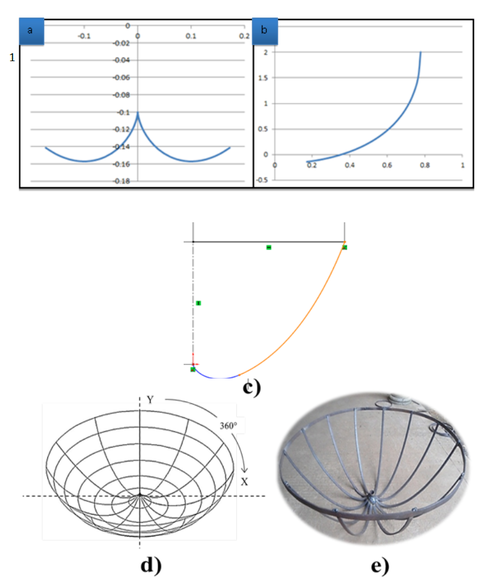
El colector de la estufa solar bajo estudio, es un dispositivo en base a un Concentrador Parabólico Compuesto (CPC) de revolución, lo que hace posible la concentración de los rayos solares en una región focal donde va colocado el recipiente de absorción. La geometría del colector está formado por dos partes, una involuta y una sección de parábola, las cuales son descritas a continuación en términos de las ecuaciones que corresponden a las coordenadas polares del CPC en el plano (x; y) para graficar la geometría señalada [10 y 11]:
Donde
, es el factor de concentración del colector. En la figura 1 se muestran las curvas graficadas.
A continuación se muestra la figura 2 mostrando las diferentes interacciones de transferencia de calor y partir de las cuales se ha planteado el modelo térmico:

Los parámetros de diseño que se han toman para realizar el análsis de sensibilidad, son las que se consideran más importantes para el funcionamiento de estufas solares. En particular, la masa de agua está de acuerdo a los valores usados en la aplicación del protocolo de evaluación de estufas solares [12]. Para los valores de la reflectancia se han tomado el valor de la lámina optimizada que se ha usado para el experimento. Del mismo modo, los valores del cociente absortancia-emitancia de la pintura selectiva absorbedora, la reflectancia del reflector del concentrador y el tamaño del colector, son tomados los que correspoden a las características de los materiales usados.
2.1. Ecuaciones del balance de energía en los componentes de la estufa solar
Considérese el caso de una estufa solar en operación, con radiación incidiendo en ella y con carga de fluido (agua) en su olla contenedora. Se plantea un modelo de transferencia de calor, que consiste en considerar el balance de energía para el recipiente absorbedor, las láminas reflectoras y el fluido, en términos de un sistema acoplado de ecuaciones diferenciales ordinarias.
2.1.1. Ecuación de transferencia de calor en el recipiente absorbedor
Realizando el balance de energía en para la superficie del recipiente absorbedor de la estufa solar, se puede expresar como:
| (1) |
Donde
Es el flujo de calor de la radiación incidente sobre la olla contenedora,
Es el flujo de calor por radiación entre la olla y el cielo,
Es el flujo de calor por convección entre la olla y el ambiente,
Es el flujo de calor por convección entre la olla y el interior de la estufa.
Es el flujo de calor por radiación entre la olla y las láminas reflectoras,
Además,
Es la temperatura ambiente.
Es la temperatura del firmamento. Y se relaciona con la temperatura ambiente como [10]:
Es la temperatura promedio del aire entre el absorbedor y la superficie reflectora.
Es la temperatura promedio del aire dentro del recipiente, Es la temperatura promedio del agua.
Es la temperatura promedio de la superficie de los reflectores.
Es la temperatura promedio de la superficial de la olla contenedora.
Es la emitancia de la película selectiva del absorbedor.
Es la constante de Stefan Boltzmann.
Es el coeficiente de calor por convección entre la olla y el ambiente.
Es el coeficiente de calor por convección entre el absorbedor y el aire dentro de la estufa solar.
Es el coeficiente de calor por convección entre la olla y el fluido.
Es el calor específico del aluminio.
Es la masa del recipiente de la olla.
Es la masa de agua.
Es la masa de las láminas reflectoras del concentrador.
Es la absortancia de los reflectores.
Es la absortancia del absorbedor.
Es el área superficial de la olla contenedora.
Es el tiempo.
Es el calor específico de las láminas reflectoras de aluminio.
Es el calor específico del agua.
Es el rendimiento óptico.
Es la reflectancia de la superficie reflectora.
Es el número promedio de reflexiones en el CPC.
Es la potencia de cocción.
Es la potencia de cocción estándar.
Es el coeficiente de calor por convección entre la superficie reflectora y el ambiente.
Es la irradiancia directa.
Es la irradiancia reflejada.
Es el flujo de calor por la radiacón incidente.
Es el flujo de calor por convección entre las láminas reflectoras y el ambiente.
2.1.2. Ecuación de transferencia de calor en la superficie reflectora
Aplicando el balance de energía en la superficie de la superficie reflectora de la estufa, se obtiene la siguiente ecuación:
| (2) |
|---|
Donde
Es el flujo de calor por radiación entre la superficie reflectora y el firmamento.
Donde
Es el área del colector solar.
Es la emitancia de las láminas reflectoras.
2.1.3. Ecuación de transferencia de calor al fluido
Finalmente, se plantea la ecuación de balance de energía en el fluido contenido en la olla:
| (3) |
Donde
Es el flujo de calor por convección entre la olla y el interior de la estufa,
Es el flujo de calor por radiación entre el fluido y la olla contenedora,
Las ecuaciones (1), (2) y (3) representan un sistema de ecuaciones diferenciales acopladas, no lineales para las variables
, y
Se han tomado los valores para los coeficientes de transferencia de calor por convección de [11 y 12].
3 SOLUCIÓN DEL SISTEMA DE ECUACIONES Y CÁLCULO DE PARÁMETROS
Para resolver el conjunto de ecuaciones diferenciales acopladas y no lineales, (1), (2) y (3), se ha usado el método de Runge-Kutta de cuarto orden, a través de un código programado en fortran. Las condiciones iniciales que se han tomado como la temperatura ambiente. Es decir;
, y
De acuerdo a los resultados obtenidos al comparar la solución numérica de la temperatura promedio del agua, con los datos experimentales, se encuentra un error menor al 5% en los casos de prueba considerados [1].
3.1 Cálculo de la potencia de cocción y del rendimiento térmico
Al resolver el sistema de ecuaciones, se obtuvieron los valores numéricos de las temperaturas promedio, de la superficie del recipiente, de la superficie reflectora y del agua, en función del tiempo. Con esta última se puede estimar la potencia de cocción mediante el uso del término de lado derecho de la ecuación (3), la potencia de cocción estándar, se define cuando la diferencia de temperatura entre la temperatura del fluido y la temperatura ambiente, es decir,
[12].
Donde , es la diferencia entre la temperatura del fluido y del ambiente ( ![]() ).
).
La potencia de cocción estándar [12]:
|
|
(4) |
El rendimiento térmico se calcula usando la expresión (8) ver por ejemplo [13].
|
|
(5) |
Donde
Es el rendimiento térmico de la estufa solar
Es la temperatura del agua en el tiempo
Es la temperatura del agua en el tiempo
4 RESULTADOS DE LAS SIMULACIONES NUMÉRICAS VARIANDO PARÁMETROS DE DISEÑO
A continuación se presenta la variación de algunos de los parámetros de diseño de la estufa solar, obteniendo las simulaciones numéricas correspondientes, para la potencia de cocción estándar y el rendimiento térmico.
El conjunto de parámetros considerados, son los siguientes: cociente absortancia-emitancia de la película selectiva absorbedora, la reflectancia del reflector del concentrador, el tamaño del colector y la cantidad fluido en la olla. Los valores fijos toman esos valores porque son los que tienen los materiales usados para la elaboración de la estufa solar. El cociente absortancia-emitancia es el de la pintura usada, del mismo modo, el valor de la reflectancia corresponde al de las láminas de la estufa solar elaborada.
A continuación se muestran las gráficas correspondientes, considerando la variación de los parámetros.
Se consideran fijos los otros parámetros, los valores numéricos tomados para la simulación, se muestran en la tabla 1.
| PARÁMETRO | VALOR |
| COCIENTE ABSORTANCIA-EMITANCIA | 2.4 |
| REFLECTANCIA | 0.93 |
| MASA DE AGUA (kg) | 5.00 |
En la figura 2, se muestra la potencia de cocción estándar y el rendimiento térmico, en función del área de captación del colector de la estufa solar, la cual se ha tomado en el intervalo (0.1, 1.5) , porque son los valores correspondientes al caso de estufas solares de pequeñas dimensiones.
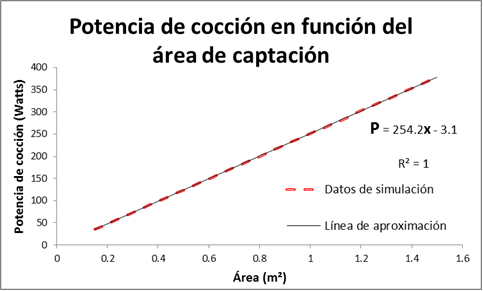 a) a)
|
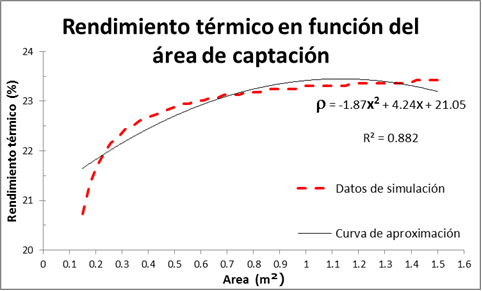 b) b)
|
| Figura 2. a) Muestra la potencia de cocción estándar y b) el rendimiento térmico, en términos del área del colector de la estufa solar. |
En ambos casos, se considera una curva de aproximación a los datos de la simulación numérica, relacionando la potencia de cocción estándar y el rendimiento térmico, en función del área de captación de la estufa solar.
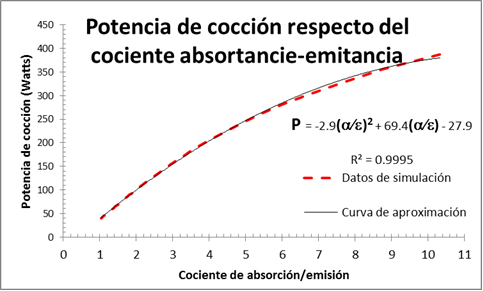
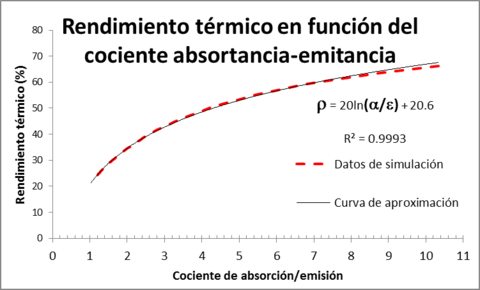
En la figura 3 se muestran, en el eje vertical la potencia de cocción estándar y el rendimiento térmico y en el eje horizontal el cociente absortancia-emitancia, que se ha tomado en el intervalo (1, 10). El límite inferior corresponde superficies que emiten lo mismo que absorben y el superior a las que absorben 10 veces más con respecto a lo que emiten. Este límite corresponde al de películas selectivas solares optimizadas [Duffie, 2013]. Los valores numéricos de los parámetros fijos se muestran en la tabla 2.
| PARÁMETRO | VALOR |
| ÁREA DEL COLECTOR ( ) | 0.60 |
| REFLECTANCIA | 0.93 |
| MASA DE AGUA (kg) | 5.00 |
 a) a)
|
 b) b)
|
| Figura 3. a) Muestra la potencia de cocción estándar y b) el rendimiento térmico, en términos del cociente emitancia-absortancia. |
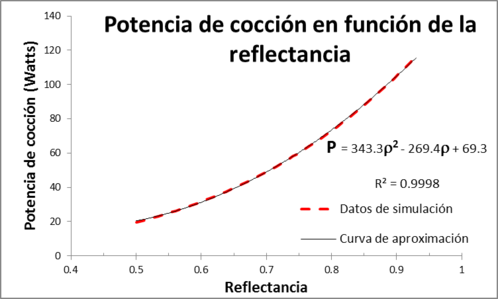
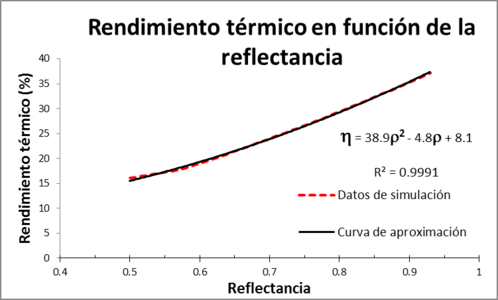
De manera similar, en la figura 4, se muestran la potencia de cocción estándar y el rendimiento térmico en función de la reflectancia de la superficie reflectora, se ha tomado en el intervalo de (0.5, 0.93). El límite inferior corresponde a la reflectancia, en el espectro solar de una superficie de acero acabado espejo y el superior a una superficie optimizada para aplicaciones solares. Los valores numéricos de los otros parámetros se muestran en la tabla 3:
| PARÁMETRO | VALOR |
| COCIENTE EMITANCIA-ABSORTANCIA | 2.20 |
| ÁREA DEL COLECTOR ( ) | 0.60 |
| MASA DE AGUA (kg) | 5.00 |
 a) a)
|
 b) b)
|
| Figura 4. a) Muestra la potencia de cocción estándar y b) el rendimiento térmico, en función de la reflectancia. |
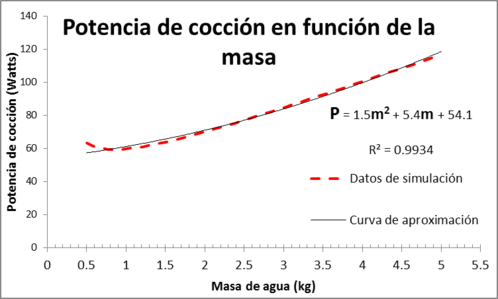
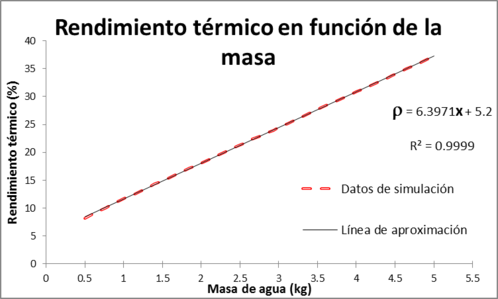
Finalmente en la figura 5, se muestran la potencia de cocción estándar y el rendimiento térmico, en función de la cantidad de agua en el recipiente contenedor. Los valores se han tomado en el intervalo (0.5, 5) kg, el límite inferior corresponde a la cantidad de alimento para una persona y el límite superior a la capacidad máxima del contenedor. Los valores para los demás parámetros se muestran en la tabla 4.
| PARÁMETRO | VALOR |
| COCIENTE EMITANCIA-ABSORTANCIA | 2.20 |
| REFLECTANCIA | 0.93 |
| ÁREA DEL COLECTOR ( ) | 0.60 |
|
|
| Figura 6. Muestra la potencia de cocción estándar y el rendimiento térmico, en función de la masa de agua en el contenedor de la estufa solar. |
En las gráficas que muestra las variación de la potencia de cocción estándar y del rendimiento térmico, en función de las diferentes variables, se han considerado una línea de ajuste a los datos obtenidos en la simulación numérica, para la potencia de cocción estándar y el rendimiento térmico, obteniendo algunas correlaciones marcadas.
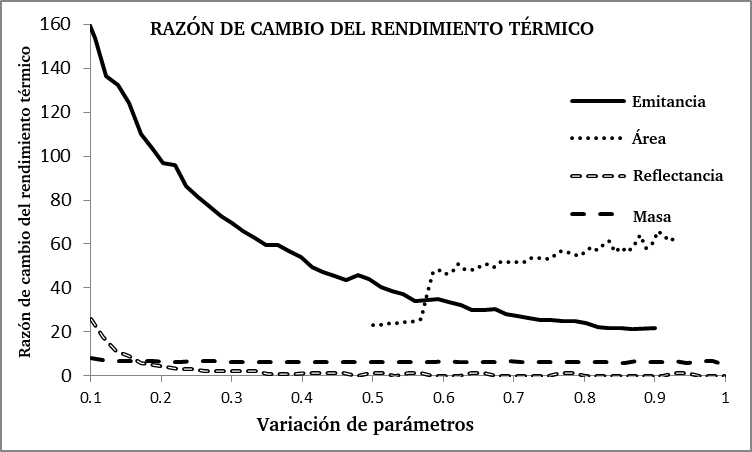
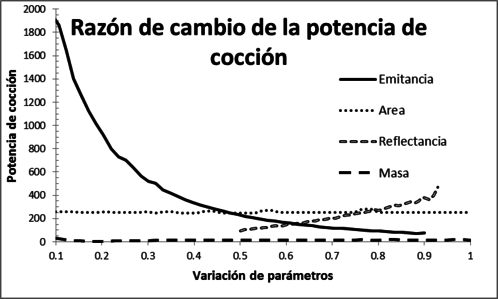
Finalmente, para estudiar las variaciones de la potencia de cocción estándar y el rendimiento térmico en función de los parámetros de diseño, se ha considera la razón de cambio. A continuación se muestra en la figura 7, la razón de cambio de potencia de cocción con respecto a cada uno de los parámetros que han sido adimensionalizados y mapeados el intervalo (0,1).
|
| Figura 7. Razón de cambio de la potencia de cocción estándar con respecto a las variables de diseño de la estufa solar. |
De la misma manera, en la figura 6, se muestra la razón de cambio del rendimiento térmico de la estufa solar, en función de cada uno de los parámetros considerados.
| Figura 8. Razón de cambio del rendimiento térmico con respecto a las variables de diseño de la estufa solar. |
En ambos casos es notorio que la razón de cambio mayor es con respecto a la emitancia de la película selectiva absorbedora, en rangos pequeños de la emitancia. En segunda instancia, la razón de cambio con respecto a la reflectancia implica cambio significativos, sobre todo cuando la reflectancia en mayor al 90%. En el caso del área del colector y de la masa en el contenedor, la razón cambio se mantiene aproximadamente constante.
5 Conclusiones
Este estudio propone un modelo térmico para simular el comportamiento térmico de la cocina de concentración solar de Jorhejpataranskua en términos de un sistema no lineal acoplado de ecuaciones diferenciales ordinarias. Las incógnitas en estas ecuaciones diferenciales son: temperaturas promedio del agua, de la superficie del recipiente absorbente y de la superficie reflectora. Se utilizó un análisis de variación de los parámetros de diseño basado en simulaciones numéricas de, específicamente, la temperatura promedio del fluido, para calcular la potencia de cocción estándar y el rendimiento térmica. El estudio consideró las variaciones en cuatro parámetros de diseño: el área del colector, la masa de fluido en la olla, el cociente absorbancia-emitancia y la reflectancia. Se obtuvieron curvas de ajuste para los datos de las simulaciones para los cálculos de potencia de cocción estándar y rendimiento térmico, con una expresión funcional de estos en términos de las variables de diseño.
Utilizando la técnica del análisis de la razón de cambio, se encontró que la mayor variación para los parámetros de diseño correspondía al caso de la emitancia de la película absorbente sobre la superficie del recipiente que contiene el alimento a cocinar con la olla de la estufa solar. También se encontró que la tasa de cambio relacionada con la reflectancia del concentrador es significativa en los casos en que es mayor que 0,9. Finalmente, las tasas de cambio obtenidas para el tamaño del colector y la cantidad de agua en la olla permanecieron prácticamente constantes.
Agradecimientos
Agradecemos el financiamiento del proyecto CONACyT número 247719 a la Universidad Intercultural Indígena de Michoacán para la realización del presente trabajo.
Referencias
- 1. M. González-Avilés & J. J. González Avilés, Thermal Model of a Solar Cooker Jorhejpatarnskua. Energy Procedia 57 (2014) 1623-1631.
- 2. A. A. El-Sebaii, R. Domański, and M. Jaworski. Experimental and theoretical investigation of a box-type solar cooker with multi-step inner reflectors. Energy 19.10 (1994) 1011-1021.
- 3. P. A. Funk & D.L. Larson. Parametric model of solar cooker performance, Solar Energy, V 62.1 (1998) 63-68.
- 4. T. C. Thulasi Das, S. Karmakar & D. P. Rao, Solar Box Cooker: part I–modeling and part II–analysis andsimulation. Solar Energy 52.3 (1994) 274.
- 5. A.H. Algifri & H.A. Al-Towaie. Efficient orientation impacts of box-type solar cooker on the cooker performance. Solar Energy 70.2 (200) 165-170.
- 6. A.K. Bidotnark & N. Türkmen. Modelling of a hot box solar cooker. Energy Conversion and Management 37.3 (1996) 303-310
- 7. E.R. Pejack. Mathematical model of the thermal performance of box-type solar cookers. Renewable Energy 1.5–6 (1991) 609-615
- 8. K. Klemens Schwarzer & M.E. Vieira da Silva. Characterisation and design methods of solar cookers. Solar Energy 82.2 (2008) 157-163
- 9. J.R. Morales, M. Gordon, M., H. Terrés, A. Ortega & A. Lizardi, A. Evaluación de reflectores internos en una estufa solar de tipo caja. Científica 12.4 (2008) 175-183
- 10. A. Rabl. Comparison of solar concentrators. Solar energy 18, no. 2 (1976) 93-111.
- 11. A. Rabl. Optical and thermal properties of compound parabolic concentrators. SPIE milestone series 54 (1993) 229-243.
- 10. J.A. Duffie & W.A. Beckman Solar engineering of thermal processes. Third ed. New York,
Wiley, 2013.
- 11. S.A. Channiwala & N.I. Doshi. Heat loss coefficients for box-type solar cookers. Solar Energy. 42.6 (1989) 495-501.
- 12. ASAE S580. Testing and Resporting Solar Cooker Performance. American Society of Agricultural Engineers, ASAE S580 JAN03 (2003) 824-826.
- 13. A. Kundapur & C.V. Sudhir. Proposal for new world standard for testing solar cookers. Journal of Engineering Science and Technology 4 (2009) 272-281.
Document information
Published on 08/02/19
Accepted on 01/11/18
Submitted on 22/01/18
Volume 35, Issue 1, 2019
DOI: 10.23967/j.rimni.2018.11.006
Licence: CC BY-NC-SA license
Share this document
Keywords
claim authorship
Are you one of the authors of this document?