Manual de Usuario de FEM2DEM
Metodología FEM-DEM para la predicción de fracturas en materiales y estructuras
International Center For Numerical Methods In Engineering (CIMNE)
Manual de Usuario de FEM2DEM
Metodología FEM-DEM para la predicción de fracturas en materiales y estructuras
International Center For Numerical Methods In Engineering (CIMNE)
Introducción 3
Interfaz de usuario 3
Datos generales 6
Definición de las funciones de tiempo 7
Asignar desplazamientos impuestos 8
Asignar velocidades impuestas 8
Asignar fuerzas puntuales 9
Asignar fuerzas uniformemente distribuidas 9
Asignar fuerzas de presión 10
Asignar propiedades del material 10
Asignar parámetros de contacto entre DEM 11
Definir gráficas en post proceso 12
Generar malla 12
Órdenes en el cálculo 13
Referencias 13
Introducción
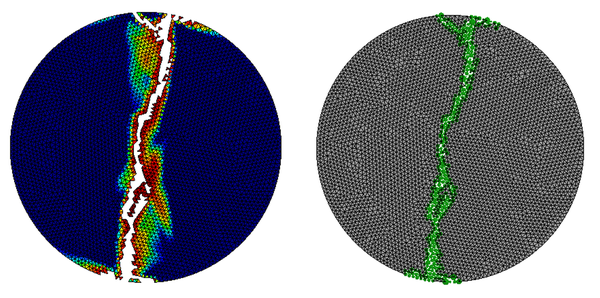
Este documento explica el funcionamiento de la interface de usuario del programa FEM2DEM para analizar sólidos bidimensionales utilizando el sencillo procedimiento FEM-DEM propuesto por Zarate & Oñate que se utiliza para predecir el inicio y la propagación de fracturas [1,2].
El método propuesto enriquece una metodología de apertura de grietas bien definida llamada Técnica de eliminación de elementos, al crear elementos discretos en los labios de la grieta. Algunos aspectos importantes inherentes a la formulación utilizada y que se presentan en varios artículos [1-5] garantizan los buenos resultados obtenidos. En particular el hecho de usar un campo de tensión suavizada, garantizar la conservación de masa y el uso de un algoritmo simple para asegurar el contacto posterior a la fractura entre el borde fracturado, son algunas de las características del procedimiento FEM-DEM.
El enfoque FEM-DEM se ha aplicado a una colección de problemas de referencia en 2D y 3D que evidencian el buen rendimiento de esta técnica numérica para el análisis no lineal de sólidos que implica situaciones de múltiples fracturas [1,2].
Es importante mencionar que la transición de FEM a DEM se realiza sin la necesidad de volver a conectar, ya que una vez que se alcanza el valor máximo de daño en cada lado de un elemento, se elimina y se reemplaza por un par de elementos discretos ubicados en los nodos del elemento.
Interfaz de usuario
El módulo de cálculo FEM2DEM se utiliza en conjunto con el programa GiD y es compatible con la versión 12.1.11 o superior.
La Figura 1 muestra la clásica pantalla de GiD
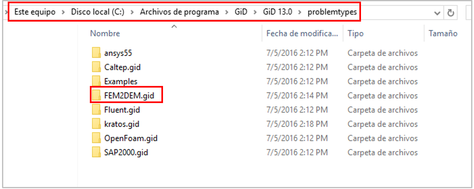
Para instalar el programa FEM2DEM en GiD, es necesario copiar la carpeta que contiene el código y la interfaz, dentro del directorio "problemtypes" de la carpeta de instalación GiD, tal y como se muestra en la Figura 2
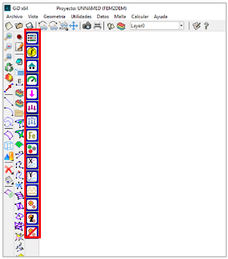
Una vez hecho esto, es necesario reiniciar el programa GiD a fin de que la interfaz de usuario del programa FEM2DEM se encuentre completamente operativa y pueda ser referenciada como se muestra en la Figura 3.
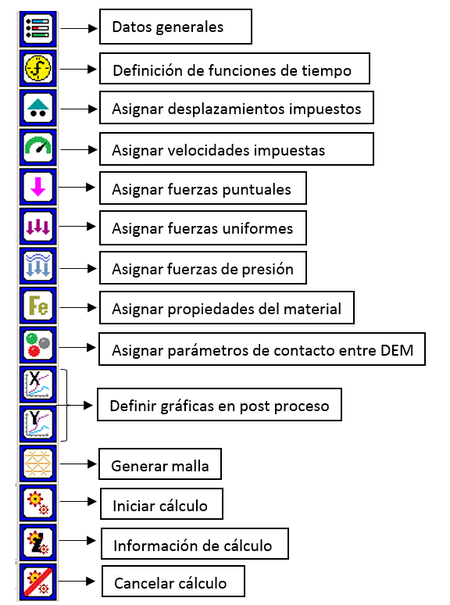
Al activarse, el módulo FEM2DEM presenta una barra de herramientas donde se puede acceder a todas las funcionalidades del programa:
Cada uno de los iconos permite acceder a una utilidad diferente. La Figura 5 muestra el uso de cada una de las funciones asociadas y que sera descritas en los siguientes apartados.
Cabe hacer mencion que el modulo FEM2DEM esta diseñado para trabajar en el sistema internacional de unidades.
Al presionar sobre el botón de “Datos generales” aparecerá la ventana siguiente:
Esta ventana posee dos pestañas. La primera corresponde a los datos generales de cálculo con las siguientes opciones:
- Problem type: Define si se trata de un cálculo de deformación o tensión plana.
- Max. Number of iterations: Número de iteraciones que realizará el solver como máximo para encontrar la convergencia en un paso de tiempo determinado. En caso de no converger, el incremento de tiempo se reduce automáticamente a una decima parte.
- Resolución: Tolerancia de convergencia en daño.
- Minimum time increment: Define el paso de tiempo más pequeño a utilizar en caso de que la solucion no converja.
- Gravity: Activa o desactiva la gravedad.
La segunda pestaña “Time control” permite modificar los parámetros mostrados en la Figura 7.
- Final analysis time: Tiempo total de la simulación.
- Default time increment: Incremento de tiempo a utilizar por defecto.
- Default postprocess interval: Intervalo de tiempo por defecto para generar información de postproceso.
- Default graph output: Intervalo de tiempo para generar datos para gráficas.
 Definición de las funciones de tiempo
Definición de las funciones de tiempo
Al presionar sobre el botón de “Definición de las funciones de tiempo” se obtiene la ventana siguiente:
En el caso que las condiciones de contorno o fuerzas aplicadas varíen de magnitud en el tiempo es necesario definir dicha información mediante la ventana de la Figura 8.
Inicalmente se debera selccionar la pestaña asociada a la variable sobre la cual se definira su variacion temporal. Dicha variacion se define mediante intervalos de tiempo y amplitud. FEM2DEM considerara una variacion lineal de la amplitud entre dos marcas temporales. Entendiendo la amplitud como el factor de amplificacion de la variable. Por otra parte es importante definir la función de tiempo desde el instante 0 hasta un un tiempo mayor al del tiempo total de la simulación.
En cada intervalo de tiempo definido es posible utilizar un paso de tiempo diferente (“DTUSER”) del definido por defecto, siempre y cuando el nuevo paso de tiempo sea menor. De la misma forma es posible definir los intervalos de postproceso “TOUTP” Y “TOUTD”. A modo de ejemplo se muestra la definicion de datos para la variacion temporal mostrada en la Figura 9. 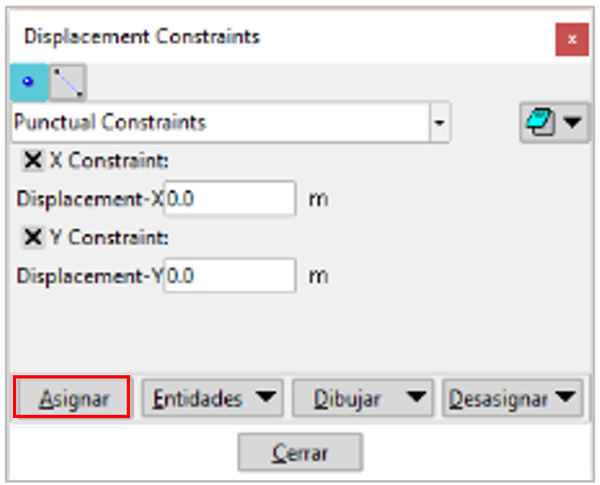
En el caso mostrado en la Figura 9 se puede observar como la función de amplitud de las fuerzas de presión tienen un máximo en t=0.0451005 s y a partir de ahí disminuye a cero en t=0.046 s.
En otro aspecto es interesante ver que el incremento de tiempo es variable siendo éste de 10-4 s en el intervalo de 0s a 0.045 s y cambiando a un valor de 10-7 s en el resto de la simulación.
Finalmente es importante comentar que un valor de 0 implica la utilización del paso de tiempo definido por defecto (Figura 7).
 Asignar desplazamientos impuestos
Asignar desplazamientos impuestos
Mediante el botón “Asignar desplazamientos impuestos” se accede a las opciones mostradas en la Figura 10, las cuales son válidas para puntos o líneas:
Para definir una condición de desplazamiento se debe activar el desplazamiento correspondiente y proporcionar su valor ya sea en la direccion X o Y o ambas. Una vez definidos estos campos, mediante el boton de “asignar” se deben seleccionar sobre la geometría los puntos o líneas asociados a dichas condiciones.
Esta ventana permite tambien desasignar, listar o dibujar las entidades a las cuales se han aplicado alguna condicion.
De la misma forma que son asignados los desplazamientos impuestos se asignan las velocidades impuestas a puntos y/o líneas mediante el botón “Asignar velocidades impuestas” tal y como se muestra en la ventana emergente de la Figura 11.
Para ello es necesario proporcionar el valor de la velocidad impuesta, proyectada sobre los ejes cartesianos y posteriormente asignar dicha velocidad a los puntos o líneas de interés.
Al igual que en el caso de los desplazamientos impuestos se puede listar entidades asignadas, dibujarlas y/o desasignarlas.
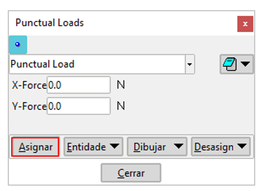
La asignación de las fuerzas puntuales se realiza mediante el uso de la ventana emergente mostrada en la Figura 12:
El mecanismo de asignacion es muy similar a lo descrto en las opciones anteriores. En esta ventana se infroma de la magnitud de la proyeccion de la fuerza sobre las coordenas cartesianas, para pasar a asignarla, mediante el correspondiente boton, a los puntos de interes de la geometría.
Igualmente, es posible eleminar cargas puntuales, dibujarlas sobre la geometría o desasignalras.
 Asignar fuerzas uniformemente distribuidas
Asignar fuerzas uniformemente distribuidas
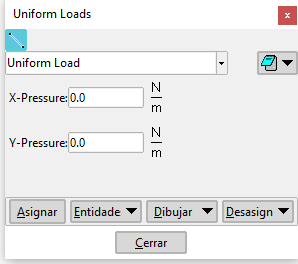
La asignación de las fuerzas uniformemente distribuidas se realiza mediante el uso de la ventana emergente mostrada en la Figura 13 y es muy similar al caso de las cargas puntuales.
La única salvedad radica en el hecho que las fuerzas distribuidades deben aplicarse únicamente a las líneas de la geometría.
La asignación de las presiones sobre las superficies del solido se realizar siguiendo el mismo modelo que las cargas uniformemente distribuidas. Con el hecho añadido que es necesario proporcionar un valor de retardo (delay). Este valor es muy útil en la simulación de voladuras donde los barrenos no estallan simultáneamente, sino que existe un cierto desfase entre ellos. Cabe mencionar que la curva de amplitud temporal asociada será la misma todas las entidades geométricas asignadas, tomando en cuenta el retardo asignado.
 Asignar propiedades del material
Asignar propiedades del material
La definición de las propiedades mecánicas asociadas a los distintos materiales que pueden ser utilizados se definen y asignan mediante el icono correspondiente el cual presenta la ventana emergente mostrada en la Figura 15
En dicha ventana se definen las siguientes variables:
- Young: Valor del módulo de elasticidad del material (Pa).
- Poisson: Coeficiente de Poisson ν.
- Self-weight: Valor del peso específico del material (N/m3).
- Thickness: Espesor del material (valor 1 m si es deformación plana).
- Material model: Modelo de superficie de fluencia a escoger: Rankine, Mohr-Coulomb, Christensen, Truncate Rankine y Mixed.
- Damage Model: Modelo de daño después de el límite elástico a escoger: lineal, exponencial y frágil.
- Failure Tension Stress: Límite elastico en tracción.
- Failure compression Stress: Límite elastico en compresión.
- Failure energy in Tension: Energía de rotura en tracción.
- Failure energy in Compression: Energía de rotura en compresión.
Al modificar cualquiera de estos valores es necesario guardarlos de forma asociada al nombre de un material. Una vez hecho esto es posible asociar un área de la geometría con un material específico. Obviamente no puede quedar ninguna área sin tener un material asociado.
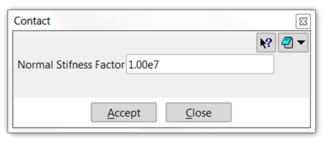
 Asignar parámetros de contacto entre DEM
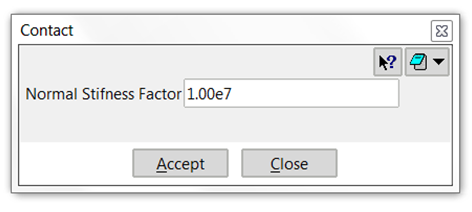
Asignar parámetros de contacto entre DEM
La rigidez del contacto normal Kn entre esferas es el parámetro que se define en este apartado. El valor por defecto es útil en la mayoría de los casos.

 Definir gráficas en post proceso
Definir gráficas en post proceso
Es posible definir un máximo de 5 gráficos distintos que permitan monitorizar el comportamiento de la simulación. En cada uno de ellos se define una variable sobre las abscisas y otra sobre las ordenadas.
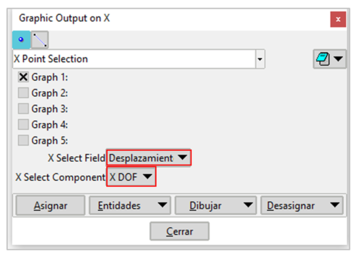
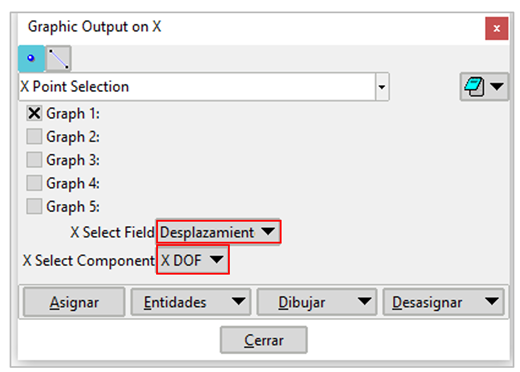
En la Figura 17 se observa la manera de seleccionar cualquiera de los 5 gráficos disponibles.
Una vez seleccionado el grafico correspondiente se elige la variable a graficar (desplazamientos, reacciones, velocidades y aceleraciones) mediante el botón “X select Field”.
De igual forma se procede utilizando el el botón correspondiente para las variables a representar sobre el eje Y.
Mediante este botón se genera la malla sobre la geometría definida, tomando en cuenta todas las condiciones de carga, desplazamiento y materiales definidos.
Los tres últimos botones se encuentran relacionados con el proceso de cálculo de FEM2DEM.
El primero de ellos sirve para iniciar el cálculo una vez completados los pasos anteriores.
El segundo botón permite obtener información del proceso que se está llevando a cabo mostrando el progreso del cálculo (tiempo de cálculo, paso de tiempo llevándose a cabo…)
El último botón se emplea para cancelar el cálculo y parar el proceso.
Referencias
[1] Zárate, F. & Oñate, E. A simple FEM–DEM technique for fracture prediction in materials and structures. Comp. Part. Mech. (2015) 2: 301-314. https://doi.org/10.1007/s40571-015-0067-2
[2] Zárate, F., Cornejo, A. & Oñate, E. A three-dimensional FEM–DEM technique for predicting the evolution of fracture in geomaterials and concrete, Comp. Part. Mech. (2017). https://doi.org/10.1007/s40571-017-0178-z
[3] Oñate E., Zárate F., Celigueta M.A., González J.M., Miquel J., Carbonell J.M., Arrufat F., Latorre S., Santasusana M., Advances in the DEM and Coupled DEM and FEM Techniques in Non Linear Solid Mechanics. In: Oñate E., Peric D., de Souza Neto E., Chiumenti M. (eds) Advances in Computational Plasticity. Computational Methods in Applied Sciences, vol 46. Springer, Cham (2018)
[4] González, J.M., Zárate, F. & Oñate, E. Pulse fracture simulation in shale rock reservoirs: DEM and FEM–DEM approaches. Comp. Part. Mech. (2017). https://doi.org/10.1007/s40571-017-0174-3
[5] Zárate, F., Gonzalez, J.M., Miquel J., Lohner, R., Oñate, E., A coupled FEM-DEM procedure for predicting blasting operations in tunnels. Papers Repository of the International Centre for Numerical Methods in Engineering (CIMNE) (2017)
Document information
Published on 01/01/2017
Licence: CC BY-NC-SA license