Abstract
Factor analysis was used to investigate the changes of dry-wet climate in the dry season in Yunnan during 1961–2007 based on observed data from 15 stations. Three common factors were extracted from the 9 climatic factors. The results showed that the dry-wet climate has evidently changed since the early 1960s. The general trends in the changes of dry-wet climate were described as slight decrease in humidity and gradual enhancement in drought intensity. The climate during 1960s–1980s was under weak-medium drought. But since early 1990s, dry conditions have markedly strengthened and continued due to uneven temporal distribution of rainfall and climate warming.
Keywords
dry-wet climate ; factor analysis ; dry season ; Yunnan
1. Introduction
Climate change is a hot subject which is a matter of concern for the international community, and which has some relations with drought disaster and natural water resources crisis [ Qin et al., 2005 ]. Dry-wet change is an important part of climate change. Generally, investigation of dry-wet climate is usually done by analyzing rainfall change, or using arid/humid indices considering temperature and precipitation, or simulating potential evapotranspiration [ Guo et al., 2008 , Li et al., 2006 , Ma and Ren, 2007 and Shi et al., 2007 ]. Though many studies have made some advances, defects still exist because of its intrinsic complexity. One of the defects is inconsiderately dealing with the income and expenditure in natural moisture balance, for instance, neglecting temporal distribution of precipitation and its validity. This would influence the objectivity of changes in dry-wet climate [ Ma and Ren, 2007 ; Shi , 2007].
Compared to most of other provinces in China, clearly dry-wet season is an important climatic character of Yunnan [ Wang, 1990 and Qin et al., 1997 ]. The total rainfall of the dry season (from November to April of the next year) only constitutes 15.4% of annual precipitation. During the dry season, monthly precipitation is from 12 to 40 mm, far less than the potential evaporation capacity at the same time [ Wang, 1990 and YPMA, 1984 ]. So, Yunnan generally suffers from drought and water shortage during dry season, especially from February to April [ Wang, 1990 and YPMA, 1984 ]. The drought in dry season restrains summer crops and fruits [ Wang, 1990 and Huo et al., 2001 ], and seriously affects sowing, transplanting and growing in spring [ Wang, 1990 , Qin et al., 1997 and Qin et al., 2000 ]. Further, it increases uncertainty in autumn yields. Moreover, the six-month-long dry season is the primary cause for frequent forest fires in Yunnan [ Qin et al., 2000 ], and also is the important factor for the fragile ecosystem which is hard to recover. In order to boost disaster prevention and reduction in Yunnan, this paper launched a research to investigate the characteristics of dry-wet climate change in dry season.
2. Data and methods
2.1. Data
After taking into account city’s heat island effect, 15 climatological stations situated in different prefectures are selected with good continuity and representativeness in meteorological observation (a.s.l. 880–2,345 m). The paper employs monthly and daily data of sunshine duration, average temperature and rainfall from November 1961 to April 2008.
2.2. Methods
At present, there are no observed elements or index calculated with observed meteorological elements that can objectively and exactly reflect the status of dry-wet climate [ Meng et al., 2004 and Yuan and Zhou, 2004 ]. As it is well known, natural dry-wet status rests with the balance of water income and expense [ Meng et al., 2004 and Zhou et al., 1997 ]. Further, effective rainfall and evaporation capacity dominate water income and expense respectively under natural condition [ Meng et al., 2004 and Zhou et al., 1997 ]. Air temperature, solar radiation (sunshine duration), and air humidity are the principal influence elements for evaporation [ Yuan and Zhou, 2004 and Zhou et al., 1997 ]. Temporal distribution and intensity of precipitation are closely related with rainfall drain (run-off) and air humidity. Bearing in mind that air humidity depends largely on temperature and moisture content in the air, together with short-term records of precisely observed evaporation capacity, 9 climatic factors are selected to synthetically express dry-wet condition for the dry season. These factors include total rainfall of the dry season (R), percentage of daily rainfall over 10 mm (R10 %), maximum rainfall for 3 successive decades (R3sx ), number of rainy days (Rn ), total rainfall from February to April (R24 ), greatest number of successive rainless days (R0n ), number of rainy days over 2 mm (R2n ), average temperature (T) and sunshine duration (S) for the dry season. R represents gross water income, and R10% and R3sx express precipitation intensity. Rn , R24 , R0n and R2n reflect temporal distribution of precipitation, and R2n is the index of agricultural effective precipitation. T and S are the leading factors for natural evaporation. Firstly, 9 climatic factors mentioned above for each station are calculated. Then, regional mean of each factor is calculated.
Factor analysis is a statistical method which can simplify and solve multivariate-colinearity problems [ Zhang, 2002 and Yu, 2003 ]. Due to the using of varimax orthogonal rotation, factor analysis interprets the physical meanings of common factors more clearly than principal component analysis [ Zhang, 2002 ]. In this paper, factor analysis is employed.
3. Preliminary results
KMO (Kaiser-Meyer-Olkin Measure of sampling adequacy) test is done before factor analysis. It is used for judging whether factor analysis is appropriate for selected climatic variables. Generally, if the KMO value is more than 0.75, factor analysis offers great utility of the selected variables [ Zhang, 2002 ]. Here, the statistical value of KMO for 9 climatic factors is 0.754, which means that the data are suitable for factor analysis. 69.8%–95.8% of the total information of 9 climatic factors were extracted. The explained variances of 3 extracted common factors before and after varimax orthogonal rotation are listed in Table 1 . Correlations between the 9 original factors and the extracted common factors are shown in Table 2 .
| Factor | Before varimax orthogonal rotation | After varimax orthogonal rotation | ||
|---|---|---|---|---|
| Variance (%) | Cumulative variance (%) | Variance (%) | Cumulative variance (%) | |
| Z1 | 56.56 | 56.56 | 29.57 | 29.57 |
| Z2 | 16.68 | 73.23 | 26.83 | 56.40 |
| Z3 | 9.57 | 82.80 | 26.40 | 82.80 |
| Factor | R | R24 | R10% | R3sx | Rn | R0n | R2n | S | T |
|---|---|---|---|---|---|---|---|---|---|
| Z1 | 0.590* | 0.300 | 0.908* | 0.873* | 0.265 | −0.101 | 0.458 | −0.242 | 0.109 |
| Z2 | 0.399 | 0.114 | −0.017 | 0.230 | 0.888* | −0.906* | 0.532* | −0.191 | −0.511 |
| Z3 | 0.418 | 0.732* | 0.093 | 0.215 | 0.173 | −0.253 | 0.617* | −0.844* | −0.652* |
Note:
- . illustrates the statistically significant level of 0.001
According to the results of factor analysis, the construction for each extracted common factor and their physical meanings are shown in Table 3 . As each variable in these expressions is standardized, the greater the absolute values of variable coefficients, the more influence on common factors. Positive and negative signs indicate positive and negative effects on common factors.
| Factor | Construction | Physical meanings |
|---|---|---|
| Z1 | Z1 = 0.460R10% + 0.390R3sx + 0.257T + 0.213R | More daily rainfall over 10 mm and heavier rain spells are in favor of drought strengthening under the premise of total rainfall keeping constant |
| Z2 | Z2 = 0.529Rn – 0.526R0n + 0.219S – 0.235R24 + 0.514R2n | More rainy days and less successive rainless days benefit for drought weakening |
| Z3 | Z3 = 0.468R24 – 0.540S – 0.343T – 0.270Rn + 0.187R2n | Less sunshine duration and lower temperature in dry season, and more total rainfall from February to April benefit for drought weakening |
Note: All variables are standardized
4. Analysis and discussion
4.1. Factor analysis reaching the expected purpose
According to the results, there are no significant correlations among the three extracted common factors. There is not much difference among the explained variances of the three factors, indicating they have nearly equal importance. The physical meanings of these common factors are definite and reasonable. Moreover, Table 2 shows that each original factor is significantly correlated with at least one of the 3 common factors. In addition, their cumulative explained variance reached 82.8%. Undoubtedly, the three common factors are able to express the changes of dry-wet climate in dry season.
4.2. Changes in common factors reflecting the characteristics of the dry-wet climate
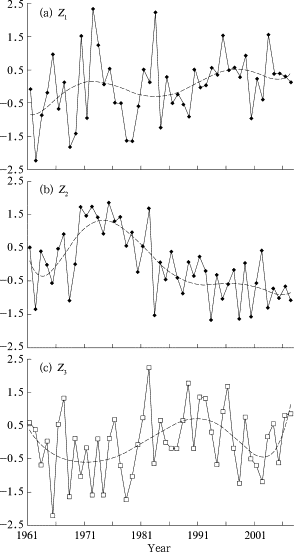
Figure 1 shows the yearly changes of the three common factors. Common factor Zi shows an obvious increasing trend, and its linear trends during 1961–2007 and 1985–2007 are 0.198 and 0.394 per 10 years respectively (at the statistically significant level of 0.1, and 0.05, respectively). Common factor Z2 presents a distinct decreasing trend since 1970s, and the decreasing trend during 1961–2007 is −0.366 per 10 years (at the statistically significant level of 0.01). The trends of Z1 and Z2 both illustrate strengthening of drought. Meanwhile, to a certain extent, common factor Z3 displays a visibly cyclical variation with an increasing trend of 0.150 per 10 years, indicating drought is weakening slightly (the linear trend fails to pass the significance test). It is completely obvious that the dry-wet climate during the dry season in Yunnan has the characteristic of slight decrease in humidity and gradual enhancing in drought over the past 47 years.
|
|
|
Figure 1. Yearly variations of the 3 common factors (1961–2007) (smoothing curves are multinomial fittings)
|
Based on the common factors, interdecadal variations of dry-wet climate for the dry season and their direct causes can be drawn (Tab. 4 ). 1960s, 1970s and 1980s are all in the status of relatively weak drought. Since early 1990s, the dry conditions have markedly strengthened and continued. The present status is still under the typical dry climate mainly due to uneven temporal distribution of precipitation.
| Years | Z1 | Z2 | Z3 | Tendency | Main reasons |
|---|---|---|---|---|---|
| 1962–1970 | −0.694 | −0.075 | −0.171 | Weak to medium drought | Proportion of relatively strong rainfall and rainfall concentration |
| 1971–1980 | 0.042 | 1.341 | −0.692 | Number of rainy days and temporal distribution | |
| 1981–1990 | −0.093 | −0.069 | 0.497 | Sunshine duration for the dry season and total rainfall from February to April | |
| 1991–2000 | 0.516 | −0.561 | 0.412 | Typical drought | Combined influence from three common factors |
| 2001-2008 | 0.199 | −0.806 | −0.077 | Number of rainy days and temporal distribution | |
| 2004-2008 | 0.547 | −0.951 | 0.355 | Number of rainy days, temporal distribution, and rainfall concentration |
4.3. Changes of original factors confirming the results
The yearly variations of the leading two original factors in each common factor were shown in Figure 2 , Figure 3 and Figure 4 .
|
|
|
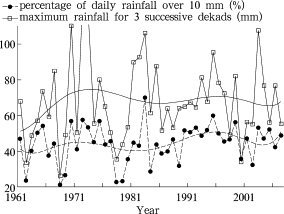
Figure 2. Yearly variations of percentage of daily rainfall over 10 mm and maximum rainfall for 3 successive dekads
|
|
|
|
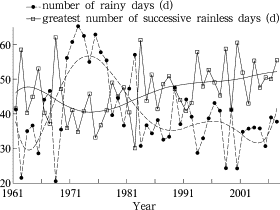
Figure 3. Yearly variations of number of rainy days and greatest number of successive rainless days over dry season
|
|
|
|
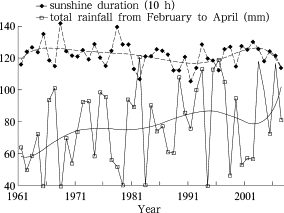
Figure 4. Yearly changes of sunshine duration for the dry season and total rainfall from February to April
|
According to Figure 2 , percentage of daily rainfall over 10 mm and the maximum rainfall for 3 successive decades show slightly increasing trends over the past 47 years, in accordance with the tendency of Z1 . Changes of the leading two original variables in Figure 3 and Figure 4 also confirm the variation of Z2 and Z3 respectively. Among all the 6 leading original variables, decrease in number of rainy days, increase in greatest number of successive rainless days, and gradual increase in total rainfall from February to April are most significant. They are likely to drive the changes of natural dry-wet status for the dry season.
4.4. Influence of total rainfall of the dry season and climate warming
It is necessary to analyze total rainfall of the dry season because it is water income. The mean value of total rainfall of the dry season over the past 47 years is 143.9 mm, its standard deviation is 42.1 mm (29.3%), its interdecadal standard deviation for the five decades is 15.9 mm (11.1%), and the linear trend in the total rainfall during the past 47 years is only 2.4 mm per 10 years which fails to pass the statistical sigificance test. Obviously, there is uncertainty in the variation of total rainfall of the dry season, but it contributes to the interannual fluctuations of natual dry-wet status.
Although annual variations in average temperature for the dry season are much less than variations in total rainfall and sunshine duration, temperature is a major element affecting natural evaporation [Zhou, 1997; Zhang and Wan, 1995 ]. Since the 1990s, average temperature for the dry season has been increasing at the rate of 0.43 °C per 10 years, being in sharp contrast to the changing rate of 0.01 °C per 10 years during 1961–1989. It is obvious that the increase in average temperature for the dry season over the past two decades has probably intensified the drought condition.
4.5. Influence of total rainfall from February to April
Among the 6 leading original factors of dry-wet climate, only the increase of total rainfall from February to April (5.67 mm per 10 years at statistically significant level of 0.05) implies weakening in drought (Fig. 4 ). However, rainfall from November to January of next year decreased at the rate of −3.23 mm per 10 years. On the other hand, climate warming in Yunnan from February to April is more significant than in summer and autumn [ Gao et al., 2008 ]. Furthermore, the months from February to April are the sunniest period of the year. Under such circumstances, increasing in total rainfall from February to April is not actually big enough to weaken the drought in the dry season.
5. Conclusions
(1) The extracted 3 common factors can reflect the changes of dry-wet climate in the dry season in Yunnan.
(2) The general trends in dry-wet climate of the dry season from 1961 to 2007 are described as decrease in humidity and gradual enhancement in drought with great interannual fluctuations. Decrease in number of rainy days, increase in greatest number of successive rainless days, and gradual increase in the proportion of total rainfall from February to April are the important elements responsible for the aridification. During the 1960s–1980s weak-medium drought was observed. Since the early 1990s, dry conditions have markedly strengthened and continued. The markedly dry climate in the dry season in recent years mainly stem from the uneven temporal distribution of rainfall.
(3) The dry season for the years 1990–2007 has a characteristic of distinct warming with an increasing rate of 0.43 °C per 10 years in average temperature, which has great impact on drought strengthening. The trend in total rainfall of the dry season has uncertainty, but its great annual fluctuation is important for the interannual variation in dry-wet climate.
Acknowledgements
This paper is supported by the program (40675045) from the National Natural Science Foundation of China.
References
- Gao et al., 2008 Z. Gao, H. Chen, J. Li; Characteristics of monthly and seasonal temperature variation distribution in Yunnan province; Yunnan Geographic Environment Research (in Chinese), 20 (5) (2008), pp. 48–52
- Guo et al., 2008 J. Guo, J. Wu, Y. Li; Climate dryness/wetness status and its variation characteristics in Guangdong province; Chinese Journal of Agrometeorology (in Chinese), 29 (2) (2008), pp. 157–161
- Huo et al., 2001 S. Huo, W. Ren, J. Cheng, et al.; Tobacco Meteorology (in Chinese), Yunnan Scientific and Technical Press (2001), p. 344
- Li et al., 2006 Y. Li, G. Yang, D. Wang; Dry and wet climatic changes in recent decades in the source regions of Yangtze, Yellow and Lancang Rivers; Journal of Northwest Sci-Tech University of Agriculture and Forestry (Natural Science Edition) (in Chinese), 34 (3) (2006), pp. 73–77
- Liu et al., 2004 G. Liu, A. Guo, S. An, et al.; Research progress in Palmer drought severity index and its application; Journal of Natural Disasters (in Chinese), 13 (4) (2004), pp. 21–27
- Ma and Ren, 2007 Z. Ma, X. Ren; Drying trend over China from 1951 to 2006. Adv. Clim. Change Res. (in ; Chinese), 3 (4) (2007), pp. 195–201
- Meng et al., 2004 M. Meng, J. Ni, Z. Zhang; Aridity index and its applications in geo-ecological study; Acta Phytoecologica Sinica (in Chinese), 28 (6) (2004), pp. 856–861
- Qin et al., 2005 D. Qin, Y. Ding, J. Su, et al.; Assessment of climate and environment changes in China (I): Climate and environment changes in China and their projection. Adv. Clim. Change Res. (in ; Chinese), 1 (1) (2005), pp. 4–9
- Qin et al., 1997 J. Qin, J. Ju, M. Xie; Weather and Climates in Low Latitude Plateau (in Chinese), China Meteorological Press (1997), p. 210
- Qin et al., 2000 J. Qin, M. Xie, Y. Liu, et al.; Pandect of Meteorological Disasters in Yunnan (in Chinese), China Meteorological Press (2000), p. 256
- Shi et al., 2007 J. Shi, H. Tang, W. Xu, et al.; Dryness/wetness changes in Qinghai province during 1959–2003; Adv. Clim. Change Res. (in Chinese), 3 (6) (2007), pp. 356–361
- Wang, 1990 Y. Wang; Agricultural Climate Resources in Yunnan and Its Regionalization (in Chinese), China Meteorological Press (1990), p. 250
- Wu et al., 2008 C. Wu, P. He, P. Dai; Seasonal characteristics of evaporation and its effects on drought; Journal of Meteorological Research and Application (in Chinese), 29 (3) (2008), pp. 8–11
- YPMA, 1984 YPMA (Yunnan Provincial Meteorology Administration); Data Booklet for Agricultural Climates in Yunnan (in Chinese), People’s Press of Yunnan (1984), p. 240
- Yu, 2003 X. Yu; X. Yu (Ed.), Factor analysis. in: Multivariate Statistical Analysis (in Chinese), China Statistics Press (2003), pp. 71–198
- Yuan and Zhou, 2004 W. Yuan, G. Zhou; Comparison between standardized precipitation index and Z-index in China; Acta Phytoecologica Sinica (in Chinese), 28 (4) (2004), pp. 523–529
- Zhang and Wan, 1995 M. Zhang, G. Wan; Model studies of calculating the amount of evaporation using different meteorological elements; Meteorological Monthly (in Chinese), 21 (2) (1995), pp. 36–40
- Zhang, 2002 W. Zhang; W. Zhang (Ed.), Factor analysis and correspondence analysis. in: Statistical Analysis Tutorial in SPSS 11 (Advanced Level) (in Chinese), Beijing Hope Electron Press (2002), pp. 190–212
- Zhou et al., 1997 S. Zhou, R. Zhang, C. Zhang; Meteorology and Climatology (in Chinese), Higher Education Press (1997), p. 260
Document information
Published on 15/05/17
Submitted on 15/05/17
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?