Simulation of Climate Negotiation Strategies between China and the U.S. Based on Game Theory

Abstract

Consensus and disagreements between China and the U.S. are the key factors influencing the direction that global climate negotiation is heading for. By taking into account the uncertainties of temperature increment and its impact on GDP growth, together with the positive, negative and spillover effects of climate change investment on utility, a strategic simulation model including China and the U.S. is developed. Based on utility and game theory, a sensitivity analysis is conducted. The results show that the first-mover disadvantage exists in the game, and the scale of each country’s climate change investment under non-cooperative scenario is too small to ensure the 2°C target. To guarantee the stability and win-win basis for global cooperation, the simulation results also indicate that it makes sense to assist and compensate technology transfer and funding to China.

Citation

Jin, Z.-G., W.-J. Cai, and C. Wang, 2014: Simulation of climate negotiation strategies between China and the U.S. based on game theory. Adv. Clim. Change Res.,  5 (1), doi: 10.3724/SP.J.1248.2014.034.

Keywords

climate negotiation ; utility ; game theory ; strategy

1. Introduction

Owing to the Doha Round talks, the second stage of the Kyoto Protocol succeeds to continue. But in reality, the countries with binding commitments only contribute about 15.0% of global greenhouse gas (GHG) emissions, while the top two economic entities, i.e., the U.S. and China, release about 41.8% of global GHG annually. With a 32.8% proportion on the global GDP (purchasing power parity-adjusted, 2010) [ IEA, 2012 ], the consensus and disagreements between China and the U.S. may greatly influence the trend in climate negotiation. The U.S. currently refuses to sign the Kyoto Protocol and emphasizes that its reduction responsibility should be based on mutual commitments including developing countries. China and other developing countries insist on the principal of common but differentiated responsibilities (CBDR), and persuade the countries with historical responsibilities to take action immediately. The potential restrictions and economic opportunities hidden behind the disagreements between the U.S. and China are essential. For the investigation of strategic actions between the U.S. and China, the application of game theory is not only necessary for a better understanding of the current global climate negotiation predicament, but also instructive for the design of a better international negotiation framework [ Eyckmans and Tulkens,  2003 ].

Wood  [2011] has already pointed out the free-rider phenomenon behind the climate negotiation from a perspective of public goods. The externalities of GHG effects provide the basis for the game research on climate negotiation. Currently, most studies focus on the theoretical amendment to solve the problem of cooperation failure, including Ostrom  [2010] and Zhang et al.  [2011] , but few researches discuss the specific individual’s decision procedure except for Hovi et al.  [2012] , who explain why the U.S. quit the Kyoto Protocol. In order to better understand the hidden purposes and strategies of the main emitters in climate negotiation, and the predictable results of such strategies, it’s necessary to combine the theoretical model with simulations. This article will not only build a strategic simulation model including the top two global emitters, but also investigate the existence of first-mover disadvantage under climate negotiation and the possibility of staying below 2°C increment.

2. Utility functions of the U.S. and China

Assume that the national utility functions of the U.S. and China meet the standards of constant relative risk aversion (CRRA), and the utility U_t  at time t can be connected with the homochromous consumption C_t , i.e.,

$U_{t}={\begin{array}{lll}{\frac {C_{t}^{1-n}}{1-\eta }},&if&\eta \not =1;\\ln\left(C_{t}\right),&if&\eta =1{\mbox{.}}\end{array}}$

( 1)

η  represents the level of risk aversion. The consumption C_t  at time t  can be further expressed as C_t  = exp(∫₀^tg_s ds ) by standardizing the initial cosumption (Here, go ,CHN and go ,US represent the stable GDP growth of China and the U.S., respectively.) The respective growth rates are 4.5% and 1.5% with a PPP-adjusted reference of global 2.5% annual GDP growth as given by Pindyck  [2012] , which means that the gross GDP of China will overtake the U.S. by 2023. This assumption is in accordance with the years of 2039 given by Wilson and Purushothaman  [2003] , 2031 by Wu  [2010] , and 2016 by the OECD [ Johansson et al.,  2012 ].

The greenhouse effect can also affect the utilities of each individual. Dell et al.  [2009] gave a simplified relation between the GDP growth g_t  and a temperature increment T_t ,  i.e., g_t = g₀  — γT_t , where γ  is the ratio of the marginal effect. Given the temperature increment T_H  at year H , the changing process of the temperature increment is calculated by T_t  = 2T_H  × [1 — (1/2)^t/H ]. However, the temperature increment T_H  at year H is uncertain. Pindyck  [2012] used the three-parameter Gamma function (r_T = 3.8. λ_T = 0.92, θ_T =–1.13) to simulate the distribution of T_H  based on the research results of the IPCC  [2007] . This method is used in our research, where the probability density function can be expressed as

$f_{T}\left(x;r_{T}{\lambda }_{T},{\theta }_{T}\right)={\frac {{\lambda }_{T}^{r_{T}}}{\Gamma \left(r_{T}\right)}}{\left(x-{\theta }_{T}\right)}^{r_{T}-1}e^{-{\lambda }_{T}\left(x-{\theta }_{T}\right)},$ $x\geq {\theta }_{T}{\mbox{.}}$

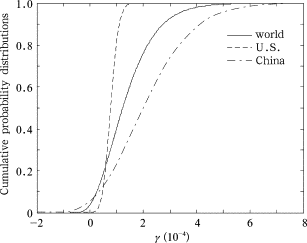
With the theoretical linear relationship between the marginal effect parameter γ  and the loss function L(T)  = exp(—βT² ), the three-parameter Gamma distribution (parameters: r_γ , λ_γ , θ_γ ) can be applied to simplify the theoretical model based on the research results of integrated assessment models (IAMs) [ Nordhaus, 1994  and Hope, 2006 ]. Table 1 summarizes the GDP loss ratios of the U.S. and China under different temperature increments. Compared to the global reference, the variance of loss under the same temperature increment follows the order: China>world>U.S., which is in accordance with the economic structure and the resistance ability to natural disasters of each country. In this research the assumptions of the global y as given by Pindyck  [2012] and Dietz and Stern  [2008] are taken as the references. Here, we assume the loss of the mean, 17% and 83% proportion of the cumulative loss function under a 2.5°C increment for China (2.00%, 1.00% and 4.80%) and the U.S. (1.20%, 0.75% and 1.40%). Table 2 further lists the respective parameters of the world, the U.S. and China. Figure 1 illustrates the parameter y  distributions. In order to enhance the robustness of our theoretical model, a sensitivity analysis of y  is further carried out in this study.

Table 1. GDP loss ratios of the world, China and the U.S. for different temperature increments

Reference	Temperature increment (°C)	Effect to global GDP (%)	Effect to GDP of China (%)	Effect to GDP of U.S. (%)
Fankhauser  [1995]	2.5	–1.4	–4.7	–0.7
Richard  [1995]	2.5	–1.9	–8.6a , –5.2b	–1.5c
Nordhaus  [1994]	3.0	–1.33	–1.0
Nordhaus and Yang  [1996]	2.5	–1.7	–2.4d
Plambeck and Hope  [1996]	2.5	–1.3 (–0.6 to –5.1)	–4 (–1 to –4.8)e	–1.2 (–1.4 to –0.8)
Nordhaus and Boyer  [2000]	2.5	–1.50, –1.88f	–0.22	–0.45
Tol  [2002]	1.0	–2.3 (1.0)	–2.1 (5.0)g	–3.4 (2.1)h
Maddison  [2003]	2.5	–0.1		–0.3
Hope  [2006]	2.5	–0.9 (–0.2 to 2.7)	–2.6 (–0.4 to 10.0)i

Notes: Data in brackets represent the 95% confidence interval;

a. including south and southeast Asia;

b. referring to the centralized countries;

c. including the U.S. and Canada;

d. including developing countries;

e. including other Asian countries;

f. the former is weighted by GDP, and the latter is weighted by population;

g. referring to the centralized countries;

h. referring to the American OECD countries except for Mexico;

i. referring to Asian countries except China

Table 2. GDP loss ratios distributions and parameters for the world, China and the U.S. under a 2.5°C increment

District	GDP loss proportion under 2.5°C increment(%)			Three parameters of Gamma
	Mean	17% distribution proportion	83% distribution proportion	rγ	λγ	θγ
World	1.92	0.63	3.15	3.96	19,645	–6.26×10–5
U.S.	1.10	0.75	1.40	103.80	411,600	–1.75×10–4
China	3.00	1.00	4.80	11.14	22,329	–2.85×10–4

Notes: The GDP loss distribution of the World is adjusted according to the results by Pindyck  [2012] and Dietz and Stern  [2008]

Figure 1. Cumulative probability distribution of parameter γ  for the world, China and the U.S.

The externality of GHG effects will affect the utilities in three ways:

First, the increase of climate change investment will lead to the decrease of disposable consumption, which will have negative impacts on the utility.

Second, the increase of climate change investment will boost the GDP growth, as it is a capital investment into the economy. Such a positive effect has already been confirmed by the EU [ Jaeger et al.,  2011 ].

Taking China as an example, if ICHN represents the proportion of climate change investment to its GDP, then the new disposable consumption and new GDP growth as the result of negative and positive effects should be modified as:

$C_{CHN,t}^{\ast }=C_{CHN,t}\times \left(1-I_{CHN}\right),$ $g_{CHN,t}^{\ast }=g_{0,CHN}\times \left(1+{\xi }_{CHN}\times I_{CHN}\right)-$${\gamma }_{CHN}T_{t}{\mbox{,}}$

where ξ_CHN  represents the multiplier of I_CHN  to the GDP growth.

And third, the spillover effect is the illustration of public goods. Assume that the global temperature increment T_up  can be controlled by the global investment I_world  in the relation T_up  = Φ(I_world ), which can be further decomposed into each country’s investment, i.e., T_up  = Φ(ω CHN × I CHN = ω US × I US + others). And ω CHN, ω US are the weighting factors of the country’s GDP. The PPP-adjusted GDP of China and the U.S. in 2010 are 10.16 trillion and 14.59 trillion international dollar each. It means the weighting factors are 13.26% and 19.02%, respectively.

3. Theoretical optimization procedure of game strategies between the U.S. and China

For China, the net present gross utility can be simplified as U CHN = Ψ CHN(U CHN, I US) by involving the three effects of climate change investments, i.e.,

$U_{CHN}={\int }_{0}^{+\infty }{\int }_{{\theta }_{\gamma -CHN}}^{+\infty }{\int }_{{\theta }_{T}}^{T_{up}}U_{CHN,t}^{\ast }\times exp\left(-\right.$$\left.{\delta }_{CHN}\times t\right)\times {\tilde {f}}_{T}\left(T;,,r_{T};,,{\lambda }_{T};,,{\theta }_{T}\right)\times f_{\gamma -CHN}\left(\gamma ;,,r_{\gamma -CHN};,,{\lambda }_{\gamma -CHN};,,{\theta }_{\gamma -CHN}\right)dTd\gamma dt$

The utility at time t  for China (U_CHN,t^⁎ ) and the Bayesian-modified probability density function of the temperature increment (${\textstyle {\tilde {f}}_{T}}$ ) can be expressed as:

$U_{CHN,t}^{\ast }={\frac {{\left\{\left(1-I_{CHN}\right)\times exp\left[{\int }_{0}^{t}g_{0,CHN}\times \left(1+{\xi }_{CHN}\times I_{CHN}\right)ds-{\int }_{0}^{t}2T_{t}\times {\gamma }_{CHN}\times \left(1-2^{-s/H}\right)ds\right]\right\}}^{-1{\eta }_{CHN}}}{1-{\eta }_{CHN}}}$ ${\tilde {f}}_{T}\left(x;,,r;,,\lambda ;,,\theta \right)=$${\frac {f_{T}\left(x;,,r;,,\lambda ;,,\theta \right)}{F\left(T_{up}\right)}},\theta \leq x\leq T_{up},\quad T_{up}=$$\Phi \left(I_{CHN},I_{US}\right),F\left(T_{up}\right)=$${\int }_{{\theta }_{r}}^{T_{up}}f_{T}\left(x;,,r;,,\lambda ;,,\theta \right)dx{\mbox{.}}$

According to the hypothesis of rationality, and given the information that the proportion of the U.S. investment is I_US , the conditional optimal strategy for China is to select the optimal scale of climate change investment to maximize its utility, i.e., ${\textstyle {\underset {I_{CHN}}{Max}}{\psi }_{CHN}\left(I_{CHN},I_{US}\right)}$ . Then the conditional optimal strategy can be expressed as O CHN, which is closely connected with the exogenous information I US, i.e., O CHN = Θ CHN(I US). Similarly, the conditional optimal strategy for the U.S. can also be expressed as O US = Θ US (I chn).

For the non-cooperative scenario, the dynamic game strategies involve three types: China moves first, China moves second, and China and the U.S. move simultaneously. Taking the first type as an example, the dynamic optimal strategy of China is to maximize its utility. Under the dynamic situation, China should take the subjective initiative of the U.S. into consideration, which means that the U.S.’s investment information should beΘ US(I US) rather than I US. Hence, the dynamic optimal strategy for China and the maximized utility can be expressed as O_CHN^first and U_CHN^first using the following equation: Max Ψ CHN(I CHN, Θ US(I   CHN)). Then the dynamic optimal strategy for the U.S. and the corresponding utility can be calculated as ${\textstyle {\underset {I_{CHN}}{Max}}{\psi }_{CHN}\left(I_{CHN},{\Theta }_{US}\left(I_{CHN}\right)\right)}$ . The theoretical optimization procedures for the second and third types of game strategies are similar.

For the cooperative scenario, the goal is to maximize the gross utility under the 2°C target and to define the optimal global allocation of investment assignments. Table 3 summarizes the theoretical equilibrium results of different game strategies.

Table 3. Game equilibrium results under different strategies

Country	Non-cooperative game			Cooperative game
	China moves first	China moves second	Simultaneously
China	OCHNfirst , UCHNfirst	OCHNsecond , UCHNsecond	OCHNsimul , UCHNsimul	OCHNcoop , UCHNcoop
U.S.	OUSsecond , UUSsecond	OUSfirst , UUSfirst	OUSsimul , UUSsimul	OUScoop , UUScoop

4. Simulation of the game theory and sensitivity analysis between the U.S. and China

Table 4 gives the initial setting of parameters for the simulation of the game theory between the U.S. and China. Apart from the GDP growth g₀ , weighting factor ω , the distribution of temperature increment T , and the probability density of parameter γ  discussed above, the discounting factor δ  and risk aversion η  still need to be calibrated. While Conceicao et al.  [2007] and Dasgupta  [2007] have different views, considering the inter-generation unfairness [ Dasgupta, 2007  and Stern and Britain, 2006 ] and proper social discounting ratio, the discounting factor and risk aversion are set as δ = 0, η = 2, which is in accordance with the results of  Seda and Tran, 2012  and Zhang, 2011 and Yang and Tao [2011] . In addition, ξ  can be theoretically proven to be equal to 1 if the climate change investment is treated as the classic investment^① .

Table 4. Initial parameters for the simulation of the China–U.S. strategic game model

Parameter	China	U.S.
go	4.5%	1.5%
ω	13.26%	19.02%
(rγ , λγ , θγ )	(11.14, 2.23×104 , –2.85×10–4 )	(103.80, 4.12×105 , –1.75×10–4 )
(η, δ, ξ, H )	(2, 0, 1, 100)	(2, 0, 1, 100)
(rT , λT , θT )	(3.80, 0.92, –1.13)	(3.80, 0.92, –1.13)

With the initial parameters calibrated, Table 5 further illustrates the results of the game simulations. First, both China and the U.S. tend to choose the second-move strategy (China: –21.77453 < –21.77451; U.S.: –66.47602 < –66.47596), which is similar to the actual situation in the climate negotiations. Both countries are trying to persuade the other to take the lead in reduction and to put off its own responsibilities.

Table 5. Simulation results of the dynamic game model

Country	Non-cooperative game			Cooperative game
	China moves first	China moves second	Simultaneously
China	1.3419% [–21.774532]	1.3368% [–21.774509]	1.3405% [–21.774532]	3.7520% [–21.794039]
U.S.	0.4548% [–66.475957]	0.5601% [–66.476019]	0.4547% [–66.475956]	1.2747% [–66.444107]

Notes: Data in brackets indicate the utility level. The EU is assumed to take the corresponding burden of climate change investment for the global 2°C target

Second, the non-cooperative scenario can hardly meet the necessary requirement of the 2°C target. In other words, the results also demonstrate the importance and necessity of cooperation in global climate negotiations.

Finally, the simulation also demonstrates that the U.S. rather than China can benefit from the cooperation scenario. China’s utility under the cooperation scenario is smaller than that under the noncooperative scenario, but the situation is different for the U.S. The reason for this is that China will have higher shares in emission reduction for maximizing the global utility, compared to the proportion under the non-cooperative scenario. China will then contribute much more to the spillover effect than receiving from it, which is quite different for the U.S. Compared to the non-cooperative scenario, China should increase the climate change investment proportion by 2.41% for the cooperative scenario, while the U.S. should only increase it by 0.82%. Without any compensation mechanisms in place, this difference makes the cooperative framework quite unstable. Therefore, necessary assistance for the developing countries, including funds and technology transfer, is of great importance. The utility differences between the cooperative and non-cooperative scenario for the U.S. and China can further confirm and explain the U.S.’s negotiation strategies. The U.S. emphasizes that its emission reduction should be bound on the condition that large developing countries participate in the allocation of the reduction targets. The U.S. prefers to establish a new platform to redistribute the reduction responsibilities beneficial for himself, and to essentially restrict the rights of emerging countries. So the developing countries need to push for their rights and have to appeal for reasonable compensation.

In order to reach more robust conclusions, Table 6 gives the results of the sensitivity analysis based on the initial parameter settings (Table 4 ). All results support the three key conclusions listed in Table 5 generally, which are: the first-mover disadvantage phenomenon does exist in the climate negotiation between the U.S. and China; it is impossible for the world to stay below the 2°C increment under the noncooperative scenario; the compensation mechanisms are quite necessary for the realization of a successful cooperation in climate change negotiations.

Table 6. Sensitivity analysis and the influences on the main conclusions

Conclusion	Original model	Higher g0	Lower g0	Higher η	Lower η	Increase variance of γ	Decrease variance of γ	Shift of γ	Higher δ	Lower ξ
Q1	Y	Y	Y	Y	Y	Y	Y	Y	Y	Y
Q2	N	N	N	N	N	N	N	N	N	N
Q3	Y	Y	Y	Y	Y	Y	Y	Y	Y	Y

Notes: Q1 indicates the existence of first-mover disadvantage; Q2 indicates the possibility to stay below the 2°C target under a non-cooperative scenario; Q3 indicates the necessity of compensation mechanisms to enhance the cooperation between the U.S. and China

5. Conclusions and policy implications

The strategic simulation model based on game theory together with the sensitivity analysis gives us a new perspective to reexamine the current climate negotiation and the U.S. strategies involved. The results indicate the necessity of compensation mechanisms, without which the 2°C target can hardly be reached whatever the strategies under the non-cooperative scenario would be.

Specifically for China, it will be reasonable and necessary to acquire technology and funding assistance, besides insisting on the principal of CBDR. On the one hand, the strategies under the non-cooperative scenario are also meaningful if the negotiations are deadlocked. On the other hand, assisting and funding the developing countries for reduction is also a favorable option for the U.S. if only an enforceable cooperation framework can be reached among the major emitters.

Acknowledgements

This study is supported by the Natural Science Foundation (No. 71273153) and the National Key Technology R&D Program (No. 2012BAC20B04). The authors appreciate the helpful suggestions and comments of the anonymous reviewers and the editors.

References

1. Conceicão et al., 2007 P. Conceicão, Y. Zhang, R. Bandura; Brief on discounting in the context of climate change economics; Human Development Report Office occasional paper (2007), pp. 1–19
2. Dasgupta, 2007 P. Dasgupta; The Stern Review’s economics of climate change; National Institute Economic Review, 199 (2007), p. 4
3. Dell et al., 2009 M. Dell, B.F. Jones, B.A. Olken; Temperature and income: Reconciling new crosssectional and panel estimates; The American Economic Review, 99 (2) (2009), pp. 198–204
4. Dietz and Stern, 2008 S. Dietz, N. Stern; Why economic analysis supports strong action on climate change: A response to the Stern Review’s critics; Review of Environmental Economics and Policy, 2 (1) (2008), pp. 94–113
5. Eyckmans and Tulkens, 2003 J. Eyckmans, H. Tulkens; Simulating coalitionally stable burden sharing agreements for the climate change problem; Resource and Energy Economics, 25 (4) (2003), pp. 299–327
6. Fankhauser, 1995 S. Fankhauser; Valuing Climate Change: The Economics of the Greenhouse; EarthScan (1995), pp. 66–90
7. Hope, 2006 C. Hope; The marginal impact of CO₂  from PAGE2002: An integrated assessment model incorporating the IPCC’s five reasons for concern  ; Integrated Assessment Journal, 6 (1) (2006), pp. 19–56
8. Hovi et al., 2012 J. Hovi, D.F. Sprinz, G. Bang; Why the United States did not become a party to the Kyoto Protocol: German, Norwegian, and US perspectives; European Journal of International Relations, 18 (1) (2012), pp. 129–150
9. IEA, 2012 IEA, 2012[2013-02-02]: Key world energy statistics. Accessed http://www.iea.org/publications/ .
10. IPCC, 2007 IPCC; Climate Change 2007: The Physical Science Basis; S. Solomon (Ed.), et al. , Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change, Cambridge University Press (2007), pp. 98–679
11. Jaeger et al., 2011 C.C. Jaeger, L. Paroussos, D. Mangalagiu, et al.; A New Growth Path for Europe, University of Oxford, ICCS, Université Paris (2011), pp. 1–27
12. Johansson et al., 2012 Johansson, A, Y. Guillemette, F. Murtin, et al., 2012[2013-02-02]: Looking to 2060: Long-term global growth prospects. Accessed http://www.astrid.eu/La-produtt/Studi-ric/OECD_2060-policy-paper-FINAL_11_2012.pdf
13. Maddison, 2003 D. Maddison; The amenity value of the climate: The household production function approach; Resource and Energy Economics, 25 (2) (2003), pp. 155–175
14. Nordhaus, 1994 W.D. Nordhaus; Expert opinion on climatic change; American Scientist, 82 (1) (1994), pp. 45–51
15. Nordhaus and Yang, 1996 W.D. Nordhaus, Z. Yang; A regional dynamic general-equilibrium model of alternative climate-change strategies; The American Economic Review (1996), pp. 741–765
16. Nordhaus and Boyer, 2000 W.D. Nordhaus, J.G. Boyer; Warming the World: The Economics of the Greenhouse Effect; MIT Press (2000), pp. 76–128
17. Ostrom, 2010 E. Ostrom; Polycentric systems for coping with collective action and global environmental change; Global Environmental Change, 20 (4) (2010), pp. 550–557
18. Pindyck, 2012 R.S. Pindyck; Uncertain outcomes and climate change policy; Journal of Environmental Economics and Management, 63 (3) (2012), pp. 289–303
19. Plambeck and Hope, 1996 E.L. Plambeck, C. Hope; PAGE95: An updated valuation of the impacts of global warming; Energy Policy, 24 (9) (1996), pp. 783–793
20. Richard, 1995 S.J.T. Richard; The damage costs of climate change toward more comprehensive calculations; Environmental and Resource Economics, 5 (4) (1995), pp. 353–374
21. Seda and Tran, 2012 K.C. Seda, C. Tran; Temptation and social security in a dynastic framework; European Economic Review, 56 (7) (2012), pp. 1422–1445
22. Stern and Britain, 2006 N.H. Stern, G. Britain; Stern Review: The Economics of Climate Change, HM Treasury (2006), pp. 179–298
23. Tol, 2002 R. Tol; Estimates of the damage costs of climate change. Part 1: Benchmark estimates; Environmental and Resource Economics, 21 (1) (2002), pp. 47–73
24. Weitzman, 2009 M. Weitzman; Additive damages, fat-tailed climate dynamics, and uncertain discounting; Economics: The Open-Access, Open-Assessment E-Journal, 3 (39) (2009), pp. 1–29
25. Wilson and Purushothaman, 2003 Wilson, D., and R. Purushothaman, 2003[2013-02-02]: Dreaming with BRICs: The path to 2050. Accessed http://www.atlanticfinancial.com/global-investing/emerging-markets-investing/goldman-sachs-bric-research-paper-2050.pdf .
26. Wood, 2011 P.J. Wood; Climate change and game theory; Annals of the New York Academy of Sciences, 1219 (1) (2011), pp. 153–170
27. Wu, 2010 Q.-J. Wu; Forcasting the change in economic strength of China and America; East China Economic Management (in Chinese), 24 (12) (2010), pp. 56–59
28. Yang and Tao, 2011 Y. Yang, Y.-C. Tao; Estimation of proper Chinese international reserves 1994–2009; Studies of International Finance (in Chinese), 6 (2011), pp. 4–13
29. Zhang et al., 2011 F.-S. Zhang, Z. Xu, J.-K. He, et al.; Gametheoretical study on international transfer of low-carbon technologies under incomplete information; Advances in Climate Change Research (in Chinese), 7 (1) (2011), pp. 41–47
30. Zhang, 2011 Zhang, T., 2011[2013-02-02]: Endogenous discounting, precautionary savings and the current account: The case of China. Accessed http://halshs.archivesouvertes.fr/docs/00/55/69/79/PDF/2007.31.pdf .

Notes

①. g  = ΔY/Y, Y  indicates the GDP. If the climate change investment is treated as the classic investment, then g*  = (ΔY + I × ΔY)/Y  = (1 + I) × g