Restructuring surface tessellation with irregular boundary conditions

Abstract

In this paper, the surface tessellation problem is explored, in particular, the task of meshing a surface with the added consideration of incorporating constructible building components. When a surface is tessellated into discrete counterparts, certain unexpected conditions usually occur at the boundary of the surface, in particular, when the surface is being trimmed. For example, irregularly shaped panels form at the trimmed edges. To reduce the number of irregular panels that may form during the tessellation process, this paper presents an algorithmic approach to restructuring the surface tessellation by investigating irregular boundary conditions. The objective of this approach is to provide an alternative way for freeform surface manifestation from a well-structured discrete model of the given surface.

Keywords

Freeform surfaces ; Irregular boundary conditions ; Boundary-driven analysis ; Quad-dominant mesh ; Surface tessellation

1. Introduction

There is increasing interest in exploring complex freeform shapes in contemporary architectural and design practice. Frank Gehry (Lindsey, 2001 ) and Zaha Hadid (Jodidio, 2009 ) are prime examples of pioneering avant-garde designers who have incorporated freeform shapes into their designs. The development of manifesting freeform designs relies heavily on a core geometry, which is used from early conceptual form finding to final detailed building assembly. Among the various techniques for freeform shape construction, a NURBS (Non-Uniform Rational Basis Spline) surface is perhaps the most commonly exploited geometrical model (Piegl and Tiller, 1997 ). To manifest a NURBS surface, a discrete model, namely a mesh model, is employed. The meshing process generates an approximation of a given freeform geometry. In design practice, the modeling and subsequent, fabrication of an intriguing, sometimes intricate, freeform shapes requires an extension of the meshing process to include considerations of incorporating constructible building components. This is referred to as the surface tessellation problem, which is the subject matter of this paper. There is a close relationship and analogy between elements of a mesh and the components of a freeform design, for example, faces associate with panels, edges to structural frames, and so on.

1.1. Objective

The features of a given surface boundaries are essential for surface tessellation. For example, boundaries (also called edges) delineate the appearance of a freeform shape, and indicate where surface analysis starts and where it ends. Boundaries also identify whether a surface has been trimmed, that is, parts of the surface have been removed. Trimming can occur in the interior, or exterior of a surface. Figure 1 illustrates an original NURBS surface on the left and a trimmed surface, with both interior and exterior edges, in the middle. When tessellating a trimmed surface into its discrete counterparts, the irregularly shaped panels emerge at these trimming edges, as shown on the right of Figure 1 . This is a commonly seen problem in NURBS-based freeform architectural designs as the simple iso-parameterization is not enough to resolve the potential irregularly shaped panels at these trimmed boundaries.

Figure 1. (Left) original NURBS surface (middle) trimmed NURBS surface (right) sub-surface patches affected by trimming edges.

By exploring the surface boundary conditions for tessellation-based patterns, we present an algorithmic approach for generating boundary-driven meshes. Specifically, the quadrilateral mesh is used to exemplify the approach applied to the formation of the tessellation structure with irregular boundary conditions. Our objective is to present a general algorithmic solution to discretize freeform surfaces with regular pattern-based elements, and to develop strategies for solving constraints from irregular surface boundaries.

1.2. Background

In applying principles from computational geometry to the manifestation of freeform design there is emphasis placed on meshing arbitrary surfaces into discrete building components. Each component is procedurally constructed from a base polygonal pattern, typically, a triangle or quadrilateral (Wang, 2009 ).

There has been a shift from using triangles as the base pattern to approximate freeform shapes towards using quadrilateral patterns, which is gaining considerable interest in both constructive geometry theory as well as in architectural practice and research (Pottmann et al., 2007b ). For reasons of physical construction, it is often preferable to convert a curvilinear surface into planar elements. There are published techniques for such conversions. For example, Pottmann et al. (2008) presents a fine-tuned approach to discretizing the freeform surface with planar quadrilateral elements. However, Pottmann׳s approach of initiating a representative mesh with merely quadrilateral faces may not always be possible, and often requires manual remodeling of the original surface. This reverse-engineering process relies heavily on the preparation of an initial coarse mesh and on how well this initial mesh represents the target shape (Pottmann et al., 2007a ). Such an approach, in one sense, is less intuitive for designers to consider in the design process yet it could be very efficient given that the initial coarse mesh truly represents the ultimate shape.

An alternative approach presented by Cutler and Whiting (2007) looks at a re-meshing technique by iteratively clustering neighboring mesh elements and fitting them onto the closest planes. Their result demonstrates an algorithmic approach to post-restructuring an originally triangulated mesh into planar elements for architectural fabrication. The outcome of this approach is organic and formulated with arbitrary polygonal shapes. The bubble mesh (Shimada and Gossard, 1995 ) presents a physics-based algorithm to automate mesh generation by simulating bubble packing. The strength of this algorithm lies in its ability to control size, anisotropy and orientation of mesh formation. As this approach initiates the bubble packing from the existing boundaries, the generated result will be close to what will be described in this paper given that the entire boundary conditions are taken into the optimization process.

In brief, aforementioned approaches explore how the mesh elements could be structured by optimizing the constraints of interest, such as, pattern, planarity, sizing, etc. However, all these approaches currently do not provide the flexibility of intervention from users/designers to inform, or direct, how surface tessellation could be further improved to facilitate design exploration, in particular, at the early design conceptual phase. Given the seminal role of the surface boundaries during the tessellation process, most of the aforementioned algorithms emphasize on the automation of the mesh element generation and overlook the potential of incorporating boundary conditions for customizable surface tessellation.

The tessellation problem becomes even more challenging as the complexity of boundary conditions grows as does the complexity of design operations. Although the emphasis in this paper is in automating the meshing process (from an underlying NURBS surface), one of the major challenges is to address the need of introducing boundary constraints procedurally to facilitate design exploration. In addition, we also focus on minimizing irregular regions that could emerge from the given boundary conditions. Our contention is that by customizing boundary conditions of a target surface, a design-oriented and well-structured mesh can be generated, and thus provide a coherent tessellation pattern to further freeform design.

2. Surface panelization

Panelization is the process of realizing a freeform surface by a collection of constructible components, specifically, by face-based panels and supporting structures. In architectural applications, this process describes how panels are utilized to construct designated freeform shapes. Here, each panel is procedurally built from a given base polygonal shape that specifies a pattern of the local boundary representation. For example, underlying a four-sided panel are four vertices that define the local boundary, namely, a quadrilateral face.

Contemporary digital approaches to modeling panels are primarily based on isoparameters from the surface domains, U and V . Isoparameterization is a process of mapping two-dimensional parameters, u and v , to a three-dimensional manifold. Figure 2 demonstrates such a mapping illustrating a sub-surface patch formed by the intervals, [u₄ , u₆ ) along U and [v₂ , v₄ ) along V .

Figure 2. Mapping from a two-dimensional UV parametric system onto a three-dimensional surface domain.

These approaches are both simple and efficient; at the same time, they are limiting. For instance, isoparameters cannot control the size of sub-surface generation. Nor can the parameters distinguish boundary conditions well, particularly at trim edges, which might affect both esthetic appearance and final manifestation. Normally, a uniform parametric interval is employed; this usually results in non-uniform sub-surface generation. The size of each panel, in fact, is closely related to the initial control polygons. Control polygons govern control points, which are used to interpolate ultimate surface presentation. If the vertices of the control polygons are uniformly distributed, an equi-dimensional patch is more likely to be generated. However, given the freedom with which control points can be modified in any modeling environment, they rarely remain uniformly distributed once designers start to manipulate the meshing in some arbitrary fashion.

There is no general way of dividing a surface into uniform sub-surfaces. Current tessellation applications rely mainly on uniform isoparametric control. That is, patches are generated according to the isoparametric domains. Figure 3 illustrates two possible segmentation schemes that generate very different sub-surface patches with variations in size. The left side figure illustrates initial surface subdivision by uniform isoparameters, with equal intervals along both the U and V domains. The right side figure illustrates an attempt to equalize the actual size of each sub-surface patch. Using a different tessellation scheme, another different exclusive mesh can be created. Yet, for architectural applications, if one takes into consideration the machining of parts, equi-dimensional surface patches are the more practical.

Figure 3. Two types of surface subdivision (left) uniform iso-parametric intervals (right) optimizing face sizes via equi-dimensional intervals.

To construct equi-dimensional sub-surface regions, one possible solution is to iteratively optimize cell sizes until they reach a specified threshold. However, with the growing complexity of increasingly irregular boundary conditions, the task of converting an arbitrarily trimmed surface into well-structured sub-surface regions is challenging. In practice, designers may, sometimes, unintentionally introduce complex boundary conditions by trimming the freeform surface for various purposes, such as entrance, view, and skylight. Our hypothesis is that by taking the boundary conditions into consideration, irregular-shaped panels at these trim edges can be removed, and a coherent underlying tessellation scheme can be achieved.

In order to solve the problem of tessellating surfaces with irregular boundary conditions, we propose a workflow based on an optimization process with the following three major stages (as shown in Figure 4 ). The workflow depends on the formation of three boundary-driven components: BDTensor , BDCurve , and BDMesh (detailed in 2.1 , 2.2  ;  2.3 ). The workflow is divided into the following three stages:

Figure 4. Proposed workflow for boundary-driven mesh optimization.

Feature selection : the first stage is to identify the featured boundaries from a given surface to be meshed. This step retrieves both the existing and trimmed boundaries from the surface of interest.

Mesh construction : the meshing process initiates from a seed, a starting BDTensor node, within the target surface domain. This can be supplied by user input, or stochastically picked from the initial feature boundaries. Accordingly, a network of BDCurves is generated and sorted by intersections. The last step in the second stage is to fit the mesh faces by iteratively traversing the sorted curve network.

Optimization : after the initial mesh has been constructed, a post-optimization process is executed to optimize with the designated constraints. For example, a mesh-smoothing algorithm is implemented to optimize the dimension of mesh edges through the constructed mesh topology.

By default, all boundary curves of the given surface are considered for the optimization. However, specific customized sources, such as partial curve(s) from the surface boundary or curves of interest on the surface, can also be specified. Further details on how to incorporate single to multiple boundaries in the meshing process are discussed in Section 4 .

2.1. Boundary-driven tensor

A boundary-driven tensor (BDTensor ) is a weighted geometric entity that pertains to information on a location of interest relative to the given surface. The output of a tensor node yields directional projections, which are used to navigate the given surface domain. The Inverse Distance Weighting (IDW) method ( Shepard, 1968 ) is adopted in interpolating the BDTensor by taking a given number of sampled values from the feature boundaries. The equation for BDTensor interpolation is as follows:

$T(x)=\lbrace {\begin{array}{cc}{\frac {{\sum }_{i=1}^{N}{\omega }_{i}(x)T_{i}}{{\sum }_{i=1}^{N}{\omega }_{i}(x)}},&if\quad d(x,x_{i})\not =0\\T_{i},&if\quad d(x,x_{i})=0\end{array}}$

( 1)

${\omega }_{i}(x)={\frac {1}{d{\left(x,x_{i}\right)}^{\rho }}},\quad 1\leq i\leq N$

( 2)

N is the number of source nodes initiated from the boundary conditions, which could be formed from all, or parts, of existing boundary edges. x denotes the target node. Each w_i is a weighting function, in which x_i is a local interpolation node on a feature boundary edge. d represents the distance function from a boundary node x_i to the target node x. ρ is the power parameter to smooth out the influence of the sampled boundary nodes.

Figure 6 illustrates a BDTensor P , which is interpolated using locally influential nodes, pA , pB , pC , and pD on the feature boundaries, respectively E_A , E_B , E_C and E_D . Each node has vector components calculated in two conjugate directions with associated weights. These directional vectors are remapped onto their local reference coordinate system where the Z -axis is normal to the node location on the surface. Once the BDTensor interpolation is complete, boundary-driven curves are constructed through iteratively tracing the path by moving along the interpolated direction from the neighboring nodes. Also illustrated in Figure 5 is the difference between the underlying curve (derived from uniform iso-parameters) and the interpolated curve (computed by local boundary influences). The iso-parametric curves are shown shaded in green using a dashed pattern. Boundary-driven curves in two conjugate directions are shown with arrows colored blue or red.

Figure 5. Conjugate curves derived from boundary-driven computation and underlying isoparametric grid.

2.2. Boundary-driven curve intersection

When boundary-driven curves (BDCurves ) are created, they are grouped by origin, namely, by the directions along which they were derived. As shown in Figure 6 , there are three kinds of curves: the original edge curve (shown shaded in green) and two directional curves in a conjugate relationship (shown shaded in blue and red).

Figure 6. BDCurve generation and curve–curve intersection to construct boundary-driven mesh nodes.

For the constructed BDCurves , curve-to-curve intersections are evaluated. These intersections are used to formalize the unsorted BDCurves through the formation of an interconnected network. In Figure 6 above, ItP_X₃Y₂ is a mesh node created by intersecting BDCrv_X₀₃ with BDCrv_Y₀₂ . Each mesh node in the network is connected to its neighboring nodes in a parametric order on the curves to which they belong. For instance, ItP_X₃Y₂ is connected to mesh nodes, ItP_X₂Y₂ and ItP_X₄Y₂ , in their parametric order on BDCrv_Y₀₂ , and is also connected to mesh nodes, ItP_X₃Y₃ and ItP_X₃Y₁ , along BDCrv_X₀₃ .

The parametric order of each node along the associative curve is determined by its parameter, t , which is often utilized for interpolating points on the governing curve domain. For practical reasons, the parametric domain of a given curve is normalized; thus, the end points of a normalized curve have t =0.0 and t =1.0 respectively. In Figure 7 , the graph node P₁ (t =0.3) has a predecessor node P₀ (t =0.2) and a successor node P₂ (t =0.4) on CURVE_{_01} ; likewise, P₁ also maintains connectedness information to its predecessor and successor nodes, P₃ and P₄ , along Curve_{_02} . These generated nodes in the network are not necessarily the same as the sampled BDTensors created in the first step. Instead, they are remapped nodes on the curve network, which governs the formation of the boundary-driven mesh (BDMesh ). More detail on how these sorted nodes are revisited to build the corresponding mesh edges and faces by the mesh topology solver is given in Section 3.1 .

Figure 7. Sorting intersecting nodes by their parametric order on the associative curve.

2.3. Meshing with the boundary-driven curve network

To optimize a target surface with discrete elements, we start from a representative curve network derived from the feature boundary conditions. A mesh topology solver is then employed to construct the corresponding mesh faces and edges from this interconnected curve network. The algorithm we propose initiates a search by visiting sorted intersecting nodes in the network and consecutively determines the shortest path between its current neighboring nodes to form corresponding faces. In a sense, an intersecting node from the sorted curve network is regarded as a mesh vertex in the mesh topology. By examining the topological connectives between intersecting nodes, mesh faces are constructed and therefore mesh edges.

2.3.1. Mesh topology solver

To create a mesh using the sorted curve network, a topology solver is employed to construct the mesh face from only local neighbor relationships. Figure 8 illustrates the topology solver. V₄ is the origin of the search, and it is connected to V₁ , V₃ , V₇ , and V₅ in counter-clockwise order. (When the mesh nodes are sorted, their topological relations are also structured in a counterclockwise fashion along the normal direction). The shortest path approach is adopted to fit a best-matched mesh face. For instance, to construct faces connected to mesh node V₄ , the process examines potential paths connecting pairs of its neighboring nodes, for example, [V₇ , V₅ ]. The objective is to find the shortest path from V₄ to V₅ via V₇ . To create the mesh face—F₁ , the algorithm searches depth first by looking at the connected neighbors of V₇ and finds three potential paths consisting of neighbors, V₆ , V₁₀ and V₈ . By continuously advancing to their consecutive nodes in the network, a shortest path of [V₄ , V₇ , V₈ , V₅ ] can be found and nodes found at this path are then utilized as the vertices for a new mesh face. This searching process terminates immediately when a valid shortest path is found, for instance path of V₄ –V₇ –V₈ –V₅ , or, when a face element that shares the same nodes in the initial search set already exists. By sweeping through all mesh nodes in the network, the initial mesh is constructed. The pseudo-code for this process is shown in Figure 9 .

Figure 8. Fitting mesh faces by shortest path search.

Figure 9. Pseudo-code for the mesh topology construction.

3. Mesh refinement

For practical purposes, we choose the quadrilateral mesh as the exemplar to demonstrate the process of mesh automation with boundary-driven optimization. Owing to the possible complexity of boundary conditions associated with any arbitrary surfaces, the preliminary boundary-driven mesh will be potentially composed of triangles, quadrilaterals and other polygonal face elements. To ensure a quad-dominant mesh, additional mesh refinement functions are required to remove skewed triangles, and to construct quad-dominant faces from arbitrary polygonal faces. Lastly, a mesh-smoothing operator is introduced to relax the constructed mesh topology. The conditions and procedures for refining the BDMesh elements to a well-structured quad-dominant mesh are discussed below.

3.1. Removing skewed triangles

To control whether a triangular face is skewed for removal is specified by a threshold parameter, which is calculated by the ratio of the smallest and largest interior angles of a triangle face. The threshold parameter may also be set by user input. When the ratio is less than the specified value, the triangle is tagged for removal. For instance, Figure 10 illustrates the removal of a skewed triangle by vertex replacement. The vertex with the largest interior angle of the triangle is removed, and is replaced by its nearest vertex in the triangle. All topological entities associated with this tagged vertex, such as edges and faces, are updated accordingly. For instance, after replacing the vertex (colored in dark gray, tagged as “V t to Remove”) by the existing vertex (shaded in light gray) in the network, edges e₁ , e₅ and face F₁ are removed and a new edge, e_new , is inserted to form the new mesh face F′₁ .

Figure 10. Skewed triangle removal.

3.2. Mesh quadrangulation

When tessellating the given surface with the constructed curve network, polygonal face elements may be produced at points where multiple boundaries meet. These polygonal faces are subdivided to convert the initial mesh into a quad-dominant mesh containing only quadrilateral faces in the network. The subdivision process is carried out by edge mid-point and face center vertex insertions. Figure 11 illustrates new quadrilateral faces being formed by recursively connecting the center of an existing polygonal face to the mid-point of the edges together with the original face vertices. A polygon with N edges will yield N corresponding quadrilateral faces. This mechanism can be applied to any arbitrary polygonal shape.

Figure 11. Quad meshing by face center and edge midpoint insertion. (left) quadrangulate a triangle face (right) quadrangulate a 5-sided polygon face.

3.3. Mesh smoothing

The quality of the resulting quad-mesh can be improved by mesh smoothing, also called mesh relaxation. We consider a Laplacian smoothing algorithm (Hermann, 1976 ) with local vertex perturbation to ensure that the smoothed result conforms to the original input surface. To start, we compute new vertex locations by a finite difference approximation of the Laplace operator, which moves a mesh vertex toward the centroid of the connected vertices. The equation for this is as follows:

$P_{new}={\frac {1}{n}}{\sum }_{i=0}^{n}{\alpha }_{i}p_{i}$

( 3)

where α_i is the weighting factor for each connected mesh vertex.

As the initial BDCurve network is generated from the conjugate relationship, the connected vertices of a BDMesh vertex will likely form a convex polyhedron. (Exceptions occur at vertices on the surface boundaries.) For interior vertices bounded by convex hulls, the new locations derived from centroids of these polygons remain inside the original boundary. This property ensures homogeneous mesh generation and maintains the original anisotropic configuration. However, for peripheral vertices on the original surface boundaries, special treatment is needed. For example, vertices that are moved away (inside or outside) the original boundaries will need to be adjusted so that the mesh stays as close as possible to the original surface. Two cases of mesh vertex replacements are illustrated in Figure 12 . Corner vertices belong to the third scenario where they will not be modified in order to keep the original boundaries intact.

Figure 12. Mesh vertex replacement (left) interior mesh vertex replaced by the centroid of a convex polyhedron (right) boundary mesh vertex moved from the original boundary and then adjusted by vertex perturbation.

After smoothing the mesh vertices, local modulation of mesh vertex location is executed through vertex perturbation. There are two types: vertex-to-edge and vertex-to-face perturbations. Vertex-to-edge perturbation moves the mesh vertex back to the closest boundary (shown in the right side image in Figure 12 ). Likewise, vertex-to-face perturbs the vertex onto the input surface. By so perturbing mesh vertices either to the nearest location on the boundaries or onto the surface, the refined BDMesh can better represent the given surface. It also conforms to the given boundary conditions.

4. Example: meshing a trimmed surface

The algorithm presented above is illustrated on a trimmed surface as the target surface for boundary-driven mesh optimization. The left side image in Figure 13 shows the original untrimmed surface and the right image delineates the relationships between the original surface and the trimming curves. The resulting trimmed surface, as shown in the right side image of Figure 13 , has new boundary edges formed by: (i) original untrimmed edges (shown shaded in green); (ii) exterior trimming edges (shown shaded in red); and (iii) interior trimming edges (shown shaded in blue).

Figure 13. (Left) original untrimmed surface (right) trimmed surface.

By taking these boundary edges into consideration, a BDCurve network is first created, as shown in the left image in Figure 14 . The right image in Figure 14 illustrates the preliminary result of meshing the trimmed surface with the constructed curve network (shown shaded red and blue lines in the left image of Figure 14 ). In Figure 15 , two smoothed mesh results are given. On the left is the smoothed result of the preliminary BDMesh , and on the right is a qaudrangulated result of the smoothed BDMesh .

Figure 14. (Left) conjugate curve network (right) preliminary BDMesh .

Figure 15. Mesh smoothing (left) smoothed BDMesh (right) smoothed quadrangulated BDMesh .

4.1. From single to multiple boundary consideration

Given a tessellation scheme that caters to the inherent boundary conditions, we examine the influences of the complex boundary conditions incrementally. In this experiment, we remodeled the west façade of Zaha Hadid׳s Next-Gene Museum in Taiwan to demonstrate the potential use of the technique in a real architectural application. The constructive procedure is initiated from a partial cone surface and then a series of trimming operations are applied to form the targeted freeform surface. In Figure 16 , there are a total of six curves utilized for the trimming operations; the resulting surface has the new boundary formed by the partial trimming curves and original boundary edges.

Figure 16. Applying trimming operations on a partial cone surface for the experiment.

In Figure 17 , a series of trimming operations coupled with the corresponding BDMesh results are illustrated. The BDMesh results are displayed in counter-clockwise order, starting from the top-left corner to the top-right corner. As shown in steps 4, 5 and 6 in Figure 17 , irregular regions start to emerge where multiple boundaries meet and thus polygon face elements, such as pentagons, are generated at these regions. These polygonal elements are later refined as quad-dominant elements. The optimized boundary-driven mesh for the west façade of the Next-Gene Museum is shown in Figure 18 .

Figure 17. Variations of BDMesh results ranging from single to multiple boundary conditions.

Figure 18. Optimized BDMesh for the western façade of the Next-Gene Museum (Hadid, 2008 ).

5. Discussions and conclusions

Customizing and controlling tessellation schemes for arbitrary surfaces is of interest to the field of computational geometry and to the architecture community. Conventionally, tessellating a surface is often limited to iso-parameterization. In this paper, we have presented an approach to automating mesh generation from a given surface with irregular boundary conditions. Our objective is to provide a distinct approach to surface tessellation and render a well-structured discretized model for further freeform surface application. In addition, the proposed approach is also expected to provide users (designers) with the flexibility to customize surface computation catering to their design intention, in this case, the surface boundary conditions.

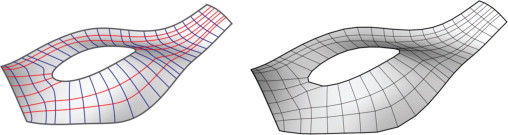
At first glance, the UV-based curve network (the left image of Figure 19 ) is in appearance similar to the boundary-driven curve network (the right image of Figure 19 ). However, they are very different in their formation. The former is interpolated solely from the underlying iso-parameters, the latter is computed from inherent boundary conditions. In a sense, the boundary-driven curve network conforms to the inherent surface boundary conditions more strictly than the UV-based curve network. This property ensures a well-configured framework for the tessellation pattern, particularly, at the boundary edges.

Figure 19. Curve network generations (left) UV-based curve network (right) boundary-driven curve network.

Although our approach looks at the entire boundary condition as the whole to optimize the tessellation result, it is also possible to specify customized sources to explore varied surface tessellation pattern generations. In Figure 20 , we demonstrate an example of utilizing an additional curve on the surface as the input for BDMesh construction. The image on the left side of Figure 20 shows an additional curve (shown shaded in red) on the given surface domain. The right image illustrates the constructed BDCurve network derived from this customized source. In this example, we illustrate the capability of introducing curve inputs as an additional constraint to create the underlying tessellation structure. This capability would afford designers a vehicle to control and experiment how they intend to discretize the freeform surfaces with pattern-based elements, such as quadrilaterals, or triangles, using customized input. In comparison to aforementioned algorithms, this proposed approach is yet another method with which we examine the surface tessellation problem. The major difference from this approach to others is to the adaptability for designers to intervene the optimization process and induce distinctive freeform surface designs.

Figure 20. (Left) customized input source for surface tessellation (right) curve network derived from it.

In summary, the capability of supplying customized sources for tessellation offers flexibility to designers to explore potential pattern generations. This paper highlights an algorithmic approach of how boundary conditions can be examined for tessellation pattern generation. The boundary constraints can be retrieved from the underlying surface boundary edges, and can be additionally customized by user input. To make this approach amendable for real design exploration, user control, from single to multiple boundary sources, is essential and plays an imperative role in the optimization process. This personalized control is treated as the key to distinguish itself from other algorithms.

As discussed in both Wang (2009) and Pottmann et al. (2008) , the base tessellated pattern is seminal for freeform surface applications and plays an important role in the constructive procedures. The development from a base tessellation pattern to real architectural manifestation can be treated as a remeshing process, which subdivides and reconfigures an initial discretized model as finer elements with added physical considerations. We claim that a well-structured model, which coheres to inherent boundary conditions, will guarantee success for surface development. In Section 4 , we demonstrated how this approach could be applied procedurally by gradually increasing the boundary complexity for surface tessellation. In addition, we have explored other surface tessellation examples to ensure robustness of our approach. For example we have employed the Archimedean patterns (Akleman et al., 2005 ) as exemplars to demonstrate the potential of subdivision applications for customizable pattern-based surface tessellation (Wang, 2012 ).

References

1. Akleman et al., 2005 Akleman, E., Srinivasan, V. and Mandal, E., 2005, Remeshing schemes for semi-regular tilings. In: Proceedings of the International Conference on Shape Modeling and Applications, pp. 44–50.
2. Cutler and Whiting, 2007 Cutler, B.B., Whiting, E.E., 2007. Constrained planar remeshing planar for architecture, In: Proceedings of the Graphics Interface Conference, Montreal, Canada, pp. 11–18.
3. Hadid, 2008 Z. Hadid; Schematic Design Report for Next-Gene Architecture Museum, Graduate Institute of Architecture, National Chiao-Tung University, Hsinchu, Taiwan (2008)
4. Hermann, 1976 L.R. Hermann; Laplacian-isoparametric grid generation scheme; J. Eng. Mech., 102 (EM5) (1976), pp. 749–756
5. Jodidio, 2009 P. Jodidio; Zaha Hadid: Complete Works, TASCHEN America Llc, Los Angeles (2009)
6. Lindsey, 2001 B. Lindsey; Digital Gehry, Birkhäuser, Basel (2001)
7. Piegl and Tiller, 1997 L. Piegl, W. Tiller; The NURBS Book; Springer-Verlag, Berlin (1997)
8. Pottmann et al., 2007a H. Pottmann, A. Asperl, M. Hofer, A. Kilian, D. Bentley (Eds.), Architectural Geometry, Bentley Institute Press, Exton, Pennsylvania (2007)
9. Pottmann et al., 2007b H. Pottmann, Y. Liu, J. Wallner, A. Bobenko, W. Wang; Geometry of multi-layer freeform structures for architecture; ACM Trans. Graph., 26 (3) (2007), pp. 1–11
10. Pottmann et al., 2008 H. Pottmann, A. Schiftner, J. Wallner; Geometry of architectural freeform structures; Int. Math. News, 209 (2008), pp. 15–28
11. Shepard, 1968 Shepard, D., 1968. A two-dimensional interpolation function for irregularly-spaced data. In: Proceedings of the 1968 ACM National Conference, pp. 517–524.
12. Shimada and Gossard, 1995 Shimada, K. and Gossard, D.C., 1995. Bubble mesh: automated triangular meshing of non-manifold geometry by sphere packing. In: Proceedings of the ACM Third Symposium on Solid Modeling and Applications, pp. 409–419.
13. Wang, 2009 Wang, T.-H., 2009. Procedural reconstruction of NURBS surfaces. In: Proceedings of the 14th International Conference on Computer Aided Architectural Design Research in Asia, Yunlin, Taiwan, pp. 597–606.
14. Wang, 2012 Wang, T.-H., 2012. Customizing Pattern-Based Panelization for Surface Reconstruction with Irregular Boundary Conditions (Ph.D. thesis). School of Architecture, Carnegie Mellon University, Pittsburgh, Pennsylvania, April 2012.