Dynamic factors for underpasses in high speed train lines

Resumen

Los pasos inferiores son muy numerosos en las líneas de ferrocarril. Su comportamiento dinámico ha recibido mucha menos atención que el de otras estructuras como los puentes, pero su elevado número hace que su estudio sea económicamente relevante con vista a optimizar su forma, manteniendo la seguridad. El proyecto de puentes según el Eurocódigo incluye comprobaciones de estados límite de tensiones bajo carga dinámica. En el caso de pasos inferiores, las comprobaciones pueden resultar tan costosas como aquellas de puentes, pese a que su coste es mucho menor. Por tanto, se impone la búsqueda de unas reglas de cálculo simplificado que pongan en consonancia el coste de la estructura con el esfuerzo necesario para su proyecto. Este artículo propone un conjunto de reglas basadas en un estudio paramétrico.

Abstract

Underpasses are common in modern railway lines. Wildlife corridors and drainage conduits often fall into this category of partially buried structures. Their dynamic behavior has received far less attention than that of other structures such as bridges, but their large number makes their study an interesting challenge from the viewpoint of safety and cost savings. The bridge design rules in accordance with the Eurocode involve checks on stresses according to dynamic loading. In the case of underpasses, those checks may be as much as those for bridges. Therefore, simplified design rules may align the design effort with their cost. Such a set of rules may provide estimations of response parameters based on the key parameters influencing the result. This paper contains a proposal based on a parametric study.

Palabras clave

Alta velocidad ; Paso inferior ; Coeficiente de impacto

Keywords

High speed train ; Underpass ; Dynamic factor

1. Introducción

Desde mediados del siglo xix , coincidiendo con la expansión del ferrocarril, se sabe que la respuesta de puentes excitados por cargas móviles puede ser bastante distinta a la estática [1]  and [2] . Este problema ha sido el objeto de numerosos estudios [3]  and [4] , teniéndose, en la actualidad, fórmulas que permiten el proyecto con un esfuerzo razonable. Por ejemplo, en el campo de la alta velocidad ferroviaria, el proyectista puede recurrir a las fórmulas del European Rail Research Institute[5] .

Con la introducción de la alta velocidad ferroviaria se puso de manifiesto que los puentes de pequeñas luces pueden sufrir aceleraciones importantes [6] . Así se tendió a proyectar estos pasos como pórticos o marcos, con objeto de aprovechar la capacidad de disipación de energía por radiación del terreno, y así reducir la respuesta. De esta manera, en general, tanto los puentes cortos como los pasos inferiores se resuelven con las mismas tipologías estructurales.

Los pasos inferiores son estructuras muy abundantes en las líneas ferroviarias. Los condicionantes del trazado imponen una gran cantidad de conductos de drenaje, pasos de fauna, y cruces con caminos y carreteras, etc., que suelen materializarse mediante marcos y tubos. Aun así, su respuesta dinámica se ha estudiado poco. Una excepción son los llamados soil-steel bridges[7] . Pese a su reducido coste, su abundancia hace que su optimización, asegurando un comportamiento adecuado, tenga un elevado interés económico.

El comportamiento dinámico de tubos y marcos es el resultado de su interacción tanto con la carga actuante como con el terreno que los rodea y sustenta. Un modelo capaz de reproducir adecuadamente estos fenómenos está fuera de lugar teniendo en cuenta el coste de estas estructuras. Más coherente con este último aspecto serían unas reglas simplificadas, que complementen a los Eurocódigos [8]  and [9] .

Este artículo plantea una propuesta en este sentido. Se trata de una serie de fórmulas que permiten la estimación de un coeficiente de impacto que facilita las comprobaciones de tensiones en la estructura.

Los resultados que aquí se presentan se apoyan en un trabajo previo, en el que se presentó un modelo de cálculo adecuado para el problema, aplicando el método de las subestructuras y haciendo uso de modelos de elementos finitos [10] . El ajuste de los modelos se hizo utilizando medidas tomadas in situ en una gran variedad de estructuras de la tipología considerada [11] .

La primera parte de este artículo resume los principales aspectos del modelo de cálculo. A continuación, se plantea un estudio paramétrico cuyos resultados sirven para establecer las relaciones que se presentan en la última parte del artículo. Algunos resultados intermedios ya han sido presentados por los autores [12] .

2. El modelo de cálculo

2.1. El método de las subestructuras

Existen numerosas propuestas para el modelado del problema. Algunos autores prefieren aplicar el llamado método directo, que consiste en construir un modelo completo [13] . La alternativa, recomendada por organismos como la Federal Transit Administration[14] , es aplicar el método de las subestructuras [15] . La gran ventaja de la segunda alternativa es que pueden evitarse los compromisos que sí se hacen en la primera, y adaptar cada componente de manera que se representen adecuadamente las longitudes de onda que allí predominen.

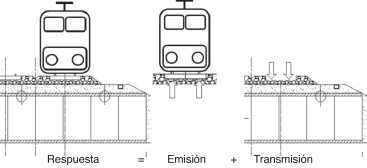
Para este estudio se ha aplicado el método de las subestructuras, considerando un modelo con 2 componentes (fig. 1 ). A continuación se presentan los principales aspectos del mismo [10] .

Figura 1. Método en 2 pasos para estimar la respuesta estructural.

En primer lugar, dado un tipo de tren y una velocidad de circulación, se determinan las historias temporales de fuerzas bajo las traviesas f_k (t ), que se evalúan en N_s puntos discretos situados bajo los ejes de los carriles.

Estos puntos se consideráran fuentes en la segunda etapa del modelo, donde se determinará la respuesta, por ejemplo el desplazamiento d (t ) o la aceleración a (t ), en un punto de interés, utilizando la ecuación ( 1 ). En ella aparecen las funciones de respuesta impulsional h_k (t ) para cada punto fuente. Estas miden la respuesta en el punto de interés debido a una carga impulsional unitaria en el punto fuente con etiqueta k , y se determinan en la segunda etapa de cálculo, con el llamado modelo de transmisión.

$a(t)=\sum _{k=1}^{N_{s}}a_{k}(t)=\sum _{k=1}^{N_{s}}h_{k}(t)\ast f_{k}(t).$

( 1)

El símbolo * en la ecuación (1 ) indica convolución en el dominio del tiempo.

2.2. Modelo de emisión

La primera etapa de cálculo, que consiste en obtener las fuerzas de reacción en los puntos fuente bajo las traviesas, se realiza con un modelo de elementos finitos que representa la mitad de la superestructura de vía (fig. 2 ). En este modelo, cada punto bajo las traviesas es un punto fuente.

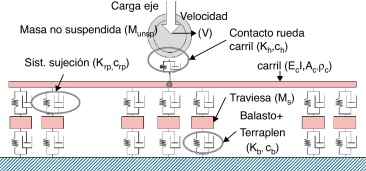
Figura 2. Esquema del modelo de emisión.

El carril se modela con elementos viga y las traviesas con masas puntuales. Resortes y amortiguadores puntuales caracterizan tanto el sistema de sujeción del carril como el conjunto formado por balasto y terraplén. Cabe destacar que si bien la interfaz de las 2 componentes del modelo se sitúa bajo la traviesa, se ha tenido en cuenta la interacción entre ambas partes al incluir la rigidez conjunta del balasto y terraplén en los elementos bajo la traviesa.

2.3. Modelo de transmisión

Una vez obtenidas las fuerzas de reacción, solo queda determinar las funciones de respuesta impulsional h_k (t ) para poder aplicar la ecuación ( 1 ). En la práctica, se determina su transformada, lo que operacionalmente es práctico, ya que en el dominio de la frecuencia la convolución se transforma en un producto:

$h_{k}(t)\ast f_{k}(t)={\int }_{-\infty }^{\infty }H_{k}(\omega )\cdot F_{k}(\omega )\cdot e^{-i\omega t}d\omega$

( 2)

donde H_k (ω ) y F_k (ω ) son, respectivamente, las transformadas de Fourier de h_k (t ) y f_k (t ). Las funciones H_k (ω ) se denominan funciones de respuesta en frecuencia (FRF).

Además, para cada frecuencia considerada, puede aplicarse el teorema de reciprocidad. Así, con un único cálculo se pueden obtener todos los H_k (ω ) de una vez. Esto se consigue aplicando una carga armónica en el punto de interés y calculándose la respuesta en cada punto fuente.

Se consideran 2 puntos fuente por traviesa, uno bajo cada carril. Así, para cada punto de interés para la estimación de la respuesta, el número de FRF es el doble del número de traviesas consideradas (N_s ).

$a(t)=\sum _{k=1}^{N_{s}}{\int }_{-\infty }^{\infty }\left(H_{k1}(\omega )\cdot F_{k1}(\omega )+\right.$$\left.H_{k2}(\omega )\cdot F_{k2}(\omega )\right)\cdot e^{-i\omega t}d\omega$

( 3)

Las FRF entre los puntos de aplicación de la carga (dos bajo cada traviesa) pueden obtenerse empleando distintas alternativas. Una solución es utilizar el método de los elementos finitos (MEF).

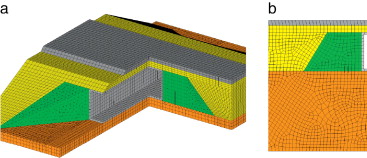
Las hipótesis de modelado pueden variar, pudiendo considerarse una geometría tridimensional o bidimensional (fig. 3 ). El modelo 3D es capaz de describir adecuadamente la dinámica del conjunto. El modelo 2D debe calibrarse para representar tan solo la porción del paso inferior más solicitada, ya que este modelo obviamente no incluye los modos tipo placa que caracterizan la respuesta de la estructura.

Figura 3. Ejemplos de mallas para el cálculo de funciones de transferencia: (a) 3D (b) 2D. Solo se ha modelado la mitad de la geometría.

2.4. Ajuste de los modelos

Como paso previo al ajuste se han llevado a cabo 2 estudios de sensibilidad. En primer lugar, se ha comprobado la enorme importancia del modelo de emisión, y dentro de él del perfil de rugosidad generado, en caso de considerarse dicho factor. El modelo de transmisión tridimensional, al contrario, tiene una influencia mucho menor, para una geometría fija, considerando tan solo variaciones en las propiedades de los materiales dentro de rangos razonables.

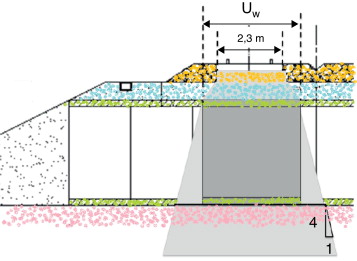
Como ya se indicó, los cálculos pueden simplificarse si en lugar de utilizar un modelo de transmisión 3D se plantea uno 2D que caracterice la parte más solicitada de la estructura, perdiendo la información en el resto de puntos. En la figura 4 se presenta conceptualmente un modelo de este último tipo. Se trata de un modelo construido con elementos de tensión plana y espesor variable. El único parámetro geométrico que se debe ajustar es el ancho equivalente del marco ${\textstyle U_{w}}$ .

Figura 4. Idealización geométrica que sirve de base para construir el modelo 2D. El parámeto de ajuste es el espesor ${\textstyle U_{w}}$ de los elementos planos que representan el marco.

Un modelo 2D puede conducir a resultados similares a los obtenidos con uno 3D. Sin embargo, debe tenerse en cuenta que cualitativamente el modelo 2D tan solo es capaz de representar modos de vibración tipo viga. En particular, el modelo caracteriza bien la respuesta de la estructura hasta la primera resonancia. Por tanto, su rango de validez en frecuencia variará en función de las dimensiones del marco, que son las que determinan su frecuencia fundamental.

Se ha buscado una expresión para determinar el valor de ancho de plataforma del modelo de transmisión 2D. Para ello, se han considerado 6 marcos distintos que cubren un rango de luces entre 2, 3 y 12 m. Se trata de estructuras para las que se dispone de registros de respuesta reales [11] . Para cada uno de ellos se ha construido un modelo de transmisión 3D y otro 2D que se ha ajustado considerando la flecha máxima registrada. Se ha llegado por tanto a un valor de ${\textstyle U_{w}}$ adecuado para cada marco.

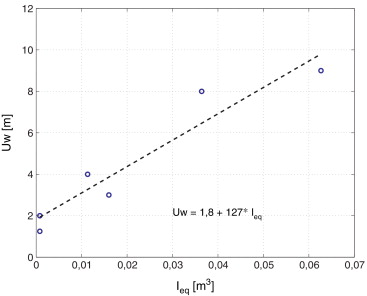
Se ha buscado una dependencia que permita al proyectista estimar el valor del ancho equivalente de plataforma sin necesidad de repetir el proceso. La inercia equivalente de la sección compuesta dintel-montera ha resultado ser el parámetro con mejor correlación para esos efectos. Para cada marco se toma una porción de un metro de ancho de dintel y montera, y esta última se reduce a las propiedades del hormigón del dintel para definir una inercia equivalente I_eq con dimensiones m⁴ /m . La luz del marco va implícita en el valor de I_eq , puesto que el espesor de la losa está directamente relacionado con aquella.

Al representar los valores del ancho en función de esta inercia equivalente para los 6 marcos, se observa una dependencia lineal según la recta ajustada por mínimos cuadrados que se presenta en la figura 5 , y cuya expresión es la siguiente:

Figura 5. Expresión del ancho de plataforma del modelo de transmisión 2D en función de la inercia equivalente de la sección compuesta.

$U_{w}=1,8+127\cdot I_{eq}$

( 4)

La ecuación (4 ) proporciona el valor ${\textstyle U_{w}}$ en metros para valores de la inercia equivalente I_eq en m⁴ /m .

3. Planteamiento del estudio paramétrico para marcos

3.1. La acción

Se han utilizado 13 trenes: 3 trenes reales (Talgo-350, ATPRD y Talgo-250) y 10 trenes de la familia HSLM-A (EN1991-2, anexo E).

Para el estudio del coeficiente de impacto es capital conocer la flecha estática de la estructura. Esta se asimila al valor que se produce cuando el tren circula a 20 km/h. El límite superior de velocidad se fija en 1,2 · 350 = 420 km/h. Entre las 2 velocidades, se considerarán velocidades con incrementos de 20 km/h. Se tienen por tanto 21 valores de velocidad de paso.

3.2. La estructura

Se han considerado las siguientes variaciones de 4 características del modelo:

• Dimensiones interiores del paso (luz × altura). Siete casos: 2 × 2 m, 3 × 3 m, 4 × 3 m, 6 × 4 m, 8 × 5 m, 10 × 5 m, 12 × 5 m.
• Razón canto-vano. Tres casos: 0,06, 0,1 y 0,14 para las 2 dimensiones menores, y 0,06, 0,75 y 0,09 para los mayores. Esta distinción se debe a que el rango fijado previamente para esta característica conduce, en los marcos de gran dimensión, a cantos alejados de los habitualmente empleados en los diseños reales.
• Monteras. Tres casos: 0,5, 1,5 y 2,5 m.
• Terrenos cimentación. Tres casos caracterizados por distintas celeridades de ondas de cortante: c_s  = 150, 250 y 350 m/s.

Con anterioridad se ha llevado a cabo un estudio estadístico de los rangos de variación habituales en las geometrías [11] . Este ha revelado que predominan las estructuras de pequeña luz: más de la mitad de las estructuras tienen menos de 4 m de luz. Sin embargo, el rango de luces llega hasta los 12 m. Además, se ha constatado la validez de la regla de predimensionamiento que consiste en atribuir al canto un valor de un décimo de la luz del vano.

Si se consideran todas las combinaciones de estos parámetros se tienen 7 × 3 × 3 × 3=189 geometrías distintas.

4. Resultados

Se han realizado alrededor de 52.000 simulaciones, que resultan de la combinación de 189 geometrías, 13 trenes y 21 velocidades. En cada caso se ha determinado la historia temporal de flechas en el dintel, y se ha determinado su valor máximo, que se estima tomando la distancia vertical entre el punto situado en el centro del vano y la recta que une los puntos de intersección entre la losa superior y los hastiales. Es decir, suponiendo conocidos los movimientos verticales en todos los puntos de la losa superior Uz (x ), siendo x la distancia respecto al centro del vano, cuya longitud es L_Φ , la flecha f se determina según:

$f=Uz(0)-0,5(Uz(-L_{\Phi }/2)+Uz(L_{\Phi }/2))$

( 5)

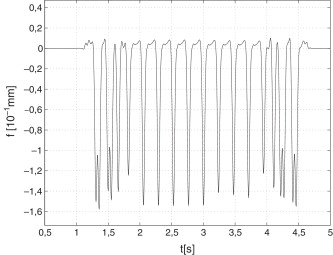
La figura 6 presenta un ejemplo de historia temporal obtenida utilizando la expresión 5 .

Figura 6. Historia temporal de la flecha. Marco 3 × 3 m, tren Talgo-250 a 200 km/h.

4.1. Caracterización de 1 + ϕ ′

Se busca, en primer lugar, caracterizar la relación entre efectos dinámicos y estáticos sin rugosidad. Es decir, el valor 1 + ϕ ′ de la expresión (C.2) de EN 1991-2.

${\frac {{\delta }_{din,real}}{{\delta }_{st,real}}}=(1+$${\phi }^{'}+0,5{\phi }^{''})$

( 6)

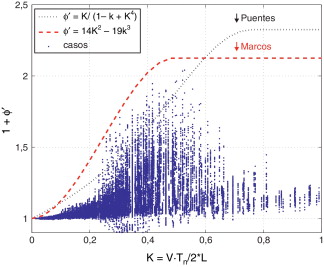
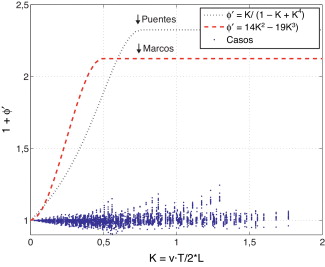
Las simulaciones se han realizado sin considerar la irregularidad del carril. Por tanto, la relación entre la flecha dinámica y la estática es directamente 1 + ϕ ′. En la figura 7 se presentan todos estos valores en función del parámetro K , que representa la velocidad adimensionalizada según la siguiente expresión:

Figura 7. Valores 1 + ϕ ′ en función del parámetro K .

$K={\frac {V\cdot T_{0}}{2L_{\Phi }}}$

( 7)

donde V es la velocidad de circulación del tren, L_Φ el vano de la estructura y T₀ el periodo fundamental de vibración.

Cada punto de la figura 7 corresponde a una de las aproximadamente 52.000 simulaciones. Junto a ellas se presenta la curva envolvente 1 + ϕ ′ obtenida mediante la expresión D.2 de EN 1991-2, de validez en el caso de puentes. Puede apreciarse que algunos valores quedan por encima de esta última curva. Como alternativa se propone la segunda curva, válida para todos los casos, y cuya dependencia con el parámetro K se presenta a continuación:

${\phi }^{'}=14K^{2}-19K^{3}$

( 8)

$K=min\left\{{\frac {V\cdot T_{0}}{2L_{\Phi }}},{\frac {1}{2}}\right\}$

( 9)

La utilización de la ecuación (8 ) para deducir una cota superior de 1 + ϕ ′ requiere conocer el periodo fundamental de vibración para poder adimensionalizar el valor de la velocidad. Su determinación requeriría construir un modelo. Para facilitar la tarea del proyectista se ha buscado una expresión sencilla, realizando un ajuste por mínimos cuadrados sobre los resultados de las 189 geometrías de las que se dispone para el estudio paramétrico.

La expresión para estimar la frecuencia fundamental n₀ obtenida depende de la luz del marco L_Φ , la montera O , y la inercia equivalente I_eq de una porción de 1 m de dintel y montera, homogeneizada a las propiedades del dintel.

$n_{0}=121\cdot L_{\Phi }^{0,8}I_{eq}^{0,1}O^{-0,3}$

( 10)

La expresión anterior proporciona valores en Hz para L_Φ y O en metros y valores de I_eq en (m⁴ /m ).

La montera incluye todo el material por encima del dintel salvo el balasto. Es decir, comprende el terraplén, la capa de forma y el sub-balasto. La inercia equivalente se determina homogeneizando a las propiedades del hormigón la sección compuesta por el dintel y la montera.

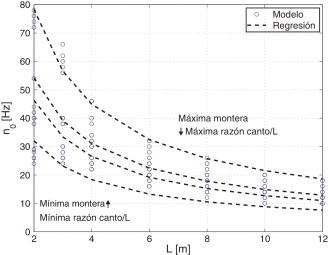
La figura 8 presenta, en función de la luz del vano, 4 curvas de nivel de la superficie de predicción de la frecuencia fundamental, junto con los 189 valores identificados en las geometrías del estudio paramétrico.

Figura 8. Líneas de nivel de la regresión para caracterizar la frecuencia fundamental de los marcos ecuación (10 ).

4.2. Caracterización del coeficiente de impacto global

A partir de los resultados anteriores se ha buscado determinar un coeficiente de impacto global para las 189 estructuras consideradas. El factor de impacto global se define como la razón entre la respuesta dinámica y la estática debida a un tren UIC71 con factor de clasificación 1,21:

$\Phi ={\frac {{\delta }_{din,real}}{{\delta }_{st,UIC71}}}=$${\frac {{\delta }_{st,real}}{{\delta }_{st,UIC71}}}(1+$${\phi }^{'}+{\phi }^{''})$

( 11)

La expresión anterior es aplicable a vías con buen mantenimiento, existiendo una similar para un mal nivel de mantenimiento.

El efecto adicional de la irregularidad se ha añadido a las simulaciones utilizando la expresión C-6 de EN 1991-2:

${\phi }^{''}={\frac {\alpha }{100}}\left[56\cdot e^{-{\left({\frac {L_{\Phi }}{10}}\right)}^{2}}+\right.$$\left.50\left({\frac {L_{\Phi }n_{0}}{80}}-1\right)e^{-{\left({\frac {L_{\Phi }}{20}}\right)}^{2}}\right]$

( 12)

El procedimiento de cálculo ha consistido en determinar ϕ ″ para cada estructura y añadirlo a 1 + ϕ ′ considerado los 2 grados de mantenimiento: bueno y normal. Posteriormente, el resultado se corrige multiplicando por la razón entre la flecha estática del tren considerado y la del tren UIC71 con factor de clasificación 1,21, según la ecuación ( 11 ). El último paso ha sido tomar, para cada estructura y cada velocidad, el mayor de los valores obtenidos para los distintos trenes. Esta sería la cota superior para cada estructura.

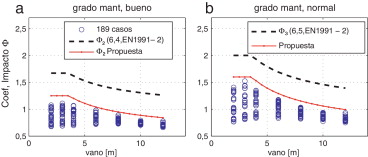
Los valores obtenidos se presentan, en función del vano, en la figura 9 . En ella se distinguen los 2 grados de mantenimiento considerados: bueno (a) y normal (b). Junto a ellos se presentan las curvas obtenidas mediante las expresiones 6,4 (gráfica a) y 6,5 (gráfica b) de EN 1991-2. Aunque estas últimas no son de aplicación en el caso de marcos, serían válidas aunque muy conservadoras.

Figura 9. Comparación de los coeficientes de impacto globales calculados para grado de mantenimiento bueno (a) y normal (b), y las expresiones 6,5 y 6,6 de EN 1991-2 respectivamente. Se incluyen además 2 propuestas.

En la misma figura 9 se presentan unas segundas curvas, resultantes de desplazar verticalmente las anteriores, ajustadas a los resultados. Sus expresiones, función únicamente de la luz del vano (m), son las siguientes:

${\Phi }_{2}={\frac {1,44}{\sqrt {L_{\Phi }-0,2}}}+0,4$

( 13)

${\Phi }_{3}={\frac {1,44}{\sqrt {L_{\Phi }-0,2}}}+0,33$

( 14)

5. Planteamiento del estudio paramétrico para tubos

5.1. Estudio paramétrico

Los tubos de drenaje son estructuras con mucha menor variación en sus dimensiones. El análisis de un tramo de línea de alta velocidad de 91 km de longitud ha permitido constatar que la mayor parte son tubos con un diámetro de Φ = 1,8 m. De hecho, el propietario de las infraestructuras ferroviarias españolas prescribe su uso, salvo situaciones excepcionales en las que puede ser sustituido por uno con Φ = 1,5 m [16] .

Por estas razones, en este estudio se han considerado solo 2 diámetros interiores 1,8 m y 1,5 m. En cada caso se considerará un único espesor del tubo, ya que su variación es, en general, bastante pequeña. Los valores adoptados son 0,18 y 0,155 m respectivamente. Se han tomado los mismos valores de montera, y los mismos tipos de suelo que en el estudio paramétrico de marcos. Se tienen por tanto 18 geometrías distintas resultantes de las combinaciones de 2 tipos de tubo, 3 monteras y 3 tipos de suelo.

Los trenes elegidos y el rango de variación de velocidades son los mismos que los empleados en el caso de los marcos.

5.2. Comprobación de la aplicabilidad de las relaciones anteriores

Se realizan 2 comprobaciones. En primer lugar, se comprueba que el coeficiente 1 + ϕ ′ queda por debajo del valor definido en la ecuación ( 8 ) (fig. 10 ). En segundo lugar, se comprueba que el coeficiente global de impacto también está por debajo de la expresión definida en la ecuación (13 ) (sustituyendo L por el diámetro del tubo) en el caso de mantenimiento bueno, y de la expresión 14 en el caso de mantenimiento normal.

Figura 10. Valores de 1 + ϕ ′ en función del parámetro K obtenidos en el estudio paramétrico.

6. Conclusiones

En este trabajo se ha estudiado la flecha dinámica en estructuras semienterradas de tipo marco bajo la acción de trenes de alta velocidad. En el estudio se han hecho variar los parámetros que más influyen en la respuesta de la estructura, dentro de unos rangos identificados en trabajos anteriores. En base a los resultados del estudio se proponen expresiones para el coeficiente de impacto sin irregularidad 1 + ϕ ′ y para el coeficiente de impacto global Φ.

El procedimiento de obtención de una cota superior para 1 + ϕ ′ comprende los siguientes pasos:

• Determinar la inercia equivalente de una porción de 1 m de ancho de dintel y montera, homogeneizando los materiales al hormigón del dintel.
• Determinar la frecuencia fundamental de la estructura con la ecuación (10 ), y adimensionalizar la velocidad de proyecto.
• Utilizar la ecuación (8 ) para determinar 1 + ϕ ′.

Si bien se ha comprobado que las expresiones Φ propuestas en el Eurocódigo para puentes son válidas, estas resultan excesivamente conservadoras. En su lugar, se han propuesto alternativas que reducen el nivel de conservadurismo: ecuación (13 ) para grado de mantenimiento normal, y 14 para malo.

Un estudio paramétrico sobre tubos Φ = 1, 8 m y Φ = 1, 5 m ha permitido comprobar que los resultados obtenidos para marcos son extensibles a estas estructuras. Sin embargo, el grado de conservadurismo es, para estas estructuras, muy importante.

Agradecimientos

Este trabajo ha sido financiado por el Ministerio de Fomento, Contrato No. A-V-ENC-E-119, y supervisado por los ingenieros Julián Santos y Antonio Corral.

References

1. [1] R. Willis, Appendix to the Report of the Commissioners Appointed to Inquire into the Application of Iron to Railway Structures, H.M. Statinery Office, London, 1849.
2. [2] G.G. Stokes; Discussion of a Differential Equation Related to the Breaking of Railway Bridges; Vol. 8, Transactions of the Cambridge Philosophical Society (1867) Part 5
3. [3] J.M. Biggs; Structural Dynamics; McGraw-Hill (1964)
4. [4] L. Fryba; Vibration of solids and structures under moving loads; Noordhoff (1972)
5. [5] D214 Committee, Ponts rails pour vitesses sur 200 km/h. Rapport Final (Railway bridges for speeds above 200 km/h, Final Report), European Rail Research Institute, 2000.
6. [6] P. Museros, M.L. Romero, A. Poy, E. Alarcón; Advances in the analysis of short span railway bridges for high-speed lines; Comput. Struct., 80 (2002), pp. 2121–2132
7. [7] G. Abdel-Sayed, B. Bakht, L.G. Jaeger; Soil-steel bridges: Design and Construction; McGraw Hill (1994)
8. [8] EN1990. EUROCODE 0. Basis of structural design. Annex A2.
9. [9] EN1991. EUROCODE 1. Actions on Structures. Part 2: Traffic loads on Bridges, 2002.
10. [10] J. Vega, A. Fraile, E. Alarcón, L. Hermanns; Dynamic response of underpasses for high-speed train lines; J. Sound Vib., 331 (2012), pp. 5125–5140
11. [11] J. Vega, L. Hermanns, E. Alarcón, A. Fraile; Measuring dynamic effects on underpasses of high-speed railway lines, Structure and Infrastructure Engineering: Maintenance, Management; Life-Cycle Design and Performance (2012) DOI:10.1080/15732479.2012.692698
12. [12] L. Hermanns, J. Vega, E. Alarcón, A. Fraile, A Parametric Study of the Dynamic Effects of Underpasses of High-Speed Railway Lines, in J. Pombo (Editor). Proceedings of the First International Conference on Railway Technology: Research, Development and Maintenance, Civil-Comp Press, Stirlingshire, UK, Paper 10. (doi:10.4203/ccp.98.10). Las Palmas de Gran Canaria. 18-20 April 2012.
13. [13] A. Romero, P. Galvín, L. Domínguez; Comportamiento dinámico de viaductos cortos considerando la interacción vehículo-vía-estructura-suelo; Rev. int. métodos numér. cálc. diseño ing., 28 (2012), pp. 55–63
14. [14] Federal Transit Administration, Transit noise and vibration impact assessment, May 2006, Report number FTA-VA-90-1003-06.
15. [15] R.R. Craig, C.C. Bampton; Coupling of substructures for dynamic analysis; American Institute of Aeronautics and Astronautics Journal, 6 (7) (1968), pp. 1313–1319
16. [16] Administrador de Infraestructuras Ferroviarias (ADIF). Instrucciones Generales de proyecto. Parte 2. Drenaje. 2008.