Numerical simulation of bulk superconductor during pulsed field magnetization based on multi-field coupled analysis

Abstract

High-temperature bulk superconductors are widely used in various superconducting devices due to their high critical current density, which enables them to trap high magnetic fields. However, the critical current density of bulk superconductors is influenced by magnetic field, temperature and stress, and both increase of stress and temperature can lead to a decrease in the critical current density. And the influence of magnetic field, current, stress are interactional. In this paper, the multi-field coupled analysis is employed to investigate the electromagnetic and mechanical behavior on bulk superconductor during pulsed field magnetization. The simulation results were compared with the present experimental results. The results showed a good agreement between the simulation and experimental results, further validating the reliability of the numerical simulation method. The magnetic field, current, temperature, and stress distribution and variation within the bulk sample during the pulsed magnetization process were calculated and analyzed. Additionally, the influence of the central crack and edge crack in the bulk superconductor was investigated. The results indicate that the region near the crack experiences a variation in current flow direction, resulting in local temperature rise and significant electromagnetic forces. The tip of the crack exhibits stress concentration, leading to a decrease in critical current density. Bulk supercondutor with edge crack case exhibits greater stress concentration compared to those with central crack case. The impact of crack length on maximum stress was analyzed, revealing that as the crack length increases, both the maximum hoop stress and radial stress within the bulk sample rise.

Keywords：Bulk superconductor, multi-field coupled analysis, critical current density, finite element method, crack

1. Introduction

Due to their high critical current density and ability to trapped higher magnetic fields, high-temperature bulk superconductors have found widespread applications in various superconducting devices [1,2,3,4]. There are three magnetization methods for bulk superconductor: field cooling (FC), zero-field cooling (ZFC), and pulse field magnetization (PFM). Although FC and ZFC can achieve higher trapped fields, they suffer from drawbacks such as long loading times, high energy losses, and the requirement of expensive equipment [5,6,7,8,9]. In contrast, the advantages of PFM are simplicity, convenience, and cost-effectiveness. It features extremely short loading times and low energy losses, while imposing minimal requirements on the equipment. However, the limitations of PFM are the rapid loading rate leading to significant temperature rises, flux jumps and making it difficult to achieve high trapped fields [10].

Due to the weak mechanical properties of bulk superconductor and the large Lorentz force in magnetization, the mechanical behavior is important in the practical application. The bulk superconductors are sometimes reinforced externally with metals to improve their mechanical performance and prevent fractures [11,12,13,14]. Ainslie and Fujishiro addressed the modeling issues of magnetizing bulk superconductors and provided a finite element method to assess and predict their magnetization characteristics [19]. In 2018, Wu et al. investigated the stress distribution in high-temperature superconductors under PFM magnetization process and proposed methods to mitigate stress [15]. Subsequently, they studied the mechanical behavior of non-uniform high-temperature superconductors under PFM magnetization, analyzing the potential for fracture and damage due to non-uniform distributions and their impacts on performance and lifespan [16]. Xia et al. studied the characteristics of thermomagnetic instability in MgB₂ bulk samples and provided numerical simulation methods to evaluate and predict their performance [17]. Building upon this research, Zhang et al. investigated the mechanical response of cylindrical superconductors under flux jumps and analyzed the mechanical response characteristics of superconductors under different conditions [18]. Wang et al. have explored the mechanical stress issues of high-temperature superconducting ring bulk samples during the PFM process [20].

During the fabrication process of bulk superconductor, the occurrence of small crack and voids is inevitable, which can have a certain impact on the mechanical properties of the bulk superconductor [30]. Therefore the study of crack in bulk superconductor is a wide field of scientific research and many researchers have done important work in this field [21,22,23,24]. Mochizuki et al. have analyzed the trapped field characteristics and fracture behavior of REBaCuO circular bulk samples during the PFM process [25]. Takahashi et al. have studied the fracture behavior of EuBaCuO superconducting circular bulk samples under different reinforcing material supports during field cooling magnetization [12]. Electromagnetic forces lead to stress concentration and crack formation within the superconductor, and the rate and direction of crack propagation depend on factors such as the magnitude and direction of the electromagnetic forces, material parameters, and geometric shape [31]. Ru et al. conducted numerical simulations to investigate the fracture behavior of bulk superconductor with pre-existing elliptical crack under the influence of electromagnetic forces, delving into the patterns of crack formation and propagation [32].

In this paper, the performance of ring bulk superconductor during the PFM magnetization process is analyzed using finite element method based on H-formulation, heat conduction equation, and the mechanical equilibrium equation. The variation in critical current density of the bulk due to variations in magnetic field intensity, temperature, and stress are considered, and the impact of these factors on the results is examined. The analysis results are in good agreement with experimental results. Furthermore, the influence of crack at different locations on the results is analyzed, providing different simulation results for trapped fields and temperatures within the bulk affected by stress and various crack configurations.

2. Numerical model and parameters

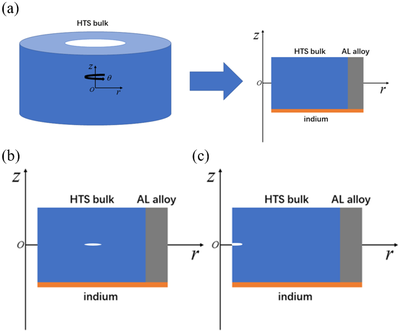
The numerical model in this paper is based on the experimental sample presented by Mochizuki [25], and the 2D axisymmetric model of the GdBCO ring bulk is adopted for simplification. Figure 1(a) depicts a three-dimensional schematic diagram and a 2D axisymmetric cross-section schematic (not to scale) of the ring GdBCO high-temperature bulk superconductor. The ring is installed in the holder with an aluminum alloy ring (5 mm in width). The lower part of the bulk is a layer of indium sheet (1 mm in thickness), which is connected to the cold head with an initial temperature of 65 K. A uniform critical current is assumed throughout the ring in this study, and the epoxy layer between the aluminum alloy ring and the superconducting ring is disregarded, assuming an ideal connection between them. In the experiment, a pulsed field of ${\textstyle B_{ex}=2.53{\mbox{ }}T}$ was applied to the bulk, with a rise time of 13 ms and a duration of 200 ms. Hall sensors were positioned at the center of the bulk to measure the trapped field, while a Hall probe was placed 1 mm above the surface of the bulk to generate the distribution of the trapped field ${\textstyle B_{z}}$ [25]. High-temperature copper oxide superconductors are relatively brittle, microcrack and defects can be generated in superconductors [36]. Cracking may occur in superconductors due to large electromagnetic body force [37]. Furthermore, the crack and defects lead to strong local enhancement of the stress which may limit the application of the superconductor. In order to investigate the impact of crack on the superconducting and mechanical properties of the bulk superconductor, elliptical crack were introduced into the model, while both central crack case and edge crack case are considered, as shown in Figures 1(b) and (c).

Figure 1. (a) Sketches of the ring GdBCO bulk (left) and two-dimensional axisymmetric model (right). (b)-(c) Two-dimensional axisymmetric modeling of bulk superconductor containing central elliptical crack case and edge semi-elliptical crack case

In this study, the magnetic field and current density were calculated using the H-formulation[38]. The governing equations are given by [26]

$\nabla \times {\boldsymbol {E}}+{\frac {{\mbox{d}}{\boldsymbol {B}}}{{\mbox{d}}t}}=$$\nabla \times \left(\rho \nabla \times {\boldsymbol {H}}\right)+$${\frac {{\mbox{d}}\left({\mu }_{0}{\mu }_{r}{\boldsymbol {H}}\right)}{{\mbox{d}}t}}=$$0$

(1)

where ${\boldsymbol {E}}$, ${\textstyle {\boldsymbol {B}}}$ and ${\textstyle {\boldsymbol {H}}}$ are electric field, magnetic flux density, and magnetic field intensity, respectively.

The Maxwell's equations, which are required for electromagnetic field calculations, are as follows

${\begin{array}{c}\nabla \times {\boldsymbol {E}}=-{\frac {\partial {\boldsymbol {B}}}{\partial t}}\\\nabla \times {\boldsymbol {H}}={\boldsymbol {J}}\\\nabla \cdot {\boldsymbol {B}}=0\end{array}}$

(2)

where ${\boldsymbol {J}}$ is the critical current density, and $t$ is the time. The electromagnetic constitutive equations for superconductors are as follows

${\begin{cases}{\boldsymbol {E}}=\rho {\boldsymbol {J}}\\{\boldsymbol {B}}={\mu }_{0}{\mu }_{r}{\boldsymbol {H}}\end{cases}}$

(3)

where $\rho$ is the equivalent resistivity; the variables ${\mu }_{0}$ and ${\textstyle {\mu }_{r}}$ are the Vacuum permeability, and the relative permeability, in this study, a value of ${\mu }_{r}=1$. Furthermore, Eq. (1) is derived by combining Eqs. (2) and (3). To prevent the electric field from becoming excessively large when the current exceeds the critical density in the ${\textstyle {\boldsymbol {E-J}}}$ model, the modified ${\textstyle {\boldsymbol {E-J}}}$ model is employed, with an effective resistivity denoted as [35]

$f(n)={\begin{cases}{\frac {{\rho }_{sc}\cdot {\rho }_{normal}}{{\rho }_{sc}+{\rho }_{normal}}},&{\mbox{    }}T\leq T_{c}\\{\rho }_{nomal},&{\mbox{              }}T>T_{c}\end{cases}}$

(4)

where ${\rho }_{normal}$ is the resistivity of the bulk superconductor in the normal state. Among them

${\rho }_{sc}=E_{c}{\left({\frac {J}{J_{c}}}\right)}^{\left(n-1\right)}J_{c}$

(5)

The critical current density could be influenced by the magnetic field intensity, temperature, and stress. In this article, the modified Kim model is employed, as follows

$J_{c}={\beta }_{0}{\left[1-{\left({\frac {T}{T_{c}}}\right)}^{2}\right]}^{1.5}{\frac {B_{0}}{\vert B\vert +B_{0}}}J\left(\sigma \right)$

(6)

where ${\beta }_{0}=1.32\times {10}^{9}{\mbox{A}}/{\mbox{m}}^{2}$ [27], is the critical current density at $B=0,\,T=0$ is determined; $T_{c}$ is the critical temperature; $B_{0}$ is the fitted parameter. $J\left(\sigma \right)$ denotes the effect of stress on the critical current density [34]. The heat transfer control equation is [28]

${\rho }_{m}C{\frac {\partial T}{\partial t}}=\nabla \cdot \left(\kappa \nabla T\right)+Q$

(7)

$Q={\boldsymbol {E}}\cdot {\boldsymbol {J}}$

(8)

where $\rho$ is the densities; $c$ is the constant pressure heat capacity; $k$ is the thermal conductivity and $Q$ is the joule heat. The thermal conductivity has different values in the ab plane (${\textstyle {\kappa }_{ab}}$) and c plane (${\textstyle {\kappa }_{c}}$). Due to the temperature-dependent specific heat and thermal conductivity of the bulk superconductor, fitting equations obtained from the literature were utilized in our program [6]. The bulk superconductor was affixed to an indium foil, and a cold head was positioned at the bottom of the indium foil, with the temperature designated as ${\textstyle T_{0}}$. Therefore, the heat transfer boundary condition is defined as the fixed temperature of ${\textstyle T_{0}}$ at the lower edge, while the remaining boundaries are subjected to thermal insulation conditions.

In the experiment, the external magnetic field on the bulk sample was applied using external coils. In the simulation, the external magnetic field was imposed at the boundary of the air domain. The applied pulse magnetic field was [29]

$B_{ex}\left(t\right)=B_{\max }t/{t_{1}}\exp \left(1-t/{t_{1}}\right)$

(9)

where $B_{max}$ is the peak value of the applied magnetic field and $t_{1}$ is the rise time of the applied magnetic field.

In the mechanical calculations, the ring bulk sample is considered as an isotropic linear elastic material. The mechanical equilibrium equation can be expressed as follows

$\nabla \cdot {\boldsymbol {\sigma }}+{\boldsymbol {F}}_{L}=0$

(10)

${\boldsymbol {F}}_{L}={\boldsymbol {J}}\times {\boldsymbol {B}}$

(11)

where ${\boldsymbol {F}}_{L}$ is the Lorentz force; ${\overline {\rho }}$ is the mass density. In the study, it is assumed that the transient behavior of the structure is quasi-static and that the second-order time derivative of the displacement variable ${\textstyle u}$. The inertia terms ${\textstyle \rho {\frac {{\mbox{d}}^{2}u}{{\mbox{d}}t^{2}}}}$ are zero. Due to the occurrence of the Lorentz force during the magnetization process of the high-temperature superconducting ring bulk sample in a pulsed field, the influence of the stress distribution caused by the Lorentz force is considered in the mechanical calculations of this study. It is assumed that the bulk superconductor is fixed on a base, thus imposing a mechanical boundary condition of zero displacement at the lower edge. The stress-strain relationship in the ring bulk sample is given by

$\left[{\begin{array}{c}{\epsilon }_{r}\\{\epsilon }_{\varphi }\\{\epsilon }_{z}\\{\gamma }_{zr}\end{array}}\right]=\left[{\begin{array}{cccc}{\frac {1}{E}}&-{\frac {\upsilon }{E}}&-{\frac {\upsilon }{E}}&0\\-{\frac {\upsilon }{E}}&{\frac {1}{E}}&-{\frac {\upsilon }{E}}&0\\-{\frac {\upsilon }{E}}&-{\frac {\upsilon }{E}}&{\frac {1}{E}}&0\\0&0&0&{\frac {1}{G}}\end{array}}\right]\left[{\begin{array}{c}{\sigma }_{r}\\{\sigma }_{\varphi }\\{\sigma }_{z}\\{\tau }_{zr}\end{array}}\right]$

(12)

where ${\textstyle \upsilon }$ is the Poisson's ratio and ${\textstyle E}$ is the Young's modulus.

The simulation and modeling of the aforementioned aspects were conducted using the finite element method. The parameter values mentioned earlier but not provided were provided in Table 1.

Table 1. Parameters in the simulation

Parameter	Description	Value
${\textstyle c}$	Specific heat of the ring bulk	[6]
${\textstyle c_{in}}$	Thermal conductivity of the indium	[15]
${\textstyle c_{al}}$	Specific heat of the reinforced ring	[33]
${\textstyle k_{ab}}$	Thermal conductivity of the bulk along the ab plane	[6]
${\textstyle k_{c}}$	Thermal conductivity of the bulk along the c plane	[6]
${\textstyle k_{in}}$	Thermal conductivity of the indium	[15]
${\textstyle k_{al}}$	Thermal conductivity of the reinforced ring	[33]
${\textstyle \rho }$	Density of the ring bulk	${\textstyle 5900\,}$ kg/m${\textstyle ^{3}}$
${\textstyle E}$	Young modulus of the ring bulk	${\textstyle {\mbox{103 }}}$ GPa
${\textstyle \upsilon }$	Poisson ratio of the ring bulk	${\textstyle 0.3}$
${\textstyle \alpha }$	Thermal expansivity of the ring bulk	${\textstyle 1\times {10}^{-5}{\mbox{ K}}^{-1}}$
${\textstyle E_{al}}$	Young modulus of the reinforced ring	${\textstyle 78}$  GPa
${\textstyle {\upsilon }_{al}}$	Poisson ratio of the reinforced ring	${\textstyle 0.34}$
${\textstyle {\alpha }_{al}}$	Thermal expansivity of the reinforced ring	${\textstyle 1.48\times {10}^{-5}{\mbox{ K}}^{-1}}$
${\textstyle B_{0}}$	Fitting parameters	${\textstyle 1.3{\mbox{ T}}}$

3. Results and discussions

3. 1 Verification of results

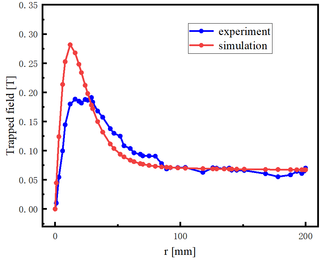
To ensure the accuracy of the simulation results, a comparative validation was conducted with experimental data [25]. The validation involved a ring bulk superconductor with an inner diameter of 36 mm and an outer diameter of 30 mm, which was reinforced with a 5 mm thick aluminum alloy and affixed to a 1 mm thick indium foil. The ambient temperature during the experiment was maintained at 65 K. Figure 2 shows the trapped field at the center of the ring superconductor obtained from both the numerical simulation and the experimental measurements. By comparing the numerical simulation results with the experimental data, it was found that the numerical results closely approximated the experimental results, providing evidence of the accuracy of the numerical simulation.

Figure 2. Comparison of numerical simulation and experimentally obtained trapped fields, where ${\textstyle B_{ex}=2.53{\mbox{ T}}}$ and ${\textstyle t_{1}=13\,{\mbox{ ms}}}$

3. 2 Calculated results for ring bulk superconductor

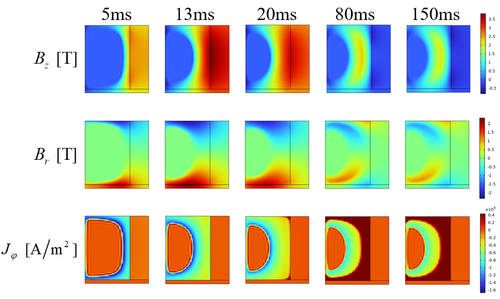
To analyze the electromagnetic characteristics of the ring bulk superconductor during the PFM process, Figure 1 shows the magnetic field, and current density distributions of the bulk superconductor at different times (5 ms, 13 ms, 20 ms, 80 ms and 150 ms). As shown in the figure, the magnetic field at the ascending stage (0-13 ms), penetrates from the upper and lower ends of the bulk superconductor towards the interior. Simultaneously, a circular current is generated within the bulk, gradually flowing from the external region into the interior. Conversely, reverse currents begin to appear simultaneously from the upper and lower ends of the bulk sample at the descending stage (after 13ms).

Figure 3. Magnetic field and current density distribution in the bulk under the PFM process

Figures 4(a) and (b) depict the distribution of the trapped field and temperature at different times during the magnetization process on the ${\textstyle z=0}$ plane. The observed variation in the trapped field aligns with the findings in [15] for cylindrical bulk samples. However, the temperature variation differs from that of cylindrical bulk samples. In the simulation results, it could be found that the temperature gradually increases inward from the right side along the radius and then decreases gradually. This phenomenon arises due to the reinforcement of the bulk sample with an aluminum alloy ring, which affects the thermal conduction between the bulk sample and the aluminum alloy, thereby influencing the temperature distribution.

Figure 4. Trapped field and temperature distribution in the ${\textstyle z=0}$ plane of the bulk at different times under the PFM process

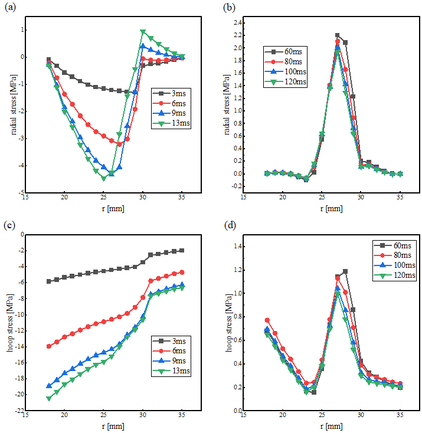
For study the mechanical response in the PFM process, Figures 5(a) and (b) present the distribution of radial stress on the ${\textstyle z=0}$ plane, corresponding to the ascending stage and descending stage of the external magnetic field, respectively. In ascending stage, compressive stress is generated within the sample when the magnetic field gradually penetrates into the bulk sample. Subsequently, during the descending stage of the external magnetic field, the radial stress undergoes a transition from compression to tension due to the variation in the direction of the current. Figures 5(c) and (d) show the distribution of hoop stress ${\textstyle {\sigma }_{\varphi }}$ on the ${\textstyle z=0}$ plane of the bulk sample during the magnetization process, corresponding to the ascending stage and descending stage, respectively. It can be observed that during the ascending stage, compressive stress exists at the inner edge of the ring bulk superconductor. As the external magnetic field decreases, the hoop stress at the inner edge gradually transitions to tensile stress. The hoop stress experienced by the inner edge of the ring bulk sample is higher than that of the outer edge. Therefore, it can be inferred that the inner edge of the ring bulk superconductor is more prone to crack formation than the outer edge. In the next section, we will introduce pre-existing crack and analyze their electromagnetic and mechanical characteristics separately, while both of central crack case and edge crack case are considered.

Figure 5. Distribution of radial and hoop stresses at different moments in the ${\textstyle z=0}$plane of a bulk under the action of a pulsed magnetic field

3. 3 Calculated results for ring bulk superconductor with crack

In this section, the simulation results are analyzed for the models of blocks containing elliptical center crack and blocks containing semi-elliptical edge crack, respectively The semi-major axis and semi-minor axis of the elliptical are ${\textstyle a=1{\mbox{ mm}}}$, ${\textstyle b={\mbox{0}}{\mbox{.1 mm}}}$, respectively.

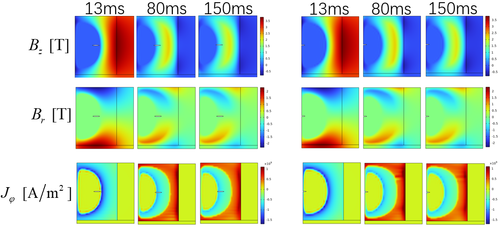
Figure 6 depict the distributions of magnetic field and current density at 13 ms, 80 ms, and 150 ms for the ring bulk sample with a central elliptical crack and the ring bulk sample with a semi-elliptical edge crack case. It can be observed that the presence of both the central crack case and edge crack case has a minor impact on the distribution of the magnetic field. However, the presence of crack changes the geometric structure of the bulk sample, leading to variations in the current distribution. Additionally, the direction of the current density also variations in the vicinity of the crack.

Figure 6. Distributions of magnetic field and current density in central crack case (left) and edge crack case (right)

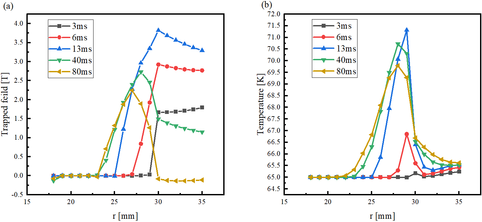
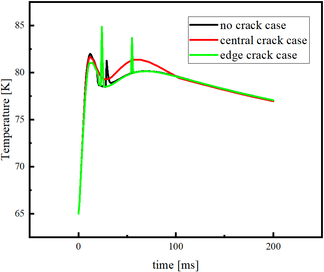
The temperature of the bulk sample gradually increases as the external magnetic field rises. However, the presence of crack also introduces certain variations to the temperature rise trend. As shown in Figure 7, when there are without crack in the bulk sample, the temperature undergoes a sudden jump during the descending stage. The central crack case has a more gradual temperature variation than edge crack case. However, in edge crack case, the temperature experiences two jumps during the descending stage, with a larger amplitude and higher jump temperature. This phenomenon indicates that the presence of edge crack case, will change the direction of the current around the crack. The current concentrated on the region near the crack, resulting in larger electric fields. Due to the strong nonlinearity ${\textstyle {\boldsymbol {E-J}}}$ relationship of the bulk superconductor, the Joule heat will rise and leads to significant local temperature increase.

Figure 7. Maximum temperature of the bulk as a function of time in the presence of a pulsed magnetic field

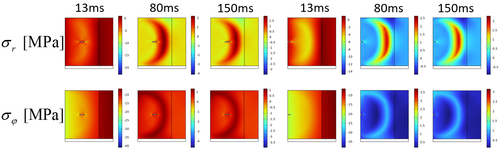
Figure 8 show the distributions of circumferential and radial stress at 13 ms, 80 ms, and 150 ms for the ring bulk sample with a central elliptical crack and the ring bulk sample with semi-elliptical edge crack case. It can be observed that stress concentration occurs at the crack tips, resulting from the alteration of the bulk sample's geometric shape due to the presence of crack. The crack lead to the stress concentration effect. And this stress concentration phenomenon also leads to the non-uniformity of the critical current density, thereby affecting the distribution of temperature.

Figure 8. Stress distributions clouds for bulk containing central crack case (left) and edge crack case (right)

Figures 9(a) and (b) depict the distribution of radial and hoop stress on the ${\textstyle z=0}$ plane at 13 ms and 50 ms, respectively, for the bulk sample without crack, with a central crack case, and with edge crack case. As shown in Figure 9, both radial and hoop stress experience a significant increase at the crack tips, indicating stress concentration. However, the stress values at the crack tips exhibit a more pronounced increase due to the presence of crack. At 13 ms, the stress concentration caused by edge crack case is more obvious than central crack case. The maximum radial stress on the ${\textstyle z=0}$ plane for the bulk sample without crack is ${\textstyle -20.7\,{\mbox{MPa}}}$, while for the bulk sample with a central crack case, it is ${\textstyle -36.1\,{\mbox{MPa}}}$, representing a 74% increase compared to the crack-free bulk sample. The bulk sample with edge crack case exhibits a maximum hoop stress on the ${\textstyle z=0}$ plane of ${\textstyle 37.1{\mbox{MPa}}}$, representing a 79% increase compared to the crack-free bulk sample. At 50 ms, the stress concentration caused by central crack case becomes more pronounced than that caused by edge crack case. However, overall, edge crack case can lead to larger stress concentrations than central crack case.

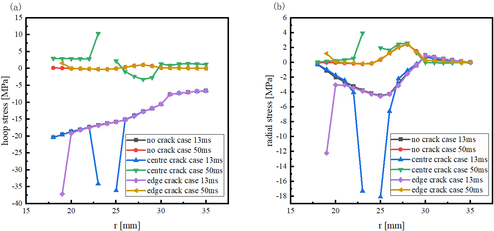
Figure 9. Distribution of radial and hoop stresses without crack and with central case and edge crack case at different times in ${\textstyle z=0}$ plane

The size of the crack length also has a certain influence on the maximum stresses. In Figure 10, we analyze the variation in the maximum radial and hoop stresses among bulk samples with different edge crack lengths case. It can be observed from the figure that both radial and hoop stresses increase with the increase in crack length, with the hoop stress exhibiting a more pronounced trend. This phenomenon occurs because as the crack length increases, the stress concentration effect becomes more prominent. When the crack is shorter, the sharpness at the crack tip is lower. However, as the crack length grows, the sharpness at the crack tip increases, and the region of high stress expands accordingly, leading to higher stresses in the sample.

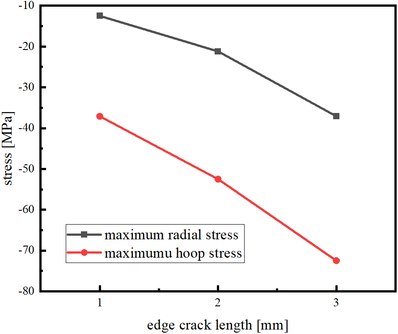
Figure 10. Maximum radial and hoop stresses during magnetization of bulk containing edge crack case of different lengths

4 Conclusions

In this study, the distribution of electromagnetic fields, temperature, and stress in ring bulk superconductor was simulated and analyzed by employing the H-formulation, heat conduction equation, and mechanical equilibrium equation. The coupled equations of force-electric-magnetic-thermal multi-field were solved to obtain the simulation results, which exhibited a good agreement with the experimental findings.

The research findings indicate that when a pulsed external magnetic field is applied, the magnetic field gradually penetrates into the bulk sample from the upper and lower ends on the right side. Induced currents are generated within the bulk sample, and the direction of these currents variations as the external magnetic field decreases. During the ascending stage of the external magnetic field, compressive stress is generated within the bulk sample. Conversely, as the external magnetic field decreases and the direction of the current variations, tensile stress is produced, leading to an influence on the critical current density of the bulk sample.

Subsequently, simulations were performed on bulk samples with central crack case and edge crack case, respectively, and the distributions of electromagnetic fields, temperature, and stress under PFM were analyzed. The results indicate the occurrence of localized stress concentration due to the presence of crack. Moreover, the crack induce variations in the direction of current and result in localized temperature elevation near the crack vicinity. The maximum radial and hoop stresses within the bulk sample also increase with the length of the crack.

Acknowledgements

The authors gratefully acknowledged the support from the Fujian Natural Science Foundation (2020J05180) and the Scientific Research Foundation of Fujian University of Technology (GY-Z19046). No part of this work has been published or submitted elsewhere. The authors declared that they have no conflicts of interest in this work.

References

[1] Murakami M. Processing and applications of bulk RE-Ba-Cu-O superconductors. Int J. Appl. Ceramic. Tech. , 2007, 4: 225–241

[2] Hull J R, Murakami M. Applications of bulk high-temperature superconductors. Proc. IEEE. , 2004, 92: 1705–1718

[3] Zou J, Ainslie M D, Fujishiro H, et al. Numerical modelling and comparison of MgB2 bulks fabricated by HIP and infiltration growth. Supercond. Sci. Technol. , 2015, 28: 075009

[4] Yokoyama K, Oka T, Okada H, et al. Solid-liquid magnetic separation using bulk superconducting magnets. IEEE Trans. Appl. Supercond. , 2003, 13: 1592–1595

[5] Ainslie M D, Fujishiro H, Ujiie T, et al. Modelling and comparison of trapped fields in (RE)BCO bulk superconductors for activation using pulsed field magnetization. Supercond. Sci. Technol. , 2014, 27: 065008

[6] Ainslie M D, Fujishiro H. Modelling of bulk superconductor magnetization. Supercond. Sci. Technol. , 2015, 28: 053002

[7] Ainslie M D, Fujishiro H, Mochizuki H, et al. Enhanced trapped field performance of bulk high-temperature superconductors using split coil, pulsed field magnetization with an iron yoke. Supercond. Sci. Technol. , 2016, 29: 074003

[8] Zhou D, Shi Y, Dennis A R, et al. Flux jumps in ring-shaped and assembled bulk superconductors during pulsed field magnetization. Supercond. Sci. Technol. , 2020, 33: 034001

[9] Zhou D, Ainslie M D, Srpčič J, et al. Exploiting flux jumps for pulsed field magnetisation. Supercond. Sci. Technol. , 2018, 31: 105005

[10] Hiroyuki Fujishiro, Tatsuya Tateiwa, et al. Higher trapped field over 5T on HTSC bulk by modified pulse field magnetizing. Physica C: Superconductivity and its Applications, 2006, 445–448: 334-338

[11] K. Takahashi, H. Fujishiro, et al. Fracture behavior analysis of EuBaCuO superconducting ring bulk reinforced by a stainless steel ring during field-cooled magnetization. Supercond. Sci. Technol. , vol. 30, no. 11, 2017, Art. no. 115006

[12] K. Takahashi, S. Namba, et al. Thermal and magnetic strain measurements on a REBaCuO ring bulk reinforced by a metal ring during field-cooled magnetization. Supercond. Sci. Technol. , vol. 32, no. 1, 2019, Art. no. 015007

[13] Ainslie M D, Huang K Y, Fujishiro H, et al. Numerical modelling of mechanical stresses in bulk superconductor magnets with and without mechanical reinforcement[J]. Superconductor Science and Technology, 2019, 32(3): 034002

[14] Li R, Fang J, Liao X, et al. Electromagnetic and Thermal Properties of HTS Bulk Combined with Different Ferromagnetic Structures under Pulsed Field Magnetization[J]. IEEE Transactions on Applied Superconductivity, 2023

[15] Haowei Wu, Huadong Yong et al. Stress analysis in high-temperature superconductors under pulsed field magnetization. Superconductor Science and Technology, 2018, 31: 045008

[16] Haowei Wu, Huadong Yong et al. Analysis of mechanical behavior in inhomogeneous high temperature superconductors under pulsed field magnetization. Superconductor Science and Technology, 2020, 33: 124002

[17] Xia J, Li M, Zhou Y. Numerical investigations on the characteristics of thermomagnetic instability in MgB2 bulks[J]. Superconductor Science and Technology, 2017, 30(7): 075004

[18] Zhang W, Xia J, Yong H, et al. Mechanical response induced by flux jump in a cylindrical superconductor[J]. AIP Advances, 2020, 10(2): 025021

[19] Ainslie M D, Fujishiro H. Modelling of bulk superconductor magnetization[J]. Superconductor Science and Technology, 2015, 28(5): 053002

[20] Wang L, Wu H W, Yong H D. Mechanical stress in high-temperature superconducting ring-shaped bulk during the pulsed-field magnetization[J]. Science China Technological Sciences, 2023: 1-12

[21] Chen H, Yong H, Zhou Y. XFEM analysis of the fracture behavior of bulk superconductor in high magnetic field[J]. Journal of Applied Physics, 2019, 125(10)

[22] Chen H, Yong H, Zhou Y. Crack detection in bulk superconductor using Genetic Algorithm[J]. Engineering Fracture Mechanics, 2022, 265: 108372

[23] Shen H, Ru Y, Wu H, et al. Three-dimensional peridynamic modeling of crack initiation and propagation in bulk superconductor during field cooling magnetization[J]. Superconductor Science and Technology, 2021, 34(8): 085020

[24] Ru Y, Yong H, Zhou Y. Numerical simulation of dynamic fracture behavior in bulk superconductors with an electromagnetic-thermal model[J]. Superconductor Science and Technology, 2019, 32(7): 074001

[25] Mochizuki H, Fujishiro H, Naito T, et al. Trapped field characteristics and fracture behavior of REBaCuO bulk ring during pulsed field magnetization[J]. IEEE Transactions on Applied Superconductivity, 2015, 26(4): 1-5

[26] Ainslie M D, Srpcic J, Zhou D, et al. Toward optimization of multipulse, pulsed field magnetization of bulk high-temperature superconductors. IEEE Trans. Appl. Supercond. , 2018, 28: 1–7

[27] Fujishiro H, Naito T. Simulation of temperature and magnetic field distribution in bulk superconductor during pulsed field magnetization. Supercond. Sci. Technol. , 2010, 23: 105021

[28] Ainslie M D, Zhou D, Fujishiro H, et al. Flux jump-assisted pulsed field magnetisation of high-Jc bulk high-temperature superconductors. Supercond. Sci. Technol. , 2016, 29: 124004

[29] Fujishiro H, Naito T, Furuta D. Analysis of temperature and magnetic field distribution in bulk superconductor during pulsed field magnetization. IEEE Trans. Appl. Supercond. , 2011, 21: 2723–2726

[30] Diko P. Cracking in melt-processed RE-Ba-Cu-O superconductors[J]. Superconductor Science and Technology, 1998, 11(1): 68

[31] Zhou Y H, Yong H D. Crack problem for a long rectangular slab of superconductor under an electromagnetic force[J]. Physical Review B, 2007, 76(9): 094523

[32] Ru Y, Yong H, Zhou Y. Fracture analysis of bulk superconductors under electromagnetic force[J]. Engineering Fracture Mechanics, 2018, 199: 257-273

[33] Callister W, David R. Material Science and Engineering—An Introduction. Danvers: WILEY, 2007

[34] van der Laan D C, Ekin J W. Large intrinsic effect of axial strain on the critical current of high-temperature superconductors for electric power applications[J]. Applied physics letters, 2007, 90(5)

[35] Duron J, Grilli F, Dutoit B, et al. Modelling the E–J relation of high-Tc superconductors in an arbitrary current range[J]. Physica C: Superconductivity, 2004, 401(1-4): 231-235

[36] Diko P, Krabbes G. Macro-cracking in melt-grown YBaCuO superconductor induced by surface oxygenation[J]. Superconductor Science and Technology, 2002, 16(1): 90.

[37] Ren Y, Weinstein R, Liu J, et al. Damage caused by magnetic pressure at high trapped field in quasi-permanent magnets composed of melt-textured Y-Ba-Cu-O superconductor[J]. Physica C: Superconductivity, 1995, 251(1-2): 15-26.

[38] Hong Z, Campbell A M, Coombs T A. Numerical solution of critical state in superconductivity by finite element software[J]. Supercond. Sci. Technol. , 2006, 19(12): 1246.