Abstract
Greater focus on sustainability across numerous industries has led to an uptick in the demand for increasingly environmentally-friendly materials. Biochar has recently come into the arena as a material that is created from biomass that has undergone pyrolysis. The benefits of this material include inputs easily found in nature (ie. pine wood), high biodegradability, and high relative strength. When combined with epoxy resin, it was hypothesized that this composite would create a stronger, more natural material than either material by itself. Through the use of ABAQUS, a finite element analysis software, representative volume elements (RVEs) were created in order to test several configurations, load magnitudes & types, variations of biochar, and mass percentages to determine the most stress-resistant material. Through analysis of the maximum and minimum von Mises Stress percentages experienced by each RVE, 4 assignable sections of spruce-fir and pine sawdust biochar collectively produced the smallest von Mises Stress percentages, indicating a low likelihood of plastic characteristics after applied stress. Across all RVEs, the median number of assignable sections (4) for biochar had the lowest von Mises Stress percentages, indicating that maintaining elastic properties is best done through a hybrid of epoxy resin and biochar. In terms of the best type of stress, hydrostatic stress gave more favorable results (decreased von Mises percentages). Differences between the reaction force from varying pressures was proportional, indicating similar behavior at different stress values. Future applications include interdisciplinary applications of epoxy resin in green-transportation, green-construction, or crack prevention across other environmentally conscious disciplines.
Introduction
As environmental issues become more pressing, it becomes imperative that composite materials be redesigned with a focus on recyclability, and the responsible use of natural materials. In fact, making the shift towards biodegradable materials can significantly reduce environmental pollution (Tian and Bilal, 2020). One way to alter a material's composition and properties is through the use of fillers, which can enhance electrical and mechanical properties, while also utilizing more affordable inputs for the material (Khan et al., 2017). Specifically, biochar filler, a type of filler that occurs from the pyrolysis of natural materials (such as textiles, wood, fibers, etc.) can be combined with other materials to decrease the mass of the material or enhance its degradation leading to more natural recycling processes, along with favorable responses to stress.
Although biochars are frequently regarded as suitable additions to soil to drastically reduce CO2 emissions (Woolf et al., 2010), biochars have become of interest to the materials science community recently, as bio-based fillers can enhance the recyclability of composite materials or lessen the amount of other materials used for structures that require stricter mechanical properties (Das, 2015). In this study, two types of biochar fillers were chosen: biochar softwood (a blend of spruce and fir wood) and pinewood sawdust. The type of wood is important to note, as there are several different types of wood, including hard and soft wood that can change mechanical outcomes. By simulating various types of softwood, this extends the applicability of this research, by considering numerous inputs for this biochar. A few notable differences between the spruce-fir blend wood and pine wood include spruce's straighter pattern, and its better weight to strength ratio (Lumber, 2018), which may come into focus as these biochars and their reactions to stress are compared with one another. Regardless of the type, biochar retains its primary property of a high carbon mass percentage, resulting from the pyrolyzation process (Downie et al., 2012).
Simulating mechanical processes has become a viable option since the inception of advanced computing technology (Bevilacqua, 2008). Although there are many options for types of mechanical simulations, ABAQUS was chosen due to its accessibility, and the scope of the variables that could be tailored to the desired experimental setup. Many different scenarios have been tested through ABAQUS, ranging from tooth mechanics (Motta et al., 2006) to pavement performance (Rahman et al., 2011). Throughout the interface, options exist to increase the strain applied to the RVE, swap the assigned sections to create different configurations, apply stress both uniaxially and hydrostatically, and combine materials to effectively test different configurations within an RVE. These features prove helpful, especially with the addition of material values to simulate certain properties, which can simulate matrices that hold polymers (Chandramohan & Marimuthu, 2011). Previous studies have checked RVEs with experimental values and found that finite element analysis accounted for a wide range of mechanical properties from the tensile strength and modulus, to the flexural strength and modulus, along with the density and Poisson’s ratio (Wallace, 2019b). Although there are alternative methods to the RVE model, such as the use of the Rule of Mixture method (RoM), this alternative method rests on three key assumptions, including the uniform dispersion of fiber, the perfect bonding between fiber and the matric, and the matrix being free of voids (Saha, 2005). As these scenarios are represent a near-perfect scenario that is not as transferable to the real world, finite element, specifically ABAQUS was deemed the more favorable option. ABAQUS obtains its unique advantages for correct calculations from the finite element method, which involves splitting the total simulated body into much smaller parts (nodes), performing calculations individually, and then recombining the results to get a much more accurate, comprehensive model. These computational features were then used to glean a wide dataset of values from the simulations completed.
For the RVEs in question, the type and amount of load was considered, as in different applications, there are different load restrictions and implications for material viability. Hydrostatic as well as uniaxial stress was applied, to simulate the different situations the biochar-epoxy resin composite may undergo. Additionally, the amount of load was changed, to determine whether there was a relationship between increased load and increased strain/plastic deformation of the material.
To measure the reaction of the material to the differing variables applied to the RVE, the von Mises percentage was chosen, as it indicates the probability of the material yielding or fracturing, leading to plastic deformation, from which any impact of further stress is permanent (Harish, 2017). In this case, the lower von Mises value is preferable, as this indicates a lesser probability of plastic deformation beyond return. It was hypothesized that by adding biochar to the epoxy resin RVE, the material would become stronger, and more resistant to stress.
Methods and Materials
In this study, the finite element analysis software (ABAQUS) was used with the standard explicit model setting. According to Roylance (2001), there are three essential parts of a finite element analysis: preprocessing, the creation of an RVE with accurate values and a fixed displacement for each node; analysis, the consideration of the force applied in relation to the displacement/deformation; and postprocessing, the process of data visualization, with graphs and other examples.
In this method’s preprocessing, to create the representative volume elements, a base model was used. This began as a cube, with triangular corners the extended to the center of each side of the cube, for a total of eight “triangular corners.” These corners were used as assignable sections, by which biochar and epoxy resin mass percentages within the total RVE would change.
To create this configuration, a 3-dimensional, deformable, solid extrusion part was created in the parts tab of ABAQUS, with the side length of 40 units throughout. For the triangular prism corners, a cell partition was created by connecting the three auto-created vertices from the center of each edge. As a control group, each “corner” was set initially to the epoxy resin values, to ensure an adequate baseline.
To obtain literature values to simulate the biochar and epoxy resin configurations, a comprehensive literature review was completed. Necessary inputs for finite element analysis included the Young’s modulus and Poisson’s ratio values to simulate the strength, and deformation behavior of these materials. These literature values were found across a wide array of literature pertaining to past experimental studies on pyrolyzed pinewood and softwood biochar, along with epoxy resin (Wallace, 2019a; Bartolucci, 2020; Das, 2015; Horabik, 2021; Smith, 1974).
Table 1: Literature Values of Mechanical Properties of Types of Biochar and Epoxy Resin
| Material | Young’s Modulus (MPa) | Poisson’s Ratio |
| Softwood (Spruce-Fir Mix) | 5640 | 0.365 |
| Pine Sawdust | 5000 | 0.35 |
| Epoxy Resin | 3850 | 0.37 |
To assign the different characters to the sections, the total amount of biochar-epoxy resin ratio was considered. For the cube configurations with triangular corners, there were four standard settings. The configurations included two alternate corners of biochar, four alternate corners of biochar, and finally all eight corners of biochar, to observe the effect of maximum biochar character. As a control, a setting with epoxy resin for all corners was considered as well. The smaller cube in the center resulting from the negative space of the corners was composed of epoxy resin in each simulation, to represent the adhesive purposes that the epoxy resin would perform for each simulation.
After the character and configuration of each RVE was set, further specifications were made to ensure a smooth simulation process. For each RVE, the boundary constant stayed the same, and was applied to every edge and partition edge (edge within the cube on the surface of the boundary) on the bottom-most surface of the RVE. The boundary condition was applied in all directions, to prevent the RVE from moving out of the frame of reference as load was applied. Whilst applying load, there were six types applied, differing in amount and applied axis. For both categories, 16, 32, and 64 units of pressure were applied in total, to determine if the relationship between the novel composite material exhibits strain results directly proportional to the amount of load added. To determine the effects of the type of stress applied, stress was applied uniaxially, from the top section, so that the pressure was perpendicular to the boundary condition, and then hydrostatically, from the top and the four sides on all parts of the biochar and epoxy so that the effect of strain in opposite axes simultaneously was accounted for. All types of loading were of the same nature, as they were mechanical and denoted as "pressure" in ABAQUS.
Finally, in order to analyze certain sections of the RVE in ABAQUS, the model was meshed. As there were irregular attributes due to the partitions and embedded regions, meshing the part (not assembly object as is the default) required first seeding the part instance (using larger seeding distances to conserve computational cost), and then selecting the "tet" feature with the hexagonal setting, to mesh each irregular part of the RVE.
To gather data from the applied stress to individual nodes, a job for each variation in pressure, configuration, and biochar percentage was created. After setting the job on a lower-memory setting (10%), results were observed, including the minimum and maximum von Mises Stress of each RVE, under the average 75% stress setting (if the values between adjacent nodes varied by upwards of 75%, the values were averaged together). From here, these ranges were compared against other RVEs with similar properties, to observe the impact of a single variable on the likelihood of the material to reach a permanent plastic state. For ranges of stress taken from the same pressure, a regression analysis was completed, to find the association between stress percentages as the amount of pressure applied to RVE increased.
Results
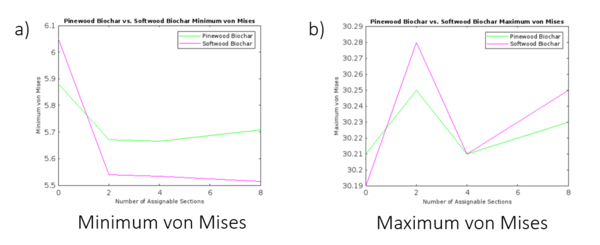Figure 5: Maximum and minimum von Mises percentages vs. number of assignable sections for pinewood and softwood blend biochar
Discussion
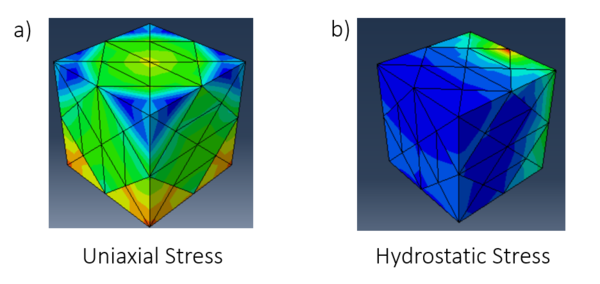
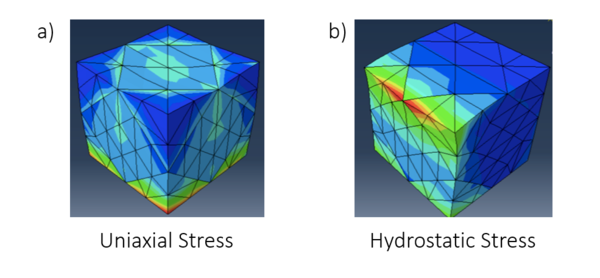
In many applications, this composite will undergo stress from several directions, whether it be uniaxial or hydrostatic. While most of the analysis performed in this study was uniaxial, the effect of a hydrostatically applied load seems to decrease von Mises percentages drastically, as seen in the difference between Figure 2a and 2b. Although at first glance, the uniaxial stress RVE may seem more favorable, as the stress is concentrated more evenly, upon looking at the maximum von Mises values, the uniaxial RVE has a maximum von Mises stress percentage tenfold greater in relation to the hydrostatic RVE (6.265e+01 in comparison with 6.622). This may be due to the spread of the softwood biochar molecules along all axes, which would lessen the concentration of applied load at any given point, thus decreasing the effective von Mises percentages. When compared to the industry standard of approximately 3000 to 5000 psi (Lysett, 2019), these composites pass this test, as 64 MPa is the primary amount of stress in this experiment. 64 MPa is equivalent to 9282 psi, meaning that this composite can withstand and exceed industry standards. In the field, this finding may be helpful to utilize biochar as an input to reduce environmental effects of leftover wildfire debris.
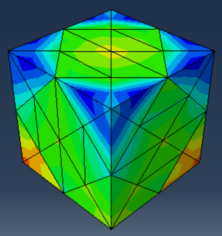
Investigating the individual nodal reactions to stress, it becomes apparent that the dispersion of force differs throughout the material. As seen in Figure 3, there is an increased concentration of force (or a higher von Mises percentage) near the alternate bottom corners in the background. This may be due to the boundary constraints, and the accumulation of force over the simulation period, due to the boundary created, and the decreased penetration of force past the boundary condition. This presents a positive finding, as when biochar and epoxy resin are put under stress whilst adjacent to each other, force buildup seems to be minimal, boding well for the strength of the material in its bulk form.
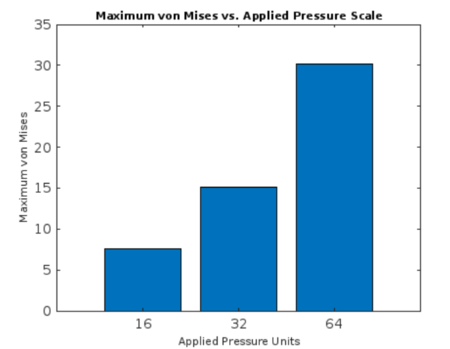
Whilst considering future applications for this novel biochar and epoxy resin composite, bulk form is important, as is scalability. Through the application of differing load amounts, the relationship between the amount of load and the RVE response to the load was determined. As seen in Figure 4, as the amount of pressure applied doubled in each increment, the average maximum von Mises percentage nearly doubled as well, demonstrating the proportionality of all biochar-epoxy resin composites reaction to increased load. This becomes helpful when implementing this material in the field, as it demonstrates a predictable relationship of strength and the probability of plastic deformation in relation to scale, a known quantity during the material construction and fabrication process.
Through several different configurations of the biochar, unique patches of high and low von Mises percentages can be observed. Through Figure 5, it seems as though the lowest maximum von Mises percentage arises when the # of assignable biochar sections is equal to four for both pinewood and softwood blend biochar. This is due to the symmetric nature of this configuration without relying heavily on the biochar epoxy resin interface. However, differences between the biochar types arise when observing the lowest minimum von Mises percentage. For pinewood biochar, this occurs when the # of assignable biochar sections is equal to 2, whilst for softwood blend biochar, this occurs when the # of assignable biochar sections is equal to 8. For pinewood biochar, the lower number of assignable sections for lower von Mises is expected, because as stated previously, pinewood has a more irregular pattern within the wood, meaning certain intersections of pinewood grain may cause concentrations of stress to build up. For the softwood blend, the minimum von Mises percentage may arise with a greater amount of biochar character, because of the increased spread of the same pressure to more boundaries between the different materials within the RVE. As Bevilacqua et al. (2008) reported, tilted implants have been associated with lower von Mises values in comparison to vertical implants. Although this study was with respect to cantilever lengths observed through finite element analysis, the same principle applies as with the configuration of 8 biochar assignable sections, they were opposite of each other, both laterally and vertically, creating an increased number of tilted surfaces. With a lower number of biochar assignable sections (such as full epoxy/biochar character or 2 assignable sections), there would be less tilted surface area within the RVE, leading to an increase in the von Mises percentage, in the case of a straighter wood configuration. Another interesting characteristic to note is the biochar’s interaction with the boundary conditions. As seen in Figure 2, with 8 assignable sections of softwood biochar, there is an increased von Mises percentage near the bottom of the corners attached to the boundary condition, signifying that much of the load is deposited in that region closer to the affixed space. This indicates that it may be better to have epoxy resin on contact corners, and biochar closer to the center, away from the contact with other hard surfaces. A similar phenomenon can be observed in Figure 3, where the 2 assignable biochar sections closest to the boundary condition are hot spots for increased von Mises percentages.
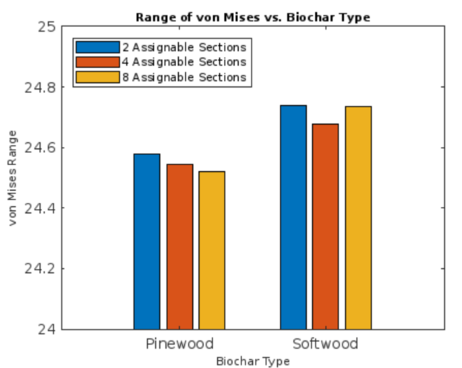
Although softwood and pinewood were tested on their own with differing configurations and amounts of load, they remain quite similar throughout each of the testing, with minor differences in range. As observed in Figure 6, the softwood biochar seems to have a greater range of von Mises percentage values, with higher maximums, and lower minimums. This could emerge from the unique properties of softwood, especially considering it is a blend of both Spruce and Fir wood, and Spruce wood is known to have straighter, more rigid patterns within itself as it matures. By integrating the two types of wood, this creates a larger range. Utilizing multiple biochar inputs may also be beneficial for material recovery, as separate circumstances or the degradation of this material may allow for a total reconstruction, or retrieval of the epoxy resin used. This is important, as one of the most prevalent problems with recyclable and biodegradable materials is the retrieval of reinforcing fibers and matrices (Yang et al., 2012).
Another interesting finding was that the blend of both softwood and pinewood produced lower von Mises percentages than either biochar by itself, as seen in Figure 7 and 8. In Figure 7a and 7b, it is evident that the concentrated locations of stress are much smaller, and less apparent than in Figure 2a and 2b which represents an “unblended” version of the biochar composite. Additionally, when compared to the pure epoxy resin in Figure 8, the minimum von Mises values of the 1:3 pinewood to softwood blend are significantly smaller, indicating a lower likelihood of fracture or plastic deformation. This supports the idea that a greater variability in the type of biochar and the interfaces between materials leads to higher mechanical properties, and a lower likelihood of plastic deformation.
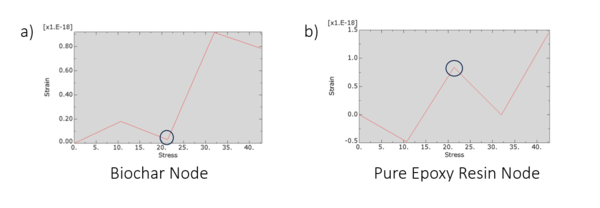
As a part of this investigation, the difference between biochar and epoxy resin’s reaction to stress was also noted. To simulate the interactions of the differing stresses, an interface between pinewood biochar and epoxy resin was tested, and differences amongst the stress vs. strain curves were noted. In Figure 9a, the derivatives of the stress strain curve are opposite that of Figure 9b, indicating that this interface represents force pairs, which act in opposite directions. The epoxy resin has a larger range of strain experienced as well, indicating that the heterogeneous particles of biochar result in a delayed reaction to the stress, and thus a further range over time.
As this experiment was centered around computational modeling, there were few sources of error that weren’t accounted for by ABAQUS, except possible human error in the form of generating the RVEs for analysis. In the future, further research may include findings considering a variety of types of biochars, including biochars from other organisms, and different tree types found in wildfire prone areas (ie. sycamore, oak, redwood). Another interesting topic of study would be including different standard materials (other than epoxy) to determine the most compatible combination of biochar composites for favorable mechanical properties.
Conclusion
Using finite element analysis and unique RVEs to simulate different configurations, types and amounts of biochar in an epoxy resin, a few major conclusions can be drawn. First, the relationship between increased load amount and the reaction to the pressure is proportional, meaning biochar-epoxy resin composites behave in a predictable fashion under higher stresses. Each time double the stress is applied, the von Mises percentage doubles as well. Secondly, as measured through lower von Mises percentages, the configuration of 4 assignable biochar sections lends itself well to lower maximum von Mises percentages, while the configuration of 8 assignable biochar sections lends itself well to lower minimum von Mises percentages, as evidenced by the pinewood RVE results for 16 MPa of applied pressure. Additionally, the location of biochar closer to boundary conditions creates higher moments of von Mises concentrations, however this can be avoided through the application of hydrostatic (instead of uniaxial) stress, as this spreads the pressure along numerous axes leading to a better dispersion of force, allowing less elastic deformation for higher pressure amounts. Furthermore, as seen by the smallest von Mises percentage of 1.375 and the highest von Mises percentage of 6.049 for 16 and 64 MPa of pressure respectively, the ranges of probability of yield and fracture seem to be more varied for the softwood blend RVEs, due to the blend’s heterogeneous makeup, that incorporates an increasing number of uneven surfaces even within the RVE that contribute to more diverse percentages ranging from lower to higher values. This contrasts from the reaction of the pure epoxy resin nodes, which act in opposite force pairs to the original biochar. Finally, the novel biochar-epoxy resin composites in this investigation withstand the industry standard of 5000 psi. These findings confirm the earlier hypothesis that the addition of biochar to epoxy resin results in a stronger and more environmentally friendly material.
Acknowledgements
Thank you to Dr. Z. Hossain for guidance on literature value collection and Mr. G. Darone for insightful discussions on data analysis and graph creation.
References
Bartolucci, B., De Rosa, A., Bertolin, C., Berto, F., Penta, F., & Siani, A. M. (2020). Mechanical properties of the most common European woods: a literature review. Frattura ed Integrità Strutturale, 14(54), 249-274.
Bevilacqua, M., Tealdo, T., Pera, F., Menini, M., Mossolov, A., Drago, C., & Pera, P. (2008). Three-dimensional finite element analysis of load transmission using different implant inclinations and cantilever lengths. International Journal of Prosthodontics, 21(6).
Chandramohan, D., & Marimuthu, K. (2011). A review on natural fibers. International Journal of Research and Reviews in Applied Sciences, 8(2), 194-206.
Das, O., Sarmah, A. K., & Bhattacharyya, D. (2015). A sustainable and resilient approach through biochar addition in wood polymer composites. Science of the total environment, 512, 326-336.
Downie, A., Crosky, A., & Munroe, P. (2012). Physical properties of biochar. In Biochar for environmental management (pp. 45-64). Routledge.
Harish, A. (2017, April 19). What Is the von Mises Stress and the Yield Criterion? SimScale. https://www.simscale.com/blog/von-mises-stress/
Horabik, J., Bańda, M., Józefaciuk, G., Adamczuk, A., Polakowski, C., Stasiak, M., ... & Molenda, M. (2021). Breakage Strength of Wood Sawdust Pellets: Measurements and Modelling. Materials, 14(12), 3273.
Khan, A., Savi, P., Quaranta, S., Rovere, M., Giorcelli, M., Tagliaferro, A., ... & Jia, C. Q. (2017). Low-cost carbon fillers to improve mechanical properties and conductivity of epoxy composites. Polymers, 9(12), 642.
Lumber, F. (2018). Construction and Usage of Spruce Lumber. Floridalumber.com. https://floridalumber.com/blog/construction-and-usage-of-spruce-lumber/#:~:text=Difference%20between%20Spruce%20and%20Pine
Lysett, T. (2019). Everything You Need to Know About Concrete Strength | Cor-Tuf. Cor Tuf. https://cor-tuf.com/everything-you-need-to-know-about-concrete-strength/
Motta, A. B., Pereira, L. C., & da Cunha, A. R. (2006, May). Finite element analysis in 2D and 3D models for sound and restored teeth. In ABAQUS Users’ conference (pp. 329-343).
Rahman, M. T., Mahmud, K., & Ahsan, S. (2011). Stress-strain characteristics of flexible pavement using finite element analysis. International Journal of Civil & Structural Engineering, 2(1), 233-240.
Roylance, D. (2001). Finite element analysis. Department of Materials Science and Engineering, Massachusetts Institute of Technology, Cambridge.
Saha, G. C. (2005). Experimental, numerical and analytical studies of smart composite materials and their applications.
Smith, A., Wilkinson, S. J., & Reynolds, W. N. (1974). The elastic constants of some epoxy resins. Journal of Materials Science, 9(4), 547-550.
Tian, K., & Bilal, M. (2020). Research progress of biodegradable materials in reducing environmental pollution. Abatement of environmental pollutants, 313-330.
Wallace, C. A., Afzal, M. T., & Saha, G. C. (2019a). Effect of feedstock and microwave pyrolysis temperature on physio-chemical and nano-scale mechanical properties of biochar. Bioresources and Bioprocessing, 6(1), 1-11.
Wallace, C. A., Saha, G. C., Afzal, M. T., & Lloyd, A. (2019b). Experimental and computational modeling of effective flexural/tensile properties of microwave pyrolysis biochar reinforced GFRP biocomposites. Composites Part B: Engineering, 175, 107180.
| Woolf, D., Amonette, J. E., Street-Perrott, F. A., Lehmann, J., & Joseph, S. (2010). Sustainable biochar to mitigate global climate change. Nature communications, 1(1), 56.
Yang, Y., Boom, R., Irion, B., Van Heerden, D. J., Kuiper, P., & De Wit, H. (2012). Recycling of composite materials. Chemical Engineering and Processing: Process Intensification, 51, 53-68. |
Appendix
Table 1: Raw Experimental Data
Legend for RVE Title:
RVE Title: XXYZA
XX - Pressure Units Applied; Y - # of Assigned Nodes (A = 8, 4 = 4, 2 = 2, _ = 0); Z - Material Used (EPOXY = Epoxy Resin, P = Pinewood Sawdust & Epoxy Resin, S = Softwood Blend & Epoxy Resin, PS = Blend of 2 Assigned Nodes of Pinewood & Softwood, Epoxy Resin filler); A - Type of Load Applied (Hydro = Hydrostatic stress, _ = Uniaxial stress)
| RVE Identification | Min. S, Mises | Max. S, Mises | Difference |
| 642S | 5.54 | 30.28 | 24.74 |
| 64AS | 5.514 | 30.25 | 24.736 |
| 644S | 5.533 | 30.21 | 24.677 |
| 642P | 5.671 | 30.25 | 24.579 |
| 644P | 5.666 | 30.21 | 24.544 |
| 64AP | 5.709 | 30.23 | 24.521 |
| 64P | 5.881 | 30.21 | 24.329 |
| 64EPOXY | 6.049 | 30.19 | 24.141 |
| 64S | 6.049 | 30.19 | 24.141 |
| 32AS | 2.572 | 15.13 | 12.558 |
| 322S | 2.77 | 15.14 | 12.37 |
| 324S | 2.763 | 15.11 | 12.347 |
| 322P | 2.832 | 15.13 | 12.298 |
| 324P | 2.83 | 15.11 | 12.28 |
| 32PS | 2.811 | 15.09 | 12.279 |
| 32AP | 2.851 | 15.12 | 12.269 |
| 32P | 2.939 | 15.11 | 12.171 |
| 32EPOXY | 3.022 | 15.1 | 12.078 |
| 32S | 3.022 | 15.1 | 12.078 |
| 16AS | 1.375 | 7.565 | 6.19 |
| 162S | 1.384 | 7.573 | 6.189 |
| 164S | 1.381 | 7.555 | 6.174 |
| 162P | 1.415 | 7.565 | 6.15 |
| 16PS | 1.405 | 7.548 | 6.143 |
| 164P | 1.414 | 7.554 | 6.14 |
| 16AP | 1.425 | 7.561 | 6.136 |
| 16P | 1.469 | 7.556 | 6.087 |
| 16EPOXY | 1.511 | 7.549 | 6.038 |
| 16S | 1.511 | 7.549 | 6.038 |
| 64PS | 5.628 | 30.18 | 24.552 |
| 16ASHydro | 0.05043 | 3.596 | 3.54557 |
| 164sHydro | 0.04846 | 3.687 | 3.63854 |
| 162SHydro | 0.04917 | 3.786 | 3.73683 |
Document information
Published on 25/09/23
Submitted on 29/08/23
Volume 5, 2023
Licence: CC BY-NC-SA license
