1 Introducción
La selección del adhesivo es un factor importante para optimizar un producto tanto en costes como en comportamiento. Sin embargo, se necesita cuantificar la aportación de la inclusión del adhesivo con modelos simples o analíticos ya que los modelos se complejizan si se tienen en cuenta el comportamiento del adhesivo para el cálculo de la estructura completa.
En este trabajo se ha cuantificado la aportación de considerar las uniones adhesivas en el modelado y cálculo de una estructura y fijado criterios de diseño que permiten desarrollar un producto con uniones adhesivas de la forma más sencilla posible. Para ello se ha realizado un estudio de los parámetros más influyentes en las uniones adhesivas utilizando el caso práctico del proceso de diseño de una base multimaterial para un ascensor, donde se tienen diferentes tipos de uniones.
2 Estudio de modelado de uniones adhesivas
Se ha realizado un estudio con el fin de analizar la influencia de diferentes tipos de modelos en uniones adhesivas. Para ello, se han planteado diferentes enfoques con distintos niveles de complejidad con los que se puede modelar una unión adhesiva utilizando el software ANSYS Workbench.
2.1 Modelos de uniones adhesivas
Los diferentes modelos planteados para el estudio se explican a continuación.
2.1.1 Adhesivo no modelado
Los substratos están en contacto directo y la unión se define mediante contactos bonded. Esta simulación asume que la unión entre las piezas es perfecta y rígida. Este tipo de modelo no tiene en cuenta la elasticidad y espesor de adhesivo.
2.1.2 Adhesivo como sólido
El adhesivo se modela como sólido de espesor tadh. Las propiedades del adhesivo se definen como isotrópico, en el que se definen dos de las siguientes tres propiedades: modulo de Young (E), módulo de cortadura (G) y Poisson (ν). Los contactos entre los adhesivos los substratos se definen como bonded o contacto perfecto. Este modelo se aproxima más a una unión adhesiva, ya que incluye términos de elasticidad y espesor.
2.1.3 Ley cohesiva simple
- 1) Contact debonding o elementos de contacto
Para este modelo se eliminan los sólidos que actuaban como adhesivo y los substratos se ponen en contacto directo, al igual que en modelo presentado en el apartado 2.1.1. Aunque este modelo no incluye términos de rigidez y espesor, sí incluye una la ley cohesiva en las intercaras, por lo que es posible analizar la rotura adhesiva. Se utilizan elementos de contacto a los que se les ha añadido la ley cohesiva.
En este modelo el contacto entre las partes se especifica como bonded de formulación pure penalty y después se incluye fractura de tipo contact debonding con las propiedades del adhesivo en las dos intercaras. Las propiedades del adhesivo se definen como separation-distance based debonding para introducir la ley cohesiva.
- 2) Interface delamination o elementos cohesivos
El mismo modelo que el anterior se puede configurar con interface delamination, en la que se incluyen elementos cohesivos en la intercara. Para eso, la definición del adhesivo se hace con propiedades tipo bilinear for interface delamination (o Exponential for Interface Delamination). El parámetro ratio, que corresponde a la rigidez inicial respecto a la separación total, será arbitrario pero muy pequeño (0.001, por ejemplo), puesto que la rigidez infinita no se puede simular en ANSYS, aspecto que se explica en el apartado 2.2. También es necesario cambiar el método del Interface delamination de VCCT a CZM (Cohesive zone modelling) y realizar un node matching. Para poder utilizar este tipo de Interface delamination, es necesario que exista un mesh match que se puede realizar como Contact match después de definir los contactos bonded de formulación pure penalty. Para esto, es necesario que los elementos sean tetraedros y del mismo tamaño en ambas caras, ya que los elementos comparten nodos.
La inserción de elementos cohesivos en es más restrictiva que los elementos de contacto, ya que es necesario que estos elementos compartan nodos en ambas caras a unir. Este modelo no tiene en cuenta la elasticidad del adhesivo. Para incluirla, es posible añadir unos resortes en la intercara o modificar la ley cohesiva, tal y como se explica en el apartado 2.1.5.
2.1.4 Adhesivo sólido con ley cohesiva
Otra opción para modelar un adhesivo es crear un modelo que combine las características de los anteriores, para poder así definir fractura del adhesivo a la vez que el espesor y la elasticidad de éste.
Para este modelo, se modifica el modelo 2.1.2 que incluye sólidos como adhesivos. Las partes que corresponden al adhesivo se parten por la mitad para reproducir una interfaz de cohesión del adhesivo. Al igual que en el modelo anterior, a ambos sólidos se les asigna el material como adhesivo isotrópico.
Se selecciona contacto bonded de tipo pure penalty para todos los contactos (entre los sólidos adhesivos y con los adherentes).
Se pueden realizar los dos tipos de fractura anteriormente mencionados:
- 1) Contact debonding à El material debe ser de tipo separation-distance based debonding (o Fracture-energies based debonding).
- 2) Interface delamination àUtiliza elementos cohesivos y requiere un material de propiedades tipo bilinear for interface delamination (o Exponential for Interface Delamination).
2.1.5 Ley cohesiva modificada
La ley cohesiva modificada corresponde a la inserción de términos de rigidez y espesor del adhesivo al modelo cohesivo analizado en 2.1.3.2 Interface delamination o elementos cohesivos. Por lo tanto, este modelo incluye tanto la rigidez como el espesor del adhesivo además de la ley cohesiva. Para ello, se modifica el parámetro ratio de las propiedades del adhesivo tipo bilinear for interface delamination.
Para determinar este ratio, se ha de calcular la deformación elástica del adhesivo. La siguiente ecuación (1) calcula el valor teórico de .
|
|
(1) |
Esta ecuación (1) sólo es aplicable al caso en el que la tracción se dé en una dirección, suponiendo que el resto de tensiones sean cero. Por lo tanto, es necesario realizar una corrección y calcular una E equivalente, que incluya efectos en otras direcciones [1], utilizando para ello la ecuación (2).
|
|
(2) |
Esta ecuación (2) se aplica en una zona adherida de ancho y largo (x y z) delimitados. Cuando la longitud de la unión es grande en comparación con el espesor, la ecuación se simplifica, obteniendo la ecuación (3).
|
|
(3) |
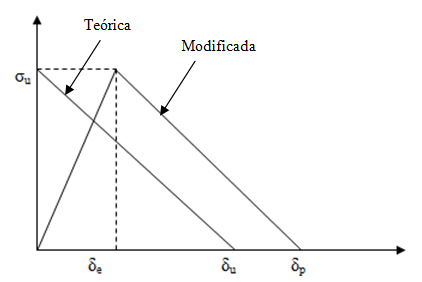
A la hora de modificar la ley cohesiva, es importante tener en cuenta que la energía de fractura deberá ser la misma que en la ley teórica, por lo que la elongación máxima del adhesivo será la elongación última a fractura más la deformación elástica (ver ecuación (4) y Figura 1).
|
|
(4) |
Por lo tanto, la ecuación (5) para calcular el ratio para las propiedades del adhesivo será:
|
|
(5) |
En el que corresponde a la elongación a rotura del adhesivo en la ley cohesiva teórica.
La elongación última a fractura ( en este caso) se introduce como Displacement jump at the completion of debonding.
A la hora de analizar los resultados, es importante considerar el tiempo de cálculo de cada modelo, ya que, si la influencia del modelado de la unión adhesiva es pequeña, se debe evitar añadir coste computacional a la simulación de un modelo más complejo.
2.2 Caso de estudio teórico
El enfoque principal de este estudio ha sido el modelado del adhesivo en uniones adhesivas, parámetros que afectan a éste y su aplicación en modelos complejos. Para ello, se ha realizado un estudio teórico previo en un modelo simple con el propósito de estudiar los diferentes métodos de modelado de uniones adhesivas y obtener recomendaciones de diseño para, después, aplicarlo en el caso práctico.
El modelo a simular es una placa bi-apoyada, en la que las uniones adhesivas se encuentran entre la placa y las bases en las que se apoya, todas de acero estructural. En la cara superior de la placa se aplica una fuerza distribuida, y las caras inferiores de las bases se fijan.
El adhesivo de referencia es H-100 de la casa Krafft, Se ha considerado, con intención de simplificar el cálculo, que las energías de fractura normal y a cortadura (modo I y modo II) tienen una relación lineal [2] y la ley cohesiva asumida lineal. Si el adhesivo es rígido, se recomienda el uso de la ley lineal aunque, si el adhesivo utilizado es elástico, la ley cohesiva lineal subestima hasta un 20% la resistencia de las uniones [2,3].
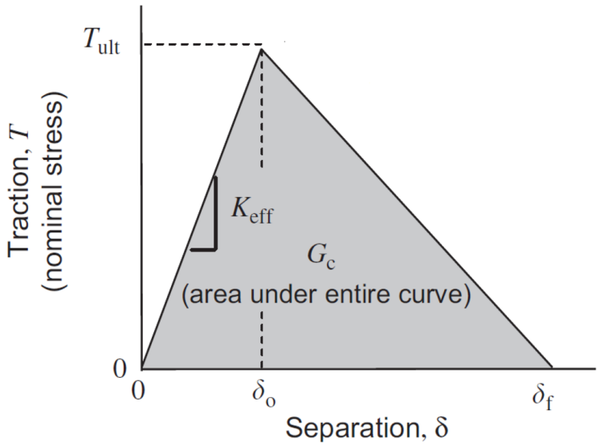
Por la imposibilidad de introducir una ley cohesiva lineal en ANSYS, en el que la rigidez inicial es infinita, es necesario introducir cierta rigidez (Keff en la Figura 2 inferior) en la ley, que corresponde a una deformación elástica casi nula. A partir de esta deformación, el adhesivo empezará a fracturarse hasta , en el que hay una separación total.
Se quiere analizar mayormente la influencia del espesor y la rigidez del adhesivo en el modelado del comportamiento de la estructura. Como parámetros de salida, se eligen tanto la deformación total como la tensión del sistema completo. También se observa la influencia en las tensiones del adhesivo, si el modelo lo permite.
2.2.1 Resultados
Se obtienen varias graficas en las que se muestran la tensión máxima y la deformación total en función de la rigidez y del espesor del adhesivo. Véanse, como ejemplo, las gráficas de la tensión y deformación máximas en función de la rigidez y el espesor del adhesivo mostradas (Figura 3 y Figura 4).
En las gráficas se puede ver que, al ser un análisis que se realiza en la región elástica, la inserción de una ley cohesiva apenas influye, ya que no llega a haber no linearidades en el adhesivo. La diferencia entre los resultados de las leyes cohesivas aplicadas de diferente modo (contact debonding o elementos de contacto e interface delamination o elementos cohesivos) se da debido a diferencias en el mallado y convergencia, ya que los elementos cohesivos requieren un mallado específico para poder compartir nodos. Se concluye que la inserción de leyes cohesivas apenas influye en el modelo en el que se añade el adhesivo, ya que no se ha llegado a la región no-lineal del mismo.
Para la fase de diseño, en el que el análisis es lineal y no se analiza rotura, se ha visto que es suficiente modelando el adhesivo como sólido, ya que influye no tanto en las tensiones máximas pero sí en la deformación total del sistema. Además, hay que tener en cuenta que el análisis lineal sobreestima las tensiones, por lo que el factor de seguridad será mayor. Con este método se puede verificar el comportamiento general del sistema e identificar zonas que podrían ser críticas y predecir el inicio del daño. Después se puede realizar un análisis en detalle de las zonas críticas, si las hubiese, introduciendo leyes cohesivas al adhesivo y simulando la rotura del mismo. El modelado del adhesivo como solido es especialmente importante para adhesivos gruesos, ya que influencia considerablemente en la deformación total. Un factor importante en el modelado como sólido es el mallado, ya que un mallado grueso puede dar problemas de singularidad en las tensiones.
Para adhesivos rígidos y de poco espesor, se ha visto que es suficiente si se define contacto perfecto (bonded) entre las caras en la fase de diseño. Como se ve en las gráficas, a partir de una rigidez de 50 MPa aproximadamente, las tensiones son similares a la simulación en la que el adhesivo no ha sido modelado.
En caso de que se quiera analizar a rotura, se deberá añadir la ley cohesiva en la unión, ya que permite observar la evolución de la grieta, desde que empieza a separarse hasta el momento de fallo catastrófico. Para ello, en caso de que el adhesivo sea rígido y de poco espesor, será suficiente utilizando un modelo cohesivo simple (tanto elementos cohesivos como de contacto). Si el adhesivo es elástico y más grueso, es recomendable utilizar un modelo cohesivo simple aplicado a un adhesivo modelado como sólido. Hay que tener en cuenta que, con la entrada de la ley cohesiva, los problemas de convergencia aumentan considerablemente, ya que la matriz de rigidez cambia entre incrementos, por lo que el coste computacional es mayor.
2.2.2 Tiempo computacional
Respecto a coste computacional, es importante cuantificar la aportación de un modelo que requiera un alto tiempo de preparación o simulación.
Los resultados muestran que la inserción del adhesivo modelado como un sólido requiere un coste computacional menor. Esto se puede dar debido a que, en un caso de carga a flexión, las uniones rígidas requieren de mayor cantidad de iteraciones para lograr la convergencia. Cuando se añade un material más elástico en el contacto, converge más fácilmente. Este mismo efecto se puede ver en los modelos sólido + ley cohesiva, en el que el tiempo de cálculo es considerablemente menor cuando los elementos de contacto unen piezas menos rígidas. Hay que mencionar que este modelo es muy simple y que añadir elementos a un modelo más complejo aumenta, normalmente, el coste computacional.
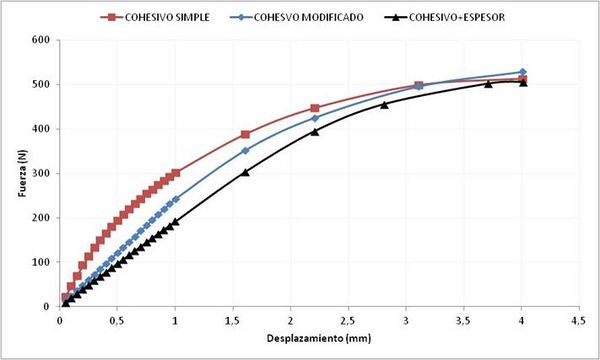
En la siguiente Figura 5 se puede ver una comparación entre modelos con elementos cohesivos en una simulación de un ensayo DCB (Double Cantilever Beam) en el que se ha simulado la propagación del daño en el adhesivo. Los tres modelos utilizados son una ley cohesiva simple (interface delamination o elementos cohesivos), la ley cohesiva modificada y el adhesivo en dos partes sólidas con elementos cohesivos.
El tiempo de cálculo de estos modelos es el siguiente:
| Modelo | Tipo de modelado | Tiempo de cálculo [s] | |
| Cohesivo simple | 2.1.3 + Elem. Coh. | 1753 | |
| Cohesivo modificado | 2.1.5 | 2985 | |
| Cohesivo con espesor | 2.1.4 + Elem. Coh. | 424 | |
La ley cohesiva modificada, aunque inicialmente parece una buena opción ya que se añaden términos de espesor y rigidez a la unión sin necesidad de añadir elementos, requiere mucho tiempo computacional en comparación con otros modelos de características similares. Su aportación no justifica su utilización para este tipo de modelos, ya que el modelo al que sustituye, que incluye la ley cohesiva a la vez que un sólido, converge más fácilmente.
Uno de los factores más difíciles de cuantificar a la hora de modelar un adhesivo es el tiempo de preparación de cada tipo de modelo. Para estructuras simples parece razonable que se añada el adhesivo en el diseño. En estructuras de geometría compleja o con gran cantidad de uniones adhesivas, el trabajo es más tedioso para el diseñador. El tiempo de preparación es un factor muy importante a la hora de realizar simulaciones, por lo que se tendrá que valorar el tipo de modelado para cada caso particular.
2.3 Influencia de las variables de fabricación de uniones adhesivas
Cuando se trabaja con uniones adhesivas, es muy común utilizar factores de seguridad altos por la incertidumbre sobre los parámetros no controlados, tales como las diferentes variables de fabricación.
En una simulación que se ha realizado utilizando un sólido que actúa como adhesivo, se supone que la unión es perfecta y que el adhesivo ocupa todo el ancho de la pieza. También se introduce un espesor constante al adhesivo. En la realidad, a la hora de fabricar una unión adhesiva, es probable que, a no ser que el pegado esté completamente controlado, se dé el caso en el que el espesor no sea constante en toda la pieza o que, aunque pueda considerarse constante, sea mayor o menor al indicado a la hora de simular. También es posible que el adhesivo no impregne todo el área deseada de las piezas a unir, por lo que el ancho o el overlap de la unión serán menores que las simuladas.
Otras variables que pueden afectar al rendimiento de la unión son el tiempo y temperatura de curado, la aparición de burbujas de aire en el adhesivo, la limpieza de las piezas a unir…
Se ha analizado el impacto que tienen en los resultados de las simulaciones las variaciones en el área y espesor de la unión en una probeta de SLJ (Single Lap Joint), obteniendo varias conclusiones:
- El factor más importante es el espesor del adhesivo. Para un adhesivo de mayor espesor, tanto las tensiones en los substratos como en el propio adhesivo disminuyen, influyendo mayoritariamente en las tensiones de los substratos.
- A mayor overlap (longitud de pegado en la dirección en la que se aplica la fuerza) disminuye la tensión en el adhesivo, aunque su influencia es considerablemente menor que la del espesor.
- Las variaciones en el ancho del adhesivo tienen menor influencia.
2.4 Conclusiones del análisis comparativo del modelado de una unión adhesiva
A continuación se presenta un resumen de las conclusiones y recomendaciones, basado en los resultados presentados previamente:
En fase de diseño, para predecir posibles inicios de rotura:
- Adhesivos rígidos y/o poco espesor à Contacto perfecto o bonded
- Adhesivos elásticos y/o de mayor espesor à Sólido
Para realizar un análisis de rotura:
- Adhesivos rígidos y/o poco espesor à Modelo cohesivo simple
- Adhesivos elásticos y/o de mayor espesor à Sólido + Modelo cohesivo simple
A la hora de insertar un modelo cohesivo, se debe elegir entre elementos cohesivos o elementos de contacto. La inserción de elementos cohesivos es más restrictiva, ya que los elementos deben compartir nodos en ambas caras a unir, por lo que es más sensible al mallado. Por ello, el tiempo de preparación de este modelo aumenta considerablemente. Además, puede ser especialmente tedioso en una estructura de geometría compleja. Los elementos de contacto, en los que la ley cohesiva se introduce mediante contact debonding, no requieren mayor trabajo que el de la inserción de la propia ley. Se recomienda, por lo tanto, utilizar elementos de contacto para introducir el modelo cohesivo en los contactos. Aún así, cabe destacar que los elementos de contacto parecen sobreestimar las tensiones y deformaciones.
Las leyes cohesivas lineales aplicadas en adhesivos elásticos, como se ha mencionado anteriormente, subestiman hasta en un 20% la resistencia de las uniones, por lo que se deberá de tener en cuenta al diseñar una unión de estas características.
Las propiedades con mayor sensibilidad son, como se ha presentado anteriormente, la rigidez y el espesor de los adhesivos, por lo que la caracterización de los adhesivos y un correcto control de la fabricación serán necesarios.
3 Caso de estudio práctico
Para comprobar los efectos estudiados en el caso simple, se ha utilizado una aplicación práctica realizando ensayos en una base multimaterial de un ascensor. Se han modelado y realizado ensayos físicos en dos prototipos diferentes.
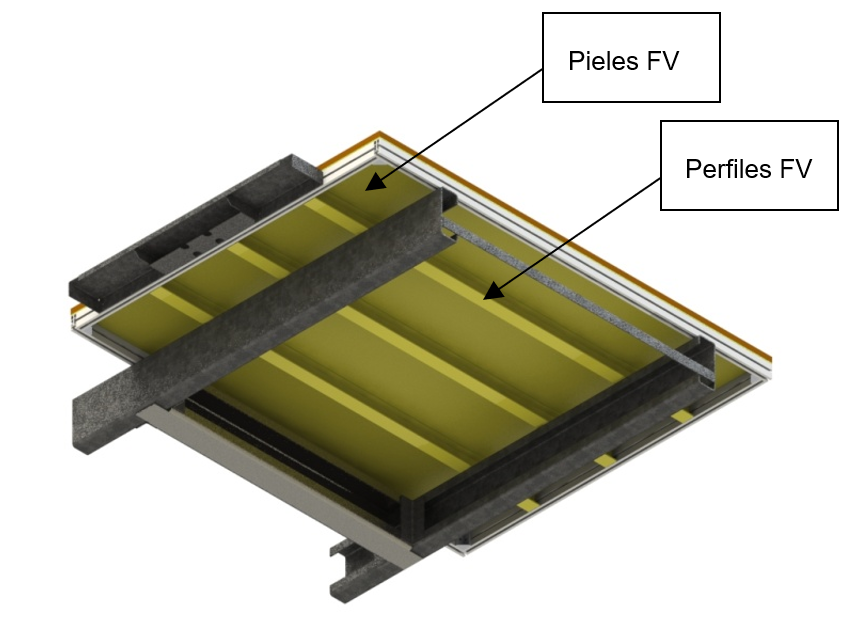
La base se compone de un marco de perfiles de aluminio comerciales al que se le añaden perfiles de pultrusión de fibra de vidrio. Encima de estos, se le coloca una placa de fibra de vidrio de 3 mm de espesor, adherida tanto al aluminio como a los perfiles de pultrusión. Por último, se le añade un panel de aglomerado encima de la base de fibra de vidrio únicamente apoyada.
3.1 Simulación sin uniones adhesivas (uniones rígidas)
En esta primera simulación, todas las uniones adhesivas fueron simuladas con contactos totalmente rígidos (bonded).
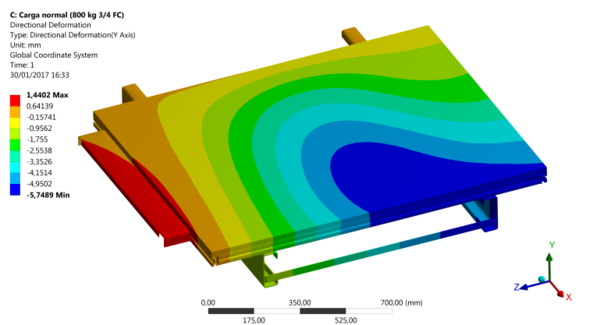
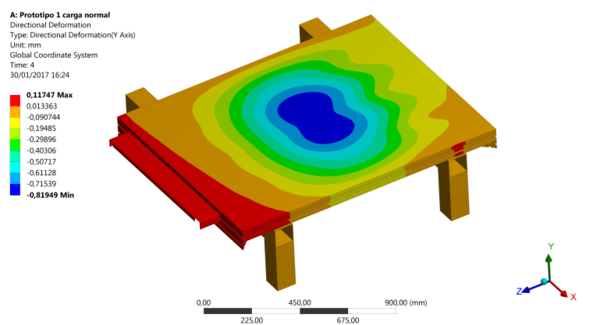
Se plantearon los dos casos de carga mostrados en la Figura 7, el de 800 kg distribuidos por ¾ del fondo de cabina (FC) y el ensayo de pisadera, 100 kg distribuidos en un área de 100 mm2.
|
Se asignaron propiedades a todos los materiales: aglomerado, pieles, perfiles de pultrusión, aluminio y acero. Mientras que para los dos últimos materiales se tomaron los valores por defecto del programa, los del resto fueron tomados de los ensayos de caracterización que se explican más adelante.
3.2 Simulación con uniones adhesivas
El modelo del apartado 3.1 se ha realizado incorporando el efecto del adhesivo, para comparar ambos modelos y su correlación con los resultados experimentales y valorar así la aportación de este tipo de modelado. Basado en las recomendaciones de los resultados obtenidos, para este modelo se ha considerado el adhesivo como sólido isotrópico de espesor de 1 mm con contactos bonded entre piezas.
Los casos de carga y las propiedades de los materiales son los mismos que en el apartado anterior.
3.3 Ensayos
3.3.1 Ensayos estructurales en los prototipos
Los casos de carga planteados para las simulaciones se llevaron a cargo en dos prototipos fabricados. Los prototipos corresponden a dos versiones diferentes de la base, siendo una más pesada y rígida que la otra. Para ambos prototipos se utilizó el adhesivo MS 9380 de Teroson, con un módulo de Young de aproximadamente 18 MPa.
3.3.2 Caracterización de materiales
Se realizaron ensayos de caracterización de materiales de todos los elementos fabricados con composites: pieles de fibra y perfiles de pultrusión. Se perseguía con ello analizar las propiedades obtenidas en los ensayos con los proporcionados por el fabricante, puesto que se utilizaron materiales tanto comerciales como fabricados para la aplicación.
Para las pieles se realizaron ensayos de compresión y tracción, mientras que los perfiles de pultrusión fueron ensayos por flexión a tres puntos y a compresión.
3.3.3 Caracterización del adhesivo
Se realizaron con la misma finalidad tres ensayos de adhesivos diferentes: DCB, Bulk Y SLJ. En los ensayos de adhesivos se utilizaron probetas metálicas y de composites para comparar los resultados. A la hora de ajustar una simulación con uniones adhesivas es recomendable caracterizar el adhesivo, ya que los fabricantes no ofrecen, en muchos casos, datos suficientes para su simulación. También se analizaron varios adhesivos para buscar el más adecuado para esta aplicación, en el que se encuentran uniones composite-composite y metal-composite.
3.4 Comparativa y discusión de resultados
En primer lugar se han comparado los modelos con y sin adhesivo con la base en voladizo, tal y como se puede observar en la Figura 8.
Con la inserción del adhesivo, la resistencia de las uniones disminuye, ya que la deformación elástica aumenta. Esto también hace que las tensiones en los componentes sean más bajas. Para la comparación se ha utilizado el adhesivo de módulo de elasticidad de 18 MPa. Los errores en el cálculo de la tensión medida en el centro del perfil central muestran que el modelo sin adhesivo sobreestima hasta en un 49% las tensiones máximas. En el cálculo de los desplazamientos de la pisadera, en cambio, se produce un error de hasta un 26% en el que el modelo sin adhesivo subestima los desplazamientos, aspecto que puede ser crítico a la hora de diseñar una estructura como un ascensor. Véanse las Figuras 9 y 10.
En cuanto al tiempo de cálculo, el modelo con adhesivo requiere algo menos de tiempo, aunque su disminución no es característica. Esta reducción, aunque pequeña, concuerda con los resultados obtenidos en el caso de estudio teórico, en el que la inserción de un material menos rígido en el contacto disminuye el tiempo de cálculo en problemas dominados por flexión. Puesto que no se trata de un problema puro de flexión, este efecto no es característico.
Respecto a la correlación FEM-experimental, se han comparado los modelos con y sin adhesivo con las mediciones que se realizaron en el prototipo de la base, que se encuentra apoyada en una estructura rígida tal y como se muestra en la Figura 11. Para este apartado ha sido muy importante la caracterización del adhesivo, ya que el modelo debe reflejar con la mayor exactitud posible el prototipo real.
Los resultados de las Figuras 12 y 13 muestran que el error en la correlación FEM-experimental es menor si el adhesivo es modelado en la unión. Aún así, al tratarse de un apoyo muy rígido, la diferencia entre ambos modelos es menor si se compara con la base en voladizo de las Figuras 9 y 10.
4 Conclusiones
En el modelado de estructuras complejas de multimaterial unidas mediante tecnologías adhesivas resulta de gran importancia considerar los efectos de espesor y elasticidad del adhesivo para obtener resultados precisos en la predicción del comportamiento de la estructura.
Del estudio comparativo realizado entre los diferentes modelos se puede concluir que, para la fase de diseño de una estructura con uniones adhesivas, no es necesario introducir leyes cohesivas en el modelo, puesto que, al introducir términos de espesor y elasticidad es posible determinar las zonas críticas y predecir el inicio del daño. Se ha comprobado este tipo de modelado en el caso de estudio práctico, validando las recomendaciones realizadas para el diseño con una buena eficiencia computacional. En cuanto al análisis de rotura, el modelo cohesivo simple requiere menor tiempo computacional que el modelo modificado, por lo que se recomienda su uso.
Respecto a la aportación de la modelización del adhesivo, se concluye que la inserción del adhesivo en el modelo de simulación por elementos finitos aproxima los resultados a los experimentales. Este efecto aumenta a medida que las cargas aumentan, puesto que los modelos sin adhesivos en el contacto no contemplan la elasticidad del mismo, subestimando los desplazamientos de la estructura.
Considerando los efectos del adhesivo en los modelos de la base se han obtenido predicciones en aproximadamente un 20% más precisas del comportamiento estructural. Además al modelar la base de ascensor, se comprueba que las propiedades de los materiales compuestos son críticas a la hora de realizar el modelo. En algunos casos, como con los perfiles de pultrusión, los resultados de la caracterización mostraban propiedades mejores que las proporcionadas por el fabricante. Al contrario sucedía al ensayar las pieles, por lo que se concluye que para obtener unas propiedades fiables, los ensayos son necesarios.
Es importante mencionar que, aunque en los modelos utilizados para el caso práctico no se analiza la fractura del adhesivo, con la inserción del adhesivo como sólido en el modelo es posible localizar las zonas críticas a sufrir rotura. Para un análisis más exhaustivo del proceso de fractura, se deberán incluir, según la naturaleza del material, leyes cohesivas en el modelo, tal y como se recomienda en el apartado 2.4.
5 Referencias
[1] Cabello, M., Zurbitu, J., Turon, A., Sarrado, C., Renar, J., & Martínez, F. Influence of the specimen width on the experimental measurement of the cohesive law using the j-integral approach. ECCM17 - 17th European Conference on Composite Materials. Munich (2016).
[2] da Silva, L., & Campilho, R. Advances in Numerical Modelling of adhesive joints. SpringerBriefs in Computational Mechanics (2012). DOI: 10.1007/978-3-642-23608-2
[3] Ridha, M., & Tan, T. Traction-separation laws for progressive failure of a bonded scarf repair of composite panels. Composite Structures, 93-4, 1239-1245 (2011). https://doi.org/10.1016/j.compstruct.2010.10.015
[4] Diehl, T. On using a penalty-based cohesive-zone finite element approach. Part I: Elastic solution benchmarks. International Journal of Adhesion and Adhesives. 28, 237–255 (2008). https://doi.org/10.1016/j.ijadhadh.2007.06.003
Document information
Published on 14/04/19
Accepted on 14/04/19
Submitted on 14/04/19
Volume 03 - Comunicaciones Matcomp17 (2019), Issue Núm. 2 - Aplicaciones, uniones y reparaciones de los materiales compuestos, 2019
DOI: 10.23967/r.matcomp.2019.04.011
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?