Modelling and predictive control for a RTM mold

1 Introducción

El presente artículo describe el proceso de modelado y control predictivo de un molde RTM calefactado a través de resistencias eléctricas. El sistema se diseña para asegurar un elevado nivel de homogeneidad en la temperatura de la cavidad, ya que la uniformidad de propiedades del material compuesto fabricado mediante esta tecnología depende en gran medida de que en el proceso de curado de la resina no existan gradientes térmicos significativos. Además, el sistema de control implementado debe ser capaz de realizar el calentamiento del molde según un ciclo térmico predefinido de acuerdo a las recomendaciones de procesado de la resina habituales.

Para el diseño del sistema de control predictivo es importante disponer de un modelo de referencia que sea capaz de reproducir el comportamiento térmico del sistema. Esto implica disponer de un modelo que prediga la evolución de las temperaturas en distintas posiciones de la cavidad a lo largo del tiempo. Teniendo en cuenta el carácter no lineal del sistema y su complejidad geométrica, la obtención del modelo no es tarea sencilla. La opción más precisa es resolver las ecuaciones de conservación de masa y energía, que gobiernan la física del problema, en modelos distribuidos, discretizados y resueltos numéricamente mediante métodos de volúmenes finitos (VOF) o elementos finitos (MEF). No obstante, estos modelos tienen demasiados grados de libertad y resultan complicados a la hora de diseñar el sistema de control. Por este motivo, se busca la obtención de un modelo de orden reducido (MOR) que pueda utilizarse en el propio control. La obtención de estos modelos puede realizarse de distintas formas. En [1] se plantea el uso de series temporales y modelos borrosos con adaptación de parámetros mediante Takagi-Sugeno. En [2] se aplican redes neuronales RBF (Radial Basis Functions) para la representación de moldes. En el presente trabajo se aplican modelos recursivos lineales ARX con observadores de perturbación para poder compensar las no linealidades del sistema. Estas se corresponden con la variabilidad en los coeficientes de convección en las paredes exteriores del molde.

Una vez obtenida una representación de orden reducido, es posible realizar el diseño del sistema de control aprovechando esta información. Así, frente a los controladores estándar existentes en el mercado [3], normalmente basados en compensadores estándar PID [4], es posible mejorar las prestaciones si se aprovecha una representación simplificada del comportamiento térmico del molde (Internal Model Control). Un segundo aspecto a tener en cuenta en el diseño de control es tomar en consideración las propias limitaciones de los actuadores, ya sean calefactores [5] o sistemas de refrigeración [6]. Por estos motivos, las soluciones más avanzadas que se encuentran en la literatura se basan en modelos previamente obtenidos o en conocimiento experto existente a priori: [1] utiliza un modelo Fuzzy para calcular un comando feedforward; [7] propone por un lado el uso de modelos neuronales para adaptar un control adaptativo basado en modelo de referencia (stochastic model reference predictive control algorithm), y por otro plantea un control adaptivo mediante PID de ganancia variable basada en control borroso; [8] aplica directamente control borroso del sistema. En el presente artículo se plantea el uso de control MPC con un algoritmo de optimización sujeto a restricciones basado en el método de Hildreth [9]. MPC no es un algoritmo nuevo en el control térmico de moldes, por ejemplo [10] y [11] aplican esos algoritmos.

La principal aportación del presente artículo es el uso de modelos lineales ARX con observadores de perturbación para poder estimar las no linealidades del sistema y compensarlas en tiempo real. Por otra parte, el uso de un algoritmo de optimización analítico sujeto a restricciones, basado en el método de Hildreth, mejorando así el coste computacional frente a métodos de optimización numéricos.

A continuación se describe el sistema de trabajo (sección 2); el modelo térmico del molde y su representación de orden reducido aparecen en la sección 3; el diseño de la arquitectura de control en la sección 4; y la posterior validación por simulación y experimentalmente se describen en las secciones 5 y 6 respectivamente.

2 Descripción del sistema

En este apartado se describen brevemente las características del molde RTM y de su hardware y software de control (Figura 1).

Figura 1. Molde RTM y hardware de control.

El molde RTM tiene una cavidad para fabricar placas de composite de dimensiones de 400x300mm y su espesor se puede ajustar a 2, 3 o 5 mm utilizando distintos espaciadores.

Se han incorporado dieciséis resistencias de cartucho internas (ocho en la cara superior y ocho en la cara inferior) y cuatro cinturones laterales, destinados a minimizar las pérdidas de calor por el perímetro. El molde cuenta además con unos paneles de aislamiento para reducir pérdidas de calor.

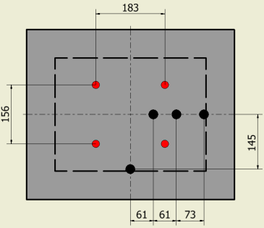
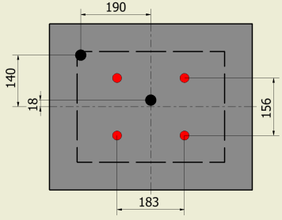
Se dispone de seis termopares permanentes en las cavidades superior e inferior del molde para el registro de temperatura y cerrar el bucle de control (cuatro en la cavidad superior y dos en la cavidad inferior). Para la comprobación de la homogeneidad de temperatura en la cavidad, se monitoriza la temperatura en ocho puntos adicionales mediante termopares accesorios provisionales. La figura 2 muestra un esquema de la posición de los termopares permanentes y provisionales en el molde.

Figura 2. Esquema de la posición de los termopares de control permanentes (en negro) y los termopares provisionales (en rojo) en la superficie de la cavidad superior (a) y de la cavidad inferior (b). La línea discontinua muestra la placa de composite.

El cuadro de control permite la actuación sobre cada una de las veinte resistencias de modo individual. El software de control se implementa en LabVIEW mediante la adaptación de algoritmos de control desarrollados en MATLAB-Simulink.

La configuración de resistencias, sensores y aislamiento se ha seleccionado en base a análisis térmicos en simulación y resultados experimentales.

3 Modelo térmico del molde

3.1 Modelo continuo

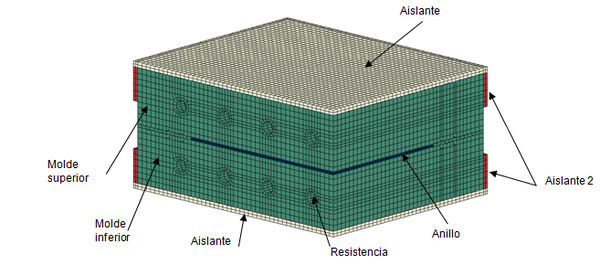
El sistema modelado consiste en un molde de acero cuyas partes superior e inferior están separadas por un anillo de 3 mm de espesor que define la cavidad donde se ubican los tejidos y se inyecta la resina. El molde está recubierto por dos tipos de aislante, un aislante de 6 mm de espesor en las partes inferior y superior y otro aislante de distintas características en el lateral, con 7 mm de espesor.

En este caso se ha elegido modelizar el comportamiento térmico del molde mediante la resolución de la ecuación de conservación de la energía únicamente en el dominio del molde, y resolverla mediante MEF. Los mecanismos de transferencia incorporados son la conducción y la convección, esta última considerada mediante coeficientes de convección efectivos en las superficies externas del molde.

En la figura 3 se muestra la discretización MEF de la geometría de un cuarto de molde utilizado para el ajuste de los distintos coeficientes de la simulación térmica.

Figura 3. Discretización MEF de la geometría de un cuarto de molde.

El material con el que se han modelado el acero del molde y el aislante se supone homogéneo e isótropo. Las propiedades térmicas del acero se recogen en la tabla 1.

Tabla 1. Propiedades térmicas del acero

Propiedad	Valor
Densidad, ρ (kg/m3)		7850
Calor específico, c (J/kgK)		520
Conductividad térmica (W/mK)		33-35.5

Con el fin de estudiar el valor de los coeficientes de convección en el exterior del molde y de los coeficientes de conducción de los aislantes se ha realizado un plan de ensayos, y las correspondientes simulaciones, en el que se ha analizado el comportamiento térmico del molde vacío, en estado estacionario, a distintos niveles de temperatura en el interior del molde.

Los coeficientes de conductividad térmica ajustados para el aislante 1 y el aislante 2 han sido, respectivamente, 0.53 W/mK y 0.26 W/mK.

La evolución de los coeficientes de convección en las caras superior e inferior (h en W/m²K) se han ajustado mediante la ecuación (1) mientras que el coeficiente en las caras laterales se ha ajustado mediante la ecuación (2). Los valores de los coeficientes (a, b y c) se muestran en la tabla 2. Según estos valores, los coeficientes de convección en la cara superior oscilan entre 6-18 W/m²K, en la cara inferior entre 1-8 W/m²K y en las caras laterales entre 2-12 W/m²K. Fuera del rango analizado se considera que los coeficientes permanecen constantes.

${\textstyle h=a{\left(\Delta T-b\right)}^{c}}$

(1)

${\textstyle h=a\left(b-{e}^{-c\Delta T}\right)}$

(2)

Tabla 2. Valores de los coeficientes de ajuste para la convección variable en las paredes del molde

	a	b	c
Superior	4.120	23.567	0.317
Inferior	0.942	22.937	0.533
Lateral	20.160	0.395	0.041

Además, el modelo térmico del molde se completa considerando el calor desprendido por el proceso de curado de la placa de composite, para lo cual se ha modelizado la cinética de curado de la resina mediante la ecuación de Kamal-Sourour. En función del grado de curado alcanzado en cada instante se considera el calor de reacción liberado.

Todo el modelo se ha implementado en el software comercial Abaqus/Standard.

3.2 Modelo de orden reducido (MOR)

A partir del modelo térmico del molde se ha obtenido una representación simplificada de orden reducido (MOR) mediante el método ARX. El algoritmo obtiene los parámetros que mejor ajustan el comportamiento térmico del modelo a partir de datos obtenidos en múltiples ensayos virtuales transitorios, representativos de la dinámica del sistema, en los que se registra la temperatura de la cavidad en seis posiciones (y, salidas) frente a las veinte potencias suministradas por las resistencias y cinturones (u, entradas). La ecuación (3) muestra la definición del modelo ARX.

${\textstyle {y}_{t+1}=\sum _{i=0}^{r-1}{{a}_{i}\cdot y}_{t-i}+\sum _{i=0}^{s}{{b}_{i}\cdot u}_{t-i}}$

(3)

Donde a y b son los parámetros del modelo y r y s son los órdenes de regresión para las salidas y las entradas, respectivamente.

Como primera aproximación se considera un coeficiente de convección constante igual a 15 W/m²K para la obtención del MOR. Al validar dicho modelo con el MEF de coeficiente de convección variable conforme a las ecuaciones (1) y (2), se obtienen errores de temperatura no despreciables (13%).

Con el fin de predecir estos efectos no recogidos por el MOR para posteriormente compensarlos, se implementa un estimador de calores de perturbación basado en el filtro de Kalman. A partir de la ecuación (3), se construye su representación en espacio de estados mostrada en la ecuación (4):

${\textstyle {\begin{matrix}{X}_{t+1}=A\cdot {X}_{t}+B\cdot {U}_{t}\\{Y}_{t}=C\cdot {X}_{t}\end{matrix}}}$

(4)

Donde

${X}_{t}=\left[{Y}_{t};{Y}_{t-1};{Y}_{t-2};\ldots {U}_{t-1};{U}_{t-2};{U}_{t-3}\ldots \right]$

Este modelo contempla internamente un coeficiente de convección constante. El hecho de que no lo sea se traduce en una perturbación que puede indicarse mediante la ecuación (5).

${\textstyle {\begin{matrix}{X}_{t+1}=A\cdot {X}_{t}+B\cdot {U}_{t}+{B}_{p}\cdot {P}_{t}\\{Y}_{t}=C\cdot {X}_{t}\end{matrix}}}$ (5)

Donde P_t representa la diferencia entre el calor de convección con coeficiente constante (15 W/m²K) y con coeficiente variable según las ecuaciones (1) y (2).

Se modifica la representación del sistema para incluir la perturbación dentro del estado asumiendo la dinámica ${\textstyle {P}_{t}{P}_{t-1}}$:

${X}_{m,t}=[{Y}_{t};{Y}_{t-1};{Y}_{t-2};\ldots {U}_{t-1};{U}_{t-2};{U}_{t-3}\ldots ;{P}_{t}]$

La ecuación de estado queda como sigue:

${\textstyle {\begin{matrix}{X}_{m,t+1}={A}_{m}\cdot {X}_{m,t}+{B}_{m}\cdot {U}_{t}\\{Y}_{m,t}={C}_{m}\cdot {X}_{m,t}\end{matrix}}}$

(6)

Donde

${A}_{m}=\left({\begin{matrix}A&{B}_{p}\\0&1\end{matrix}}\right)$

${B}_{m}=\left({\begin{matrix}B\\0\end{matrix}}\right)$

${C}_{m}=\left({\begin{matrix}C\,&0\end{matrix}}\right)$

A partir del sistema de la ecuación (6), se aplica un estimador de filtro de Kalman para predecir las variables de estado e identificar el valor de la perturbación en tiempo real:

Predicción:

${\textstyle {\tilde {X}}_{m,t}={A}_{m}\cdot {\hat {X}}_{m,t-1}+{B}_{m}\cdot {U}_{t}}$

(7)

${\textstyle {\tilde {P}}_{k,t}={{A}_{m}\cdot P}_{k,t-1}\cdot {A}_{m}^{t}+}$${C}_{q}$

(8)

Actualización:

${\textstyle {K}_{t}={\tilde {P}}_{k,t}\cdot {C}_{m}^{t}\cdot {\left({C}_{m}{\cdot {\tilde {P}}}_{k,t}\cdot {C}_{m}^{t}+{C}_{s}\right)}^{-1}}$

(9)

${\textstyle {\hat {X}}_{m,t}={\tilde {X}}_{m,t}+{K}_{t}\cdot \left({z}_{t}-\right.}$$\left.{C}_{m}\cdot {\tilde {X}}_{m,t}\right)$

(10)

${\textstyle {P}_{k,t}={\left(I-{K}_{t}\cdot {C}_{m}\right){\tilde {P}}}_{k,t}}$

(11)

Donde C_q y C_s son las incertidumbres del modelo de estimación y de los sensores de medida respectivamente; P es la covarianza del estado estimado; K es la ganancia del filtro de Kalman; y z es la medida de temperatura de los sensores.

Compensando las perturbaciones, se consiguen errores de temperatura en la validación del MOR inferiores al 6%.

4 Arquitectura de control

Se diseña un controlador MPC capaz de optimizar las consignas de los calefactores para conseguir una temperatura homogénea en los sensores de medida del molde. Este controlador calcula la potencia a suministrar a partir de la estimación de los estados siguientes, basada en el MOR.

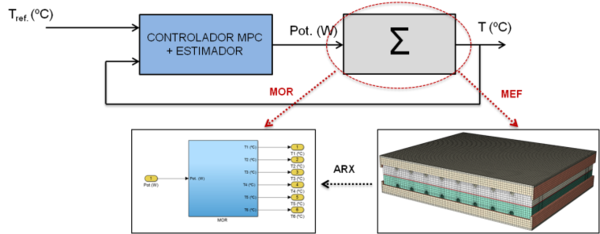
La entrada del controlador MPC es la estimación del estado del sistema tras pasar por el estimador de perturbaciones descrito en el apartado anterior, es decir, tras compensar los efectos no recogidos por el MOR. El esquema de la arquitectura de control se muestra en la figura 4.

Figura 4. Arquitectura de control: Controlador MPC y estimador de perturbaciones.

El controlador MPC cuenta con dos algoritmos: por una parte, la estimación de la evolución del sistema a partir del MOR hasta un horizonte temporal Np; y por otra, el cálculo de las potencias a suministrar mediante una función de optimización basada en dicha estimación de la evolución del sistema.

Para su implementación, se modifica previamente la representación del espacio de estados de la ecuación (6) de forma que ahora las entradas son los incrementos de potencia ( ${\textstyle {\Delta U}_{t}=}$${U}_{t}-{U}_{t-1}$) y las salidas se integran dentro del vector de estados, tal como se indica en la ecuación (12).

${\textstyle {X}_{e,t}=[\Delta {X}_{m,t};{Y}_{m,t}]}$

(12)

Donde ${\textstyle \Delta {X}_{m,t}=\,{X}_{m,t}-{X}_{m.t-1}\,}$

De esta forma, se obtiene la siguiente representación extendida del espacio de estados:

${\textstyle {\begin{matrix}{X}_{e,t+1}={A}_{e}\cdot {X}_{e,t}+{B}_{e}\cdot {\Delta U}_{t}\\{Y}_{e,t}={C}_{e}\cdot {X}_{e,t}\end{matrix}}}$

(13)

Donde

${A}_{e}=\left({\begin{matrix}{A}_{m}&0\\{C}_{m}{\,A}_{m}&1\end{matrix}}\right)$

${B}_{e}=\left({\begin{matrix}{B}_{m}\\{C}_{m}\,{B}_{m}\end{matrix}}\right)$

${C}_{e}=\left({\begin{matrix}0\,&1\end{matrix}}\right)$

Para la construcción del espacio de estados del MPC, se incluye la evolución de los estados siguientes hasta el horizonte temporal Np mediante la siguiente ecuación:

${\textstyle Y=F\,X+G\,\Delta U}$

(14)

Donde

$X=[{X}_{e,t};{X}_{e,t+1};{X}_{e,t+2};\ldots ;{X}_{e,t+Np-1}]$

$Y=[{Y}_{e.t+1};{Y}_{e,t+2};{Y}_{e,t+3};\ldots ;{Y}_{e,t+Np}]$

$\Delta U=[{\Delta U}_{t};{\Delta U}_{t+1};{\Delta U}_{t+2};\ldots ;{\Delta U}_{t+Np-1}]$

$F=\left({\begin{matrix}{\begin{matrix}{\begin{matrix}{C}_{e}{A}_{e}\\{C}_{e}{{A}_{e}}^{2}\\{C}_{e}{{A}_{e}}^{3}\end{matrix}}\\\vdots \end{matrix}}\\{C}_{e}{{A}_{e}}^{{N}_{p}}\end{matrix}}\right)$

$G=\left({\begin{matrix}{C}_{e}{B}_{e}&0&0&\ldots &0\\{C}_{e}{A}_{e}{B}_{e}&{C}_{e}{B}_{e}&0&\ldots &0\\{C}_{e}{{A}_{e}}^{2}{B}_{e}&{C}_{e}{A}_{e}{B}_{e}&{C}_{e}{B}_{e}&\ldots &0\\\vdots &\vdots &\vdots &\ldots &\vdots \\{C}_{e}{{A}_{e}}^{{N}_{p}-1}{B}_{e}&{C}_{e}{{A}_{e}}^{{N}_{p}-2}{B}_{e}&{C}_{e}{{A}_{e}}^{{N}_{p}-3}{B}_{e}&\ldots &{C}_{e}{B}_{e}\end{matrix}}\right)$

La función de optimización J depende de dos términos según la ecuación (15): el término de error cuadrático de temperatura de los sensores y el término cuadrático de eficiencia en los incrementos de potencia, ponderados por las matrices Q y R respectivamente. Para estos ensayos, el peso de la matriz Q es dos órdenes de magnitud menor que el peso de la matriz R (Q=1, R=0.01).

${\textstyle J={\left(Ref-Y\right)}^{T}\,Q\,\left(Ref-Y\right)\,+}$$\,{\Delta U}^{T}\,R\,\Delta U\,$

(15)

Donde ${\textstyle Ref}$es el vector de temperaturas de consigna hasta el horizonte temporal Np.

Para resolver la función de optimización se recurre al método de Hildreth. Se trata de una aproximación analítica para modelos lineales sujeta a restricciones basadas en inecuaciones. La ventaja con respecto a métodos de optimización numéricos es que el coste computacional se reduce considerablemente. El método se basa en implementar la expresión analítica que cumple:

${\textstyle {\frac {d\,J}{d\,\Delta U}}=0}$

(16)

A partir la igualdad de la ecuación (16), y reescribiendo las ecuaciones (14) y (15), se puede obtener el valor de los incrementos de potencia óptimos mediante la ecuación (17).

${\textstyle \Delta U={\left({G}^{T}G+R\right)}^{-1}\,{G}^{T}\,\left(Ref-\right.}$$\left.F\,X\right)\,$

(17)

Durante la optimización, el cálculo de las potencias está sujeto a restricciones: la potencia de los calefactores ha de ser inferior a su potencia de saturación y superior a cero. En caso de que las variables de optimización no cumplan las restricciones, el algoritmo las recalcula según el procedimiento descrito en [9].

5 Validación por simulación

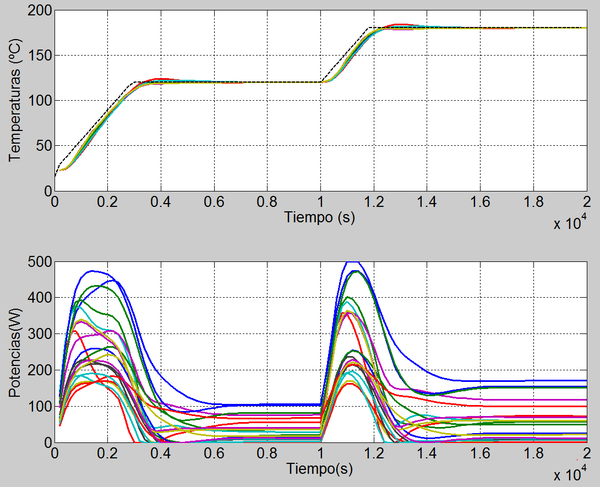
El algoritmo de control se ha validado por simulación. Inicialmente, considerando el MOR como modelo del sistema y, posteriormente, considerando directamente el MEF (Figura 5). Al enfrentar el algoritmo de control al MEF, se tienen en cuenta los efectos no lineales propios del sistema y la complejidad de la geometría. Para dicha validación, se realiza una co-simulación entre el algoritmo de control programado en MATLAB-Simulink y el MEF modelado en Abaqus.

Figura 5. Esquema de validación por simulación.

La simulación muestra un ensayo característico de inyección y curado de una resina. La evolución de la consigna de temperaturas es la siguiente:

• El molde se calienta desde temperatura ambiente (23 ºC) hasta una temperatura de 120 ºC con una rampa de 2 ºC/min.

• La temperatura de 120 ºC se mantiene constante hasta los 10000 segundos.

• El molde se calienta hasta la temperatura de curado (180 ºC) con una rampa de 2 ºC/min.

• La temperatura de 180 ºC se mantiene constante hasta los 20000 segundos.

La potencia máxima que los calefactores son capaces de suministrar es 500 W para las dieciséis resistencias internas, 750 W para los dos cinturones de los laterales largos y 550 W para los dos cinturones de los laterales cortos.

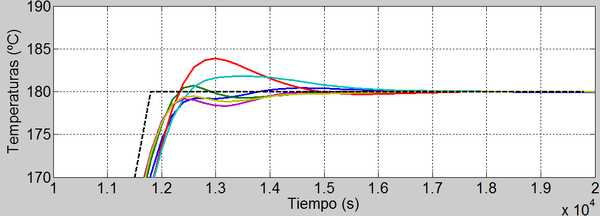
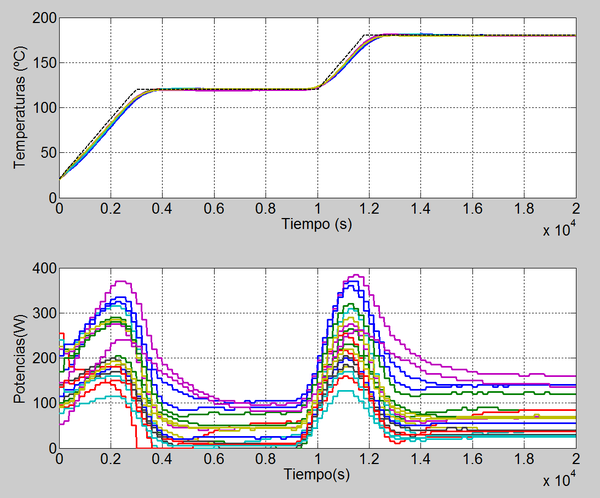
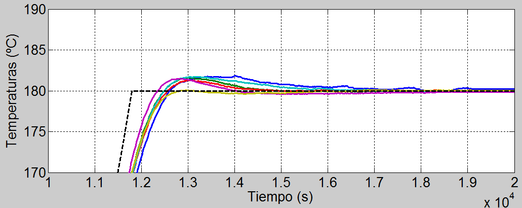
La figura 6 muestra el seguimiento de las temperaturas en los seis puntos de medida al aplicar las potencias a los calefactores demandadas por el controlador MPC. En la figura 7 se muestra un detalle del seguimiento de temperaturas para la consigna de 180ºC.

Figura 6. Evolución de las temperaturas de los sensores (arriba) y de las demandas de potencia (abajo) en la validación por simulación.

Figura 7. Detalle de las temperaturas de los sensores para una consigna de 180ºC en la validación por simulación.

En la tabla 3 se resumen los valores medios y máximos de los picos de sobreoscilación y del error de temperatura en estacionario con respecto a la consigna de 180 ºC.

Tabla 3. Valores medios y máximos de pico de sobreoscilación y error en estacionario para las temperaturas de los sensores en la validación por simulación

Indicador	Valor
Pico sobreoscilación medio (ºC)	1.07
Pico sobreoscilación máximo (ºC)	3.9
Error estacionario medio (ºC)	0.0017
Error estacionario máximo (ºC)	0.02

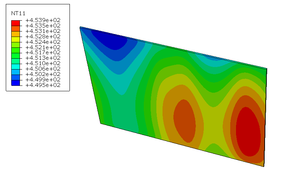
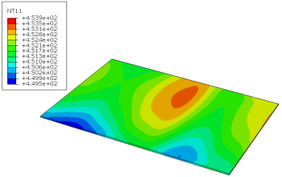
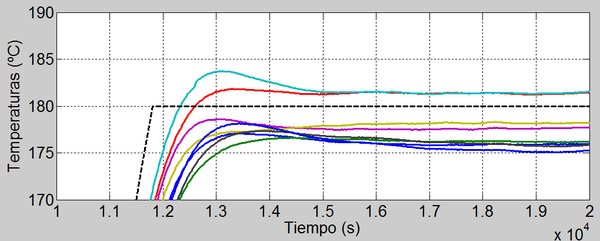
La simulación muestra que el algoritmo es capaz de controlar las temperaturas de los puntos de los que recibe información (sensores de control) con un error máximo en estacionario de 0.02ºC. El error máximo de temperatura en los puntos de la superficie de la cavidad medidos por los termopares provisionales (Figura 2), que no intervienen en el control, es de 5.5 ºC (desde 175.9ºC a 181.4ºC, media en 178.5 ºC), y en el conjunto de nodos de la placa de composite es de 4.4 ºC (desde 176.5ºC a 180.9ºC) según la distribución de temperaturas de la Figura 8.

Figura 8. Distribución de temperaturas en la placa de composite en la validación por simulación: cara superior (a la izquierda) y cara inferior (a la derecha).

Este resultado muestra que, aunque el controlador MPC es muy preciso, la posición de los sensores inicialmente seleccionada todavía podría optimizarse para asegurar homogeneidad de temperatura en la toda la cavidad.

6 Validación experimental

Se realiza la validación experimental en vacío con las mismas condiciones que en la validación por simulación. La figura 9 muestra el seguimiento de las temperaturas en los seis puntos de medida al aplicar las potencias a los calefactores demandadas por el controlador MPC.

Figura 9. Evolución de las temperaturas de los sensores (arriba) y de las demandas de potencia (abajo) en la validación experimental.

En las figuras 10 y 11 se muestra un detalle del seguimiento de las temperaturas de los sensores y de los termopares provisionales respectivamente. El error máximo de temperatura en estacionario es de 0.4 ºC en los sensores (desde 179.8 ºC a 180.2 ºC, media en 180.0 ºC) y de 5.9 ºC en los termopares provisionales (desde 175.5 ºC a 181.4ºC, media en 177.8 ºC).

Figura 10. Detalle de las temperaturas de los sensores para una consigna de 180ºC en la validación experimental.

Figura 11. Detalle de las temperaturas de los sensores provisionales para una consigna de 180ºC en la validación experimental.

7 Conclusiones

Se han validado tanto por simulación como experimentalmente los algoritmos de control MPC y de estimación de perturbaciones desarrollados, que permiten obtener diferencias de temperatura en la cavidad mucho más ajustadas que con controladores PID convencionales. El error máximo de temperatura en estacionario es de 0.4 ºC en los seis sensores de control simultáneamente; en otros puntos de la cavidad, que no intervienen en el control, se muestran diferencias máximas de 5.9 ºC (termopares provisionales).

A pesar de los buenos resultados mostrados por el control desarrollado, todavía se está trabajando en incorporar mejoras adicionales para reducir los gradientes térmicos en los puntos en los que no hay sensores de control. Por ejemplo, se plantea investigar, en este caso concreto, el aprovechamiento de condiciones de simetría del molde en los algoritmos de control. También se plantea como línea futura trabajar en la redefinición del número y distribución óptima de los sensores o en la introducción de puntos de control adicionales. No obstante, la gran ventaja de la aproximación propuesta es que se pueden definir sensores virtuales, añadiendo salidas adicionales en el MOR en otros puntos de la cavidad en los que no hay sensores físicos, suministrando una estimación de la temperatura de esos puntos de la cavidad no medidos. De esta forma el controlador suministrará potencia a los calefactores en base a información tanto de los sensores físicos como de los virtuales. Actualmente se está trabajando en esta última estrategia, cuyos resultados serán mostrados en una próxima publicación.

Agradecimientos

Este proyecto (referencia RTC-2014-1958-4) ha sido financiado por el Ministerio de Economía, Industria y Competitividad, dentro de la convocatoria Retos Colaboración del Programa Estatal de Investigación, Desarrollo e Innovación Orientada a los Retos de la Sociedad, en el marco del Plan Estatal de Investigación Científica y Técnica y de Innovación 2013-2016.

Referencias

[1] Y.-T.Wang, S.-L.Wu, “Modeling and Control for a Thermal Barrel in Plastic Molding Processes,” Tamkang Journal of Science and Engineering, 9, 2, pág. 129-140 (2006).

[2] J.Deng, Z.Yang, K.Li, G.Menary, E.Harkin-Jones, “Heuristically optimized RBF neural model for the control of section weights in stretch blow moulding,” UKACC International Conference on Control, pág. 24-29 (2012). doi: 10.1109/CONTROL.2012.6334596

[3] Cuadros de control comerciales de la marca Watlow (http://www.watlow.es/common/catalogs/files/esplc0604.pdf) (último acceso: 05.05.2017).

[4] T.Akashi, “Temperature Control of Heating Cylinder of Injection Moulding Machine by Decoupling Method,” Trans. of the Society of Instrument and Control Engineers Vol.E-1, No.1, 51/59 (2001).

[5] Calefactores comerciales de la marca Watlow (http://www.watlow.com/products/heaters/ht_cart.cfm)(último acceso: 05.05.2017).

[6] Sistema de refrigeración mediante agua a presión SINGLE (http://www.single-temp.co.uk/products/water-operated-temperature-control-technology/water-advanced.html) (último acceso: 05.05.2017).

[7] Q.Cai “Development of an accurate temperature controller for an injector of PET bottles,” NSC 98-2221-E-005-045-MY2 (1999).

[8] B.Muñoz-Barron, L.Morales-Velazquez, R.J.Romero-Troncoso, C.Rodriguez-Donate, M.Trejo-Hernandez, J.P.Benitez-Rangel, R.A.Osornio-Rios, “FPGA-Based Multiprocessor System for Injection Molding Control,” Sensors 2012, 12, 14068-14083; doi:10.3390/s121014068

[9] L.Wang, “Model Predictive Control System Design and Implementation using MATLAB,” Springer Publishing Company (2009).

[10] K.Lakshmi, D.Manamalli, M.M.Rafiq, “Design of Multimodel based MPC and IMC control schemes applied to injection molding machine”, International Journal of Engineer and Technology (2014).

[11] D.E.Gustafson ; W.M.Lebow, “Model predictive control (MPC) of injection molding machines,” 26th IEEE Conference on Decision and Control (1987). doi: 10.1109/CDC.1987.272888