Abstract
Slope stability problem is one of the most common problems in construction design. The application of tools often follows a pattern, using only fixed input parameters and resulting in a factor of safety according to the parameters themselves. This calculation model is only correct during the time when the shear resistance parameter (c, φ) of the ground does not change and is no accurate after the structure put into use, leading to slope instability, causing landslides and damage to the slope after a period of exploitation and use. The experimental studies have shown that the shear resistance parameter (c, φ) of the soil ground changes randomly with depth. As a result, current mechanical computational models are no accurate. This paper proposes a new model to analyze stability based on reliability theory with the change of shear resistance parameters by depth. Firstly, by using Karhunen – Loeve series, the result of slope stability coefficient of proposed model is smaller than these when not considering the change of shear resistance (c, φ) by depth. Then, by using Monte - Carlo simulations (n=1000) combined Karhunen – Loeve series, the forecast results are different from those only considering the static problem and the problem of random quantities, the probability of failure increase significantly.
Key words: reliability, slope stability, shear resistance, simulation,
Introduction
The problem of slope stability is one of the most common problems in construction design. The years of the twentieth century have researchers and methods proposed by Bishop (1955) [1] , Janbu (1954) [2]. From limit equilibrium theory to complex methods with high accuracy of Morgenstern - Price (1965) [3], Spencer (1973) [4], Janbu (1973) [5], the application of the above methods through the commercial software such as: Slope/W, Plaxis-2D or Plaxis-3D…However the input is static parameters. According to the method of dividing soil columns, the sliding mass above each hypothetical sliding surface divided into vertical soil columns, then analyze the force and moment balance conditions for the force system acting on the earth column to find the slope stability coefficient (FoS). Stability coefficient defined as the ratio of the total shear resistance moment to the total shearing moment acting on the sliding surface. After that, the researchers improved, supplemented, and proposed new calculation methods suitable to the real situation such as Janbu method (1954), Bishop method (1955), Spencer method (1973). The Janbu method does not completely satisfy the force and moment balance equations. Characteristic for the line of action method, in cases it is difficult to converge. At the same time, Janbu gave the coefficient ƒo without any specific basis, so it does not use in practice. The Bishop method is a popular method today, however, this method does not fully consider the vertical forces on both sides of the soil mass, and at the same time it is necessary to find out which sliding arc (sliding center) is the most dangerous, having the lowest factor of safety to evaluate the instability of the slope, so further research is needed. The Spencer method is a method that fully considers the force components of a soil element, strictly satisfies the static equilibrium, fully considers the force and moment balance equations, and may be use for circular sliding surfaces and not round. However, Spencer only calculates the moment equilibrium equation at the bottom of the soil column, thereby not simulating the sliding center and dangerous sliding arc of the slope. This method is quite complicated when the unknowns and the number of equations is large. Zhang and Zhou (2018) [6] use Monte - Carlo (MC) simulation, the LEM limit balance method finds the FoS factor of safety and the failure probability Pf, then compares their method with the classical methods of Bishop and Janbu. The obtained FoS factor of the UD-LASSO method is lower than that of Bishop and Janbu. The simple Bishop and Janbu methods of slope stability analysis have widely used since their presentation in the 1950s. Although Bishop's method does not satisfy the lateral force balance and the method of Janbu does not satisfy moment equilibrium, but FoS factor can easily calculated for most slope types. However, FoS values can differ by up to ±15% from results calculated by methods that satisfy force and moment balance such as Spencer's method or the Morgenstern-Price method. Although a direct comparison between different methods is not always possible, the FoS value determined using Bishop's simplified method for the expected circular sliding surface may differ slightly 5% more than the Spencer or Morgenstem - Price methods. The simple Janbu method used for non-circular surfaces, often giving FoS values up to 30% lower for the more rigorous methods. In contrast, the simplified Janbu method can give up to 5% higher FoS values for slopes and uncommon sliding surface shapes (Fredlund and Krahn, 1977) [7]. Currently, in the world, the researchers more fully evaluate the factors when calculating slope stability, considering the random change of shear resistance (c, γ, φ) of the soil as well as determining the probability of failure, however, very few studies have considered the random variation in depth. Therefore, the article proposes to simulate and evaluate the behavior of random factors in depth. These models usually adopt fixed input parameters for one or more separate locations, then through calculation methods to make general conclusions about the ability to ensure the overall stability of the slope.
Soil is a natural material and is sensitive to its surroundings, so its physical properties change from one location to another. This variation can be as part of a heterogeneous soil state. The random change of the shear resistance parameters of the soil is one of the most important problems in the analysis of geotechnical works. The field experiments with different soils have shown that the shear strength of the soil can view as a random quantity and simulated by the Normal distribution function (Lumb, 1966 [8]; Tan et al., 1993 [9]). This random variation characterized by the coefficient of variation (COV).
|
|
(1) |
As in slope stability calculations, resistance parameters, soil bearing capacity are the most important indicators in geotechnical design. The calculation methods are based on the input parameters of the soil. Therefore, it is important to identify certainly these parameters.
Through the research results on the change index of the soil's physical parameters in the calculation of geotechnical works, it is necessary to consider the physical properties of the soil as a random variable and accurately reflect the working condition of the soil. Phoon and Kulhawy (1999) [10] confirmed that the use of the Normal distribution model to simulate the random changes of mechanical properties is consistent with the experimental results.
Building a model to calculate the stability coefficient
Within the scope of the paper, the Bishop method to determine the slope stability coefficient is used and the problem considers the following parameters: weight density γ; unit cohesion c; internal friction angle φ; soil element width b; soil element self-weight W; inclined angle of the soil element to the horizontal θ; frictional force T; elemental force U; reaction N to give the factor of safety FoS without considering the shear force S between the soil elements, passive and active soil pressures E1, E2, and the presence of water in the slope.
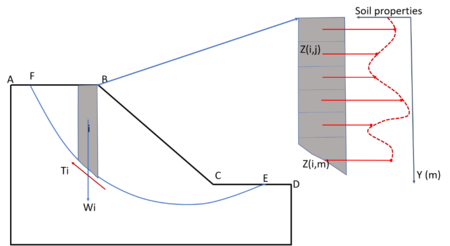
Consider the slope ABCD as shown in Figure 1, with a dangerous sliding arc EF. To determine the FoS coefficient by the Bishop method, the sliding arc region will be divided into n different pieces and the stability coefficient FoS is determined. The Bishop method does not take into account the variation of shear resistance with depth. However, when considering the change with depth of the soil shear resistance parameter in the same ith piece, according to the depth, the soil shear resistance parameter (c, φ) is different (Fig 1). This change is simulated by Karhunen-Loeve series and simulated by Matlab software. At this time, the stability coefficient FoS will be redefined as follow :
Considering the ith element fragment is divided into m subdivisions according to the depth (∆y), then the weight of the soil block i (Wi) is calculated :
Where: Δxᄌᄃ?õ;? Δy - width and thickness of element ij,
γij - density of the ijth soil element corresponding to the depth Yj
At the position of the sliding surface of the ith soil element, we will have the values of the cohesion force Ci and the internal friction angle φ which are different according to the depth Yi of the ith fragment sliding arc. At this time, the shear resistance of the ith soil element is determined as follow :
The stability factor FoS is determined in this case :
|
Results and conclusions
Analyze stability coefficient using Kahunen -Loeve serives
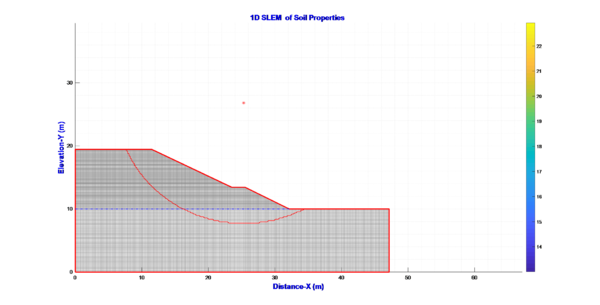
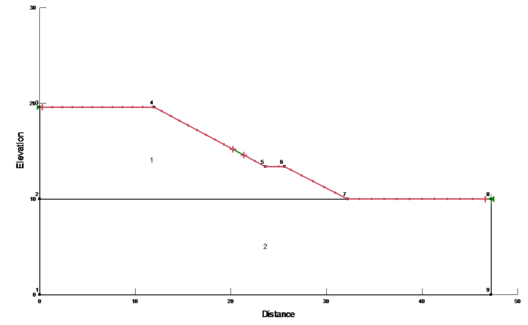
A numerical example of slope is considered in Fig 2. The avaraged values of weight of density, cohension, internal friction angle are hypothesized in Table 1. The value of CoV and width b is also selected in Table 1.
|
| Physical properties | Average | CoV | b (m) |
| Weight Density (KN/m3) | 19.5 | 0.1 | 1 |
| Cohension (KN/cm2) | 18.4 | 0.1 | 1 |
| Internal friction angle (o) | 18.4 | 0.1 | 1 |
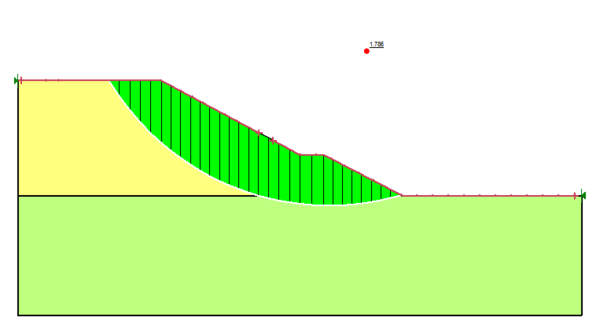
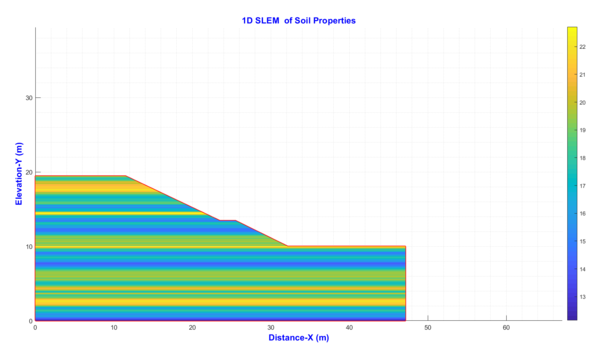
Simulation results of the change with depth of cohesion C by Kahunen -Loeve serives are showed in Fig 3. The changed value of cohesion from 13 to 22 kN/m3. The blue area show cohesion is smaller than the average value.
|
|
(4a) |
|
(4b) |
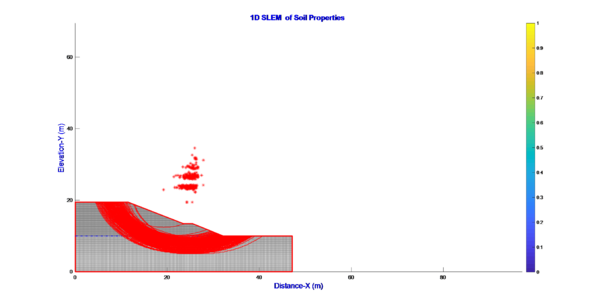
After using the Karhunen-Loeve series to simulate the change of parameters (γ, c, φ), we have the coefficient FoS is 1.48. This value is smaller than results (1.68) run using software GeoStudio 2020. These results showed in Fig 4a and Fig 4b). The results compared with the case that do not consider this change show that there is a difference in the sliding arc and the stability coefficient. This is explained because in the area of sliding arc, there are many values of density larger than the average value, while in the area of sliding arc, the load capacity is smaller than the average value (blue area in Fig 3) which make decrease in the load capacity of the slope.
Reliability analysis of slope stability considering the random change by depth of shear resistance
To analyze the reliability of the problem, using Karhunen - Loeve series to simulate the change with depth of the soil shear resistance. After using the Karhunen - Loeve series, we get the following results as Fig 5a and Fig 5b. The results of simulation times for shear resistance parameters are different. From this result, it is necessary to perform simulations for accurate analysis results, according to previous studies, the number of simulations from 1000 to 10000 will give reliable results.

(5a) |

(5b) |
After simulation, the process of determining the stability coefficient (FOS) performed. However, because the properties of the soil change randomly (with constraints), for analysis and evaluation, it is necessary to use Monte - Carlo simulation to predict all possible cases, in the article, we use 1000 times of Monte - Carlo simulation to change the quantity ξ_i (θ) in the Karhunen - Loeve simulation and the result is 1000 FoS values. The analysis process shows in Fig 6.
To determine the reliability, from the results of 1000 FOS values, the failure probability value Pf is determined as in the following formula:
In which: mean and standard deviation are determined from 1000 analyzed FOS values based on the formula:
The steps to analyze the reliability in the above problem are as follows:
Step 1: Input the parameter values from geological data.
Step 2: Use the Karhunen - Loeve series to simulate a random field X that varies with the depth of the roadbed with the following characteristics: mean (μ), standard deviation (σ) and correlation characteristic (b).
Step 3: From the combination of variables {c, φ, γ} randomly generated in step 2, using the Bishop problem and Matlab software to calculate the factor of safety FOSmin
Step 4: Use the Monte - Carlo simulation to repeat steps 2 and 3 with the number of simulations n=1000, the result will be a set of 1000 FOSmin values.
Step 5: Apply the theory of reliability and failure probability to evaluate the influence of shear resistance on slope stability.
| Parameters | µ | σ=0.1µ | σ=0.2µ | σ=0.3µ | µ | σ=0.1µ | σ=0.2µ | σ=0.3µ | |||
| Density γ (kN/m3) | 19.58 | 1.958 | 3.916 | 5.874 | 19.54 | 1.954 | 3.908 | 5.862 | |||
Cohesion
|
18.4 | 1.84 | 3.68 | 5.52 | 18.4 | 1.84 | 3.68 | 5.52 | |||
| Internal friction angle (độ) | 18.4 | 1.84 | 3.68 | 5.52 | 18.4 | 1.84 | 3.68 | 5.52 |
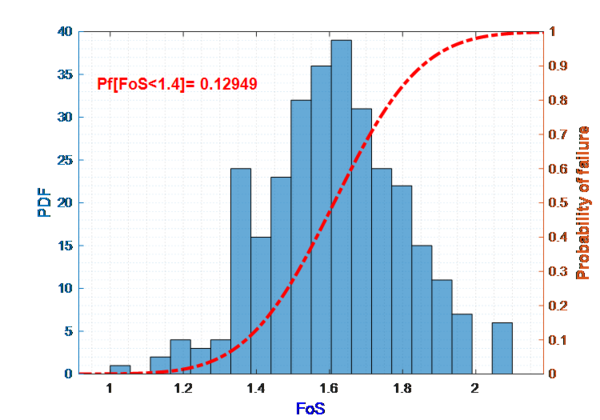
With data in table 2, after performing the five above steps, we get the result as shown in Fig 7a and Fig 7b. From the analysis results, we find that, when not considering random change, value FoS=1.68 > 1.4, slope ensures stability, however, when considering random change of basic properties, we found up to 12.95% ability of failure of the slope. This shows that when considering the random change with the depth, the slope is unstable, and the distribution is stable when considering the random change with the depth of the shear resistance parameter (c, φ) of the soil is need.
(7a) |
(7b) |
Conclusions
The article has built a model to analyze the slope stability when considering the change of shear resistance with depth based on the Bishop’s equation using Karhunen – Loeve series. With a proposed numerical model, the results compared with the case that do not consider this change (results run using software GeoStudio 2020) show that there is a difference in the sliding arc and the stability coefficient. Specifically, the results show that the value of the stability coefficient of the proposed model is 1.48, which is smaller than 1.68 of the models run with GeoStudio 2020 software. By using Monte - Carlo simulations combined with Karhunen - Loeve series, when considering the random change in depth of soil shear resistance, the forecast results are different from those only when considering the static problem and random quantity problems, the probability of failure will increase significantly (12.95%). The research results open a new direction in the calculation and quality control of slope stability.
Acknowledgements
The authors thank the Ministry of Education and Training of Vietnam, the University of Danang, University of Science and Technology, Vietnam, for supporting for this work.
Conflict of interest
All authors certify that they have participated sufficiently in the work to take public responsibility for the content, including participation in the concept, design, analysis, writing, or revision of the manuscript. Furthermore, all authors also certify that this material or similar material has not been and will not be submitted to or published in any other publication before its appearance in the Indian Geotechnical Journal.
References
1. Bishop. A.W. (1955) The Use of the Slip Circle in the Stability Analysis of Slope. Geotechnique, 10, 129-150.
2. Janbu. N (1954). Application of composite slip surfaces for stability analysis. Eur Conf Stabil Earth Slopes 3 pp 43–49
3. Morgenstern. N. R. and Price, V. E. (1965). The Analysis of the Stability of General Slip Surfaces. Geotechnique, Vol. 15, No. 1 pp. 77‐93.
4. Spencer. (1973). Thrust line criterion in embankment stability analysis.
Géotechnique. Volume 23 Issue 1, March 1973, pp. 85-100
5. Janbu. N. (1973). Slope Stability Computations. Embankment Dam Engineering, Casagrande Volume, pp. 47‐86.
6. Zhang. X, Zhou. X. (2018) Analysis of the numerical stability of soil slope using virtual-bond general particle dynamics Eng. Geol., 243 (2018), pp. 101-110.
7. Fredlund. D.G. and Krahn, J. (1977) Comparison of Slope Stability Methods of Analysis. Canadian Geotechnical Journal, 14, 429-439.
8. Lumb. P (1966). The variability of natural soils. Can Geotech J3(2):74–97.
9. Tan. CP, Donald. IB, Melchers. RE (1993) Probabilistic slip circleanalysis of earth and rockfill dams. In: Proceedings of theconference on probabilistic methods in geotechnicalengineering, Canberra, Australia, pp 281–288.
10. Phoon. K.K; Kulhawy. F.H. (1999b). Evaluation of geotechnical property variability. Canadian Geotechnical Journal, vol. 36(4): 625-639.
Document information
Published on 30/09/22
Submitted on 22/09/22
Licence: CC BY-NC-SA license
Share this document
claim authorship
Are you one of the authors of this document?