Abstract:The unsteady large-scale vortex near the turbine rim has an important influence on the sealing performance. Characteristics and performance of four sealing structures are researched in this paper. Three-dimensional unsteady numerical simulation was adopted to deeply reveal the characteristics of the rim sealing vortex and its influence mechanism on the rim sealing performance. The results show that the rim seal vortex structure induced by the interaction between ingested gas and sealing flow in the gap is the leading cause of unsteady flow in the rim. The vortex size is suppressed with the increasing seal flow rate or a Chute seal structure. However, the rim seal vortex exit in the cavity gap under a low seal flow rate can suppress the gas intrusion and improve the sealing efficiency of the turbine cavity even with a simple sealing structure. The Chute sealing structure achieves better performance among the four sealing structures studied in this paper. It can achieve complete sealing under a low sealing flow rate of 0.5% and has less impact on the aerodynamic performance of the mainstream even with high sealing flow rate. The research of this paper has guiding significance for further understanding the sealing mechanism and optimizing the design of the sealing structures.

Key Words: turbine rim seal, rim seal vortex, unsteady frequency, sealing efficiency, turbine acronymic performance

1 Introduction

The higher-temperature gas ingests into the cavity from the gap will cause a severe threat to the cavity and shaft of the turbine with the increase in turbine operating temperature. Introducing air from the compressor into the cavity effectively prevents gas ingestion and cooling the wall surface. It is still of great significance to clarify the mechanism of gas ingest and the interaction between sealed air and mainstream for the design of a secondary air systems with good performance. It is generally believed the factors that caused gas ingestion can be summarized into three aspects. (1) nonuniform distribution of mainstream pressure caused by unsteady interaction between rotor and stator, called the EI effect (2) The radial pressure gradient caused by rotor rotation will cause gas ingestion, even when the mainstream pressure is uniform. This effect is called RI. (3) Unsteady effect of rim seal, such as K-H vortex, inertia wave, etc.[1-2].

Many studies have shown that the EI is the main factor inducing gas ingestion compared with RI [3-4]. The main reason for the EI effect is the alternating high and low pressure formed in the main flow channel by the interaction between the rotor leading edge and the stator wake. Chew et al.[5] studied the influence of the axial position of the vane blade on the gas ingestion without rotor blades, and the research showed that the degree of gas ingestion weaken with the vane blades away from the disk cavity device. Bohn et al.[6-7]. reached a similar conclusion about the influence of the position of the vane on the gas ingestion. They also pointed out that both rotor blades and vane wake have a significant effect on gas ingestion and the degree of their impact was related to the sealing structure. Green and Turner et al.[3] believed that the existence of rotor blades would weaken the nonuniform pressure field caused by vane blade wake. Therefore, the presence of rotor blades improved the sealing efficiency of the cavity. Hills.[8] hold opposite views that the rotor blade will aggravate the gas ingestion rather than repress it.

Recent research on turbine cavities found that the unsteady effect of the rim is also considered to be an essential factor affecting the performance of the rim seals. Cao et al. [9] first confirmed the existence of unsteady the large-scale flow structure in the cavity through experimental research. They believed that the low-pressure region of large-scale vortex core was the main reason for increasing gas intrusion; subsequently, Jakoby, Savov, and Town. [10-12] believed that the three-dimensional unsteady flow at the rim was induced by K-H instability. The K-H vortex found by Rabs et al. [13] in an actual three-dimensional turbine device made the location of gas intrusion and purged air outflow different from the classical theory. Horwood et al. [14] found that the depth and width of gas intrusion increased at a lower seal flow rate because of the increased size and strength of the K-H vortex. Chew, Savov , and Gaofeng. [15-17] considered that the unsteady flow of the rim was closely related to the sealing structure. The more complex sealing structure corresponds to a higher unsteady frequency. The above research has reached a relatively consistent conclusion on the formation of K-H; that is, it is formed by the shear caused by the tangential velocity gradient difference between the ingesting gas and the purged flow. However, there is no clear conclusion about the interaction mechanism between gas intrusion and the K-H vortex and its influence on rim seal performance.

In addition, the formation of mixing shear near the cavity gap and outlet will affect the aerodynamic performance of the turbine by changing the upstream and downstream pressure potential fields, the downstream rotor inlet angle of attack, and the channel vortex strength. Ziqing Zhang et al.[18] pointed out that the K-H vortex weakens the tangential velocity in the rotor channel and have a particular inhibitory effect on the mainstream channel vortex. Regina et al. [19] showed that every 1% increase in the sealing flow would reduce the turbine efficiency by 0.8%. Jenny et al. [20] believed that the main reason for the rise in the aerodynamic loss of the turbine is the shear mixing of the sealed air and the mainstream and its enhancement of the channel vortex. Yang Fan.[21] believed that the loss caused by the mixing and shearing of sealing air and mainstream was relatively significant, but they considered that the impact of the change of the sealing structure on the shear loss could be ignored. In contrast, Gao Jie. [22] showed that the chute sealing structure was superior to the axial and radial sealing structure in rim seal performance.

In general, the flow in the rim seal gap has a crucial impact on the gas intrusion and turbine aerodynamic performance and is closely related to the sealing structure. In this paper, the gas intrusion mechanism and rim flow conditions with different seal structures are analyzed in detail, as well as the influence mechanism of sealing flow on the mainstream loss characteristics. The main intention of this paper is to make a deeply explore the sealing mechanism and provide reference data for the design of the sealing structure.

2. Computational Models and Numerical Approach

2.1 Geometries and Models

The numerically invested sections include a 1.5-stage turbine with a vane-blade-vane configuration. The number of blades in the numerical simulation molded as 2:3:2 since the number of blades in the whole annulus was36,54,36 respectively. Therefore, the 1/18 sector was adopted in the unsteady calculation. For more detailed instructions, refer [23]. This paper took the turbine front cavity as the research object, and the sealing structure located in the stator domain upstream of the rotor- stator interface. The sealing structures studied were axial, radial ,and chute with the angle of 30^。and 40^。. The inclination angle is between the seal structure and the axial direction. The turbine devices with four sealing structures were described as Axial, Radial,

Chute_45° ,Chute_30°in the paper, as illustrated in Fig. 1

Fig. 1.Cross section of calculated model

2.2 Numerical Approach and Mesh

Numerical simulations were performed in ANSYS CFX software. Reynolds-averaged Navier–Stokes equations and shear stress transfer (SST) turbulence model for fully three-dimensional (3D), unsteady flow were solved. The working medium was defined as the mixture of an ideal gas and CO2 tracer gas, and there was no chemical reaction between them. Structured grid generation was undertaken using NUMECA AutoGrid5 and ICEM, as displayed in Fig. 2. To minimize the interpolation error, a matching grid interface was defined between the stator and cavity domains. The circumferential grid resolution was set as 0.4 °/cell; A boundary layer grid characterized grids near the wall with the first cell height of approximately y+<1. The total number of nodes was 8.0 million after grid independence verification. Among them, the number of grids in the circumferential, axial, and spanwise directions of the calculation channels of S1, R1, and S2 blade rows were: 100×109×85、100×134×85、95×82×85.



Fig. 2. Computation mesh of 1.5-stage turbine with seal cavities

2.3 Boundary conditions

The boundary condition of the research model setting was referenced [23]. A total pressure (140Kpa) and total temperature (328K) boundary condition were used at the main path inlet, whereas an average static pressure condition was set at the main path outlet. The sealing flow rate (purge flow) represented by parameter IR, defined as the cavity inlet mass to the main flow rate, was set as 0.25%, 0.5%, 1.0%, or 1.5% in the cavity inlet. Simultaneously, the total temperature was also placed at the inlet of the cavity. The CO2 tracer gas was employed, set to o in the mainstream inlet while 1 in the cavity inlet. In the unsteady calculation, a rotor blade channel was divided into 42 steps; the physical time step was 0.00978us. It can be determined that the unsteady data converges after about 45 rotor rotation cycles through the pressure on the monitoring point at the outlet of the disk cavity, shown in Fig. 3, and the statistical average value was output in the subsequent nine rotor rotation cycles.

Fig. 3 Unsteady pressure at the monitoring point

2.4 Validation of Numerical Model

To validate the simulation method, the comparison of numerical simulation and experimental results date was shown in Fig. 4 and Fig. 5. The total pressure coefficient is defined as formula (1), where $p_{t}$ is the local total pressure on the outlet of the rotor, $p_{t,inlet}$ is the average total pressure at the pitch diameter at 50% of the axial chord length upstream of the leading edge of S1 blade, and $p_{s,exit}$ is the average static pressure at the hub position at 15% of the axial chord length downstream of the trailing edge of S2 blade. The flow angle is the angle between the flow and the axial direction.

(1)

The passage vortices near the hub and shroud can be well captured by the simulation method, which presented in Fig. 4. The experimental measurement and numerical prediction of the outlet flow angle along the radial distribution are also in good agreement, especially below 60% blade height. The relative error between the numerical value and the experimental results is less than 2.5%. This study focuses on the mainstream gas intrusion and sealing air outflow, mainly concentrated near the hub. Therefore, the numerical simulation method used is reasonable and reliable for solving the flow field distribution near the end wall of axial the turbine hub.


Fig. 4 Total pressure coefficient	Fig. 5 Flow angle of rotor exit

3 Research and Discuss

3.1 Gas ingestion and rim seal vortex

To show the circumferential position of gas ingestion, the radial velocity distribution of the cavity exit was displayed in Fig. 6 for IR=0.5%. The red area in the figure indicates that the radial velocity is positive, representing the purged flow; the blue area means gas intrusion. For the four sealing structures studied in this paper, gas intrusion occurs in circumferential regions with high pressure, such as the upstream of the rotor leading edge, the downstream of the stator wake, or the place where the rotor and stator are close to each other. The gas intrusion is the most serious when the rotor sweeps the stator wake, as displayed by the rectangular wireframe in the figure. Although the effect of the sealing structure on the circumferential position of gas intrusion is minimal, the circumferential range of gas intrusion is evident. Among the above structures, the Axial sealing structure has the most extensive intrusion circumferential field, while the Chute_30°sealing structure has the smallest intrusion range.

Fig. 6 Radial velocity contour at the outlet of the cavity（IR=0.5%，t=0T）

The Pressure nonuniformity distributed along the streamwise from stator wake to rotor leading edge(1-9) shown in 12, which can reflect the degree of gas ingestion, is defined as the difference between the maximum pressure and the minimum pressure in the circumferential direction. The nonuniformity produced by stator wake reduces rapidly along the flow direction due to its viscous dissipation, although it is enormous near the wake of the stator. The above characteristics of pressure nonuniformity attenuation can explain why the axial position of the cavity is significant for gas ingress and consistent with chew.[5] and Bohn’s [6]study work. Therefore, the rotor leading edge in this research model might mainly affect the pressure distribution at the cavity exit.

Fig. 7 Time-averaged pressure nonuniformity distributed along the streamline

To provide further insight into gas intrusion in the cavity, the circumferential region of the rectangular box identified in Fig. 6 was divided into seven parts, each accounting for 0.5 degrees. The radial velocity contour and streamline on the seven planes for four seal structures were presented in Fig. 8-.Fig. 11.

The sealing gap on the cutting planes 1 and 2 of the Axial sealing structure shown in Fig. 8 is dominated by egress flow, and no vortex is generated in the gap. 4-7 cutting planes gap is mainly governed by ingress gas; in particular, the gas intrusion at planes 5 and 6 goes deep into the inner cavity; meanwhile, there is still a part of sealing flow near the stationary wall in the gap. It is noteworthy that vortices of varies sizes are formed in the gap, and the vortex size increases with the enlarged proportion of sealing flow, such as in plane 7. The gas ingress degree of Radial and Chute_45°, Chute_30°sealing structures is weaker than that of Axial sealing structures and only occurs in the rim seal gap; correspondingly, a smaller vortex structure is formed in the gap.

According to EI induced gas ingested theory and the characteristics of the rim seal vortex analyzed above, the formation of the rim seal vortex can be summarized as follows: The gas enters the cavity gap from the rotor side under the action of high pressure close to the leading edge of the rotor. It then rolls up the vortex structure because of the interaction of ingested gas near the rotor side and egress air close to the stator side in the gap. The shear vortices can only be formed in the time when there is both ingress gas and egress flow in the clearance. According to the physical causes of vortex generation, that is to say, the radial velocity gradient and circumferential velocity gradient caused by purged flow and ingested gas in the gap are the main reasons for the formation of rim seal vortex. It is seems to be somewhat different from the traditional K-H vortex, which is considered to be generated by the tangential velocity gradient.

Wall corner vortex structure is also found in the buffer cavity except for the rim seal vortex in the upper gap for the Radial structure. For plane1 and 2, the vortex in the buffer cavity is mainly formed by the radially outward sealing flow. The wall corner vortex enlarged for sections3-7 as the interaction between the ingress gas and the egress flow in the buffer cavity. To sum up, the wall corner vortex structure in the buffer chamber is affected by the streamline curvature of the buffer chamber and the velocity gradient of the ingested gas and the egress air. Compared with the Axial seal structure, the gas intrusion depth of the Radial seal structure is reduced due to the wall corner vortex structure in the buffer cavity having a hinder effect on the radial velocity of gas ingestion.

In the research of this paper, the gas ingestion of the Chute sealing structure is the smallest because the reverse pressure gradient along spanwise produced by the sealing structure is a damping effect for gas intrusion. Only a slight gas intrusion occurs, and a small rim seal vortex structure is formed near the gap where the gas ingestion exists, for the Chute_30°.

Fig. 8 Velocity and streamline distribution in the cavity for IR=0.5%,t=0T（Axial）

Fig. 9 Velocity and streamline distribution in the cavity for IR=0.5%,t=0T（Radial）

Fig. 10 Velocity and streamline distribution in the cavity for IR=0.5%,t=0T（Chute_45°）

Fig. 11 Velocity and streamline distribution in the cavity for IR=0.5%,t=0T（Chute_30°）

3.2 Rim sealing performance

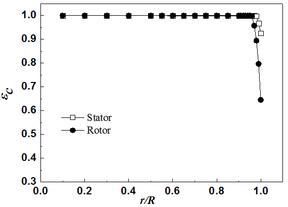
To further reveal the interaction between gas ingestion and rim seal vortex and its influence on the sealing performance of the rim seal, the radial distribution of sealing efficiency near the rotor and stationary wall of the cavity for four sealing structures was displayed in Fig. 12. The sealing efficiency defined as formula (2), where $c_{s}$ is the local tracer gas (CO2) concentration, $c_{a}$ is the mainstream inlet tracer gas concentration, $c_{0}$ is the tracer gas concentration of the purged flow in the cavity inlet.

(2)

It can be found that the sealing efficiency near the rotor wall is lower than that near the stationary wall in the clearance of rim seal for four sealing structures. According to the formation of rim seal vortices above, this phenomenon can be clarified as that the rolled-up rim seal vortex makes the ingested gas flow from the rotor side to the stationary side. As a result, the sealing efficiency near the rotor wall side is significantly lower than that near the stationary wall side. Moreover, the upward driving effect of the rotor rotation on the sealing flow has a specific blocking effect on the mainstream gas ingested from the rotor wall side. Also, it promotes the formation of the rim seal vortex. In other words, the rim seal vortices have positive significance for controlling gas ingress under low seal flow rate. The sealing efficiency of the rotor side is much lower than that of the stator side in the cavity gap for Chute sealing structure because of the smaller scale rim seal vortex, which can be proved from the above analysis. The sealing efficiency of the rotor wall side is only 52.3% of that of the stator wall side at the exit of the cavity for the Chute_30°sealing structure, while 69.2% for Radial construction, 85.3%for Axial structure.

The wall vortex effect in the buffer cavity and the pressure damping effect in the cavity makes the sealing efficiency of the rotor and stator wall side of the Radial and Chute sealing structure significantly higher than that of the Axial sealing structure.


（a）Axial	（b）Radial

（c）Chute_45°	（d）Chute_30°
Fig. 12 Time-averaged sealing efficiency distribution（IR=0.5%）

To evaluate the effect of sealing structure on sealing performance at different sealing flow rates, time-average sealing efficiency of a specific isosurface is shown in Fig. 13. This surface is located at 92% height of the disk cavity, the junction of the cavity and the cavity gap. The cavity is considered to achieve a completed sealing state when the sealing efficiency reaches 99.9%.

The sealing efficiency of the Radial and Chute structures is higher than the Axial sealing structure until the disk cavity is completely sealed. It is completely sealed for the Chute_30°when the seal flow rate reaches 0.5%, while 1.0 for the Chute_45° and Radial seal structure. In other words, the minimum sealing flow decreases with the more considerable inclination of the sealing structure for the Chute sealing structure. Furthermore, the sealing efficiency of the Chute sealing structure is significantly higher than that of Axial and Radial sealing constructions when the sealing flow rate is lower. The sealing efficiency can reach 93% for Chute_30°, even if the sealing flow is only 0.25%.

Fig. 13 Sealing efficiency for various sealing flow rates

3.3 Unsteady characteristics of rim seal

Through Fourier transform of the unsteady pressure in 9 cycles at the monitor points set in the middle of cavity clearance, the unsteady signals in the gaps of different sealing structures for IR=0.5% were obtained, as shown in Fig. 14. It indicates that the unsteady effect in the gap of the four sealing structures is mainly affected by the rotor frequency, especially for the Chute sealing structure. In addition to the rotor frequency, other unsteady frequency signals are also found in the Axial and Radial seal structure.

According to the above analysis of the flow field in the cavity gap, the rim seal vortex is obvious in the Axial and Radial seal structure gap when the seal flow rate is set as 0.5% due to the fierce gas ingress and sealing air outflow. In contrast, the vortex structure size of the Chute seal structure is tiny. What needs further attention is that almost completely sealed is achieved for Chute seal structures from Fig. 13. It can be inferred that the rim seal vortex is the cause of the unsteady frequency of the rim seal.



Fig. 14 Unsteady frequency signal of monitoring point in the gap（IR=0.5%）

To further prove this inference, Figure 16 shows the unsteady signal on the monitoring point in the gap when the sealing flow is 1.5%. The Axial and Radial sealing structures are completely sealed under this cavity inlet flow rate, and the rim seal vortex becomes weaker or disappears. Thus, unsteady signals in the gap except the rotor rotation frequency could not appear in the figure.

Some conclusions can be drawn: the rim seal vortex is the cause of the unsteady phenomenon of the rim seal, and the intermittent rim effect is both affected by the seal flow and seal structure. With the increase of the sealing flow, the unstable large-scale vortex structure of the rim seal is restrained. More importantly, even at low sealing flow, the unsteady frequency of the Chute sealing structure is not apparent.

Fig. 15 Unsteady frequency signal of monitoring point in the gap（IR=1.5%）

3.4 The influence of sealing flow on the turbine aerodynamic loss

To describe the interference loss between the sealing air and the mainstream with the different seal structures, the viscous work is introduced as a quantitative parameter. The definition of viscous work referred to Zlatinov[24], which represents the change of loss along the flow direction. The viscous work gradually increases along the flow direction due to the cumulative effect of losses shown in Fig. 16.

.

Fig. 16 Viscous work distribution along the flow direction

The variation curve of the difference between the viscous work of the Axial sealing structure and the viscous work of the Radial or Chute sealing structure along the flow direction for IR=0.5% is drawn in Fig. 17 for consideration of the sealing structure’s influence on the turbine loss in detail based on the Axial sealing structures. The viscous work of the stator region with different sealing structures is almost equal; i.e., the sealing air blocking effect on the stator channel is minimal at this flow rate. The losses of the Radial and Chute sealing structure begin to decrease compared with the Axial sealing structure from the outlet of the sealing gap, and the viscous work of Chute_ 30°is the smallest. It can be seen from the figure that the losses in the two areas marked A and B change sharply, and the corresponding positions of these two areas are at the outlet of the cavity exit and the rotor exit.

Fig. 17 Viscous work difference along the flow direction (based on the Axial sealing structure, IR=0.5%)

The variation curve of the difference between the viscous work Yang Fan and Zlatinov’s study indicates that the loss in the area is mainly caused by the mixing of sealing air and mainstream, which is affected primarily by the velocity gradient. The above research shows that the sealing air mostly flows out from the side of the cavity close to the stationary wall. The flow radial velocity near the stator wall in the cavity distributed along the spanwise was displayed in Fig. 18. The interference of the sealing air to the mainstream will aggravate with the increase of the radial velocity of the purged air, leading to the rise of loss. It can be seen from the figure that the radial velocity of the sealing air flowing out of the cavity with the Axial sealing structure is the largest. In contrast, it is the smallest for the Chute sealing structure; of course, the most negligible loss for Chute_30°in region A.

Fig. 18 Radial velocity distribution on the stationary wall side of the cavity

The interaction between sealing air and channel vortex is another reason for the increase in losses. Figure 19 shows the axial vorticity of rotor exit with different seal structures. It can be found that the size of the vortex core area of the Axial and Radial sealing structures is relatively close. In contrast, the vortex core area of the Chute sealing structure is significantly smaller than that of the Axial sealing structure, especially for the Chute_30°sealing structure. The above might have been the reason for the viscous work of Radial sealing structure does not change; however, the viscous work of Chute sealing structure decreases compared with the Axial sealing structure in region B.

Fig. 19 Axial vorticity contour at rotor exit（Below 50% span）

Figure 20 shows the distribution of turbine aerodynamic efficiency under different sealing flow rates for four seal structures. To further consider the influence of sealing air outflow on turbine aerodynamic efficiency, turbine efficiency is defined as:

{\textstyle \eta ={\frac {T_{q}\omega }{{\dot {m}}_{m}c_{p}T_{t}{}_{01}(1-{\left({\frac {\overline {P_{t}{}_{03}}}{\overline {P_{t01}}}}\right)}^{\frac {\gamma -1}{\gamma }})+{\dot {m}}_{s}c_{p}T_{t01s}(1-{\left({\frac {\overline {P_{t}{}_{03}}}{\overline {P_{t}{}_{01s}}}}\right)}^{\frac {\gamma -1}{\gamma }})}}}

(3)

Where $T_{q}$ is the torque on the moving blade, ${\dot {m}}_{m}$ is the mainstream flow, ${\textstyle {\overline {P_{t03}}}}$ is the total pressure of the average area of the rotor outlet, ${\textstyle {\overline {P_{t01s}}}}$ is the total pressure of the turbine cavity inlet, ${\dot {m}}_{s}$ Is the sealed flow.

With the increase of the sealing flow, the interference between the sealing air and the mainstream will reduce the aerodynamic efficiency of the turbine. The aerodynamic efficiency of the turbine with a Radial or Chute seal structure decreases more slowly than the Axial seal structure with the increasing purged flow rate. The turbine with a Chute_ 30°.sealing structure maintains high aerodynamic efficiency in the studied flow rate range. The aerodynamic efficiency of Chute_30° would increase by 0.43% compared with the simple Axial sealing structure when the sealing flow is 1.0%.

Fig. 20 Turbine aerodynamic efficiency

4. Conclusion

A three-dimensional unsteady numerical method was used to analyze the flow mechanism near the turbine rim with different sealing structures. The research shows that the rim seal vortex structure in the cavity gap has an essential influence on the sealing performance of the rim seal. The turbine with a Chute seal structure has a good performance in cavity sealing efficiency and turbine aerodynamic efficiency, although its design is straightforward. The specific conclusions are summarized as follows:

1) The rim seal vortex structure is formed by the interaction between the ingested gas and the purged flow in the sealing gap and is affected by both the sealing flow rate and the sealing structure. The strength of the rim seal vortex decreased with the increase of the sealing flow and was the smallest for the Chute_30°sealing structure under the same sealing flow rate. Moreover, the interaction between the rim seal vortex and the rotating pump effect blocks the gas ingested from the rotating side. Therefore, the rim seal vortex has a positive significance for controlling the gas intrusion in the turbine cavity at a low seal flow rate.

2) Through the frequency spectrum analysis of unsteady pressure in the gap, it can be considered that the rim seal vortex is the leading cause of unsteady flow in the rim seal. Thus, the intermittent frequency signal of the rim disappears when the sealing flow is 1.5, i.e., fully sealed, and the Chute sealing structure has a positive significance for restraining the unsteady flow of the rim.

3) The Chute sealing structure has high sealing efficiency in the range of sealing flow studied. The complete sealing flow of Chute_30°is only 0.5%, while it is 1.5% for Axial construction.

4) The viscosity loss of the turbine with a Chute seal structure is significantly reduced compared to the turbine with an Axial structure due to the lower radial velocity at the outlet of the turbine cavity and the weaker interaction between sealing air and channel vortex. The aerodynamic efficiency of the turbine with a Chute_30°sealing structure increased by 0.43% compared with Axial sealing structure when the sealing flow is 1.0%.

Reference

[1]. James A.Scobie,Carl M.Sangan,J.Michael Owen, et al, Review of ingress in gas turbine[J], Journal of Engineering for Gas Turbine and Power, 2016,Vol.138:120801-1:16.

[2]. John W Chew,Feng Gao,Donato M Palermo, Flow mechanism in axial turbine rim sealing[J],Proc IMechE Part C:J Mechanical Engineering Science,2019, 233(23-24):7368-7655.

[3]. Green, T., and Turner, A.B., 1994, “Ingestion Into the Upstream Wheelspace of an Axial Turbine Stage.” J. Turbomach., 116(2): 327-332.

[4]. Bohn, D. E., Decker, A., Ohlendorf, N., and Jakoby, R., 2006, “Influence of an Axial and Radial Rim Seal Geometry on Hot Gas Ingestion Into the Upstream Cavity of a 1.5-Stage Turbine,” ASME Paper No. GT2006-90453.

[5]. Chew, J. W., Green, T., and Turner, A. B., 1994, “Rim Sealing of Rotor-Stator Wheelspaces in the Presence of External Flow,” ASME Paper No. 94-GT-126.

[6]. Bohn, D. E., Rudzinski, B., S€urken, N., and G€artner, W., 2000, “Experimental and Numerical Investigation of the Influence of Rotor Blades on Hot Gas Ingestion Into the Upstream Cavity of an Axial Turbine Stage,” ASME Paper No.000-GT-0284.

[7]. Bohn, D. E., Decker, A., Ma, H., and Wolff, M., 2003, “Influence of Sealing Air Mass Flow on the Velocity Distribution in and Inside the Rim Seal of the Upstream Cavity of a 1.5-Stage Turbine,” ASME Paper No. GT2003-38459

[8]. Hills, N. J., Chew, J. W., and Turner, A. B., 2002, “Computational and Mathematical Modeling of Turbine Rim Seal Ingestion,” ASME J. Turbomach.,124(2), pp. 306–315

[9]. Cao C, Chew JW, Millington PR, et al. Interaction of rim seal and annulus flows in an axial flow turbine. In:Proceedings of the ASME Turbo Expo 2003, 2003, paper no. GT2003-38368. Also ASME J Eng Gas Turbines Power 2003; 126: 786–793.

[10]. Jakoby R, Zierer T, Lindblad K, et al. Numerical simulation of the unsteady flow field in an axial gas turbine rim seal configuration. In: Proceedings of the ASME turbo expo 2004, 2004, paper no. GT2004-53829.

[11]. Savov SS, Atkins NJ and Uchida SA. Comparison of single and double lip rim seal geometries. ASME J Eng Gas Turbines Power 2017; 139: 112601–112601-13.

[12]. Town J, Averbach M and Camci C. Experimental and numerical investigation of unsteady structures within the rim seal cavity in the presence of purge mass flow. In: ASME turbo expo, 2016, paper no.GT2016-56500.

[13]. M. Rabs, F.-K. Benra, H. J. Dohmen, and O. Schneider. Investigation of flow instabilities near the rim cavity of a 1.5 stage gas turbine. In Proceedings of the ASME Turbo Expo 2009: Power for Land, Sea, and Air, 2009. Paper No.GT2009-59965

[14]. Horwood J T, Hualca F P, Scobie J A, et al. Experimental and Computational Investigation of Flow Instabilities in Turbine Rim Seals[J].Journal of Engineering for Gas Turbines and Power-transactions of The Asme, 2019, 141(1)

[15]. Savov SS, Atkins NJ and Uchida SA. Comparison of single and double lip rim seal geometries. ASME J Eng Gas Turbines Power 2017; 139: 112601–112601-13.

[16]. J. W. Chew, F. Gao, and D. M. Palermo. Flow mechanisms in axial turbine rim sealing. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2018.

[17]. F. Gao, J. W. Chew, P. F. Beard, D. Amirante, and N. J. Hills. Large-eddy simulation of unsteady turbine rim sealing flows. International Journal of Heat and Fluid Flow, 70:160–170, 2018.

[18]. Ziqing Zhang,Yingjie Zhang,Xu Dong et al,Flow mechanism between purge flow and mainstream in different turbine rim seal configurations.[J],Chinese Journal of Aeronautics,2020,33(8):2162-2175

[19]. Regina.K, Kalfas A L, Abhari R S, Experiment investigation of purge flow effects on a high pressure turbine stage[J],Journal of Turbomachinery,2015,Vol.137:041006:1-7

[20]. Jenny P, Abhari R S,Rose M G,Unsteady rotor hub passage vortex behavior in the presence of purge flow in an axial low pressure turbine[J] Journal of turbomachinery,2013,135(05): 051022-1:9

[21]. Fan Yang , Li Zhou and Zhanxue Wang.Unsteady numerical investigation on viscous shear loss caused by rim seal purge flow[J],Journal of Power and Energy,2019,0(0)1-12

[22]. Gao Jie,Cao FuKun,Chu ZhaoFeng,et al, Unsteady flow characteristics and structural optimization of rotary induced rim seal[J],Science China Press:Scientia, 2019,49(07):753-766

[23]. Behr T. Control of rotor tip leakage and secondary flow by casing air injection in unshrouded axial turbines

[24]. Zlatinov M B,Tan V S,Montgomery M，et al. Turbine Hub and Shroud Sealing Flow Loss Mechanisms［J］.Journal of Turbomachinery，2012，134（11）：1-12.