Analysis of bending-twisting coupling in angle-ply laminates

J. de Gracia^a, A. Boyano^a, A. Arrese^b, F. Mujika^b

GRUPO MATERIALES + TECNOLOGÍAS / MECÁNICA DE MATERIALES

^aDepartamento de Ingeniería Mecánica, Escuela de Ingeniería de Vitoria-Gasteiz.

Universidad del País Vasco. Nieves Cano, 12, 01006 Vitoria-Gasteiz, España.

^b Departamento de Ingeniería Mecánica, Escuela de Ingeniería de Guipúzcoa.

Universidad del País Vasco. Plaza de Europa, 1, 20018. San Sebastián, España

Análisis del acoplamiento flexión-torsión en laminados angulares
Historia del artículo: Recibido 6 de Junio 2019 En la versión revisada 20 de Junio 2019 Aceptado 5 de Julio 2019 Accesible online 18 de Enero de 2021	El objetivo del presente estudio es la evaluación del efecto del acoplamiento flexión-torsión en el análisis del ensayo DCB mediante la determinación analítica de la tasa de liberación de energía de composites laminados angulares. Se trata de ampliar un estudio anterior de los mismos autores a nuevas configuraciones de laminado. Se analizan laminados angulares de brazos simétricos, ya que, en este caso la aplicación de un momento flector por medio de las bisagras provoca una rotación de torsión en cada uno de los brazos. Dicha torsión es impedida por las bisagras, debido a la propia configuración del ensayo. Por tanto, existe una distribución de cargas no uniforme aplicada por las bisagras, cuya resultante es la carga aplicada P y el momento resultante un momento torsor desconocido mt, que evita la rotación en el punto de aplicación. La resolución del sistema de fuerzas y momentos resultante permite obtener analíticamente la tasa de liberación de energía, y analizar los términos debidos exclusivamente al acoplamiento flexión-torsión.
Palabras clave: Fractura interlaminar Double Cantilever Beam Multidireccional Efectos de acoplamiento
Analysis of bending-twisting coupling in angle-ply laminates
Keywords: Delamination Double Cantilever Beam Multidireccional Coupling effects	The purpose of the present study is the evaluation of the bending-twisting coupling effect in the analysis of the DCB test by means of the analytical determination of the energy release rate of angle-ply laminated composites. The aim is to extend a previous work done by the same authors to new laminate configurations. Angle-ply laminates with symmetrical arms are analyzed, since in this case the application of a bending moment by means of the piano hinges causes a torsional rotation in each of the arms. That torsion is prevented by the hinges, due to the configuration of the test. Therefore, there is a non-uniform load distribution applied by the hinges, whose resultant is the applied load P and the resultant moment is an unknown twisting moment mt, which prevents rotation at the point of application. The resolution of the resulting system of forces and moments allows obtaining analytically the energy release rate, and analyzing the terms due exclusively to the bending-twisting coupling

1 Introducción

A pesar de que el ensayo DCB ha sido normalizado para laminados unidireccionales, a menudo son usados para calcular la tasa de liberación de energía de laminados multidireccionales [1, 2, 3].

Sin embargo, algunos factores que carecen de importancia en el ensayo de laminados unidireccionales, pueden afectar seriamente el comportamiento y los resultados en laminados multidireccionales , tales como la secuencia de apilamiento, la simetría del laminado, la curvatura del frente de grieta, la mezcla de modos de fractura, las tensiones residuales debidas a los efectos higrotérmicos o los daños que se van produciendo durante el avance de la grieta, como la rotura de fibras o los puentes de fibra que se forman.

Algunos estudios concluyen que el valor de iniciación G_Ic de laminados multidireccionales es prácticamente independiente de la orientación de las láminas que forman el plano de deslaminación [3, 4] , mientras que otros concluyen lo contrario [5, 6].

La mayoría de los trabajos que se realizan con laminados multidireccionales se aplican, en general, a secuencias de apilamiento que evitan los acoplamientos flexión-torsión debido a las dificultades relacionadas con las curvaturas de torsión.

En el presente trabajo se incluye el efecto del acoplamiento flexión-torsión en el análisis del ensayo DCB. Se analizan laminados angulares simétricos con brazos simétricos, de manera que las tensiones residuales sean mínimas y se puedan aislar los acoplamientos.

Al ser los brazos laminados simétricos, la existencia del acoplamiento flexión-torsión se traduce en que al aplicar un momento flector por medio de las bisagras se provoca una rotación de torsión en cada uno de los brazos de la probeta.

2 Laminados simétricos

2.1 Campo de desplazamientos y deformaciones

Fig. 1 Geometría de la probeta y sistema de referencia adoptado

Con el objetivo de modelar las probetas, se adopta una geometría tipo banda, con los ejes tal y como aparecen en la [[#_Ref10028596|Fig. 1. Se asume que el campo de desplazamientos es el siguiente:

${\textstyle \,<math>{\begin{array}{c}u=u_{0}(x,y)+z{\theta }_{x}(x,y)\\v=v_{0}(x,y)+z{\theta }_{y}(x,y)\\w=w_{0}(x,y)=w_{0}(x)-y{\theta }_{y}(x)\end{array}}}$</math>

(1)

Donde u₀, v₀ y w₀, funciones de x e y, son los desplazamientos del plano medio en las direcciones x, y y z, respectivamente, mientras que θ_x y θ_y son los ángulos de flexión y torsión respectivamente. Este campo de desplazamientos tiene en cuenta tanto la flexión como la torsión. Las deformaciones asociadas a este campo se obtienen derivando los desplazamientos:

${\textstyle \,<math>{\begin{array}{c}{\epsilon }_{x}=u_{,x}={\epsilon }_{x}^{0}+z{\kappa }_{x}\\{\epsilon }_{y}=v_{,y}={\epsilon }_{y}^{0}+z{\kappa }_{y}\\{\epsilon }_{z}=0\\{\gamma }_{s}={\gamma }_{s}=u_{,y}+v_{,x}={\gamma }_{xy}^{0}+z{\kappa }_{xy}\\{\gamma }_{r}=0=u_{,z}+w_{,x}={\theta }_{x}+w_{0,x}-y{\theta }_{y}^{'}\\{\gamma }_{q}=0=v_{,z}+w_{,y}={\theta }_{y}-{\theta }_{y}=0\end{array}}}$</math>

(2)

Las deformaciones y curvaturas del plano medio en (2) se definen como:

${\textstyle \,<math>{\begin{array}{c}{\epsilon }_{x}^{0}=u_{0}{}_{,x}{\mbox{; }}{\epsilon }_{y}^{0}=v_{0}{}_{,y}{\mbox{; }}{\gamma }_{s}^{0}=u_{0}{}_{,y}+v_{0}{}_{,x}\\{\kappa }_{x}={\theta }_{x}{}_{,x};{\mbox{ }}{\kappa }_{y}={\theta }_{y}{}_{,y}=0\\{\kappa }_{xy}={\kappa }_{s}={\theta }_{x}{}_{,y}+{\theta }_{y}{}_{,x}={\theta }_{x}{}_{,y}+{{\theta }^{'}}_{y}\end{array}}}$</math>

(3)

2.2 Relaciones carga-desplazamiento

2.2.1 Comportamiento en el plano

Los laminados simétricos se forman mediante pares de láminas iguales y orientadas en la misma dirección a ambos lados del plano medio. Si además todas las láminas están orientadas en direcciones +θ y -θ se denomina laminado simétrico angular.

La ecuación constitutiva en este caso viene dada por [7]:

File:Igelmo et al 2021a-image11.png

Como las matrices de flexibilidad [b] y [c] son nulas, no existe acoplamiento entre fuerzas de membrana y curvaturas del laminado ni entre momentos y deformaciones de membrana. Sin embargo, si existirá acoplamiento flexión-torsión ya que los coeficientes d_xs y d_ys no son nulos.

El hecho de que probetas que se ensayan en este trabajo tengan un ángulo θ=45º resulta en que a_xx=a_yy y que d_xx=d_yy.

En cuanto a los efectos higrotérmicos, para esta secuencia de apilamiento las únicas cargas equivalentes que aparecen una vez el material se ha enfriado hasta la temperatura ambiente son fuerzas axiales en x e y, que además son iguales debido al ángulo de 45º.

2.2.2 Comportamiento fuera del plano

En esta sección se va a utilizar la notación de Daniel e Ishai [7], siendo los subíndices yz = q y zx = r. La relación constitutiva correspondiente a las componentes de deformación cortante fuera del plano, g_q y g_r es independiente de la relación en el plano, y viene dada por:

${\textstyle \,{\left\{{\begin{array}{c}{\gamma }_{q}\\{\gamma }_{r}\end{array}}\right\}}_{k}={\left[{\begin{array}{cc}S_{qq}&S_{qr}\\S_{qr}&S_{rr}\end{array}}\right]}_{k}{\left\{{\begin{array}{c}{\tau }_{q}\\{\tau }_{r}\end{array}}\right\}}_{k}}$

(4)

En el campo de desplazamientos adoptado, que tiene en cuenta tanto la flexión como la torsión, g_q y g_r son independientes de z y por tanto la relación anterior puede expresarse en términos de los valores medios de las deformaciones en el espesor:

${\textstyle {\mathit {\boldsymbol {\,}}}\left\{{\begin{array}{c}{\overline {\gamma }}_{q}\\{\overline {\gamma }}_{r}\end{array}}\right\}={\frac {1}{h}}\left[{\begin{array}{cc}{\overline {S}}_{qq}&{\overline {S}}_{qr}\\{\overline {S}}_{qr}&{\overline {S}}_{rr}\end{array}}\right]\left\{{\begin{array}{c}V_{q}\\V_{r}\end{array}}\right\}{\mathit {\boldsymbol {\quad }}}}$

(5)

Donde V_q y V_r son las resultantes de los esfuerzos cortantes por unidad de longitud y h es el espesor del laminado. Los coeficientes de flexibilidad equivalentes corresponden al valor medio de todo el laminado [8]. Dado que en los laminados estudiados en este trabajo todas las láminas están orientadas a θ =45º y θ =-45º, los valores absolutos de ${\textstyle \,{\overline {S}}_{ij}}$ con i, j = q, r son iguales.

2.3 Distribución de Ms

La distribución a través de la anchura del laminado de M_s se puede obtener de las ecuaciones de equilibrio sobre uno de los brazos de la probeta, teniendo en cuenta la ecuación constitutiva de los laminados estudiados y que las únicas cargas por unidad de longitud aplicadas en este caso son M_x y M_s.

${\textstyle \,<math>M_{s}={\frac {d_{xs}M_{x}-2{{\theta }^{'}}_{y}}{d_{ss}}}\left({\frac {coshky}{cosh\lambda }}-\right.}$$\left.1\right)$</math>

(6)

Donde d_xs y d_ss son coeficientes de flexibilidad del laminado y l y k son parámetros relacionados con los coeficientes de flexibilidad equivalentes Failed to parse (syntax error): {\textstyle \, <math display="inline">{\overline{S}}_{ij}} </math> definidos en el anterior apartado.

3 Aproximación analítica

3.1 Cargas aplicadas y reacciones

3.1.1 Momento flector

La distribución de momentos flectores se calcula mediante la aproximación presentada en [9]. La Fig. 2 muestra un modelo de la mitad inferior de una probeta DCB con las fuerzas distribuidas que equilibran la carga P aplicada en el ensayo.

File:Igelmo et al 2021a-image17-c.png

Fig. 2 Fuerza distribuida sobre la viga

El método señalado permite determinar las distribuciones de momentos flectores en función de la grieta a, de parámetros geométricos de la probeta y de propiedades mecánicas del material.

3.1.2 Momento torsor

En la configuración estudiada, el hecho de que exista un acoplamiento entre la flexión y la torsión lleva a que los brazos del laminado sufran una torsión dependiente de la carga P aplicada durante el ensayo. Esta curvatura tendrá sentido opuesto en cada uno de los brazos del laminado, ya que el laminado es simétrico (Fig. 3).

Fig. 3 Rotación en el frente de grieta

Al estar la rotación en el punto de aplicación de la carga impedida por las bisagras, se está aplicando un momento torsor que induce un momento reactivo, el cual se va a suponer concentrado en el frente de grieta.

La distribución del momento torsor por unidad de longitud es la presentada 2.3:

${\textstyle \,M_{s}={\frac {d_{xs}M_{x_{a}}-2{{\theta }^{'}}_{y}}{d_{ss}}}\left({\frac {coshky}{cosh\lambda }}-\right.\left.1\right)}$

(7)

Donde M_xa es el momento flector por unidad de longitud en el frente de grieta.

La mitad del momento torsor de una sección rectangular corresponde a M_s y la otra mitad corresponde a la resultante de la fuerza cortante fuera del plano ${\textstyle \,V_{r}^{t}}$ [10]:

${\textstyle \,m_{t}={\int }_{L_{y}}M_{s}dy+{\int }_{L_{y}}V_{r}^{t}ydy}$

(8)

Y, por tanto:

${\textstyle \,m_{t}=2{\int }_{L_{y}}M_{s}dy={\frac {2\left(d_{xs}M_{x_{a}}-2{{\theta }^{'}}_{y}\right)}{d_{ss}}}b(\xi -1)}$

(9)

Donde:

${\textstyle \,\xi ={\frac {1}{\lambda }}tanh\lambda }$

(10)

La relación entre M_s y m_t es:

${\textstyle \,M_{s}={\frac {1}{2b(\xi -1)}}\left({\frac {coshky}{cosh\lambda }}-\right.\left.1\right)m_{t}}$

(11)

Los momentos resultantes vienen dados por:

${\textstyle \,\left\{{\overline {M}}\right\}=\left\{{\begin{array}{c}M_{x}\\0\\M_{s}\end{array}}\right\}}$

(12)

La expresión de la energía complementaria de un laminado multidireccional debida a un estado de tension plana [11] es la siguiente:

${\textstyle \,U^{\ast }={\frac {1}{2}}{\int }_{L_{x}}{\int }_{L_{y}}\left(\right)dxdy-{\frac {1}{2}}LbB}$

(13)

Sabiendo que la rotación en la sección de aplicación de la carga es nula, se aplica el teorema de Engesser-Castigliano con el objetivo de determinar el momento torsor aplicado por las bisagras:

${\textstyle \,U_{,m_{t_{a}}}^{\ast }={\int }_{L_{x}}{\int }_{L_{y}}\left(\right)dxdy=0\,}$

(14)

Resolviendo la ecuación anterior se obtiene M_s :

${\textstyle \,M_{s}={\frac {d_{xs}}{d_{ss}}}{\frac {\xi -1}{3(1-\xi )-{\lambda }^{2}{\xi }^{2}}}\left({\frac {coshky}{cosh\lambda }}-\right.\left.1\right){\frac {Pa}{b}}}$

(15)

Y teniendo en cuenta la relación de M_s y m_t, el momento torsor aplicado por las bisagras es:

${\textstyle \,m_{t_{a}}={\frac {d_{xs}}{d_{ss}}}{\frac {2{\left(\xi -1\right)}^{2}}{3(1-\xi )-{\lambda }^{2}{\xi }^{2}}}Pa}$

(16)

Fig. 4 Distribución del momento torsor en el ancho

La Fig. 4 muestra la distribución en el ancho para diferentes anchuras (10, 15 y 20mm) del momento torsor normalizado respecto a la carga aplicada, para el material T6T/F593 y secuencia estudiada cuando la longitud de grieta es a = 50mm.

3.2 Tasa de liberación de energía

La relación entre la energía de relajación y la energía complementaria es la siguiente [12]:

${\textstyle \,G={\frac {1}{b}}{\left({\frac {\partial U^{\ast }}{\partial a}}\right)}_{F_{i}}}$

(17)

Derivando, por tanto, la expresión de la energía complementaria (13), en la que se sustituyen las cargas aplicadas, ecuación (12), y teniendo en cuenta las relaciones entre coeficientes de flexibilidad de los laminados simétricos, se obtiene la siguiente expresión de G:

${\textstyle \,G={\frac {2}{b}}{\int }_{L_{x}}{\int }_{L_{y}}\left(\right)dxdy+}$${\frac {1}{b}}{\int }_{L_{y}}d_{ss}M_{s}^{2}dy$

(18)

El término precedido por d_xx está directamente relacionado con el momento flector aplicado y por tanto corresponde a la parte predominante de la tasa de liberación de energía debida al modo I de fractura. Los términos con coeficiente d_xs están relacionados con el acoplamiento flexión-torsión. Por último, los términos que contienen el coeficiente d_ss están relacionados con la torsión.

Teniendo en cuenta estas consideraciones, si se sustituyen en la expresión (18) las distribuciones de los momentos flectores y torsores calculados anteriormente, se obtiene:

${\textstyle \,G_{I}(flexi{\acute {o}}n)={\frac {P^{2}d_{xx}}{b^{2}}}\left({\varphi }_{0}+\right.\left.{\varphi }_{1}a+a^{2}\right)-{\frac {d_{xs}^{2}}{d_{ss}}}{\frac {{\left(\xi -1\right)}^{2}}{3(1-\xi )-{\lambda }^{2}{\xi }^{2}}}{\left({\frac {Pa}{b}}\right)}^{2}}$

(19)

${\textstyle \,G_{I}(torsi{\acute {o}}n)=-{\frac {1}{2}}{\frac {d_{xs}^{2}}{d_{ss}}}{\frac {{\left(\xi -1\right)}^{2}}{3(1-\xi )-{\lambda }^{2}{\xi }^{2}}}{\left({\frac {Pa}{b}}\right)}^{2}}$

(20)

Los factores f₀ y f₁ son los definidos en la referencia [9]. El signo negativo es debido a que el momento torsor es inducido por el momento flector facilitando el crecimiento de grieta. El momento torsor provoca que la distribución de las tensiones normales en el frente de grieta no sea uniforme, con la consecuente apertura lateral.

3.3 Desplazamiento del punto de aplicación de la carga

La distancia, en el ensayo DCB, entre los puntos de aplicación de la carga (2d) se ve afectada, en el caso de los laminados estudiados en este trabajo, debido al acoplamiento flexión-torsión.

Teniendo en cuenta la la energía complementaria del laminado dada en (13), se aplica el teorema de Engesser-Castigliano obteniendo, para la configuración estudiada, la siguiente expresión en función de los momentos flectores y torsores:

$\,\delta ={\int }_{L_{x}}{\int }_{L_{y}}\left(\right)dxdy$

Resolviendo la integral con las expresiones de los momentos calculadas anteriormente:

$\,\delta =d_{xx}{\frac {P}{b}}({\frac {1}{3}}a^{3}+{\frac {{\beta }_{1}}{4}}a^{2}+$${\frac {{\beta }_{2}}{12}}a+~{\frac {{\beta }_{3}}{60}})-{\frac {1}{2}}{\frac {d_{xs}^{2}}{d_{ss}}}{\frac {{\left(\xi -1\right)}^{2}}{3(1-\xi )-{\lambda }^{2}{\xi }^{2}}}{\frac {P}{b}}a^{3}$

Donde b₁, b₂ y b₃ son parámetros dependientes de la geometría y propiedades mecánicas de la pieza. El primer término es la solución para laminados unidireccionales obtenida en [9] y por tanto debida unicamente al momento flector. El segundo térmico se corresponde con el acoplamiento flexión-torsión.

4 Experimental

Se han fabricado 4 probetas de material T6T/F593 con la configuración ${\textstyle \,{\left[{\left(\pm {45}_{2}\right)}_{s}\right]}_{s}}$ .Previamente a los ensayos DCB, se ha medido el módulo de flexión de cada una de las probetas de cada secuencia mediante ensayos de flexión de tres puntos [11], obteniendo el valor: ${\textstyle {E}_{f}=14118\pm 266\,MPa}$.

Los resultados obtenidos con el método presentado se han comparado con los obtenidos por medio tanto del método de Williams (MBT) y con el método de las áreas.

Fig. 5 Tasa crítica de liberación de energía.

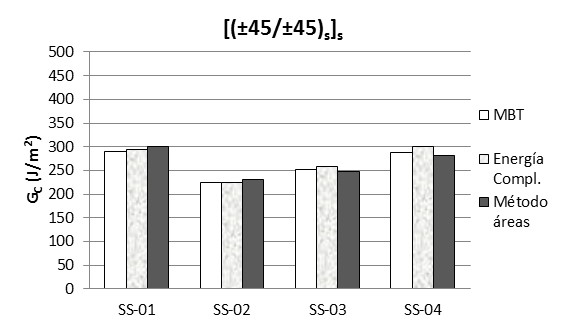
Se han determinado las propiedades interlaminares únicamente en la iniciación del crecimiento de grieta. La Fig. 5 muestra la comparación de los valores de Gc obtenidos para cuatro probetas simétricas. Como se puede observar, aunque los resultados para diferentes probetas varían significativamente, los valores son similares para cada una de ellas mediante los tres métodos de reducción de datos utilizados.

El valor medio obtenido mediante la energía complementaria es ${\textstyle \,G_{c}=270\pm 35J/m^{2}}$ , mientras que el máximo valor del efecto de acoplamiento flexión-torsión obtenido ha sido ${\textstyle \,G_{I}(acoplamiento)=-2,3J/m^{2}}$ . Este valor incluye los términos con coeficiente d_xs en las ecuaciones (19) y (20).

5 Conclusiones

Se han analizado probetas DCB de laminados angulares simétricos con brazos simétricos, obteniendo una solución analítica de la tasa de liberación de energía. El acoplamiento flexión-torsión provoca rotaciones de torsión, que son de sentido contrario en los brazos de la probeta.

Se ha determinado la influencia del acoplamiento y se ha incluido en los cálculos, considerando una distribución del momento torsor por unidad de longitud no uniforme en la anchura de la probeta. Además, el acoplamiento flexión-torsión tiene influencia en el desplazamiento del punto de aplicación de la carga, que también se ha determinado.

Las expresiones obtenidas se han validado experimentalmente, comparando los resultados con los obtenidos por medio del método de las áreas y por el de la teoría de vigas modificada. Se observa que, en los materiales ensayados, la influencia de los nuevos términos obtenidos no es mayor del 3%. Teniendo en cuenta la dispersión de los resultados del ensayo DCB, principalmente en laminados multidireccionales, la influencia puede considerarse despreciable.

Agradecimientos

Los autores agradecen a la Universidad del País Vasco (UPV/EHU) la financiación del Grupo de Investigación Mecánica de Materiales GIU 16/51 en la convocatoria de 2016.

Referencias

[1]	A. B. De Morais, «Double cantilever beam testing of multidirectional laminates,» Composites: Part A, vol. 34, nº 12, p. 1135–1142, 2003.
[2]	M. J. Hiley, «Delamination between multi-directional ply interfaces in carbon-epoxy composites under static and fatigue loading,» European Structural Integrity Society, vol. 27, pp. 61-72, 2000.
[3]	A. B. Pereira y A. B. de Morais, «Mode I interlaminar fracture of carbon/epoxy multidirectional laminates,» Composites Science & Technology, vol. 64, pp. 2261-2270, 2004.
[4]	A. Laksimi, A. Ahmed Benyahia, M. L. Benzeggagh y X. L. Gong, «Initiation and bifurcation mechanisms of cracks in multi-directional laminates,» Composites Science and Technology, vol. 60, pp. 597-604, 2000.
[5]	N. S. Choi, A. J. Kinloch y J. G. Williams, «Delamination Fracture of Multidirectional Carbon-Fiber/Epoxy Composites under Mode I, Mode II and Mixed Mode I/II Loading,» Journal of Composite Materials, vol. 33, nº 1, pp. 73-100, 1999.
[6]	P. Robinson y D. Q. Song, «Robinson, Song. A Modified DCB Specimen for Mode I Testing of Multidirectional Laminates,» Journal of Composite Materials, vol. 26, nº 11, pp. 1554-1577, 1992.
[7]	I. Daniel y O. Ishai, Engineering mechanics of composite materials, New York: Oxford university press , 2006.
[8]	J. Romera, M. Cantera, I. Adarraga y F. Mujika, «A top-down analytic approach for the analysis of edge effects of angle-ply symmetric laminates,» Composite Structures, vol. 104, pp. 60-70, 2013.
[9]	J. De Gracia, A. Boyano, A. Arrese y F. Mujika, «A new approach for determining the R-curve in DCB tests without optical measurements,» Engineering Fracture Mechanics, vol. 135, pp. 274-285, 2015.
[10]	V. V. Vasilev y E. V. Morozov, Mechanics And Analysis Of Composite Materials, Oxford: ElsevierScience Limited, 2001.
[11]	F. Mujika, «A novel approach for the three point flexure test of multidirectional laminates,» Journal of Composite Materials, vol. 46, nº 3, pp. 259-274, 2011.
[12]	A. Boyano, J. de Gracia, A. Arrese y F. Mujika, «Equivalent energy release rate and crack stability in the End Notched Flexure with inserted roller mixed mode I/II test,» Theoretical and Applied Fracture Mechanics, vol. 87, pp. 99-109, 2017.