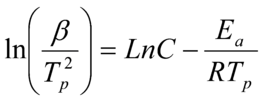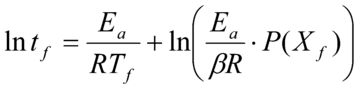Decomposition kinetics and lifetime estimation on natural fibre reinforced thermoplastic composites

B. Enciso^a, J. Abenojar^a, G.M. Aparicio^b, M.A. Martínez^a

^aDepartamento de Ciencia e Ingeniería de Materiales e Ingeniería Química, IAAB, Grupo de Comportamiento en Servicio de Materiales, Universidad Carlos III de Madrid, España

^bGinsai Group, Universidad Autónoma de Occidente, Cali, Colombia

Cinética de descomposición y estimación de vida en servicio de materiales compuestos termoplásticos reforzados con fibras naturales
Historia del artículo: Recibido 23 de Mayo 2019 En la versión revisada 20 de Junio 2019 Aceptado 5 de Julio 2019 Accesible online 18 de Enero de 2021	El presente estudio pretende analizar la influencia del tipo de fibra natural y del tratamiento superficial de plasma de baja presión, sobre la cinética de descomposición de materiales compuestos de matriz termoplástica, así como estimar su vida en servicio. Para ello se compararon dos modelos cinéticos, Kissinger y Model Free Kinetics. Los materiales se prepararon utilizando LDPE como matriz y fibras naturales de lino y coco, tratadas con plasma y sin tratar y a un 20 y un 30% en peso, como refuerzo. Se fabricaron empleando una mezcladora de rotores y una prensa de platos calientes. Posteriormente, para cada material, se llevaron a cabo los ensayos termogravimétricos a seis velocidades diferentes y mediante un espectrómetro de masas se identificaron los elementos desprendidos durante el proceso y la temperatura a la cual lo hacían. A partir de las energías de activación del proceso de descomposición y mediante la ecuación de Toop, se estimó la vida en servicio de cada uno de los nueve materiales objeto de estudio. Se ha demostrado que el tratamiento de plasma no tiene una influencia notable en la cinética de descomposición de los materiales, si bien, tiende a aumentar ligeramente la vida en servicio en todos ellos. La variable decisiva a este respecto es la composición de las fibras naturales, aumentando de manera significativa la vida útil de los materiales cuanto mayor es el contenido de celulosa de las fibras de refuerzo.
Palabras clave: Fibras naturales Termoplástico Cinética Plasma Vida en servicio
Decomposition kinetics and lifetime estimation on natural fibre reinforced thermoplastic composites
Keywords: Natural fibres Thermoplastic Kinetics Plasma Life in service	Through this study two different natural fibres composites were characterized from the point of view of decomposition kinetics comparing two kinetics models, Kissinger and Model Free Kinetics in order to estimate the lifetime of the composites. Composite materials were prepared with low density polyethylene as matrix and as reinforcements, plasma treated and untreated natural fibres with 20 and 30 wt.% of fibre content. Composites were manufactured using a rotor mixer and a hot plates press. Afterwards, thermogravimetric analysis was carried out for each material at six different rates with a coupled Mass Spectrometry device to identify detached elements in a specific temperature range. The influence of the low pressure plasma treatment, as well as the fibre type, was taken into account to evaluate the activation energy of the decomposition processes of each material. Besides, lifetime was estimated from the obtained decomposition energies and the Toop equation. It was found that plasma treatment does not have a meaningful influence on decomposition kinetics but, the main composition of the natural fibres is decisive in this aspect, giving rise to much longer lifetimes when the cellulose content of the fibre is higher.

1 Introducción

El empleo de fibras naturales derivadas de las plantas como refuerzo de estructuras formadas por distintos materiales se ha llevado a cabo con éxito por múltiples civilizaciones a lo largo de la historia para mejorar la resistencia, rigidez y resistencia al impacto de determinados materiales. Sin embargo, desde hace tres décadas ha resurgido este interés en las fibras naturales centrándose su aplicación en el refuerzo de materiales compuestos de matriz polimérica.

Los principales factores que han desencadenado recientemente el interés en este tipo de materiales son reducir la cantidad de materiales basados en la industria petroquímica, impulsar las economías rurales y ser más respetuosos con el medio ambiente a la hora de gestionar los residuos generados al final de la vida en servicio de los materiales. Su elevada disponibilidad, bajo coste, buenas propiedades mecánicas y baja densidad complementan sus prestaciones para posicionarse como alternativa a las fibras sintéticas de carbono o vidrio [1]. De manera general, y al margen de la enorme variabilidad de las fibras naturales, el mayor problema reside en la débil unión existente entre las fibras naturales y las matrices poliméricas, lo que repercute en una mala transmisión de esfuerzos y una mayor absorción de humedad por parte del material compuesto, provocando la pérdida de propiedades. La baja temperatura que admiten durante el procesado es otro factor a tener en cuenta durante el diseño de materiales compuestos reforzados con fibras naturales.

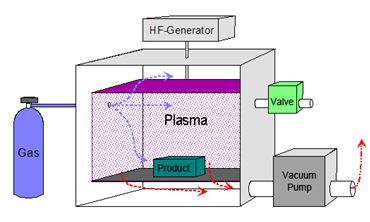
La modificación superficial de las fibras naturales cuando se emplean como refuerzo de materiales compuestos, es un paso imprescindible en la fabricación del material para mejorar la adhesión entre las fibras y la matriz, conseguir una mejor transmisión de esfuerzos y, por lo tanto, evitar una débil interfase [2]. Las fuentes de plasma son una excelente alternativa para este tipo de materiales ya que se trata de procesos sin residuos respetuosos con el medio ambiente [3].

El proceso de descomposición de los polímeros, así como de los materiales compuestos, puede llegar a ser muy complejo y en muchas ocasiones resulta complicada la obtención de los parámetros cinéticos. El análisis termogravimétrico permite de una manera rápida y sencilla determinar la estabilidad térmica de muchos materiales.

La predicción de la vida útil de los materiales es un dato de gran ayuda a la hora de diseñar y proyectar nuevos componentes, pero no siempre es tarea fácil. El análisis termogravimétrico junto con la ecuación de Toop [4] proporciona un método rápido y eficaz para estimar la vida en servicio de los materiales poliméricos.

2 Método experimental

2.1 Materiales y preparación de muestras

Se utilizaron como refuerzo de los materiales compuestos, fibras cortas de lino y coco al 20 y al 30% en peso (Procotex, Dottignies, Bélgica), y poletileno de baja densidad, LDPE, como matriz (DOW 780E).

Las mezclas se prepararon en una mezcladora de rotores, Haake Rheomix 252P (Massachusetts, USA), durante 40 minutos a una temperatura de 150ºC. Después se prensaron en una prensa de plastos calientes Fontune Presses TPB374 (Barendrecht, Netherlands).

2.2 Plasma de baja presión

Antes de mezclar las fibras con la matriz, las fibras fueron tratadas con plasma de baja presión en una cámara Plasma Cleaner (Ithaca, NY, EE.UU.) utilizando aire como gas a ionizar a una presión de 300 mtorr. Una vez realizado el vacío en la cámara las fibras estuvieron sometidas al tratamiento durante 1 min. A 30 W de potencia del equipo.

Figura 1. Esquema de cámara de plasma de baja presión

2.3 Análisis termogravimétrico

Para el estudio de las cinéticas de reacción y la estimación de vida útil de los materiales compuestos de fibras cortas de lino y coco, se realizaron análisis termogravimétricos utilizando un equipo TGA Q500 de TA Instruments (New Castle, EE.UU.) que tiene incorporado un espectrómetro de masas MS Discovery (TA Instruments). Para cada material se realizaron seis ensayos a distintas velocidades de calentamiento 5, 7, 10, 13, 15 y 20 ºC/min. Mediante el software STAR de Mettler Toledo y a partir de los termogramas obtenidos para cada velocidad, es posible calcular la energía de activación (E_a) en función del grado de degradación del material (α) mediante el modelo cinético incorporado en el software, Model Free Kinetics (MFK), y compararla con la obtenida mediante el modelo de Kissinger [5]. En este modelo se calcula la energía de activación a partir de la temperatura del pico de la derivada de la curva de descomposición como una función de la velocidad de calentamiento, según la ecuación (1):

(1)

Donde β es la velocidad de calentamiento, T_p, la temperatura (K), R, la constante de los gases (8.314 J/mol K) y E_a, la energía de activación (J/mol) que se desea calcular.

A partir de aquí, y aplicando la ecuación de Toop, ecuación (2), es posible calcular la vida útil de cada material en función de la temperatura.

(2)

Donde β es la velocidad de calentamiento, R, la constante de los gases, E_a, la energía de activación calculada para el grado de descomposición (obtenida mediante MEK) que se considere fallo del material, en este caso un 5%, T_f, las temperaturas de servicio elegidas para el cálculo de la vida útil, P(X_f), una función que viene dada por los valores E_a/RT_c (donde T_c es la temperatura al porcentaje de descomposición que se considera fallo, 5%) y por último t_f, el tiempo estimado hasta fallo del material, es decir, la vida útil del mismo.

3 Resultados y discusión

En primer lugar se obtuvieron los resultados de energía de activación de los nueve materiales a partír del modelo de Kissinger asumiendo un mecanismo de reacción de orden 1 y por lo tanto un valor de energía constante durante todo el proceso de descomposición. Los valores de energía no proporcionaron una tendencia clara ni en cuanto a influencia del tipo de fibra ni referente al tratamiento LPP. De manera general los materiales de lino proporcionaron valores de energía de descomposición mayores a los de coco, y estos valores aumentaban tanto con el contenido de refuerzo como con el tratamiento de plasma. Sin embargo, para comprobar esta hipótesis se recurrió al modelo cinético MFK, obteniendo valores de energía de descomposición en función del grado de descomposición.

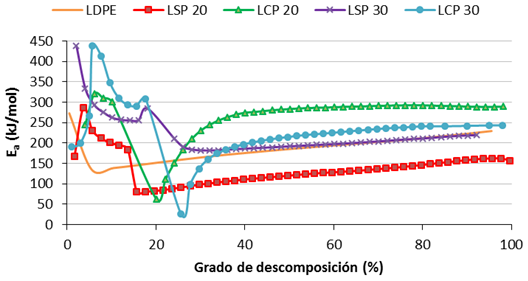
En la Figura 2. Se muestran las curvas de energía de descomposición de los amteriales compuestos de lino en comparación con la del LDPE.

Figura 2. Energía de descomposición de los composites de lino y LDPE

Al inicio del proceso se observa un comportamiento variable que se estabiliza a partir del 20 o 25% de descomposición. Sin embargo, en todos los casos se necesita mayor energía para iniciar el proceso y después se produce una bajada importante. Si se comparan los materiales compuestos de lino con el LDPE se observa que, en la zona estabilizada, todos los composites presentan un valor de energía superior o similar al del LDPE.

Los materiales de coco presentaron el comportamiento opuesto a los composites de lino en comparación con el LDPE. En este caso todos requieren una energía de descomposición inferior al LDPE durante todo el proceso, incluso al inicio del proceso. Por lo tanto parece que la composición de las fibras naturales juega un papel importante en los procesos de descomposición y que puede dar lugar a comportamiento muy diferentes.

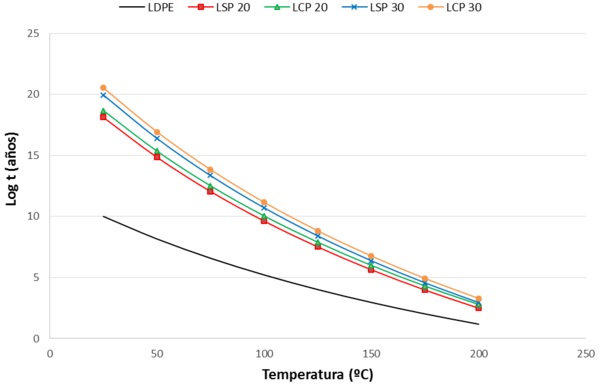
Para estimar la vida útil de los materiales se definió el fallo de los mismos en un 5% de descomposición y para este grado de descomposición se obtuvieron los valores de energía de activación y de temperatura a la cual ocurre este fallo. Aplicando la ecuación de Toop se estimó la vida en servicio de los materiales cuyos resultados para los materiales de lino se muestran en la figura 3.

Figura 3. Tiempo estimado de vida útil de los composites de lino

Los materiales de lino presentaron valores de vida útil muy superiores a los del LDPE y también se observaron variaciones entre los composites reforzados al 30 y al 20%.. El hecho de que haya una mayor cantidad de refuerzo implica que sea necesaria mayor energía de activación para iniciar el proceso de descomposición y por lo tanto la vida útil de los materiales es mayor. El tratamiento de plasma también parece tener un efecto positivo en la duración de los materiales, siendo el material con un mayor tiempo en servicio el reforzado con lino tratado al 30 % en peso (LCP 30).

Los composites de coco, en línea con los valores de energía de descomposición obtenidos, mostraron un tiempo de vida muy inferior con respecto a los materiales compuestos de lino y al LDPE. . En la Tabla 1. se muestra el tiempo estimado en años para cada uno de los nueve materiales estudiados a una temperatura de servicio de 25 ºC. Se observa, que en los materiales de coco, a pesar de presentar una durabildiad en servicio menor, mantienen la tendencia observada en los materiales de lino, y tanto el tratamiento de plasma como un mayor refuerzo favorecen el tiempo útil de vida.

Tabla 1. Tiempo de vida estimado a 25ºC

Material	t estimado (años)
LDPE	1010
LSP20	1018
LCP20	1018
CSP 20	290
CCP20	418
LSP 30	1019
LCP 30	1020
CSP 30	300
CCP 30	494

4 Conclusiones

Se puede concluir que la composición del tipo de fibra de refuerzo influye de manera considerable en la vida útil de los materiales, así como el tratamiento de plasma, aunque éste último en menor medida. En contra de lo esperado, pues al haber mayor contenido de fibras naturales y menos de LDPE cabría esperar una descomposición más rápida por parte de los materiales compuestos, el tiempo estimado de vida en servicio de los composites es muy superior al del LDPE. Sin embargo los materiales de coco presentaron una durabilidad muy baja con respecto a este último. Por lo tanto se puede concluir que a mayor contenido de celulosa de las fibras naturales, mayor tiempo de vida útil de los materiales compuestos de los que son refuerzo.

5 Referencias

[1] Pickering KL, Efendy MGA, Le TM. 2016. A review of recent developments in natural fibre composites and their mechanical performance. Compos. Part A Appl. Sci. Manuf. 83, 98–112.

[2] Bledzki AK, Reihmane S, Gassan J. 1996. Properties and modification methods for vegetable fibers for natural fiber composites. J. Appl. Polym. Sci. 59, 1329–1336.

[3] Conrads H, Schmidt M. 2000. Plasma generation and plasma sources. Plasma Sources Sci. Technol. 9, 441–454.

[4] Toop DJ. 1971. Theory of Life Testing and Use of Thermogravimetric Analysis to Predict the Thermal Life of Wire Enamels. IEEE Trans. Electr. Insul. EI-6, 2–14.

[5] Blaine RL, Kissinger HE. 2012. Homer Kissinger and the Kissinger equation. Thermochim. Acta 540, 1–6